Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-assembly of freely-rotating polydisperse cuboids: unveiling the boundaries of the biaxial nematic phase†
Effran
Mirzad Rafael
 a,
Daniel
Corbett
a,
Alejandro
Cuetos
a,
Daniel
Corbett
a,
Alejandro
Cuetos
 b and
Alessandro
Patti
b and
Alessandro
Patti
 *a
*a
aDepartment of Chemical Engineering and Analytical Science, The University of Manchester, Manchester, M13 9PL, UK. E-mail: alessandro.patti@manchester.ac.uk
bDepartment of Physical, Chemical and Natural Systems, Pablo de Olavide University, 41013 Sevilla, Spain
First published on 15th June 2020
Abstract
Colloidal cuboids have the potential to self-assemble into biaxial liquid crystal phases, which exhibit two independent optical axes. Over the last few decades, several theoretical works have predicted the existence of a wide region of the phase diagram where the biaxial nematic phase would be stable, but imposed rather strong constraints on the particle rotational degrees of freedom. In this work, we use molecular simulation to investigate the impact of size dispersity on the phase behaviour of freely-rotating hard cuboids, here modelled as self-dual-shaped nanoboards. This peculiar anisotropy, exactly in between the oblate and prolate geometry, has been proposed as the most appropriate to promote phase biaxiality. We observe that size dispersity radically changes the phase behaviour of monodisperse systems and leads to the formation of an elusive biaxial nematic phase, being found in a large region of the packing fraction vs. polydispersity phase diagram. Although our results confirm the tendencies reported in past experimental observations on colloidal dispersions of slightly prolate goethite particles, they cannot reproduce the direct isotropic-to-biaxial nematic phase transition observed in these experiments.
The first known theory on entropy-driven phase transitions was proposed by Onsager in his seminal work dating back to the 1940s.1 Onsager demonstrated that systems of infinitely long hard rods exhibit an isotropic-to-nematic phase transition as a result of mere volume effects. Later on, experiments and computer simulations showed that entropy-driven phase transitions can also lead to the formation of positionally ordered liquid crystals (LCs), such as smectic and columnar phases.2,3 The equilibrium structures stemming from the self-assembly of colloidal particles are especially determined by the architecture of their building blocks. In particular, biaxial particles, such as bent-core and cuboidal particles, have been reported to form biaxial nematic (NB) LCs.4–6 First theorised by Freiser in 1970,7 the NB phase has attracted widespread attention for being a promising candidate to be engineered into next generation liquid crystal displays. In contrast to uniaxial nematics (NU), where long-range orientational order exists only along one direction, the NB phase possesses three orthogonal directors and hence two distinct optical axes that can pave the path to high-performance displays.8–10 Despite having been extensively studied over the past 50 years, the stability of the NB phase still remains an open question, predominantly, but not only, at the molecular scale. Answering this question is hampered by the fact that the NB phase tends to be metastable with respect to other morphologies, such as the NU and Sm phases.11
About a decade ago, Vroege and coworkers reported the first experimental evidence of the NB phase in a system of colloidal goethite (roughly board-like) particles.6 The stability of this NB phase was ascribed to the particles’ quasi self-dual shape, a geometry in between oblate and prolate, and to their significant size dispersity, which hinders the formation of the Sm phase. This key work has reignited recent interest, sparking numerous theoretical, experimental and computer simulation studies on hard board-like particles (HBPs)12–27 and other biaxial geometries.24,28–32 Theoretical and computational studies on monodisperse systems have suggested that self-dual-shaped particles exhibit a higher tendency to form biaxial nematics. However, these studies applied rather strong approximations, limiting the particle orientation to six orthogonal directions,11–13 freezing the rotation of the long axes of the particle,33 or neglecting the occurrence of positionally ordered LC phases.34–37 Our recent theoretical work and computer simulations of freely-rotating HBPs suggested that these approximations might artificially magnify the stability of the NB phase.22,23 We note that stable NB phases have been found in systems of cuboids with rounded corners (spheroplatelets) with a length-to-thickness ratio of L* ≡ L/T > 916,17 and L* ≥ 23 in systems of especially elongated HBPs.24 Sedimentation experiments on highly uniform and monodisperse colloidal cuboids with 15 ≤ L* ≤ 180 did not report the formation of an NB phase, which, for self-dual-shaped cuboids, was found to be pre-empted by biaxial smectic (SmB) or crystal-B phases, depending on the solvent used.25 We stress that these conditions, probing stacking behaviour, are very different from those of ref. 24, studying bulk behaviour, and thus their conclusions are not expected to necessarily match. This lack of agreement between experiments, theories and simulations keeps the discussion on the ability of HBPs to form the NB phase alive.
Size dispersity has been identified as a key ingredient to destabilise the Sm phase and thus promote the formation of biaxial nematics. In particular, the effect of size dispersity in systems of HBPs was investigated by Onsager's theory within the restricted-orientation (Zwanzig) approximation.13 This theory provided an elegant and solid explanation on the origin of the NB stability experimentally observed in colloidal dispersions of goethite particles.6 Nevertheless, its conclusions were strongly determined by the use of the Zwanzig model, which only allows six orthogonal particle orientations and cannot describe the phase behaviour of cuboids accurately, as recent simulations and theory have indicated.22,23 Consequently, fully unlocking the particle rotational degrees of freedom is of paramount importance to ascertain the impact of polydispersity on the phase behaviour of HBPs and accurately map the boundaries of the NB phase. While it is extremely challenging to formulate a theory that simultaneously incorporates particle size dispersity and unrestricted orientations, molecular simulation can provide an insightful contribution to shed light on this combined effect. To this end, we have performed Monte Carlo (MC) simulations of freely-rotating HBPs with Gaussian size distribution peaked at L* = 12. The particle thickness, T, is the system unit length and is the same for all HBPs, whereas L* changes with standard deviation σL 〈L*〉, where 0.05 ≤ σL ≤ 0.30 measures the particle length dispersity. Finally, the particle width dispersity is linked to the length dispersity by  , which ensures the self-dual shape for all particles. Our systems consist of Np = 2000 to 3000 HBPs that are initially arranged in cubic or rectangular boxes with periodic boundaries and are equilibrated in the isothermal–isobaric ensemble. Phase transitions have been assessed by expansion or compression of a perfect biaxial nematic phase at extensive range of pressures. To ensure that the equilibrium configurations were independent of the initial configuration, expansion of Sm phases and compression of isotropic (I) phases have also been carried out. We have also simulated significantly larger systems, with Np = 6000, to discard the occurrence of finite-size effects, where these could especially influence the symmetry of the phases observed, that is at the I–N transition. Additionally, the potential occurrence of fractionation has been assessed by evaluating the space distribution of particles whose size is one standard deviation above or below the average size distribution and the space dependence of the order parameters. No evidence of fractionation, including N+U/N−U separation in the NB region, has been detected. Other more sophisticated techniques, such as isobaric semigrand MC simulations,38 are perhaps better suited to assess the occurrence of fractionation in polydisperse systems. Generally, up to 107 MC cycles were needed to equilibrate the systems, with a cycle consisting of Np attempts of displacing and/or rotating randomly selected particles and one trial volume change. Because the force field used here consists only of a hard-core potential, these moves were accepted if no overlaps were detected, according to the separating axes theorem.39,40 Systems were considered to be at equilibrium if packing fraction (η) and uniaxial (S2) and biaxial (B2) order parameters achieved steady values within reasonable statistical uncertainty. In particular,
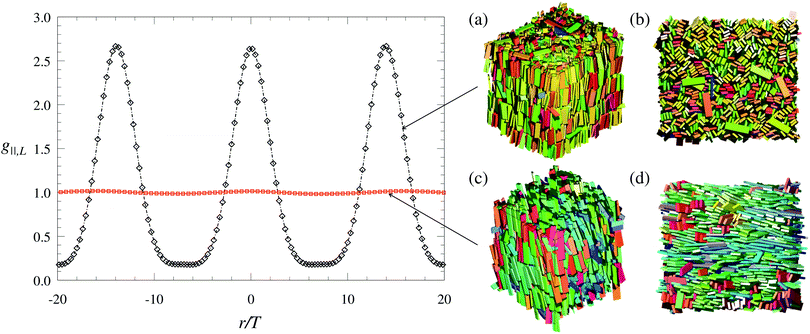
, which ensures the self-dual shape for all particles. Our systems consist of Np = 2000 to 3000 HBPs that are initially arranged in cubic or rectangular boxes with periodic boundaries and are equilibrated in the isothermal–isobaric ensemble. Phase transitions have been assessed by expansion or compression of a perfect biaxial nematic phase at extensive range of pressures. To ensure that the equilibrium configurations were independent of the initial configuration, expansion of Sm phases and compression of isotropic (I) phases have also been carried out. We have also simulated significantly larger systems, with Np = 6000, to discard the occurrence of finite-size effects, where these could especially influence the symmetry of the phases observed, that is at the I–N transition. Additionally, the potential occurrence of fractionation has been assessed by evaluating the space distribution of particles whose size is one standard deviation above or below the average size distribution and the space dependence of the order parameters. No evidence of fractionation, including N+U/N−U separation in the NB region, has been detected. Other more sophisticated techniques, such as isobaric semigrand MC simulations,38 are perhaps better suited to assess the occurrence of fractionation in polydisperse systems. Generally, up to 107 MC cycles were needed to equilibrate the systems, with a cycle consisting of Np attempts of displacing and/or rotating randomly selected particles and one trial volume change. Because the force field used here consists only of a hard-core potential, these moves were accepted if no overlaps were detected, according to the separating axes theorem.39,40 Systems were considered to be at equilibrium if packing fraction (η) and uniaxial (S2) and biaxial (B2) order parameters achieved steady values within reasonable statistical uncertainty. In particular,  , where V is the box volume and vi is the volume of a generic particle i. The calculation of S2 and B2 was done by diagonalisation of the traceless second-rank symmetric tensor
, where V is the box volume and vi is the volume of a generic particle i. The calculation of S2 and B2 was done by diagonalisation of the traceless second-rank symmetric tensor 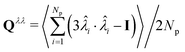 , where I is the second-rank unit tensor,
, where I is the second-rank unit tensor, ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e11a.gif) i =
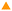
i = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , ŷ and ẑ is the particle unit orientation vector and angular brackets denotes ensemble average. Isotropic, perfect uniaxial and perfect biaxial phases are observed at (S2,B2) = (0,0), (1,0) and (1,1), respectively. An illustrative example of the dependence of the order parameters on the packing fraction is given in Fig. 1, for different values of σL. Finally, to assess the long-range ordering of the phases at equilibrium, we have analysed the spatial correlations along and perpendicularly to the relevant phase directors by computing the longitudinal, g‖(r‖), and transverse, g⊥(r⊥), pair distribution functions, where r‖ and r⊥ are the corresponding projections of the inter-particle distance. Interested readers can refer to the ESI† for further details on the calculation of order parameters and pair correlation functions.
, ŷ and ẑ is the particle unit orientation vector and angular brackets denotes ensemble average. Isotropic, perfect uniaxial and perfect biaxial phases are observed at (S2,B2) = (0,0), (1,0) and (1,1), respectively. An illustrative example of the dependence of the order parameters on the packing fraction is given in Fig. 1, for different values of σL. Finally, to assess the long-range ordering of the phases at equilibrium, we have analysed the spatial correlations along and perpendicularly to the relevant phase directors by computing the longitudinal, g‖(r‖), and transverse, g⊥(r⊥), pair distribution functions, where r‖ and r⊥ are the corresponding projections of the inter-particle distance. Interested readers can refer to the ESI† for further details on the calculation of order parameters and pair correlation functions.
Bearing in mind these introductory considerations, we now report on the LC phases that polydisperse HBPs are able to form at the equilibrium, with specific interest in the critical polydispersity that stabilizes the NB phase and the extent of this stability. For consistency with our former work,26 we defined the axial symmetry of the NB and Sm phases according to the magnitude of the order parameters (see the ESI† for additional details). The σL–η phase diagram of polydisperse and self-dual-shaped HBPs is shown in Fig. 2. All points at σL = 0 refer to monodisperse systems, obtained from previous simulation results22 and included here as a reference. The diagram reveals the existence of uniaxial and biaxial LC phases at η ≳ 0.30. At a lower density and regardless of the size dispersity, we only detect I phases, in good agreement with the Zwanzig-based Onsager theory by Belli et al., who predicted stable I phases for η ≲ 0.28 and 0 ≤ σL ≤0.4.13 We stress that these authors studied slightly prolate particles with 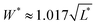 or ν ≡ L/W − W/T = 0.1. This slight deviation from the self-dual shape, for which ν = 0, might appear insignificant, but in fact it determines the oblate or prolate symmetry of the nematic phase, at least in monodisperse systems, as established by Mulder in the 1980s.35
or ν ≡ L/W − W/T = 0.1. This slight deviation from the self-dual shape, for which ν = 0, might appear insignificant, but in fact it determines the oblate or prolate symmetry of the nematic phase, at least in monodisperse systems, as established by Mulder in the 1980s.35
As far as the NU phase is concerned, its stability region (orange-shaded area in Fig. 2) is not especially influenced by the polydispersity of the particle, with the lower and upper boundaries approximately constrained between η = 0.30 and 0.35, similar to those observed in monodisperse systems (σL = 0). A slight difference is detected at 0.15 ≤ σL ≤ 0.20, where four different phases seem to converge and the region of stability of uniaxial nematics expands up to η = 0.41 at σL = 0.18. In former simulation studies on monodisperse systems of self-dual-shaped HBPs with L* = 12, the NU stability was also observed to be relatively small,24 and even to vanish in binary mixtures.23 Within the NU domain, we came across nematic LCs with oblate and prolate symmetries, respectively labelled as N−U and N+U. The occurrence of the N−U phase is predominantly detected close to the I–N transition and also far from it for σL ≥ 0.25. In contrast, the N+U phase is mostly observed at larger packing fractions for 0 ≤ σL ≤ 0.20. Consequently, at a given polydispersity, increasing the system density can produce an inversion of the nematic phase symmetry. Meanwhile, the prolate and oblate particles commonly tend to trigger the N+U and N−U phases, respectively.11,18,34,35,37,41 Although a significant polydispersity can counteract this tendency,13 the self-dual shape is, in principle, not expected to exhibit a clear oblate or prolate nature, but rather an ambivalent nature. By applying our Onsager-like theory,22 we observed that, close to the I–N transition, the free-energy difference between N+U and N−U phases is very small and not much larger at increasing η (see ESI†). Although this theory is strictly valid for monodisperse systems and serves here as a mere qualitative guideline, it confirms the very small free-energy differences between oblate and prolate symmetries that had also been reported by Martnez-Ratón and co-workers, who applied density-functional theory to study the phase behaviour of nearly self-dual-shaped monodisperse HBPs.12
Uniaxial and biaxial smectic phases are obtained at larger packing fractions. To distinguish them from the nematic phases, we calculated the density distribution function along the nematic director, g‖(r‖), identified by the order parameters. Uniaxial smectic (SmU) phases (green area in Fig. 2) only exhibit a prolate symmetry (Sm+U), in agreement with former simulations of monodisperse systems.22 In particular, their layers, whose thickness is roughly 13T to 15T, are perpendicular to the average direction of the particle length. The g‖(r‖), calculated along this direction, displays periodically peaked profiles of the type reported in Fig. 3 and displays no indication of structural order in the other directions. In contrast, biaxial smectics, found at η > 0.50 and 0.05 ≤ σL ≤ 0.20 (blue area in Fig. 2), can present a prolate (Sm+B) or oblate (Sm−B) symmetry. The former is characterised by layers piling along the particle length, and the latter by layers piling along the particle thickness. Upon increasing polydispersity, the SmB phase acquires a more and more defined structural identity, with a weak-to-strong biaxiality crossover at approximately 0.05 < σL < 0.10 and a full biaxial character (B2 > 0.6) at σL ≥ 0.18. At this value of size dispersity, our simulations highlighted a particularly rich phase behaviour, unveiling an I → NU → NB → SmB sequence of phases that is exemplarily shown in Fig. 4. In qualitative agreement with theory and experiments, we found the NB phase to be stabilised by a substantial degree of particle size dispersity. In particular, our simulation results indicate σL = 0.18 as the critical polydispersity above which the NB phase can form. Close to the NU–NB phase boundary, we find nematics with a relatively weak (but non-negligible) biaxiality and a residual oblate or prolate character. These phases, here referred to as weak biaxial nematics, are characterised by a biaxial order parameter in the range 0.2 ≤ B2 ≤ 0.30 and one predominant uniaxial order parameter granting them prolate (N+B) or oblate (N−B) symmetry.
In contrast with the experiments on goethite particles,6 we do not observe a direct I–NB phase transition here. This apparent lack of agreement deserves some comments. First of all, the cuboids studied in these experiments are not self-dual-shaped. Their shape parameter, ν = 0.1, indicates a prolate geometry, which in monodisperse systems is expected to promote an I–N+U, rather than I–NB, transition as predicted by theories spanning almost five decades.11,18,34,35,37,41 However, the goethite particles utilized by Vroege and co-workers are not monodisperse, but exhibit a polydispersity between 20% and 25% in the three directions. Because polydispersity can lead to fractionation42 and these authors studied the phase behaviour in capillaries, the longer particles tend to accumulate towards the bottom, where the NB phase was found, de facto increasing the shape parameter of this subset of particles to the effective value of ν = 0.6.6 This particle geometry, evidently prolate, is very different from the self-dual shape applied here and a quantitative analogy is therefore not directly possible. The Onsager theory within the Zwanzig approximation does not predict a direct I–NB transition in systems of polydisperse HBPs with ν = 0.1, but it suggests the existence of the NB phase in a wide region of the η–σL phase diagram, including for σL < 0.1.13 While it is known that restricting orientations can significantly enhance the stability of the NB phase, both Belli's theoretical work and our simulations do not report a direct I–NB phase transition, whose existence has never been unambiguously confirmed by off-lattice simulations spanning more than twenty years.16,24,30,37,43–46 Indeed, our recent MC simulations and generalised fifth-virial Onsager theory applied to freely-rotating monodisperse HBPs with L* ≤ 12 had even excluded the existence of the NB phase, also at the self-dual shape. A third-virial theory for monodisperse cuboids with continuum orientations predicted a direct I–NB transition at L* = 64, which was not observed in the simulations by the same authors.24 To the best of our knowledge, there are no theoretical works on freely-rotating polydisperse HBPs that might help resolve this conundrum. While the phase diagram in Fig. 2 illustrates the relevant discrepancies of the work proposed by Belli, both works agree very well on the key role of polydispersity in the stabilisation of the NB phase. This is especially evident at σL ≥ 0.18, where the stability region of the NB phase widens, remarkably reducing that of the Sm and NU phases. This is not surprising as a large size dispersity is expected to hinder the formation of layered structures due to the absence of well-defined structural periodicity in the longitudinal direction.
In summary, our MC simulations of freely-rotating HBPs have revealed a rich phase behaviour that is characterised by three key results: (i) a significant degree of particle size dispersity is needed to stabilise the NB phase; (ii) self-dual-shaped HBPs do not exhibit a direct I–NB phase transition in the range of size dispersities studied here; (iii) the ambivalent nature of the self-dual shape provides uniaxial nematics that, in a relatively wide region of the η–σL phase diagram, might well be oblate or prolate. More specifically, a significant polydispersity (σL ≥ 0.18) prevents the discretization of the space along the nematic director and thus enfeebles the stability of the Sm phase, practically enhancing that of the nematic phase. This result is in line with the experiments and theories, but on a merely qualitative basis only. The lack of a direct I–NB phase transition might appear in evident disagreement with previous experimental observations, which anyway used prolate rather than self-dual-shaped particles, but agrees with a relevant number of simulation studies that could not confirm its occurrence in a reasonable range of particle anisotropies. As far as the ambivalence of the self-dual shape is concerned, it is interesting to observe an oblate-to-prolate symmetry inversion in the NU domain upon increasing density. Our modified version of the Onsager theory for monodisperse biaxial particles suggests that the free-energy difference between the N−U and N+U phases is very small, offering a possible explanation for the symmetry inversions observed in our simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
EMR would like to thank the Malaysian Government Agency Majlis Amanah Rakyat for funding his PhD at the University of Manchester. AC acknowledges the Spanish Ministerio de Ciencia, Innovación y Universidades and FEDER for funding (project PGC2018-097151-B-I00) and C3UPO for the HPC facilities provided. AP acknowledges financial support from the EPSRC under grant agreement EP/N02690X/1 and the Leverhulme Trust Research Project Grant RPG-2018-415. We would like to thank Andrew Masters and Matthew Dennison for sharing the code to calculate the virial coefficients. Finally, EMR, DC and AP acknowledge the assistance given by IT Services and the use of the Computational Shared Facility at the University of Manchester.Notes and references
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- D. Frenkel, H. Lekkerkerker and A. Stroobants, Nature, 1988, 332, 822 CrossRef CAS.
- F. van der Kooij and H. Lekkerkerker, Phys. Rev. Lett., 2000, 84, 781 CrossRef CAS PubMed.
- B. R. Acharya, A. Primak and S. Kumar, Phys. Rev. Lett., 2004, 92, 145506 CrossRef PubMed.
- L. A. Madsen, T. J. Dingemans, M. Nakata and E. T. Samulski, Phys. Rev. Lett., 2004, 92, 145505 CrossRef CAS PubMed.
- E. van den Pol, A. Petukhov, D. Thies-Weesie, D. Byelov and G. Vroege, Phys. Rev. Lett., 2009, 103, 258301 CrossRef CAS PubMed.
- M. Freiser, Phys. Rev. Lett., 1970, 24, 1041 CrossRef CAS.
- J.-H. Lee, T.-K. Lim, W.-T. Kim and J.-I. Jin, J. Appl. Phys., 2007, 101, 034105 CrossRef.
- R. Berardi, L. Muccioli and C. Zannoni, J. Chem. Phys., 2008, 128, 024905 CrossRef PubMed.
- M. Ricci, R. Berardi and C. Zannoni, J. Chem. Phys., 2015, 143, 084705 CrossRef PubMed.
- M. P. Taylor and J. Herzfeld, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 3742 CrossRef.
- Y. Martnez-Ratón, S. Varga and E. Velasco, Phys. Chem. Chem. Phys., 2011, 13, 13247–13254 RSC.
- S. Belli, A. Patti, M. Dijkstra and R. van Roij, Phys. Rev. Lett., 2011, 107, 148303 CrossRef CAS.
- S. Belli, M. Dijkstra and R. van Roij, J. Phys.: Condens. Matter, 2012, 24, 284128 CrossRef CAS PubMed.
- S. D. Peroukidis and A. G. Vanakaras, Soft Matter, 2013, 9, 7419–7423 RSC.
- S. D. Peroukidis, A. G. Vanakaras and D. J. Photinos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062508 CrossRef PubMed.
- S. D. Peroukidis, Soft Matter, 2014, 10, 4199–4207 RSC.
- A. B. G. M. Leferink op Reinink, S. Belli, R. van Roij, M. Dijkstra, A. V. Petukhov and G. J. Vroege, Soft Matter, 2014, 10, 446–456 RSC.
- Y. Martnez-Ratón, S. Varga and E. Velasco, J. Chem. Phys., 2014, 140, 204906 CrossRef PubMed.
- L. Mederos, E. Velasco and Y. Martnez-Ratón, J. Phys.: Condens. Matter, 2014, 26, 463101 CrossRef PubMed.
- M. González-Pinto, Y. Martnez-Ratón, E. Velasco and S. Varga, Phys. Chem. Chem. Phys., 2015, 17, 6389–6400 RSC.
- A. Cuetos, M. Dennison, A. Masters and A. Patti, Soft Matter, 2017, 13, 4720–4732 RSC.
- A. Patti and A. Cuetos, Mol. Simul., 2018, 44, 516–522 CrossRef CAS.
- S. Dussi, N. Tasios, T. Drwenski, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2018, 120, 177801 CrossRef CAS PubMed.
- Y. Yang, G. Chen, S. Thanneeru, J. He, K. Liu and Z. Nie, Nat. Commun., 2018, 9, 4513 CrossRef PubMed.
- A. Cuetos, E. M. Rafael, D. Corbett and A. Patti, Soft Matter, 2019, 15, 1922–1926 RSC.
- R. A. Skutnik, I. S. Geier and M. Schoen, Mol. Phys., 2020, 1–21 CrossRef.
- N. Tasios and M. Dijkstra, J. Chem. Phys., 2017, 146, 144901 CrossRef CAS PubMed.
- L. Querciagrossa, M. Ricci, R. Berardi and C. Zannoni, Phys. Chem. Chem. Phys., 2017, 19, 2383–2391 RSC.
- S. Orlandi, L. Muccioli and R. Berardi, Liq. Cryst., 2018, 45, 2400–2415 CrossRef CAS.
- T. Drwenski and R. van Roij, Mol. Phys., 2018, 116, 2812–2822 CrossRef CAS.
- M. Chiappini, T. Drwenski, R. Van Roij and M. Dijkstra, Phys. Rev. Lett., 2019, 123, 068001 CrossRef CAS PubMed.
- A. Vanakaras, M. Bates and D. Photinos, Phys. Chem. Chem. Phys., 2003, 5, 3700–3706 RSC.
- J. P. Straley, Phys. Rev. A: At., Mol., Opt. Phys., 1974, 10, 1881 CrossRef.
- B. Mulder, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 360 CrossRef PubMed.
- M. P. Allen, Liq. Cryst., 1990, 8, 499–511 CrossRef.
- P. J. Camp and M. P. Allen, J. Chem. Phys., 1997, 106, 6681–6688 CrossRef CAS.
- M. A. Bates and D. Frenkel, J. Chem. Phys., 1998, 109, 6193–6199 CrossRef CAS.
- S. Gottschalk, M. C. Lin and D. Manocha, Comput. Graph, 1996, 30, 171–180 Search PubMed.
- B. S. John, C. Juhlin and F. A. Escobedo, J. Chem. Phys., 2008, 128, 044909 CrossRef PubMed.
- R. Alben, Phys. Rev. Lett., 1973, 30, 778 CrossRef.
- E. van den Pol, D. Thies-Weesie, A. Petukhov, G. Vroege and K. Kvashnina, J. Chem. Phys., 2008, 129, 164715 CrossRef CAS PubMed.
- R. Berardi and C. Zannoni, J. Chem. Phys., 2000, 113, 5971–5979 CrossRef CAS.
- G. S. Preeti, K. Murthy, V. Sastry, C. Chiccoli, P. Pasini, R. Berardi and C. Zannoni, Soft Matter, 2011, 7, 11483–11487 RSC.
- L. Querciagrossa, M. Ricci, R. Berardi and C. Zannoni, Phys. Chem. Chem. Phys., 2013, 15, 19065–19072 RSC.
- L. Querciagrossa, R. Berardi and C. Zannoni, Soft Matter, 2018, 14, 2245–2253 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of order parameters, pair distribution functions, smectic layer thicknesses, free energies and equation of state. See DOI: 10.1039/d0sm00484g |
| This journal is © The Royal Society of Chemistry 2020 |