Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Degenerate states, emergent dynamics and fluid mixing by magnetic rotors†
Takuma
Kawai
a,
Daiki
Matsunaga
 *ab,
Fanlong
Meng
*ab,
Fanlong
Meng
 *bcd,
Julia M.
Yeomans
b and
Ramin
Golestanian
*bcd,
Julia M.
Yeomans
b and
Ramin
Golestanian
 bd
bd
aGraduate School of Engineering Science, Osaka University, Toyonaka 5608531, Japan. E-mail: daiki.matsunaga@me.es.osaka-u.ac.jp
bRudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3PU, UK
cCAS Key Laboratory for Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: fanlong.meng@itp.ac.cn
dMax Planck Institute for Dynamics and Self-Organization (MPIDS), Göttingen 37077, Germany
First published on 11th June 2020
Abstract
We investigate the collective motion of magnetic rotors suspended in a viscous fluid under a uniform rotating magnetic field. The rotors are positioned on a square lattice, and low Reynolds hydrodynamics is assumed. For a 3 × 3 array of magnets, we observe three characteristic dynamical patterns as the external field strength is varied: a synchronized pattern, an oscillating pattern, and a chessboard pattern. The relative stability of these depends on the competition between the energy due to the external magnetic field and the energy of the magnetic dipole–dipole interactions among the rotors. We argue that the chessboard pattern can be understood as an alternation in the stability of two degenerate states, characterized by striped and spin-ice configurations, as the applied magnetic field rotates. For larger arrays, we observe propagation of slip waves that are similar to metachronal waves. The rotor arrays have potential as microfluidic devices that can mix fluids and create vortices of different sizes.
1 Introduction
Magnetic forces provide a useful way of driving small units in viscous fluids. For example, in recent years magnetic driving has been extensively used in microfluidic devices, for applications such as magnetic swimmers,1–4 magnetic spinners,5–7 magnetic pumps8,9 and cilia,10–14 and to facilitate particle sorting and segregation.15–18 Many of the approaches are designed to control a single magnetic unit or to actuate many units in exactly the same manner. For further development of magnetically-actuated devices, it would be desirable to be able to control the dynamics of the magnetic units just by changing the external magnetic field. However, it is not immediately obvious how to achieve different behaviors among different magnetic units when they are driven by the same external magnetic driving mechanism.In a recent work,9 we analyzed the collective motion of a square array of magnetic rotors and found a surprisingly rich dynamics under an external magnetic field which oscillated along one axis of the array. By changing the relative strength of the external field and the dipolar interactions between the rotors, different collective rotational patterns emerged. When the dipole interaction was dominant the rotors swung back and forth, clockwise or counterclockwise in alternating stripes. When the external field dominated over the dipolar interactions, the rotors underwent full rotations with different quadrants of the array turning in different directions.
In the present paper, we extend these results by changing the external magnetic field from a 1D oscillatory to a 2D rotating field (see Fig. 1 for a schematic representation of our system), and find richer dynamics that did not emerge in the previous setup. The current setup enables us to identify three different collective rotational patterns as the balance of the torque due to the external field and the torque due to dipolar interactions is varied. In the first regime that occurs for strong fields, we observe synchronized patterns in which all the magnetic units rotate in the same direction as the external field. We observe oscillating patterns for weak field strengths, when the rotors cannot achieve net rotation. We also observe a most interesting chessboard pattern, which appears when the contributions of the two torques are comparable. In this pattern, the rotors rotate in a direction opposite to their closest neighbouring rotors, which is counter-intuitive because half of the rotors rotate in the opposite direction to the external field. It is also surprising that the dynamics of the square array (N × N) is strongly dependent on whether N is an even or an odd number.
The other new finding using the rotational magnetic field is a novel slip wave propagation. We examine system sizes up to 100 × 100 rotors, and report the observation of the propagation of slip waves that are similar to the metachronal waves that arise from coordinated motion of cilia.19–25 We demonstrate that our system can be used as a microfluidic device for mixing and pumping, as it can drive flow fields with different vortex sizes and mixing length scales.
2 Description of the system and governing equations
2.1 The system
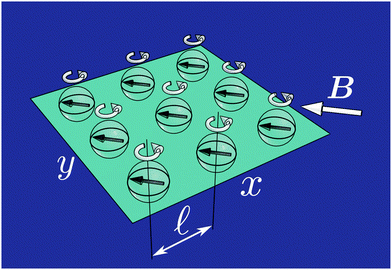
Our system consists of magnetic rotors positioned on a square lattice in xy-plane with a lattice spacing![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as shown in Fig. 1. The total number of rotors is N = NxNy, where Nx and Ny are the number of rotors in the x- and y-directions, respectively. The rotors are embedded in an unbounded fluid domain with viscosity η and density ρ. The magnetic dipoles have no translational degrees of freedom because they are fixed in space, but each has a single rotational degree of freedom about the z-axis. Every rotor is taken to be a sphere with radius a, which has a magnetic dipole moment
as shown in Fig. 1. The total number of rotors is N = NxNy, where Nx and Ny are the number of rotors in the x- and y-directions, respectively. The rotors are embedded in an unbounded fluid domain with viscosity η and density ρ. The magnetic dipoles have no translational degrees of freedom because they are fixed in space, but each has a single rotational degree of freedom about the z-axis. Every rotor is taken to be a sphere with radius a, which has a magnetic dipole momentmi = (m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,m ϕi,m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,0), ϕi,0), | (1) |
The rotors are driven by a rotating magnetic field
B(t) = (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,B θ,B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,0) θ,0) | (2) |
2.2 Governing equations
Each rotor experiences a magnetic torque that comprises contributions from the external field Text, and the dipole–dipole interactions Tdd. The torque contributions on the i-th rotor areTexti = (mi × B)·êz = mB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ − ϕi), sin(θ − ϕi), | (3) |
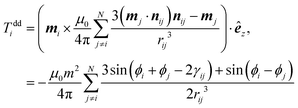 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij,sin
γij,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij,0) = (rj − ri)/rij, and êz is the unit vector along the z direction. Torque balance in the viscous regime gives the angular velocity ωi of a rotor as
γij,0) = (rj − ri)/rij, and êz is the unit vector along the z direction. Torque balance in the viscous regime gives the angular velocity ωi of a rotor as | (5) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The leading order effect of hydrodynamic coupling is discussed in Appendix A.
. The leading order effect of hydrodynamic coupling is discussed in Appendix A.
The potential energies due to the external magnetic field, Uext, and magnetic interaction, Udd, are
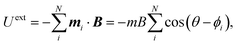 | (6) |
 | (7) |
The velocity field and the vorticity field at a position x are described by the rotlet26
 | (8) |
| Ω(x) = ∇ × v(x). | (9) |
 | (10) |
2.3 Dimensionless parameters
We introduce two dimensionless parameters: | (11) |
 | (12) |
Eqn (5) can then be rewritten in non-dimensional form:
 | (13) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , Texti* = Texti/(mB), and Tddi* = Tddi × 4π
, Texti* = Texti/(mB), and Tddi* = Tddi × 4π![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3/(μ0m2). Similarly, we define the dimensionless potential energies as Uext* = Uext/(mB) and Udd* = Udd × 4π
3/(μ0m2). Similarly, we define the dimensionless potential energies as Uext* = Uext/(mB) and Udd* = Udd × 4π![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3/(μ0m2).
3/(μ0m2).
2.4 Numerical method
We discretize eqn (13) and follow the time evolution of the rotor angles using a first-order Euler method with a time step fΔt = 10−4, and the initial orientation angles ϕi are set randomly. Note that we confirmed that the time step is small enough: the simulation result did not change when the time step was reduced by a factor 10 (data not shown). Before the main simulation process starts, a strong external field corresponding to 1/(τrf) = 104 is applied in the +x-direction for a dimensionless time ft = 1 to align the rotors. When we analyze the average motion of the rotors or the flow field, we run the simulation for 50 cycles and take the average of the last 30 cycles.3 Results
3.1 Motion of a single rotor
For completeness, we first summarize the results for a single rotor. In the absence of dipole interaction, the rotational velocity is determined purely by the torque from the external field Text. The rotational velocity is therefore simply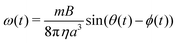 | (14) |
 | (15) |
For 1/(τrf) > 2π the stable solution has 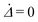 and the rotor follows the external field with a constant angular velocity ω = 2πf. For 1/(τrf) < 2π, however, there is no solution with
and the rotor follows the external field with a constant angular velocity ω = 2πf. For 1/(τrf) < 2π, however, there is no solution with  : the rotor does not reach a constant velocity but periodically slips to move backwards as it fails to keep up with the external field.2,14,28
: the rotor does not reach a constant velocity but periodically slips to move backwards as it fails to keep up with the external field.2,14,28
3.2 3 × 3 array
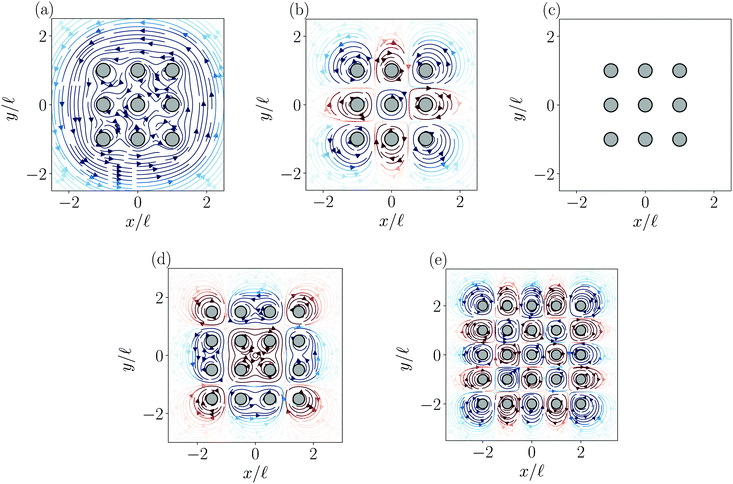
Fig. 2(a) is a phase diagram showing the dynamical configurations of 3 × 3 arrays of magnetic rotors (see also Movie S1, ESI†). The competition between the two torques Text and Tdd, which are controlled by the two dimensionless parameters 1/(τrf) and 1/Mn, respectively, determines the rotational patterns. We identify three different responses to the field: “synchronized” (Fig. 2(b)), “chessboard” (Fig. 2(c)), and “oscillating” (Fig. 2(d)) patterns. Note that we introduce a parameter R to characterize the rotational pattern,9 defined as. | (16) |
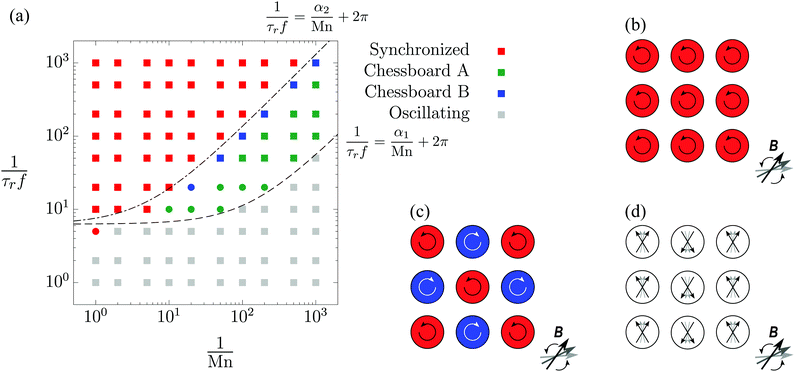 | ||
| Fig. 2 Rotational patterns for the 3 × 3 array of rotors. (a) Phase diagram in the space of the two parameters 1/Mn and 1/(τrf). Square markers represent |R| = 0 or 1 and circle markers represent 0 < |R| < 1. The difference between chessboards A and B is in the transient orientation of the rotors as shown later in Fig. 3(b) and Movie S2 (ESI†). (b) Synchronized pattern: all rotors rotate in the same direction as the external field. (c) Chessboard pattern: all rotors rotate in the opposite direction to their nearest neighbours. The colors represent the rotational direction: clockwise (blue) and counterclockwise (red). (d) Oscillating pattern: the rotors oscillate instead of performing full rotations. The arrows on the rotors represent the magnetic moment of the rotors. | ||
The synchronized pattern appears when the torque due to the external field is dominant over the dipolar interactions 1/(τrf) > 1/Mn, which corresponds to the top left corner of Fig. 2(a). In this regime, all rotors rotate in the direction of the external field as shown in Fig. 2(b). The oscillating pattern appears when the dipolar interaction is dominant 1/Mn ≫ 1/(τrf), or when the rotors cannot catch up with the external field 1/(τrf) < 2π as also seen in the motion of a single rotor. The rotors simply oscillate and cannot achieve a net rotation because the external field is not strong enough to destroy the configurations favoured by the magnetic interaction, such as the spin-ice pattern.9,29,30
The chessboard pattern appears when the contributions of the two torques are comparable, namely, 1/Mn ∼ 1/(τrf). In this regime, all rotors rotate in a direction opposite to their closest neighbours. This is counter-intuitive because half of the rotors are rotating in the opposite direction to the magnetic field. There have been reports of such chessboard-like behaviour in other active matter systems, such as bacterial suspensions,31–33 although they do not operate under the effect of an external driving mechanism unlike our system.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0,B
θ0,B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0,0) where 0 ≤ θ0 < 2π, and analyze the equilibrium orientation configuration for each angle θ0. Since the rotors are in the equilibrium state, there is only one relevant dimensionless parameter in the system, namely
θ0,0) where 0 ≤ θ0 < 2π, and analyze the equilibrium orientation configuration for each angle θ0. Since the rotors are in the equilibrium state, there is only one relevant dimensionless parameter in the system, namely | (17) |
When there is no applied external field (i.e., α = 0) there exist several equilibrium configurations for a square rotor array such as the stripe and spin-ice configurations shown in Fig. 3(a). In a 3 × 3 array, the magnetic dipole–dipole interaction energy Udd* is in fact the same in these two configurations for regular alignment of the magnetic moments, i.e., ϕi = nπ/4 with n as integers. Note, however, that the directions of the magnetic dipoles in finite systems can have minor deviations from the regular alignment defined by ϕi = nπ/4, which corresponds to infinite systems. This leads to the stripe configuration having slightly lower dipolar potential energy (Udd* ≈ −16.51) than the spin-ice configuration (Udd* ≈ −16.45) in the 3 × 3 array.
Starting from random rotor orientations without an external field, namely α = 0, the simulation results in one of these equilibrium configurations depend on the details of the initial angles. If we now impose a static external magnetic field that is comparable to the dipolar field, namely α ∼ 1, the system changes the pattern to that dictated by the external field direction θ. As shown in the chessboard A pattern in Fig. 3(b), the system prefers stripe-like configurations for external field directions θ0 = nπ/2 where n is an integer, while it prefers spin-ice-like configurations for θ0 = (2n + 1)π/4 (see Appendix B). Since the chessboard rotational pattern can be obtained by following the sequence of 8 configurations in Fig. 3(b), we can understand that it is a consequence of alternate switching between stripe and spin-ice ordering.
Note that we classified chessboard patterns into two different patterns, chessboard A (that corresponds to smaller α) and chessboard B (that corresponds to larger α), depending on the transient configurations in Fig. 3(b). In the chessboard B pattern, configurations at θ0 = nπ/2 are not stripe-like patterns (such as chessboard A), as shown in Movie S2 (ESI†).
The chessboard pattern can be seen only for α ∼ 1. Fig. 3(d) shows the potential of dipolar interactions Udd*. When the external field is weak (α ≪ 1), as for α = 0.05 in Fig. 3(d), the system cannot transit from the stripe pattern to the spin-ice pattern because the external field strength is not sufficiently strong for the rotors to jump across the energy barrier ΔUdd* between the two configurations. As the result, they stay on a single stripe pattern and just result in the oscillating pattern. When the external field is moderately strong, say for α = 0.2, the system can make the transition into all 8 patterns as shown in Fig. 3(b) and (d). When the external field is strong (α ≫ 1) on the other hand, the chessboard pattern cannot be seen because the rotors all align to the external field direction and the stripe or the vortex configurations disappear.
 | (18) |
Analytical estimates for the values of α1 and α2 can be obtained by considering the energies of the different patterns. For simplicity, we consider only rotor orientations that satisfy ϕi = nπ/4 where n is an integer, thus approximating the stripe and spin-ice configurations as shown in Fig. 3(a). The corresponding dipole interaction energy Udd* is also shown in the figure. For a given orientation patterns ϕi, the total dimensionless energy can be estimated as
| Utot*(ϕi,θ0,α) = Udd*(ϕi) + αUext*(ϕi,θ0). | (19) |
An estimate of α1 is obtained by comparing the total energy of the stripe and spin-ice configurations for an external field direction θ0 = π/4. This is based on the observation that the chessboard pattern appears when the total energy of spin-ice configurations is lower than that of stripe configurations. Using  and Uext*(ϕicei,π/4) = −3, and assuming that the energy varies monotonically as a function of α, we obtain α1 = 0.068, which is in good agreement with the simulation result.
and Uext*(ϕicei,π/4) = −3, and assuming that the energy varies monotonically as a function of α, we obtain α1 = 0.068, which is in good agreement with the simulation result.
For α2, the estimate follows from comparing the total energy of the striped and aligned (Fig. 3(a)) configurations, for an external field at θ0 = 0 noting that the synchronized pattern appears when the total energy of aligned configurations is lower than that of the striped ones. Using Uext*(ϕstripei,0) = −3 and Uext*(ϕalignedi,0) = −9, we obtain α2 = 1.36, which is again in good agreement with the numerical value obtained from our simulations.
It is well known that mixing at small Reynolds numbers is challenging,34–36 because of the absence of inertia. This device would allow the vortex size and the mixing length scale to be controlled by the external magnetic field. Other types of flow fields are also possible for oscillatory magnetic driving mechanisms.9
3.3 The effect of lattice size
Fig. 5 shows the phase diagrams for different sizes of the rotor arrays. The value of R as defined in eqn (16) is always in the range − 1 ≤ R ≤ 1, and the color in Fig. 5 represents the rotational directions: red (R = 1) corresponds to rotation along with the external field, blue (R = −1) shows the opposite rotation and gray (R = 0) shows rotors with no net rotation. | ||
| Fig. 5 Phase diagrams for rotor arrays with different sizes: (a) 2 × 2, (b) 3 × 3, (c) 4 × 4, (d) 5 × 5. The color reflects the value of R. | ||
Although the basic structure of the phase diagram does not depend on the array size, the rotational patterns are different around the regions where the two torque contributions are comparable, namely 1/(τrf) ∼ 1/Mn. The arrays that have odd values of Nx and Ny show the same chessboard pattern as the 3 × 3 array (see also Movie S3, ESI†). By comparing arrays of 3 × 3, 5 × 5, and 7 × 7 (data not shown), we find that the parameter range over which the chessboard pattern is stable becomes smaller with increasing system size. For 4 × 4 arrays, there are equal numbers of clockwise and counterclockwise rotors for 1/(τrf) ∼ 1/Mn. However, the pattern differs from the chessboard pattern: each rotor takes three periods to complete a single full rotation. Moreover, a 2 × 2 array shows only synchronized or oscillating patterns.
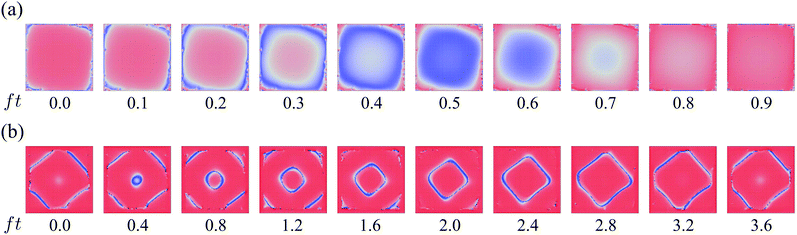
When interactions mediated by the fluid are negligible a* = a/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≪ 1, the slipping motion is first triggered at the outer edges of the system and slowly propagates inwards, as shown in Fig. 6(a) and Movie S4 (ESI†). This is because the alignment of the outer layers is strongly distorted due to the open boundary. If we now include the first-order hydrodynamic coupling between the rotors (see Appendix A) and increase the effective density by using the parameter a* = 0.45, the direction of the wave propagation reverses and the rotors first slip at the inner layers as shown in Fig. 6(b) and Movie S5 (ESI†). This occurs because the hydrodynamic effects are stronger at the centre of the array. As shown by eqn (10), each rotor creates a flow field with vorticity that is opposite to the rotating direction of the rotor. Therefore the hydrodynamic interactions tend to slow down neighbouring rotors. Since the inner layers have a larger number of neighbours, the slip starts from this region.
≪ 1, the slipping motion is first triggered at the outer edges of the system and slowly propagates inwards, as shown in Fig. 6(a) and Movie S4 (ESI†). This is because the alignment of the outer layers is strongly distorted due to the open boundary. If we now include the first-order hydrodynamic coupling between the rotors (see Appendix A) and increase the effective density by using the parameter a* = 0.45, the direction of the wave propagation reverses and the rotors first slip at the inner layers as shown in Fig. 6(b) and Movie S5 (ESI†). This occurs because the hydrodynamic effects are stronger at the centre of the array. As shown by eqn (10), each rotor creates a flow field with vorticity that is opposite to the rotating direction of the rotor. Therefore the hydrodynamic interactions tend to slow down neighbouring rotors. Since the inner layers have a larger number of neighbours, the slip starts from this region.
4 Conclusion
In this paper, we describe the collective motion of magnetic rotors under a rotational magnetic field. We mainly focus on a 3 × 3 array of magnets, and observe three characteristic dynamical rotor patterns as the external field strength is varied. In the synchronized regime, which appears when the magnetic torque due to the external field is dominant, all magnets rotate in the same direction as the field. If, however, the dipolar interaction between the rotors is dominant, all rotors exhibit oscillations (rather than full rotations) during a cycle. When the contributions from the external field and the dipolar interaction are comparable, there is an unexpected chessboard pattern of rotations where the magnets rotate in opposite directions to their closest neighbours. The chessboard is counter-intuitive because half of the rotors rotate in the opposite direction to the external field. We argue that the chessboard pattern appears as a consequence of the rotor array switching between stripe and spin-ice configurations: essentially the field lifts the degeneracy of these two states. For large system sizes, we observe the propagation of slip waves reminiscent of the metachronal waves observed in natural systems.19–25The rotational patterns in this paper emerge because of the competition between the external magnetic field and the dipolar interactions. Although it is intuitive to understand the rotor dynamics when either effect is dominant, it is difficult to analyse the complex dynamics when the two effects compete.9 The novelty of this work is not only finding these new rotational patterns, but also the constructing of a theoretical framework to understand the dynamics and to predict the phase boundaries. In future work, it would be interesting to investigate changes in the lattice geometry,9 or to consider the effect of inertia.
Such rotor arrays have potential as microfluidic devices that can create various flow fields and vortices of different sizes. Depending on the external field condition, the flow around the device considered here can vary from a single large vortex, to small alternating vortices around each rotor. We believe that our work sheds light on new collective dynamics of magnetic rotors and opens possibilities for future experiments and applications.
Conflicts of interest
There are no conflicts to declare.Appendix
A Effect of hydrodynamics
Considering the hydrodynamic coupling between rotors to the leading order,9,26 the angular velocity of the i-th rotor is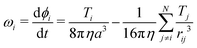 | (20) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as is evident from the following dimensionless form:
as is evident from the following dimensionless form: | (21) |
 | (22) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the hydrodynamic coupling can be neglected, resulting in eqn (13).
, the hydrodynamic coupling can be neglected, resulting in eqn (13).
B Favourable configurations
Since it is difficult to analyze the energy of a system that has 9 degree of freedoms (the 3 × 3 array), we consider a simplified description with a single degree of freedom, the deviation angle Δϕ, and discuss the resulting energy landscape in this Appendix. We consider the stripe pattern as a reference configuration, with Δϕ = 0, and define the deviation of the orientation of the i-th rotor, located at the p-th row and q-th column of the array, asϕi = ϕp,q(Δϕ) = π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(qπ/2) + (−1)p+qΔϕ. cos(qπ/2) + (−1)p+qΔϕ. | (23) |
Varying the deviation Δϕ from 0 to 2π, we find that the magnetic dipole–dipole interaction energy Udd is constant for odd N′ = Nx = Ny, not only for the stripe and spin-ice configurations, but also for all other angles. On the other hand, the potential Udd for even arrays is not constant. The potentials due to the external magnetic field, Uext, are
 | (24) |
As the result, Uext is dominant when N′ is odd, and the orientational pattern prefers Δϕ = θ0. For arrays with even N′, there is no preferred configuration because Uext is constant.
Acknowledgements
This work has received funding from the Horizon 2020 Research and Innovation Programme of the EU under Grant Agreement No. 665440. T. K. acknowledges the support of Osaka University Engineering Science Student Dispatch Program 2018, D. M. acknowledges the support of Multidisciplinary Research Laboratory System for Future Developments (MIRAI LAB), and F. M. acknowledges the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA17010504) and the Alexander von Humboldt Foundation for the partial support.Notes and references
- F. Y. Ogrin, P. G. Petrov and C. P. Winlove, Phys. Rev. Lett., 2008, 100, 218102 CrossRef PubMed
.
- L. Zhang, J. J. Abbott, L. Dong, K. E. Peyer, B. E. Kratochvil, H. Zhang, C. Bergeles and B. J. Nelson, Nano Lett., 2009, 9, 3663–3667 CrossRef CAS PubMed
.
- F. Meng, D. Matsunaga and R. Golestanian, Phys. Rev. Lett., 2018, 120, 188101 CrossRef CAS PubMed
.
- J. K. Hamilton, A. D. Gilbert, P. G. Petrov and F. Y. Ogrin, Phys. Fluids, 2018, 30, 092001 CrossRef
.
- B. A. Grzybowski and G. M. Whitesides, Science, 2002, 296, 718–721 CrossRef PubMed
.
- G. Kokot, S. Das, R. G. Winkler, G. Gompper, I. S. Aranson and A. Snezhko, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12870–12875 CrossRef CAS PubMed
.
- K. Han, G. Kokot, S. Das, R. G. Winkler, G. Gompper and A. Snezhko, Sci. Adv., 2020, 6, eaaz8535 CrossRef PubMed
.
- J. Leach, H. Mushfique, R. di Leonardo, M. Padgett and J. Cooper, Lab Chip, 2006, 6, 735–739 RSC
.
- D. Matsunaga, J. K. Hamilton, F. Meng, N. Bukin, E. L. Martin, F. Y. Ogrin, J. M. Yeomans and R. Golestanian, Nat. Commun., 2019, 10, 4696 CrossRef PubMed
.
- N. Coq, A. Bricard, F.-D. Delapierre, L. Malaquin, O. Du Roure, M. Fermigier and D. Bartolo, Phys. Rev. Lett., 2011, 107, 014501 CrossRef PubMed
.
- Y. Wang, Y. Gao, H. Wyss, P. Anderson and J. den Toonder, Lab Chip, 2013, 13, 3360–3366 RSC
.
- F. Tsumori, R. Marume, A. Saijou, K. Kudo, T. Osada and H. Miura, Jpn. J. Appl. Phys., 2016, 55, 06GP19 CrossRef
.
- S. Hanasoge, P. J. Hesketh and A. Alexeev, Soft Matter, 2018, 14, 3689–3693 RSC
.
- F. Meng, D. Matsunaga, J. M. Yeomans and R. Golestanian, Soft Matter, 2019, 15, 3864–3871 RSC
.
- D. Matsunaga, F. Meng, A. Zöttl, R. Golestanian and J. M. Yeomans, Phys. Rev. Lett., 2017, 119, 198002 CrossRef PubMed
.
- D. Matsunaga, A. Zöttl, F. Meng, R. Golestanian and J. M. Yeomans, IMA J. Appl. Math., 2018, 83, 767–782 CrossRef
.
- R. Zhou, C. A. Sobecki, J. Zhang, Y. Zhang and C. Wang, Phys. Rev. Appl., 2017, 8, 024019 CrossRef
.
- J. Zhang, M. R. Hassan, B. Rallabandi and C. Wang, Soft Matter, 2019, 15, 2439–2446 RSC
.
- N. Uchida and R. Golestanian, Phys. Rev. Lett., 2010, 104, 178103 CrossRef PubMed
.
- N. Osterman and A. Vilfan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15727–15732 CrossRef CAS PubMed
.
- R. Golestanian, J. M. Yeomans and N. Uchida, Soft Matter, 2011, 7, 3074 RSC
.
- D. R. Brumley, M. Polin, T. J. Pedley and R. E. Goldstein, Phys. Rev. Lett., 2012, 109, 268102 CrossRef PubMed
.
- J. Elgeti and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4470–4475 CrossRef CAS PubMed
.
- N. Narematsu, R. Quek, K.-H. Chiam and Y. Iwadate, Cytoskeleton, 2015, 72, 633–646 CrossRef PubMed
.
- D. R. Brumley, M. Polin, T. J. Pedley and R. E. Goldstein, J. R. Soc., Interface, 2015, 12, 20141358 CrossRef PubMed
.
-
S. Kim, S. J. Karrila and S. J. Karrila, Microhydrodynamics: principles and selected applications, Newnes, 1991, p. 507 Search PubMed
.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nat. Phys., 2017, 13, 375–379 Search PubMed
.
- K. E. Peyer, L. Zhang and B. J. Nelson, Nanoscale, 2013, 5, 1259–1272 RSC
.
- S. T. Bramwell and M. J. Gingras, Science, 2001, 294, 1495–1501 CrossRef CAS PubMed
.
- C. Castelnovo, R. Moessner and S. L. Sondhi, Nature, 2008, 451, 42 CrossRef CAS PubMed
.
- H. Wioland, F. G. Woodhouse, J. Dunkel and R. E. Goldstein, Nat. Phys., 2016, 12, 341 Search PubMed
.
- S. P. Thampi, A. Doostmohammadi, T. N. Shendruk, R. Golestanian and J. M. Yeomans, Sci. Adv., 2016, 2, e1501854 Search PubMed
.
- D. Nishiguchi, I. S. Aranson, A. Snezhko and A. Sokolov, Nat. Commun., 2018, 9, 4486 Search PubMed
.
- N.-T. Nguyen and Z. Wu, J. Micromech. Microeng., 2004, 15, R1 CrossRef
.
- C.-Y. Lee, C.-L. Chang, Y.-N. Wang and L.-M. Fu, Int. J. Mol. Sci., 2011, 12, 3263–3287 CrossRef CAS PubMed
.
- H. Aref, J. R. Blake, M. Budišić, S. S. Cardoso, J. H. Cartwright, H. J. Clercx, K. El Omari, U. Feudel, R. Golestanian and E. Gouillart,
et al.
, Rev. Mod. Phys., 2017, 89, 025007 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Movie_S1: typical rotational patterns in a 3 × 3 array of magnetic rotors: (a) synchronized pattern (1/Mn = 100, 1/(τrf) = 500), (b) chessboard pattern (1/Mn = 100, 1/(τrf) = 50) and (c) oscillating pattern (1/Mn = 100, 1/(τrf) = 10). The arrows at the bottom right indicate the direction of the external magnetic field. Bold arrows at the beginning of the movie indicate that a strong magnetic field 1/(τrf) = 104 is applied to align the rotors. Movie_S2: three different types of chessboard pattern: (a) chessboard A (1/Mn = 500, 1/(τrf) = 100), (b) chessboard A but with |R| < 1 (1/Mn = 200, 1/(τrf) = 20) and (c) chessboard B (1/Mn = 100, 1/(τrf) = 100). Movie_S3: chessboard pattern in a (a) 5 × 5 array and (b) 7 × 7 array, for dimensionless parameters 1/Mn = 100 and 1/(τrf) = 100. Movie_S4: slip wave propagation from outer to inner rotors in a 100 × 100 array, for dimensionless parameters 1/Mn = 1, 1/(τrf) = 5 and a* = 0. Note that the rotor size is set as a* = 0.5 for the visualization. Movie_S5: slip wave propagation from outer to inner rotors in a 100 × 100 array, for dimensionless parameters 1/Mn = 1, 1/(τrf) = 10 and a* = 0.45. See DOI: 10.1039/d0sm00454e |
| This journal is © The Royal Society of Chemistry 2020 |