Thermodynamics and ordering kinetics in asymmetric PS-b-PMMA block copolymer thin films

Abstract

The ordering kinetics of standing cylinder-forming polystyrene-block-poly(methyl methacrylate) block copolymers (molecular weight: 39 kg mol⁻¹) close to the order–disorder transition is experimentally investigated following the temporal evolution of the correlation length at different annealing temperatures. The growth exponent of the grain-coarsening process is determined to be 1/2, signature of a curvature-driven ordering mechanism. The measured activation enthalpy and the resulting Meyer–Neldel temperature for this specific copolymer along with the data already known for PS-b-PMMA block copolymers in strong segregation limit allow investigation of the interplay between the ordering kinetics and the thermodynamic driving force during the grain coarsening. These findings unveil various phenomena concomitantly occurring during the thermally activated ordering kinetics at segmental, single chain, and collective levels.

---

A. Introduction

Block copolymers (BCPs) are a single component system composed of two covalently bonded and repelling macromolecules. The chain connectivity frustrates the macro phase separation arising from block repulsion. Low temperature, low symmetrical, and spatially modulated phases self-assemble upon phase separation of the homogenous phase. The equilibrium morphologies, such as lamellae, cylinders, gyroids, and spheres, are mainly determined by the relative volume fraction of one component quantified by the chain disproportion (f). The degree of polymerization, i.e. the number of monomeric units (N), dictates the domain spacing (L₀) characterizing the periodicity of the self-assembled domains. The change in local free energy due to the interaction between the two distinct monomers is quantified by the Flory–Huggins parameter (χ).^1–9

The BCP free energy is composed of nearly specular entropic (÷1/N) and enthalpic (÷χ) contributions.⁴ At the order–disorder transition (ODT), these contributions are balanced. The segregation strength (χN) determines the strength of the repulsive interaction between the two blocks. The χN governs the phase separation as well as the degree of segregation between the two blocks upon phase separation. Increasing the χN above the χN_ODT, the transition to the ordered phase is driven by the free energy gain associated with the phase separation. This free energy gain results from the balance between the enthalpic gain and the entropic penalty in the transition to the phase-separated state from the homogeneous phase. The potential describing the phase separation in BCP self-assembly is short-range attractive and long-range repulsive (SALR) along the backbone of the polymer chain.³ In particular, the long-range repulsion has entropic origin.¹ The entropic penalty contributions, such as the chain stretching and the interface localization between the incompatible polymeric chains, determine the polymeric chain features of the phase-separated state. The chain stretching increases when the interface localization narrows, increasing χN and moving away from χN_ODT.^4,9–11

Above ODT, the degree of segregation between the two blocks is usually categorized into three regimes: weak, intermediate, and strong according to the concentration gradient across the interface between microphase-separated domains as a function of χ and N. The weak segregation regime occurs close to ODT (χN ≈ χN_ODT) when the composition profile is almost sinusoidal. Conversely, the strong segregation regime takes place far from the ODT (χN > χN_ODT) and is characterized by a nearly flat composition profile as well as strongly stretched chains and narrow interfaces. The weak to intermediate crossover is commonly placed slightly above ODT before the onset of the strong segregation. However, considering a mean field-based approach, strong segregation conditions have been demonstrated to be valid over most of the intermediate regime. Overall, the segregation regimes can be classified as weak (WSL) and strong (SSL) segregation limits with a smooth transition between the two limits. The degree of segregation in the two regimes can be effectively characterized by L₀ and the interfacial width, w: in particular w/L₀ ≈ 1 in the WSL, while w/L₀ ≪ 1 with L₀ ≈ N^2/3 in the SSL.^9–12

The phase diagram properties for the BCP system at thermodynamic equilibrium have been widely investigated.^3,10,13 However, the final equilibrium state is not reached instantaneously and the kinetics of equilibrium structure formation proceeds through the coarsening of the polycrystalline pattern by the progressive annihilation of the topological defects and the reorientation of the ordered domains. Up to now, the major focus has been on the dynamics of the coarsening process.^13–16 Ordering kinetics has been described in the framework of nucleation and growth of ordered mesophases^17–19 as well as focusing on the reduced chain diffusivity increasing the chain length.^20,21 However, an in depth experimental investigation of the relationship between the thermodynamic driving force and the ordering kinetics is still missing.

The weak dependence on the temperature (T) of the Flory–Huggins parameter χ_S–MMA for a polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) BCP^22,23 defines a peculiar experimental configuration: the speed of the ordering kinetics is modulated by changing the annealing temperature T without affecting the thermodynamic driving force χN that is independently defined by N of the selected copolymer. This peculiarity allows investigation of the specific interplay between the ordering kinetics and the thermodynamic driving force during the coarsening process. Recently, within this experimental approach, cylinder-forming PS-b-PMMA BCP thin films in SSL have been scrutinized.¹⁴ Further reducing N of the investigated BCP allows one to approach ODT, where the system is thermodynamically less stable, and to reduce L₀ toward the lower limit.²⁴ Moreover, reduced L₀ and effective ordering are crucial for the exploitation of BCPs as a valuable technological platform for the fabrication of dense and ordered nanostructures.^25–31 All these fundamental and practical characteristics make such a system very interesting to investigate.

In this work, we investigate the thermally activated ordering for a cylinder forming PS-b-PMMA BCP with χN ≈ χN_ODT measuring the evolution of the level of order as a function of the different time and temperature combinations of the thermal treatment. The data herein reported allow comprehensive clarification of the kinetic and thermodynamic mechanisms occurring at collective, single chain, and segmental levels, in the ordering process of a BCP-based two-dimensional hexagonal pattern for all the segregation regimes.^16,32–35

B. Experimental

Poly(styrene-random-methyl methacrylate) (P(S-r-MMA), molecular weight, M_n = 1.7 and 69 kg mol⁻¹, f_s = 0.61, and polydispersity index, PDI = 1.19) random copolymer (RCP) was grafted by means of a rapid thermal annealing (RTA) (T = 310 °C, and t = 60 s) on a hydroxyl terminated, flat, and unpatterned Si surface to form a neutral brush layer.³⁶ When deposited in the form of thin films, these RCPs exhibit an extremely high thermal stability.^37,38 In addition, high temperature RTA treatments have been demonstrated to effectively promote the grafting of these macromolecules, further increasing the thermal stability of the RCP brush layer compared to conventional furnace annealing.^39,40 The composition of the RCP brush layer guarantees the neutralization of the substrate, inducing the perpendicular orientation of the PMMA cylinders in the self-assembled asymmetric BCPs.^41,42 PS-b-PMMA BCPs with styrene fraction, f_s = 0.69, PDI = 1.07, and N = 379 (M_n = 39 kg mol⁻¹) in toluene solution were spun on the RCP-grafted layer to obtain a ≈ 30 nm BCP thick layer. The spin coated films underwent a thermal treatment using RTA in order to enhance the polymeric chain mobility and to drive the system toward the ordered equilibrium morphology.^24,43,44 The ordering process in the BCP thin films was studied considering different combinations of annealing time (t_A = 1–900 s) and temperature (T_A = 160–220 °C). Surface morphology after the RTA treatment was investigated by scanning electron microscopy (SEM). Top down SEM images provide real-space information of the BCP domains at the free surface. Considering the limited BCP film thickness, the cylindrical domains are expected to propagate throughout the entire thin film depth.⁴⁵ Magnification and resolution of the SEM images were selected to provide information over an area of the sample that is much larger than the measured correlation length (ξ). Several SEM images in different areas of the sample were acquired and analysed for each sample, offering statistically valuable information about the morphology of the sample under investigation. After SEM image binarization, the centroid of every cylinder was localized by software analysis and a Delaunay triangulation was performed to detect the coordinates of the vertex of the hexagons. These analyses allowed investigating the pattern orientation in real space. The level of order of the two-dimensional hexagonal pattern was quantified by measuring ξ, fitting the resulting autocorrelation function with an exponential decay function. More details about the analysis procedure are reported in previous papers.^{24,43,44,46,47}

C. Results and discussion

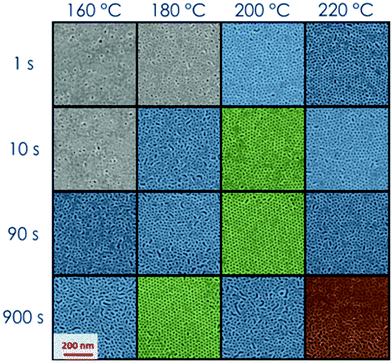
During the deposition process by spin casting from a dilute solution, the BCP thin films reach a kinetically trapped state far from the thermodynamic equilibrium state due to the slow dynamics of the polymeric chains.^43,47 A thermal or solvent annealing process is necessary to drive the system from this metastable state towards the thermodynamic equilibrium. Solvent and temperature effects on the BCP self-assembly process can be mapped on the phase diagram with proper definition of the parameter χ.^8,48 Recently we demonstrated that the grafted layer of RCP, that is commonly used to neutralize the surface, can trap a wealth of residual solvent in the polymeric film. This reservoir of solvent can be exploited during the thermal annealing to promote phase separation and grain coarsening in thin films of PS-b-PMMA in the SSL regime.^8,14 The capability of the RTA treatment to reach the target temperature in a very short time, even though not instantaneous, reduces solvent evaporation during the heating step and maximizes the effect of the residual solvent trapped in the polymeric film to enhance the polymeric chain mobility, increasing the ordering kinetics.^14,43,44 It has been evidenced that the amount of residual solvent in the overall RCP + BCP system is proportional to the brush layer thickness (h) that, indeed, is proportional to the RCP M_n.^43,47 The characteristic dimensions in the self-assembled BCP thin films, i.e. diameter (d) and L₀ of the PMMA cylinders have been found to be the same in all the samples, irrespective of the initial amount of residual solvent trapped in these RCP + BCP systems.⁴³

The effect of the residual solvent on the self-assembly process of a thin film of PS-b-PMMA with low N (=379) have been investigated. Fig. 1 shows the SEM plan view images of the self-assembled BCP over a “thick” brush layer (M_n(RCP) = 69 kg mol⁻¹, h ≈ 19 nm).⁴³ The investigated surfaces are phase separated but poorly ordered irrespective of the specific combination of T_A and t_A. In these samples, even in the best conditions, ξ values are very low and it is not possible to detect valuable ordering kinetics as a function of (t_A, T_A). This fact indicates that for a BCP system with low N, an excessive amount of solvent in the overall RCP + BCP system dilutes the investigated BCP system, shielding the block interaction forces, reducing the segregation strength, and driving the BCP towards the homogenous phase. On the other hand, using a “thin” brush layer (M_n(RCP) = 1.7 kg mol⁻¹, h ≈ 2 nm) as the neutralizing layer the reduced amount of solvent makes it possible to achieve the phase separation along with a valuable level of order as evidenced by the SEM images reported in Fig. 2.^14,43 In particular, Fig. 2 shows that, for very short processing times (t_A = 1–10 s) and relatively low temperatures (T_A = 160–180 °C), lateral order is very limited (gray SEM images with ξ < L₀). Increasing T_A (≥180 °C) and/or t_A (≥10 s), the level of order increases with ξ values well above L₀ (1 < ξ < 2L₀ blue, and ξ > 2L₀ green SEM images). Finally, for T_A = 220 °C and t_A = 900 s, the BCP surface shows inhomogeneities, suggesting the occurrence of a degradation process in the polymer film (red SEM images). The periodicity of the self-assembled domains was evaluated to be L₀ = 24.0 ± 1.0 nm and the diameter of the hexagonal packed cylinders was determined to be d = 12.0 ± 2.0 nm.^24,43 These results are in agreement with data previously collected on the same BCP, using a RCP brush layer with h ≈ 7 nm. From a thermodynamic point of view, the equilibrium morphology of the self-assembled BCP thin film is unaffected by the different reservoirs of solvent, which are present in these two BCP/RCP systems.⁴⁸ Thus, the self-assembly of this PS-b-PMMA BCP is possible only if the amount of solvent initially trapped in the system is not too high to shield the block interaction forces and to reduce χN. This phenomenon has not been observed in PS-b-PMMA BCP with M_n > 39 kg mol⁻¹, even increasing the amount of the retained solvent by means of “thick” brush layers. This fact suggests that the shift in the χ parameter that is determined by the excess of the retained solvent is quite limited. Overall, these data indicate that the low N of the PS-b-PMMA corresponds to a χN value that is very close to ODT, providing a signature of WSL.^24,43

Fig. 1 Plan view high-magnification SEM images of 39 kg mol⁻¹ BCP thin films annealed at different temperatures T_A for different t_A values on “thick” RCP (69 kg mol⁻¹, brush layer ≈ 19 nm). ξ < L₀ gray images.

Fig. 2 Plan view high-magnification SEM images of 39 kg mol⁻¹ BCP thin films annealed at different temperatures T_A for different t_A values on “thin” RCP (1.7 kg mol⁻¹, brush layer ≈ 2 nm). ξ < L₀ gray images, 1 < ξ < 2L₀ blue images, ξ > 2L₀ green images, and inhomogeneities red images.

All the following data were obtained by self-assembling the BCP film over a “thin” RCP layer with a RTA treatment in a range of temperatures between 180 and 200 °C. Fig. 3 reports ξ as a function of t_A at different T_A values (180, 190, 195, and 200 °C). The data evidence a regular increase of ξ as a function of t_A at the different T_A values, while for the same t_A, ξ increases increasing T_A. This regularity induces one to treat the measured ξ values by applying the time–temperature superposition (tTS) procedure. ξ values as a function of t_A for different T_A values are collected in a master curve reporting ξ versus an equivalent time (t_EQ) at the reference temperature T_A = 180 °C (Fig. 4). The master curve results by multiplying for a proper rigid shift factor the time scale of ξ(t_A) curves for every T_A > 180 °C in order to match ξ values to the reference curve at T_A = 180 °C.¹⁴ Although the absolute ξ values may appear not to be very high, normalizing ξ by the periodicity L₀ of the BCP, a maximum value of ξ/L₀ ≈ 10 is obtained. This ξ/L₀ value is perfectly consistent with the results for perpendicularly oriented cylinder-forming PS-b-PMMA BCP thin films that were reported in previous papers.¹⁴ The master curve is well fitted with a power law t^ϕ, evidencing the self-similarity of the system. The measured growth exponent is ϕ = 0.50 ± 0.02.

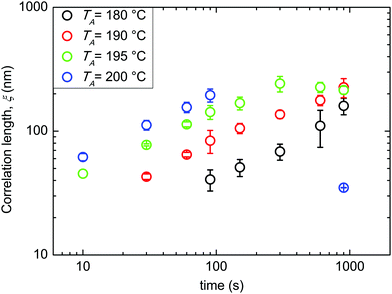Fig. 3 Evolution of the correlation length ξ as a function of t_A at different T_A values (180, 190, 195, and 200 °C).

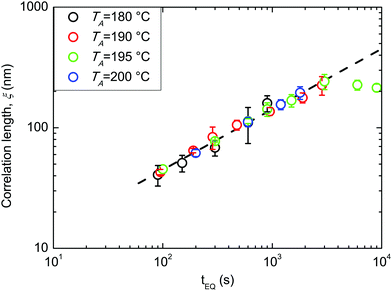Fig. 4 Master curve from time–temperature-superposition of the correlation length data. The slope of the curve represents the growth exponent ϕ.

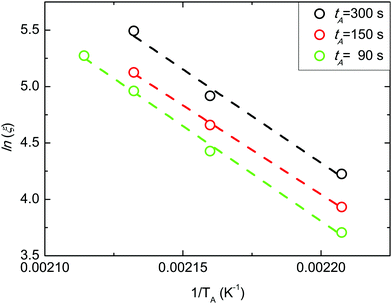
The evolution of ln ξ as a function of 1/T_A at different t_A values is reported in Fig. 5. Experimental data were fitted using an Arrhenius equation ln ξ = ln A − H_A/(K_B·T_A), where H_A corresponds to the activation enthalpy of the grain-coarsening process, K_B is the Boltzmann constant, and A is the pre-exponential factor that is related to the activation entropy S_A. The linear evolution of ln ξ as a function of 1/T_A indicates that the grain-coarsening process is a thermally activated process with a kinetic barrier. Limited variations of H_A with t_A have been observed, as previously reported also in the case of PS-b-PMMA in SSL.¹⁴ The mean H_A value is 136.5 ± 5.0 kJ mol⁻¹.

Fig. 5 Arrhenius plots of ξ data at different t_A values.

These data for a PS-b-PMMA BCP close to ODT along with the previously published data for PS-b-PMMA BCP in SSL allow a comprehensive description of the system.¹⁴ In particular, considering the BCP ordering process as an outcome of various phenomena concomitantly occurring at different levels (collective, single chain, and segmental) it is possible to map out a profitable route for the rationalization of the experimental data.

Collective dynamics

In Fig. 6 (data in SSL from ref. 14) ϕ values for BCP with 39 < M_n < 132 kg mol⁻¹ are depicted as a function of N_MMA, i.e. the number of monomeric units in the minor component of the BCP. The absolute ϕ value progressively increases when decreasing N_MMA. In particular, for the BCPs in SSL with f_s = 0.69, ϕ exhibits an analytical dependence exp(−χN_MMA), with χ = 0.028 ± 0.002. This effective χ parameter is in excellent agreement with χ_S–MMA values reported in the literature.^14,22 Moreover, the exponential dependence of ϕ on χN_MMA mimics the one of a single chain diffusion, suggesting that this mechanism drives the grain-coarsening process. For the 39 kg mol⁻¹ BCP (N_MMA = 122, f_s = 0.69), i.e. when entering into WSL, the ϕ value further increases but with a value, which is lower compared to that expected according to the extrapolated exponential curve. This dissimilarity evidences that, approaching ODT, a supplemental rate limiting mechanism frustrates the diffusion limited grain coarsening mechanism observed in SSL.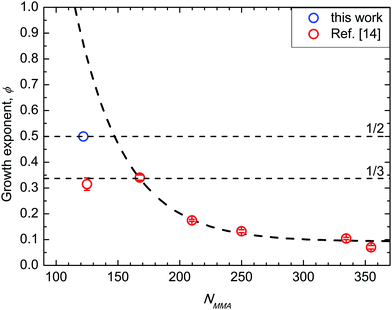

Fig. 6 Growth exponent ϕ as a function of N_MMA. Data in strong segregation limit (N_MMA ≥ 167) are reported from ref. 14.

This frustration can be rationalized as follows. Approaching ODT, the chains are less stretched and the interface between PS and PMMA components is not sharp, hindering the expected accelerated kinetics associated with the increased diffusivity of BCP chains when decreasing N.^15,49 Growth exponents of 1/2 and 1/3 are widely recognized as maximum values for curvature-driven and diffusion-limited coarsening, respectively, for systems with short-range attractive potential that macro phase separate.^50–53 In the data herein reported, the same maximum growth exponents are experimentally measured for a system described by a SALR potential inducing the microphase separation and the inherent thermally activated ordering. It is worth noticing the subtle dependence of these data on f_s. In fact, the ϕ value that was obtained for the 48 kg mol⁻¹ BCP (N_MMA = 125, and f_s = 0.74) is clearly outside this exponential trend. This is ascribed to the dependence of the self-diffusion coefficient on 1/N, further supporting the interpretation of these data as a marker of a diffusion-limited mechanism.⁴⁹ A subtle difference in f_s for two BCPs could result in a similar N_MMA of the minor block, even if the N values of the BCPs is significantly different. This corresponds to a different N_S value of the major PS block in the two PS-b-PMMA BCPs, modifying the volume of the PS region that the PMMA component has to cross during the diffusion process associated with the grain coarsening; the larger the volume of this region, the slower the diffusion process. Namely, the different behaviour of these two samples indicates that the dependence on N_MMA we depicted in Fig. 6 holds only for samples with f_s = 0.69. Changing f_s we expect to have a different exponential curve describing the evolution of the grain-coarsening process as a function of N_MMA.

Single chain kinetics and thermodynamic driving force coupling

Fig. 7 compares the H_A value herein achieved with those previously reported in the case of BCP in SSL.¹⁴H_A values are reported as a function of N_MMA, and follow the same exponential decay exp(−χN_MMA) irrespective of the segregation regime. The χ value obtained from the overall fitting is 0.024 ± 0.001, in excellent agreement with the previously reported value in the case of SSL (N_MMA ≥ 167, χ = 0.024) and with χ_S–MMA values reported in the literature.^14,22 This fact further supports the idea that the amount of solvent initially trapped in this specific BCP/RCP combination effectively enhances the kinetics of the grain coarsening-process without significantly affecting the thermodynamics of the BCP interactions.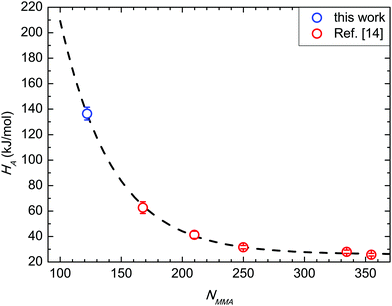

Fig. 7 Activation enthalpy H_A as a function of N_MMA. Data in strong segregation limit (N_MMA ≥ 167) are reported from ref. 14.

This analysis highlights that the energetics associated with the thermally activated grain-coarsening process is the same in WSL and SSL. Indeed, the kinetic barrier evolution is described by the same exponential dependence on −χN_MMA in both regimes. This feature suggests the same basic process irrespective of N. It can be depicted as a hindered diffusion mechanism similar either to the single chain hopping in sphere-based systems or to the perpendicular diffusion in lamellar systems.^49,54–57 Actually, the two-dimensional hexagonally packed lattice of the BCP film is represented as a system with zero dimensional connectivity where the energy penalty for hopping diffusion describes the experimental data.

The effect of the thermodynamic driving force on the kinetic process can be rationalized considering the specular mechanisms of chain unmixing and mixing. The free energy gain in unmixing corresponds to a free energy penalty in mixing. Experimentally, phase separation and ordering are two consecutive steps of the self-assembly process; early stage phase separation is assumed to take place when ξ ≤ L₀ and late stage ordering when ξ > L₀.^14,43 However, the same thermodynamic driving force χN determines nucleation and growth during the phase separation at the expense of the homogenous phase (ξ ≤ L₀) and coarsening of the ordered phase at the expense of a less-ordered phase during ordering (ξ > L₀).^17–19 In this respect, the framework of nucleation accounts for the herein reported experimental data. Nucleation corresponds to a thermally activated transition from a less stable to a more stable state, moving through a transition state at high energy, which represents the nucleation barrier.^58–62 Indeed, the basic features of nucleation are a free energy variation, with competing gain and penalty components, along with a nucleation barrier that inversely depends on the free energy gain during nucleation. All these features match our experimental results. Indeed, in their seminal work about the kinetics of metastable states in BCPs, Fredrickson and Binder disclosed that “the barrier for homogeneous nucleation in symmetric diblocks decreases with increasing molecular weight”,¹⁷ in agreement with our experimental findings. Alternatively, a theoretical approach based on single-chain in mean field simulations evidenced peculiarities that describe our experimental results as well. In particular, focusing on the local densities of the blocks as collective variables, such a theoretical approach evidences that the slowness of the ordering kinetics originates not from a collective variable but from a small Onsager coefficient, that connects the thermodynamic driving force to an order parameter flux. Within this approach, the exponential dependence of the barrier on −χN_MMA is reported to be related to the single chain dynamics without a collective free energy barrier in the minimum free energy path.^54,56,63 Indeed, Müller and de Pablo reported that “the kinetics can be protracted in strongly segregated systems, even if there is a strong thermodynamic driving force”, consistent with our observations showing that by increasing the thermodynamic driving force the kinetics gets slower.⁶³

Segmental activation

Fig. 8 reports the relationship between H_A and ln A, i.e. ln of the pre-exponential factor A of the Arrhenius equation that is related to the activation entropy S_A. Present data are compared with those obtained in SSL from ref. 14. The overall linear relationship indicates that the data follow the Meyer–Neldel (MN) rule ΔS = ΔH/T_MN, where T_MN is the MN temperature.^64,65 From the linear fitting, T_MN is found to be 447 K (174 °C). Considering the reported mean bulky glass transition temperature T_G for these BCPs, it descends so that T_MN ≈ 1.2T_G. This fact evidences the same behaviour in SSL and WSL, indeed T_MN ≈ 1.2T_G in both cases.

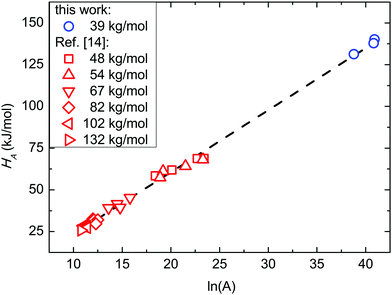Fig. 8 H _A as a function of the pre-exponential factor (ln A) of the Arrhenius plot corresponding to the activation entropy (S_A). Data in the strong segregation limit are reported from ref. 14.

The same T_MN value, irrespective of WSL or SSL, refers the ordering kinetics to a thermally activated process that begins at the same temperature without any dependence on N. The value of T_MN ≈ 1.2T_G ascribes this thermally activated process to the glass transition (GT) where segmental dynamics, which is the basic kinetic step, becomes active. Above this threshold, the inverse relationship between diffusivity and viscosity holds. This segmental feature originates the collective tTS behaviour of BCP systems, which has been exploited following the ordering kinetics.^66,67 From a thermodynamic point of view, it has been shown that T_MN is a consequence of a balance between repulsive and attractive interactions.⁶⁸ This balance at the kinetic GT mimics the balance between entropic and enthalpic contributions at the thermodynamic ODT.^4,5

Overall view

The experimental decoupling of the kinetic and thermodynamic controls indicates the two different phase transitions (ODT and GT) that define BCP ordering. The distance from ODT (N_ODT) is determined by N. Considering that χ_S–MMA is almost independent of T, N also dictates χN that determines the thermodynamic driving force affecting phase separation and ordering. T measures the distance from GT (T_MN) and it originates thermal fluctuations to activate the cross of the kinetic barriers. Overall, the ordering process is enclosed in these landmarks and its effective rate originates from the coupling of these thermodynamic and kinetic factors. As evidenced by the unique analytical dependence of H_A and the single T_MN, thermodynamically, WSL and SSL are not distinguishable. On the other hand, approaching ODT, in WSL, the collective dynamics (quantified by ϕ) is hindered by a supplemental rate-limiting process that switches the ordering process from a diffusion-limited (in SSL) to a curvature-driven mechanism (in WSL).

The grain coarsening occurs by local rearrangement of single chains. Their mobility determines the cooperative diffusion (as quasi particles) and annihilation of topological defects that dominate the grain coarsening.^8,49,55 The apparent discrepancy of the trends of experimental kinetic barriers for the grain-coarsening process (single chain based), decreasing with N, and the simulated free energy barriers for an overall defect removal, increasing with N, is recomposed considering that a collection of many molecules contributes to a defect. Both single chain and collective motions comply with the extensively evidenced kinetics-limited coarsening and the reduced diffusivity, increasing N and moving away from ODT, and, conversely, with the thermodynamics-limited coarsening and the enhanced diffusivity, decreasing N and moving towards ODT.^{12,21,48,49,54,57,63}

Generally, an inverse coupling between kinetic barriers and thermodynamic driving force either in a two state kinetic model or in a flux–force relationship is a ubiquitous concept in different scientific and technological fields such as metallurgy, protein folding, structural transitions, and metabolism. In particular, in the latter case, enzymes instead of stochastic forces (as thermal fluctuations) are used to activate the crossing of the barrier.^69–76

Perspectives

A direct extrapolation of these results to other PS-b-PMMA morphologies is not straightforward because of the different connectivity in spheres, cylinders and lamellae forming BCP thin films. In particular, hexagonally packed cylinders perpendicularly oriented with respect to the surface are characterized by a zero-dimensional connectivity, so that hopping diffusion drives the grain-coarsening process. Conversely, perpendicularly oriented lamellae are characterized by a one-dimensional connectivity that results in both an interface diffusion along the lamellae and a hopping diffusion normal to the lamellae.⁴⁹ The interplay of these effects during the grain coarsening introduces an additional degree of freedom in the system, increasing the level of complexity. Due to this fact, it is difficult to extrapolate the evolution of a lamellar system on the basis of the behaviour of the perpendicularly oriented cylinders.

Nevertheless, irrespective of their morphology upon self-assembly, all PS-b-PMMA BCPs exhibit the same weak dependence of χ_S–MMA on T. Consequently, the same experimental approach based on a tTS procedure could be used to investigate the grain coarsening of other PS-b-PMMA systems. In particular, we already reported the kinetics of grain coarsening in a lamellae-forming PS-b-PMMA BCP with M_n = 51 kg mol⁻¹.^77,78 To clearly disclose this behaviour, further experiments using lamellae forming BCPs with different M_n and RCP brush layers with different h are needed.

The application of this methodology is questionable in the case of high-χ BCP systems that are usually characterized by a temperature dependent χ. Actually, operating at different T values, the variation of χ is expected to modify χN, changing the thermodynamics of the system and affecting its kinetic evolution as well. In a previous work, we investigated the kinetics of grain coarsening in a cylinder forming PS-b-PDMS BCP at constant T. Data highlighted that a power law dependence perfectly describes the evolution of ξ as a function of time during the thermal treatment.⁷⁹ The investigation of grain coarsening evolution at different T values would be extremely interesting to understand how the variation of χN affects the kinetics of the process, eventually modifying ϕ. Similarly, a dedicated approach for the dependence of χ on T should be implemented to investigate the thermodynamics of the system.

From the point of view of the integration of PS-b-PMMA in a standard lithographic process, the understanding and optimization of the self-assembly process of BCP films deposited on unpatterned substrates is essential. In particular, the perfect order in BCP thin films confined into topographically defined trenches requires a corresponding minimum level of order on an unpatterned surface.²⁹ Moreover, measuring the correlation length of unguided self-assembled BCP thin films, Ellison et al. demonstrated that it is possible to directly predict the density of kinetically trapped defects in BCP thin films deposited on a fixed chemical pattern and self-assembled under the same process conditions.³¹ Therefore, the understanding of the self-assembling process for a BCP deposited on an unpatterned substrate is fundamental for the development of any directed self-assembly based nanolithograpic application.^25,26,31

D. Conclusions

From the measure of the evolution with time and temperature of a collective variable, the correlation length ξ, it was possible to experimentally evidence the basic thermodynamics that affects the ordering as well as the temperature where the polymer is not yet glassy identifying the onset of segmental activation. The coupling between kinetics and thermodynamic driving forces has been comprehensively scrutinized by studying the ordering of a two-dimensional hexagonal pattern on a flat and unpatterned surface within a proper experimental PS-b-PMMA BCP-based platform. These results are relevant both considering the paradigmatic properties of self-assembling BCP systems described by SALR competing interactions and the technological applications in order to plan better strategies to increase the order of dense nanostructures.^{28,30,80–85}

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge: M. Laus, K. Sparnacci, V. Gianotti, and D. Antonioli (Università Del Piemonte Orientale, Italy) for the RCP synthesis; M. Alia (CNR-IMM, Italy) for assistance with the experimental part; and T. J. Giammaria (CNR-IMM, Italy, present address: CEA-LETI, France) and F. Ferrarese Lupi (CNR-IMM, Italy, present address: INRIM, Italy) for fruitful discussions. This research has been partially supported by the project IONS4SET funded from the European Union's Horizon 2020 Research and Innovation Program under Grant No. 688072.

References

1. D. Andelman and R. E. Rosensweig, J. Phys. Chem. B, 2009, 113, 3785–3798.
2. C. B. Muratov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 066108.
3. D. Pini and A. Parola, Soft Matter, 2017, 13, 9259–9272.
4. F. S. Bates, Science, 1990, 251, 898–905.
5. A. Kumar and V. Molinero, J. Phys. Chem. Lett., 2017, 8, 5053–5058.
6. A. Ciach, J. Pekalski and W. T. Góźdź, Soft Matter, 2013, 9, 6301–6308.
7. F. A. Lavergne, D. G. A. L. Aarts and R. P. A. Dullens, Phys. Rev. X, 2017, 7, 041064.
8. P. W. Majewski and K. G. Yager, J. Phys.: Condens. Matter, 2016, 28, 403002.
9. K. Koo, H. Ahn, S.-W. Kim, D. Y. Ryu and T. P. Russell, Soft Matter, 2013, 9, 9059.
10. M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098.
11. R. L. Lescanec and M. Muthukumar, Macromolecules, 1993, 26, 3908–3916.
12. W. Li, P. F. Nealey, J. J. de Pablo and M. Muller, Phys. Rev. Lett., 2014, 113, 168301.
13. R. A. Segalman, A. Hexemer, R. C. Hayward and E. J. Kramer, Macromolecules, 2003, 36, 3272–3288.
14. G. Seguini, F. Zanenga, M. Laus and M. Perego, Phys. Rev. Mater., 2018, 2, 055605.
15. D. A. Vega, C. K. Harrison, D. E. Angelescu, M. L. Trawick, D. A. Huse, P. M. Chaikin and R. A. Register, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061803.
16. S. Ji, C. Liu, W. Liao, A. L. Fenske, G. S. W. Craig and P. F. Nealey, Macromolecules, 2011, 44, 4291–4300.
17. G. H. Fredrickson and K. Binder, J. Chem. Phys., 1989, 91, 7265–7275.
18. H. J. Dai, N. P. Balsara, B. A. Garetz and M. C. Newstein, Phys. Rev. Lett., 1996, 77, 3677–3680.
19. K. Aissou, M. Kogelschatz and T. Baron, Nanotechnology, 2009, 20, 095602.
20. H. Yokoyama and E. J. Kramer, Macromolecules, 1998, 31, 7871–7876.
21. K. A. Cavicchi and T. P. Lodge, Macromolecules, 2003, 36, 7158–7164.
22. T. P. Russell, R. P. Hjelm and P. A. Seeger, Macromolecules, 1990, 23, 890–893.
23. T. P. Russell, Macromolecules, 1993, 26, 5819.
24. G. Seguini, T. J. Giammaria, F. Ferrarese Lupi, K. Sparnacci, D. Antonioli, V. Gianotti, F. Vita, I. F. Placentino, J. Hilhorst, C. Ferrero, O. Francescangeli, M. Laus and M. Perego, Nanotechnology, 2014, 25, 045301.
25. J. Y. Cheng, A. M. Mayes and C. A. Ross, Nat. Mater., 2004, 3, 823–828.
26. M. Kim, E. Han, D. P. Sweat and P. Gopalan, Soft Matter, 2013, 9, 6135–6141.
27. M. Perego, A. Andreozzi, A. Vellei, F. Ferrarese Lupi and G. Seguini, Nanotechnology, 2013, 24, 245301.
28. J. Frascaroli, S. Brivio, F. Ferrarese Lupi, G. Seguini, L. Boarino, M. Perego and S. Spiga, ACS Nano, 2015, 9, 2518–2529.
29. G. Aprile, F. Ferrarese Lupi, M. Fretto, E. Enrico, N. De Leo, L. Boarino, F. G. Volpe, G. Seguini, K. Sparnacci, V. Gianotti, M. Laus, J. Garnæs and M. Perego, ACS Appl. Mater. Interfaces, 2017, 9, 15685–15697.
30. F. Delachat, A. Gharbi, P. Pimenta-Barros, A. Fouquet, G. Claveau, N. Posseme, L. Pain, C. Nicolet, C. Navarro, I. Cayrefourcq and R. Tiron, Nanoscale, 2018, 10, 10900–10910.
31. J. Doise, J. H. Koh, J. Y. Kim, Q. Zhu, N. Kinoshita, H. S. Suh, G. Vandenberghe, C. G. Willson and C. J. Ellison, ACS Appl. Mater. Interfaces, 2019, 11, 48419–48427.
32. W. T. M. Irvine, V. Vitelli and P. M. Chaikin, Nature, 2010, 468, 947–951.
33. N. A. García, A. D. Pezzutti, R. A. Register, D. A. Vega and L. R. Gómez, Soft Matter, 2015, 11, 898–907.
34. A. M. Welander, H. Kang, K. O. Stuen, H. H. Solak, M. Müller, J. J. De Pablo and P. F. Nealey, Macromolecules, 2008, 41, 2759–2761.
35. P. W. Majewski and K. G. Yager, Soft Matter, 2015, 12, 281–294.
36. K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus, F. Ferrarese Lupi, T. J. Giammaria, G. Seguini and M. Perego, ACS Appl. Mater. Interfaces, 2015, 7, 10944–10951.
37. V. Gianotti, D. Antonioli, K. Sparnacci, M. Laus, T. J. Giammaria, F. Ferrarese Lupi, G. Seguini and M. Perego, Macromolecules, 2013, 46, 8224–8234.
38. K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus, G. Zuccheri, F. Ferrarese Lupi, T. J. Giammaria, G. Seguini, M. Ceresoli and M. Perego, ACS Appl. Mater. Interfaces, 2015, 7, 3920–3930.
39. K. Sparnacci, D. Antonioli, M. Perego, T. J. Giammaria, G. Seguini, F. Ferrarese Lupi, G. Zuccheri, V. Gianotti and M. Laus, Polym. Int., 2017, 66, 459–467.
40. F. Ferrarese Lupi, T. J. Giammaria, G. Seguini, M. Ceresoli, M. Perego, D. Antonioli, V. Gianotti, K. Sparnacci and M. Laus, J. Mater. Chem. C, 2014, 2, 4909–4917.
41. E. Han, K. O. Stuen, Y. H. La, P. F. Nealey and P. Gopalan, Macromolecules, 2008, 41, 9090–9097.
42. S. Ham, C. Shin, E. Kim, D. Y. Ryu, U. Jeong, T. P. Russell and C. J. Hawker, Macromolecules, 2008, 41, 6431–6437.
43. G. Seguini, F. Zanenga, T. J. Giammaria, M. Ceresoli, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2016, 8, 8280–8288.
44. F. Ferrarese Lupi, T. J. Giammaria, M. Ceresoli, G. Seguini, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, Nanotechnology, 2013, 24, 315601.
45. F. Ferrarese Lupi, T. J. Giammaria, F. G. Volpe, F. Lotto, G. Seguini, B. Pivac, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2014, 6, 21389–21396.
46. F. Ferrarese Lupi, T. J. Giammaria, G. Seguini, F. Vita, O. Francescangeli, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2014, 6, 7180–7188.
47. T. J. Giammaria, F. Ferrarese Lupi, G. Seguini, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, ACS Appl. Mater. Interfaces, 2017, 9, 31215–31223.
48. W. Li and M. Müller, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 187–216.
49. H. Yokoyama, Mater. Sci. Eng., R, 2006, 53, 199–248.
50. L. R. Gómez, E. M. Vallés and D. A. Vega, Phys. A, 2007, 386, 648–654.
51. A. Adland, Y. Xu and A. Karma, Phys. Rev. Lett., 2013, 110, 265504.
52. C. Sagui and R. C. Desai, Phys. Rev. Lett., 1995, 74, 1119–1122.
53. C. Sagui and R. C. Desai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 52, 2807.
54. W. Li and M. Müller, Macromolecules, 2016, 49, 6126–6138.
55. Q. Tong and S. J. Sibener, Macromolecules, 2013, 46, 8538–8544.
56. S.-M. Hur, V. Thapar, A. Ramírez-Hernández, G. Khaira, T. Segal-Peretz, P. A. Rincon-Delgadillo, W. Li, M. Müller, P. F. Nealey and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14144–14149.
57. H. Takahashi, N. Laachi, K. T. Delaney, S. M. Hur, C. J. Weinheimer, D. Shykind and G. H. Fredrickson, Macromolecules, 2012, 45, 6253–6265.
58. M. Iwamatsu, J. Chem. Phys., 2009, 130, 244507.
59. J. M. Rubí and A. Pérez-Madrid, J. Non-Equilib. Thermodyn., 2015, 40, 275–281.
60. D. Michel, Phys. A, 2018, 503, 26–44.
61. F. Sicard, Phys. Rev. E, 2018, 98, 052408.
62. X. Cheng, L. Lin, W. E, P. Zhang and A.-C. Shi, Phys. Rev. Lett., 2010, 104, 148301.
63. M. Müller and J. J. de Pablo, Annu. Rev. Mater. Res., 2013, 43, 1–34.
64. A. Yelon and B. Movaghar, Phys. Rev. Lett., 1990, 65, 618.
65. H. J. Ryu, Q. Tong and S. J. Sibener, J. Phys. Chem. Lett., 2013, 4, 2890–2895.
66. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267.
67. A. P. Sokolov and K. S. Schweizer, Phys. Rev. Lett., 2009, 102, 248301.
68. J. F. Douglas, J. Dudowicz and K. F. Freed, Phys. Rev. Lett., 2009, 103, 135701.
69. R. Zwanzig, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 148–150.
70. H. Yu, A. N. Gupta, X. Liu, K. Neupane, A. M. Brigley, I. Sosova and M. T. Woodside, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14452–14457.
71. D. A. Beard and H. Qian, PLoS One, 2007, 2, e144.
72. E. Noor, A. Bar-Even, A. Flamholz, E. Reznik, W. Liebermeister and R. Milo, PLoS Comput. Biol., 2014, 10, e1003483.
73. Q. Li and Y.-S. Jun, Commun. Chem., 2018, 1, 56.
74. J. Kao, K. Thorkelsson, P. Bai, Z. Zhang, C. Sun and T. Xu, Nat. Commun., 2014, 5, 4053.
75. Y. H. Lee, S. D. Hyun, H. J. Kim, J. S. Kim, C. Yoo, T. Moon, K. Do Kim, H. W. Park, Y. Bin Lee, B. S. Kim, J. Roh, M. H. Park and C. S. Hwang, Adv. Electron. Mater., 2019, 5, 1800436.
76. M. H. Park, Y. H. Lee, T. Mikolajick, U. Schroeder and C. S. Hwang, Adv. Electron. Mater., 2019, 5, 1800522.
77. M. Perego, F. Ferrarese Lupi, M. Ceresoli, T. J. Giammaria, G. Seguini, E. Enrico, L. Boarino, D. Antonioli, V. Gianotti, K. Sparnacci and M. Laus, J. Mater. Chem. C, 2014, 2, 6655.
78. M. Ceresoli, F. G. Volpe, G. Seguini, D. Antonioli, V. Gianotti, K. Sparnacci, M. Laus and M. Perego, J. Mater. Chem. C, 2015, 3, 8618–8624.
79. T. J. Giammaria, F. Ferrarese Lupi, G. Seguini, M. Perego, F. Vita, O. Francescangeli, B. Wenning, C. K. Ober, K. Sparnacci, D. Antonioli, V. Gianotti and M. Laus, ACS Appl. Mater. Interfaces, 2016, 8, 9897–9908.
80. C.-C. Liu, E. Franke, Y. Mignot, R. Xie, C. W. Yeung, J. Zhang, C. Chi, C. Zhang, R. Farrell, K. Lai, H. Tsai, N. Felix and D. Corliss, Nat. Electron., 2018, 1, 562–569.
81. I. Gunkel, Small, 2018, 14, 1802872.
82. M. Perego, G. Seguini, E. Arduca, A. Nomellini, K. Sparnacci, D. Antonioli, V. Gianotti and M. Laus, ACS Nano, 2018, 12, 178–186.
83. K. Brassat, D. Kool, J. Bürger and J. K. N. Lindner, Nanoscale, 2018, 10, 10005–10017.
84. P. W. Majewski and K. G. Yager, Nano Lett., 2015, 15, 5221–5228.
85. Y. Choo, P. W. Majewski, M. Fukuto, C. O. Osuji and K. G. Yager, Nanoscale, 2018, 10, 416–427.

---