Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Orientational order in dense suspensions of elliptical particles in the non-Stokesian regime
György
Tegze
 *a,
Frigyes
Podmaniczky
a,
Ellák
Somfai
*a,
Frigyes
Podmaniczky
a,
Ellák
Somfai
 a,
Tamás
Börzsönyi
a,
Tamás
Börzsönyi
 a and
László
Gránásy
ab
a and
László
Gránásy
ab
aInstitute for Solid State Physics and Optics, Wigner Research Center for Physics, P.O. Box 49, H-1525 Budapest, Hungary. E-mail: tegze.gyorgy@wigner.hu
bBCAST, Brunel University, Uxbridge, Middlesex UB8 PH3, UK
First published on 2nd September 2020
Abstract
Suspensions of neutrally buoyant elliptic particles are modeled in 2D using fully resolved simulations that provide two-way interaction between the particle and the fluid medium. Forces due to particle collisions are represented by a diffuse interface approach that allows the investigation of dense suspensions (up to 47% packing fraction). We focus on the role inertial forces play at low and high particle Reynolds numbers termed low Reynolds number and inertial regimes, respectively. The suspensions are characterized by the orientation distribution function (ODF) that reflects shear induced rotation of the particles at low Reynolds numbers, and nearly stationary (swaying) particles at high Reynolds numbers. In both cases, orientational ordering differs qualitatively from the behavior observed in the Stokesian-regime. The ODF becomes flatter with increasing packing fraction, as opposed to the sharpening previous work predicted in the Stokesian regime. The ODF at low particle concentrations differs significantly for the low Reynolds number and inertial regimes, whereas with increasing packing fraction convergence is observed. For dense suspensions, the particle–particle interactions dominate the particle motion.
1 Introduction
The collective behaviour of elongated particles or molecules in flowing fluids plays an important role in a number of industrial processes including hydrodynamic alignment of cellulose fibers1 and composite materials2 and aligning biological filaments3 or nematic liquid crystals.4 The distribution of particle orientations in these systems can be important in tuning materials properties, for example, it may define anisotropic optical or mechanical properties. Despite the fact that the behaviour of particles in fluid flow has long been studied, the related phenomena are so complex that some experimental observations are understood only phenomenologically, or even considered counterintuitive. Generally, it was found in various systems that the average orientation of the particles is nearly parallel to the fluid streamlines. However, elongated particles passing through a narrow channel tend to align perpendicularly to the flow direction,5 and transverse alignment was also observed in periodically sheared suspensions.6A single non-Brownian ellipsoid immersed in a simple shear flow of a Stokesian fluid rotates with modulated angular velocity resulting in a time averaged orientation parallel to the streamlines.7 The case of interacting non-Brownian rods placed into shear flow was studied by several authors mostly for fiber like objects, i.e., for aspect ratios above 10. Stover et al. investigated experimentally the orientation distribution in a semi-dilute non-Brownian fiber suspension (nL2d ≪ 1) of particle aspect ratios L/d = 17–30 in cylindrical Couette geometry and found a slight misalignment relative to the flow direction.8 Rahnama et al. calculated the effect of hydrodynamic interactions between non-Brownian fibers using slender body theory and found good agreement with Stover's results.9 Yamane et al. carried out numerical simulations to explore the semidilute regime (1/L3 < n < 1/L2d), where short range hydrodynamic interaction between the particles cannot be neglected.10 These simulations showed that entering the semidilute regime does not bring strong changes in the behaviour of the suspension. Sundararajakumar and Koch performed numerical calculations to study the effect of direct mechanical contacts in semi-concentrated suspensions (nL2d = O(1)) of non-Brownian fibers11 and found a slight misalingment for L/d = 30. We note, however, that the addition of Brownian noise results in a deviation of the time averaged orientation from the flow direction already for a single ellipsoid.12,13 Brownian suspensions or single component Brownian systems (thermotropic nematics) also show a slight misalingment in shear flow.1,3,4,12,13 In this case the orienting effect of the shear flow is competing with the Brownian noise. The dynamical behavior and rheological properties of such systems were investigated by Doi, Edwards, Marrucci, Dhont and others14–18 and it was shown that the rotational diffusion coefficient rapidly decreases with increasing concentration and elongation of the particles. This is due to a hindering effect which neighboring rods exert on the rotational motion of the particle. Shaqfeh and Fredrickson quantitatively analyzed how the surrounding particles screen the hydrodynamic disturbance induced by the particle in the large elongation limit.19,20 Despite the similar behaviour observed in the systems mentioned above, they often show distinct features, which depend on the forces (e.g., contact, hydrodynamic, viscous or inertial) that dominate the particle trajectories. An interesting comparison could be made with the flow of dry granular matter,21 where particles are also known to misalign with respect to the flow direction.
In the present work, we explore ensemble averaged alignment of non-Brownian elliptic particles of aspect ratio L/d = 3, while varying the volume fraction of the particles in a wide range. We focus on how particle–particle interactions perturb single particle dynamics. Our results will be compared to the angular distribution measured for dry granular materials,21 in which the particles’ motion is driven exclusively by contact forces owing to the absence of a fluid medium.
2 Background
The behaviour of particles in flowing suspensions is fully characterized by the trajectory and orientation of each particle. For certain idealistic cases there exist models based on first principles, which describe particle translation and possibly rotation as well. The Maxey–Riley equation,22 a more generic form of the Stokes equation, proved successful in describing particle translation in complex flows. It provides insight into the chaotic nature of finite sized particles both in simple time-periodic23 and turbulent flows.24 However the model has limitations; the Maxey–Riley equation was derived for spherical particles only, and is valid, when the particle is small compared to the fluid flow structures (i.e., the velocity difference across the particle is small). It provides a one way coupling to fluid flow, therefore, no wall-particle, or particle–particle hydrodynamic interaction is included. The model describes dilute systems; however, particle–particle interaction can be approximated by assuming simple rules for the coagulation and fragmentation of particle clusters.25 Also, particle rotation is absent in the Maxey–Riley model, although it would be very important for non-spherical particles.The first theoretical description of a rotating ellipsoidal particle in sheared fluid medium was developed by Jeffery.7 The calculation assumes no-slip boundary conditions and was made in the Stokes limit, where the inertial effects are negligible. His findings were confirmed experimentally,26 and the description was extended to more general shapes.27,28 According to Jeffery's formula, the particle undergoes a periodic rotation with modulated angular velocity that shows maxima, when the major axis is perpendicular to the streamlines, and minima when it is parallel with them. We note, that due to the time reversal symmetry in overdamped dynamics, the alignment angle, defined as the angle between the average orientation of the particle major axis and the streamlines, is zero for an orbital period. Therefore the misalignment found in various experiments cannot be attributed to viscous stresses.
There is no first principles theory that accounts for the inertial effect on particle orientation, although there are a number of fully resolved simulations that address the motion of ellipsoidal29,30 or elliptic particles31,32 in a Newtonian fluid. On the particle scale the ratio of inertial and viscous forces can be characterized by the particle Reynolds number Rep = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) d2η, where
d2η, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the macroscopic shear rate of the colloid suspension, d is the largest diameter of the particle (i.e., the major axis for an ellipse) and η is the kinematic viscosity. It was found that with increasing Rep the orbital period of a single isolated particle increases, while at a critical value Recrp of the particle rotation, there is a transition from time periodic rotation to a steady motion through a saddle-node bifurcation.29 The fluid flow pattern around the particle is also different for the two cases: while a rotating particle involves crossing streamlines outside the particle and the flow pattern is characterized by two stagnation points,33 in the steady, torque free case the streamlines are separated.34 In general, the torque-free orientation of the particle is not aligned with the streamlines, the orientation angle increases with Rep − Recrp.32 These works provide evidence that inertial forces can cause nonzero averaged orientation angle, which is observed experimentally as well.35
is the macroscopic shear rate of the colloid suspension, d is the largest diameter of the particle (i.e., the major axis for an ellipse) and η is the kinematic viscosity. It was found that with increasing Rep the orbital period of a single isolated particle increases, while at a critical value Recrp of the particle rotation, there is a transition from time periodic rotation to a steady motion through a saddle-node bifurcation.29 The fluid flow pattern around the particle is also different for the two cases: while a rotating particle involves crossing streamlines outside the particle and the flow pattern is characterized by two stagnation points,33 in the steady, torque free case the streamlines are separated.34 In general, the torque-free orientation of the particle is not aligned with the streamlines, the orientation angle increases with Rep − Recrp.32 These works provide evidence that inertial forces can cause nonzero averaged orientation angle, which is observed experimentally as well.35
The above discussion is valid for very dilute suspensions, in which the particle–particle interaction is negligible. In this work, we analyze how the hydrodynamic interaction and contact forces in suspensions modify this picture while varying the packing fraction. Herein, we investigate both the Rep < Recrp domain, termed here “low Rep regime”, and Recrp < Rep, termed the “inertial regime”. We control the average strength of the particle interaction by varying the particle volume fraction,† changing thus the average distance between the rigid particles. We explore a relatively wide range of volume fractions 0 < ϕ < 0.48, which is below the critical volume fraction reported by Cuesta et al. corresponding to the isotropic–nematic transition in a system of ellipses interacting with hard core interaction in the presence of thermal noise in the absence of shear. This critical volume fraction was found to be around 0.6 for 2D ellipses with aspect ratio L/d = 3.0.36
3 Simulation methods
3.1 Eulerian–Lagrangian approaches
Jeffery's approach, as mentioned in the previous section, is valid in the Stokes flow limit. Despite this limitation, it can be used, in principle, in Eulerian–Lagrangian models to simulate dilute suspensions of ellipsoids in complex flows,37 that realizes one-way coupling (particle trajectories do not affect fluid flow). It was shown that two-way (mutual interaction between fluid and particle), or even four way coupling (that also accounts for particle–particle and particle wall interactions)38 is needed to model semi-dilute suspensions, at ≈1% volume fraction. Recently, four-way coupling simulations were extended to non-spherical particles,39 however, some features were modeled on phenomenological basis, including the rotation of the ellipsoids, whereas the torque acting on the fluid near the particle was neglected.It is characteristic to all Stokesian or Maxey–Riley-type models22 that the characteristic length scale of fluid flow must be larger than the particle size. Therefore, the model is not applicable for high density suspensions, where complex flow patterns evolve due to the hydrodynamic interaction of particles. In such cases, a more detailed Eulerian–Eulerian approach is needed, which resolves fluid flow on the particle scale.
3.2 Fully resolved simulations
Recent advancements of fully resolved techniques provide various options to account for hydrodynamic interaction among immersed particles, including the Lattice–Boltzmann Method,40 the immersed boundary method,41 the “fluid particle” method42 and Patankar's fictitious–domain method.43 These techniques allow solving the fluid flow equations while applying a deformation-free velocity field inside a particle volume (rigid body). Herein, we adopt the fictitious-domain method to perform fully resolved simulations in modelling particulate flows. This formulation has option to avoid the explicit computation of the distributed Lagrangian multipliers that enforce rigidity constraint over the particle; a two step operator splitting can be employed to compute translational and angular velocities for each particle. Contact forces arising from particle–particle interaction are modelled using the diffuse interface field approach (DIFA),44 that allows computing forces and torques acting on arbitrary shaped particles. We note here, that without any explicit particle–particle or particle-wall collision models using sufficiently high numerical resolution the particle overlap is negligible up to approx. 10% volume fraction.The equations governing fluid flow incorporate the Navier–Stokes eqn (1) along with the incompressibilty constraint (2), both of which were solved in the whole computational domain, and the rigidity constraint (3) that was applied in the volume of the particles (Γp):
 | (1) |
| 0 = −∇·v, | (2) |
 | (3) |
In the model the i-th particle is represented by a continuum field (ϕi), that is constructed to give zero outside the particle and one inside. The boundary of the particle is represented by a diffuse interface, with a thickness larger than the actual grid spacing, typically 3–4 grid spacing in thickness. Following Wang's DIFA method44 we apply a steric repulsion force density (4). This results in a force and torque on the particles; for the i-th particle these are given by eqn (5) and (6) respectively.
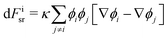 | (4) |
 | (5) |
 | (6) |
Contact forces generated by the above formulae affect both particle trajectories, and the fluid's velocity field thus representing two-way particle–fluid coupling.
3.3 Numerics and implementation
Spatiotemporal discretization of the equations of motion was done by combining the finite volume method with an explicit finite difference time stepping. Coupling between the equations was implemented using a simple variant of Chorin's projection method,45 whereas Goda's incremental pressure correction method46 was chosen to solve the governing set of equations. Using these schemes, the discretization of the Navier–Stokes eqn (1) leads to a trivial set of linear systems. Substituting the latter into the continuity eqn (2), one obtains a matrix equation. In solving the respective linear system, a multigrid (MG) scheme was used, which was, however, adjusted to fit better to modern computer architectures. | ||
| Fig. 1 Schematic view of the setup, with the definition of the orientation angle θ and rotation angular velocity ω. According to our conventions typically 〈ω〉 ≤ 0. | ||
To model the behaviour of elongated particles in 2D in a uniform shear flow, we set fixed velocity boundary conditions on the top and bottom boundaries, while at the left and right boundaries periodic boundary condition was prescribed (Fig. 1). The dimensions of the computational domain were 2160 grid points in transverse and 3840 grid points in flow direction. The particles immersed in the fluid were neutrally buoyant, had an elliptical shape with major and minor axis of 30 and 10 grid points, respectively; i.e., their aspect ratio was L/d = 3.0. We examined their behaviour at two Reynolds numbers Re = 103 and Re = 104, which correspond to particle Reynolds numbers of Rep = 0.772 and Rep = 7.72, respectively. We expect different behaviors in these two regimes: at the smaller shear rate (in the low Rep regime) a single particle rotates similarly to the Jeffery orbits, though with small deviations due to the nonzero shear rate. The larger shear rate falls above Recrp, the system is in the inertial regime, in which isolated particles moves with a constant orientation angle that varies with Rep.
4 Results
Fig. 2 displays snapshots of two simulations performed with different particle densities (ϕ = 0.1125 and 0.3937). Visual inspection indicates that the orientation distribution of the particles is not uniform. The rotation velocity is indicated by colors and the insets show the distribution of the rotation velocity. We quantify these observations in the following sections.4.1 Particle orientation
First, we discuss the alignment of the particles relative to the streamlines. In Fig. 3(a), we present the orientation distribution functions (ODF) for a broad range of volume fractions in the low Reynolds number regime (Rep = 0.772). We find that with increasing volume fraction (i) the distribution is widening, and (ii) the mode of the distribution is shifting, as well as its average, 〈ϕ〉, to larger angles [see also Fig. 3(c)]. Inspecting the nematic order parameter (S) as a function of the volume fraction ϕ, we find a monotonically increasing trend [Fig. 3(d)]. This contradicts the widening of the main peak observed with increasing ϕ [Fig. 3(a)], as widening of the main peak alone would yield an opposite tendency, namely a decreasing order parameter with ϕ. However, there is another stronger effect which is the suppression of flipping events due to particle–particle interactions reflected by a decreased height of the distribution tails at larger ϕ [see inset of Fig. 3(a)].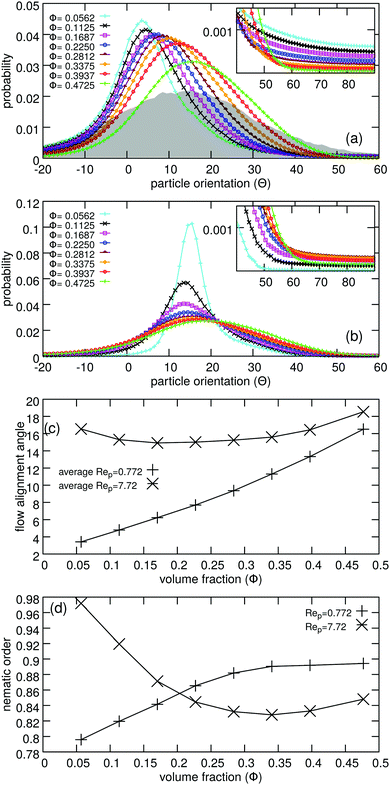 | ||
| Fig. 3 Alignment of suspended particles in shear flow. (a) and (b) Probability density of the particle orientation for various volume fractions ϕ in the investigated regimes: (a) low Reynolds number at Rep = 0.772 and (b) inertial at Rep = 7.72. Panel (c) shows the average orientation angle for both shear rates as a function of volume fraction. For comparison, in panels (a) and (b), experimental results21 for dry rice particles (of aspect ratio 3.4) are also shown (gray shaded areas). (d) Nematic order parameter as a function of the packing fraction. | ||
Since the macroscopic fluid flow conditions (i.e., the global shear rate and fluid viscosity) do not change, the variations in the angular distribution can be attributed exclusively to hydrodynamic and contact forces amongst the particles. Even in the dilute case (5.6% volume fraction) doublets and clusters form, and these inter-particle interactions cannot be neglected. The same conclusion was drawn for the Stokesian limit in a previous work.47 We note, however, that the effect of ordering on the angular distribution differs considerably at low Rp and in the overdamped limit of the Stokesian regime: in the latter case the peak of the angular distribution becomes narrower with increasing volume fraction.47 In turn, the shift in the peak position seems to be generic for both for nonzero Reynolds numbers and in the Stokesian regime. Our data is based on high parfticle number simulations, thus the distributions are smooth even for the lowest volume fraction case. We also note that, as shown in Fig. 3(a), the ODF does not just flatten with increasing volume fraction, but it's skewness is positive and increases.
In the inertial regime (Rep = 7.72 > Recrp), where an isolated particle would attain a steady orientation, the change of the ODF with volume fraction is more pronounced, see Fig. 3(b). This is not surprising since a standalone particle would yield a delta function ODF, while hydrodynamic interaction can either cause swaying or rotating motion of the particles, which result in a stronger widening of the ODFs, when increasing the volume fraction. This results in a strong decrease of the nematic order parameter (S) as a function of ϕ up to volume fractions of about 0.25 [Fig. 3(d)]. For larger volume fractions S increases slightly due to the suppression of flipping events by particle–particle interactions. The probability of finding flipping particles is also non-monotonic with ϕ [see inset of Fig. 3(b)]. At low ϕ it is increasing due to the disturbance of the steady orientation, while it is decreasing in dense systems due to the hindering effect of near neighbours. Interestingly, the change of the mean alignment angle is non-monotonic, at low volume fractions both the mean and the mode of the distribution is shifting towards lower angles, while above ϕ = 0.15 the mean alignment angle is increasing [see Fig. 3(c)].‡ Similarly to the low Rep regime the orientation distributions are strongly skewed: the orientation distributions show more pronounced right tails in all cases. For the sake of comparison, in Fig. 3 we also present data for quasistatic shear flows of dry granular particles taken from experiments21 with rice grains of aspect ratio 3.4. This dataset can be regarded as the high volume fraction limit (with ϕ = 0.59 in 3D), where contact forces drive the evolution of the orientation distribution. At high volume fractions, our simulations predict higher average alignment angles then observed in the experiments. The difference can be mostly attributed to the skewness of the computed distributions, which may stem from the reduced degrees of freedom of the particles in 2D.
4.2 Particle angular velocity and particle correlations in the low Reynolds number regime
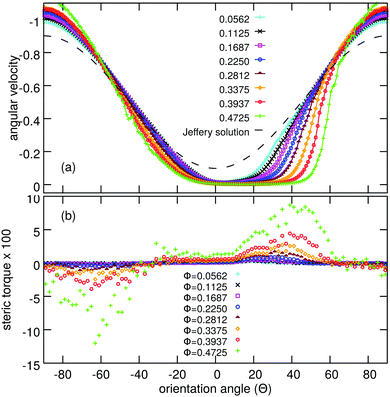
To understand the specific features of the ODF and the microscopic mechanisms behind them, we now focus on the dynamics. Fig. 4(a) shows the average angular velocity of the particles as a function of their orientation in the low Rep regime. We note here, that due to particle conservation, the angular velocity is inversely proportional to the ODF. The respective curves are periodic, as in the case of Jeffery's solution, although there are notable differences. At nonzero Reynolds number the minima of the angular velocity are lower, leading to longer orbital periods32 and sharper ODFs. Even at low volume fractions, there is a notable interaction amongst the particles that causes deviation from Jeffery's solution. We note here that for single particle simulations convergence to Jeffery's formula was observed with decreasing Reynolds number.To assess the role of the particle interactions, we varied the volume fraction from 5.6% to 47.3%. It was found that below about −60° the angular velocity varies non-monotonically with volume fraction, whereas for θ > −60° the angular velocity decreases with increasing volume fraction. This decrease is particularly prominent for 20° < θ < 70°, while the curves become flat close to zero. This behavior is reflected in the enhanced skewness of the respective ODFs [Fig. 3(a)].
In order to identify the origin of this behavior, we quantify the effect of collisions with nearby particles via computing a spatial correlation function (SCF), which is defined as the average volume fraction of nearby particles (∑ϕi) as a function of the position relative to the centre of a reference particle, whose orientation falls in the neighbourhood of a given angle θ (i.e., between θ − 1° and θ + 1°). Besides providing a visual representation of the average local structure around the particles, the SCF allows the computation of the average net torque acting on the particle at a given angle due to particle collisions.
As can be seen in Fig. 4(b), the average torque is large between 20° ≲ θ ≲ 70°, especially for high volume fractions. It can be, therefore, concluded that the particle interactions significantly block the rotation due to shear flow and reduce the average angular velocity of the particle at these angles. One may also conclude that the pronounced tail on the right side of the ODF originates from the particle collisions in this orientation regime. In contrast, for θ ≲ −20° the torque attributed to particle collisions is negative, which enhances the rotation of the particles. As a result, the angular velocity curves intersect each other at negative angles.
Visual analysis of the SDF's (Fig. 5) reveals, that the torque characteristic to a given angle originates from the local arrangement of the particles. For particles, whose orientation falls close to the average orientation, the rotation is hindered/blocked by neighbors represented by well defined peaks in the SDF.
4.3 Particle angular velocity and correlations in the inertial regime
We computed the same quantities in the inertial regime as well. In Fig. 6, we show the average angular velocity (normalized by the shear rate) as a function of the orientation. Dilute cases behave differently when compared to the low Reynolds number regime.Adding more particles (increasing the particle volume fraction) leads to larger angular velocities outside the 0° ≲ θ ≲ 70° range. The abrupt change in the angular velocity indicates a complex particle–particle interaction: at higher concentrations nearby particles pass by each other at smaller distances, which causes disturbances that may lead to eventual overturn (flipping) of some of the particles. The presence of stable orientation of particles is visible even at the highest volume fractions we used: the angular velocity is very small in the angular range 0° ≲ θ ≲ 50°.
Since single particle hydrodynamic effects are significant at these Reynolds numbers, the pair correlation function, and consequently the particle hindrance is less relevant in this regime.
4.4 Spatial heterogeneities
Snapshots of the simulated suspensions (see Fig. 2) provide visual information on slight inhomogeneities in the density and particle orientation. A weak chain-like clustering with particles touching each other in the direction of the smaller axis can also be recognized. This feature is consistent with the structure of the spatial pair correlation function (Fig. 5) that shows higher densities parallel to the reference particle. This phenomenon appears to be more pronounced for particles oriented about 40 degrees [see Fig. 5(d)], where even the third neighbor positions are visible. The spatial structure of the distribution indicates that the chains are sheared. Various definitions of clusters are possible, however, due to the dynamic behavior of the heterogeneities under shearing (formation, deformation, and dissolution), characterization of the clusters needs a complex approach, therefore, a detailed analysis of these phenomena is relegated to another paper.5 Summary
We performed simulations for a large number of ellipses immersed in a sheared 2D fluid to investigate the effects of nonzero particle volume fraction. Similarly to the case of a single particle, we found two regimes of different behavior: the low Reynolds number regime, and the inertial regime at moderate Reynolds numbers.We have shown that in the low Reynolds number regime, the motion of the particles resembles the predictions of the analytically solvable reference case by Jeffery, however, with the following essential differences:
(i) At nonzero Reynolds numbers, due to strong inertial effects in the surrounding fluid flow, the rotation of an isolated particle is the slowest when it is somewhat misaligned relative to the streamlines. A narrower ODF is observed, which is no longer symmetric around zero angle.
(ii) The other type of deviation is due to the particle–particle interaction. As the volume fraction of the particles increases, it becomes progressively prevalent that a nearby particle hinders the rotation of a given reference particle, especially when it is oriented at a small positive angle from the streamlines. This is clearly visible in the pair correlation plots, and is well captured by the average steric torque computed from spatial correlation functions. The particle–particle interaction leads to an asymmetric pronounced tail of the ODF, and further reduced angular velocities for the respective angles.
We note that in the inertial regime, an isolated particle attains a constant, stable orientation instead of rotating with an angular velocity depending on the momentary orientation. In this regime, the particles are slightly tilted from the streamlines by an angle that depends on the Reynolds number. When the volume fraction of the particles is increased to a level that is still so low that the particles pass by each other at a distance, the disturbance due to the hydrodynamic interaction makes them sway back and forth. This results in a broadened ODF; however, the average angular velocity stays zero. Increasing further the volume fraction, the disturbances reach a point, where some of the particles start to flip over. This results in a dramatic broadening of the ODF, and a sharp increase in the angular velocity contrasting the originally stable alignment relative to the streamlines.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Agency for Research, Development, and Innovation, Hungary (NKFIH) under Contract No. K-115959, K-116036 and KKP-126749.References
- K. M. O. Håkansson, A. B. Fall, F. Lundell, S. Yu, C. Krywka, S. V. Roth, G. Santoro, M. Kvick, L. Prahl Wittberg, L. Wågberg and L. D. Söderberg, Nat. Commun., 2014, 5, 4018 CrossRef.
- T. Papathanasiou and D. Guell, Flow Induced Alignment in Composite Materials, Taylor & Francis, 1997 Search PubMed.
- T. Sugiyama, D. Miyashiro, D. Takao, H. Iwamoto, Y. Sugimoto, K. Wakabayashi and S. Kamimura, Biophys. J., 2009, 97, 3132–3138 CrossRef CAS.
- D. Forster, Phys. Rev. Lett., 1974, 32, 1161–1164 CrossRef CAS.
- M. Trebbin, D. Steinhauser, J. Perlich, A. Buffet, S. V. Roth, W. Zimmermann, J. Thiele and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6706–6711 CrossRef CAS.
- A. Franceschini, E. Filippidi, E. Guazzelli and D. J. Pine, Phys. Rev. Lett., 2011, 107, 250603 CrossRef.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- C. A. Stover, D. L. Koch and C. Cohen, J. Fluid Mech., 1992, 238, 277–296 CrossRef CAS.
- M. Rahnama, D. Koch and E. Shaqfeh, Phys. Fluids, 1995, 7, 487 CrossRef CAS.
- Y. Yamane, Y. Kaneda and M. Dio, J. Non-Newtonian Fluid Mech., 1994, 54, 405–421 CrossRef CAS.
- R. Sundararajakumar and D. Koch, J. Non-Newtonian Fluid Mech., 1997, 73, 205–239 CrossRef CAS.
- J. K. G. Dhont and W. J. Briels, in Soft Matter, Sections 3.1–3.9, Complex Colloidal Suspensions, ed. G. Gompper and M. Schick, Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim, Germany, 2005, vol. 2 Search PubMed.
- E. J. Hinch and L. G. Leal, J. Fluid Mech., 1972, 52, 683–712 CrossRef.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 918–932 RSC.
- M. Doi, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 229–243 CrossRef CAS.
- G. Marrucci and N. Grizzuti, J. Non-Newtonian Fluid Mech., 1984, 14, 103–119 CrossRef CAS.
- G. Marrucci and P. L. Maffettone, Macromolecules, 1989, 22, 4076–4082 CrossRef CAS.
- J. K. G. Dhont and W. J. Briels, Rod-Like Brownian Particles in Shear Flow: Sections 3.1 - 3.9, John Wiley & Sons, Ltd, 2007, ch. 3a, pp. 147–216 Search PubMed.
- G. H. Fredrickson and E. S. G. Shaqfeh, Phys. Fluids A, 1989, 1, 3–20 CrossRef CAS.
- E. S. G. Shaqfeh and G. H. Fredrickson, Phys. Fluids A, 1990, 2, 7–24 CrossRef CAS.
- T. Börzsönyi, B. Szabó, S. Wegner, K. Harth, J. Török, E. Somfai, T. Bien and R. Stannarius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 051304 CrossRef.
- M. R. Maxey and J. J. Riley, Phys. Fluids, 1983, 26, 883–889 CrossRef.
- J. H. E. Cartwright, U. Feudel, G. Károlyi, A. de Moura, O. Piro and T. Tél, Dynamics of Finite-Size Particles in Chaotic Fluid Flows, in Nonlinear Dynamics and Chaos: Advances and Perspectives, ed. M. Thiel, J. Kurths, C. M. Romano, G. Károlyi and A. Moura, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 51–87 Search PubMed.
- J. Bec, L. Biferale, G. Boffetta, A. Celani, M. Cencini, A. Lanotte, S. Musacchio and F. Toschi, J. Fluid Mech., 2006, 550, 349–358 CrossRef.
- J. C. Zahnow, R. D. Vilela, U. Feudel and T. Tél, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 026311 CrossRef.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1923, 103, 58–61 Search PubMed.
- F. P. Bretherton, J. Fluid Mech., 1962, 14, 284–304 CrossRef.
- M. Junk and R. Illner, J. Math. Fluid Mech., 2007, 9, 455 CrossRef.
- E.-J. Ding and C. K. Aidun, J. Fluid Mech., 2000, 423, 317–344 CrossRef CAS.
- Z. Yu, N. Phan-Thien and R. I. Tanner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026310 CrossRef.
- J. Zhang, X. Xu and T. Qian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 033016 CrossRef.
- S.-L. Huang, S.-D. Chen, T.-W. Pan, C.-C. Chang and C.-C. Chu, Phys. Fluids, 2015, 27, 083303 CrossRef.
- J. Cao, Engineering, Experimental Study of Migration of Shape-specific Particles and Its Applications in Fluidic Self-assembly, Purdue University, 2008 Search PubMed.
- D. R. Mikulencak and J. F. Morris, J. Fluid Mech., 2004, 520, 215–242 CrossRef.
- C. M. Zettner and M. Yoda, J. Fluid Mech., 2001, 442, 241–266 CrossRef.
- J. A. Cuesta, C. F. Tejero and M. Baus, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6498–6506 CrossRef.
- P. Mortensen, H. Andersson, J. Gillissen and B. Boersma, Int. J. Multiphase Flow, 2008, 34, 678–683 CrossRef CAS.
- B. Vreman, B. J. Geurts, N. Deen, J. Kuipers and J. Kuerten, Flow, Turbul. Combust., 2009, 82, 47–71 CrossRef.
- B. van Wachem, M. Zastawny, F. Zhao and G. Mallouppas, Int. J. Multiphase Flow, 2015, 68, 80–92 CrossRef CAS.
- A. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS.
- Z. Zhang and A. Prosperetti, J. Comput. Phys., 2005, 210, 292–324 CrossRef.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS.
- S. V. Apte, M. Martin and N. A. Patankar, J. Comput. Phys., 2009, 228, 2712–2738 CrossRef CAS.
- Y. U. Wang, Acta Mater., 2007, 55, 3835–3844 CrossRef CAS.
- A. J. Chorin, Math. Comput., 1968, 22, 745–762 CrossRef.
- K. Goda, J. Comput. Phys., 1979, 30, 76–93 CrossRef.
- C. Pozrikidis, Eur. J. Mech. B Fluids, 2005, 24, 125–136 CrossRef.
Footnotes |
| † We use the widely accepted term “volume fraction,” even though in our 2D simulation “area fraction” would be more precise. |
| ‡ A continuous transition is expected between the monotonic/non-monotonic behaviors observed at low and high Reynolds numbers. Further work is, however, needed to clarify whether this transition happens at the same critical Reynolds number as in the single particle case. |
| This journal is © The Royal Society of Chemistry 2020 |