Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crossover from mean-field compression to collective phenomena in low-density foam-formed fiber material
Tero
Mäkinen
 *a,
Juha
Koivisto
*a,
Juha
Koivisto
 a,
Elina
Pääkkönen
b,
Jukka A.
Ketoja
a,
Elina
Pääkkönen
b,
Jukka A.
Ketoja
 b and
Mikko J.
Alava
ac
b and
Mikko J.
Alava
ac
aDepartment of Applied Physics, Aalto University, P.O. Box 11100, 00076 Aalto, Espoo, Finland. E-mail: tero.j.makinen@aalto.fi
bVTT Technical Research Centre of Finland Ltd, Solutions for Natural Resources and Environment, P.O. Box 1000, FI-02044 VTT, Espoo, Finland
cNOMATEN Centre of Excellence, National Centre for Nuclear Research, A. Śoltana 7, 05-400 Otwock-S’wierk, Poland
First published on 29th June 2020
Abstract
We study the compression of low-weight foam-formed materials made out of wood fibers. Initially the stress–strain behavior follows mean-field like response, related to the buckling of fiber segments as dictated by the random three-dimensional geometry. Our Acoustic Emission (AE) measurements correlate with the predicted number of segment bucklings for increasing strain. However, the experiments reveal a transition to collective phenomena as the strain increases sufficiently. This is also seen in the gradual failure of the theory to account for the stress–strain curves. The collective avalanches exhibit scale-free features both as regards the AE energy distribution and the AE waiting time distributions with both exponents having values close to 2. In cyclic compression tests, significant increases in the accumulated acoustic energy are found only when the compression exceeds the displacement of the previous cycle, which further confirms other sources of acoustic events than fiber bending.
1 Introduction
Soft, bio-based materials offer a wide range of material combinations and likewise a wide range of methods for synthesizing such. Networks based on fibers with high aspect ratio form as such a class of interesting examples. In particular, one interesting route is using aqueous foams to set up the fiber network geometry,1–5 whereby the air bubbles of the carrier foam determine to a large degree the porous structure of the “fiber foam” after drying.6The mechanics of random fiber networks depend first and foremost on the network density, or likewise on the number of contacts per fiber.7 Beyond that, the mechanical properties of the individual fibers and their variation play an important role,8 as does often the nature of the fiber-to-fiber bonds,9 in particular the character of the stress transfer and the bond failure mechanism. In what follows we study (see Fig. 1) the compression deformation of low-weight foam-formed wood fiber structures, in the density of 60 kg m−3. These structures have a random structure typically, and a low number of contacts per fiber. Using geometric arguments,7,8 the average contact number would be 5–7 for homogeneous fiber distribution. However, the true number of inter-fiber bonds is probably somewhat higher because of voids and large pores left in samples after foam forming.
Earlier simulations10 have shown the build up of significant axial stress in non-bonded fiber networks at high compaction levels. The axial stress should develop more rapidly in well-bonded networks with high fiber bending stiffness. Besides normal bending11 and bond opening, possible local stress release mechanisms in this case are also the sudden buckling of the whole fiber segment or a localized buckling failure e.g. in the heterogeneous fiber wall of a hollow wood fiber. The latter could take place also in the case of fiber bending, where axial stress outside the neutral plane can be high. Ketoja et al.8 postulated that the mean stress–strain behavior during compression could be related to buckling failures of fiber segments. Effectively fiber segments that undergo a buckling failure would act as “stress sensors” that relate mean geometrical changes of the network with the applied stress. The postulate allows to solve for the stress–strain response using simple mean-field arguments to account for the gradually increasing fraction of fiber segments that have buckled.
In this work, we study what happens beyond the validity of such theory, at large compressional strains, while also providing further evidence for the mean-field argument at small strains. A large literature has grown recently around the presence of complex, collective phenomena in deformation under compression.12–26 The main idea is the presence of “labquakes” or bursts of deformation analogous in many ways to earthquakes. Stress–strain curves and concomitant Acoustic Emission (AE) and digital image correlation analyses allow to characterize the burstiness and classify materials according to the statistics observed. The purpose of our work is to both explore the avalanches during the deformation of the foam-formed fiber structures and to relate the changes in stress–strain curves from mean-field-like behavior to the AE activity.
The next section discusses the experimental details, and then we in section Results show for two kinds of foam-formed fiber structures what kind of stress–strain behavior is found and what kind of AE statistics are obtained. Finally, we present conclusions and ideas for further study.
2 Experimental
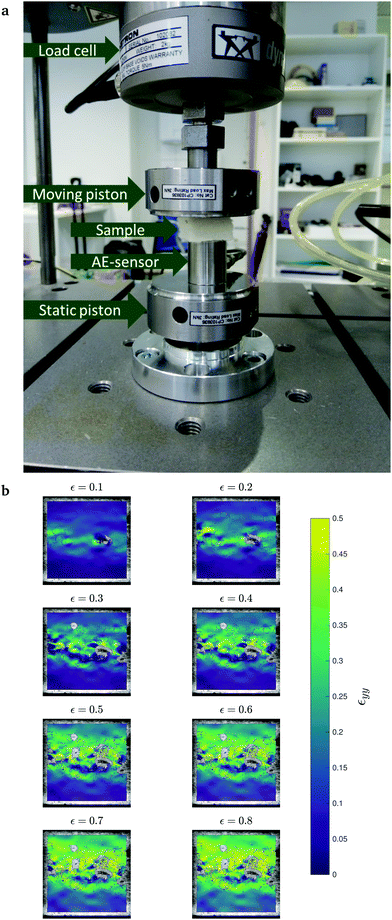
The experimental setup is depicted in Fig. 1a where the foam-formed block of 19 × 20 × 20 mm3 is compressed between a compression piston and an AE sensor ensuring a good acoustic coupling. To obtain uniform compression a thin plastic plate wider than the sample was placed between the sample and the AE sensor. The AE sensor is a wideband sensor F30α connected to a preamplifier by Physical Acoustics Corporation. The steel and ceramic casing of the sensors is rigid within measurements accuracy under the small loads during the compression. The amplified signal is then digitized by National Instruments 6040E digital acquisition card with f = 100 kHz sample rate. The compressive piston is connected to a load cell with nominal maximum load of 250 N with 1% repeatability. The cell is connected to the Instron E1000 tensile testing machine that digitizes the load displacement data in compliance with the ASTM standards.Additionally one face of the sample was imaged for Digital Image Correlation analysis. The Fig. 1b shows some typical compressive strain maps obtained using this method. The plotted εyy is the yy-component (where y is the compression direction) of the Green–Lagrange strain tensor obtained with the ncorr27 software. The displacement calculations were done using circular regions of interest with radius of 25 pixels and grid spacing of 1 pixel which correspond to 0.75 mm and 0.03 mm. The component of the strain tensor considered is then calculated from the displacements u = (u,v) as
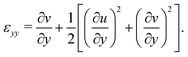 | (1) |
2.1 Sample preparation
Two types of fiber materials were used to prepare the foam-formed samples: unrefined bleached softwood kraft pulp (BSKP) and bleached spruce chemi-thermomechanical pulp (CTMP) (see Fig. 2). BSKP was obtained from a Finnish pulp mill (Metsä Fibre Oy, Äänekoski Bioproduct Mill, Finland) with the Schopper–Riegler (SR) freeness value of 13, and CTMP was gained from a Swedish pulp mill (Rottneros AB, Rottneros Mill, Sweden) with the Canadian Standard Freeness value of 650. Both freeness values describe dewaterability of pulp and indirectly indicate fiber flexibility and fines content. The average (length-weighted) fiber length was 1.98 ± 0.02 mm for BSKP and 1.86 ± 0.03 mm for CTMP. The mean fiber widths were 28.3 ± 0.1 μm (BSKP) and 38.2 ± 0.2 μm (CTMP). However, the CTMP pulp included a much higher proportion of submicron fine particles than the BSKP pulp.In sample preparation, a nonionic surfactant polyethylene sorbitan monolaurate (TWEEN 20, Sigma-Aldrich, St. Louis, MO, USA) with the dosage of 6.5 g l−1 was used as foaming agent. The high surfactant concentration, exceeding the critical micelle concentration of 0.074 g l−1,28 was necessary to achieve the target air content of wet foam. The wet fiber foams were generated by mixing the pulp, surfactant and water in a vessel with a starting volume of 3.08 liters, with a mixer (Netzsch, Hedensted, Denmark). A rotational speed of 3800 rpm was used to make the foam at the air content of 58%. After foaming, the wet foam was poured into a hand-sheet mold along a tilted plate and was left to drain for about 20 min by gravity. The sheets were dried over night at 70 °C in an oven. The final targeted thickness level was adjusted in a separate phase. The dried sheets were firstly re-wetted to a 50% moisture content and then pressed to the desired thickness (20 mm) and finally dried in an oven (70 °C). This resulted in porous random fiber networks with broad pore size distributions. Basis weights of the sheets were about 1200 g m−2. Density of the CTMP and BSKP sheets were 60.6 and 63.6 kg m−3, respectively. For the experiments, blocks of the size of 20 × 20 mm2 were cut from the sheets.
2.2 Acoustic emission
The observed acoustic emission signal A is divided into discrete events by thresholding it just above the noise level. The energy of each event is then calculated as the square integral of the amplitude over the event duration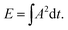 | (2) |
The event count n denotes the cumulative number of acoustic events and similarly the cumulative energy 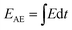 is the sum of the energies of the acoustic events. Similarly the event rate ṅ and the energy rate ĖAE at time t are calculated by counting the number of events per unit time or the sum of their energies per unit time in a 0.5 s window around the time t.
is the sum of the energies of the acoustic events. Similarly the event rate ṅ and the energy rate ĖAE at time t are calculated by counting the number of events per unit time or the sum of their energies per unit time in a 0.5 s window around the time t.
2.3 Compression testing
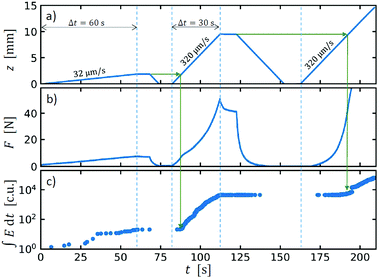
The compression protocol consists of three displacement controlled cycles illustrated in Fig. 3a. The first compression is a slow one with a displacement rate of ż = 32 μm s−1 lasting 60 seconds corresponding to a strain rate of![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 10% min−1 (strain rate being calculated just as the displacement rate divided by the initial sample height). The first loading protocol up to 10% strain is based on a standard for thermal insulation materials.29 The strain rate for the next loading phases is increased by the factor 10 in order to speed up the measurement. We observe the nearly linear increase in stress (which is proportional to the force F shown in Fig. 3b) and few individual acoustic emission events (Fig. 3c). After the loading has reached ε = 10% strain, the sample is unloaded with a faster rate ż = 320 μm s−1 (
= 10% min−1 (strain rate being calculated just as the displacement rate divided by the initial sample height). The first loading protocol up to 10% strain is based on a standard for thermal insulation materials.29 The strain rate for the next loading phases is increased by the factor 10 in order to speed up the measurement. We observe the nearly linear increase in stress (which is proportional to the force F shown in Fig. 3b) and few individual acoustic emission events (Fig. 3c). After the loading has reached ε = 10% strain, the sample is unloaded with a faster rate ż = 320 μm s−1 (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 100% min−1). This return to the starting position is done manually with a few second delay after the loading has ended.
= 100% min−1). This return to the starting position is done manually with a few second delay after the loading has ended.
The second compression cycle uses a faster displacement rate ż = 320 μm s−1. Here, we observe clearly a non-linear stress–strain behavior and significantly more acoustic events. It also looks like the behavior changes as the strain exceeds the strain of the previous cycle and we start to compress the “virgin strain” portion of the sample. The green arrows highlight the location with a bump in the stress and significant increase in acoustic activity. The loading lasts for 30 seconds and the sample reaches ε = 50% strain. Again, after a few seconds we manually start the unloading ramp with the same faster displacement rate.
The third cycle is similar to the second one, except we compress until the stress limit of the load cell is reached. Also here we observe a bump in the stress data and a significant increase in acoustic activity as we move to “virgin strain” region of the sample.
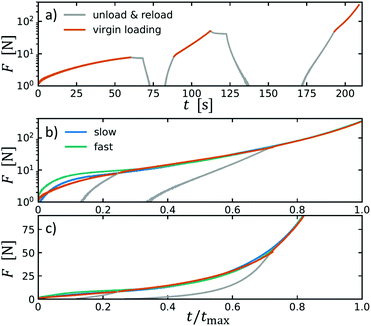
In the analysis that follows we have excluded all other parts except the virgin loading by stitching together the corresponding parts of the loading. This is done by attaching the end of one portion of virgin loading to the beginning of the next one as seen in Fig. 4. We can compare the resulting force curve to two reference experiments (which are not included in the further analysis) with continuous loading and different strain rates (slower one done with ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 10% min−1 and faster one with
= 10% min−1 and faster one with ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 100% min−1). This is done by normalizing the time-axis with the maximum time tmax (which for all experiments corresponds to the same stress). The force response is the same for both cases and we lose only a very tiny part of the acoustic emission data.
= 100% min−1). This is done by normalizing the time-axis with the maximum time tmax (which for all experiments corresponds to the same stress). The force response is the same for both cases and we lose only a very tiny part of the acoustic emission data.
3 Results
3.1 Stress–strain response
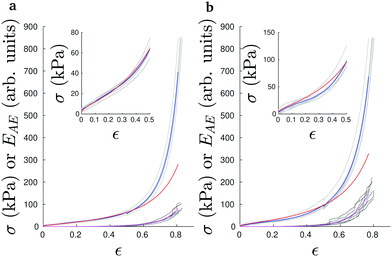
Fig. 5 shows the resulting averaged response for both sets of samples and zoomed-in views of the initial parts in the Insets. The curves are obtained from the cyclic experiments by joining together the parts of increasing compression. Ketoja et al.8 explained similar data for an extended set of trial points by making assumptions on the average order in which fiber segments (from a bond to subsequent bond) buckle during compression. The segment lengths a of the random network are exponentially distributed,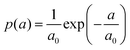 | (3) |
| [s(ε) + 1]exp[−s(ε)] = ε. | (4) |
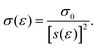 | (5) |
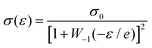 | (6) |
3.2 Acoustic emission and heterogeneous deformation
In cyclic compression tests, we observed a significant increase in the accumulated acoustic energy only when the compression exceeded the displacement of the previous cycle. Moreover, very few events were observed during the unloading of the sample between the cycles (see Fig. 3c). This suggests that acoustic events correspond to other failure mechanisms than fiber bending, which takes place also during unloading. The above mean-field theory based on fiber segment failures allows estimating the AE accumulation during compression. The proportion of buckled segments at strain ε is given by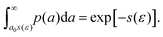 | (7) |
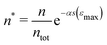 | (8) |
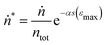 . The normalized measured values of n* and ṅ* agree with the theoretical predictions e−αs(ε) and
. The normalized measured values of n* and ṅ* agree with the theoretical predictions e−αs(ε) and 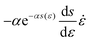 , respectively, up to the strain level at which deviation between the measured and predicted stress–strain behavior was seen in Fig. 5.
, respectively, up to the strain level at which deviation between the measured and predicted stress–strain behavior was seen in Fig. 5.
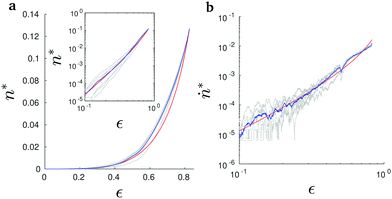 | ||
Fig. 6 (a) Cumulative event counts (grey), their average (blue) and the theoretical prediction e−αs(ε) (red) for varied strain ε. Here the measured values n have been normalized to 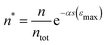 according to eqn (8). The inset shows the same plot with logarithmic axes. (b) Event rates (grey) with the same normalization according to eqn (8). The inset shows the same plot with logarithmic axes. (b) Event rates (grey) with the same normalization 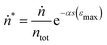 , their average (blue) and the theoretical prediction (red). , their average (blue) and the theoretical prediction (red). | ||
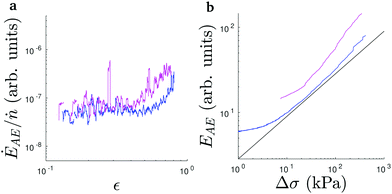
Moreover, the accumulated AE energy followed quite closely the total number of events for strains in the range of 10–50% (see Fig. 7a). In other words, the mean released acoustic energy per event was fairly constant in this region. For small strains below 10% this correspondence was lost but in this region there are only rather few events and the deformation is far from homogeneous as shown by Fig. 1b.
Beyond ε = 0.5, the energy integral increases rapidly (see Fig. 5). This coincides for both fiber structures with the deviations of the stress–strain curve from the mean-field like. Plotting the deviation
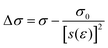 | (9) |
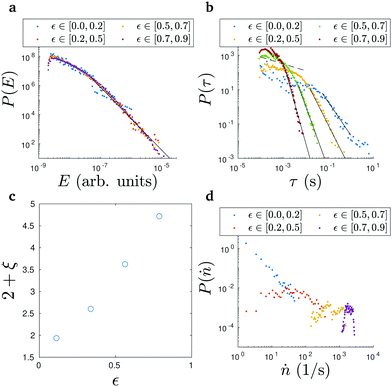
The statistics of the AE are quite different as regards the development with increasing strain. We therefore have divided the experiments into four strain bins (see Fig. 8) and consider the statistics of the events occurring in each strain bin separately. For the event energies we find in general P(E) ∼ E−2.1, which is larger than what is found in the compression avalanches of other materials (Fig. 8a). Xu et al.31 have pointed out the possible existence of two different universality classes with more homogeneous materials tested (e.g. Vycor, wood19) resulting in a value of about 1.4 whereas more disorder leads in some cases (charcoal) to about 1.7, both in other words values again lower than 2.1. Here the fit is done as an maximum likelihood estimate to the set of all event energies (as the exponent does not change between the strain bins) and on the part of the distribution where the black line in Fig. 8a is drawn.
The waiting time distribution evolves during the compression (Fig. 8b). As usual for AE waiting time statistics cut-off behavior is seen, so that at small strains the maximum times are larger and a power-law P(τ) ∼ τ−(2+ξ) with an exponent close to −2 is found for the tail (Fig. 8c shows the results of fitting to distributions binned to strain windows). Again the fit is done as a maximum likelihood estimate and on the part where the solid black lines in Fig. 8b are drawn. The strong dependence of the distribution makes us expect that this is connected to the variations of event rate.14 If the probability distribution of the rates is broad enough this will show up in the waiting time distribution due to the rescaling of the waiting times even without any inter-event correlations as such. Fig. 6b demonstrates indeed that there is a change in the evolution of the rate, which grows approximately as a power-law in strain. Another typical feature of waiting time statistics in compression is that with small τ a small portion of the distribution seems to follow P(τ) ∼ τ−(1−ν), here ν being close to 0.6 as seen from the dashed black line in Fig. 8b. This is related to Omori-type aftershock sequences with an event rate proportional to t−(1−ν) when time is measured from the mainshock,14 and indicates correlations in the waiting times at short times. The tail of the P(τ) is on the other hand linked to the rate distributions, Fig. 8d, which has the easy interpretation that the probability of a large waiting time is dominated by the periods in the time series when the event rate is small.
4 Conclusions
We have studied the compression of foam formed fiber-based low-weight structures. These materials deform in their own, particular way which can be to a quite large degree be described by mean-field arguments. This includes not only the stress–strain behavior but also the measured accumulated AE events during compression. We found an explicit mathematical coupling between these two properties.However, as one might expect, with increasing compression the deformation behavior changes. The main empirical observation is the hardening of the response as seen in the stress–strain curve, compared to the mean-field-picture. This change in behavior can be easily detected by AE observations. In a strain region around 50% the avalanche activity increases tremendously.
The AE bursts exhibit energy statistics that are not much dependent on the strain window of observation, thus on the main mode of deformation. Instead, the temporal, waiting time statistics show substantial changes. This is connected with the ramp-up of the AE event rate, and our results show that this is the fundamental reason behind the change in the waiting time statistics. We thus conclude that these materials differ from what has thus been observed in “non-soft” matter, including wood.
As the mean-field argument is very general, it will be interesting to seek for other similar systems where it could be applicable. In this context, a further topic is to investigate mechanisms by which the theory breaks because of possible collective or other complex phenomena, as seems to happen here at larger strains.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Eduard Vives for useful discussions. We acknowledge the financial support from the Academy of Finland through the Centers of Excellence program (Project No. 251748), and the postdoctoral grant 308235 (J. K). M. A. acknowledges support from the European Union Horizon 2020 research and innovation programme under grant agreement No. 857470 and from European Regional Development Fund via Foundation for Polish Science International Research Agenda PLUS programme grant No. MAB PLUS/2018/8. The work has been partly supported by the European Regional Development Fund (grant number A73089, A73092). We are also grateful for the support by the FinnCERES Materials Bioeconomy Ecosystem. We acknowledge the computational resources provided by the Aalto University School of Science “Science-IT” project.Notes and references
- B. Radvan and A. P. J. Gatward, Tappi J., 1972, 55, 748–751 CAS.
- J. Lehmonen, P. Jetsu, K. Kinnunen and T. Hjelt, Nord. Pulp Pap. Res. J., 2013, 28, 392–398 CAS.
- A. Madani, S. Zeinoddini, S. Varahmi, H. Turnbull, A. B. Phillion, J. A. Olson and D. M. Martinez, Cellulose, 2014, 21, 2023–2031 CrossRef CAS.
- M. Alimadadi and T. Uesaka, Cellulose, 2016, 23, 661–671 CrossRef CAS.
- S. Burke, M. Möbius, T. Hjelt and S. Hutzler, Cellulose, 2019, 26, 2529–2539 CrossRef.
- A. M. Al-Qararah, A. Ekman, T. Hjelt, J. A. Ketoja, H. Kiiskinen, A. Koponen and J. Timonen, Colloids Surf., A, 2015, 482, 544–553 CrossRef CAS.
- T. Komori and K. Makishima, Text. Res. J., 1977, 47, 13–17 CrossRef.
- J. A. Ketoja, S. Paunonen, P. Jetsu and E. Pääkkönen, Materials, 2019, 12, 384 CrossRef CAS PubMed.
- T. Sormunen, A. Ketola, A. Miettinen, J. Parkkonen and E. Retulainen, Sci. Rep., 2019, 9, 4258 CrossRef CAS PubMed.
- G. Subramanian and C. R. Picu, Phys. Rev. E, 2011, 83, 056120 CrossRef PubMed.
- M. Alimadadi, S. B. Lindström and A. Kulachenko, Soft Matter, 2018, 14, 8945–8955 RSC.
- M. J. Alava, P. K. V. V. Nukala and S. Zapperi, Adv. Phys., 2006, 55, 349 CrossRef.
- L. Girard, J. Weiss and D. Amitrano, Phys. Rev. Lett., 2012, 108, 225502 CrossRef PubMed.
- J. Baró, A. Corral, X. Illa, A. Planes, E. K. H. Salje, W. Schranz, D. Soto-Parra and E. Vives, Phys. Rev. Lett., 2013, 110, 088702 CrossRef PubMed.
- F. Kun, I. Varga, S. Lennartz-Sassinek and I. G. Main, Phys. Rev. Lett., 2014, 112, 065501 CrossRef PubMed.
- S. Lennartz-Sassinek, I. G. Main, M. Zaiser and C. C. Graham, Phys. Rev. E, 2014, 90, 052401 CrossRef CAS PubMed.
- G. Nataf, P. Castillo-Villa, J. Baró, X. Illa, E. Vives, A. Planes and E. K. H. Salje, Phys. Rev. E, 2014, 90, 022405 CrossRef PubMed.
- J. Weiss, L. Girard, F. Gimbert, D. Amitrano and D. Vandembroucq, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6231–6236 CrossRef CAS PubMed.
- T. Mäkinen, A. Miksic, M. Ovaska and M. J. Alava, Phys. Rev. Lett., 2015, 115, 055501 CrossRef PubMed.
- J. Vasseur, F. B. Wadsworth, Y. Lavallée, A. F. Bell, I. G. Main and D. B. Dingwell, Sci. Rep., 2015, 5, 13259 CrossRef CAS PubMed.
- J. Baró, P. Shyu, S. Pang, I. M. Jasiuk, E. Vives, E. K. H. Salje and A. Planes, Phys. Rev. E, 2016, 93, 053001 CrossRef PubMed.
- L. Viitanen, M. Ovaska, M. J. Alava and P. Karppinen, J. Stat. Mech.: Theory Exp., 2017, 053401 CrossRef.
- J. Baró, K. A. Dahmen, J. Davidsen, A. Planes, P. O. Castillo, G. F. Nataf, E. K. Salje and E. Vives, Phys. Rev. Lett., 2018, 120, 245501 CrossRef PubMed.
- F. Renard, J. Weiss, J. Mathiesen, Y. Ben-Zion, N. Kandula and B. Cordonnier, J. Geophys. Res., 2018, 123, JB014964 Search PubMed.
- C. Vu, D. Amitrano, O. Plé and J. Weiss, Phys. Rev. Lett., 2019, 122, 015502 CrossRef CAS PubMed.
- R. C. Picu and G. Subramanian, Phys. Rev. E, 2011, 84, 031904 CrossRef CAS PubMed.
- J. Blaber, B. Adair and A. Antoniou, Exp. Mech., 2015, 55, 1105–1122 CrossRef.
- A. Patist, S. S. Bhagwat, K. W. Penfield, P. Aikens and D. O. Shah, J. Surfactants Deterg., 2000, 3, 53–58 CrossRef CAS.
- Standard EN826:2013, Thermal insulating products for building applications – Determination of compression behaviour, 2013.
- T. Pöhler, J. A. Ketoja, T. Lappalainen, V.-M. Luukkainen, I. Nurminen, P. Lahtinen and K. Torvinen, Cellulose, 2020 DOI:10.1007/s10570-020-03263-x.
- Y. Xu, A. G. Borrego, A. Planes, X. Ding and E. Vives, Phys. Rev. E, 2019, 99, 033001 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |