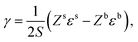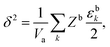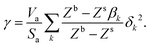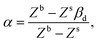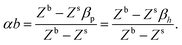DOI:
10.1039/D0SM00197J
(Paper)
Soft Matter, 2020,
16, 4299-4310
Systematic approach for wettability prediction using molecular dynamics simulations†
Received
3rd February 2020
, Accepted 13th April 2020
First published on 13th April 2020
Abstract
We present a fast and efficient approach to predict the wettability and spreading of liquids on polymeric substrates. First, a molecular dynamics parameterization is proposed for the calculation of the solubility parameter for 74 compounds including surfactants typically used in inkjet printing. Then, we introduce a molecular geometrical factor to relate the solubility parameter to the surface tension, obtaining estimates in remarkable agreement with experiments. By using a modified Young–Fowkes equation, the contact angles of liquids on various polymeric substrates are determined and their dependence on the hydrogen bonding, dispersion and polar contribution of the solubility parameter are investigated. We find that wetting properties are obtained with a good accuracy when taking into account the hydrogen-bonding and polar interactions in the geometric sum of the solubility parameter. Based on these findings, a 3D wetting space is proposed to evaluate liquids wettability and judge their suitability for specific substrates. This will enable easy formulation of liquids with wettability tailored for a particular surface and application.
1 Introduction
Wettability and spreading of liquid drops on solid substrates is a fundamental phenomenon in nature, important for diverse applications, including inkjet printing,1,2 oil recovery,3 agriculture4 and textiles.5,6 In inkjet printing for instance, the lack of liquid spreading may lead to print quality artefacts such as streakiness, while over-wetting may lead to bleeding and reduced sharpness.7–9 As a consequence, optimizing inkjet processes requires formulating ink mixtures that have a specific predefined range of wetting, which is a time-consuming and prohibitively expensive process. Therefore, a rapid and economical approach for the prediction of the wetting properties of liquids is necessary, especially when the screening of thousands of potential mixture components is required.
The wettability of a liquid droplet on a solid surface is determined by the molecular interactions of the materials involved. Strong attractions between the molecules of the liquid and the solid favors the spreading of the liquid on the surface. Conversely, weak attractions cause the liquid drop to bead off. Under static conditions, wettability is commonly described in terms of the contact angle θ (see Fig. 1) by Young's equation, which has been proved recently to be valid down to the nanometer scale,10,11
| | 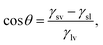 | (1) |
where
γsv,
γsl and
γlv are, respectively, the solid–vapor, solid–liquid, and liquid–vapor interfacial energies. Tuning the wettability requires the balance between these energies to be manipulated. However, difficulties in obtaining reproducible contact angles have been reported by many investigators, and both
γsv and
γsl cannot be measured reliably.
12,13 As a consequence, several semi-empirical approximations have been proposed to predict the contact angle and the surface energy of solids and liquids. These include the critical surface tension approach by Zisman and co-workers,
14,15 harmonic-mean approximation by Wu,
16,17 the acid–base approach by van Oss
18 and the geometric-mean approximation proposed by Girifalco and Good,
19 and by Fowkes.
20 Fowkes
20 and later, Owen and Wendt
21 suggested that the surface free energy of a material is the sum of different intermolecular interactions, namely polar, dispersive and hydrogen-bonding interactions. On the other hand, Neumann
22,23 proposed a model based on macroscopic thermodynamics that disregards the concept of surface free energy components. Neuman's approach remains controversial and several works are in favor of Fowkes and Owen–Wendt theories.
13,24–28 Other recent studies were directed toward the development of numerical frameworks for the computation of the surface energy.
29–32 Sgouros
et al.29 developed a simulation strategy for the prediction of the interfacial free energies and wetting properties of polyethylene–graphite interfaces. Aqra
et al.31 proposed a theoretical model based on classical statistical thermodynamics for calculating surface tension of liquid metals. Despite these efforts, there is still little consensus on the determination of interfacial energies, and the separate effect of the disperse, polar and hydrogen-bonding interactions on wettability is still not well understood.
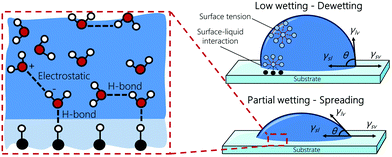 |
| | Fig. 1 Schematic of the wetting of a droplet on a substrate (right). High wetting is characterized by a low contact angle. Wetting is determined by the interactions at the atomistic scale (left). | |
One important thermodynamic property of a material is the Cohesive Energy Density (CED). This property, coined by Hildebrand and Scott as the “solubility parameter”,33 is equal to the amount of energy per unit volume required to separate a molecule from its surrounding environment, toward a distance where it approaches zero potential energy. Because it contains all the intermolecular energies holding the liquid together, it represents an important descriptor for liquid wettability. The solubility parameter has been correlated to a variety of properties such as the surface tension, refractive index and viscosity,30,34,35 and has been proven useful for several applications in areas ranging from material design to pharmaceutics and chemical processes.34,36–40 Yet, its experimental determination is still difficult, and the solubility parameter of a large number of liquids and miscible mixtures, commonly used in inkjet printing processes, are still unknown.
Typical modeling approaches for the determination of the solubility parameters of molecules are based on theoretical calculations via group contribution methods proposed by Van Krevelen,41 Hansen,42,43 Yamamoto (Y-MB)44,45 and Hoy,46 where all contributions of the functional groups (e.g. –CH3 and –OH) are summed up. These methods are semi-empirical, ignore the stereochemistry of the molecule, and often fails for large or complex molecules or when there are two or more strong functional groups in close proximity.47–49 Molecular Dynamics (MD) simulations is a promising more robust alternative to compute the molecule's solubility parameter. It has the advantage of making predictions as functions of pressure and temperature, and can deal with complex mixtures.50–52 MD has proven a convenient tool for the calculation of solubility parameters for pharmaceutical products,53 solvents,54 CO2-expanded mixtures,55 non-ionic surfactants,54 ionic liquids,56 and polymers,36,57–59 but its use for wettability-related applications has been largely unexplored.
In this paper, we propose a simple and fast approach to predict the wetting properties of liquids. By performing short molecular dynamics simulations, the Hansen solubility parameters42,43 of molecules are computed more accurately than in methods purely based on the atomic structures of the molecules. The solubility parameter of liquids, surfactants and polymers (74 compounds) obtained from MD are compared against experimental data, showing good agreement. An alternative form of the equation of Beerbower60 relating surface tension to the solubility parameter is proposed, by including details of the geometry of the molecule, resulting in a better fit to the experimental data. The expression for the contact angle by Owens and Wendt21 is extended to include all three Hansen solubility parameters, to improve its predictive value. Akin to the miscibility spheres of liquids in the Hansen's 3D space, the revised contact angle expression is represented by 3D wettability spheres that allows to evaluate the performance of liquids in terms of wetting properties on a given substrate.
2 Methods and approaches
2.1 Solubility parameter and Hansen 3D space
A molecule which “evaporates” escapes from the droplet to the vapour phase when its energy becomes high enough to overcome the cohesive energy of the surrounding molecules. This energy of vaporization can be obtained experimentally from the molar enthalpy of evaporation, which, if the vapor phase in equilibrium with the liquid behaves ideally, can be related to the cohesive energy density, whose square root is known as the solubility parameter,33,61| | 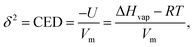 | (2) |
where U is the molar internal energy of the liquid phase, Hvap is the molar enthalpy of vaporization, R is the gas constant, Vm the molar volume of the liquid and T is the temperature. Crowley et al.62 and later Hansen42 proposed to split the solubility parameter δ into three components based on intermolecular interactions. The first component δd is related to the van der Waals dispersion interactions, the second component, δp, is related to the coulombic interactions (excluding hydrogen-bonding interactions), and the last one, δh, represents the hydrogen-bonding interactions. The total solubility parameter is the geometric sum of these components,| | 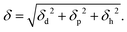 | (3) |
Following this scheme, Hansen42 developed what is now the most widely used three-dimensional interaction space, wherein all the solid and liquid substances are localized. The basic premise of Hansen's theory is that substances that are closer to each other in Hansen space generally have higher miscibility, see Fig. 2. For a solid substance to be soluble in a liquid, or two liquids to be miscible, it is necessary that their positions in the Hansen space are close, that is to say that their three solubility parameters are similar. Once a wide range of substances are placed in the Hansen space, it will become a useful tool for liquids formulation with less empirical front-end testing.
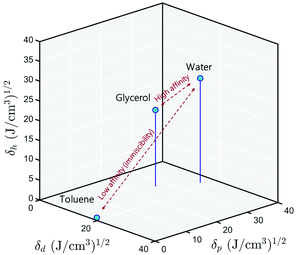 |
| | Fig. 2 3D representation of the Hansen solubility parameters. Water and glycerol are miscible because their positions are close in this space. Toluene, on the other hand, has a lower affinity for water because they are far from each other. | |
2.2 All-atom molecular dynamics
Molecular dynamics simulations were conducted using LAMMPS.63 The atomic charges of each molecule were obtained using the charge equilibration (Qeq) method of Rappé and Goddard,64 except for carbonyls (e.g., ethylene carbonate and acetic acid) where the Electrostatic Potential Fitting (ESP)54,63 was used since it produces better results for these molecules. The initial amorphous configurations were generated using a Monte-Carlo algorithm available in the Scienomics MAPS package.65,66 The energies of the amorphous configurations were minimized using the steepest descent method, followed by the conjugate gradient method with a maximum number of iterations equal to 1000. After generating the molecular simulation cell with periodic boundaries, DREIDING67,68 forcefield was applied to the molecules, where 12-6 Lennard-Jones and Coulomb electric potentials account for the van der Waals and electrostatic interactions, respectively, and a 12-10 Lennard-Jones potential accounts for the hydrogen-bonding interactions. This latter was included through a donor–acceptor distance-angle dependent definition.69,70 As the hydrogen-bonding term is short-ranged, it was truncated at a distance of 3.5 Å and smoothly shifted to zero at 4 Å, following the recommendations and settings of earlier MD and quantum-mechanical studies.71–74 We set the angle cutoff to 140° to limit the scope of the Lennard-Jones hydrogen-bonding potential, see Fig. 3. All oxygen and nitrogen atoms were considered to be potential hydrogen bond acceptors and donors. The hydrogen bond Lennard-Jones potential was parametrized with a zero-crossing distance Rhb = 2.75 Å and a hydrogen-bond energy Dhb = 4 kcal mol−1, with a cosine angle periodicity equaling 4 as suggested by Mayo et al.67
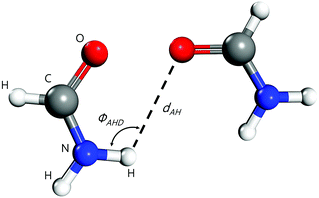 |
| | Fig. 3 Geometrical MD parameters for describing hydrogen-bonding between two formamide molecules: ϕAHD is the hydrogen bond angle. Here, nitrogen (in blue) is the donor atom and oxygen (in red) is the acceptor atom. | |
A cutoff distance of 10 Å smoothed at 11 Å was used for the 12-6 Lennard-Jones and Coulomb interactions. Long-range electrostatic interactions were handled by the Ewald summation,75 making the Coulomb cutoff distance effectively infinite. The total number of molecules in the simulation cell varies between 100 for the smallest molecules and 10 for the largest ones. All initial configurations were relaxed to adjust the coordinates of the atoms, where the experimental density of the different compounds was used to set the simulation box volume. Molecular dynamics simulations were launched in the canonical ensemble NVT for 200 ps, with a time step of 1 fs. The temperature was set at room temperature T = 298.15 K and controlled by a Nose–Hoover thermostat. For polymeric substrates, we followed the same protocol used by Jawalkar et al.,58 Diaz et al.76 and Jarray et al.36 Although a degree of polymerization of 8 with four polymer chains are sufficient to compute solubility parameters,36,54 all our simulations were performed with at least 10 polymer chains in the simulation box with 8 repetition units each. To ensure that the equilibration and sampling durations are adequate, we created independent initial configurations following the same recipe as well as performed longer simulations of 1 ns. We found that the solubility parameter values were well reproduced and can be established in relatively short runs of 200 ps to within a standard deviation of about 0.25 (J cm−3)0.5 (more details in the ESI,† Section S1), which is consistent with other studies.53,77–79 Once molecules with promising properties have been identified, they can be subject to longer simulations for more accurate estimates and/or tested experimentally.
The solubility parameter values, with units of [energy density0.5], where calculated by averaging the intermolecular energy54 over the last 20 ps of the simulation,
| | 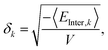 | (4) |
where
k runs over the dispersive, coulombic and hydrogen-bonding energies. The brackets denote a time average, and
V denotes the simulation box volume.
2.3 Surface tension and wettability prediction
Surface tension, i.e. the imbalance of the cohesive forces between molecules at the liquid–vapour interface, is an important parameter for assessing the wettability of liquids. It can be related to the solubility parameter using the empirical equation60,61where k is a constant equal to 0.0171. Although this equation gives satisfactory values of the surface tension for several liquids, its accuracy can be improved by discerning the types of interactions. Beerbower60 provided, on the basis of a computer regression of experimental data, a more accurate correlation that differentiates the three components of the solubility parameter,| | | γ = kVm1/3(δd2 + b(δp2 + δh2)), | (6) |
with k the same constant as in eqn (5), and b equal to 0.632. Since these constants were derived empirically, it would be nice to derive their physical origin. Becher80 attributed the constant k to the geometrical properties of the liquid molecule. The difficulty, as seen at that time by Hildebrand and Scott,61 lies in the evaluation of the surfaces and volumes of the molecules. Becher assumed that the molecules are highly convoluted and used the characteristic dimensions of the molecule.80 We propose to extend this argument by including the molecule details. Taking into account the three components of the solubility parameters, we define the solubility parameter-surface tension relation as| | 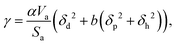 | (7) |
with Va the volume of the molecule, Sa the surface area of the molecule, and α a parameter that depends on the ratio of the number of neighboring molecules on the surface to that in the bulk. Roughly speaking, molecules at the surface of a droplet lose about half of their cohesion energy,81 hence, α ≈ 0.5 as it will be shown in this work. A detailed derivation of eqn (7), explaining the origin of α and b, is presented in Appendix A. For the computation of Va and Sa, the procedure of Richmond82 and Richard83,84 was used. The approach consists of rolling a spherical probe on the molecule atoms while in contact with the van der Waals surface, which is defined by the boundary of the union of the atomic van der Waals spheres. The rolling probe center provides the total accessible area of the molecule, see Fig. 4. The probe radius suggested by Richard83 and often used by many authors85–88 is ra = 1.4 Å, and corresponds to the average radius of a water molecule. However, recent studies89–91 suggested the use of a probe that depends on the atom types of the molecule to get better accuracy of the solvent accessible area. Here, we will use a probe radius that corresponds to the average atomistic radii of the molecule, which are provided by Wang and Hou90 (1.4 Å for oxygen, 1.72 Å for carbon, 1.54 Å for nitrogen, 2.1 Å for silicon, 1.6 Å for fluorine and 2 Å for bromine). As we will show, a constant probe radius of ra = 1.4 Å also gives good results, indicating that 1.4 Å is an acceptable average radius.
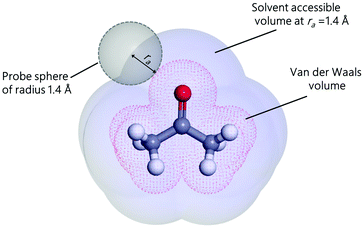 |
| | Fig. 4 Solvent accessible surface area and volume of acetone molecule generated by rolling a probe. | |
Based on Fowkes' approximation20,92 of additive contribution to the surface energy and Good–Girifalco's geometric mean approximation93 of interaction energies, Owens and Wendt21 used the Young equation to postulate the following equation for estimating either the interfacial energy or the contact angle of liquids on solid surfaces:
| | 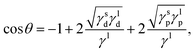 | (8) |
where
γs and
γl are the interfacial energies of the substrate and liquid, respectively, and the subscripts d and p denote, respectively, the dispersive and polar components of the interfacial energy.
γl is the total liquid surface tension given by the sum of
γld and
γlp. This geometrical mean approach uses only two categories of interactions instead of three (
i.e., polar and dispersive interactions). By taking into account the hydrogen-bonding contribution and equating the last three equations, we obtain the wettability in terms of the three solubility parameter components:
| | 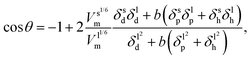 | (9) |
| | 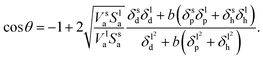 | (10) |
Eqn (9) derived from the empirical
eqn (6) uses the molar volume, while
eqn (10) derived from
eqn (7) uses the molecular geometrical factor
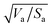
and assumes identical values of
α for solids and liquids (
i.e.,
αl =
αs). While keeping in mind that both of these equations ignore the effect of surface roughness and inhomogeneities, they can be used to predict
θ if the various dispersion, polar and hydrogen bonding components of the solubility parameter are known.
3 Results and discussion
We show in Fig. 5 the solubility parameters of solvents, polymers and surfactants typically used in inkjet printing, obtained using molecular dynamics plotted against experimental data gathered from the literature.94–96 Solubility parameter values are summarized in Table 1. Obtaining the three components of the solubility parameters is difficult experimentally, which is why only the total experimental solubility parameters are listed for comparison with the numerical results. A pictorial of the molecular structure of all the compounds used in this study is provided in Section S2 of the ESI.† MD gives solubility parameter values in agreement with experiments with an overall deviation of 1.1%. The largest deviations of 5–10% are observed for amine-based liquids (e.g., formamide) and carbonyls (e.g., ethyl acetate). As previously pointed out by Belmares et al.,54 this discrepancy is because the Lennard-Jones potential of the hydrogen-bonding interactions in the DREIDING forcefield is not well adjusted for nitrogen and double-bonded oxygen atoms.
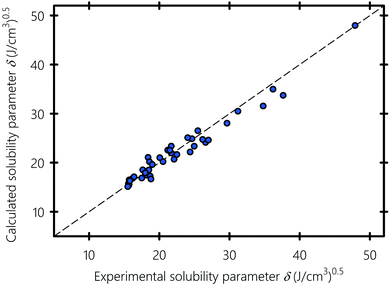 |
| | Fig. 5 MD-calculated versus experimental solubility parameters. Experimental values of the solubility parameter are gathered from ref. 94–97. | |
Table 1 Experimental and computed solubility parameters in (J cm−3)0.5 obtained using MD simulations, volume (Å3) and surface accessible area (Å2), experimental and calculated surface tensions (mN m−1) at 298.15 K, obtained using eqn (6) and (7)
|
|
MD simulations |
Exp. |
Calculated γ |
|
δ
|
δ
d
|
δ
p
|
δ
h
|
V
a
|
S
a
|
δ
|
γ
|
Eqn (6)
|
Eqn (7)
|
| Abbreviation: PC: polycarbonate, PET: polyethylene terephthalate, DPGME: di(propylene glycol)methyl ether, PMMA: polymethyl methacrylate, POM: polyoxymethylene, PP: polypropylene, PTFE: polytetrafluoroethylene, PS: polystyrene, and PVA: polyvinyl alcohol. For the computed solubility parameters, the standard deviation is in the range of ∼0.2 (J cm−3)0.5 for small molecules and ∼0.25 (J cm−3)0.5 for polymers, see Section S1 of the ESI. The corresponding deviation in the surface tension is in the range of ∼0.6 mN m−1 for small molecules and ∼0.8 mN m−1 for polymers. Calculated from experimental enthalpy of vaporization, ΔHvap from ref. 95 and 98, using eqn (2). Experimental surface tensions at 293.15 K. Dispersed experimental values in the literature. Experimental solubility parameters are obtained from ref. 94–97. Experimental surface tension values are obtained from ref. 94 and 96–102. Eqn (7) with a probe radius that depends on the atom types of the molecules. |
|
Polar and H-bonding liquids
|
| Acetic acid |
24.1 |
14.9 |
15.5 |
10.9 |
305.3 |
232.2 |
26.6 |
27.1 |
29.6 |
29.5 |
| Acetaldehyde |
20.2 |
15.0 |
12.9 |
4.1 |
280.1 |
215.5 |
20.5a |
20.5 |
22.1 |
22.2 |
| Acetone |
20.7 |
15.2 |
11.7 |
7.8 |
349.4 |
253.6 |
23.4 |
23.5–25.2c |
25.3 |
24.5 |
| Acetophenone |
22.5 |
20.6 |
9.1 |
0.2 |
562.9 |
360.3 |
21.2 |
38.9–39.1c |
39.9 |
37.5 |
| Allyl alcohol |
23.3 |
14.9 |
14.8 |
10.1 |
354.1 |
256.1 |
24.9 |
25.3 |
29.8 |
29.4 |
| Anisole |
21.0 |
19.1 |
8.1 |
3.3 |
519.0 |
338.4 |
20.1a |
35.1 |
33.8 |
31.8 |
| Benzyl alcohol |
24.9 |
19.8 |
13.1 |
7.5 |
525.4 |
342.4 |
24.6 |
39.3 |
42.9 |
41.2 |
| 1-Bromonaphthalene |
24.5 |
21.9 |
10.9 |
0.0 |
669.5 |
406.2 |
|
44.6 |
49.2 |
46.2 |
| Butanal |
20.4 |
16.8 |
11.5 |
0.5 |
416.7 |
288.5 |
|
24.3b |
28.0 |
26.6 |
| Butanol |
20.8 |
15.3 |
11.7 |
7.9 |
437.0 |
298.0 |
23.1 |
24.9–25.7c |
27.9 |
26.6 |
| Cyclobutanone |
23.1 |
19.3 |
12.5 |
0.7 |
374.9 |
265.0 |
|
31.9 |
33.2 |
33.7 |
| Cyclopentanone |
21.9 |
19.3 |
10.5 |
0.3 |
429.4 |
291.6 |
21.7 |
33.3 |
33.2 |
32.7 |
| Diethylene glycol |
31.0 |
14.1 |
23.2 |
15.0 |
496.4 |
339.0 |
|
45.2 |
50.5 |
49.1 |
| Dipropyl ether |
15.4 |
14.5 |
4.3 |
3.0 |
578.7 |
376.4 |
15.7a |
20.0 |
19.9 |
17.6 |
| Ethanol |
24.7 |
12.8 |
17.8 |
11.3 |
289.6 |
221.0 |
26.2 |
22.0 |
29.6 |
29.2 |
| Ethanolamine |
30.5 |
10.3 |
21.5 |
19.0 |
341.5 |
249.5 |
31.2a |
48.3 |
42.5 |
42.7 |
| Ethyl acetate |
21.1 |
17.1 |
12.2 |
0.9 |
445.6 |
309.5 |
18.4 |
23.4 |
30.6 |
28.1 |
| Ethylene carbonate |
28.0 |
18.0 |
17.9 |
11.8 |
350.8 |
254.7 |
29.6 |
|
42.6 |
42.5 |
| Ethylene glycol |
31.5 |
13.2 |
22.9 |
17.1 |
322.3 |
240.1 |
34.8 |
48.0 |
45.4 |
46.4 |
| Formamide |
33.7 |
12.7 |
26.5 |
16.5 |
252.8 |
202.2 |
37.6 |
57.0 |
46.8 |
48.4 |
| Furan |
20.1 |
17.9 |
9.1 |
0.7 |
353.2 |
253.3 |
|
24.1 |
27.4 |
26.2 |
| Furfuryl alcohol |
26.5 |
18.8 |
15.9 |
9.8 |
445.3 |
304.6 |
25.5 |
38.2 |
43.7 |
42.1 |
| Glycerol |
34.9 |
11.7 |
26.7 |
19.3 |
406.8 |
284.1 |
36.2 |
63.4 |
59.3 |
58.6 |
| Glycerol carbonate |
31.2 |
19.2 |
22.2 |
10.6 |
440.8 |
302.1 |
|
|
56.4 |
54.8 |
| 2-Methyl-3-pentanol |
18.8 |
15.8 |
8.3 |
5.9 |
530.2 |
337.9 |
|
24.4 |
27.0 |
24.9 |
| Methyl salicylate |
23.3 |
20.1 |
11.5 |
2.9 |
608.5 |
386.6 |
21.7 |
39.0 |
42.6 |
39.1 |
| Methyl vinyl ether |
17.9 |
15.1 |
9.0 |
3.5 |
357.8 |
260.1 |
|
15.7 |
20.9 |
19.8 |
| Pentanal |
20.1 |
17.2 |
10.5 |
0.3 |
483.6 |
323.2 |
18.6 |
24.8–25.4c |
29.6 |
27.5 |
| Pentanol |
21.6 |
16.2 |
11.7 |
8.2 |
500.1 |
330.6 |
22.5 |
25.4–26.7c |
32.1 |
29.8 |
| Propanol |
22.1 |
14.3 |
13.7 |
9.9 |
366.2 |
260.3 |
24.4a |
23.3 |
27.9 |
27.1 |
| Propylamine |
17.4 |
12.5 |
6.5 |
10.2 |
380.2 |
268.9 |
18.2a |
21.7–22.4c |
18.5 |
17.7 |
| Propylene oxide |
20.8 |
15.1 |
13.5 |
4.5 |
336.7 |
245.0 |
|
24.5 |
25.3 |
24.6 |
| Tetramethylsilane |
13.3 |
13.2 |
0.9 |
0.0 |
555.6 |
347.3 |
|
12.3 |
15.2 |
14.2 |
| Triethylsilane |
15.9 |
15.9 |
0.6 |
0.0 |
499.0 |
322.7 |
|
20.3 |
20.9 |
19.6 |
| Trioxane |
23.7 |
17.0 |
15.8 |
4.7 |
360.7 |
257.0 |
|
|
33.7 |
32.5 |
| Trisilane |
15.2 |
15.2 |
0.6 |
0.0 |
605.0 |
67.5 |
|
18.7b |
20.3 |
19.2 |
| Water |
47.9 |
17.2 |
36.2 |
26.4 |
130.4 |
126.3 |
47.9 |
72.0 |
69.9 |
80.2 |
|
|
|
Surfactants
|
| DPGME |
22.3 |
16.8 |
13.2 |
6.4 |
659.3 |
411.3 |
|
|
38.3 |
33.5 |
| Dynol 607 |
19.4 |
14.9 |
10.7 |
6.2 |
2911.2 |
1450.2 |
|
|
51.3 |
32.2 |
| Heptanediol |
22.2 |
16.9 |
12.3 |
7.4 |
647.6 |
405.9 |
|
37.0 |
37.6 |
33.4 |
| 1,2-Hexanediol |
25.1 |
16.0 |
15.9 |
11.0 |
571.0 |
366.6 |
24.0 |
36.2 |
42.1 |
38.3 |
| Pentanediol |
28.0 |
16.1 |
19.1 |
12.6 |
528.5 |
348.3 |
|
44.0 |
47.7 |
44.8 |
| Surfynol 104 |
18.6 |
16.6 |
7.4 |
4.3 |
1002.4 |
571.8 |
|
33.1 |
34.4 |
28.2 |
| Tergitol NP-9 |
20.4 |
16.7 |
9.8 |
6.3 |
2553.4 |
1456.4 |
|
32.0 |
51.9 |
32.0 |
|
|
|
Polymeric substrates
|
| PC |
20.1 |
17.9 |
7.7 |
4.6 |
5679.2 |
2280.9 |
|
42.7 |
38.9 |
46.7 |
| PET |
22.5 |
18.5 |
11.3 |
5.9 |
5044.1 |
2733.7 |
19.9–21.9c |
40.0–43.0c |
41.0 |
41.3 |
| PMMA |
19.9 |
13.8 |
13.2 |
5.5 |
2186.6 |
1001.3 |
18.6–26.2c |
39.2 |
26.5 |
35.1 |
| POM |
23.6 |
15.9 |
15.6 |
8.0 |
1738.2 |
1040.0 |
|
38.0–39.6c |
30.3 |
37.3 |
| PP |
16.8 |
16.3 |
3.9 |
0.0 |
1447.7 |
760.0 |
16.8–18.8c |
29.6–32.0c |
19.9 |
26.4 |
| PS |
17.9 |
16.9 |
5.8 |
0.0 |
2192.9 |
1207.1 |
17.4–19.0c |
33.0–36.0c |
26.0 |
35.3 |
| PTFE |
14.0 |
13.5 |
3.8 |
0.0 |
1357.3 |
738.3 |
|
18.5 |
13.8 |
17.7 |
| PVA |
24.6 |
14.2 |
16.5 |
11.4 |
1189.5 |
658.2 |
25.8–29.1c |
37.0 |
32.0 |
41.2 |
|
|
|
Hydrocarbons
|
| Benzene |
17.2 |
17.2 |
1.5 |
0.0 |
439.4 |
296.7 |
18.7 |
28.2 |
23.9 |
22.1 |
| Cumene |
17.9 |
17.8 |
1.4 |
0.0 |
607.8 |
376.3 |
|
27.7 |
28.4 |
26.1 |
| Cycloheptene |
18.6 |
18.5 |
1.6 |
0.0 |
515.1 |
328.1 |
|
28.0b |
28.7 |
27.2 |
| Cyclohexene |
18.5 |
18.4 |
1.6 |
0.0 |
467.0 |
307.3 |
17.6a |
26.2 |
27.2 |
26.2 |
| Decane |
16.6 |
16.4 |
2.5 |
0.0 |
806.5 |
487.0 |
18.8 |
23.7 |
27.2 |
22.9 |
| Dimethylbutane |
14.4 |
14.3 |
2.0 |
0.0 |
504.7 |
320.4 |
|
15.8 |
17.9 |
16.4 |
| Dodecane |
16.8 |
16.6 |
2.7 |
0.0 |
936.5 |
554.3 |
16.2 |
25.3 |
29.2 |
23.8 |
| Fluorene |
22.2 |
22.1 |
1.2 |
0.0 |
726.4 |
436.0 |
|
|
44.5 |
41.2 |
| Heptane |
15.7 |
15.5 |
2.3 |
0.0 |
611.5 |
386.0 |
15.6 |
19.6 |
22.0 |
19.5 |
| Hexadecane |
17.1 |
16.9 |
2.7 |
0.0 |
1196.3 |
688.6 |
16.4 |
27.2 |
32.9 |
25.3 |
| Hexane |
15.6 |
15.5 |
1.2 |
0.0 |
546.5 |
352.3 |
15.7a |
17.9 |
20.8 |
18.9 |
| Hexatriene |
17.1 |
16.9 |
2.2 |
0.0 |
509.5 |
340.1 |
|
|
23.7 |
22.0 |
| Mesitylene |
18.6 |
18.5 |
1.6 |
0.0 |
633.7 |
395.0 |
|
27.5 |
30.2 |
27.6 |
| Methylnaphthalene |
20.8 |
20.6 |
2.7 |
0.0 |
657.9 |
400.6 |
|
37.5 |
38.1 |
35.5 |
| Nonane |
16.5 |
16.3 |
2.4 |
0.0 |
741.9 |
453.4 |
15.7 |
22.7 |
25.8 |
22.1 |
| Octane |
16.3 |
16.1 |
2.4 |
0.0 |
676.2 |
419.7 |
15.8 |
21.5 |
24.5 |
21.3 |
| 1-Octyne |
17.1 |
17.1 |
0.9 |
0.0 |
662.4 |
423.3 |
|
23.9 |
26.5 |
23.1 |
| Paraffin oil |
19.9 |
17.9 |
1.1 |
0.0 |
1327.5 |
756.2 |
|
27.7–28.9c |
37.8 |
28.3 |
| Pentane |
15.1 |
15.6 |
1.2 |
0.0 |
481.1 |
319.0 |
15.5 |
15.5 |
18.6 |
17.3 |
| Spiropentane |
19.0 |
19.0 |
1.6 |
0.0 |
396.4 |
272.1 |
|
22.8 |
25.5 |
26.5 |
| Styrene |
19.6 |
19.5 |
1.8 |
0.0 |
544.7 |
350.3 |
19.0 |
30.9b |
31.9 |
29.9 |
| Toluene |
18.5 |
18.4 |
1.3 |
0.0 |
504.3 |
329.8 |
18.5 |
28.5 |
27.5 |
26.3 |
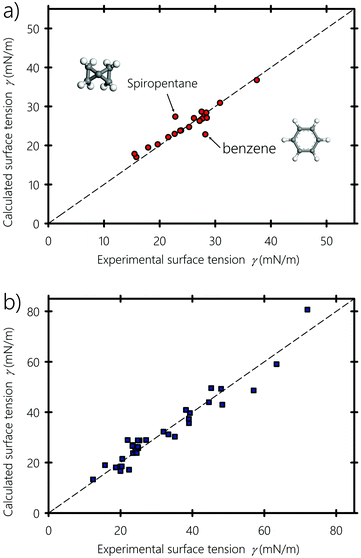
Fig. 6(a and b) show the experimental surface tension of typical liquids, polymers and surfactants used in inkjet printing, plotted against the surface tension values obtained using eqn (6) and (7), respectively. Nonpolar (e.g., hydrocarbons, halogenated – carbons), partially polar (e.g., acetone and ethyl acetate) and hydrogen-bonding compounds (e.g., formamide, glycerol and water) liquids are shown with different symbols. Calculated and experimental surface tension values of these liquids are listed in Table 1. For some compounds showing dispersed experimental surface tensions in the literature (deviation ranges ∼1 mN m−1 for liquids and ∼2 mN m−1 for polymers), the average value was taken when plotting Fig. 6. Fitting α and b of eqn (7) to the experimental surface tension values gives b = 0.6225, which is almost equal to the value proposed by Beerbower60 (b = 0.632), and a value of α = 0.504, showing that molecules on the surface lose about half their cohesive energy. We point out that the value of α depends on the interplay between the number of neighboring molecules on the surface of the liquid and the anisotropic interactions bearing on the surface molecules (see Appendix A). Both equations give surface tension values in good agreement with experiments, but eqn (7) shows an overall better agreement, especially when predicting the interfacial energy of polymeric substrates: In fact, eqn (6) and (7) agree with the experimental values with 4.3% and 2.4% deviation in comparison to the experimental values, respectively. This endorses the argument of the molecular geometrical origin of the constant k in Hildebrand–Scott61 and Beerbower60 equations, previously derived from experimental extrapolation. The agreement also confirms that better predictive accuracy is obtained when taking into account the type of interaction, namely polar, disperse and hydrogen-bonding. In particular, the surface tension of hydrocarbons is well reproduced and fitting eqn (7) to only hydrocarbons gives b = 0.96 and α = 0.52 (see Appendix B). Alkane molecules are dominantly dispersive, and have weak orientational ordering due to their weak polar and hydrogen-bonding interactions, which explains why b has a low effect on their surface tension. For the case of liquids containing polar groups, such as COOH, OH, and NH2, both the molecular surface polarization and the preference of breaking hydrogen acceptor over donor would cause the polar end of the molecule to be oriented toward the inner side of the surface.103–105 From this standpoint, we can infer that the constant b in the Beerbower60 equation takes into account the polar and hydrogen-bonding interactions lost by the similarly oriented molecules at the vapour–liquid interface.
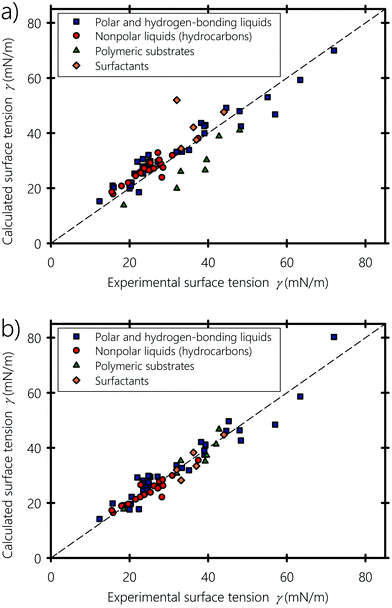 |
| | Fig. 6 Calculated versus experimental surface tensions, (a) obtained using Beerbower's60eqn (6), and (b) obtained using our eqn (7). Experimental data of the surface tension are obtained from ref. 94, 96 and 98–101. | |
When using a constant probe radius ra = 1.4 Å for the calculation of the solvent accessible area in eqn (7), good results were also obtained as shown in the ESI† (Section S3), with a 3% deviation in comparison to the experimental values. Solubility parameter and surface tension values obtained using the Yamamoto-Molecular Break (Y-MB) method44,45 are also provided in the ESI† (Section S4). These results show that the Y-MB method works equally well for small molecules such as glycerol and cyclobutanone, but becomes less accurate for polymers and large molecules such as tergitol. Overall, better results are obtained when using the solubility parameters components computed from MD.
Next, we explore the wetting properties of liquids on different smooth polymeric substrates namely PMMA: polymethyl methacrylate, PTFE: polytetrafluoroethylene, PP: polypropylene, PC: polycarbonate, PET: polyethylene terephthalate, POM: polyoxymethylene, PS: polystyrene, and PVA: polyvinyl alcohol. In Fig. 7, the calculated contact angles obtained using eqn (10) are plotted against experimental data from literature, obtained using the sessile drop method and the one-liquid contact angle method.100,107 All contact angle data are tabulated in the ESI† along with a version of Fig. 7 where liquids are labeled with their name (Sections S5 and S6, respectively, ESI†). The polymeric substrates are smooth with a surface roughness factors below 1.05, i.e. the ratio of the actual surface area of the substrate to its horizontal projection, thereby minimizing the estimated roughness-induced enhancement of the experimental contact angle value to less than 2 degrees.108 The calculated and reported experimental contact angles are equilibrium values, which usually lie in between the receding and advancing angles of moving droplets.109,110 Our equation, with b = 0.6225, gives results in reasonable agreement with experiments, which favors Good's93 geometric mean in eqn (8). The Teflon (PTFE) substrate, a well-known low-surface-energy materials that is frequently used in fusing components in the printing industry,111,112 shows the best agreement. Similarly, the computed contact angle values of polar and H-bonding polymers, such as PC and PET, are close to the experimental values. However, for PS and PP, there is an overestimation of the contact angle when they are in contact with highly polar liquids, but the equation correctly predicts the expected trend. This may have several causes: for instance, on the experimental side, beside the difficulty of the acquisition of precise contact angle values, the effects of surface heterogeneity can easily overshadow the influence of interfacial interactions.113,114 On the theoretical side, as stated by Wu102 the geometric mean in eqn (8), sometimes does not perform well for interactions between low energy materials (e.g., hydrocarbons) and highly polar liquids (e.g., water and glycerol), especially if they involve molecular rearrangement at the solid–liquid interface resulting from weak H-bonds formed between the hydrogen atoms of the substrate and the hydrogen acceptors of the liquids. In this particular type of overwhelmingly dispersive hydrocarbon substrates, we recommend modeling their interactions with polar liquids on the basis of the total solubility parameter rather than with their individual separate interaction components, which curiously gave slightly better results for PS and PP (and for these two only), as shown in the ESI† (Section S7). Alternatively, considering the orientation of the molecules at the solid–liquid interface and taking into account the dependence of α and b on the type of the interface in eqn (10) (i.e., taking αs ≠ αl rather than assuming a constant α) may provide more accurate predictions.
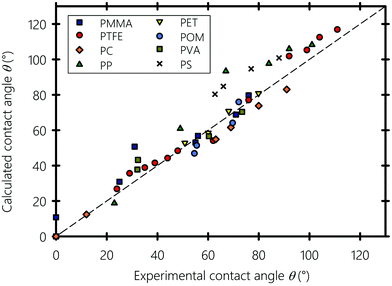 |
| | Fig. 7 Experimental versus calculated contact angles of liquids on different polymeric substrates. PMMA: polymethyl methacrylate, PTFE: polytetrafluoroethylene, PP: polypropylene, PC: polycarbonate, PET: polyethylene terephthalate, POM: polyoxymethylene, PS: polystyrene and PVA: polyvinyl alcohol. Experimental contact angle values are gathered from ref. 100, 106 and 107. | |
To enable numerical vs. experimental comparison of the spreading behaviour of the liquids, we will consider next that liquids completely spread on the substrate if the calculated contact angle value is lower than 15°. The wetting behaviour is summarized in Fig. 8. Bottom-right and upper-left oriented triangles denote experiments and numerical calculations, respectively. Red and blue triangles denote dewetting and spreading liquids, respectively. To interpret the significance of the contact angle results, components are sorted according to the magnitude of their hydrogen-bonding interactions. Wetting behaviour computed numerically agrees with experiments in all cases. According to Fig. 8, strongly hydrogen-bonding liquids dewet or partially wet all the polymeric substrates. PTFE is neither a hydrogen bonding nor a polar substrate, which explains why no liquids spreads on it. Even for the strongly hydrogen-bonding liquids, polar and dispersion interactions still play a role. For instance, the latter explains why bromonaphthalene partially wets PMMA but spreads on the less polar PC surface, in agreement with experiments (see Table S3 in the ESI†).
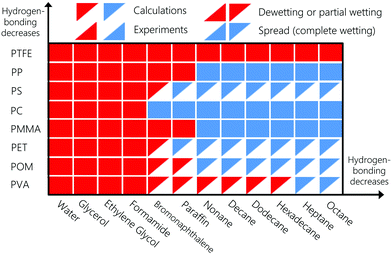 |
| | Fig. 8 Spreading behaviour of various liquids on different substrates, namely: PMMA: polymethyl methacrylate, PTFE: polytetrafluoroethylene, PP: polypropylene, PC: polycarbonate, PET: polyethylene terephthalate, POM: polyoxymethylene, PS: polystyrene, and PVA: polyvinyl alcohol. Experimental spreading behaviour are obtained from ref. 100, 106 and 107. | |
Similarly to the Hansen 3D space approach, the three parameters δd, δp and δh, multiplied by the square root of the ratio of the solvent volume to the accessible solvent area 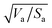 , can be treated as coordinates of a point in three-dimensional space. Then, by solving eqn (10) for a specific substrate and a predefined contact angle, a wettability sphere is obtained as shown in Fig. 9. Note that the coefficient b of eqn (10) is taken into account in the coordinates of the polar and hydrogen-bonding components to generate a sphere instead of a spheroid. Here again, in eqn (10), we consider b to be a constant equal to 0.6255. Liquids that lie inside the resulting sphere for a certain predefined low contact angle, will spread on the corresponding substrate.
, can be treated as coordinates of a point in three-dimensional space. Then, by solving eqn (10) for a specific substrate and a predefined contact angle, a wettability sphere is obtained as shown in Fig. 9. Note that the coefficient b of eqn (10) is taken into account in the coordinates of the polar and hydrogen-bonding components to generate a sphere instead of a spheroid. Here again, in eqn (10), we consider b to be a constant equal to 0.6255. Liquids that lie inside the resulting sphere for a certain predefined low contact angle, will spread on the corresponding substrate.
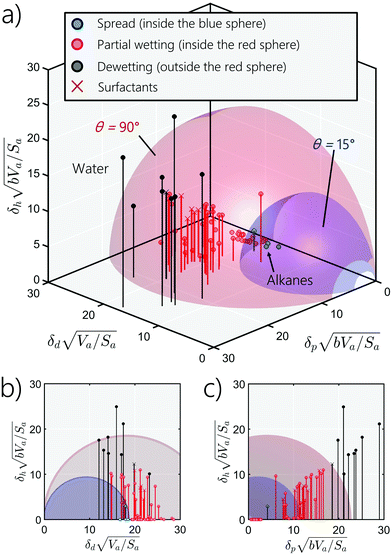 |
| | Fig. 9 (a) Wettability spheres for PTFE, (b) projection on the hydrogen-bonding-dispersive plan, and (c) projection on the-hydrogen-bonding-polar plan. All data are in (J cm−2)1/2. Liquid dots inside the blue sphere spread on PTFE, while those outside but still inside the red sphere partially spread on PTFE. Dewetting happens for liquids outside the red sphere. | |
In Fig. 9, we plot two wetting blue and red spheres of PTFE (Teflon) corresponding to contact angles of 15° and 90°, respectively, and we place the coordinates of the 66 liquids investigated in this study, whose properties are tabulated in Table 1. The blue and red dots in Fig. 9 present, respectively, liquids which are inside the blue and the red wetting spheres. The blue dots, inside the blue sphere, mark liquids that spread; the red dots, in between the red and blue spheres, indicate liquids that form less well spread droplets up to hemi-spherical droplets, while the black dots represent liquids that dewet the substrate (i.e., form a spherical droplets on the substrate). We notice that as we go further from the origin of the 3D wetting space, liquids spreading decreases because the polar, dispersive and hydrogen-bonding contributions to the cohesive force between the molecules of the liquid increases. In the specific case of PTFE, almost all liquids lie outside the blue wetting sphere, indicating dewetting or partial wetting. Only a few hydrocarbon liquids (e.g., toluene) are near the edge of the blue sphere and will likely spread. The other liquids, in particular water and glycerol, exhibit a high polar contribution hindering the wetting of PTFE. We also provide the wetting spheres of all the other polymers in the ESI† (Sections S8). From Fig. 9(c), it is interesting to see that for many liquids the hydrogen-bonding component increases almost linearly with the polar components of the solubility parameter.
Knowledge of the wetting sphere allows easy wettability determination and fast screening of adequate solvents and surfactants for many applications including inkjet printing. Here for instance, the wetting sphere of PTFE needs to be enlarged to improve the spreading, for example, by means of surface treatment, or in the case of water and glycerol, by selecting a surfactant whose polar contribution is low. Furthermore, this approach can also be applied to a combination of miscible liquids, since MD allows the computation of the solubility parameter of miscible mixtures. For rough surfaces, eqn (10) can be extended by using for example the Wenzel model,108 simply by multiplying its right side by the roughness factor.
4 Conclusions
We introduced a straightforward, low-cost, molecular dynamics-based approach for characterizing the wetting behavior of liquids, speeding up the screening of adequate molecules that meet predefined wettability and spreading requirements encountered in various industrial applications. We proposed an MD framework that predicts well the solubility parameter components of popular liquids and polymeric substrates. Then, we showed that the empirically derived Hildebrand–Scott constant in Beerbower's correlation relating the surface tension to the solubility parameter,60 is based on geometrical properties of the liquid molecule. By separating the solubility parameter components in Owens and Wendt21 equation and including the hydrogen-bonding interactions, we proposed a new 3D wettability space that is inspired by the Hansen solubility parameter space,42 to generate the wetting spheres of substrates. This allows to categorize the wetting behaviour of liquids or mixtures and select or design suitable substrates for specific applications.
The proposed approach is fast and yields Hansen solubility parameters, surface tensions and contact angles in good agreements with experimental data. One may therefore expect the method to give reasonable predictions for compounds that were not part of the current study. Compared to group contribution methods such as Y-MB,44 the method is not as fast but it is more accurate, accounts for conformation changes in molecular structure, and can be applied to polymers and large molecules. In comparison to studies extracting Hansen parameters, surface tensions or contact angles by simulating long polymer chains or explicit droplets,29,115–118 the current method is much faster. There are a few limitations that need to be addressed in future studies. For instance, the DREIDING67 hydrogen-bonding potential is still not well parametrized for nitrogen and bromine atoms, and can be adjusted for higher accuracy. Additionally, Good's93 geometrical mean approximation implemented in our equation sometimes overestimates the contact angles between dominantly dispersive substrates and highly polar liquids. Consequently, it would be interesting to further universalize our equation to accurately predict liquid wettability while taking into account these specific interactions.
Conflicts of interest
The authors declare no conflict of interest.
Appendix A: surface tension as a function of the solubility parameters
We want to determine the physical origin of the constants α and b in eqn (7). The surface energy of a pure liquid is the energy needed to increase the interfacial area by one unit. It can therefore be approximated as the energy required to bring one individual molecule from the bulk to the surface of the liquid,119 see Fig. 10,| | 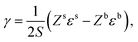 | (11) |
where ε is the average pairwise intermolecular energy, S is the surface area of the molecule exposed to the vapour phase, and Z is the coordination number. The denominator “2” is due to the double-counting of the pairwise interactions, and the superscripts s and b refer to the surface and bulk of the liquid, respectively. Similar equations were proposed by several authors.31,120,121 However, these authors assumed that the molecules on the surface interact the same way as in the bulk (i.e., εs = εb). This should not be the case, particularly for polar and hydrogen-bonding molecules as their orientation may change on the vapour–liquid interface, subsequently affecting the intermolecular interactions undergone by the molecule on the surface. Assuming that the intermolecular interactions are equally distributed over the surface of the molecule, the surface area exposed to the vapour phase can be written in terms of the total accessible area of the molecule as S = Sa(Zb − Zs)/Zb. Introducing the ratio βk = εsk/εbk, where k runs over the van der Waals dispersion, the coulombic, and the hydrogen-bonding energies, and using| | 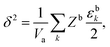 | (12) |
we get| | 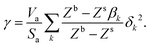 | (13) |
The ratio βk takes into account the excess binding energy. This latter equation translates into eqn (7), when taking| | 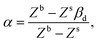 | (14) |
| | 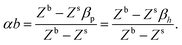 | (15) |
Here, α depends on both the number of neighboring molecules as well as on the intermolecular energy on the bulk and on the surface. Note that this derivation of the surface tension as a function of the solubility parameter is energy-based and disregard the effect of the entropy, which is taken into account in the fitting of α and b in eqn (7) against experimental data.
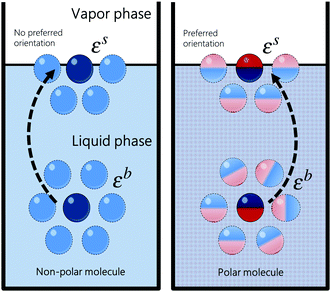 |
| | Fig. 10 Schematic representation of a molecule on the surface and in the bulk of the liquid. Polar molecules do not interact the same way on the surface as in the bulk because they exhibit a preferred orientation on the surface. | |
Appendix B: surface tension of hydrocarbons and polar liquids
In Fig. 11(a and b), we show the fitting of eqn (7) to hydrocarbons and polar molecules, respectively. Fitting to only hydrocarbons gives b = 0.96 and α = 0.52. For polar liquids, b = 0.67 and α = 0.46. It is interesting to see that the hydrocarbons with the highest deviations relative to the experimental values are cyclic hydrocarbons (e.g., benzene and spiropentane). This can be explained by the unusual orientation of these molecules on the surface of the liquid due to their non-linear molecular geometry.
 |
| | Fig. 11 Calculated versus experimental surface tension obtained using eqn (7), for (a) hydrocarbons and (b) polar and hydrogen-bonding liquids. Experimental values of the surface tension are obtained from ref. 94, 96 and 98–101. | |
Acknowledgements
We thank Stefan Luding, Nicolae Tomozeiu and Anton A. Darhuber for their help and advice. Financial support through the NWO (STW 14666) is also acknowledged.
References
- B. He, S. Yang, Z. Qin, B. Wen and C. Zhang, Sci. Rep., 2017, 7, 11841 CrossRef PubMed.
- D. Tian, Y. Song and L. Jiang, Chem. Soc. Rev., 2013, 42, 5184–5209 RSC.
- E. Bertrand, D. Bonn, D. Broseta, H. Dobbs, J. Indekeu, J. Meunier, K. Ragil and N. Shahidzadeh, J. Pet. Sci. Eng., 2002, 33, 217–222 CrossRef CAS.
- V. Bergeron, D. Bonn, J. Y. Martin and L. Vovelle, Nature, 2000, 405, 772–775 CrossRef CAS PubMed.
- S. Li, J. Huang, Z. Chen, G. Chen and Y. Lai, J. Mater. Chem. A, 2017, 5, 31–55 RSC.
- G. Zhang, M. A. Quetzeri-Santiago, C. A. Stone, L. Botto and J. R. Castrejón-Pita, Soft Matter, 2018, 14, 8182–8190 RSC.
-
S. D. Hoath, Fundamentals of inkjet printing: the science of inkjet and droplets, John Wiley & Sons, 2016 Search PubMed.
-
M. Shlomo, The chemistry of inkjet inks, World Scientific, 2009 Search PubMed.
- H. Wijshoff, Curr. Opin. Colloid Interface Sci., 2018, 36, 20–27 CrossRef CAS.
- J.-C. Fernandez-Toledano, T. Blake, P. Lambert and J. De Coninck, Adv. Colloid Interface Sci., 2017, 245, 102–107 CrossRef CAS PubMed.
- J. De Coninck, F. Dunlop and T. Huillet, Phys. Rev. E, 2017, 95, 052805 CrossRef PubMed.
- H. Fox and W. Zisman, J. Colloid Sci., 1950, 5, 514–531 CrossRef CAS.
- R. J. Good, J. Adhes. Sci. Technol., 1992, 6, 1269–1302 CrossRef CAS.
- A. Ellison and W. Zisman, J. Phys. Chem., 1954, 58, 503–506 CrossRef CAS.
- W. A. Zisman, Adv. Chem., 1964, 43, 1–51 CAS.
- S. Wu, J. Polym. Sci., Part C: Polym. Symp., 1971, 34, 19–30 CrossRef.
- S. Wu, J. Phys. Chem., 1970, 74, 632–638 CrossRef CAS.
-
C. J. Van Oss, Interfacial forces in aqueous media, CRC Press, 2006 Search PubMed.
- L. Girifalco and R. J. Good, J. Phys. Chem. A, 1957, 61, 904–909 CrossRef CAS.
-
F. M. Fowkes, Contact Angle, Wettability, and Adhesion, ACS Publications, 1964 Search PubMed.
- D. K. Owens and R. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- A. Neumann, J. Spelt, R. Smith, D. Francis, Y. Rotenberg and D. Absolom, J. Colloid Interface Sci., 1984, 102, 278–284 CrossRef CAS.
- D. Li and A. Neumann, Adv. Colloid Interface Sci., 1991, 36, 125–151 CrossRef CAS.
- L. H. Lee, Langmuir, 1993, 9, 1898–1905 CrossRef CAS.
- M. Morra, E. Occhiello and F. Garbassi, Adv. Colloid Interface Sci., 1990, 32, 79–116 CrossRef CAS.
- H. Y. Erbil, Surf. Sci. Rep., 2014, 69, 325–365 CrossRef CAS.
- L.-H. Lee, Langmuir, 1994, 10, 3368 CrossRef CAS.
- C. Van Oss, R. Good and M. Chaudhury, Langmuir, 1988, 4, 884–891 CrossRef CAS.
- A. Sgouros, G. G. Vogiatzis, G. Kritikos, A. Boziki, A. Nikolakopoulou, D. Liveris and D. Theodorou, Macromolecules, 2017, 50, 8827–8844 CrossRef CAS.
- C. N. Pereira and G. C. Vebber, J. Mol. Liq., 2018, 272, 520–527 CrossRef CAS.
- F. Aqra and A. Ayyad, Appl. Surf. Sci., 2011, 257, 6372–6379 CrossRef CAS.
- V. Goussard, F. Duprat, V. Gerbaud, J.-L. Ploix, G. Dreyfus, V. Nardello-Rataj and J.-M. Aubry, J. Chem. Inf. Model., 2017, 57, 2986–2995 CrossRef CAS PubMed.
-
J. Hildebrand and R. Scott, The solubility of nonelectrolytes, Reinhold Pub, 1950, vol. 3 Search PubMed.
-
R. Fedors, D. Van Krevelen, P. Hoftyzer and C. In, Handbook of solubility parameters and other cohesion parameters, 1983 Search PubMed.
- P. Bustamante, J. Navarro-Lupión and B. Escalera, Eur. J. Pharm. Sci., 2005, 24, 229–237 CrossRef CAS PubMed.
- A. Jarray, V. Gerbaud and M. Hemati, Prog. Org. Coat., 2016, 101, 195–206 CrossRef CAS.
- J. Bonnet, G. Suissa, M. Raynal and L. Bouteiller, Soft Matter, 2014, 10, 3154–3160 RSC.
- V. B. Souza and C. R. Mansur, Energy Fuels, 2015, 29, 7855–7865 CrossRef CAS.
- S. Tsutsumi, Y. Kato, K. Namba and H. Yamamoto, Results Mater., 2019, 4, 100046 CrossRef.
- I. Rodriguez-Donis, S. Thiebaud-Roux, S. Lavoine and V. Gerbaud, C. R. Chim., 2018, 21, 606–621 CrossRef CAS.
- D. Vankreve, Fuel, 1965, 44, 229 Search PubMed.
-
C. M. Hansen, The three dimensional solubility parameter, 1967, vol. 14 Search PubMed.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151 CrossRef CAS.
- H. Yamamoto, JCPE J., 1999, 11, 65–76 Search PubMed.
-
C. Hansen, S. Abbott and H. Yamamoto, HSPiP Software. Hansen solubility parameters web site, 2014 Search PubMed.
- K. Hoy, J. Paint Technol., 1970, 42, 76–118 CAS.
-
J. Wei, M. M. Denn, J. H. Seinfeld, A. Chakraborty, J. Ying, N. Peppas and G. Stephanopoulos, Molecular Modeling and Theory in Chemical Engineering, Elsevier, 2001, vol. 28 Search PubMed.
- P. Choi, T. A. Kavassalis and A. Rudin, Ind. Eng. Chem. Res., 1994, 33, 3154–3159 CrossRef CAS.
- M. R. Shah and G. D. Yadav, J. Membr. Sci., 2013, 427, 108–117 CrossRef CAS.
- J. L. Lewin, K. A. Maerzke, N. E. Schultz, R. B. Ross and J. I. Siepmann, J. Appl. Polym. Sci., 2010, 116, 1–9 CrossRef CAS.
- X. Chen, C. Yuan, C. K. Wong and G. Zhang, J. Mol. Model., 2012, 18, 2333–2341 CrossRef CAS PubMed.
- H. Yang, L. Ze-Sheng, H.-j. Qian, Y.-b. Yang, X.-b. Zhang and C.-c. Sun, Polymer, 2004, 45, 453–457 CrossRef CAS.
- A. Jarray, V. Gerbaud and M. Hémati, Powder Technol., 2015, 271, 61–75 CrossRef.
- M. Belmares, M. Blanco, W. Goddard Iii, R. Ross, G. Caldwell, S.-H. Chou, J. Pham, P. Olofson and C. Thomas, J. Comput. Chem., 2004, 25, 1814–1826 CrossRef CAS PubMed.
- Y. Medina-Gonzalez, A. Jarray, S. Camy, J.-S. Condoret and V. Gerbaud, J. Solution Chem., 2017, 46, 259–280 CrossRef CAS.
- Y. S. Sistla, L. Jain and A. Khanna, Sep. Purif. Technol., 2012, 97, 51–64 CrossRef CAS.
- T. Spyriouni, C. Tzoumanekas, D. Theodorou, F. Müller-Plathe and G. Milano, Macromolecules, 2007, 40, 3876–3885 CrossRef CAS.
- S. S. Jawalkar, S. G. Adoor, M. Sairam, M. N. Nadagouda and T. M. Aminabhavi, J. Phys. Chem. B, 2005, 109, 15611–15620 CrossRef CAS PubMed.
- A. Jarray, V. Gerbaud and M. Hemati, Powder Technol., 2016, 291, 244–261 CrossRef CAS.
- A. Beerbower, J. Colloid Interface Sci., 1971, 35, 126–132 CrossRef CAS.
-
J. Hildebrand and R. Scott, The Solubility of Non-Electrolytes, Reinhold, New York, 1950 Search PubMed.
- J. D. Crowley, G. Teague Jr and J. W. Lowe Jr, J. Paint Technol., 1966, 38, 269–280 CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. K. Rappe and W. A. Goddard III, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478 CrossRef CAS.
- Scienomics, MAPS Platform 4.2, 2019, http://www.scienomics.com/.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- A. R. Kulkarni and D. S. Sholl, Langmuir, 2015, 31, 8453–8468 CrossRef CAS PubMed.
- J. Marti, J. Chem. Phys., 1999, 110, 6876–6886 CrossRef CAS.
- A. Luzar and D. Chandler, Phys. Rev. Lett., 1996, 76, 928 CrossRef CAS PubMed.
- G. Bahlakeh, M. Nikazar and M. M. Hasani-Sadrabadi, J. Membr. Sci., 2013, 429, 384–395 CrossRef CAS.
- F. Fabiola, R. Bertram, A. Korostelev and M. S. Chapman, Protein Sci., 2002, 11, 1415–1423 CrossRef CAS PubMed.
- X. Wu, R. J. Moon and A. Martini, Cellulose, 2013, 20, 43–55 CrossRef CAS.
- J. B. Mitchell and S. L. Price, J. Comput. Chem., 1990, 11, 1217–1233 CrossRef CAS.
- P. T. Kiss, M. Sega and A. Baranyai, J. Chem. Theory Comput., 2014, 10, 5513–5519 CrossRef CAS PubMed.
- I. Daz, E. Dez, J. Camacho, S. León and G. Ovejero, Fluid Phase Equilib., 2013, 337, 6–10 CrossRef.
- F. Frigerio and D. Molinari, Comput. Theor. Chem., 2011, 975, 76–82 CrossRef CAS.
- J. Yang, X. Gong and G. Wang, Comput. Mater. Sci., 2015, 102, 1–6 CrossRef CAS.
- S. Sridhar, B. Smitha, S. Mayor, B. Prathab and T. Aminabhavi, J. Mater. Sci., 2007, 42, 9392–9401 CrossRef CAS.
- P. Becher, J. Colloid Interface Sci., 1972, 38, 291–293 CrossRef CAS.
-
M. Kleman and O. D. Laverntovich, Soft matter physics: an introduction, Springer Science & Business Media, 2007 Search PubMed.
- T. J. Richmond, J. Mol. Biol., 1984, 178, 63–89 CrossRef CAS PubMed.
- F. M. Richards, Annu. Rev. Biophys. Bioeng., 1977, 6, 151–176 CrossRef CAS PubMed.
- B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379–400 CrossRef CAS.
- T. Hou, J. Wang, Y. Li and W. Wang, J. Chem. Inf. Model., 2010, 51, 69–82 CrossRef PubMed.
- F. Palazzesi, M. Calvaresi and F. Zerbetto, Soft Matter, 2011, 7, 9148–9156 RSC.
- C. Balasubramanian, R. P. Ojha and S. Maiti, Biochem. Biophys. Res. Commun., 2007, 355, 1081–1086 CrossRef CAS PubMed.
- P. S. Redmill, S. L. Capps, P. T. Cummings and C. McCabe, Carbon, 2009, 47, 2865–2874 CrossRef CAS.
- S. Bhat and E. O. Purisima, Proteins: Struct., Funct., Bioinf., 2006, 62, 244–261 CrossRef CAS PubMed.
- J. Wang and T. Hou, J. Chem. Inf. Model., 2012, 52, 1199–1212 CrossRef CAS PubMed.
- A.-J. Li and R. Nussinov, Proteins: Struct., Funct., Bioinf., 1998, 32, 111–127 CrossRef CAS.
-
F. M. Fowkes, Chemistry and physics of interfaces, American Chemical Society, Washington, D. C., 1965, pp. 1–12 Search PubMed.
- R. J. Good and L. Girifalco, J. Phys. Chem., 1960, 64, 561–565 CrossRef CAS.
-
R. C. Weast, M. J. Astle and W. H. Beyer, et al., CRC handbook of chemistry and physics, CRC Press, Boca Raton, FL, 1988, vol. 69 Search PubMed.
-
A. F. Barton, CRC handbook of solubility parameters and other cohesion parameters, Routledge, 2017 Search PubMed.
-
C. L. Yaws, Thermophysical properties of chemicals and hydrocarbons, William Andrew, 2008 Search PubMed.
-
D. W. Van Krevelen and K. Te Nijenhuis, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier, 2009 Search PubMed.
-
D. R. Lide, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, 1995 Search PubMed.
-
M. Lechner, C. Wohlfarth and B. Wohlfarth, Surface tension of pure liquids and binary liquid mixtures, Springer, 2015 Search PubMed.
- O. Ozkan and H. Y. Erbil, Surf. Topogr.: Metrol. Prop., 2017, 5, 024002 CrossRef.
-
E. W. Flick, Industrial solvents handbook, 1998 Search PubMed.
-
S. Wu, Polymer interface and adhesion, M. Dekker, New York, 1982, vol. 188 Search PubMed.
- C. M. Phan, C. V. Nguyen and T. T. Pham, J. Phys. Chem. B, 2016, 120, 3914–3919 CrossRef CAS PubMed.
- W. D. Harkins, E. C. Davies and G. L. Clark, J. Am. Chem. Soc., 1917, 39, 541–596 CrossRef CAS.
- S. Sugden, J. Chem. Soc., Trans., 1924, 125, 1167–1177 RSC.
- A. Burdzik, M. Stähler, M. Carmo and D. Stolten, Int. J. Adhes. Adhes., 2018, 82, 1–7 CrossRef CAS.
- B. Jańczuk, T. Białopiotrowicz and A. Zdziennicka, J. Colloid Interface Sci., 1999, 211, 96–103 CrossRef PubMed.
- R. N. Wenzel, J. Phys. Chem., 1949, 53, 1466–1467 CrossRef CAS.
- J. Göhl, A. Mark, S. Sasic and F. Edelvik, Int. J. Multiphase Flow, 2018, 109, 164–177 CrossRef.
- V. Starov, Colloid Polym. Sci., 2013, 291, 261–270 CrossRef CAS.
-
K.-Y. Law and H. Zhao, Surface wetting: characterization, contact angle, and fundamentals, Springer, Switzerland, 2016 Search PubMed.
- S. Hasebe, Proc. NIP & Digital Fabrication Conference, 2008, 2, 519–522 Search PubMed.
- A. Neumann, Adv. Colloid Interface Sci., 1974, 4, 105–191 CrossRef CAS.
-
C. Bischof, R.-D. Schulze, W. Possart and H. Kamusewitz, The influence of the surface state of polymers on the determination of the contact angle, in Adhesion 12, ed. K. W. Allen, Elsevier Applied Science, London, 1988, pp. 1–16 Search PubMed.
- C. F. Fan and T. Cagin, J. Chem. Phys., 1995, 103, 9053–9061 CrossRef CAS.
- M. Latva-Kokko and D. H. Rothman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 046701 CrossRef CAS PubMed.
- M. Lundgren, N. L. Allan, T. Cosgrove and N. George, Langmuir, 2002, 18, 10462–10466 CrossRef CAS.
- B. Kong and X. Yang, Langmuir, 2006, 22, 2065–2073 CrossRef CAS PubMed.
-
H.-J. Butt, K. Graf and M. Kappl, Physics and chemistry of interfaces, John Wiley & Sons, 2013 Search PubMed.
- G. Navascues, Rep. Prog. Phys., 1979, 42, 1131 CrossRef.
- R. Oriani, J. Chem. Phys., 1950, 18, 575–578 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Wettability spheres for all polymers, surface tensions results using a constant probe radius, plot of the experimental vs. calculated contact angles of different liquids on polystyrene and polypropylene, molecular structure of the studied compounds, results using Y-MD method, and tabulated contact angles values. See DOI: 10.1039/d0sm00197j |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Herman
Wijshoff
bc,
Jurriaan A.
Luiken
b and
Wouter K.
den Otter
*a,
Herman
Wijshoff
bc,
Jurriaan A.
Luiken
b and
Wouter K.
den Otter
 a
a
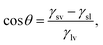

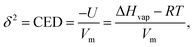
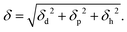
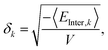
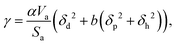
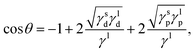
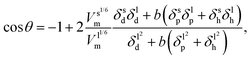
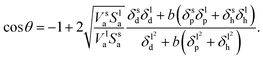
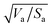 and assumes identical values of α for solids and liquids (i.e., αl = αs). While keeping in mind that both of these equations ignore the effect of surface roughness and inhomogeneities, they can be used to predict θ if the various dispersion, polar and hydrogen bonding components of the solubility parameter are known.
and assumes identical values of α for solids and liquids (i.e., αl = αs). While keeping in mind that both of these equations ignore the effect of surface roughness and inhomogeneities, they can be used to predict θ if the various dispersion, polar and hydrogen bonding components of the solubility parameter are known.




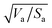 , can be treated as coordinates of a point in three-dimensional space. Then, by solving eqn (10) for a specific substrate and a predefined contact angle, a wettability sphere is obtained as shown in Fig. 9. Note that the coefficient b of eqn (10) is taken into account in the coordinates of the polar and hydrogen-bonding components to generate a sphere instead of a spheroid. Here again, in eqn (10), we consider b to be a constant equal to 0.6255. Liquids that lie inside the resulting sphere for a certain predefined low contact angle, will spread on the corresponding substrate.
, can be treated as coordinates of a point in three-dimensional space. Then, by solving eqn (10) for a specific substrate and a predefined contact angle, a wettability sphere is obtained as shown in Fig. 9. Note that the coefficient b of eqn (10) is taken into account in the coordinates of the polar and hydrogen-bonding components to generate a sphere instead of a spheroid. Here again, in eqn (10), we consider b to be a constant equal to 0.6255. Liquids that lie inside the resulting sphere for a certain predefined low contact angle, will spread on the corresponding substrate.