Impact of wormlike micelles on nano and macroscopic structure of TEMPO-oxidized cellulose nanofibril hydrogels

Abstract

In this work, we investigated the effect of adding surfactant mixtures on the rheological properties of TEMPO-oxidized cellulose nanofibril (OCNF) saline dispersions. Three surfactant mixtures were studied: cocamidopropyl betaine (CAPB)/sodium dodecyl sulfate (SDS), which forms wormlike micelles (WLMs); cocamidopropylamine oxide (CAPOx)/SDS, which forms long rods; and CAPB/sodium lauroyl sarcosinate (SLS), which forms spherical micelles. The presence of micelles in these surfactant mixtures, independent of their morphology, leads to an increase of tan δ, making the gels less solid-like, therefore acting as a plasticizer. WLMs were able to suppress strain stiffening normally observed in OCNF gels at large strains. OCNF/WLM gels have lower G′ values than OCNF gels while the other micellar morphologies have a reduced impact on G′. The presence of unconnected micelles leads to increased dissipative deformation in OCNF gels without affecting the connectivity of the fibrils, while the presence of entangled micelles interferes with the OCNF network.

---

1 Introduction

Soft materials and complex fluids are ubiquitous materials in modern life. Ever present in food and health-care products, additives are employed as tools to tailor the right rheological response according to the end applications. The rheological behaviour of these additives is not simply determined by the intrinsic properties of their components, but how their 3D structure interacts and is shaped at different length-scales. Physical hydrogels are of particular interest, as their self-assembled 3D-structures are maintained by a fine balance of transient interactions. By playing with this balance, the physical properties can be tuned. One way to influence the gel network self-assembly is to combine different types of networks in order to guide or restrict their self-assembly.¹ Cellulose nanofibrils, a type of nanocellulose, can form colloidal networks.^2,3 In plants, cellulose is found as a tightly bound pack of nanosized fibrils, which, once individualized, provide a renewable source of nanoparticles, also called nanocelluloses.^4,5 These nanocelluloses can be roughly divided into two main groups: cellulose nanofibrils (CNFs), obtained via mechanical disintegration, and cellulose nanocrystals (CNCs), obtained from acid hydrolysis of plant-based cellulose. CNFs have lengths of a few hundred nanometres and cross-sections of up to tens of nanometres, leading to particles with very large aspect ratios, while CNCs are generally shorter cylinders.⁵ Nanocelluloses can be readily surface modified, allowing an exceptional level of tailoring to specific applications.^6–10 A common modification is TEMPO-mediated oxidation,¹¹ a chemo-selective oxidation of the glucosyl C6 primary hydroxyl groups by NaOCl mediated by (2,2,6,6-tetramethyl-piperidin-1-yl)oxyl (TEMPO)/NaBr in water. The resulting oxidized cellulose nanofibrils (OCNFs) are anionic nanoparticles capable of forming stable dispersions of individualized nanofibrils in water. OCNF dispersions can undergo gelation due to changes in the aqueous environment such as addition of alcohols,¹² surfactants,^13,14 salts,^15–18 or block copolymers,¹⁹ and changes in pH^20–22 or temperature.²³ Surfactants are capable of self-assembling in solution to form supra-molecular aggregates that can adopt a myriad of forms.²⁴ Spherical micelles are the most common morphology, but cylindrical, lamellar and vesicle morphologies can form given the right environment.²⁵ Of particular interest are the long and flexible cylindrical micelles, commonly named wormlike micelles (WLMs), as their rheological behaviour is similar to that of polymers and they are able to form entangled networks, imparting strong viscoelastic properties to the solution.^25,26 A convenient way to obtain WLMs is through surfactant mixtures, as the range of mixed micellar aggregates accessible can be controlled by tuning the mixture composition. Also, the system can benefit from the surfactants' individual properties.²⁶ Combinations of surfactants are also more relevant to commercial and technological products, which usually contain a multitude of components.²⁷ To obtain the WLMs, we chose to work with the mixture of cocamidopropyl betaine and sodium dodecyl sulphate under saline conditions.²⁸ Cocamidopropyl betaine is one of the most common foam boosters used in shampoos, mainly due to its mildness and ability to form WLMs.²⁹ In this work, we combine both contributions: colloidal networks from OCNFs and WLM entangled networks from the surfactant mixtures. We studied the influence of surfactant mixtures on the gelation behaviour of OCNFs under saline conditions. Three mixtures, offering three different micellar morphologies were studied: cocamidopropyl betaine (CAPB)/sodium dodecyl sulphate (SDS), cocamidopropylamine oxide³⁰ (CAPOx)/SDS and CAPB/sodium lauroyl sarcosinate³¹ (SLS). Under saline conditions, CAPB/SDS mixtures will form long rodlike micelles and, under the right conditions,²⁸ generate an entangled network of wormlike micelles (WLMs), while CAPOx/SDS formed shorter cylinders and CAPB/SLS formed spherical micelles. OCNF alone also gels under saline conditions.¹⁸ Salt is a common component in formulations where these surfactants and their mixtures are employed. The use of sodium chloride as the salt of choice both serves to induce the different micellar morphologies observed as well as imitate a common environment in applied uses. We explored the impact of the WLM entangled network on the OCNF network in contrast with other micellar aggregates also obtained from these surfactant mixtures. The gels obtained were studied via rheology and small-angle neutron scattering, providing insights on the benefits of combining these two networks and the presence or absence of cross-interactions between the micellar and nanoparticle networks.

2 Materials and methods

2.1 Materials

TEMPO oxidized cellulose nanofibrils, OCNFs, with an ∼25% degree of oxidation, produced from purified softwood fibre processed via high pressure homogenization, were kindly provided by Croda Europe Ltd. These were further purified by dialysis against ultra-pure water (DI water), 18.2 MΩ cm, for 24 h. Then, the dispersion was acidified to pH 3 using HCl solution and dialysed (cellulose dialysis tubing MWCO 12400) against DI water for 24 h. The dialysed OCNF was processed via mechanical shear (ULTRA TURRAX, IKA T25 digital, for 30 minutes at 6500 rpm) and the pH was adjusted to 7 using NaOH solution and further dialysed against DI water for 3 days. The DI water was replaced twice a day. This leads to the formation of a sodium-salt, as all –COOH groups on the OCNF are now converted to –COONa. After a second dialysis step, the dispersion was diluted to ca. 2 wt% and dispersed using a sonication probe (Ultrasonic Processor, FB-505, Fisher). 40 mL of the 2 wt% dispersion was sonicated via a series of 1 s on 1 s off pulses for a total time of 60 min at 30% amplitude in an ice bath. Sodium dodecyl sulfate, SDS, (≥99.0%), N-lauroylsarcosine sodium salt, SLS, (≥99.0%) and sodium chloride, NaCl, (≥99%) were obtained from Sigma-Aldrich and used without further treatment. Commercial grade cocamidopropyl betaine (CAPB, Crodateric CAB 30-LQ-(MH), 30% aqueous solution, batch No. 1189504) and cocamidopropylamine oxide (CAPOx, Incromine Oxide C-LQ-(MH), 25% aqueous solution, batch No. 838616) were kindly donated by Croda Europe Ltd. CAPB and CAPOx were freeze-dried and redispersed before use. All samples were prepared by dilution of the aqueous stock dispersions and concentrations are given in weight/weight. Samples for small-angle neutron scattering experiments were redispersed in D₂O (Sigma-Aldrich, 99.9 atom% D) from freeze-dried stock. All samples are in 1 wt% (ca. 173 mM) NaCl solutions. Samples were measured within 4 days of preparation. This time window allows the samples to reach a steady-state while minimizing chances of microbial contamination.

2.2 Methods

Rheological measurements were conducted using a stress-controlled Discovery Hybrid Rheometer, Model HR-3 (TA Instruments, USA) equipped with a sand-blasted 40 mm parallel plate geometry over a sand-blasted lower plate. Temperature was controlled via a Peltier unit (±0.1 °C) and kept at 25 °C. A thin layer of low viscosity mineral-oil was added to the edge of the geometry to prevent sample evaporation. Oscillatory amplitude sweeps were done at a fixed angular frequency (ω) of 6.28 rad s⁻¹ and amplitude strain (γ) from 0.01 to 100%. Frequency sweeps were conducted at an γ of 0.1%, within the linear viscoelastic range, covering the ω of 0.01 to 50 rad s⁻¹. All samples were measured between 24 and 48 h after preparation. Small-angle neutron scattering (SANS) measurements were conducted using the time-of-flight diffractometer instrument SANS2d at the STFC ISIS Neutron and Muon Source (Didcot, UK).³² Incident wavelengths from 1.75 to 16.5 Å were used with a sample-to-detector distance of 4 m, corresponding to a total scattering vector range q from 4.5 × 10⁻³ to 0.75 Å ⁻¹. The sample temperature was controlled using an external circulating thermal bath (Julabo, DE). The scattering intensity was converted to the differential scattering cross-section in absolute units using ISIS standard procedures.³³ Samples were loaded in 1 mm path length, 1 cm wide optical quartz cells.^34,35 Contrast match experiments were done at 15 wt% D₂O, which is the contrast match point for the surfactant mixtures. All other SANS experiments were done in 100 wt% D₂O. SANS data were fitted using SASView³⁶ or internally developed routines written in FORTRAN.¹⁸ The intensity I(q) can be written as follows:

I(q) ∝ P(q)S(q) (1)

with P(q) being the form factor of the objects studied, giving information about their shape and S(q) being the structure factor associated with the interactions between the objects probed. Concerning OCNF, a detailed description of the data treatment for oxidized cellulose nanofibrils under water or saline conditions has been published by Schmitt et al.¹⁸ Briefly, the nanofibrils are modelled as rigid cylinders with an elliptical cross-section (eqn (2)),^37,38 wherein R_maj (Å) is the major radius of the fibrils, ε is the ellipticity of the cross-section (ε = R_min/R_maj), and L (Å) is the length of the fibrils.

P(q) = P(q,R_maj,ε,L,σ) = 〈F_CS²(q,R_maj,ε)〉_σP_rod(q,L) (2)

where
is the contribution associated with the elliptical cross-section and
is the contribution from the length of the fibrils, with
J₁ is a first order Bessel function and σ represents the polydispersity in size of the cross-section, following the Schulz–Zimm distribution.¹⁸

This decoupling between length and cross-section can be achieved due to the random distribution of orientation of the fibrils, and because R_maj < L/5.

Fibril–fibril attraction was modelled using the PRISM model,³⁹ with ν_RPA < 0 being the strength of the attraction.

Depending on the surfactant used, micelles in saline solution can be shaped as spheres, (CAPB/SLS), rodlike particles (CAPOx/SDS) or even WLMs (CAPB/SDS). Spherical micelles are defined by their radius R (Å), and the polydispersity in size σ.⁴⁰ The form factor used to describe spheres (eqn (3)) is:

P(q,R,σ) = 〈F_sphere²(q,R)〉_σ (3)

where
where V(R) is the volume of a sphere of radius R.

Interactions between spherical micelles are modelled using the hard-sphere repulsion model, with ϕ_HS being the volume fraction of micelles interacting (in %) and R_HS > R being the hard-sphere radius of interaction. For SLS, the Hayter–Penfold mean spherical approximation was used instead of hard-spheres to model the electrostatic interactions between micelles. This model uses the parameter Z, the value of the charge (in electrons), and ϕ_int, the volume fraction of micelles interacting (in %), to describe the interactions.^41,42

For rodlike micelles with a cross-section radius R, length L and polydispersity in radius σ, the intensity can be described similarly to that for OCNFs without interaction, hence using the form factor given in eqn (2), with ε = 1 for a spherical cross section. Finally, wormlike micelles can be modelled as flexible cylinders. This can be obtained by replacing the term P_rod in eqn (2) by P_flex = (q,L,b_Kuhn), which depends on the length, L, of the flexible cylinder and b_Kuhn, the Kuhn length of the wormlike micelle. A complete description of P_flex can be found in ref. 37 and is not repeated here.

Similar to OCNFs, rodlike micelles can experience repulsion, modelled via the PRISM model,³⁹ where ν_RPA > 0 is the strength of the repulsion and R_c ≥ R is the cross-section radius of interaction. WLMs are modelled using the same parameters, but adding the Kuhn length b_Kuhn (in Å; with R < b_Kuhn < L). The Kuhn length is defined as twice the persistence length of the WLMs, i.e., the length scale where WLMs can be considered as rigid. Details of modelling of spherical,^41,42 rodlike⁴³ or wormlike micelles³⁷ can be found elsewhere. Radial polydispersity improved the fittings for the CAPB/SLS mixtures. For the other systems, polydispersity was not considered as it did not result in better fitting of the data. In the case of mixtures of OCNFs and micelles, the signal is modelled as a sum of the two contributions, without adding any extra contributions from OCNF–micelle interactions. This is a simplified calculation of the intensity but one that is sufficient to describe the data accurately.

Raw data is available on University of Bath Research Data Archive.⁴⁴

3 Results and discussion

3.1 Surfactant behaviour

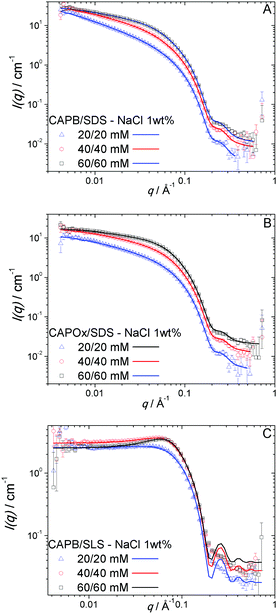
In this work, we studied the impact of the micellar morphology on the gelation properties of TEMPO-oxidized cellulose nanofibrils (OCNFs). We focused on three surfactant mixtures, CAPB/SDS, CAPOx/SDS and CAPB/SLS, as each of these forms a different type of micelle. Before covering the OCNF/surfactant hydrogel systems, we present a brief characterisation of the surfactant solutions on their own. Here, we establish the baseline behaviour of the individual surfactants first, as a prerequisite to determining how they interact with the OCNF network. The solution behaviour of SDS micelles is well established.^13,43,45,46 They are expected to be ellipsoidal objects with half axes of 13 × 23 × 23 Å, in solutions with salt concentrations smaller than 0.5 M NaCl.⁴³ For the three other surfactants studied in this work, CAPB,^{28,31,47–49} CAPOx, and SLS,^47,50 the information available is more limited. We conducted SANS experiments at three different concentrations above the critical micellar concentration (CMC) for each of these surfactants. The CMC value for SLS at 25 °C in water is 12.7 mM;⁴⁷ for CAPB, at 25 °C in 0.2 M NaCl, it is 5.6 mM;⁵¹ and for CAPOx at room temperature in 1 wt% NaCl, it is 0.06 mM (measured as part of this work via surface tension – Fig. S1, ESI†). The SANS data for the CAPB and CAPOx solutions at all concentrations can be adequately fitted using a spherical model with a hard-sphere structure factor^40,52 (Fig. 1A and B). They form spherical micelles of similar dimensions, radius R = 23 ± 1 and 24 ± 1 Å for CAPB and CAPOx, respectively. No interaction was needed to fit the lowest concentration while a small increase in the repulsion is observed with concentration; nonetheless, this is found to be very weak (fitted parameters are in Table S1A and B, ESI†). The anionic surfactant, SLS, forms spheres of radius R = 19 ± 1 Å and evidenced stronger interactions, which are better described using a structure factor for charged spheres, in this case the Hayter–Penfold mean spherical approximation (MSA)^41,42 (Fig. 1C and Table S1C, ESI†). Overall, the shape and dimensions of the micelles did not show any significant change over the concentration range studied: 20 to 60 mM (Fig. 1A–C). All surfactants studied have a hydrocarbon tail containing twelve carbon atoms, thus the difference between them lies in the headgroups. CAPB and CAPOx micelles, within the error, have the same shape and size. The headgroups are of a similar nature, betaine for CAPB and an amine oxide for CAPOx. The main difference between these surfactants lies in the charge distribution in the headgroup, CAPOx has a N→O dative bond, which has higher polarity than a covalent bond but not a formal charge separation, making CAPOx a non-ionic surfactant. For CAPB, charge separation is present in the betaine headgroup, but the net charge is zero. However, the differences between them are small enough to not affect the morphology of the single surfactant micelles. SLS micelles are significantly smaller, having a shorter and more compact headgroup than the other surfactants. A more in-depth discussion of the pure surfactant phase diagrams is outside the scope of this work, but this topic has been studied in depth elsewhere.⁵³ The mixtures of surfactants, however, showed a wider range of micellar morphology. In Fig. 2, the SANS data and fittings are presented for the mixtures CAPB/SDS, CAPOx/SDS and CAPB/SLS as a function of the concentration. We kept an equimolar ratio while changing the overall concentrations to give solutions at 20/20, 40/40 and 60/60 mM surfactants. At first glance, the mixtures can be split into two groups depending on the cosurfactant, with either SDS (Fig. 2A and B) or with SLS (Fig. 2C). For CAPB/SDS and CAPOx/SDS, the data were fitted using a combination of a semi-flexible cylinder³⁷ form factor and a random-phase approximation structure factor.^18,54,55

Fig. 1 SANS curves and fits for (A) CAPB, (B) CAPOx and (C) SLS as a function of the surfactant concentration in 1 wt% NaCl.

Fig. 2 SANS curves and fits for (A) CAPB/SDS, (B) CAPOx/SDS and (C) CAPB/SLS as a function of the surfactant concentration in 1 wt% NaCl.

The fittings suggest long, rodlike, strongly interacting micelles for both CAPB/SDS and CAPOx/SDS mixtures. The length of the micelles, however, lies outside of the q-range accessible by the measurement and cannot be determined from the SANS data. It was arbitrarily fixed as 1000 Å. From the fittings (Table S2A and B, ESI†), we obtained the cross-sectional radius for the rodlike micelles, R = 18 Å, for both CAPB/SDS and CAPOx/SDS, and the ν_RPA coefficient, which provides insights on the magnitude and type of interactions (ν_RPA > 0 repulsive, ν_RPA < 0 attractive). However, the magnitude of ν_RPA depends on the micelle length, which was arbitrarily fixed. Therefore, only relative changes within a given series will be discussed. At 20/20 mM, ν_RPA = 16.2 was obtained for CAPB/SDS and ν_RPA = 64.2 was obtained for CAPOx/SDS, showing that strong interactions are present in both cases but CAPOx/SDS micelles show apparently stronger repulsive interactions. As the actual value of ν_RPA will depend on the length of the micelle, the stronger repulsive interactions for CAPOx/SDS compared to CAPB/SDS at the same concentration can either be described by a stronger interaction or longer micelles, or even both. While the SANS data cannot provide information about the length of the micelles, the rheological behaviour of the mixtures can add further clarification. Systems formed by long flexible cylinders such as polymers and WLMs will form entangled networks above an overlap concentration. These entangled networks have a characteristic rheological profile. They follow the behaviour expected for a Maxwell fluid.^25,26 In Fig. 3, we present the frequency sweep for both CAPB/SDS and CAPOx/SDS at 60/60 mM in 1 wt% NaCl. All of the single surfactants and the mixture CAPB/SLS showed Newtonian behaviour, however the CAPB/SDS solution shows the characteristic behaviour of a Maxwell fluid, associated with wormlike micelles.^25,26 In this case, a two-element Maxwell model was used to satisfactorily fit the data. CAPOx/SDS solutions showed very weak viscoelasticity close to the operational limit of the rheometer, which could not be satisfactorily fitted with a Maxwell model. A likely explanation is that CAPOx/SDS micelles are short rods, not long enough to generate an entangled network at the concentration assayed. The high repulsion observed via SANS also suggests they are not flexible cylinders. One cause for the lack of flexibility is a highly charged surface, since repulsive electrostatic interactions would lead to a loss of flexibility. As discussed earlier, the amine oxide group from the CAPOx headgroup has a N→O dative bond, which has no formal charge separation, which could result in weaker electrostatic interactions with SDS than the betaine headgroup in CAPB, where formal charges are present. Even though CAPB and CAPOx have no net charge at the experimental pH (neutral), the local charge distribution of the CAPB headgroup should be more effective at reducing electrostatic repulsion than the CAPOx headgroup.

Fig. 3 Oscillatory shear frequency sweeps for CAPB/SDS and CAPOx/SDS solutions at 60/60 mM surfactant in 1 wt% NaCl (G′ closed symbols, G′′ open symbols). Lines displaying the fitting to a two-element Maxwell model are drawn to guide the eye.

For the CAPB/SLS mixture, as shown in Fig. 2C, the data were fitted with a combination of a sphere form factor⁴⁰ and a Hayter–Penfold MSA (charged spheres) structure factor.^41,42 The fittings resulted in spherical micelles of R = 24 ± 1 Å in radius, essentially identical to CAPB micelles except for the enhanced interactions, due to the charge contribution of SLS.

3.2 OCNF/surfactant systems

The effect of anionic surfactants on OCNF gelation has been previously studied by our group.^13,14 In this work, we focus on the contribution of CAPB and CAPOx, both alone and in mixtures with either SDS or SLS. In Fig. 4, the SANS curves for CAPB, CAPOx and SLS in 1 wt% OCNF/1 wt% NaCl are presented for three surfactant concentrations, 20, 40 and 60 mM. The surfactant contribution is strong in the SANS pattern dominating the overall signal, however the OCNF signal is still clearly present. The curves can be described by the addition of spherical micelles, using the previously established behaviour for CAPB, CAPOx and SLS (Fig. 1), plus the contribution from OCNF (without polydispersity for the cross-section), R_maj = 53 ± 1 Å, fixed length = 1600 Å and ε = 0.24 ± 0.02, as established in a previous study,¹⁸ adjusting the scale factor and ν_RPA. These results show that the OCNFs and the surfactant micelles in these systems are not disturbed by the other's presence and that no strong interactions (either attractive or repulsive) between them are present at this length scale. The extracted ν_RPA parameter associated with OCNF is negative, −1.9, in all of the scattering patterns from OCNF/CAPB, OCNF/CAPOx and OCNF/SLS, which is in line with the expected attractive interactions of OCNFs in saline solutions.¹⁸ The OCNF does not affect the morphology of the single surfactant micelles, nor is the OCNF network sensitive to the type of surfactant used. The rheological behaviour, however, is strongly affected by the presence of the surfactants (Fig. 5A–C). OCNF in saline solutions is known to form gels due to strong attractive interactions.¹⁸ The addition of either CAPB or CAPOx leads to a significant reduction of G′ and G′′ but without affecting the overall gel behaviour, with G′ ≫ G′′ for all concentrations of surfactant, suggesting that the micelles disrupt the OCNF network. SLS (Fig. 5C) has a smaller effect, increasing G′ slightly at 20 mM, with a further concentration increase leading to a reduction of G′. A likely scenario is that the micelles populate the interstices of the OCNF network and disrupt the network connectivity by imposing a steric barrier to OCNF interactions.

Fig. 4 SANS curves and fits for (A) CAPB, (B) CAPOx and (C) SLS mixtures as a function of the surfactant concentration in 1 wt% OCNF/1 wt% NaCl.

Fig. 5 Oscillatory shear frequency sweeps for (A) CAPB, (B) CAPOx and (C) SLS mixtures as a function of surfactant concentration in 1 wt% OCNF/1 wt% NaCl (G′ closed symbols, G′′ open symbols).

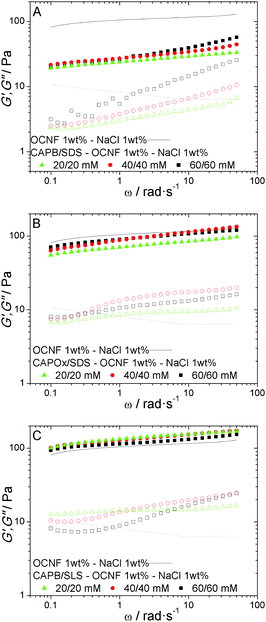
The combination of OCNF and the surfactant mixtures (CAPB/SDS, CAPOx/SDS and CAPB/SLS), however, leads to more visible changes in the OCNF gel behaviour. In Fig. 6A–C, oscillatory frequency behaviour for the three mixtures as a function of the surfactant concentration is shown. Based on the previously discussed SANS and rheological data (Fig. 2A–C and 3), WLMs, long rods and spherical micelles are formed in CAPB/SDS, CAPOx/SDS and CAPB/SLS mixtures, respectively. For the OCNF/CAPB/SDS mixtures (Fig. 6A), containing WLMs, we observe a significant drop in G′ and G′′ when compared to OCNF gels (Fig. 5A). An inversion of the G′′ frequency dependence is also observed. In the presence of WLMs, an exponential increase, which decreases with the surfactant concentration, is observed, while without WLMs, G′′ values decayed exponentially with increasing frequency. Moreover, G′′ is also more sensitive to the surfactant concentration than G′. For both CAPOx/SDS and CAPB/SLS (Fig. 6B and C), the impact of the micellar aggregates on the OCNF gel network is smaller than that with the WLMs (Fig. 6A) or single surfactant micelles (Fig. 5A and B). WLMs, under the right conditions, form entangled networks, adding a new relaxation process, reptation, which is not present in the OCNF network. Based on the rheological behaviour of the CAPB/SDS solution (Fig. 3), one can assume that the entangled network has a shorter relaxation time than the OCNF network (Fig. 5 – black line). OCNF forms physical gels, and their frequency sweeps show a weak frequency dependency that translates to finite but very long relaxation times for the OCNF network. Meanwhile, as can be seen from Fig. 3, CAPB/SDS WLMs have a G′, G′′ cross-over at 1 rad s⁻¹, therefore a relaxation time of ca. 150 ms. Hence, in OCNF/CAPB/SDS hydrogels, the WLM entangled network is capable of undergoing mechanical relaxation in a time frame much shorter than that of the OCNF network, adding extra dissipative contributions, in the form of reptation and breaking/reforming micellar dynamics, to the system. This leads to the observed increase of G′′ in addition to the drop in G′ due to the steric constraints imposed on the OCNF network by the micelles.

Fig. 6 Oscillatory shear frequency sweeps for (A) CAPB/SDS, (B) CAPOx/SDS and (C) CAPB/SLS mixtures as a function of surfactant concentration in 1 wt% OCNF/1 wt% NaCl (G′ closed symbols, G′′ open symbols).

Only a small drop in G′ is observed for CAPOx/SDS (rodlike micelles) in the presence of OCNF and a slight increase is observed for CAPB/SLS (spherical micelles). G′′ is more sensitive to the surfactant presence, as, in both cases, an increase in the frequency dependence of G′′ is observed. Curiously, when comparing spherical micelles of the single surfactant and mixtures (Fig. 5A–C and 6C), their behaviour is dissimilar. Surfactant mixtures have a smaller effect on G′ than single surfactants and a more significant impact on G′′ when comparing systems with OCNF at the same total surfactant concentration; 40 mM single surfactants vs. 20/20 mM mixtures, with the exception of CAPB/SLS mixtures, which showed little effect. The literature⁵⁶ suggests that synergism between CAPB and anionic surfactants results in lower free surfactant concentrations in their mixtures than alone, so this is unlikely to be due to free surfactant binding to the OCNFs and changing inter-fibrillar interactions. Another visible change in OCNF gel behaviour in the presence of WLMs can be seen in the deformation behaviour. In Fig. 7A–C, oscillatory strain sweeps are presented for OCNF dispersions and OCNF/surfactant mixtures. In the nonlinear region of the strain sweep, G′′ shows strain stiffening, i.e., an increase in magnitude of G′′ or overshooting⁵⁷ in OCNF gels (Fig. 7 – black line), which is suppressed when WLMs are present (Fig. 7A), but the gels are unaffected by rodlike or spherical micelles (Fig. 7B and C), apart from a decrease of the strain value at which the stiffening of the gel occurs. This strain stiffening, during strain deformation, reflects an additional resistance to the applied strain from the system.⁵⁸ For the OCNF case, or generally speaking, for charged anisotropic particles, the applied deformation leads to an increase in the orientation of the particles; below the linear viscoelastic range (LVR), this shear induced orientation is within the normal range of movement of the particles at rest. Past the LVR, the shear induced orientation is hindered by the repulsive interactions of the charged OCNFs, leading to the strain stiffening. The WLMs could be suppressing the strain stiffening in two ways. The added relaxation through reptation could help to offset the stiffening as observed in interpenetrating networks,⁵⁹ or the physical presence of the WLMs could affect the OCNF shear orientation. We note that both systems are likely to be similar in terms of changes in ionic strength arising from the surfactant counterions; as CAPB/SDS and CAPB/SLS are sodium salts, they do not appear to play a role in suppressing the strain stiffening. However, rheological data do not provide molecular insights into these systems and since the SANS data were collected in a quiescent state, it is therefore not possible to provide an unambiguous clear pictorial view of the actual mechanism or mechanisms taking place.

Fig. 7 Oscillatory shear amplitude sweeps of (A) CAPB/SDS, (B) CAPOx/SDS and (C) CAPB/SLS mixtures as a function of surfactant concentration in 1 wt% OCNF/1 wt% NaCl (G′′ closed symbols, G′′ open symbols).

The SANS data for OCNF/surfactant mixtures, however, show that the OCNF and micelle contributions to the scattering patterns are still additive. In Fig. 8A and B, SANS curves for OCNF/CAPB/SDS and OCNF/CAPOx/SDS systems are presented. In both cases, the curves can be fitted using the previous surfactant mixture scattering patterns (Fig. 2A and B) and the previously established OCNF profile.¹⁸ To clarify the effect of the WLMs on the OCNF network in these mixtures, SANS data were also collected in 15/85 wt% D₂O/H₂O mixtures (Fig. 8C). At this D₂O/H₂O ratio, the scattering length density of the surfactant is matched to that of the solvent and the surfactant is no longer visible. Therefore, the SANS signal originates only, or in majority, from the OCNFs. The OCNF scattering is not affected by the concentration of the surfactant mixtures, from 20/20 to 60/60 mM, and it shows a weaker attractive interaction than expected at 1 wt% NaCl, ν_RPA = −1.1 vs. ν_RPAca. −1.8, respectively.¹⁸ This suggests that the WLMs, once in place, slightly reduce the attractive forces between the OCNFs, but do not change the OCNF dispersion behaviour, which would be in line with the WLMs just creating an excluded-volume barrier to the OCNF–OCNF interactions without specific WLM–OCNF interactions.

Fig. 8 SANS curves and fits for (A) CAPB/SDS in 100 wt% D₂O, (B) CAPOx/SDS in 100 wt% D₂O and (C) CAPB/SDS in 15 wt% D₂O mixtures as a function of the surfactant concentration in 1 wt% OCNF/1 wt% NaCl.

4 Conclusions

In this work, we studied the effect of micellar morphology on the gel behaviour of OCNFs under saline conditions. We observed that both micellar morphology and the presence of single surfactants or surfactant mixtures can have an impact on OCNF gel behaviour. Small-angle neutron scattering was used to probe the structure of the micellar aggregates within the OCNF network, showing both that the micelles are unperturbed by the presence of the OCNF network and that they are not interacting with the fibrils at the length scale probed in SANS. This shows that the rheological modulation provided by the micelles is likely due to excluded-volume effects rather than molecular interactions. Wormlike micelles (CAPB/SDS mixtures) had the largest impact, both reducing G′ and G′′ as well as changing the moduli frequency dependence, making the gel less stiff and more plastic. WLMs also suppressed strain stiffening normally observed in OCNF gels at large oscillatory strains. For spherical micelles, the single surfactants studied (CAPB and CAPOx) lowered both G′ and G′′, while the mixtures CAPB/SLS and CAPOx/SDS lead to small variations in G′ and a large effect on G′′ frequency dependency. These results suggest that unconnected spherical and rodlike micelles present within the OCNF network only add to the dissipative deformation (increase in G′′) without major impacts on the structure of the OCNF network (G′), while the WLMs affect the connectivity of the OCNF network, leading to the drop of G′ and G′′ observed. In summary, small, unconnected micellar aggregates occupy space within the OCNF network, weakening it, likely by reducing the connectivity of the fibril network. For long, interconnected micellar aggregates, in our case WLMs, the system behaves as a sum of the fibril and entangled network contributions, both reducing the OCNF network connectivity and adding reptation relaxation to the hybrid hydrogel.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank EPRSC for funding this project (grant number EP/N033310/1). V. Calabrese thanks the University of Bath for supporting his PhD. Experiments at the ISIS Pulsed Neutron and Muon Source were supported by beam time allocations for SANS2D from the Science and Technology Facilities Council under proposal numbers RB1820265³⁴ and RB1910353.³⁵ This work benefited from the use of the SasView application, originally developed under NSF Award DMR-0520547. SasView also contains code developed with funding from the EU Horizon 2020 programme under the SINE2020 project Grant No. 654000. Data supporting this work are freely accessible in the Bath research data archive system at DOI: 10.15125/BATH-00797.

Notes and references

1. M. A. da Silva and C. A. Dreiss, Polym. Int., 2016, 65, 268–279.
2. D. Klemm, B. Heublein, H.-P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393.
3. K. Tan, S. Heo, M. Foo, I. M. Chew and C. Yoo, Sci. Total Environ, 2019, 650, 1309–1326.
4. D. Klemm, F. Kramer, S. Moritz, T. Lindstrom, M. Ankerfors, D. Gray and A. Dorris, Angew. Chem., Int. Ed., 2011, 50, 5438–5466.
5. A. Dufresne, Mater. Today, 2013, 16, 220–227.
6. S. Eyley and W. Thielemans, Nanoscale, 2014, 6, 7764–7779.
7. S. Kalia, S. Boufi, A. Celli and S. Kango, Colloid Polym. Sci., 2014, 292, 5–31.
8. V. Calabrese, M. A. da Silva, J. Schmitt, J. C. Munoz-Garcia, V. Gabrielli, J. L. Scott, J. Angulo, Y. Z. Khimyak and K. J. Edler, Soft Matter, 2018, 14, 7793–7800.
9. R. Nigmatullin, V. Gabrielli, J. C. Munoz-Garcia, A. E. Lewandowska, R. Harniman, Y. Z. Khimyak, J. Angulo and S. J. Eichhorn, Cellulose, 2019, 26, 529–542.
10. F. Rol, M. N. Belgacem, A. Gandini and J. Bras, Prog. Polym. Sci., 2019, 88, 241–264.
11. T. Saito, S. Kimura, Y. Nishiyama and A. Isogai, Biomacromolecules, 2007, 8, 2485–2491.
12. M. A. da Silva, V. Calabrese, J. Schmitt, D. Celebi, J. L. Scott and K. J. Edler, Soft Matter, 2018, 14, 9243–9249.
13. R. J. Crawford, K. J. Edler, S. Lindhoud, J. L. Scott and G. Unali, Green Chem., 2012, 14, 300–303.
14. J. Scott, C. Smith and G. Unali, Aqueous Gels, WO2012171725, A61K8/04, A61K8/34, A61K8/60, A61K8/73, A61Q17/00, A61Q19/00, 2012.
15. H. Dong, J. F. Snyder, K. S. Williams and J. W. Andzelm, Biomacromolecules, 2013, 14, 3338–3345.
16. H. Fukuzumi, R. Tanaka, T. Saito and A. Isogai, Cellulose, 2014, 21, 1553–1559.
17. A. Sone, T. Saito and A. Isogai, ACS Macro Lett., 2016, 5, 1402–1405.
18. J. Schmitt, V. Calabrese, M. A. da Silva, S. Lindhoud, V. Alfredsson, J. L. Scott and K. J. Edler, Phys. Chem. Chem. Phys., 2018, 20, 16012–16020.
19. T. Ingverud, E. Larsson, G. Hemmer, R. Rojas, M. Malkoch and A. Carlmark, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 3415–3424.
20. K. Abe and H. Yano, Carbohydr. Polym., 2011, 85, 733–737.
21. T. Saito, T. Uematsu, S. Kimura, T. Enomae and A. Isogai, Soft Matter, 2011, 7, 8804–8809.
22. L. Mendoza, W. Batchelor, R. F. Tabor and G. Garnier, J. Colloid Interface Sci., 2018, 509, 39–46.
23. V. Calabrese, J. C. Munoz-Garcia, J. Schmitt, M. A. da Silva, J. L. Scott, J. Angulo, Y. Z. Khimyak and K. J. Edler, J. Colloid Interface Sci., 2019, 535, 205–213.
24. H. Hoffmann and G. Ebert, Angew. Chem., Int. Ed. Engl., 1988, 27, 902–912.
25. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
26. S. Ezrahi, E. Tuval and A. Aserin, Adv. Colloid Interface Sci., 2006, 128-130, 77–102.
27. R. G. Laughlin, The Aqueous phase behavior of surfactants, Academic Press, London, 1996.
28. N. C. Christov, N. D. Denkov, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2004, 20, 565–571.
29. P. A. Cornwell, Int. J. Cosmet. Sci., 2018, 40, 16–30.
30. C. L. Burnett, Int. J. Toxicol., 2008, 27, 55–62.
31. H. Lu, M. Yuan, B. Fang, J. Wang and Y. Guo, J. Surfactants Deterg., 2015, 18, 589–596.
32. R. K. Heenan, S. E. Rogers, D. Turner, A. E. Terry, J. Treadgold and S. M. King, J. Neutron Res., 2011, 22, 19–21.
33. ISIS SANS Data Reduction in Mantid, http://www.mantidproject.org/ISIS_SANS.
34. K. J. Edler, N. Mahmoudi, M. A. da Silva, J. Schmitt, V. Calabrese and Z. Hossain, Surfactant induced gelation of TEMPO-oxidized cellulose; Using betaine-based wormlike micelles to modulate rheological behaviour, 2018,  DOI:10.5286/ISIS.E.RB1820265.
35. K. J. Edler, N. Mahmoudi, M. A. da Silva, Z. Hossain, V. Calabrese and J. Schmitt, Gelation of oxidised cellulose nanofibrils with industrially relevant anionic surfactants, 2019,  DOI:10.5286/ISIS.E.RB1910353.
36. M. Doucet, J. H. Cho, G. Alina, J. Bakker, W. Bouwman, P. Butler, K. Campbell, T. Cooper-Benun, C. Durniak, L. Forster, M. Gonzales, R. Heenan, A. Jackson, S. King, P. Kienzle, J. Krzywon, T. Nielsen, L. O'Driscoll, W. Potrzebowski, R. Ferraz Leal, P. Rozycko, T. Snow and A. Washington, SasView version 5.0, available from http://www.sasview.org, 2019.
37. J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612.
38. W.-R. Chen, P. D. Butler and L. J. Magid, Langmuir, 2006, 22, 6539–6548.
39. K. S. Schweizer and J. G. Curro, in PRISM theory of the structure, thermodynamics, and phase transitions of polymer liquids and alloys, ed. L. Monnerie and U. W. Suter, Springer Berlin Heidelberg, Berlin, Heidelberg, 1994, pp. 319–377.
40. A. Guinier, G. Fournet, C. B. Walker and K. L. Yudowitch, Small-Angle Scattering of X-Rays, New York, Chapman & Hall, London, John Wiley & Sons, 1955.
41. J. B. Hayter and J. Penfold, Mol. Phys., 1981, 42, 109–118.
42. J.-P. Hansen and J. B. Hayter, Mol. Phys., 1982, 46, 651–656.
43. M. Bergström and J. Skov Pedersen, Phys. Chem. Chem. Phys., 1999, 1, 4437–4446.
44. M. A. da Silva, V. Calabrese, K. M. Z. Hossain, S. J. Bryant, N. Mahmoudi, J. L. Scott and J. K. Edler, Dataset for “Impact of wormlike micelles on nano and macroscopic structure of TEMPO-oxidized cellulose nanofibrils hydrogels”, University of Bath Research Data Archive, Bath, 2020,  DOI:10.15125/BATH-00797.
45. V. Y. Bezzobotnov, S. Borbely, L. Cser, B. Farago, I. A. Gladkih, Y. M. Ostanevich and S. Vass, J. Phys. Chem., 1988, 92, 5738–5743.
46. Y. Rharbi, L. Chen and M. A. Winnik, J. Am. Chem. Soc., 2004, 126, 6025–6034.
47. G. B. Ray, S. Ghosh and S. P. Moulik, J. Surfactants Deterg., 2009, 12, 131–143.
48. S. Rozanska, Colloids Surf., A, 2015, 482, 394–402.
49. W. Zou, G. Tan, H. Jiang, K. Vogtt, M. Weaver, P. Koenig, G. Beaucage and R. G. Larson, Soft Matter, 2019, 15, 642–655.
50. M. V. Popova and D. Michel, Appl. Magn. Reson., 2014, 45, 353–364.
51. K. Staszak, D. Wieczorek and K. Michocka, J. Surfactants Deterg., 2015, 18, 321–328.
52. J. K. Percus and G. J. Yevick, Phys. Rev., 1958, 110, 1–13.
53. K. D. Danov, P. A. Kralchevsky, S. D. Stoyanov, J. L. Cook, I. P. Stott and E. G. Pelan, Adv. Colloid Interface Sci., 2018, 256, 1–22.
54. S. F. Edwards, Proc. Phys. Soc., London, 1966, 88, 265–280.
55. T. Shimada, M. Doi and K. Okano, J. Chem. Phys., 1988, 88, 2815–2821.
56. G. Szewczyk and K. Wisniewski, in B.2.I - Dish and Household Cleaning, ed. I. Johansson and P. Somasundaran, Elsevier Science B. V., Amsterdam, 2007, pp. 125–195.
57. S. Precha-Atsawanan, D. Uttapap and L. M. C. Sagis, Food Hydrocolloids, 2018, 85, 1–9.
58. K. Hyun, S. H. Kim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2002, 107, 51–65.
59. L. H. Sperling and V. Mishra, Polym. Adv. Technol., 1996, 7, 197–208.

---

Footnote

† Electronic supplementary information (ESI) available: SANS fitting parameters and CMC data. See DOI: 10.1039/d0sm00135j

---