 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatio-temporal heterogeneities in nanosegregated single-molecule polymeric nanoparticles†
Petra
Bačová
 *a,
Emmanouil
Glynos
*a,
Emmanouil
Glynos
 b,
Spiros H.
Anastasiadis
b,
Spiros H.
Anastasiadis
 bc and
Vagelis
Harmandaris
bc and
Vagelis
Harmandaris
 *ad
*ad
aInstitute of Applied and Computational Mathematics (IACM), Foundation for Research and Technology Hellas (FORTH), GR-70013 Heraklion, Crete, Greece. E-mail: pbacova@iacm.forth.gr
bInstitute of Electronic Structure and Laser, Foundation for Research and Technology Hellas (FORTH), GR-70013 Heraklion, Crete, Greece
cDepartment of Chemistry, University of Crete, GR-70013 Heraklion, Crete, Greece
dDepartment of Mathematics and Applied Mathematics, University of Crete, GR-70013 Heraklion, Crete, Greece. E-mail: harman@uoc.gr
First published on 7th April 2020
Abstract
The study of the coupling between structural and dynamical heterogeneities in nanostructured systems is essential for the design of hybrid materials with the desired properties. Here, we use atomistic molecular dynamics simulations to closely examine the dynamical heterogeneities in nanostructured single-molecule nanoparticles consisting of mikto-arm star copolymers with poly(ethylene oxide), PEO, and polystyrene, PS, arms. The particles exhibit an internally nanostructured morphology, resembling either “Janus-like” or “patchy-like” morphology when the functionality of the stars varies. The differences in the local environment result in strong intramolecular dynamical heterogeneities. In the proximity of the star core, geometric constraints promote unfavorable PEO:PS contacts that lead to a behavior similar to dynamically asymmetric miscible polymer blends or disordered copolymers. In contrast, further away from the core, the nanosegregation induces segmental dynamics very similar to the one found in the homopolymer star analogues.
1 Introduction
In an attempt to achieve dynamically rich materials, with complex relaxation spectra tailored for a specific application, two concepts proved to be quite successful: mixing of dynamically dissimilar polymers and modifying the polymer architecture. The first method covers the range of materials such as miscible polymer blends,1–12 linear block copolymers13,14 or nanostructured materials, in which the mutual arrangement of the segregated domains turned out to be the key factor in their dynamical response.15–17 Concerning the polymer architecture, the presence of branch points restricts the motion of the molecule and results in a wide distribution of relaxation processes, which are extended to much longer time scales than in the case of their linear analogues.18–23 In this family of materials, multi-component star polymers serve as a promising example of nanostructured materials, which could combine both approaches, i.e., incorporating dynamically contrasting chains in a complex polymer architecture. However, apart from a demanding synthetic effort, an actual quantification of the dynamical heterogeneities at the local scale in these materials is very challenging. Experimental studies are scarce and they mostly involve the use of dielectric spectroscopy in the studies of asymmetric mikto-arm stars with low functionalities (number of arms).24,25 Molecular simulation studies can provide a direct investigation of such systems at the atomic level. However, due to the complexity of the systems most of the works focus almost exclusively on the structural properties of copolymer stars; moreover, they lack the necessary atomistic details to describe the specific chemical composition.26–29Very recently we showed that regular mikto-arm stars consisting of immiscible polymer arms, more specifically polystyrene (PS) and poly(ethylene oxide) (PEO), form nanostructured particles with either Janus-like or patchy-like morphologies under bad solvent conditions.30 Two types of environments were used to mimic poor solvent conditions for both components of the mikto-arm stars, namely vacuum and a polybutadiene (PB) matrix. The mikto-arm stars with f < 32 form Janus-like nanoparticles in both types of environments, while the stars with f = 32 nanosegregate into patchy-like structures.30
In this work we provide a detailed investigation about the effect of the functionality f and the internal morphology on the (local) segmental dynamics of model mikto-arm stars in these two environments. To this end, we model single-molecule stars with the same arm length but varying functionality in a PB matrix and in vacuum through atomistic molecular dynamics simulations. We also investigate the effect of the internal morphology (i.e., Janus vs. patchy) on the segmental dynamics by examining two types of 32-arm star in vacuum with different attachment of the arms to the core. Mikto-arm stars in vacuum represent an ideal system, in which the absence of an explicit solvent allows us to neglect the environmental factors, such as the specific star-solvent interactions, and to focus solely on the internal interplay between the nanosegregated PEO and PS arms.
2 Model
In the first part of our study we simulated 4 systems of mikto-arm stars with f = 4, 8, 16, 32 arms attached to the core in the alternating way (see Fig. 1(a)). Each copolymer star contains (f/2) PEO arms and (f/2) PS arms and a dendritic core. Both types of arms are 40 monomers long. The core consists of C, CH or CH2 carbon units connected into a dendritic-like architecture, the number of carbon units depends on the star functionality (see Fig. 1). The notation of the mikto-arm stars is f/40. Each system contains one star in a PB matrix or in vacuum. The length of PB chains is 30 monomeric units. In the second part, in order to investigate the effect of the internal morphology (i.e., Janus vs. patchy), we created one additional system of 32-arm star in vacuum with PEO and PS arms connected, by construction, to the core atoms in the Janus-like manner (see Fig. 1(b)). The 32/40 star with the PEO and PS arms attached to the different “hemispheres” of the core retains Janus-like fashion after nanosegregation and therefore it can be seen as a “complementary” morphology to the star with the same composition (32/40) but with the alternating arm attachment, which forms a patchy-like pattern.30 To avoid confusion, we refer to the 32/40 star with alternating attachment as “alternating” and to the 32/40 star with the Janus-like geometry by construction as “hemisphere”. We have also studied homopolymer (PEO)f and (PS)f stars with f = 4, 8, 16, 32 in both types of environments (PB matrix and vacuum) as reference systems. The simulations were performed at a temperature of 400 K with the Gromacs simulation package.31 The preparation of the systems as well as the details about the equilibration process can be found elsewhere.30 The interactions in the systems are described by the TRAPPE united-atom force field.32–35 The typical simulation run is 150 ns long for the vacuum systems and around 300 ns for the systems in PB matrix. The time step is 1 fs.3 Results
To quantify intramolecular dynamical heterogeneities, each arm is divided into 5 regions, with 8 monomers per region, labeled from the core to the free end of each arm (see the inset of Fig. 2(a) and Fig. S1(a), ESI†). We define a segmental vector v as a vector connecting two extremes of the monomer (i.e., 1–3 vector for PEO arms and a vector along the backbone for PS arm, see Fig. S1(a), ESI†) and calculate the first Legendre polynomial (correlation function) through: | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(t/τKWWi)βi), where A is a prefactor, βi the stretch exponent, τKWWi the segmental relaxation time and index i corresponds to the label of the region (i = 1–5). The characteristic average relaxation time of the segments in the given region τi is then obtained as
exp(−(t/τKWWi)βi), where A is a prefactor, βi the stretch exponent, τKWWi the segmental relaxation time and index i corresponds to the label of the region (i = 1–5). The characteristic average relaxation time of the segments in the given region τi is then obtained as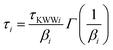 | (2) |
3.1 Effect of the functionality
Concerning the dynamical heterogeneities along the arm, our data reveal a noticeable deceleration of the segmental dynamics close to the core in comparison to the middle segments, which smoothly turns into a plateau in the middle region of the arm and ends up with a slight acceleration of the outer segments with respect to the plateau (see the values of τKWWi parameter in Fig. 2(a)). This intramolecular dynamical heterogeneity is qualitatively similar for both PEO and PS arms; however, the PS segmental dynamics is almost one order or magnitude slower than the corresponding dynamics of PEO arms. Such a disparity in the segmental relaxation times between PS and PEO is expected due to the large difference in their glass transition temperatures, i.e., about 150 K between PEO and PS.36 The actual degree of the dynamical slowing down in the vicinity of the core with respect to the middle arm segments depends on the functionality for both PEO and PS arms. The slower dynamics in the first region is not surprising if we consider the higher density at the core region which increases with increasing the functionality (see the density profiles in Fig. S2 of the ESI†), and has been also reported in a previous simulation work on the relaxation dynamics for melts of homopolymer stars, using a bead-spring model.37 The same trend (i.e., more pronounced internal heterogeneities with increasing f and decreasing distance to the star core) is captured in the values of the stretch exponent βi for the given star and/or region along the arm, shown in Fig. 2(b): the smaller β values near to the core region denote a broader distribution of relaxation times. Note that the values of the stretch exponents are in all regions smaller for PEO segments than for PS segments. The same trend is observed in their homopolymer analogues in PB matrix. In what follows we report values of the characteristic average relaxation time of the segments in the given region τi, which combines both τKWWi and βi through eqn (2).In Fig. 3 the segmental relaxation times τi are plotted as a function of the position along the arm, normalized by the respective segmental relaxation times of the corresponding homopolymer stars in the PB matrix, τhi. The error bars were estimated by using the standard block averaging method and for clarity we show the error bars only for the first and the third region. The error bars in the remaining regions are of the same order or smaller. This representation allows us to rule out the effect of the star-like architecture on the segmental dynamics and to understand the interdependence of the PEO and PS dynamics. Interestingly, for functionalities higher than 8 (Fig. 3(c and d)) there is a clear deviation in the dynamical behavior of the PEO and PS segments in the first (nearest to the core) region of mikto-arm stars, from that of the homopolymer stars. Namely, the PEO segments in mikto-arm stars are slower than the corresponding segments in (PEO)f stars. On the other side, the relaxation of the PS segments in the first region of mikto-arm stars is faster than the one measured in (PS)f stars. This can be explained by the fact that in the vicinity of the core of the mikto-arm star the immiscible PEO and PS monomers are enforced, due to geometric constraints, to maintain a large number of (unfavorable) contacts between each other. This structural characteristic along with the dynamical asymmetry of the two components (i.e., PS has a high Tg while PEO has a much lower Tg) results in a behavior akin to that seen only in dynamically asymmetric miscible binary polymer blends or disordered block copolymers. Indeed, for a miscible polymer blend, or for a disordered copolymer, a speed-up of the segmental dynamics of the slower component is expected and an associated slowing-down of the dynamics of the faster component (compared to the bulk one-component systems), due to the change in the local environment.1,2,13,14 As one moves away from the core, the immiscible PEO and PS arms microphase separate, as they are less geometrically constrained, forming either “Janus-like” or “patchy” nanostructures (see the insets in Fig. 3). In this case, the associated segmental dynamics becomes very similar to the corresponding homopolymer stars, i.e., as one would expect in regular phase separated immiscible systems.
To further quantify the above observation, i.e., from miscible to immiscible-like, we calculate the monomer pair probability distribution functions g(r), which are shown in Fig. S3 in the ESI.† As expected, there is a much higher number of PS:PEO contacts in the first region than in the other regions along the arm, confirming the previous statement about “enforced mixing” (all the systems follow the trend shown for 32/40 star in Fig. S3(a) in the ESI†). Moreover, the first maximum in the g(r) functions for the first region increases with the functionality for the mikto-arm stars nanosegregated into Janus-like morphology (f < 32, Fig. S3(b) in the ESI†). Interestingly, the distribution of the PS:PEO contacts in the first region for the 32/40 mikto-arm star exhibits a smaller maximum than for the 16/40, demonstrating that despite the geometric constraints the patchy-like morphology of this star facilitates the avoidance of PS and PEO segments in the region closest to the core (compare the blue and the magenta curve in Fig. S3(b), ESI†). Note, that the magnitude of the deviation in the dynamical behavior of the PEO and PS segments in the first region in comparison to the homopolymer analogues, may be also affected by a slighly different density close to the core (notice the smaller density for (PEO)f and higher density for (PS)f systems in Fig. S2 of the ESI† for r < 0.5 nm in comparison to mikto-arm stars).
Concerning the mikto-arm stars in vacuum, qualitatively the same behavior as the one described above for the stars in the PB matrix was observed for all measured quantities, therefore we only report τi/τhi as a function of the position along the arm in Fig. S4 of the ESI.†
3.2 Effect of the internal morphology
To further investigate the effect of the internal morphology on the dynamics of the nanosegregated star nanoparticles we study two types of mikto-arm stars with f = 32 in vacuum. More specifically, we compare two types of 32-arm copolymer stars, one with the patchy-like morphology following the “alternating” arm attachment, discussed up to now and one with a Janus-like morphology “by design” (“hemisphere” arm attachment). Randomly selected snapshots of both morphologies are shown in inset of Fig. 4(b). These two copolymer stars differ only in the attachment of the arms to the core (see the scheme in Fig. 1) and so, by construction, this fact fully determines the nanosegregation processes in the closest vicinity of the core and consequently the dynamics. Since their density profiles are very similar (see Fig. S5 in the ESI†) and there is no explicit polymer matrix in the systems, the segmental dynamics in both mikto-arm stars will be mostly governed by the mutual interaction of PEO and PS arms. The probability distributions of the PS:PEO and PEO:PEO distances in the first region along the arm for both stars are shown in Fig. 4(a). Due to the predetermined attachment, the number of unfavorable PS:PEO contacts in the first region is much smaller in the Janus morphology where the PS and PEO arms are arranged in hemispheres than in the patchy particle, where the alternating attachment drives the arm mixing near the core. Consequently, predominantly homogeneous environment close to the star core is found in the stars that form the Janus-like morphology, i.e., with higher percentage of PEO:PEO pairs in this region (open triangles in Fig. 4(a)). This is mainly reflected in the relaxation times of the PEO segments in this region, which are by a factor of 2 faster in the Janus-like than in the patchy-like nanoparticles (compare red crosses and orange triangles in Fig. 4(b)). Interestingly, the dynamics of the PS segments in both types of morphologies is very similar (compare blue circles and green squares in Fig. 4(b)). The curves for the PEO:PEO and PS:PEO pair distributions for the third region in both morphologies approximate each other (see Fig. S6 in the ESI†), confirming the observation that the differences in the local heterogeneities in both morphologies vanish with increasing distance from the central part of the star (observe the plateau for regions 2–5 in Fig. 4(b)).The above analysis concerns the coupling between structural and dynamical heterogeneities in the segmental (nanoscale) level, studied via orientational dynamical modes. In addition, the local environment as the main factor of the heterogeneous translational dynamics in the nanosegregated particles can be further examined by a detailed analysis of the displacement of every monomer in the star. More specifically, we calculated the average displacement (using multiple-time origin method) of each monomeric unit in the mikto-arm stars at a specific time tc, corresponding roughly to a half of the relaxation time of the PEO segments in vacuum (here tc = 1 ns). The same procedure was repeated for the homopolymer stars, however, we also averaged over equally placed monomers on each arm. Then the relative acceleration and/or slowing down of the monomers in the copolymer stars with respect to their homopolymer analogues were projected on a randomly selected configuration shown in Fig. 5 and in Fig. S7 of the ESI.† The relative error of the procedure is ±20%, thus we highlight only the monomers with higher differences in dynamics. In this representation the internal dynamical heterogeneity in the nanosegregated domains is much more evident. It is obvious that the monomers of the PEO arm whose environment consists mostly of the immiscible, dynamically contrasting PS component (close to the core in both stars and in a single segregated arm in the Janus particle) are slower than those located in PEO-rich domains (patches). Accordingly, the fastest monomers in the PS segregated domains can be found in the domains placed in the closest vicinity with the PEO monomers, thus in the domains with the highest number of unfavorable PS:PEO contacts (see Fig S7 in the ESI†).
4 Conclusions
In summary, the results reported here propose that nanoparticles with nanosegregated, dynamically heterogeneous domains can be designed by combining incompatible dynamically asymmetric polymers of different glass transition temperature in a mikto-arm architecture. By increasing the number of arms in the mikto-arm stars, the effect of the geometric constraints becomes more pronounced and the full nanosegregation of the immiscible arms is obstructed, promoting a formation of regions with mutually correlated dynamics. Moreover, the alternating attachment of the arms favors the dynamic heterogeneities in the vicinity of the star core.This work is a part of an extensive bottom-up study concerning structural and dynamical properties of nanosegregated materials consisting of mikto-arm stars. Building up on the information obtained from single-star simulations, the aim is to detect and quantify factors affecting the properties on intra- and intermolecular level in more complex systems, as for example in self-assembled structures.16,17 Due to their spatio-temporal heterogeneities, such materials consisting of mikto-arm stars have been tested as possible candidates for high performance solid polymer electrolytes for next generation of energy storage materials.17 Moreover, due to the analogous arrangement of the immiscible components, we believe that our results can be extended to the systems of binary hairy nanoparticles in the same environment, with high grafting density and the size of the nanoparticle much smaller than the size of the grafted arms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. B. and E. G. acknowledge the financial support of the Stavros Niarchos Foundation within the framework of the project ARCHERS (“Advancing Young Researchers' Human Capital in Cutting Edge Technologies in the Preservation of Cultural Heritage and the Tackling of Societal Challenges”). This research is partially supported by the project “National Research Infrastructure on nanotechnology, advanced materials and micro/nanoelectronics” (MIS 5002772) implemented under the “Action for the Strategic Development on the Research and Technological Sector”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund).Notes and references
- V. A. Harmandaris and M. Doxastakis, J. Chem. Phys., 2013, 139, 034904 CrossRef PubMed.
- V. A. Harmandaris, G. Floudas and K. Kremer, Phys. Rev. Lett., 2013, 110, 165701 CrossRef PubMed.
- R. H. Colby, Polymer, 1989, 30, 1275–1278 CrossRef CAS.
- C. M. Roland and K. L. Ngai, Macromolecules, 1991, 24, 2261–2265 CrossRef CAS.
- Y. H. Chin, C. Zhang, P. Wang, P. T. Inglefield, A. A. Jones, R. P. Kambour, J. T. Bendler and D. M. White, Macromolecules, 1992, 25, 3031–3038 CrossRef CAS.
- J. A. Pathak, R. H. Colby, G. Floudas and R. Jérôme, Macromolecules, 1999, 32, 2553–2561 CrossRef CAS.
- Y. He, T. R. Lutz and M. D. Ediger, J. Chem. Phys., 2003, 119, 9956–9965 CrossRef CAS.
- E. Krygier, G. Lin, J. Mendes, G. Mukandela, D. Azar, A. A. Jones, J. A. Pathak, R. H. Colby, S. K. Kumar, G. Floudas, R. Krishnamoorti and R. Faust, Macromolecules, 2005, 38, 7721–7729 CrossRef CAS.
- K. L. Ngai and C. M. Roland, Rubber Chem. Technol., 2004, 77, 579–590 CrossRef CAS.
- R. H. Colby and J. E. G. Lipson, Macromolecules, 2005, 38, 4919–4928 CrossRef CAS.
- W. Liu, D. Bedrov, S. K. Kumar, B. Veytsman and R. H. Colby, Phys. Rev. Lett., 2009, 103, 037801 CrossRef PubMed.
- S. Salaniwal, R. Kant, R. H. Colby and S. K. Kumar, Macromolecules, 2002, 35, 9211–9218 CrossRef CAS.
- G. Fytas, S. H. Anastasiadis, K. Karatasos and N. Hadjichristidis, Phys. Scr., 1993, 1993, 237–241 CrossRef.
- K. Karatasos, S. H. Anastasiadis, A. N. Semenov, G. Fytas, M. Pitsikalis and N. Hadjichristidis, Macromolecules, 1994, 27, 3543–3552 CrossRef CAS.
- H. Yang, X. C. Chen, G. R. Jun and P. F. Green, Macromolecules, 2013, 46, 5036–5043 CrossRef CAS.
- P. Bačová, R. Foskinis, E. Glynos, A. N. Rissanou, S. H. Anastasiadis and V. Harmandaris, Soft Matter, 2018, 14, 9562–9570 RSC.
- E. Glynos, L. Papoutsakis, W. Pan, E. P. Giannelis, A. D. Nega, E. Mygiakis, G. Sakellariou and S. H. Anastasiadis, Macromolecules, 2017, 50, 4699–4706 CrossRef CAS.
- D. J. Read, D. Auhl, C. Das, J. den Doelder, M. Kapnistos, I. Vittorias and T. C. B. McLeish, Science, 2011, 333, 1871–1874 CrossRef CAS PubMed.
- P. Bačová, L. G. D. Hawke, D. J. Read and A. J. Moreno, Macromolecules, 2013, 46, 4633–4650 CrossRef.
- D. Vlassopoulos, Rheol. Acta, 2016, 55, 613–632 CrossRef CAS.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855–R876 CrossRef CAS.
- T. Pakula, D. Vlassopoulos, G. Fytas and J. Roovers, Macromolecules, 1998, 31, 8931–8940 CrossRef CAS.
- K. J. Johnson, E. Glynos, G. Sakellariou and P. Green, Macromolecules, 2016, 49, 5669–5676 CrossRef CAS.
- G. Floudas, N. Hadjichristidis, H. Iatrou and T. Pakula, Macromolecules, 1996, 29, 3139–3146 CrossRef CAS.
- T. Kinsey, E. U. Mapesa, W. Wang, K. Hong, J. Mays, S. M. Kilbey and J. Sangoro, Macromolecules, 2018, 51, 5401–5408 CrossRef CAS.
- P. Hebbeker, F. A. Plamper and S. Schneider, Macromol. Theory Simul., 2015, 24, 110–116 CrossRef CAS.
- J. Havránková, Z. Limpouchová, M. Štěpánek and K. Procházka, Macromol. Theory Simul., 2007, 16, 386–398 CrossRef.
- Y. Chang, W.-C. Chen, Y.-J. Sheng, S. Jiang and H.-K. Tsao, Macromolecules, 2005, 38, 6201–6209 CrossRef CAS.
- L. Rovigatti, B. Capone and C. N. Likos, Nanoscale, 2016, 8, 3288–3295 RSC.
- P. Bačová, E. Glynos, S. H. Anastasiadis and V. A. Harmandaris, ACS Nano, 2019, 13, 2439–2449 Search PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- C. D. Wick, M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 2000, 104, 8008–8016 CrossRef CAS.
- J. Fischer, D. Paschek, A. Geiger and G. Sadowski, J. Phys. Chem. B, 2008, 112, 2388–2398 CrossRef CAS PubMed.
- V. A. Harmandaris, N. P. Adhikari, N. F. A. van der Vegt and K. Kremer, Macromolecules, 2006, 39, 6708–6719 CrossRef CAS.
- J. Bicerano, Glass Transition, Encyclopedia of Polymer Science and Technology, American Cancer Society, 2001 Search PubMed.
- A. Chremos, E. Glynos and P. F. Green, J. Chem. Phys., 2015, 142, 044901 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00079e |
| This journal is © The Royal Society of Chemistry 2020 |





