Probing particle heteroaggregation using analytical centrifugation

Abstract

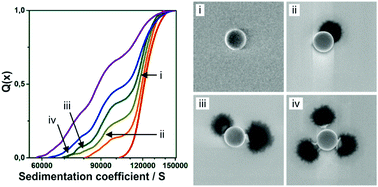
The controlled aggregation of colloidal particles is not only a widespread natural phenomenon but also serves as a tool to design complex building blocks with tailored shape and functionalities. However, the quantitative characterization of such heteroaggregation processes remains challenging. Here, we demonstrate the use of analytical centrifugation to characterize the heteroaggregation of silica particles and soft microgels bearing similar surface charges. We investigate the attachment as well as the stability of the formed heteroaggregates as a function of particle to microgel surface ratio, microgel size and the influence of temperature. The attachment of microgels onto the colloidal particles induces a change in the sedimentation coefficient, which is used to quantitatively identify the number of attached microgels. We corroborate the shift in sedimentation coefficient by computer simulations of the frictional properties of heteroaggregates via a modified Brownian dynamic algorithm. The comparison between theoretical investigations and experiments suggest that the microgels deform and flatten upon attachment.