Growth of a bubble cloud in CO2-saturated water under microgravity†
Abstract
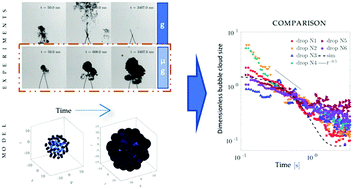
The diffusion-driven growth of a dense cloud of bubbles immersed in a gas-supersaturated liquid is a problem that finds applications in several modern technologies such as solvent-exchange micro-reactors, nanotechnology or the manufacturing of foamy materials. However, under Earth's gravity conditions, these dynamics can only be observed for a very limited time if the cloud is not attached to a surface, due to the action of buoyancy, i.e. of gravity effects. Here, we present experimental observations of the time evolution of dense bubble clouds growing in CO2-supersaturated water under microgravity conditions. We report the existence of three regimes where the bubble cloud exhibits different growth rates. At short times, each bubble grows independently following the Epstein–Plesset equation. Later on, bubbles start to interact with each other and their growth rate diminishes as they compete for the available CO2. When this happens, the growth rate slows down. This occurs earlier the deeper the bubble is in the cloud. Finally, at long times, only those bubbles on the husk continue growing. These regimes may be qualitatively described by a mathematical model where each individual bubble grows in the presence of a constellation of point mass sinks. Despite the model being only valid for dilute bubble clouds, its predictions are consistent with the experimental observations, even though the bubble clouds we observe are rather dense.


 Please wait while we load your content...
Please wait while we load your content...