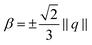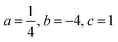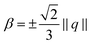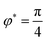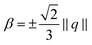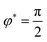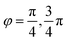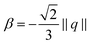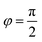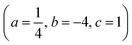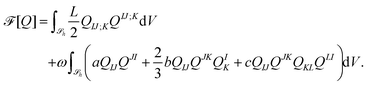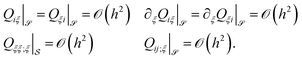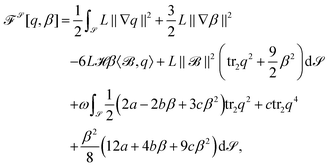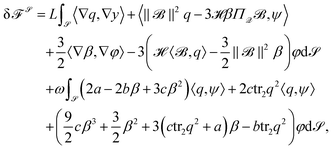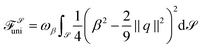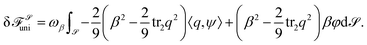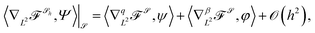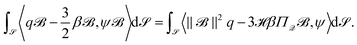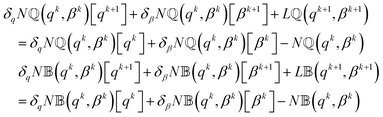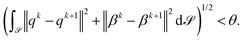Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Properties of surface Landau–de Gennes Q-tensor models
Michael
Nestler
*a,
Ingo
Nitschke
a,
Hartmut
Löwen
b and
Axel
Voigt
 acd
acd
aInstitut für Wissenschaftliches Rechnen, Technische Universität Dresden, 01062 Dresden, Germany. E-mail: michael.nestler@tu-dresden.de
bInstitut für Theoretische Physik II – Soft Matter, Heinrich-Heine-Universität Düsseldorf, 40225 Düsseldorf, Germany
cDresden Center for Computational Materials Science (DCMS), Technische Universität Dresden, 01062 Dresden, Germany
dCenter for Systems Biology Dresden (CSBD), Pfotenhauerstr. 108, 01307 Dresden, Germany
First published on 9th April 2020
Abstract
Uniaxial nematic liquid crystals whose molecular orientation is subjected to tangential anchoring on a curved surface offer a non trivial interplay between the geometry and the topology of the surface and the orientational degree of freedom. We consider a general thin film limit of a Landau–de Gennes Q-tensor model which retains the characteristics of the 3D model. From this, previously proposed surface models follow as special cases. We compare fundamental properties, such as the alignment of the orientational degrees of freedom with principle curvature lines, order parameter symmetry and phase transition type for these models, and suggest experiments to identify suitable model assumptions.
1 Introduction
Liquid crystals1,2 consist of particles that possess both translational and orientational degrees of freedom. If these particles are constrained to the tangent bundle of a curved surface interesting phenomena emerge, which result from the tight coupling of the elastic and bulk free energies of the liquid crystal with the topological and geometrical properties of the surface. There are various experimental realization3–13 and particle-based computer simulations,14–30 which mainly focus on the emergence and position of topological defects on spherical or more complex surfaces. However, not only defects are tightly linked to the topological and geometrical properties of the surface, but also other fundamental issues, such as the alignment of the orientational degree of freedom with principle curvature lines, order parameter symmetries, phase transition type and curvature induced phase transitions are of fundamental interest, but are much less explored. We will address these issues for uniaxial nematic liquid crystals within a field-theoretical description of a surface Landau–de Gennes Q-tensor model. Various such models have been proposed.31–38 They strongly differ in the coupling mechanism between the orientational ordering of the nematic liquid crystal and the geometric properties of the surface. These coupling terms strongly depend on the assumptions made in the derivation and, as will be shown, have strong consequences on the fundamental properties of the phase transition type and order parameter symmetries.Liquid crystals on curved surfaces are in a certain sense between 2D and 3D and could thus show properties of both dimensions. Lets first compare such properties of the established Landau–de Gennes Q-tensor theory for nematic liquid crystals in 2D and 3D:1 the nematic phase can be stable in both dimensions. However, already the isotropic-to-nematic phase transition qualitatively differs between 2D and 3D. While it is of first-order in 3D, it is controversially discussed if this generally holds in 2D. Even if it can be proven that first-order isotropic-to-nematic phase transitions are possible in 2D,39,40 computer simulations and experiments indicate qualitatively different behaviour including continuous, first-order and even the absence of phase transitions, see e.g.ref. 41–43. In ref. 44 an overview of these theoretical arguments, computer simulations and experimental observations for thin films and 2D systems is provided. The situation on curved surfaces should somehow reflect these properties. However, in some of the proposed surface models first-order phase transitions are not possible. Another aspect highlighting the differences is discussed in ref. 45 by comparing mean field theories in 2D46 and 3D.47 The definitions yield different eigenvalue spectra in the order tensor, which corresponds to either a symmetry under in plane rotations by 90° in 2D or a rotational symmetry (w.r.t. the average particle direction) in 3D. How a nematic liquid crystal on a curved surface fits into this picture is open. A similar situation arises for Landau–de Gennes models. Some of the proposed surface models yield an eigenvalue spectrum as in 2D, others as in 3D. In 2D uniaxial nematics is the only possible nematic state, in 3D it is the energetically most favourable state under weak assumptions on the state potential.45 A proper classification of uniaxiality in a surface Landau–de Gennes model is open, but one might ask, if, as in 2D, only uniaxial nematics should be allowed. The third aspect considers the mean orientation. If not induced by external fields or boundary conditions the mean orientation in nematic liquid crystals is arbitrary in 2D and 3D. This changes on curved surfaces, where it should be preferential to align with the principle curvature lines. This aspect has been discussed previously and is identified with the influence of extrinsic curvature terms32,33 in surface models, which again are considered in some but not all of the proposed models.
We will review the proposed surface Landau–de Gennes Q-tensor models with the aspect of these fundamental properties. Furthermore we propose a version of a surface Landau–de Gennes Q-tensor model which effectively describes surface liquid crystals retaining the 3D phase transition type and uniaxial eigenvalue spectra. Most previously proposed models follow as special cases and we discuss under which assumptions the fundamental properties get lost. The paper is structured as follows. In Section 2 we briefly review the 3D Landau–de Gennes Q-tensor model1 and propose its thin film limit under generic anchoring conditions. Solving this model indicates a strong influence of geometry on fundamental properties. In particular, it is established that curvature can induce biaxiality, even if parameters in the original 3D model enforce state potential minima to be uniaxial. To overcome this problem we modify the derived energy by adding a penalty term which enforces uniaxiality weakly. In Section 3 this model together with its special cases is discussed in a flat 2D scenario with respect to their fundamental properties. We demonstrate the general model to retain the 3D properties. With this established, we apply the models to curved surfaces and discuss the effects of curvature on the ordering of the liquid crystal in Section 4. We summarize our findings and discuss them in a general framework in Section 5. As all these results do not depend on specific material parameters, we only consider a one-constant approximation. Details on derivations and used numeric methods can be found in the Appendix.
2 Thin film limit of the Q-tensor model
In this section we present essential notions and properties of the Landau–de Gennes Q-tensor model in 3D1 and derive a generic surface model as a thin film limit. Restrictions to enforce uniaxiality and special cases, which link the model to the previously proposed surface Landau–de Gennes Q-tensor models, follow.Q-Tensor model in 3D
We consider rod like particles with a head–tail symmetry in a volume V ⊂![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. We consider the symmetric and trace free tensorial order parameter Q. In the special case of a uniaxial eigenvalue spectrum it is defined by
3. We consider the symmetric and trace free tensorial order parameter Q. In the special case of a uniaxial eigenvalue spectrum it is defined by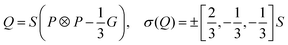 | (1) |
![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) 3. The phase of prevalent liquid like material properties is characterized by an isotropic ordering of particles and S = 0. In the nematic phase the particles tend to preferentially align with the average direction and S → S* > 0. The Landau–de Gennes Q-tensor model is based on the free energy
3. The phase of prevalent liquid like material properties is characterized by an isotropic ordering of particles and S = 0. In the nematic phase the particles tend to preferentially align with the average direction and S → S* > 0. The Landau–de Gennes Q-tensor model is based on the free energy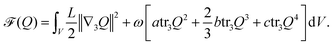 | (2) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 and ‖·‖ the Frobenius norm. For more general models see e.g.ref. 48–52. In the remaining terms, the state potential, we have factored out ω > 0 such that classic phenomenological constants are given by a* = ωa, b* = ωb and c* = ωc. For the sake of readability we use an index free tensor notation,53 where e.g. · denotes the inner product, regardless of the tensorial degree. We define trace notion by tr3Q = Q·G. Such full contraction with the space metric coincides with the Frobenius tensor norm by
3 and ‖·‖ the Frobenius norm. For more general models see e.g.ref. 48–52. In the remaining terms, the state potential, we have factored out ω > 0 such that classic phenomenological constants are given by a* = ωa, b* = ωb and c* = ωc. For the sake of readability we use an index free tensor notation,53 where e.g. · denotes the inner product, regardless of the tensorial degree. We define trace notion by tr3Q = Q·G. Such full contraction with the space metric coincides with the Frobenius tensor norm by 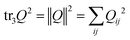 . The state potential can be expressed in terms of S such that the choice of a, b and c defines the preferred ordering S* as local minima of the state potential.
. The state potential can be expressed in terms of S such that the choice of a, b and c defines the preferred ordering S* as local minima of the state potential.
Following ref. 45 and 52 we point out that the tensorial order parameter Q in this model is not restricted to the uniaxial eigenvalue spectra σ(Q) as defined in (1). To track such situations, a biaxiality measure is introduced54
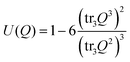 | (3) |
Planar anchoring and tensor decomposition
For the boundary of the volume V, ∂V, with outward pointing normal ν, planar anchoring of uniaxial Q-tensors is modeled by a bare surface energy as discussed in ref. 35–37,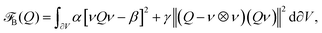 | (4) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +. The formulation can be interpreted as a penalty energy enforcing ν as an eigenvector of Q with eigenvalue β. In the case of a tangential aligned uniaxial Q-tensor (P·ν = 0) this would translate into β = −⅓S. Given this concept of prescribing a specific eigenvalue in the boundary normal direction motivates the separation of Q in a normal part β and tangential parts q (‖qν‖ = ‖νq‖ = 0). Analogous to ref. 35–37 we thereby choose a separation such that q is symmetric and trace free (in the boundary domain sense)
+. The formulation can be interpreted as a penalty energy enforcing ν as an eigenvector of Q with eigenvalue β. In the case of a tangential aligned uniaxial Q-tensor (P·ν = 0) this would translate into β = −⅓S. Given this concept of prescribing a specific eigenvalue in the boundary normal direction motivates the separation of Q in a normal part β and tangential parts q (‖qν‖ = ‖νq‖ = 0). Analogous to ref. 35–37 we thereby choose a separation such that q is symmetric and trace free (in the boundary domain sense)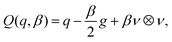 | (5) |
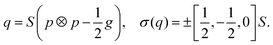 | (6) |
Thin film limit models
Lets consider V =![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h as a thin film with thickness h, such that
h as a thin film with thickness h, such that 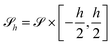 and
and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) a regular surface. We perform the thin film limit
a regular surface. We perform the thin film limit 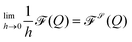 in the spirit of ref. 38 under boundary condition ‖(G − ν ⊗ ν)(Qν)‖ = 0, which corresponds to α = 0 and γ → ∞ in eqn (4) and keeps β as a degree of freedom. For details see the Appendix. By averaging out the normal direction we yield a surface model. Inserting (5) in (2) leads to
in the spirit of ref. 38 under boundary condition ‖(G − ν ⊗ ν)(Qν)‖ = 0, which corresponds to α = 0 and γ → ∞ in eqn (4) and keeps β as a degree of freedom. For details see the Appendix. By averaging out the normal direction we yield a surface model. Inserting (5) in (2) leads to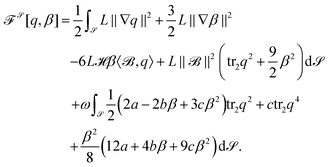 | (7) |
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) denotes the shape operator and
denotes the shape operator and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) the mean curvature of
the mean curvature of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , for details see the Appendix. These are extrinsic curvature contributions, the term 6
, for details see the Appendix. These are extrinsic curvature contributions, the term 6![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) β〈
β〈![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,q〉 induces an alignment of p with one of the lines of principle curvatures depending on the sign of
,q〉 induces an alignment of p with one of the lines of principle curvatures depending on the sign of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . The second term
. The second term 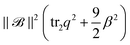 poses an isotropic coupling between curvature and ordering. The term is closely related to the state potential such that the curvature can locally deform the potential and can induce phase transition or violate uniaxiality even if b < 0, a setting guarantees state potential minima to be uniaxial in the initial 3D model.45 An example is provided in the Appendix.
poses an isotropic coupling between curvature and ordering. The term is closely related to the state potential such that the curvature can locally deform the potential and can induce phase transition or violate uniaxiality even if b < 0, a setting guarantees state potential minima to be uniaxial in the initial 3D model.45 An example is provided in the Appendix.
As we are only interested in uniaxial nematic liquid crystals, we require a constraint, which suppresses curvature induced biaxiality. Inserting the decomposition (5) in the biaxiality measure (3) leads to a condition for β enforcing uniaxial eigenvalue spectra of Q-tensors, for details see the Appendix. It reads
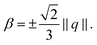 | (8) |
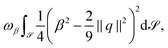 | (9) |
As evolution laws we propose L2-gradient flows of the energy (7) with (9) with independent variables q and β, which read
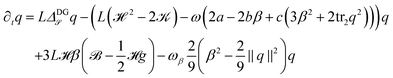 | (10) |
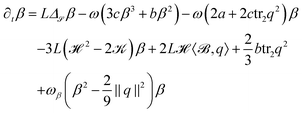 | (11) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) denotes the surface Div-Grad (Bochner) Laplace operator, Δ
denotes the surface Div-Grad (Bochner) Laplace operator, Δ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the Laplace–Beltrami operator and
the Laplace–Beltrami operator and ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) the Gaussian curvature. Details of the derivation can be found in the Appendix. Eqn (10) and (11) provide a general surface Landau–de Gennes Q-tensor model with uniaxial eigenvalue spectra with a minimum of a priori assumptions. This system can be solved numerically, see the Appendix.
the Gaussian curvature. Details of the derivation can be found in the Appendix. Eqn (10) and (11) provide a general surface Landau–de Gennes Q-tensor model with uniaxial eigenvalue spectra with a minimum of a priori assumptions. This system can be solved numerically, see the Appendix.
Previously proposed models consider special choices for β. They result as a thin film limit by considering the boundary conditions νQν − β = 0 and ‖(G − ν ⊗ ν)(Qν)‖ = 0, corresponding to α → ∞ and γ → ∞ in eqn (4), which specifies β. β = 0 yields a model with degenerate Q-tensors Q = q as in ref. 31 and 34, for β = −⅓S* we yield the model of approximate uniaxial Q-tensors,32,37,56,57 where some consider a different constant value for β, and the one-constant approximation of the derived models in ref. 35, 36 and 38. The resulting evolution equations are special cases of eqn (10). In the following we will compare the three models:
1. 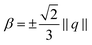 (eqn (10) and (11))
(eqn (10) and (11))
2. β = −⅓S* (eqn (10) with β = −⅓S* and ωβ = 0)
3. β = 0 (eqn (10) with β = 0 and ωβ = 0).
(1) ensures 3D uniaxial eigenvalue spectra, (2) approximates this condition, and (3) essentially has a biaxial eigenvalue spectrum in 3D and is only uniaxial if considered as a 2D model.
3 Fundamental properties of the surface models
To keep the discussion as simple as possible we start with planar surfaces, which already show fundamental differences.Eigenvalue spectra and symmetries
We recall the results of the mean field modeling approach for 3D systems, see e.g.ref. 47,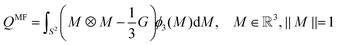 | (12) |
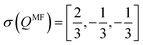 . The mean field model in 2D, e.g.ref. 46, reads similar
. The mean field model in 2D, e.g.ref. 46, reads similar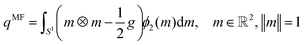 | (13) |
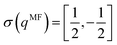 . Considering the eigenvalue spectrum for the decomposed Q tensor (5)
. Considering the eigenvalue spectrum for the decomposed Q tensor (5)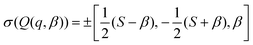 | (14) |
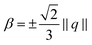 conform to 3D theory.
conform to 3D theory.
Phase transition type
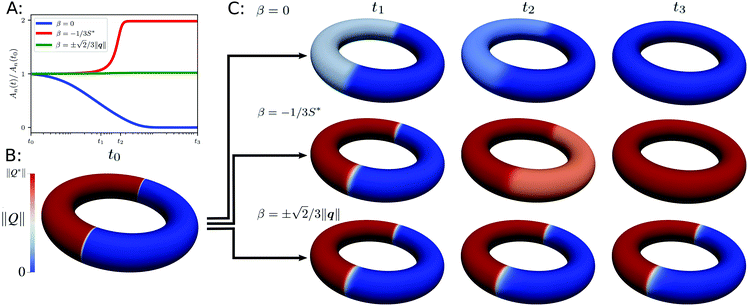
We now turn to the isotropic-to-nematic phase transition. In the Landau–de Gennes Q-tensor model such transitions can be accounted for by a temperature dependent coefficient a = a(T) = a0(T − T*) where T* denotes the critical temperature where the isotropic phase is stable for T > T*. Fig. 1A shows the phase portrait of the Landau–de Gennes Q-tensor model for the 3D case w.r.t.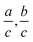 with a typical transient for increasing T from the pure nematic phase, via phase coexistence of the nematic and isotropic phase to the pure isotropic phase. T° denotes the critical temperature where the nematic phase ceases to exist. In this framework the transition is discontinuous/first-order.
with a typical transient for increasing T from the pure nematic phase, via phase coexistence of the nematic and isotropic phase to the pure isotropic phase. T° denotes the critical temperature where the nematic phase ceases to exist. In this framework the transition is discontinuous/first-order.
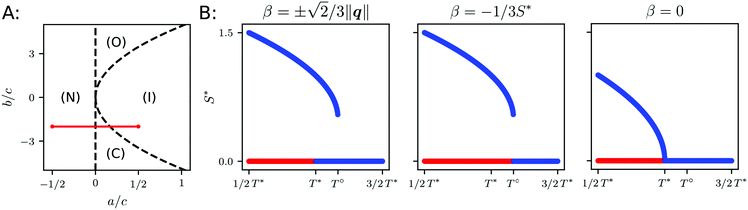 | ||
Fig. 1 Types of phase transition in surface models: (A) phase portrait for bulk Landau–de Gennes Q-tensor model as defined in (2). Four distinct phases w.r.t. state potential parameters a, b and c exist. Only the isotropic phase is stable (I), only the nematic phase is stable (N) isotropic-to-nematic phase coexistence (C) and orthogonal ordering (O). The red line indicates a typical phase transition for a(T) = α(T − T*), T ∈ [1/2T*,3/2T*] where T* denotes critical temperature such that the isotropic phase loses stability, (I)-to-(N) transition. Here, the temperature T° marks the transition from only the isotropic stable regime to coexistence, (I)–(C) transition. (O) denotes also a region of coexistence but due to 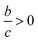 a preferred ordering S* < 0 is observed. Such a situation of orthogonal ordering (w.r.t. P) is not discussed here. (B) Stability of minima S = {0,S*} of state potential w.r.t. to temperature for a(T) and choice of the β model. Blue lines denote stable minima while red lines indicate unstable minima. a preferred ordering S* < 0 is observed. Such a situation of orthogonal ordering (w.r.t. P) is not discussed here. (B) Stability of minima S = {0,S*} of state potential w.r.t. to temperature for a(T) and choice of the β model. Blue lines denote stable minima while red lines indicate unstable minima. | ||
We transfer this investigation of the transient from 3D to the surface models. For this purpose we consider states of uniform Q(q,β) and evaluate the minima of the state potential contribution in (7) w.r.t. to a(T) and the choice of β. In Fig. 1B we have plotted the minima and their stability. Reviewing the results for 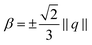 we observe a behavior identical to the 3D case. This is quite natural, since inserting the Q-tensor decomposition in 3D state potential energy density yields directly the surface counterpart. Therefore this surface model exhibits a first order phase transition type and enables phase coexistence. For the model of fixed β = −⅓S* we observe a first-order transition at T° as in a previous model but no phase coexistence for T ∈ [T*,T°]. In the case of β = 0 the transition type changes to continuous/second-order and shifts to the lower temperature T*.
we observe a behavior identical to the 3D case. This is quite natural, since inserting the Q-tensor decomposition in 3D state potential energy density yields directly the surface counterpart. Therefore this surface model exhibits a first order phase transition type and enables phase coexistence. For the model of fixed β = −⅓S* we observe a first-order transition at T° as in a previous model but no phase coexistence for T ∈ [T*,T°]. In the case of β = 0 the transition type changes to continuous/second-order and shifts to the lower temperature T*.
Fig. 2 further highlights the qualitative differences of the three models on a torus (with two major radii r, R), which is chosen as a prototypical surface with varying curvature, which avoids the presence of topological defects.
4 Impact of curvature in surface models
To investigate the impact of β on the geometry coupling mechanisms and to demonstrate the sketched effects we consider two numerical experiments.Distortion energy minima
To focus on the first coupling term in the surface Landau–de Gennes Q-tensor energy (7), 6![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) β〈
β〈![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,q〉, we consider a uniform director field P(φ) = cos(φ)pr − sin(φ)pR on a torus defined by the linear combination of two director modes pr and pR as shown in Fig. 3A. With this director field we define q(φ) = (p(φ) ⊗ p(φ) − ½g) with fixed norm. For given β we can now variate φ and evaluate the distortion energy contributions. In this set up the isotropic coupling term is constant as well as ‖∇β‖2, furthermore the models β = −⅓S* and
,q〉, we consider a uniform director field P(φ) = cos(φ)pr − sin(φ)pR on a torus defined by the linear combination of two director modes pr and pR as shown in Fig. 3A. With this director field we define q(φ) = (p(φ) ⊗ p(φ) − ½g) with fixed norm. For given β we can now variate φ and evaluate the distortion energy contributions. In this set up the isotropic coupling term is constant as well as ‖∇β‖2, furthermore the models β = −⅓S* and 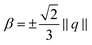 coincide. For β = 0 the directed coupling term vanishes and the minimum of distortion energy is defined by the ‖∇q‖2 contribution. As shown in Fig. 3C (top) two minima exist. The minimum
coincide. For β = 0 the directed coupling term vanishes and the minimum of distortion energy is defined by the ‖∇q‖2 contribution. As shown in Fig. 3C (top) two minima exist. The minimum 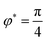 results in a surprising q configuration, shown in Fig. 3B (left). The second minimum
results in a surprising q configuration, shown in Fig. 3B (left). The second minimum 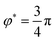 yields a corresponding configuration with in-plane 90° rotated eigenvectors. In the model
yields a corresponding configuration with in-plane 90° rotated eigenvectors. In the model 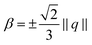 and on the chosen geometry the −3βL
and on the chosen geometry the −3βL![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 〈
〈![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,q〉 contribution dominates the distortion energy, see Fig. 3C (bottom) such that the minimum is achieved for
,q〉 contribution dominates the distortion energy, see Fig. 3C (bottom) such that the minimum is achieved for 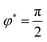 . The corresponding Q-tensor configuration consists of principal eigenvectors aligned with lines of minimal curvature, see Fig. 3B (right).
. The corresponding Q-tensor configuration consists of principal eigenvectors aligned with lines of minimal curvature, see Fig. 3B (right).
Reviewing these results we conclude, once more, that degenerate (β = 0) surface Landau–de Gennes Q-tensor models describe a substantial different type of physical systems than surface models with non-degenerate Q-tensors. Retaining the 3D nature of liquid crystals in the surface model yields an intensified geometry-ordering coupling.
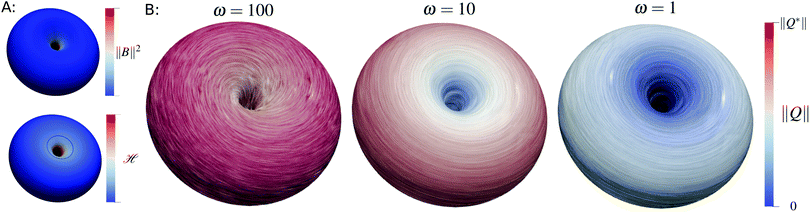
Balancing curvature effects for 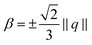
To obtain an intuition on the possible interactions of the geometry-order couplings we consider a thick torus (R = 0.55, r = 0.45) where ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) changes sign, see Fig. 4A. On this surface we evaluate the equilibrium states Q of the
changes sign, see Fig. 4A. On this surface we evaluate the equilibrium states Q of the 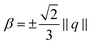 model for several values of ω, see Fig. 4B. Recalling ω as factor weighting the distortion contribution versus the state potential we observe for ω = 100 a dominant state potential such that a uniform nematic phase, ‖Q‖ = ‖Q*‖, as prescribed by the state potential, is enforced across the entire surface, suppressing the effects of the isotropic geometry coupling. In contrast, the directed geometry coupling is not affected and we observe a strong forcing towards the – geometry induced – preferred alignment such that a non uniform ordering of principal directors is yielded, see Fig. 4B (left). For regions of positive
model for several values of ω, see Fig. 4B. Recalling ω as factor weighting the distortion contribution versus the state potential we observe for ω = 100 a dominant state potential such that a uniform nematic phase, ‖Q‖ = ‖Q*‖, as prescribed by the state potential, is enforced across the entire surface, suppressing the effects of the isotropic geometry coupling. In contrast, the directed geometry coupling is not affected and we observe a strong forcing towards the – geometry induced – preferred alignment such that a non uniform ordering of principal directors is yielded, see Fig. 4B (left). For regions of positive ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) the alignment is with minimal curvature lines (outer part), whereas for negative
the alignment is with minimal curvature lines (outer part), whereas for negative ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) the alignment is with maximal curvature lines (inner part). Similar effects have also been reported for polar liquid crystals within a surface Frank–Oseen model.58,59 Weakening the state potential by choosing ω = 10 we observe a curvature induced phase transition with a localized isotropic phase at the inner part of the torus, where ‖
the alignment is with maximal curvature lines (inner part). Similar effects have also been reported for polar liquid crystals within a surface Frank–Oseen model.58,59 Weakening the state potential by choosing ω = 10 we observe a curvature induced phase transition with a localized isotropic phase at the inner part of the torus, where ‖![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ‖2 has its maximum. This area coincides with the area of the strongest directed geometry coupling. Finally matching the distortion contribution and state potential by ω = 1 we yield a global isotropic phase since the isotropic coupling distorts the state potential such that only the isotropic Q = 0 phase remains stable.
‖2 has its maximum. This area coincides with the area of the strongest directed geometry coupling. Finally matching the distortion contribution and state potential by ω = 1 we yield a global isotropic phase since the isotropic coupling distorts the state potential such that only the isotropic Q = 0 phase remains stable.
The isotropic geometry coupling term, 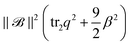 , turns out to be the dominating effect compared to the directed geometry coupling term 6
, turns out to be the dominating effect compared to the directed geometry coupling term 6![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) β〈
β〈![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,q〉. Only in situations where the state potential is strong enough to suppress the isotropic coupling the effects of directed coupling become traceable. In this situation the geometry induces a preferred alignment, see also ref. 38 for similar results on ellipsoidal geometries. For geometries with strong variations in
,q〉. Only in situations where the state potential is strong enough to suppress the isotropic coupling the effects of directed coupling become traceable. In this situation the geometry induces a preferred alignment, see also ref. 38 for similar results on ellipsoidal geometries. For geometries with strong variations in ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , including sign changes, this leads to nonuniform ordering. An effect is obviously possible only in models with β ≠ 0.
, including sign changes, this leads to nonuniform ordering. An effect is obviously possible only in models with β ≠ 0.
5 Discussion and conclusions
Exploring a thin film limit of the 3D Landau–de Gennes Q-tensor model allows bridging the gap to previously proposed surface models. Planar anchoring at the boundary of the thin film was thereby used to fix the boundary normal as eigenvector with eigenvalue β, which motivated the decomposition of the tensorial order parameter Q in tangential q and normal β parts. We will now review the central results of the models with different choices of β, discuss suitable application scenarios, assess their inherent couplings to the curvature of the surface and discuss possible experiments to confirm these results.Discussion
The first class of surface Landau–de Gennes Q-tensor models considers β = 0 and is usually labeled as planar degenerate Q-tensors.31,34 We observed the models to exhibit essentially 2D characteristics like eigenvalue spectra of Q matching 2D mean field theory. These models also show a continuous/second-order isotropic-to-nematic phase transition, which contradictory results on the existence of first-order isotropic-to-nematic phase transitions in 2D.39,40 Concerning the coupling with geometric properties the model in ref. 31 and 34 did only account for intrinsic curvature effects.For the second class, where β ≠ 0, the obtained models retain the characteristics of the 3D Landau–de Gennes Q-tensor model. As the resulting thin film limit in the general case of variable β shows a distortion of uniaxiality by curvature, we use a 3D biaxiality measure to fix 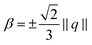 , which enforces uniaxial Q also in the surface model. Further investigations confirmed that in this modified model for uniaxial Q-tensors the fundamental properties of eigenvalue spectra, first order isotropic-to-nematic phase transition and phase coexistence stay preserved. The model β = −⅓S*, as proposed in ref. 36 and 38, has been proven to reproduce the 3D characteristics, under the assumption of ‖Q‖ = ‖Q*‖, except for phase coexistence. It can be considered as a simplified surface Landau–de Gennes Q-tensor model suitable for uniaxial nematic liquid crystals far from phase transition temperature. Furthermore β ≠ 0 introduces additional curvature coupling terms. In addition to isotropic geometry coupling, the alignment of the director field with the principle curvature lines is considered, which had already been shown in ref. 32, 36, 38 and 60. Parameter studies for a torus indicate that, depending on the strength of the curvature, phase transitions can be enforced, leading to phase coexistence and locally confined isotropic regions within a nematic phase or even a uniform isotropic phase if the curvature effect is strong enough. The derived thin film limit (without the introduced penalization to enforce uniaxiality) shows even stronger curvature coupling, e.g. curvature induced biaxiality, see the Appendix. Other implications of this model are not explored.
, which enforces uniaxial Q also in the surface model. Further investigations confirmed that in this modified model for uniaxial Q-tensors the fundamental properties of eigenvalue spectra, first order isotropic-to-nematic phase transition and phase coexistence stay preserved. The model β = −⅓S*, as proposed in ref. 36 and 38, has been proven to reproduce the 3D characteristics, under the assumption of ‖Q‖ = ‖Q*‖, except for phase coexistence. It can be considered as a simplified surface Landau–de Gennes Q-tensor model suitable for uniaxial nematic liquid crystals far from phase transition temperature. Furthermore β ≠ 0 introduces additional curvature coupling terms. In addition to isotropic geometry coupling, the alignment of the director field with the principle curvature lines is considered, which had already been shown in ref. 32, 36, 38 and 60. Parameter studies for a torus indicate that, depending on the strength of the curvature, phase transitions can be enforced, leading to phase coexistence and locally confined isotropic regions within a nematic phase or even a uniform isotropic phase if the curvature effect is strong enough. The derived thin film limit (without the introduced penalization to enforce uniaxiality) shows even stronger curvature coupling, e.g. curvature induced biaxiality, see the Appendix. Other implications of this model are not explored.
These discrepancies in response to the curvature of the β = 0 and β ≠ 0 models provide a motivation for in vitro experiments to assess the prevalent 2D or 3D nature of liquid crystals which are confined to curved surfaces.
Conclusions
With the presented derivations and arguments we have provided a comprehensive study unifying recent approaches for surface Landau–de Gennes Q-tensor theories for uniaxial nematic liquid crystals confined to curved surfaces. By introducing a surface parameter β we have classified different surface limits for nematic phases on curved manifolds. Essentially, β measures the ability of the orientational degrees of freedom to fluctuate in the direction perpendicular to the curved surface while the particle centers are constrained on the manifold in the thin-film limit. In terms of physics, these are the imposed anchoring conditions at the surface. In particular, we have identified two classes of models as special limits which could be related to liquid crystals with prevalent 2D or 3D characteristics. The distinct response to curvature of these two model classes enables a path to determine suitable models for the liquid crystal systems by in vitro experiments. In the future it would be interesting to link the classes of surface Landau–de Gennes Q-tensor models studied in this paper to particle-resolved models where anisotropic apolar particles are bound to curved interfaces. It remains to be understood how different anchoring conditions of the particles at the surface can be mapped and described effectively by the coarse-grained mean-field-like approach. In principle, varying the anchoring conditions should result in different coupling parameters used in the surface free energy (4). In particle-resolved computer simulations, different anchoring conditions can just be implemented by an explicit orientational coupling to the curved interface. In actual experiments on colloids bound to curved interfaces (see e.g.ref. 61), on Pickering emulsion droplets62 the anchoring conditions can be conveniently changed by the pH63 or by changing the thermodynamic parameters.Conflicts of interest
There are no conflicts to declare.A Appendix
A.1 Details on the uniaxiality condition
To obtain the surface uniaxiality condition (8) we can insert the Q-tensor decomposition (5) into the biaxiality measure (2). Another elegant approach is to consider the eigenvalue spectrum (14) and insert it into the biaxiality measure: Q uniaxial ⇔ U(Q) = 0 ⇔ 6(tr3Q3)2 = (tr3Q2)3. We obtain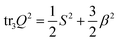 and
and 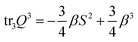 such that the uniaxiality condition U(Q) = 0 can be expressed by, assuming S ≠ 0, β2(18S2 − 81β2) = S4. This holds if and only if
such that the uniaxiality condition U(Q) = 0 can be expressed by, assuming S ≠ 0, β2(18S2 − 81β2) = S4. This holds if and only if 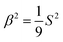 which translates to
which translates to 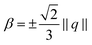 .
.
A.2 Derivation of the thin film limit
Thin film limits require a reduction of the degrees of freedom. We deal with this issue by setting Dirichlet boundary conditions for the normal parts of Q and postulate a priori a minimum of the free energy on the boundary of the thin film. This is achieved by considering the natural boundary condition of the weak Euler–Lagrange equation. In this setting we restrict the density of![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) to the surface and integrate in the normal direction to obtain the surface energy
to the surface and integrate in the normal direction to obtain the surface energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . We closely follow ref. 38, use the notation introduced there and only point out differences. Following this notation we define the shape operator by
. We closely follow ref. 38, use the notation introduced there and only point out differences. Following this notation we define the shape operator by ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = −[(G − ν ⊗ ν)∇3]ν.
= −[(G − ν ⊗ ν)∇3]ν.
The free energy (2) in the thin film ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h in index notation reads
h in index notation reads
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h a pure covariant representation of Q at the boundary is
h a pure covariant representation of Q at the boundary is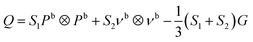 | (15) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h. According to the normal eigenvalue β of Q at
h. According to the normal eigenvalue β of Q at ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , we extend this scalar field to the thin film
, we extend this scalar field to the thin film ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h, i.e., Qξξ =
h, i.e., Qξξ = ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) with
with ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) |
|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = β.
= β.
We can relate the anchoring conditions to surface identities by sums and differences of Taylor expansions at the upper and lower boundaries, see ref. 38. This results in
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) } ∈ T(2)
} ∈ T(2)![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is not a Q-tensor. We have tr2{Qij|
is not a Q-tensor. We have tr2{Qij|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) } = tr3Q|
} = tr3Q|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) − Qξξ|
− Qξξ|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = −β. To ensure Q-tensor properties we introduce the projection Π
= −β. To ensure Q-tensor properties we introduce the projection Π![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) : t → ½(t + tT − (tr2t)g), and define
: t → ½(t + tT − (tr2t)g), and define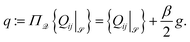 | (16) |
We can determine all remaining covariant derivatives restricted to the surface by
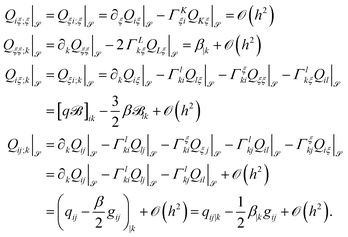 | (17) |
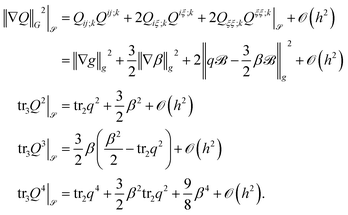 | (18) |
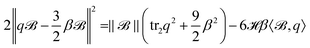 | (19) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , we obtain for h → 0
, we obtain for h → 0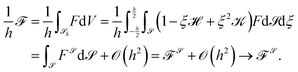 | (20) |
A.3 Variational derivatives
The first variation ofw.r.t. surface Q-tensor ψ and scalar φ perturbations for q and β reads
where β is independent. If β is constant, or prescribed generally, the associated perturbation φ vanishes. To enforce uniaxiality (8), we add the penalty energy
to
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , with ωβ > 0. Its first variation reads
, with ωβ > 0. Its first variation readsFrom this, the L2-gradient flows lead to the considered evolution equations for q and β.
A.4 L 2-Gradient flows
Instead of relating the energies![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , also the evolution equations in
, also the evolution equations in ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) h and on
h and on ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) can be related. Similar calculations as in Section A.2 give
can be related. Similar calculations as in Section A.2 givewith appropriate bulk and surface Q-tensors Ψ and ψ and scalar φ perturbations, s.t. Ψξξ|
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = φ. This condition is the principal difference to the calculations in ref. 38. Note that we used (19) in the derivation, weakly in the Q-tensor direction ψ, i.e.
= φ. This condition is the principal difference to the calculations in ref. 38. Note that we used (19) in the derivation, weakly in the Q-tensor direction ψ, i.e.Moreover, as ∂tg = 0 for a stationary surface, we obtain 〈∂tQ,Ψ〉G|
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 〈∂tq,ψ〉g +
= 〈∂tq,ψ〉g + ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) (∂tβ)ϕ +
(∂tβ)ϕ + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (h2) and as in (20)
(h2) and as in (20)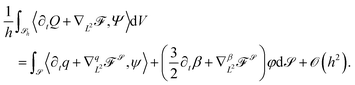 | (21) |
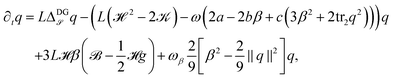 | (22) |
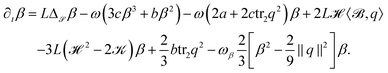 | (23) |
A.5 Numeric solution procedure
To numerically solve the tensor- and scalar-valued surface PDEs (22) and (23), we use the surface FEM approaches of ref. 64 and 65, respectively. The approach in ref. 64 extends previous ideas for vector-valued surface PDEs59,66,67 to tensors of arbitrary degree. The idea of these approaches is to reformulate the problems in Cartesian coordinates and to penalize normal components. This allows for a componentwise solution using tools for scalar-valued surface PDEs, e.g.ref. 65. The penalty term added to![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) reads
reads 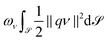 with ων > 0. This leads to an additional term in (22) reading ων(ν ⊗ ν)q.
with ων > 0. This leads to an additional term in (22) reading ων(ν ⊗ ν)q.
To address the nonlinearity of the system of PDEs we consider a Newton method. We solve the temporal discretized problem as a sequence of time steps [![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ,
,![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) ] → q,β, where ∂tq ≈ (q −
] → q,β, where ∂tq ≈ (q − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) )/τ and ∂tβ ≈ (β −
)/τ and ∂tβ ≈ (β − ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) )/τ. We denote with L
)/τ. We denote with L![[Doublestruck Q]](https://www.rsc.org/images/entities/char_e174.gif) , L
, L![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) and N
and N![[Doublestruck Q]](https://www.rsc.org/images/entities/char_e174.gif) , N
, N![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) the collections of linear and nonlinear operators of the time step problems, where
the collections of linear and nonlinear operators of the time step problems, where ![[Doublestruck Q]](https://www.rsc.org/images/entities/char_e174.gif) and
and ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) refer to the q and β state equations. The single Newton iteration k → k + 1 reads
refer to the q and β state equations. The single Newton iteration k → k + 1 reads
The resulting linear surface PDEs are solved by the surface FEM methods64,65 which are implemented in the adaptive FEM toolbox AMDiS.68,69
To assess the quality of enforcing tangentiality and uniaxiality by the introduced penalty terms, simulations are performed with ων ∈ [101,103] and ωβ ∈ [101,103] on a torus (R = 2, r = 0.5) for ω = 10, 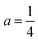 , b = −4 and c = 1. Across the studied parameters we obtain for tangential alignment ‖qν‖ < 10−3 and for uniaxiality
, b = −4 and c = 1. Across the studied parameters we obtain for tangential alignment ‖qν‖ < 10−3 and for uniaxiality 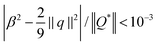 at each point of
at each point of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) .
.
A.6 Curvature induced biaxiality
Without the penalization (9) the solution space for the tensorial order parameter Q(q,β) is not restricted to the uniaxial eigenvalue spectrum σ(Q) as defined in (1). To demonstrate this we solve (10) and (11) without the penalization term (ωβ = 0). Fig. 5A and B shows the equilibrium solution on a flat (2D) and a curved surface, respectively, demonstrating the distortion of uniaxiality by curvature.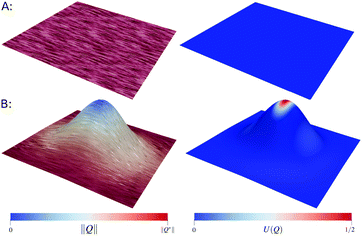 | ||
Fig. 5 Curvature distorts uniaxiality in unconstrained surface Landau–de Gennes Q-tensor model: (A) in 3D energetic minima of unconstrained surface Q-tensors ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (Q(q,β)) are uniaxial (for b < 0, see e.g.ref. 45), which also holds for the thin film limit for a flat surface. (left) 2D yields uniform alignment of the principal director (lines, obtained by line integral convolution (LIC) and constant ‖Q‖ (color scale)). (right) Uniform values of biaxiality measure U(Q) ≈ 0. (B) Curvature in domain distorts ‖Q‖ and also uniaxiality. (left) Norm deficiency in high curvature areas. (right) Uniaxiality is substantially violated in high curvature regions where U(Q) ≈ ½. The geometry is defined by a Gaussian bump h(x,y) = h0 (Q(q,β)) are uniaxial (for b < 0, see e.g.ref. 45), which also holds for the thin film limit for a flat surface. (left) 2D yields uniform alignment of the principal director (lines, obtained by line integral convolution (LIC) and constant ‖Q‖ (color scale)). (right) Uniform values of biaxiality measure U(Q) ≈ 0. (B) Curvature in domain distorts ‖Q‖ and also uniaxiality. (left) Norm deficiency in high curvature areas. (right) Uniaxiality is substantially violated in high curvature regions where U(Q) ≈ ½. The geometry is defined by a Gaussian bump h(x,y) = h0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(x2 + y2)/w02) where h0 = w0 = ½ and (x,y) ∈ [−1,1]2 and ω = 10. exp(−(x2 + y2)/w02) where h0 = w0 = ½ and (x,y) ∈ [−1,1]2 and ω = 10. | ||
Acknowledgements
AV acknowledges financial support from DFG through VO899/19. HL acknowledges financial support from DFG through LO418/20. We further acknowledge computing resources provided by JSC under grant HDR06 and ZIH/TUDresden.References
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford Science Publications, 2nd edn, 1993 Search PubMed.
- P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge University Press, 1995 Search PubMed.
- A. Fernandez-Nieves, V. Vitelli, A. S. Utada, D. R. Link, M. Marquez, D. R. Nelson and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 157801 CrossRef CAS PubMed.
- T. Lopez-Leon, A. Fernandez-Nieves, M. Nobili and C. Blanc, J. Phys.: Condens. Matter, 2012, 24, 284122 CrossRef PubMed.
- H. L. Liang, J. Noh, R. Zentel, P. Rudquist and J. P. F. Lagerwall, Philos. Trans. R. Soc., A, 2013, 371, 20120258 CrossRef PubMed.
- H. L. Liang, S. Schymura, P. Rudquist and J. Lagerwall, Phys. Rev. Lett., 2011, 106, 247801 CrossRef PubMed.
- K. May, K. Harth, T. Trittel and R. Stannarius, EPL, 2012, 100, 16003 CrossRef.
- J. P. F. Lagerwall, C. Schütz, M. Salajkova, J. H. Noh, J. H. Park, G. Scalia and L. Bergström, NPG Asia Mater., 2014, 6, e80 CrossRef CAS.
- L. Jia, A. Cao, D. Lévy, B. Xu, P.-A. Albouy, X. Xiangjun, M. J. Bowick and M.-H. Li, Soft Matter, 2009, 5, 3446 RSC.
- B. Xu, R. Piñol, M. Nono-Djamen, S. Pensec, P. Keller, P.-A. Albouy, D. Lévy and M.-H. Li, Faraday Discuss., 2009, 143, 235 RSC.
- L. Jia, D. Lévy, D. Durnad, M. Imperor-Clerc, A. Cao and M.-H. Li, Soft Matter, 2011, 7, 7395 RSC.
- L. B. G. Cortes, Y. Gao, R. P. A. Dullens and D. G. A. L. Aarts, J. Phys.: Condens. Matter, 2017, 29, 064003 CrossRef PubMed.
- R. E. Guerra, C. P. Kelleher, A. D. Hollingsworth and P. M. Chaikin, Nature, 2018, 554, 346 CrossRef CAS PubMed.
- J. Dzubiella, M. Schmidt and H. Löwen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5081–5091 CrossRef CAS PubMed.
- M. A. Bates, G. Skacej and C. Zannoni, Soft Matter, 2010, 6, 665 RSC.
- H. Shin, M. J. Bowick and X. Xing, Phys. Rev. Lett., 2008, 101, 037802 CrossRef PubMed.
- S. Dhakal, F. J. Solis and M. Olvera de la Cruz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011709 CrossRef PubMed.
- V. Koning, T. Lopez-Leon, A. Fernandez-Nieves and V. Vitelli, Soft Matter, 2013, 9, 4993 RSC.
- S. Paquay, G.-J. Both and P. van der Schoot, Phys. Rev. E, 2017, 96, 012611 CrossRef.
- N. D. Bade, R. Kamien, R. Assoian and K. Stebe, Biophys. J., 2017, 112, 536a CrossRef.
- H. Stark, Phys. Rep., 2001, 351, 378 CrossRef.
- P. Prinsen and P. van der Schoot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 68, 021701 CrossRef.
- A. Martinez, M. Ravnik, B. Lucero, R. Visvanathan, S. Zumer and I. I. Smalyukh, Nat. Mater., 2014, 13, 259 CrossRef.
- T. Geigenfeind, S. Rosenzweig, M. Schmidt and D. de las Heras, J. Chem. Phys., 2015, 142, 174701 CrossRef PubMed.
- D. Matsunaga, F. Meng, A. Zöttl, R. Golestanian and J. M. Yeomans, Phys. Rev. Lett., 2017, 119, 198002 CrossRef PubMed.
- R. Sknepnek and S. Henkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022306 CrossRef PubMed.
- F. Alaimo, C. Köhler and A. Voigt, Sci. Rep., 2017, 7, 5211 CrossRef PubMed.
- E. Allahyarov, A. Voigt and H. Löwen, Soft Matter, 2017, 13, 8120–8135 RSC.
- C. E. Sitta, F. Smallenburg, R. Wittkowski and H. Loewen, Phys. Chem. Chem. Phys., 2018, 20, 5285–5294 RSC.
- E. Allahyarov and H. Löwen, Soft Matter, 2018, 14, 8962–8973 RSC.
- S. Kralj, R. Rosso and E. G. Virga, Soft Matter, 2011, 7, 670–683 RSC.
- G. Napoli and L. Vergori, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061701 CrossRef PubMed.
- G. Napoli and L. Vergori, Phys. Rev. Lett., 2012, 108, 207803 CrossRef PubMed.
- D. Jesenek, S. Kralj, R. Rosso and E. G. Virga, Soft Matter, 2015, 11, 2434–2444 RSC.
- D. Golovaty, J. A. Montero and P. Sternberg, J. Nonlinear Sci., 2015, 25, 1431–1451 CrossRef CAS.
- D. Golovaty, J. A. Montero and P. Sternberg, J. Nonlinear Sci., 2017, 27, 1905–1932 CrossRef CAS.
- M. R. Novack, SIAM J. Math. Anal., 2018, 50, 6007–6048 CrossRef.
- I. Nitschke, M. Nestler, S. Praetorius, H. Löwen and A. Voigt, Proc. R. Soc. A, 2018, 474, 20170686 Search PubMed.
- A. C. Van Enter and S. B. Shlosman, Phys. Rev. Lett., 2002, 89, 285702 CrossRef.
- A. C. Van Enter, S. Romano and V. A. Zagrebnov, J. Phys. A: Math. Gen., 2006, 39, L439 CrossRef.
- H. H. Wensink and R. L. C. Vink, J. Phys.: Condens. Matter, 2007, 19, 466109 CrossRef.
- R. L. C. Vink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062132 CrossRef.
- R. Wittmann, C. E. Sitta, F. Smallenburg and H. Löwen, J. Chem. Phys., 2017, 147, 134908 CrossRef.
- J. Fish and R. Vink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021705 CrossRef CAS PubMed.
- A. Majumdar, Eur. J. Appl. Math., 2010, 21, 181–203 CrossRef.
- J. Straley, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 675 CrossRef.
- M. J. Stephen and J. P. Straley, Rev. Mod. Phys., 1974, 46, 617 CrossRef CAS.
- K. Schiele and S. Trimper, Phys. Status Solidi B, 1983, 118, 267–274 CrossRef CAS.
- D. W. Berreman and S. Meiboom, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 1955–1959 CrossRef CAS.
- T. C. Lubensky, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 2497–2514 CrossRef.
- L. Longa, D. Monselesan and H.-R. Trebin, Liq. Cryst., 1987, 2, 769–796 CrossRef.
- J. M. Ball and A. Majumdar, Mol. Cryst. Liq. Cryst., 2010, 525, 1–11 CrossRef CAS.
- M. E. Gurtin and A. I. Murdoch, Arch. Ration. Mech. Anal., 1975, 57, 291–323 CrossRef.
- P. Kaiser, W. Wiese and S. Hess, J. Non-Equilib. Thermodyn., 1992, 17, 153–169 CAS.
- W. Kühnel, Differential geometry, American Mathematical Soc., 2015, vol. 77 Search PubMed.
- I. Nitschke, S. Reuther and A. Voigt, Phys. Rev. Fluids, 2019, 4, 044002 CrossRef.
- I. Nitschke, S. Reuther and A. Voigt, 2019, arXiv:1911.11859.
- A. Segatti, Math. Models Methods Appl. Sci., 2016, 26, 1865 CrossRef CAS.
- M. Nestler, I. Nitschke, S. Praetorius and A. Voigt, J. Nonlinear Sci., 2018, 28, 147–191 CrossRef.
- G. Napoli and L. Vergori, Int. J. Non Linear Mech., 2013, 49, 66–71 CrossRef.
- I. B. Liu, N. Sharifi-Mood and K. J. Stebe, Annu. Rev. Condens. Matter Phys., 2018, 9, 283–305 CrossRef CAS.
- F. Lou, L. Ye, M. Kong, Q. Yang, G. Lia and Y. Huang, RSC Adv., 2016, 6, 24195 RSC.
- S. Qin and X. Yong, Soft Matter, 2019, 15, 3291–3300 RSC.
- M. Nestler, I. Nitschke and A. Voigt, J. Comput. Phys., 2019, 389, 48–61 CrossRef.
- G. Dziuk and C. M. Elliott, Acta Numer., 2013, 22, 289–396 CrossRef.
- T. Jankuhn, M. A. Olshanskii and A. Reusken, Interface. Free Bound., 2018, 20, 353–377 CrossRef.
- P. Hanbo, M. G. Larson and K. Larsson, IMA J. Num. Anal., 2019 DOI:10.1093/imanum/drz018.
- S. Vey and A. Voigt, Comput. Visualization Sci., 2007, 10, 57–67 CrossRef.
- T. Witkowski, S. Ling, S. Praetorius and A. Voigt, Adv. Comput. Math., 2015, 41, 1145 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |