Open Access Article
Open Access ArticleENTH domain-dependent membrane remodelling
Claudia
Steinem
 *ab and
Michael
Meinecke
*ab and
Michael
Meinecke
 *bc
*bc
aInstitute for Organic and Biomolecular Chemistry, University of Göttingen, Tammannstr. 2, 37077 Göttingen, Germany
bGöttinger Zentrum für Molekulare Biowissenschaften – GZMB, 37077 Göttingen, Germany. E-mail: csteine@gwdg.de; mmeinec@gwdg.de
cDepartment of Cellular Biochemistry, University Medical Center Göttingen, Humboldtallee 23, 37073 Göttingen, Germany
First published on 12th May 2020
Abstract
Cellular membranes are anything but flat structures. They display a wide variety of complex and beautiful shapes, most of which have evolved for a particular physiological reason and are adapted to accommodate certain cellular demands. In membrane trafficking events, the dynamic remodelling of cellular membranes is apparent. In clathrin-mediated endocytosis for example, the plasma membrane undergoes heavy deformation to generate and internalize a highly curved clathrin-coated vesicle. This process has become a model system to study proteins with the ability to sense and induce membrane curvature and over the last two decades numerous membrane remodelling molecules and molecular mechanisms have been identified in this process. In this review, we discuss the interaction of epsin1 ENTH domain with membranes, which is one of the best-studied examples of a peripheral and transiently membrane bending protein important for clathrin-mediated endocytosis.
1 Introduction
Cells of higher organisms are able to take up receptors, nutrients and other molecules by a process called clathrin-mediated endocytosis (CME).1–3 Over the course of some ten seconds, cargo molecules are clustered together with membrane patches. The recruitment of cargos, adaptor proteins and finally clathrin itself, leads to the formation of a clathrin-coated pit. As more and more molecules are recruited, the pit acquires a more pronounced shape and matures into a clathrin-coated vesicle, which is finally pinched of the plasma membrane with the help of dynamin.4,5 After internalization, the vesicles get depleted of clathrin and become part of the endosomal pathway or might be recycled to fuse again with the plasma membrane.Many adaptor molecules are peripheral membrane proteins with the ability to induce membrane curvature. Several molecular mechanisms of protein-dependent membrane deformation have been described.6–9 Epsins belong to such adaptor molecules as they facilitate membrane binding and protein recruitment. They are part of a conserved family of proteins that are involved in CME and other membrane trafficking events. The best studied member of this family is the mammalian epsin1, though in animals at least three other proteins, epsin2, epsin3 and epsinR, have been identified.10 The general domain structure of epsins is similar (Fig. 1). At the very N-terminus a tightly folded, membrane-binding ENTH (epsin N-terminal homology) domain is found. The C-terminus is comprised of multiple protein–protein interaction domains and is believed to mainly contain intrinsically disordered amino acid stretches.11,12 Through short protein–protein interaction motifs, epsin1 is able to bind to the α-ear of the adaptor complex AP2, to clathrin heavy chains and to Eps15 and intersectin,13–16 all proteins involved in CME. It also contains ubiquitin binding motifs, most probably to recruit ubiquitinated receptors destined for degradation into clathrin-coated vesicles.17–20 There is however a debate if epsin's role in CME might be more general.21,22 Overall, the membrane remodelling activity of epsins has been studied much more extensively than their physiological role in specific membrane trafficking pathways.
The N-terminal ENTH domain has been studied in some detail and multiple high-resolution structures are available.23 At its very N-terminus, the compact globular, α-helical domain shows in solution an unstructured amino acid stretch.24 The ENTH domain binds to membranes in an phosphoinositide-dependent manner with a preference for phosphatidylinositol-4,5-bisphosphate (PIP2).25 Upon binding to PIP2 the unstructured N-terminus folds into an amphipathic helix referred to as α0 (Fig. 2A and B).26 Basic residues on the inner side of α0 stabilize PIP2 binding and position the hydrophobic side of α0 in contact with the membrane to bind.26–28
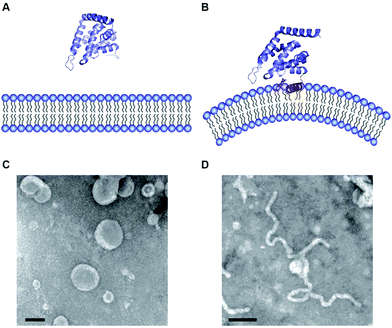 | ||
| Fig. 2 (A and B) Atomic structure of ENTH domains in the absence (A) and presence (B) of PIP2. (C and D) Electron micrographs of liposomes in the presence of ENTH domains under the same conditions shown above (pictures taken from Tarasenko et al.35). | ||
It was noted early on that membrane binding of the ENTH domain leads to membrane deformation (Fig. 2C and D).26 This effect was classically studied using various model membrane systems discussed in Section 3. Another class of proteins that are found in CME and many other membrane trafficking events are the BAR (bin/amphiphysin/rvs) domain containing proteins.29 BAR domain containing proteins also transiently interact with membranes and have the ability to induce membrane curvature.30–32 The reader is referred to excellent reviews on BAR domains.4,29,33,34 The discovery of peripheral membrane proteins that transiently interact with and have the ability to change the morphology of membranes sparked the publication of a wealth of papers identifying proteins that are important to shape the complex and beautiful structure variety of cellular membranes.
2 Molecular models for membrane remodelling by ENTH domains
The finding that binding to PIP2 containing membranes triggers the formation of an amphipathic α-helix within the ENTH domain and that this interaction generates membrane deformation demanded a molecular explanation. In order to deform a lipid bilayer, energy has to be supplied. The first widely accepted model that explained the induction of curvature by ENTH domains was that the shallow insertion of α0 at one side of the bilayer leads to non-zero spontaneous curvature.26 The amphipathic domain would hereby adopt a wedge-like structure and perturbs the packing of lipid-head groups in one monolayer of the membrane (Fig. 3, hydrophobic insertion).9,36 In line with this notion, analysing of the insertion depth revealed that α0 was located at the phosphate head-group region of the membrane.37 Later EPR studies found α0 to penetrate into the hydrophobic region of the lipid bilayer in a slanted orientation, which leads to self-association described to be distinct from simple molecular crowding.38 Interestingly, different insertion depth were also found for the amphipathic helix of the amphiphysin N-BAR domain.39 Altered insertion depths should have different impacts on membrane curvature.40,41 No conclusive explanations were so far made for how α0 of epsins could achieve different insertion depths or how this might be regulated in a physiological context.Epsin1 not only binds and deforms membranes but is also able to recruit clathrin and promote its oligomerisation into cage-like structures.26 It is hence believed that the local curvature generated by epsin is stabilized by clathrin.8 Some N-BAR domain containing proteins might have evolved to harbour both, curvature induction and stabilization in one molecule.34,42 These molecules display amphipathic helices at the N-terminus of their crescent-shape BAR domains (hence their name N-BAR) and as such can induce and stabilize membrane curvature.
Although, theoretical and structural studies have confirmed that α0 indeed inserts into the bilayer and structure-to-function mutants, with decreased hydrophobicity of the amphipathic α0 show less pronounced effects on membrane morphology,26,37,38,43 the view that the insertion of a small amphipathic domain is the main driving force behind membrane curvature generation by epsin1 and other proteins was challenged several times. Campelo et al.41 presented calculations based on a numerical solution of an analytical continuum mechanics model that suggests conditions under which α0 alone can drive membrane curvature. However, in order to induce high degrees of membrane curvature, an incredibly high protein density on the membrane would have to be established.41,44,45 In case of amphiphysin, it was even shown that α0 did not generate significant membrane curvature in the absence of the BAR domains.46 Similarly, shallow membrane insertion by the N-terminal amphipathic helix of the N-BAR domain of endophilin, another endocytic accessory molecule, was found to have no direct impact on membrane remodelling.42 Hence, a generally agreed consensus regarding the role of α0 has not been reached.
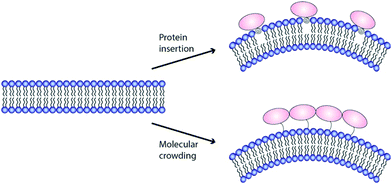
Stackowiak et al.47,48 proposed macromolecular crowding to be the main driving force for membrane deformation (Fig. 3). Similar results were shown by the Baumgart group.49 In these studies, the generation of membrane curvature could be uncoupled from amphipathic helix insertion. Even in the absence of α0, membrane deformation could be detected if protein coverage of a membrane was above 20%.48 In this crowding model, the energy to remodel a lipid bilayer is generated by collisions between membrane bound proteins. The notion that intrinsically disordered protein domains, like found in the C-terminal domain of epsin1, enhances membrane curvature sensing, is in favour of such crowding model.12
Our own results, showing that ENTH domains decrease lateral membrane tension and thereby lower the needed energy to induce membrane curvature, is in line with both models.50 We also recently found that the membrane lipid composition plays a crucial role in epsin1 dependent membrane remodelling. Phosphatidylserine (PS) induces the oligomerisation of ENTH domains and therefore high local protein densities. This in turn is a prerequisite for membrane deformation and efficient CME (Steinem and Meinecke, manuscript in revision). It might very well be that the molecular mechanism used by epsin1 to deform membranes is a combination of different effects relying on a cooperativity between protein–protein and protein–membrane interactions.
Lately, the degree of membrane curvature induced by epsins has gained renewed attention. As discussed, multiple studies found that the addition of epsin1 ENTH domain to membranes results in the induction of membrane curvature. This was classically shown by tubulation of large unilamellar vesicles (Fig. 2C and D). A recent study found though, that the ultimate consequence of ENTH–membrane interaction, and here especially the insertion of α0, is vesiculation rather than tubulation.21 The authors claim to have observed this vesiculation phenotype before26 when they used ENTH domain mutants with increased hydrophobicity at the polar side of α0. They now concluded that the insertion of amphipathic helices results in membrane fission and could hence facilitate the final steps of CME, where a clathrin-coated vesicle is internalised by a scission reaction. Epsin shows a similar recruitment profile during clathrin-mediated endocytosis as clathrin.51 Hence, it is not clear if epsin is particularly enriched at the late fission stage of clathrin mediated endocytosis and it will be interesting to see if it really facilitates the fission reaction. In light of results showing protein crowding rather than shallow insertion drives membrane curvature,42,52 and that only high concentrations of the ENTH domain generate curvature and lead to membrane fission, although less efficient than dynamin mediated fission,53 more work will be needed to fully understand the molecular mechanism of ENTH-dependent membrane remodelling and its physiological function.
3 ENTH induced membrane curvature generation and sensing investigated with different model membrane systems
Since the discovery that membrane curvature is an active means to control spatial organization and activity of cells, several model membranes have been envisioned and developed to investigate protein-induced membrane curvature sensing and generation. A very classical approach is to incubate liposomes with a diameter of 50–200 nm (small and large unilamellar vesicles) in the presence of high protein concentrations. This method allows many important parameters to be controlled such as protein concentration and lipid composition. Morphological changes of the incubated liposomes are then observed by electron microscopy (EM) using negative staining or even better cryo-EM. In an early study from 2002, Ford et al.26 used liposomes composed of total brain lipids (Folch extract containing 10% phosphoinositides) to explore the influence of ENTH domain on morphological changes of the liposomes. They indeed found that the addition of ENTH domain converted round shaped liposomes into tubules. In an advanced study of the groups of McMahon and Kozlov,21 it was reported that ENTH domain forms not only extremely narrow tubules with diameters of only 20 nm diameter but also many small nanovesicles, which means that not only tubulation but also vesiculation can occur upon ENTH interaction with the membrane. As they again used the Folch extract spiked with 5% PIP2, they asked the question of whether this lipid mixture can be replaced by a synthetic lipid composition. They prepared a mixture containing 10% cholesterol, 5% PIP2, 55% phosphatidylcholine (PC), and 30% PS. Of note, the authors state that they used 30% PS to achieve a strong electrostatic interaction for epsin, as would be expected in the plasma membrane inner leaflet where the protein binds in vivo. Their results demonstrated that addition of epsin resulted in robust vesiculation as determined by a simple sedimentation assay.Compared to small and large unilamellar vesicles with a large intrinsic curvature, giant unilamellar vesicles (GUVs) with a size of 5–50 μm in diameter are quasi-planar on the scale of individual proteins, large enough to be observed by optical microscopy and amenable to micromanipulation. In the most basic approach, GUVs labelled with a fluorescent dye are incubated with fluorescently tagged protein. Under certain conditions, i.e., at rather low membrane tension and high protein concentration, membrane tubulation or invagination can be observed by confocal laser scanning microscopy.54 For the ENTH domain we are only aware of two studies, in which tubules, generated by the interaction of ENTH with GUVs, have been described.38,48 This is probably due to the fact that the insertion of α0 of ENTH destabilizes the membranes resulting in bursting of the vesicles rather than tubule formation like observed for other membrane shaping proteins such as BAR domains.
Another membrane model that is based on GUVs is to use micropipette-assisted pulling of cylindrical tethers. In this experimental setup, a GUV is aspirated in a micropipette that sets the membrane tension σ. A membrane nanotube is pulled out from the GUV by tethering the vesicle via streptavidin–biotin to a micrometre sized bead held by a second pipette55 or trapped in optical tweezers (Fig. 4A).56 Using this approach, connected membrane regions differing in curvature by orders of magnitude are obtained, which allows quantifying the partitioning of peripherally binding proteins in membrane curvature gradients.55,57 With this membrane system, Baumgart and co-workers quantified systematically the curvature dependence of the ENTH area density on cylindrical membranes with controlled curvature.58 They adjusted the curvature by changing the membrane tension σ and monitored the fluorescence intensity of a construct composed of ENTH and green fluorescent protein (GFP) (ENTH–GFP) bound to membrane tethers composed of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/PIP2 (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (Fig. 4B and C). If ENTH bound curvature-independently, the GFP fluorescence would be expected to decrease as σ is increased. However, they observed that the GFP-fluorescence on the tether markedly increased with increasing σ indicating curvature sensing of the protein.
1) (Fig. 4B and C). If ENTH bound curvature-independently, the GFP fluorescence would be expected to decrease as σ is increased. However, they observed that the GFP-fluorescence on the tether markedly increased with increasing σ indicating curvature sensing of the protein.
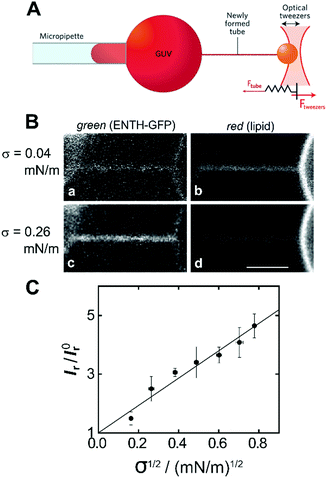 | ||
Fig. 4 Curvature partitioning of ENTH–GFP on tubular membranes. (A) Schematic drawing of a membrane tether that is formed from a GUV using optical tweezers. Image taken from Bassereau et al.59 (B) A membrane tether composed of POPC/PIP2 (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was formed by micropipette pulling from a GUV. (a and c) Green channel detecting ENTH–GFP fluorescence; (b and d) red channel detecting Texas Red DPPE fluorescence at two different membrane tensions. Scale bar: 3 μm. (C) Plot of the normalized ratio of green and red channel fluorescence intensities (Ir = Igreen/Ired) as a function of the square root of membrane tension revealing a linear relationship according to eqn (1) and (2). Images taken from Capraro et al.58 1) was formed by micropipette pulling from a GUV. (a and c) Green channel detecting ENTH–GFP fluorescence; (b and d) red channel detecting Texas Red DPPE fluorescence at two different membrane tensions. Scale bar: 3 μm. (C) Plot of the normalized ratio of green and red channel fluorescence intensities (Ir = Igreen/Ired) as a function of the square root of membrane tension revealing a linear relationship according to eqn (1) and (2). Images taken from Capraro et al.58 | ||
From the normalized fluorescence intensity ratios Ir/I0r, with Ir = Igreen/Ired as a function of membrane tension, Baumgart and co-workers were able to extract Leibler's thermodynamic curvature–composition coupling coefficient Λ according to the following relation (eqn (1) and (2)):58,60
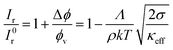 | (1) |
| κeff = κ0 − Λ2χ | (2) |
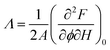 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) complex) and A the total area of the membrane. The index 0 indicates that the derivative has to be evaluated for a flat membrane.58 From the slope in Fig. 4C, Λ = −146 ± 3 pN was calculated. Eqn (1) quantifies curvature sensing as a function of the molecular property Λ and curvature generation as a function of Λ and the concentration of curvature generators ϕv, given by the ENTH/PIP2 (1
1) complex) and A the total area of the membrane. The index 0 indicates that the derivative has to be evaluated for a flat membrane.58 From the slope in Fig. 4C, Λ = −146 ± 3 pN was calculated. Eqn (1) quantifies curvature sensing as a function of the molecular property Λ and curvature generation as a function of Λ and the concentration of curvature generators ϕv, given by the ENTH/PIP2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) complexes, through a reduction in bending rigidity from κ0 to κeff. As described by Baumgart et al.,60 the Leibler-type curvature sorting model is identical to the Helfrich model with locally varying spontaneous curvature under certain assumptions, which generates the identity of Λ = −κ0Cα, with Cα being the molecular spontaneous curvature of the ENTH/PIP2 (1
1) complexes, through a reduction in bending rigidity from κ0 to κeff. As described by Baumgart et al.,60 the Leibler-type curvature sorting model is identical to the Helfrich model with locally varying spontaneous curvature under certain assumptions, which generates the identity of Λ = −κ0Cα, with Cα being the molecular spontaneous curvature of the ENTH/PIP2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) complex. Owing to the Λ2-term the effective stiffness κeff is observed to be always smaller than the bare stiffness κ0 independent of whether the spontaneous curvature of a curvature-sensing molecule is negative or positive. In their publication,58 Baumgart and co-workers reported for the first time, based on an experimental measurement, on a negative curvature–composition coupling constant for a membrane binding protein demonstrating that ENTH binds preferentially to highly curved membranes. This result indicates the possibility that ENTH contributes to cellular membrane curvature sensing and generation.
1) complex. Owing to the Λ2-term the effective stiffness κeff is observed to be always smaller than the bare stiffness κ0 independent of whether the spontaneous curvature of a curvature-sensing molecule is negative or positive. In their publication,58 Baumgart and co-workers reported for the first time, based on an experimental measurement, on a negative curvature–composition coupling constant for a membrane binding protein demonstrating that ENTH binds preferentially to highly curved membranes. This result indicates the possibility that ENTH contributes to cellular membrane curvature sensing and generation.
In another study Baumgart and coworkers61 made use of wavy surfaces to focus only on the curvature sensing properties of ENTH. They engineered a solid supported wavy membrane with continuous curvatures bearing positive and negative regions allowing an evaluation of the curvature sensitivity of ENTH. A topographical pattern with a wavelength of 1 μm and a depth of 110 nm was generated on a glass support onto which fluid lipid membranes composed of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/PIP2 (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were attached to. ENTH was found to preferentially partition into positively curved membrane regions with a protein density that varied monotonically in the curvature range yielding an increase in the normalized (relative to the average) fluorescence intensity of ENTH–GFP from 0.79 (at the most negative curvature) to 1.46 (at the most positive curvature). As they worked with the same protein construct, they also compared the curvature sensing of ENTH–GFP between free-floating (tether–GUV system) and the supported wavy membranes. In the tether–GUV system, membrane curvatures are accessible from about 0.01–0.11 nm−1 compared to −0.002–0.003 nm−1 for wavy membranes. It turned out that the supported wavy membranes sorted the protein more strongly than the tether–GUV system, which was hypothesized in terms of out-of-plane undulations occurring in freestanding membranes, which do not occur in the supported case. Of note, both membrane systems are under high tension so that this hypothesis needs to be further proven. The tether–GUV experiments with ϕv ≠ 0 show the fundamental coupling between membrane curvature sensing and generation. They are synergistically coupled phenomena both quantified through the parameter Λ.
1) were attached to. ENTH was found to preferentially partition into positively curved membrane regions with a protein density that varied monotonically in the curvature range yielding an increase in the normalized (relative to the average) fluorescence intensity of ENTH–GFP from 0.79 (at the most negative curvature) to 1.46 (at the most positive curvature). As they worked with the same protein construct, they also compared the curvature sensing of ENTH–GFP between free-floating (tether–GUV system) and the supported wavy membranes. In the tether–GUV system, membrane curvatures are accessible from about 0.01–0.11 nm−1 compared to −0.002–0.003 nm−1 for wavy membranes. It turned out that the supported wavy membranes sorted the protein more strongly than the tether–GUV system, which was hypothesized in terms of out-of-plane undulations occurring in freestanding membranes, which do not occur in the supported case. Of note, both membrane systems are under high tension so that this hypothesis needs to be further proven. The tether–GUV experiments with ϕv ≠ 0 show the fundamental coupling between membrane curvature sensing and generation. They are synergistically coupled phenomena both quantified through the parameter Λ.
More proof of the ENTH domain's curvature sensing activity was delivered by Pucadyil and co-workers.62 In this study the authors used a different low-tension model membrane system called SUPER templates. Here, a membrane reservoir is tubulated either by epsin or by extrusion through buffer flow. In the latter case, epsin was found to preferentially bind to membrane tubes. Interestingly, the authors could also show the recruitment of clathrin to highly curved membrane areas via epsin.
To investigate the influence of ENTH binding on the mechanical properties of membranes in the absence of strongly curved membranes, we established a GUV system, where the GUVs are adhered to a surface via biotin–avidin and Mg2+.50 These GUV membranes are quasi-planar. A change in the Mg2+ concentration then allowed us to adjust the lateral membrane tension by tuning the adhesion strength of the GUV to the surface mediated by Mg2+ ions. With this approach, we covered a lateral membrane tension regime of 0.08–1.02 mN m−1. To investigate the influence of ENTH binding on the adhered vesicles, we prepared GUVs composed of DOPC/1,2-dioleoyl-sn-glycero-3phosphoethanolamine (DOPE)/cap-biotin-PE/Atto488-1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (DPPE) doped with PIP2 (66.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8) in the presence of 0.5 mM and 2 mM MgCl2. The resulting mean membrane tensions σ were 0.08 mN m−1 and 0.52 mN m−1, respectively. Dependent on the pre-adjusted lateral membrane tension, two different behaviours were observed after ENTH-addition. At low lateral membrane tension (σ = 0.08 mN m−1, cMg = 0.5 mM), part of the GUVs showed tubule formation upon ENTH binding (Fig. 5A). Major part of the GUVs, however showed an increase in adhesion area indicative of transient reduction in lateral membrane tension. If GUVs with a larger membrane tension of σ = 0.52 mN m−1 (cMg = 2 mM) were incubated with ENTH, only an increase in contact adhesion area was observed (Fig. 5B).
0.8) in the presence of 0.5 mM and 2 mM MgCl2. The resulting mean membrane tensions σ were 0.08 mN m−1 and 0.52 mN m−1, respectively. Dependent on the pre-adjusted lateral membrane tension, two different behaviours were observed after ENTH-addition. At low lateral membrane tension (σ = 0.08 mN m−1, cMg = 0.5 mM), part of the GUVs showed tubule formation upon ENTH binding (Fig. 5A). Major part of the GUVs, however showed an increase in adhesion area indicative of transient reduction in lateral membrane tension. If GUVs with a larger membrane tension of σ = 0.52 mN m−1 (cMg = 2 mM) were incubated with ENTH, only an increase in contact adhesion area was observed (Fig. 5B).
 | ||
| Fig. 5 (A) Tubulation after ENTH binding to a GUV with low membrane tension. Time series of three-dimensional reconstructions of spinning disk confocal images of an adhered GUV adhered at low membrane tension. After ENTH addition (t = 0 min), the GUV starts tubulating and forms tethers. Scale bars: 10 μm. (B) Flattening of a GUV after ENTH binding at larger membrane tension. Time series of three-dimensional reconstructions of spinning disk images of an adhered GUV at higher membrane tension. The GUV starts to flatten after ENTH addition (t = 0 min). Scale bars: 20 μm. Figure adapted from Gleisner et al.50 | ||
From our results and theoretical considerations, we concluded that a substantially reduced area compressibility modulus KA is responsible for the observed flattening (increased adhesion area) of the adhered GUVs. We calculated that KA is reduced from 265 mN m−1 to 145 mN m−1 independent of the initial lateral membrane tension. In terms of thin plate theory of a continuous sheet, this implies that also the bending rigidity κ is reduced, as KA is related to κ according to eqn (4):
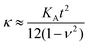 | (4) |
A membrane system different from GUVs has been developed in recent years by our groups to investigate ENTH-membrane interactions. The idea was to generate a setup that provides slightly curved membranes, which are free-standing but still rather stable and well localized on a surface.64 To achieve this, we established planar and curved pore-spanning membranes (PSMs)65–67 that suspend a highly ordered array of cavities with pore diameters of 850 nm in a Si/SiO2 substrate, which separate an aqueous compartment (Fig. 6). If an osmotic gradient ΔO is applied across the planar membranes, the bilayers start protruding leading to curved membranes. By using different osmotic gradients, the heights of the protruded membranes can be controlled (Fig. 6A). The protrusions are readily visible in the confocal fluorescence images, while the membrane on the Si/SiO2 support are barely discernible owing to the quenching of the fluorescence on the support.
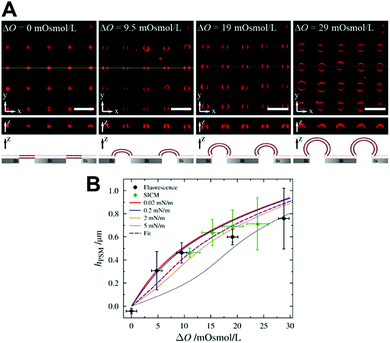 | ||
| Fig. 6 (A) Confocal z-stack fluorescence microscopy images of an array of Texas Red DPPE labelled PSMs composed of POPC at different osmolarity gradients. The yellow lines (x–y-plane) show the positions of the z-profiles depicted below. The schematic drawings at the bottom illustrates the different stages of membrane protrusions as a function of osmotic pressure difference. Scale bars: 5 μm, height of z-sections: 5 μm. (B) Heights of the protrusions of PSMs as a function of the applied osmolarity gradient ΔO obtained by confocal laser scanning fluorescence microscopy (black circles) and scanning ion conductance microscopy (green diamonds). The solid lines are simulations with different lateral membrane tensions, the dotted line is the best fit. Figure adapted from Gleisner et al.64 | ||
Compared to wavy membranes on a solid support and membrane tubes, these bilayers are only slightly curved. Compared to the adhered GUVs, the major difference is that the GUVs are assumed to enclose a constant volume, while in case of PSMs, the entire membrane patch slides on the surface and upon an osmotic change, the entrapped volume underneath the membranes change. Area dilation in this regime is negligible. We treated the protrusions as a function of the osmotic pressure difference ΔΠeq = RTΔO with the Young–Laplace equation (eqn (5)):
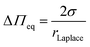 | (5) |
With this approach, we calculated a constant lateral membrane tension of this membrane system of σ = 2.1 mN m−1 in agreement with previous studies, where we used atomic force microscopy indentation experiments to determine the lateral membrane tension of planar PSMs.63,67 We asked the question how ENTH binding to these membranes alters their properties. Besides ENTH interaction, which was verified by fluorescently labelled ENTH, we also observed morphological changes of the protruded PSMs. Dependent on the lipid composition, the protrusions grew considerably owing to ENTH domain–membrane interaction, and/or disappeared. As the height of the protruded membranes is only governed by the lateral tension of the membrane (Fig. 6B) and the initial osmolarity gradient is constant, the only parameter that can explain an increase in height of the protrusions is a decrease in lateral membrane tension. That the protruded membranes disappear is probably a matter of the insertion of α0 of ENTH that forms defects in the membrane, so that the osmolarity gradient is cancelled and the membrane protrusion deflates resulting in the observed disappearance of the protrusion from the focal plane.
4 Open questions and conclusions
Over the last two decades, clathrin-mediated endocytosis was a treasure chest to identify proteins with the ability to shape membranes. The fact that virtually all of these proteins are peripheral and only transiently membrane-attached molecules, made their expression, purification as well as biochemical and structural analysis rather straight forward. For the ENTH domain of epsin1, it was proposed that the shallow membrane insertion of an amphipathic helix leads to curvature induction by a wedging mechanism. It was however also observed that the protein–membrane interaction leads to a decrease in lateral membrane tension, which renders the membrane more flexible. Recently, macromolecular crowding rather than helix insertion was suggested to drive membrane remodelling by ENTH domains. It is worthwhile noticing, that none of the above effects have to be mutually exclusive and that they might very well work in parallel. In such a model, the amphipathic α0 of ENTH domains might sense local curvatures in undulating membranes. Helix insertion would lead to increased bilayer asymmetry and a reduced membrane bending modulus. Lipid-dependent protein clustering increases the protein density on the membrane, which in turn could lead to more pronounced macromolecular crowding induced membrane deformation.The notion, that in clathrin-mediated endocytosis various membrane curvature inducing proteins work not only consecutively but also in parallel displays the necessity to analyse cooperativity within this network. Currently, it is poorly understood how these proteins influence each other and how they are regulated. It will be exciting to see how future studies address the spatial and temporal fidelity of this complex network of proteins and lipids involved in CME.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (SFB 803, project B09) for financial support.Notes and references
- G. J. Doherty and H. T. McMahon, Annu. Rev. Biochem., 2009, 78, 857–902 CrossRef CAS PubMed.
- T. Kirchhausen, D. Owen and S. C. Harrison, Cold Spring Harbor Perspect. Biol., 2014, 6, a016725 CrossRef PubMed.
- Y. Saheki and P. De Camilli, Cold Spring Harbor Perspect. Biol., 2012, 4, a005645 Search PubMed.
- O. Daumke, A. Roux and V. Haucke, Cell, 2014, 156, 882–892 CrossRef CAS PubMed.
- S. Morlot and A. Roux, Annu. Rev. Biophys., 2013, 42, 629–649 CrossRef CAS PubMed.
- M. Barbot and M. Meinecke, J. Struct. Biol., 2016, 196, 20–28 CrossRef CAS PubMed.
- V. Haucke and M. M. Kozlov, J. Cell Sci., 2018, 131, jcs216812 CrossRef PubMed.
- H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596 CrossRef CAS PubMed.
- J. Zimmerberg and K. Gawrisch, Nat. Chem. Biol., 2006, 2, 564–567 CrossRef CAS PubMed.
- V. Legendre-Guillemin, S. Wasiak, N. K. Hussain, A. Angers and P. S. McPherson, J. Cell Sci., 2004, 117, 9–18 CrossRef CAS PubMed.
- C. Kalthoff, J. Alves, C. Urbanke, R. Knorr and E. J. Ungewickell, J. Biol. Chem., 2002, 277, 8209–8216 CrossRef CAS PubMed.
- W. F. Zeno, U. Baul, W. T. Snead, A. C. M. DeGroot, L. Wang, E. M. Lafer, D. Thirumalai and J. C. Stachowiak, Nat. Commun., 2018, 9, 4152 CrossRef PubMed.
- H. Chen, S. Fre, V. I. Slepnev, M. R. Capua, K. Takei, M. H. Butler, P. P. Di Fiore and P. De Camilli, Nature, 1998, 394, 793–797 CrossRef CAS PubMed.
- M. T. Drake, M. A. Downs and L. M. Traub, J. Biol. Chem., 2000, 275, 6479–6489 CrossRef CAS PubMed.
- E. Overstreet, X. Chen, B. Wendland and J. A. Fischer, Curr. Biol., 2003, 13, 854–860 CrossRef CAS PubMed.
- J. A. Rosenthal, H. Chen, V. I. Slepnev, L. Pellegrini, A. E. Salcini, P. P. Di Fiore and P. De Camilli, J. Biol. Chem., 1999, 274, 33959–33965 CrossRef CAS PubMed.
- A. L. M. Cadavid, A. Ginzel and J. A. Fischer, Development, 2000, 127, 1727–1736 CAS.
- X. Chen, B. Zhang and J. A. Fischer, Genes Dev., 2002, 16, 289–294 CrossRef CAS PubMed.
- S. Polo, S. Sigismund, M. Faretta, M. Guidi, M. R. Capua, G. Bossi, H. Chen, P. De Camilli and P. P. Di Fiore, Nature, 2002, 416, 451–455 CrossRef CAS PubMed.
- S. C. Shih, D. J. Katzmann, J. D. Schnell, M. Sutanto, S. D. Emr and L. Hicke, Nat. Cell Biol., 2002, 4, 389–393 CrossRef CAS PubMed.
- E. Boucrot, A. Pick, G. Camdere, N. Liska, E. Evergren, H. T. McMahon and M. M. Kozlov, Cell, 2012, 149, 124–136 CrossRef CAS PubMed.
- M. Messa, R. Fernandez-Busnadiego, E. W. Sun, H. Chen, H. Czapla, K. Wrasman, Y. Wu, G. Ko, T. Ross, B. Wendland and P. De Camilli, eLife, 2014, 3, e03311 CrossRef PubMed.
- P. De Camilli, H. Chen, J. Hyman, E. Panepucci, A. Bateman and A. T. Brunger, FEBS Lett., 2002, 513, 11–18 CrossRef CAS PubMed.
- T. Itoh, S. Koshiba, T. Kigawa, A. Kikuchi, S. Yokoyama and T. Takenawa, Science, 2001, 291, 1047–1051 CrossRef CAS PubMed.
- M. M. Garcia-Alai, J. Heidemann, M. Skruzny, A. Gieras, H. D. T. Mertens, D. I. Svergun, M. Kaksonen, C. Uetrecht and R. Meijers, Nat. Commun., 2018, 9, 328 CrossRef PubMed.
- M. G. J. Ford, I. G. Mills, B. J. Peter, Y. Vallis, G. J. K. Praefcke, P. R. Evans and H. T. McMahon, Nature, 2002, 419, 361–366 CrossRef CAS PubMed.
- J. H. Hurley and B. Wendland, Cell, 2002, 111, 143–146 CrossRef CAS PubMed.
- M. Skruzny, A. Desfosses, S. Prinz, S. O. Dodonova, A. Gieras, C. Uetrecht, A. J. Jakobi, M. Abella, W. J. Hagen, J. Schulz, R. Meijers, V. Rybin, J. A. Briggs, C. Sachse and M. Kaksonen, Dev. Cell, 2015, 33, 150–162 CrossRef CAS PubMed.
- A. Frost, V. M. Unger and P. De Camilli, Cell, 2009, 137, 191–196 CrossRef CAS PubMed.
- M. Barbot, D. C. Jans, C. Schulz, N. Denkert, B. Kroppen, M. Hoppert, S. Jakobs and M. Meinecke, Cell Metab., 2015, 21, 756–763 CrossRef CAS PubMed.
- W. M. Henne, E. Boucrot, M. Meinecke, E. Evergren, Y. Vallis, R. Mittal and H. T. McMahon, Science, 2010, 328, 1281–1284 CrossRef CAS PubMed.
- M. Meinecke, E. Boucrot, G. Camdere, W. C. Hon, R. Mittal and H. T. McMahon, J. Biol. Chem., 2013, 288, 6651–6661 CrossRef CAS PubMed.
- Y. Rao and V. Haucke, Cell. Mol. Life Sci., 2011, 68, 3983–3993 CrossRef CAS PubMed.
- M. Simunovic, E. Evergren, A. Callan-Jones and P. Bassereau, Annu. Rev. Cell Dev. Biol., 2019, 35, 111–129 CrossRef CAS PubMed.
- D. Tarasenko, M. Barbot, D. C. Jans, B. Kroppen, B. Sadowski, G. Heim, W. Mobius, S. Jakobs and M. Meinecke, J. Cell Biol., 2017, 216, 889–899 CrossRef CAS PubMed.
- H. T. McMahon and E. Boucrot, J. Cell Sci., 2015, 128, 1065–1070 CrossRef CAS PubMed.
- D. H. Kweon, Y. K. Shin, J. Y. Shin, J. H. Lee, J. B. Lee, J. H. Seo and Y. S. Kim, Mol. Cells, 2006, 21, 428–435 CAS.
- Y. Yoon, J. Tong, P. J. Lee, A. Albanese, N. Bhardwaj, M. Kallberg, M. A. Digman, H. Lu, E. Gratton, Y. K. Shin and W. Cho, J. Biol. Chem., 2010, 285, 531–540 CrossRef CAS PubMed.
- J. M. Isas, M. R. Ambroso, P. B. Hegde, J. Langen and R. Langen, Structure, 2015, 23, 873–881 CrossRef CAS PubMed.
- F. Campelo, G. Fabrikant, H. T. McMahon and M. M. Kozlov, FEBS Lett., 2010, 584, 1830–1839 CrossRef CAS PubMed.
- F. Campelo, H. T. McMahon and M. M. Kozlov, Biophys. J., 2008, 95, 2325–2339 CrossRef CAS PubMed.
- Z. Chen, C. Zhu, C. J. Kuo, J. Robustelli and T. Baumgart, J. Am. Chem. Soc., 2016, 138, 14616–14622 CrossRef CAS PubMed.
- F. Campelo and M. M. Kozlov, PLoS Comput. Biol., 2014, 10, e1003556 CrossRef PubMed.
- P. D. Blood, R. D. Swenson and G. A. Voth, Biophys. J., 2008, 95, 1866–1876 CrossRef CAS PubMed.
- G. Drin and B. Antonny, FEBS Lett., 2010, 584, 1840–1847 CrossRef CAS PubMed.
- F. Fernandes, L. M. S. Loura, F. J. Chichon, J. L. Carrascosa, A. Fedorov and M. Prieto, Biophys. J., 2008, 94, 3065–3073 CrossRef CAS.
- J. C. Stachowiak, F. M. Brodsky and E. A. Miller, Nat. Cell Biol., 2013, 15, 1019–1027 CrossRef CAS PubMed.
- J. C. Stachowiak, E. M. Schmid, C. J. Ryan, H. S. Ann, D. Y. Sasaki, M. B. Sherman, P. L. Geissler, D. A. Fletcher and C. C. Hayden, Nat. Cell Biol., 2012, 14, 944–949 CrossRef CAS PubMed.
- Z. Chen, E. Atefi and T. Baumgart, Biophys. J., 2016, 111, 1823–1826 CrossRef CAS PubMed.
- M. Gleisner, B. Kroppen, C. Fricke, N. Teske, T. T. Kliesch, A. Janshoff, M. Meinecke and C. Steinem, J. Biol. Chem., 2016, 291, 19953–19961 CrossRef CAS PubMed.
- M. J. Taylor, D. Perrais and C. J. Merrifield, PLoS Biol., 2011, 9, e1000604 CrossRef CAS PubMed.
- W. T. Snead, C. C. Hayden, A. K. Gadok, C. Zhao, E. M. Lafer, P. Rangamani and J. C. Stachowiak, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3258–E3267 CrossRef CAS PubMed.
- S. Neumann and S. L. Schmid, J. Biol. Chem., 2013, 288, 25119–25128 CrossRef CAS PubMed.
- P. Sens, L. Johannes and P. Bassereau, Curr. Opin. Cell Biol., 2008, 20, 476–482 CrossRef CAS PubMed.
- A. Tian and T. Baumgart, Biophys. J., 2009, 96, 2676–2688 CrossRef CAS PubMed.
- M. Simunovic, C. Prevost, A. Callan-Jones and P. Bassereau, Philos. Trans. R. Soc., A, 2016, 374, 20160034 CrossRef PubMed.
- B. Sorre, A. Callan-Jones, J. B. Manneville, P. Nassoy, J. F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626 CrossRef CAS PubMed.
- B. R. Capraro, Y. Yoon, W. Cho and T. Baumgart, J. Am. Chem. Soc., 2010, 132, 1200–1201 CrossRef CAS PubMed.
- P. Bassereau and B. Goud, F1000Biol. Rep., 2011, 3, 7 Search PubMed.
- T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–506 CrossRef CAS PubMed.
- W. T. Hsieh, C. J. Hsu, B. R. Capraro, T. Wu, C. M. Chen, S. Yang and T. Baumgart, Langmuir, 2012, 28, 12838–12843 CrossRef CAS PubMed.
- S. S. Holkar, S. C. Kamerkar and T. J. Pucadyil, J. Biol. Chem., 2015, 290, 14267–14276 CrossRef CAS.
- A. Janshoff and C. Steinem, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 2977–2983 CrossRef CAS PubMed.
- M. Gleisner, I. Mey, M. Barbot, C. Dreker, M. Meinecke and C. Steinem, Soft Matter, 2014, 10, 6228–6236 RSC.
- N. Teske, J. Sibold, J. Schumacher, N. K. Teiwes, M. Gleisner, I. Mey and C. Steinem, Langmuir, 2017, 33, 14175–14183 CrossRef CAS PubMed.
- O. M. Schütte, I. Mey, J. Enderlein, F. Savic, B. Geil, A. Janshoff and C. Steinem, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E6064–E6071 CrossRef PubMed.
- M. Kocun, T. D. Lazzara, C. Steinem and A. Janshoff, Langmuir, 2011, 27, 7672–7680 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |