DOI:
10.1039/C9SM02367D
(Paper)
Soft Matter, 2021,
17, 298-307
Particle engulfment by strongly asymmetric membranes with area reservoirs
Received
2nd December 2019
, Accepted 18th February 2020
First published on 19th February 2020
Abstract
Biological cells are capable of undergoing extensive shape transformations thanks to the existence of membrane area reservoirs from which they can pull out membrane when required. A particularly relevant example of such membrane remodelling is given by endocytic and phagocytic processes, during which the cell membrane engulfs nano- and micrometer sized particles. Recently, it was shown that cell-like membrane reservoirs can be mimicked in giant vesicles with nanotubes stabilized by strong bilayer asymmetry, as quantified by the membrane's spontaneous curvature. Here, we theoretically investigate particle engulfment by such strongly-asymmetric membranes. We find that, depending on the sign of the spontaneous curvature, the engulfment transition may be continuous or discontinuous. Moreover, we find that, in the case of particle engulfment, the presence of asymmetry-stabilized reservoirs is not well captured by the constant-tension model typically used to describe cell-membrane deformations. This highlights the need for a better understanding of the nature of cellular membrane reservoirs, in order to accurately describe membrane remodelling processes.
1 Introduction
The cell membrane is the gateway to the cell interior. In order to shed light on and gain control over how viruses infect cells,1,2 how white blood cells protect the body by ‘eating’ foreign objects,3,4 or how to successfully deliver drug-carrying nanoparticles and imaging agents to cells,5,6 it is of fundamental importance to understand the interactions between solid particles and cellular membranes. In particular, the processes just described (known as endocytosis and phagocytosis) involve the membrane adhering to, spreading over, and ultimately engulfing the particle in question. Reliably replicating these processes in purely synthetic systems, such as lipid vesicles7–9 or polymersomes,10 in a controlled manner is a major goal of bottom-up synthetic biology, which aims to reconstruct cellular functions using minimal ingredients.11,12
A particularly important feature of biological cells, which underlies their ability to repeatedly undergo endocytosis and phagocytosis, is the existence of hidden area reservoirs connected to the cell membrane.13–17 These area reservoirs allow cells to undergo large deformations while keeping their enclosed volume unchanged. For example, it has been shown that specialized phagocytic cells can increase their apparent surface area by up to 400% when engulfing a large particle, implying that up to 80% of their total membrane area is stored in hidden reservoirs.4,18 The mechanism, or mechanisms, used by cells to stabilize and regulate these reservoirs are not yet fully understood.13–17 In the absence of such reservoirs, cells would be completely unable to undergo large deformations, given that a lipid membrane can only stretch up to about 4% before rupturing.19
Indeed, the inability to undergo large deformations is a major limitation of standard vesicle-based artificial protocells as developed in synthetic biology, which lack any area reservoirs. Recently, however, it was discovered that vesicles with strongly asymmetric lipid bilayers spontaneously develop stable area reservoirs in the form of nanotubes, see Fig. 1. The required bilayer asymmetry, which in turns leads to a non-zero membrane spontaneous curvature, may be generated in many ways,20 such as by an asymmetric concentration of lipids in each of the monolayers,21,22 or by asymmetric concentrations of particles in solution that create adsorption or depletion layers near the membrane.21,23,24 Thus, spontaneous formation of nanotubes has been observed for membranes with lipid asymmetry,25 in particular of lipids with bulky headgroups such as GM-1;26,27 for asymmetric concentrations of ions or sugars in the inner and outer aqueous solutions;28,29 for asymmetric concentrations of polymers such as PEG that adsorb to the membrane;30,31 or for membranes in contact with specialized curvature-inducing proteins such as BAR domains.32 Importantly, it has been shown26 that these artificial membrane reservoirs confer cell-like mechanical responses to the vesicles, such as the liquid-droplet-like instability in micropipette aspiration undergone by white blood cells.33–35
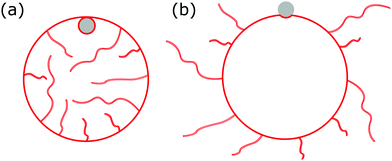 |
| | Fig. 1 We consider the engulfment of particles by strongly asymmetric membranes that develop stable area reservoirs, such as the giant vesicles with nanotubes shown here. In (a), the spontaneous curvature is negative, leading to in-tubes; in (b) the spontaneous curvature is positive, leading to out-tubes. The membrane area stored in the nanotubes is the reservoir, whereas the rest is the apparent membrane area. A completely engulfed particle (grey) is shown in (a), a partially engulfed particle in (b). The vesicle can only engulf the particle by extracting membrane area from the reservoir. | |
When developing theoretical models of membrane deformation in the context of biological cells, the existence of area reservoirs is typically modelled by assuming that area reservoirs are kept at a constant tension Σ (presumably actively regulated by the cell), with a free energy cost associated to extracting an amount of area ΔA out of this reservoir given by ΣΔA. The tension Σ thus acts as a chemical potential for membrane area. This constant-tension model has been extensively used in the context of modelling particle engulfment by cells.36–41 Interestingly, in ref. 26 it was found that vesicles with area reservoirs stabilized by strong membrane asymmetry behave, to a leading order approximation, just as if they had a constant-tension reservoir, with tension given by the spontaneous tension 2κm2, where κ and m are the bending rigidity and the spontaneous curvature of the membrane, respectively. This observation raises intriguing questions: Could membrane asymmetry be one of the mechanisms that cells exploit to stabilize their membrane reservoirs? And, can asymmetry-stabilized reservoirs always be modelled as effective constant-tension reservoirs, or are there processes in which the nature of the reservoir stabilization mechanism plays a key role?
In this article, we theoretically investigate particle engulfment by membranes with area reservoirs stabilized by strong membrane asymmetry, see Fig. 1. The presence of these reservoirs results in qualitatively and quantitatively different engulfment behaviour to that obtained for weakly asymmetric membranes,42–44 which lack such reservoirs. We obtain analytic expressions for the free energy landscapes of engulfment and the transition lines between the different engulfment regimes, valid in the limit of strongly asymmetric membranes, and compare them to numerical results. The underlying purpose is twofold. Firstly, vesicles with asymmetry-stabilized reservoirs are promising candidates for versatile protocells in synthetic biology. Understanding engulfment by these vesicles is thus important in order to develop synthetic endo-, exo-, and phagocytic systems for such minimal cells. Secondly, the asymmetry-based stabilization mechanism for area reservoirs might leave tell-tale signs in the engulfment phenomenology, that could in turn be used to elucidate whether membrane asymmetry is one of the mechanisms exploited by cells to stabilize their area reservoirs.
Indeed, we have found that, whereas to leading order O(m2Rpa2), where Rpa is the radius of the particle, area reservoirs stabilized by membrane asymmetry behave just like those modelled as having constant tension, the next order corrections O(mRpa) are fundamentally different. In fact, we find that the sign of the spontaneous curvature strongly affects the energetics of the highly-curved membrane rim around the particle, and determines whether the engulfment transition proceeds continuously or discontinuously. In the context of synthetic protocells with asymmetry-stabilized area reservoirs, this implies that those with outward-facing reservoirs behave differently than those with inward-facing reservoirs with respect to particle engulfment, see Fig. 1. In the context of biological cells, our results imply that accurate modelling of some processes involving strong membrane deformations may require a more detailed understanding of the mechanisms stabilizing membrane reservoirs, beyond the usual constant-tension model.
2 Methods
2.1 Model
2.1.1 Membrane with asymmetry-stabilized reservoirs.
Consider a large spherical vesicle with area reservoirs in the form of nanotubules, which are stabilized by spontaneous curvature, see Fig. 1.20,26,45 The total membrane area of the vesicle, including both the spherical part of the vesicle and the reservoirs, is fixed. In the presence of osmotically active particles such as salts or sugars, which is the typical experimentally-relevant condition, the volume enclosed by the vesicle is also fixed.19 The free energy associated with the membrane shape is then purely due to bending, and given by| | 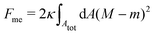 | (1) |
where the integral runs over the whole membrane area Atot, including both the spherical surface as well as the nanotubules (reservoir). Here, M is the mean curvature of the membrane at any given point. The bending properties of the membrane are defined by two parameters, namely the bending rigidity κ, and the spontaneous curvature m. The spontaneous curvature represents the preferred curvature of the membrane due to asymmetries in the composition of the two leaflets of the bilayer, or of the aqueous compartments on each side of the bilayer. By convention, we say that the spontaneous curvature is positive (negative) if the membrane prefers to bulge towards (away from) the exterior compartment.
As observed in experiment and well-understood theoretically, the nanotubules may take cylindrical or necklace-like morphologies depending on their length.31 Imposing normal and tangential balance for the tubules as well as for the mother vesicle one finds that, no matter their shape, at mechanical equilibrium tubules have a mean curvature Mtu = m + O(Mmv), where Mmv is the mean curvature of the mother vesicle.45 Moreover, one finds that the mechanical tension of the membrane goes as Σ = O(κmMmv). In this work, we will focus on the limit of a planar membrane with Mmv → 0, representing a very large mother vesicle, in which case we find Mtu → m and Σ → 0. This implies that the nanotubules perfectly adapt their mean curvature to the spontaneous curvature, and thus do not contribute to the bending energy of the system. The free energy of the membrane (1) can then be rewritten as
| | 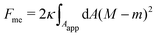 | (2) |
where now the integral runs over the apparent membrane area
Aapp,
i.e. ignoring the nanotubules (reservoir).
2.1.2 Membrane with constant-tension reservoirs.
In the constant-tension model for area reservoirs, it is typically assumed that the membrane has no spontaneous curvature, and the reservoir exists only implicitly.36 The free energy associated with the shape of the membrane then includes contributions from bending as well as from the cost of extracting area from the reservoir, with| | 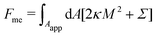 | (3) |
where again the integral is only over the apparent membrane area. Here, the tension Σ is a constant parameter that behaves as a chemical potential for membrane area, characterizing the energetic cost of extracting area from the reservoir.
2.1.3 Membrane-particle adhesion.
The adhesion between the particle and the membrane is taken into account using a contact potential with adhesive strength |W|, so that the particle-membrane adhesion free energy is given bywhere Abo is the area of the membrane segment that is bound to the particle, which depends on the extent of engulfment as determined by the wrapping angle ϕ, see Fig. 2.
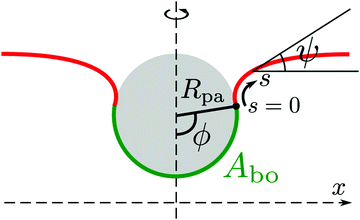 |
| | Fig. 2 Axisymmetric geometry used for the calculation of membrane shapes. The particle of radius Rpa is engulfed up to a wrapping angle ϕ, which defines the area Abo of the particle-bound membrane segment (green). The shape of the unbound membrane segment (red) is determined by the angle ψ as a function of the arc-length s, where s = 0 corresponds to the contact line with the particle. The distance from the symmetry axis is denoted by x. | |
2.2 Calculation of energy landscapes for engulfment
2.2.1 Unbound segment: full shape equations.
In order to obtain the shape of the unbound membrane segment that minimizes the free energy of the system, while satisfying appropriate boundary conditions at the contact line with the particle, we need to consider the Euler–Lagrange equations of the corresponding free energy functional. To include both cases of asymmetry-stabilized and constant-tension reservoirs side by side, we consider the free energy| | 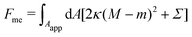 | (5) |
from which we can recover the asymmetry-stabilized case by setting Σ = 0, and the constant-tension case by setting m = 0.
For an axisymmetric geometry as considered here, see Fig. 2, the Euler–Lagrange equations corresponding to (5) are given by the well-known axisymmetric shape equations,46 in the particular case of zero osmotic pressure difference. Using the notation described in Fig. 2, the axisymmetric shape equations can be written as
| | ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) = u = u | (6) |
| | 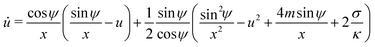 | (7) |
| | ẋ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ ψ | (8) |
where the dot above a variable indicates a derivative with respect to the arc length
s, and we have defined
which lumps together the mechanical tension
Σ and the spontaneous tension 2
κm2.
These equations can be solved numerically by means of the usual shooting method.46,47 The initial conditions correspond to a smooth matching with the surface of the particle so that u(0) = u0, ψ(0) = ϕ, and x(0) = Rpa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, see Fig. 2. We shoot until the point s = s* at which the profile becomes flat with ψ(s*) = 0, and use the initial meridional curvature u0 as shooting parameter to also ensure that u(s*) = 0. This ensures a condition of asymptotic flatness ψ =
ϕ, see Fig. 2. We shoot until the point s = s* at which the profile becomes flat with ψ(s*) = 0, and use the initial meridional curvature u0 as shooting parameter to also ensure that u(s*) = 0. This ensures a condition of asymptotic flatness ψ = ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) = 0 for the membrane as s → ∞, within numerical precision.
= 0 for the membrane as s → ∞, within numerical precision.
The shape eqn (6)–(8) can be augmented with an equation for the membrane free energy (calculated with respect to the energy of a flat membrane reference state), given by
| | 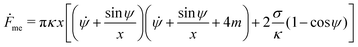 | (10) |
which serves to calculate the engulfment free energy landscapes. In particular, integrating
(10) from
s = 0 to
s =
s* gives the free energy of the unbound membrane segment
Funme(
ϕ) for any given value of the wrapping angle
ϕ.
2.2.2 Unbound segment: limit of strong asymmetry or high tension.
The full shape equations above can only be solved numerically. However, further analytical progress is possible if we focus on the limit of strongly asymmetric membranes (in the asymmetry-stabilized model) or high tension (in the constant-tension model). To this end, we consider an expansion of the shape equations in terms of the small parameter| | 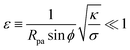 | (11) |
which in particular requires that |m|Rpa ≫ 1 in the asymmetry-stabilized model, or 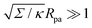 in the constant-tension model.
in the constant-tension model.
The length scale 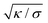 can be viewed as the characteristic distance over which the membrane becomes flat, i.e. the width of the highly curved rim around the particle, which arises from the competition between bending and tension (either mechanical Σ or spontaneous 2κm2) contributions, the former favouring a weakly-curved rim, the latter a sharp kink.36,48 As we move along the rim starting from the contact line with the particle, until the membrane becomes flat, the curvature
can be viewed as the characteristic distance over which the membrane becomes flat, i.e. the width of the highly curved rim around the particle, which arises from the competition between bending and tension (either mechanical Σ or spontaneous 2κm2) contributions, the former favouring a weakly-curved rim, the latter a sharp kink.36,48 As we move along the rim starting from the contact line with the particle, until the membrane becomes flat, the curvature ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) will thus go as the inverse of
will thus go as the inverse of 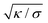 , and the distance from the symmetry axis x will change only by an amount of the order of
, and the distance from the symmetry axis x will change only by an amount of the order of 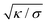 . We therefore expect the following asymptotic forms for
. We therefore expect the following asymptotic forms for ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) and x
and x
| | 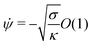 | (12) |
| | x = Rpa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ[1 + O(ε)] ϕ[1 + O(ε)] | (13) |
Combining
eqn (6) and (7), and evaluating the different contributions according to
(12) and (13), we obtain the simplified shape equation
| | 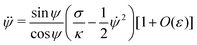 | (14) |
to lowest order. This equation is equivalent to Euler's elastica equation,
48 and can be solved analytically. We can integrate it once to obtain
| | 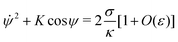 | (15) |
where
K is an integration constant. In order to enforce flatness of the membrane far away from the particle, we must require that
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif)
= 0 when
ψ = 0, which implies that
K = 2
σ/
κ[1 +
O(
ε)], so that we can write
| | 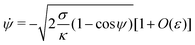 | (16) |
Within the same order of approximation, the
eqn (10) for the membrane free energy can be written as
| | 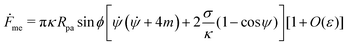 | (17) |
Now, noting that d
s = d
ψ/
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif)
, we can calculate the free energy of the unbound membrane segment
Funme as
| | 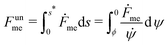 | (18) |
which finally results in
| | 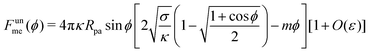 | (19) |
3 Results and discussion
3.1 Engulfment by membranes with constant-tension area reservoirs
The engulfment of a spherical particle by a planar membrane with constant-tension area reservoirs has been considered in great detail by Deserno,36 through numerical solution of the full shape equations, so we will only summarize the main results here. For any non-zero tension, the engulfment transition proceeds discontinuously with increasing adhesive strength |W|, in the following manner. For very low |W|, only the free particle state is stable, and the energy landscapes have only a boundary minimum at ϕ = 0. Increasing |W| beyond a certain value |W|ace, a metastable state corresponding to almost complete engulfment develops at ϕ ≲ π. Further increasing |W|, one finds that at a value |W|fr = |W|ce = 2κ/Rpa2, simultaneously the free state at ϕ = 0 becomes unstable towards a partially engulfed state with ϕ ≳ 0, and the almost completely engulfed state at ϕ ≲ π becomes a completely engulfed state corresponding to a boundary minimum at ϕ = π. This simultaneous destabilization and stabilization of the free and completely engulfed states, respectively, can be understood through the exact instability conditions for free and completely engulfed states developed in ref. 42. As the adhesive strength |W| is further increased, the partially and completely engulfed states switch (meta)stability at a value 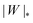 corresponding to a discontinuous transition between the two. Finally, at an even larger value |W|pe the partially engulfed state becomes unstable towards the completely engulfed state.
corresponding to a discontinuous transition between the two. Finally, at an even larger value |W|pe the partially engulfed state becomes unstable towards the completely engulfed state.
It is worth pointing out that the results of Deserno36 are very well approximated, quantitatively, by the high tension approximation developed above. We remind that, in order to recover the constant-tension model for area reservoirs, we must set m = 0 and thus σ = Σ in the above description. The energy of the unbound segment then goes as
| | 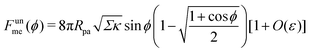 | (23) |
In
Fig. 3(a), we plot this energy (in yellow) and compare it to the one calculated from the numerical solution of the full equations for two different values of the tension. We find good agreement between the numerical results and the approximation and, as expected, the agreement gets better with increasing tension, as demonstrated quantitatively in
Fig. 3(b), which displays the relative error of the approximate energy to the numerically-calculated energy as a function of tension, both taken at the location of the high-tension energy maximum
ϕmax ≈ 0.714π. Note that, as found in
ref. 36, at high values of the wrapping angle
ϕ, there can be multiple coexisting branches of solutions so that the energy is not uniquely defined, which occurs for
ϕ beyond the value marked by the cross for the dashed line corresponding to
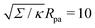
in
Fig. 3(a). Typical values for the tension of cellular membranes reported in the literature can range from 0.003 mN m
−1 for epithelial cells to 0.3 mN m
−1 for keratocytes.
17 Using a typical value of the bending rigidity
κ = 20
kBT, we find that the length scale
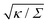
would range between 16 nm for keratocytes to 165 nm for epithelial cells. The values of
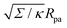
used in
Fig. 3 thus correspond to particle sizes in the range of hundreds of nanometers to several microns.
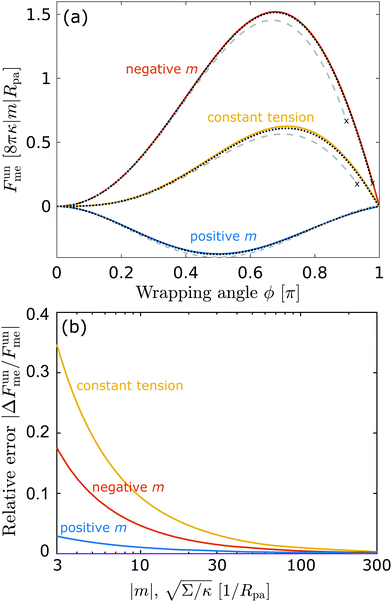 |
| | Fig. 3 (a) Energy of the unbound segment Funme for asymmetry-stabilized area reservoirs with negative (red) and positive (blue) spontaneous curvature, as well as for the equivalent constant-tension reservoir with Σ = 2κm2. The coloured lines correspond to the strong asymmetry (24) and high tension (23) limits. The grey-dashed and black-dotted lines correspond to numerical solution of the full shape equations at finite spontaneous curvature or tension, showing how they tend to the strong asymmetry or strong tension limit with increasing |m| or Σ. For negative m, the grey-dashed and black-dotted lines correspond to mRpa = −10 and −100, respectively, for positive m to mRpa = 1 and 10, and for constant tension to 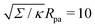 and 100. (b) Relative error of the approximation with respect to the numerical result, as a function of |m| (in the asymmetry-stabilized cases) or and 100. (b) Relative error of the approximation with respect to the numerical result, as a function of |m| (in the asymmetry-stabilized cases) or 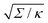 (in the constant tension case), at the location of the maximum or minimum of the coloured lines in (a), which are at ϕmax ≈ 0.678π for negative m, ϕmin ≈ 0.5π for positive m, and ϕmax ≈ 0.714π for constant tension. (in the constant tension case), at the location of the maximum or minimum of the coloured lines in (a), which are at ϕmax ≈ 0.678π for negative m, ϕmin ≈ 0.5π for positive m, and ϕmax ≈ 0.714π for constant tension. | |
As another particularly enlightening example of how eqn (23) correctly captures the physics at high tension, in ref. 36 it was observed that many important scaling relations at high tension stem from the fact that the energy of the unbound segment scales near complete engulfment as 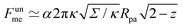 , where z ≡ 1 − cos
, where z ≡ 1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and α is a dimensionless number, which was found from a fit to the numerical results to be α ≈ 5.650. From (23), we directly obtain that near complete engulfment (ϕ ≈ π and z ≈ 2) the energy behaves as
ϕ and α is a dimensionless number, which was found from a fit to the numerical results to be α ≈ 5.650. From (23), we directly obtain that near complete engulfment (ϕ ≈ π and z ≈ 2) the energy behaves as 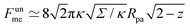 . Thus, we find analytically that
. Thus, we find analytically that 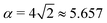 , which compares well with Deserno's numerical value. Other non-trivial results of ref. 36 that are well captured by the high-tension approximation (23) include the location of partially engulfed states and energy barriers in energy landscapes, the barrier heights, as well as the tension-dependent critical values of the adhesion strength
, which compares well with Deserno's numerical value. Other non-trivial results of ref. 36 that are well captured by the high-tension approximation (23) include the location of partially engulfed states and energy barriers in energy landscapes, the barrier heights, as well as the tension-dependent critical values of the adhesion strength 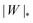 and |W|pe at which the discontinuous transition and the instability of the partially engulfed state take place, respectively. For an extensive comparison of the approximation (23) against numerical results, albeit within the slightly different context of protein-coat assembly, we refer the reader to ref. 48.
and |W|pe at which the discontinuous transition and the instability of the partially engulfed state take place, respectively. For an extensive comparison of the approximation (23) against numerical results, albeit within the slightly different context of protein-coat assembly, we refer the reader to ref. 48.
3.2 Engulfment by membranes with asymmetry-stabilized area reservoirs
3.2.1 Energy of the unbound segment.
We now turn to membranes with asymmetry-stabilized area reservoirs, which coincides with setting Σ = 0 and thus σ = 2κm2 in the results of the Methods section. The energy of the unbound segment therefore goes as| | 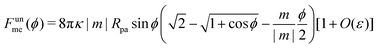 | (24) |
for strong asymmetries, which constitutes one of the key results of this paper. We note that this result implies the separation of lengthscales Rmv ≫ Rpa ≫ 1/|m|. The first inequality is required to approximate the membrane as planar, while the second inequality is required by the strong asymmetry approximation.
Crucially, while the first two terms in (24) would lead to an energy of the unbound segment equivalent to that of a constant-tension reservoir (see eqn (23)) with an effective tension Σ = 2κm2, this symmetry is broken by the third term. This third term also breaks the symmetry between positive and negative spontaneous curvatures, leading to radically different behaviour between the two. In Fig. 3(a), we plot (24) for positive and negative spontaneous curvatures, and also compare these with the energy of the unbound segment (23) for the equivalent constant-tension reservoir. We find that, while for negative spontaneous curvature the unbound segment incurs an energy cost, for positive spontaneous curvature the unbound segment decreases the energy of the system. For the case of a constant-tension reservoir, the unbound segment also incurs an energy cost, but this cost is about 60% smaller than for a negative spontaneous curvature reservoir.
Interestingly, we find that the strong curvature result (24) does a better job at approximating the full numerical solution for positive spontaneous curvatures than for negative ones. While the approximation always becomes accurate for sufficiently large curvatures |m|Rpa ≫ 1, we find that it is still rather accurate for positive spontaneous curvatures as small as mRpa = 1, while this is not the case for small negative spontaneous curvatures. The better agreement of the strong asymmetry approximation for positive spontaneous curvatures is confirmed by a systematic analysis of the relative error of the approximation with increasing |m|, see Fig. 3(b). This implies that the next order contributions O(κ) to the energy of the unbound segment are more significant for negative spontaneous curvatures than for positive spontaneous curvatures. Moreover, in our numerical analysis we find that, for negative spontaneous curvatures, at high values of the wrapping angle ϕ close to π, there is a second coexisting branch of solutions corresponding to the particle being contained in a bud with a closed neck (even if the wrapping angle is still smaller than π). At sufficiently high values of the wrapping angle, the open-neck solution becomes unstable towards the closed-neck solution, as indicated by the crosses at which the dashed and dotted lines stop in Fig. 3. However, this instability moves closer to π, and thus becomes less relevant, as m becomes more negative.
3.2.2 Continuous vs. discontinuous engulfment.
The different sign of the contributions of the unbound segment to the free energy of the system depending on the sign of the spontaneous curvature suggests that negative spontaneous curvatures will favour discontinuous engulfment with a bistable coexistence between free/partially-engulfed states and completely engulfed states, because the unbound segment creates an energy barrier at intermediate wrapping angles; whereas positive spontaneous curvatures will favour a continuous engulfment transition, because partially engulfed states are stabilized by the decrease in free energy of the unbound segment.
This intuitive picture is confirmed by a detailed analysis of the energy landscapes for engulfment Ftot(ϕ). In Fig. 4, we plot the equilibria dFtot/dϕ = 0 of these landscapes as a function of the adhesive strength |W|, for fixed values mRpa = +10 and −10 of the spontaneous curvature. The values obtained from numerical solution of the full shape equations are compared with the analytical result obtained from the strong asymmetry limit, which reads
| | 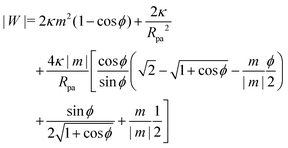 | (25) |
The first term in
(25) corresponds to the Young equation for wetting with effective tension given by the spontaneous tension 2
κm2, whereas the remaining terms represent higher order corrections due to membrane bending.
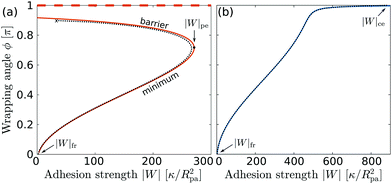 |
| | Fig. 4 Wrapping angles ϕ corresponding to the equilibria of the energy landscapes as a function of the adhesive strength |W|, for (a) negative spontaneous curvature mRpa = −10 and (b) positive spontaneous curvature mRpa = +10. For negative m, the engulfment transition is discontinuous, with coexistence between a (meta)stable free/partially engulfed state and a completely engulfed state (dashed line at ϕ = π), both separated by an energy barrier. For positive m, the transition is continuous. The colored lines correspond to the strong asymmetry limit (25), whereas the black dotted lines are the numerical solution of the full shape equations. | |
For negative spontaneous curvature, see Fig. 4(a), we find that there is (i) a coexistence between (meta)stable free and completely engulfed states at low |W| < |W|fr, (ii) a coexistence between (meta)stable partially and completely engulfed states at intermediate |W| with |W|fr < |W| < |W|pe, and (iii) complete engulfment for |W| > |W|pe. The engulfment transition is thus discontinuous and shows very strong hysteresis: in fact, we find that the completely engulfed state is stable for all values of |W|. For positive spontaneous curvature, see Fig. 4(b), we instead find that there is (i) a stable free state for |W| < |W|fr, (ii) a stable partially engulfed state for |W|fr < |W| < |W|ce, and (iii) a completely engulfed state for |W| > |W|ce. The transition is in this case continuous. Moreover, we note that the adhesive strength required to achieve complete engulfment is much larger for positive spontaneous curvature than for negative spontaneous curvature, even if both correspond to the same effective spontaneous tension 2κm2.
The analytical approximation matches the full numerical results very closely, and predicts correctly the critical value
| | | |W| = |W|fr ≡ 2κ/Rpa2 | (26) |
for the instability of the free state, which is independent of spontaneous curvature, and coincides with that obtained for weakly-asymmetric membranes in
ref. 42. The instability of the partially engulfed state |
W|
pe for negative spontaneous curvature, which does not exist for weakly-asymmetric membranes because these never show a coexistence between partially and completely engulfed states,
42–44 is also well captured by the approximation. The only significant deviations from the numerical results are observed near complete engulfment, for
ϕ ≲ π. In particular, for positive spontaneous curvatures, the analytical approximation predicts that the completely engulfed state is only reached in the limit |
W| → ∞, whereas numerical results show that the completely engulfed state becomes stable at
| | 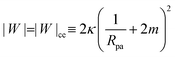 | (27) |
which coincides with the exact stability limit of the completely engulfed state as obtained in
ref. 42 and 47 in the context of weakly-asymmetric membranes. For negative spontaneous curvatures, we again find that the numerical branch of solutions becomes unstable towards a branch with closed neck at high
ϕ, see the cross terminating the dotted line in
Fig. 4(a).
3.2.3 Morphology diagrams for engulfment.
We can now summarize our results into morphology diagrams in the adhesive strength-spontaneous curvature plane (|W|,m), as shown in Fig. 5 for positive (a) and negative (b) spontaneous curvature. For positive spontaneous curvature, the transition from the free to the completely engulfed state is continuous with increasing |W|. The stability lines |W|fr and |W|ce at which the free state becomes unstable and the completely engulfed state becomes stable are given by (26) and (27), respectively. For negative spontaneous curvatures, the completely engulfed state is always (meta)stable. The free state again becomes unstable towards a partially engulfed state at the stability line |W|fr. The switch in metastability between partially and completely engulfed states takes place at the transition line 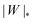 , which can be obtained from the strong asymmetry approximation by requiring that
, which can be obtained from the strong asymmetry approximation by requiring that 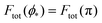 , where
, where 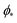 is the wrapping angle corresponding to the partially engulfed state obtained from
is the wrapping angle corresponding to the partially engulfed state obtained from 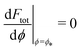 . The partially engulfed state then becomes unstable towards the completely engulfed state at the line |W|pe, which can be straightforwardly obtained from the strong asymmetry approximation by requiring
. The partially engulfed state then becomes unstable towards the completely engulfed state at the line |W|pe, which can be straightforwardly obtained from the strong asymmetry approximation by requiring 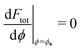 and
and 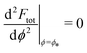 . The critical values for the adhesive strength obtained analytically are in very good agreement with those obtained from numerical solution of the full shape equations, which are given by the red symbols in Fig. 5. The most significant deviations, although still small, are found for the stability line of the partially-engulfed state |W|pe at small negative m, e.g. compare the asterisk and the solid line at mRpa = −3.
. The critical values for the adhesive strength obtained analytically are in very good agreement with those obtained from numerical solution of the full shape equations, which are given by the red symbols in Fig. 5. The most significant deviations, although still small, are found for the stability line of the partially-engulfed state |W|pe at small negative m, e.g. compare the asterisk and the solid line at mRpa = −3.
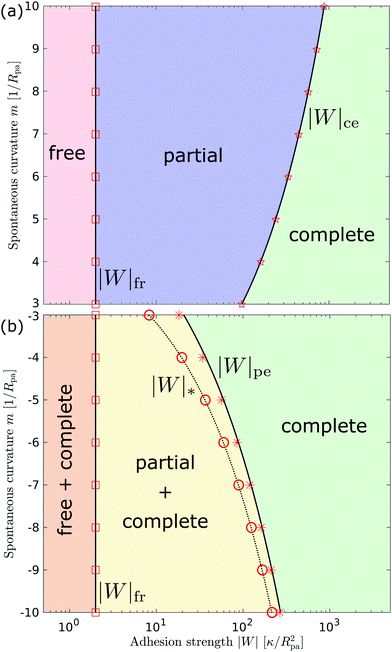 |
| | Fig. 5 Morphology diagrams for engulfment by strongly asymmetric membranes with area reservoirs, as a function of adhesive strength |W| and spontaneous curvature m; (a) for positive spontaneous curvatures and (b) for negative spontaneous curvatures. The engulfment transition is continuous for positive m, and discontinuous for negative m. For negative m, the completely engulfed state is always (meta)stable. The solid lines indicate the stability limits of the different states as explained in detail in the text, the dotted line 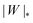 in (b) marks the discontinuous transition at which partially and completely engulfed states have equal energy. The lines |W|fr and |W|ce correspond to the stability limits (26) and (27), respectively, whereas the lines in (b) marks the discontinuous transition at which partially and completely engulfed states have equal energy. The lines |W|fr and |W|ce correspond to the stability limits (26) and (27), respectively, whereas the lines 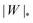 and |W|pe are obtained from the strong asymmetry approximation as described in the text. The red symbols are obtained from numerical solution of the full shape equations. and |W|pe are obtained from the strong asymmetry approximation as described in the text. The red symbols are obtained from numerical solution of the full shape equations. | |
Besides the two qualitatively different types of transition, a key difference between positive and negative spontaneous curvatures is that much higher adhesion (close to one order of magnitude higher) is needed to achieve complete engulfment for positive than for negative spontaneous curvature. That is, we generally find that the value of |W|ce relevant for a given positive spontaneous curvature m = +|m| is substantially larger than the corresponding |W|pe relevant for an equivalent negative spontaneous curvature m = −|m|.
3.2.4 Relevance to experiments.
As discussed in the introduction, spontaneous curvature can be generated in many ways. Its value can vary over several orders of magnitude,20 ranging from weak spontaneous curvatures ∼1/(10 μm) comparable to the inverse vesicle size, e.g. in the case of weakly asymmetric sugar solutions on the two sides of the bilayer, to very strong spontaneous curvatures ∼1/(10 nm) comparable to the inverse membrane thickness, as obtained using curvature-generating proteins such as BAR domains. The limit of a large mother vesicle considered in this paper corresponds to cases in which the inverse spontaneous curvature, which is also the typical radius of the tubular reservoirs, is much smaller than the vesicle size, i.e. when |m|−1 is of the order of a few hundred nanometers or smaller. This range coincides with the radius of nanotubes typically observed in experiments with tubulated giant vesicles,25–27,29–32 which are generally just below optical resolution. Using |m|−1 = 100 nm as a typical value, the results for particle engulfment obtained here will be valid for particles with sizes ranging from several hundred nanometers to a few microns, and thus our predictions should be well within the range accessible to experimental testing.
4 Conclusions
In summary, we have found that the nature of the membrane area reservoir has a strong effect on the engulfment of particles by membranes. In particular, modelling the area reservoirs as constant-tension reservoirs does not accurately capture the engulfment behaviour of reservoirs which are stabilized by a strong membrane asymmetry (spontaneous curvature), as in the case of tubulated giant vesicles.26 Moreover, the sign of the spontaneous curvature has a very strong effect on the engulfment process. Membranes with negative spontaneous curvature for which reservoirs are in-tubes, see Fig. 1(a), behave most similarly to constant-tension reservoirs, in that the engulfment transition is predicted to be discontinuous. There are still qualitative differences, however, such as that for negative spontaneous curvature reservoirs the completely engulfed state is always (meta)stable, independently of the adhesive strength of the particle, as well as quantitative differences in the adhesive strength required for complete engulfment. The behaviour of positive spontaneous curvature membranes for which reservoirs are out-tubes, see Fig. 1(b), is completely different: the engulfment transition is now continuous, and the adhesive strength required for complete engulfment is close to an order of magnitude larger.
A further distinction between positive and negative spontaneous curvature should be observable in the behavior of the narrow neck that connects a completely engulfed particle to the rest of the membrane. In ref. 47, it was predicted that this neck will experience a constriction force due to the particle-membrane adhesion as well as the spontaneous curvature of the membrane. Recently, it has been shown experimentally49 that this force (in the latter experiments, due only to spontaneous curvature) is capable of inducing neck fission when it reaches values above ∼30 pN. In the present context of particle engulfment by a planar membrane, the force is given by 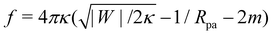 .47 This implies that, for identical conditions with equal particle size and adhesive strength, a membrane with negative spontaneous curvature m = −|m| will exert a significantly higher constriction force on the neck than the equivalent positive spontaneous curvature membrane with m = +|m|. The force difference will be Δf = 16πκ|m| which, using κ = 10−19 J and |m|−1 = 100 nm as typical values, results in a rather large force difference of 50 pN. Thus, we expect that fission of the neck and full internalization of the particle will be much more likely when a particle is engulfed by a vesicle with in-tubes (negative spontaneous curvature) than by a vesicle with out-tubes (positive spontaneous curvature).
.47 This implies that, for identical conditions with equal particle size and adhesive strength, a membrane with negative spontaneous curvature m = −|m| will exert a significantly higher constriction force on the neck than the equivalent positive spontaneous curvature membrane with m = +|m|. The force difference will be Δf = 16πκ|m| which, using κ = 10−19 J and |m|−1 = 100 nm as typical values, results in a rather large force difference of 50 pN. Thus, we expect that fission of the neck and full internalization of the particle will be much more likely when a particle is engulfed by a vesicle with in-tubes (negative spontaneous curvature) than by a vesicle with out-tubes (positive spontaneous curvature).
The existence of a discontinuous transition for negative spontaneous curvature, and a continuous one for positive spontaneous curvature, mirrors our previous findings for weakly asymmetric membranes with |m| ∼ 1/Rmv ≪ 1/Rpa.42–44 In both cases, the nature of the engulfment transition is determined by whether the contribution of the unbound membrane segment, i.e. the strongly curved rim around the particle, to the free energy of the system is positive or negative. The two regimes, of weak and strong asymmetry, are otherwise qualitatively and quantitatively different. For weak asymmetries, vesicles do not form area reservoirs and instead take non-spherical (prolate, oblate, stomatocyte) shapes,46,47 and we found different engulfment regimes depending on the local membrane curvature.43,44 The corresponding energy landscapes, for which we obtained analytical results in ref. 44, have a rather different form to those obtained here. Now that engulfment of particles by membranes with both weak and strong spontaneous curvatures is well understood, the only regime left to be studied is that of intermediate spontaneous curvatures, comparable to the inverse particle radius |m| ∼ 1/Rpa. However, we anticipate this to be a difficult and rather subtle problem, because in this regime the membrane is expected to form buds with size comparable to the particle size. Particle engulfment will thus involve a non-trivial competition between the adhering particle and the bud for the available membrane area.
We note that we have focused above on the case on endocytic engulfment, i.e. of particles originating from the exterior compartment. The case of exocytic engulfment, i.e. of particles originating from the interior compartment, simply requires that we swap the sign of the spontaneous curvature. Therefore, for exocytic engulfment, positive spontaneous curvatures will lead to a discontinuous engulfment transition, whereas negative spontaneous curvatures will lead to a continuous transition.
Our work shows that tubulated giant vesicles26 could be a versatile tool for artificial phagocytosis, allowing for controllable storage of solid particles within a biomimetic (and biocompatible) membrane compartment. In the absence of nanotubes, an initially spherical vesicle will always undergo rupture when put into contact with a strongly adhesive particle. This can be easily understood, as lipid membranes can only stretch by typically 4% before rupturing. The engulfment of a particle of radius Rpa requires a spherical vesicle of radius Rmv to stretch by a factor Rpa2/Rmv2. This implies that a vesicle will rupture when brought in contact with strongly adhesive particles if the particle radius is larger than 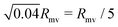 . In contrast, a spherical vesicle with apparent radius Rmv and 20% of its area stored in nanotubes could in principle engulf of the order of 0.2Rmv2/Rpa2 particles of radius Rpa before starting to stretch.
. In contrast, a spherical vesicle with apparent radius Rmv and 20% of its area stored in nanotubes could in principle engulf of the order of 0.2Rmv2/Rpa2 particles of radius Rpa before starting to stretch.
Throughout the paper, we have compared the predictions for engulfment in a model with non-zero tension and zero spontaneous curvature, against those for a model with zero tension and non-zero spontaneous curvature. These two limiting cases are significant because the former represents the model most commonly used when discussing engulfment by cells,36–41 whereas the latter is the model which applies to tubulated giant vesicles.20,26,45 In both cases, tension and spontaneous curvature were considered to be laterally homogeneous over the whole membrane surface. In a real cell membrane, in general both a non-zero tension as well as a non-zero spontaneous curvature can be simultaneously maintained, and moreover the two will typically be laterally inhomogeneous, e.g. depending on the local concentration of curvature-inducing proteins or the local environment to which the membrane is exposed.
While in this work we have focused on particle engulfment, the lessons learned here should be applicable to other membrane remodelling processes. In particular, our results highlight that understanding the nature of the area reservoirs can be crucial in order to correctly model certain processes involving membrane deformation. Because the mechanisms underlying the stabilization of area reservoirs in real biological cells are complex and still poorly understood, one should be mindful of the possible pitfalls underlying the use of an effective constant-tension model. We note, however, that whether or not the constant-tension model for the area reservoirs constitutes a valid approximation may depend on the specific remodelling process under consideraton. As described in the introduction, in ref. 26 we showed that micropipette aspiration of tubulated vesicles is well described within a constant-tension model with effective tension Σ = 2κm2, in contrast to the result obtained here for particle engulfment, in which higher order effects lead to qualitative differences in the engulfment behaviour. In any case, perhaps a detailed study of the effect of different stabilization mechanisms on various membrane remodelling processes could serve as a tool to shed light on, and ultimately pin down, which mechanisms are put to use by the cell.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The author thanks Reinhard Lipowsky for inspiring discussions about particle engulfment and tubulated vesicles. Open Access funding provided by the Max Planck Society.
Notes and references
- M. Marsh and A. Helenius, Cell, 2006, 124, 729–740 CrossRef CAS PubMed.
- J. Mercer, M. Schelhaas and A. Helenius, Annu. Rev. Biochem., 2010, 79, 803–833 CrossRef CAS PubMed.
- P. L. Rodriguez, T. Harada, D. A. Christian, D. A. Pantano, R. K. Tsai and D. E. Discher, Science, 2013, 339, 971–975 CrossRef CAS PubMed.
- M. Herant, V. Heinrich and M. Dembo, J. Cell Sci., 2005, 118, 1789–1797 CrossRef CAS PubMed.
- K. Cho, X. Wang, S. Nie, Z. G. Chen and D. M. Shin, Clin. Cancer Res., 2008, 14, 1310–1316 CrossRef CAS PubMed.
- C. Sun, J. S. H. Lee and M. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252–1265 CrossRef CAS PubMed.
- C. Dietrich, M. Angelova and B. Pouligny, J. Phys. II, 1997, 7, 1651–1682 CrossRef CAS.
- R. Michel and M. Gradzielski, Int. J. Mol. Sci., 2012, 13, 11610–11642 CrossRef CAS PubMed.
- C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS PubMed.
- K. Jaskiewicz, A. Larsen, D. Schaeffel, K. Koynov, I. Lieberwirth, G. Fytas, K. Landfester and A. Kroeger, ACS Nano, 2012, 6, 7254–7262 CrossRef CAS PubMed.
- P. Schwille, Science, 2011, 333, 1252–1254 CrossRef CAS PubMed.
- P. Schwille, J. Spatz, K. Landfester, E. Bodenschatz, S. Herminghaus, V. Sourjik, T. J. Erb, P. Bastiaens, R. Lipowsky, A. Hyman, P. Dabrock, J.-C. Baret, T. Vidakovic-Koch, P. Bieling, R. Dimova, H. Mutschler, T. Robinson, T.-Y. D. Tang, S. Wegner and K. Sundmacher, Angew. Chem., Int. Ed., 2018, 57, 13382–13392 CrossRef CAS PubMed.
- D. Raucher and M. P. Sheetz, Biophys. J., 1999, 77, 1992–2002 CrossRef CAS PubMed.
- C. E. Morris and U. Homann, J. Membr. Biol., 2001, 179, 79–102 CrossRef CAS PubMed.
- N. C. Gauthier, T. A. Masters and M. P. Sheetz, Trends Cell Biol., 2012, 22, 527–535 CrossRef CAS PubMed.
- L. Figard and A. M. Sokac, BioArchitecture, 2014, 4, 39–46 CrossRef PubMed.
- P. Sens and J. Plastino, J. Phys.: Condens. Matter, 2015, 27, 273103 CrossRef PubMed.
- J. Lam, M. Herant, M. Dembo and V. Heinrich, Biophys. J., 2009, 96, 248–254 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101 CrossRef PubMed.
- A. Sreekumari and R. Lipowsky, J. Chem. Phys., 2018, 149, 084901 CrossRef PubMed.
- B. Rózycki and R. Lipowsky, J. Chem. Phys., 2016, 145, 074117 CrossRef PubMed.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- J. Steinkühler, P. De Tillieux, R. L. Knorr, R. Lipowsky and R. Dimova, Sci. Rep., 2018, 8, 11838 CrossRef PubMed.
- T. Bhatia, J. Agudo-Canalejo, R. Dimova and R. Lipowsky, ACS Nano, 2018, 12, 4478–4485 CrossRef CAS PubMed.
- R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761 CrossRef CAS PubMed.
- B. Ali Doosti, W. Pezeshkian, D. S. Bruhn, J. H. Ipsen, H. Khandelia, G. D. M. Jeffries and T. Lobovkina, Langmuir, 2017, 33, 11010–11017 CrossRef CAS PubMed.
- M. Karimi, J. Steinkühler, D. Roy, R. Dasgupta, R. Lipowsky and R. Dimova, Nano Lett., 2018, 18, 7816–7821 CrossRef CAS PubMed.
- Y. Li, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4731–4736 CrossRef CAS PubMed.
- Y. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474 CrossRef CAS PubMed.
- Z. Shi and T. Baumgart, Nat. Commun., 2015, 6, 5974 CrossRef CAS PubMed.
- E. Evans and A. Yeung, Biophys. J., 1989, 56, 151–160 CrossRef CAS PubMed.
- R. M. Hochmuth, J. Biomech., 2000, 33, 15–22 CrossRef CAS PubMed.
- J.-Y. Tinevez, U. Schulze, G. Salbreux, J. Roensch, J.-F. Joanny and E. Paluch, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18581–18586 CrossRef CAS PubMed.
- M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef PubMed.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469–9474 CrossRef CAS PubMed.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419–424 CrossRef CAS PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS PubMed.
- F. Frey, F. Ziebert and U. S. Schwarz, Phys. Rev. Lett., 2019, 122, 088102 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Nano Lett., 2015, 15, 7168–7173 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2017, 13, 2155–2173 RSC.
- R. Lipowsky, Adv. Colloid Interface Sci., 2014, 208, 14–24 CrossRef CAS PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2016, 12, 8155–8166 RSC.
- L. Foret, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 42 CrossRef PubMed.
- J. Steinkühler, R. L. Knorr, Z. Zhao, T. Bhatia, S. M. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nat. Commun., 2020, 11, 905 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
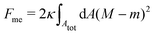
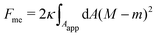
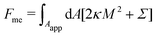
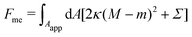
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) = u
= u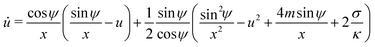
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, see Fig. 2. We shoot until the point s = s* at which the profile becomes flat with ψ(s*) = 0, and use the initial meridional curvature u0 as shooting parameter to also ensure that u(s*) = 0. This ensures a condition of asymptotic flatness ψ =
ϕ, see Fig. 2. We shoot until the point s = s* at which the profile becomes flat with ψ(s*) = 0, and use the initial meridional curvature u0 as shooting parameter to also ensure that u(s*) = 0. This ensures a condition of asymptotic flatness ψ = ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) = 0 for the membrane as s → ∞, within numerical precision.
= 0 for the membrane as s → ∞, within numerical precision.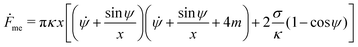
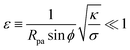
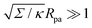 in the constant-tension model.
in the constant-tension model.
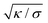 can be viewed as the characteristic distance over which the membrane becomes flat, i.e. the width of the highly curved rim around the particle, which arises from the competition between bending and tension (either mechanical Σ or spontaneous 2κm2) contributions, the former favouring a weakly-curved rim, the latter a sharp kink.36,48 As we move along the rim starting from the contact line with the particle, until the membrane becomes flat, the curvature
can be viewed as the characteristic distance over which the membrane becomes flat, i.e. the width of the highly curved rim around the particle, which arises from the competition between bending and tension (either mechanical Σ or spontaneous 2κm2) contributions, the former favouring a weakly-curved rim, the latter a sharp kink.36,48 As we move along the rim starting from the contact line with the particle, until the membrane becomes flat, the curvature ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) will thus go as the inverse of
will thus go as the inverse of 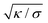 , and the distance from the symmetry axis x will change only by an amount of the order of
, and the distance from the symmetry axis x will change only by an amount of the order of 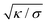 . We therefore expect the following asymptotic forms for
. We therefore expect the following asymptotic forms for ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) and x
and x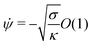
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ[1 + O(ε)]
ϕ[1 + O(ε)]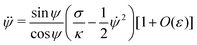
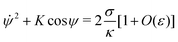
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) = 0 when ψ = 0, which implies that K = 2σ/κ[1 + O(ε)], so that we can write
= 0 when ψ = 0, which implies that K = 2σ/κ[1 + O(ε)], so that we can write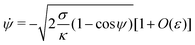
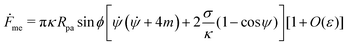
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) , we can calculate the free energy of the unbound membrane segment Funme as
, we can calculate the free energy of the unbound membrane segment Funme as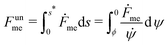
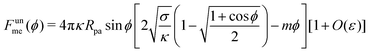
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) + σπRpa2(1 − cos
ϕ) + σπRpa2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)2
ϕ)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)
ϕ)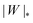 corresponding to a discontinuous transition between the two. Finally, at an even larger value |W|pe the partially engulfed state becomes unstable towards the completely engulfed state.
corresponding to a discontinuous transition between the two. Finally, at an even larger value |W|pe the partially engulfed state becomes unstable towards the completely engulfed state.
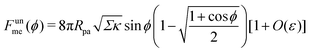
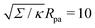 in Fig. 3(a). Typical values for the tension of cellular membranes reported in the literature can range from 0.003 mN m−1 for epithelial cells to 0.3 mN m−1 for keratocytes.17 Using a typical value of the bending rigidity κ = 20kBT, we find that the length scale
in Fig. 3(a). Typical values for the tension of cellular membranes reported in the literature can range from 0.003 mN m−1 for epithelial cells to 0.3 mN m−1 for keratocytes.17 Using a typical value of the bending rigidity κ = 20kBT, we find that the length scale 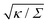 would range between 16 nm for keratocytes to 165 nm for epithelial cells. The values of
would range between 16 nm for keratocytes to 165 nm for epithelial cells. The values of 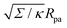 used in Fig. 3 thus correspond to particle sizes in the range of hundreds of nanometers to several microns.
used in Fig. 3 thus correspond to particle sizes in the range of hundreds of nanometers to several microns.

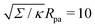 and 100. (b) Relative error of the approximation with respect to the numerical result, as a function of |m| (in the asymmetry-stabilized cases) or
and 100. (b) Relative error of the approximation with respect to the numerical result, as a function of |m| (in the asymmetry-stabilized cases) or 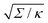 (in the constant tension case), at the location of the maximum or minimum of the coloured lines in (a), which are at ϕmax ≈ 0.678π for negative m, ϕmin ≈ 0.5π for positive m, and ϕmax ≈ 0.714π for constant tension.
(in the constant tension case), at the location of the maximum or minimum of the coloured lines in (a), which are at ϕmax ≈ 0.678π for negative m, ϕmin ≈ 0.5π for positive m, and ϕmax ≈ 0.714π for constant tension.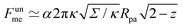 , where z ≡ 1 − cos
, where z ≡ 1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and α is a dimensionless number, which was found from a fit to the numerical results to be α ≈ 5.650. From (23), we directly obtain that near complete engulfment (ϕ ≈ π and z ≈ 2) the energy behaves as
ϕ and α is a dimensionless number, which was found from a fit to the numerical results to be α ≈ 5.650. From (23), we directly obtain that near complete engulfment (ϕ ≈ π and z ≈ 2) the energy behaves as 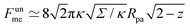 . Thus, we find analytically that
. Thus, we find analytically that 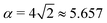 , which compares well with Deserno's numerical value. Other non-trivial results of ref. 36 that are well captured by the high-tension approximation (23) include the location of partially engulfed states and energy barriers in energy landscapes, the barrier heights, as well as the tension-dependent critical values of the adhesion strength
, which compares well with Deserno's numerical value. Other non-trivial results of ref. 36 that are well captured by the high-tension approximation (23) include the location of partially engulfed states and energy barriers in energy landscapes, the barrier heights, as well as the tension-dependent critical values of the adhesion strength 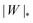 and |W|pe at which the discontinuous transition and the instability of the partially engulfed state take place, respectively. For an extensive comparison of the approximation (23) against numerical results, albeit within the slightly different context of protein-coat assembly, we refer the reader to ref. 48.
and |W|pe at which the discontinuous transition and the instability of the partially engulfed state take place, respectively. For an extensive comparison of the approximation (23) against numerical results, albeit within the slightly different context of protein-coat assembly, we refer the reader to ref. 48.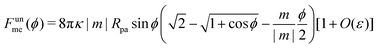
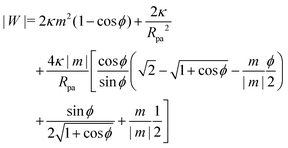

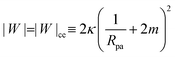
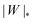 , which can be obtained from the strong asymmetry approximation by requiring that
, which can be obtained from the strong asymmetry approximation by requiring that 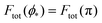 , where
, where 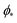 is the wrapping angle corresponding to the partially engulfed state obtained from
is the wrapping angle corresponding to the partially engulfed state obtained from 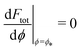 . The partially engulfed state then becomes unstable towards the completely engulfed state at the line |W|pe, which can be straightforwardly obtained from the strong asymmetry approximation by requiring
. The partially engulfed state then becomes unstable towards the completely engulfed state at the line |W|pe, which can be straightforwardly obtained from the strong asymmetry approximation by requiring 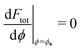 and
and 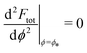 . The critical values for the adhesive strength obtained analytically are in very good agreement with those obtained from numerical solution of the full shape equations, which are given by the red symbols in Fig. 5. The most significant deviations, although still small, are found for the stability line of the partially-engulfed state |W|pe at small negative m, e.g. compare the asterisk and the solid line at mRpa = −3.
. The critical values for the adhesive strength obtained analytically are in very good agreement with those obtained from numerical solution of the full shape equations, which are given by the red symbols in Fig. 5. The most significant deviations, although still small, are found for the stability line of the partially-engulfed state |W|pe at small negative m, e.g. compare the asterisk and the solid line at mRpa = −3.

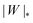 in (b) marks the discontinuous transition at which partially and completely engulfed states have equal energy. The lines |W|fr and |W|ce correspond to the stability limits (26) and (27), respectively, whereas the lines
in (b) marks the discontinuous transition at which partially and completely engulfed states have equal energy. The lines |W|fr and |W|ce correspond to the stability limits (26) and (27), respectively, whereas the lines 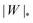 and |W|pe are obtained from the strong asymmetry approximation as described in the text. The red symbols are obtained from numerical solution of the full shape equations.
and |W|pe are obtained from the strong asymmetry approximation as described in the text. The red symbols are obtained from numerical solution of the full shape equations.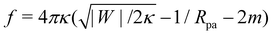 .47 This implies that, for identical conditions with equal particle size and adhesive strength, a membrane with negative spontaneous curvature m = −|m| will exert a significantly higher constriction force on the neck than the equivalent positive spontaneous curvature membrane with m = +|m|. The force difference will be Δf = 16πκ|m| which, using κ = 10−19 J and |m|−1 = 100 nm as typical values, results in a rather large force difference of 50 pN. Thus, we expect that fission of the neck and full internalization of the particle will be much more likely when a particle is engulfed by a vesicle with in-tubes (negative spontaneous curvature) than by a vesicle with out-tubes (positive spontaneous curvature).
.47 This implies that, for identical conditions with equal particle size and adhesive strength, a membrane with negative spontaneous curvature m = −|m| will exert a significantly higher constriction force on the neck than the equivalent positive spontaneous curvature membrane with m = +|m|. The force difference will be Δf = 16πκ|m| which, using κ = 10−19 J and |m|−1 = 100 nm as typical values, results in a rather large force difference of 50 pN. Thus, we expect that fission of the neck and full internalization of the particle will be much more likely when a particle is engulfed by a vesicle with in-tubes (negative spontaneous curvature) than by a vesicle with out-tubes (positive spontaneous curvature).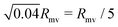 . In contrast, a spherical vesicle with apparent radius Rmv and 20% of its area stored in nanotubes could in principle engulf of the order of 0.2Rmv2/Rpa2 particles of radius Rpa before starting to stretch.
. In contrast, a spherical vesicle with apparent radius Rmv and 20% of its area stored in nanotubes could in principle engulf of the order of 0.2Rmv2/Rpa2 particles of radius Rpa before starting to stretch.

