Open Access Article
Open Access ArticleDesign principles for metamorphic block copolymer assemblies
Alessandro
Ianiro
 ab,
Steven P.
Armes
ab,
Steven P.
Armes
 c and
Remco
Tuinier
c and
Remco
Tuinier
 *ab
*ab
aLaboratory of Physical Chemistry, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: r.tuinier@tue.nl
bInstitute for Complex Molecular Systems (ICMS), Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
cDepartment of Chemistry, Dainton Building, University of Sheffield, Brook Hill, South Yorkshire S3 7HF, UK
First published on 3rd February 2020
Abstract
Certain block copolymer assemblies in selective solvents undergo dynamic morphology transitions (metamorphism) on varying the solution temperature. Despite the great application potential, there is a lack of fundamental understanding of the relationship between copolymer composition and the thermally-induced metamorphic behavior. Herein this relationship is studied by applying Scheutjens-Fleer Self-Consistent Field (SF-SCF) theory to develop fundamental design principles for thermoresponsive diblock copolymers exhibiting metamorphic behavior. It is found that metamorphism is caused by variation in the degree of stretching of the lyophobic blocks in response to changes in solvency. An optimal lyophobic/lyophilic block length ratio interval 3.5 ≲ fB ≲ 5.5 is identified. Such a fB window allows switching between spheres, cylinders and vesicles as preferred morphologies, with relatively small changes in the lyophobic block solvency. The transition from spheres to cylinders and from cylinders to bilayers can be controlled by varying fB, the overall degree of polymerization of the diblock copolymer, and by choosing an appropriate lyophilic block. Empirical relationships are provided to establish a connection between the SCF–SCF predictions and experimental observations.
Introduction
When dispersed in selective solvents, block copolymers (BCPs) form supramolecular colloidal structures whose equilibrium characteristics are dictated by the copolymer composition and how each block interacts with the solvent.1–4 Such self-assembly is spontaneous and is driven by the tendency of the lyophobic block to minimize its contact with the solvent owing to a finite block-solvent interfacial tension (γ). This leads to the formation of structures, where collapsed lyophobic chains and the well-solvated lyophilic chains are segregated into different domains. Various morphologies have been observed experimentally, including spherical micelles, worm-like micelles, vesicles, platelets, and other more complex architectures.3,5,6 To modulate self-assembly, the copolymer composition (i.e., the relative degrees of polymerization of each block) is usually varied. This is, however, hardly a reversible process. In this context, stimulus-responsive block copolymers7–9 have been given considerable recent attention because of their rich, versatile and often reversible self-assembly behavior. In some cases, the equilibrium morphology can be switched by using external stimuli such as the solution temperature (i.e., without modifying the copolymer composition).8,10–13 We refer to such assemblies as metamorphic.Metamorphic block copolymer assemblies have several potential applications, including drug delivery,7,8 preparation of thermoreversible hydrogels10 and as stimuli-responsive oil thickeners.12 The design of metamorphic assemblies is challenging because the underlying mechanisms regulating the transitions between different copolymer morphologies are only partially understood, particularly in relation to the copolymer (structural and chemical) composition. From an applications perspective, it would be useful to be able to predict metamorphic self-assembly behavior for a given new diblock copolymer in order to avoid extensive trial-and-error investigations.
Numerical self-consistent field computations have been used in the past to study morphology transitions exhibited by self-assembled block copolymer nano-objects. For example, morphology transitions can be induced by changing the size of the solvent molecules,14 varying the solution temperature15 or by the addition of nanoparticles when the block copolymer chains are under confinement.16 Numerical self-consistent field methods are appealing for their low computational cost and, unlike full computer simulations, are suitable for extensive systematic studies using a wide range of parameters. In this work, the metamorphic self-assembly of AB diblock copolymers is studied using Scheutjens-Fleer Self-Consistent Field (SF-SCF) theory.17,18 This approach is based on Flory–Huggins mean-field theory,19 but accounts for inhomogeneity and concentration gradients in the system, enabling the formation of self-assembled structures to be studied. Lattices with different geometries (spherical, cylindrical or planar) can be used to study spherical micelles, worm-like micelles or vesicles in order to determine which morphology is thermodynamically preferred under a given set of conditions (e.g., copolymer composition, solvent, temperature, etc.). With this strategy, the evolution in metamorphic assemblies on changing the degree of solvation for the structure-directing block can be examined. Furthermore, relatively short computational times enable systematic studies and provide a detailed structural description of the diblock copolymer nano-objects. This information can be translated into novel design principles for metamorphic BCP self-assembly.
Methods
Modeling approach
Metamorphism can be achieved in several ways, for example by changing the solvent itself,13 by varying temperature,10,12 and using light11,20 (a pH switch can also be used, but this case is not discussed here). Herein we focus on thermally-induced metamorphism. In this case, a change in solvency for at least one of the blocks triggers the (usually) reversible transition between two (or more) morphologies. Such changes can be mapped onto variations of a set of interaction parameters, called Flory–Huggins χ parameters,19 which are a measure of the compatibility (miscibility) between the individual components in the system. Hence they can be regarded as general indicators for solvency. Conveniently, these χ values are input parameters for the SF-SCF computations.The SF-SCF approach is based on Flory–Huggins mean-field theory and utilizes numerical lattice computations. This accounts for concentration gradients by means of the Edwards formalism.21 For each component i in the system, there is a segment potential ui(r) at each position in the lattice (here r is a coordinate vector indicating the position in the lattice). The normalized probability Pi(r) of finding the component i at the position r is proportional to a Boltzmann factor e−ui(r)/kBT. The potential at a given position r is influenced by the composition of the adjacent sites, hence it depends on the distribution of segments and molecules, φi(r). Given this mutual dependence between φi(r) and ui(r), an iterative procedure is used to determine the equilibrium segment distribution in order to minimize the free energy of the system.
This problem can be simplified if concentration gradients are considered in one direction only. In this case, the lattice can be envisaged as a collection of layers situated at a distance r from an initial layer. In this configuration, the potential ui(r) varies only in the direction of r and the normalized probability Pi(r) of finding a certain segment in the lattice layer (r) corresponds to its volume fraction φi(r) within the layer. The incompressibility ensures that  for each layer. Further details of the calculation of ui[φi(r)] and φi[ui(r)] can be found in the original study by Scheutjens and Fleer18,22 and related publications.4
for each layer. Further details of the calculation of ui[φi(r)] and φi[ui(r)] can be found in the original study by Scheutjens and Fleer18,22 and related publications.4
The SF-SCF is a general method to study the phase behaviour of multicomponent systems,4 as well as interfacial phenomena such as adsorption23 or depletion.24 Here we apply this method for the first time to systematically study the metamorphic behaviour of self-assembled block copolymer nano-objects in aqueous solution as a function of the solvency of the water-insoluble structure-directing block.
Thus, the self-assembly of an AB diblock copolymer is studied in a solvent S. The lyophilic A block and the lyophobic B block are composed of NA and NB segments, respectively. As the system comprises three components (A, B and S), three pairwise interaction parameters χAS, χBS, χAB need to be specified in the calculations. A full description of the computational set-up is reported below.
Metamorphism is often observed in systems with stimuli-responsive lyophobic blocks. In the SF-SCF computations, metamorphism is induced here by varying the interaction parameter between solvent and the lyophobic block χBS, which is varied between 0.5 and 2.5. Practically, the interval 0.5 ≲ χBS ≲ 1.5 is the most relevant regime for thermoreversible metamorphic behavior, as for χBS ≲ 0.5 the copolymer is expected to be always soluble,19 while for χBS ≳ 1.5 the assemblies are likely to be kinetically frozen, thus losing their ability to switch morphology owing to a vanishing critical aggregation concentration (i.e. the concentration of free copolymer chains that are in equilibrium with the assemblies).25–27 It is emphasized that the SF-SCF computations performed here do not account for kinetic effects – it is not possible to assess the time scales that might be required for the observation of metamorphic behavior.
Lattice and boundary conditions
Numerical SF-SCF lattice computations were performed with the SFbox program provided by Prof. F. A. M. Leermakers (Wageningen University, The Netherlands). The settings of the boundary conditions, the lattice and interaction parameters are described below.Unless specified, SCF computations were performed on lattices containing L = 200 lattice layers and either spherical, cylindrical or planar geometries to study spherical micelles, cylindrical micelles or vesicles, respectively. It was confirmed that variation of L to larger values did not affect the computed equilibrium properties; no lattice size-related artifacts were observed. A lattice coordination number (z) of 3 was used for each geometry and the lattice constant l (i.e. the size of the lattice unit) was set to unity. For a flat geometry, two mirrors are placed at the first and the last lattice sites. For the spherical and cylindrical geometries, a mirror was located at the last lattice layer (with the first layer corresponding to the center of the lattice).
All compounds (the solvent molecule S and the A and B monomer segments) were assumed to occupy a single lattice site. The diblock copolymer chains were assumed to be neutral (uncharged) in character and perfectly homogeneous in chain length (i.e. Mw/Mn = 1.00).
Interaction parameters
The system is composed of three components so three pairwise interaction parameters χ (χAS, χBS, χAB) must be specified in the calculations. The parameter χBS is varied between 0.5 and 2.5 to simulate changes in the solubility of the lyophobic block in response to the applied stimulus. Several numerical values for χAS and χAB were examined; these values are specified each time during the discussion of the results.Determination of the equilibrium properties of the assemblies
For each copolymer and each set of interaction parameters, the equilibrium self-assembled structure was determined by optimizing the free energy of the (lattice) system of interest with respect to the spatial distribution of each component (concentration profile), and with respect to the copolymer lattice occupancy θ (i.e. the number of lattice sites occupied by copolymer molecules in the lattice).28 This minimization is performed by assuming that only a single self-assembled structure is formed in the lattice. Justification of this protocol has been discussed in the literature.17,18 At equilibrium, the copolymer chains in the lattice are distributed between bulk solution (θbulk) and self-assembled structure (θexcess), θ = θexcess + θbulk, as specified by the equilibrium concentration profile. The copolymer bulk concentration (φbulkBCP) can be expressed as a function of the total lattice volume V: | (1) |
 | (2) |
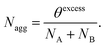 | (3) |
To determine the thermodynamically preferred morphology, the calculations are repeated in lattices with differing geometries (spherical, cylindrical and planar). The copolymer φbulkAB values are computed for each morphology and then compared. The geometry that has the lowest critical aggregation concentration (φbulkAB) corresponds to the preferred morphology, since the dimensionless free energy of a copolymer chain within a self-assembled structure ( ) is approximately given by29
) is approximately given by29
 | (4) |
Calculation of φcoreS, α and ε
The solvent volume fraction in the core φcoreS can be estimated from the solvent equilibrium concentration profile at the center of the insoluble B core. From the values of φcoreS and Nagg the surface area α occupied by each copolymer chain at the core–corona interface can be calculated. For the different lattice symmetries, geometric arguments can be used to show that | (5) |
 | (6) |
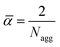 | (7) |
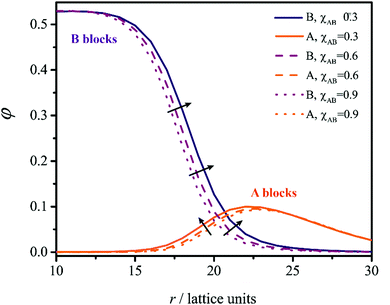
In principle, the end-to-end distance of the B blocks, ε, could be determined by the concentration profiles from the thickness of the B core. In practice, the existence of a wide interface (Fig. 4) makes it difficult to formally define the boundary of the core region. Therefore, we have also derived the following expressions for:
 | (8) |
 | (9) |
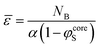 | (10) |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) and
and ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) imply that the molecular packing parameters30 of the assemblies, are P ≡ 1/3 for the spherical morphology, P ≡ 1/2 for the cylindrical morphology and P ≡ 1 for the bilayer (vesicle) morphology.
imply that the molecular packing parameters30 of the assemblies, are P ≡ 1/3 for the spherical morphology, P ≡ 1/2 for the cylindrical morphology and P ≡ 1 for the bilayer (vesicle) morphology.
Determination of χSP from φPS
The SCF computations have been used to derive an empirical relationship that allows the polymer–solvent interaction parameter χSP to be determined for an insoluble homopolymer P in a solvent S. According to this method, χSP can be evaluated by measuring the volume fraction φPS of S taken up by P when these two species are in contact. This can be achieved gravimetrically by using a microbalance if the density of the homopolymer and the solvent are known.SF-SCF calculations have been used to compute equilibrium concentration profiles for homopolymer-solvent systems for a planar geometry (L = 100, l = 1) as a function of χSP in the range 0.5 ≤ χSP < 2. Various homopolymers (P), with 100 ≤ NP ≤ 800, have been simulated. A total polymer volume fraction in the lattice φP = 0.1 was used for each computation. For χSP ≳ 0.7 phase separation into P-rich and S-rich phases is predicted. The solvent concentration in the P-rich phase, φPS, is fitted with χSP to provide the empirical relationship shown in eqn (11) (in Results and discussion).
Results and discussion
SCF results
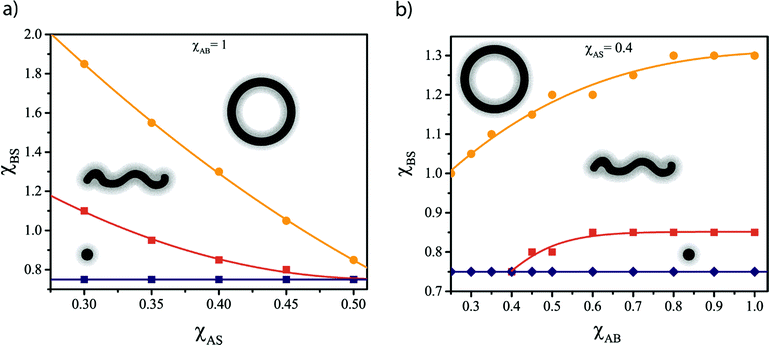
The SF-SCF computations have been first performed to evaluate the preferred morphology of AB diblock copolymers with NA = 50 and various relative block lengths fB = NB/NA. The calculations are performed assuming χAS = 0.4 and χAB = 1, corresponding to a moderately soluble A block, well segregated from the B block. The results are summarized in a phase diagram (Fig. 1a) that reveals an optimal fB window (3.5 ≲ fB ≲ 5.5 for the selected parameters), where several possible (di)block copolymer morphologies can be obtained within a reasonably narrow χBS range. Outside of this fB interval, only one (fB ≲ 2) or two (2 ≲ fB ≲ 3, fB ≳ 5.5) morphologies are predicted for 0.5 ≲ χBS ≲ 2.5.The χBS values marking the sphere-to-cylinder (χS→CBS) and cylinder-to-bilayer (χC→BBS) transitions are also influenced by the total copolymer chain length N = NA + NB (Fig. 1b). As shown in Fig. 1b, χS→CBS is only weakly dependent on N, while a marked, linear χC→BBS increase is observed when increasing N at a fixed fB value of 4. When increasing the overall copolymer chain length, the stability windows for the various morphologies become wider (Fig. 1b).
Together with the preferred morphology, the SF-SCF computations provide structural information, such as the mean aggregation number Nagg and the amount of solvent present in the core of the self-assembled structure φcoreS (see Methods for further details). These quantities can be used to estimate the average end-to-end distance of the lyophobic B block (ε) and the area that each copolymer chain occupies at the core–corona interface (α). The calculations for ε and α are described in Methods. The χBSdependence of these quantities, illustrated in Fig. 2 for A50-B200 (fB = 4, χAS = 0.4, χAB = 1), provide a molecular-level interpretation of the metamorphic behaviour. Increasing χBS causes a reduction in compatibility between B and S, which in turn drives the expulsion of solvent from the nano-objects (Fig. 2a); this is in agreement with previous experimental studies of self-assembled diblock copolymer nano-objects.10,31 As a result, the copolymer chains come into closer proximity (increasing the aggregation number with a consequent reduction in α, Fig. 2b) and are forced to stretch (increase in ε, see Fig. 2c). Such chain stretching triggers the morphology transition. The equilibrium morphology adopted is determined by the balance between interfacial energy (Δginterface = γα), core elastic energy (Δgcore) and corona elastic energy32,33 (Δgcorona).
Core and corona elastic energies are entropic contributions. They account for variation in the configurational entropy caused by perturbations of the core (ε) and corona (δ) end-to-end distances (Fig. 2d). For a fixed α value, Δginterface is morphology-independent and the preferred morphology is dictated by the balance between Δgcorona and Δgcore. The spherical morphology is associated with the lowest Δgcorona but the highest Δgcore (Fig. 2d). Conversely, bilayer morphologies such as vesicles exhibit the highest Δgcorona but the lowest Δgcore. Therefore, an increase in ε modifies the energetic balance between any given pair of assemblies, thus driving the morphology transition (first to cylindrical, then to bilayer morphology). Each transition is accompanied by a steep reduction in ε (Fig. 2c) at the expense of an increasing δ (Fig. 2d).
In contrast, lower χAB values (which correspond to greater inter-block compatibility) are associated with a reduction in χS→CBS and χC→BBS because the lyophilic chains are partially embedded at the core–corona interface (Fig. 4) and hence screen the cores from the solvent to some extent. As χAB is reduced, contact between the A and B blocks becomes more favorable and the core screening more effective. This leads to a broader core–corona interface, as indicated by the concentration profiles shown in Fig. 4. Entrapment of more A segments through the interface can be interpreted as an effective reduction in the corona chain length, with the consequent increase in fB shifting the morphology transitions towards lower χBS values (Fig. 1a). These results suggest that the choice of the particular lyophilic block can strongly influence the metamorphic behavior.
The effect of varying the lyophilic block solubility (χAS) and the degree of compatibility between A and B (χAS) was also investigated. A reduction in χAS (increase in solubility) leads to expansion of the corona chains because the effective excluded volume of the segments in the A block increases.18,34 As a result, the energy penalty associated with stretching these lyophilic chains is lower. This affects the balance between Δgcorona and Δgcore, which in turn shifts the morphology transitions towards higher χBS values (Fig. 3a).
Translating the SF-SCF results into design principles
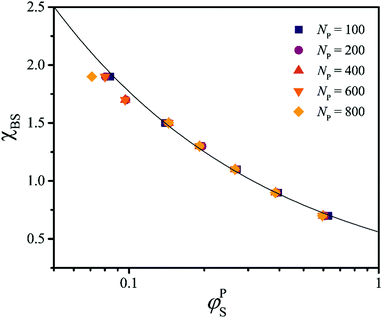
As discussed above, SF-SCF theory can be used to guide the design of new experimental systems that exhibit the desired metamorphic behavior. It appears that a composition window (expressed in terms of the relative block length) of 3.5 ≲ fB ≲ 5.5 is optimal as the resulting assemblies exhibit metamorphic behavior within a useful χBS range. This agrees with recent experimental results,31,35 where two types of block copolymers with temperature-responsive lyophobic blocks and 4.5 ≲ fB ≲ 5 exhibited the ability to form spheres, cylinders or vesicles in water depending on the solution temperature. The values of χS→CBS and χC→BBS can be controlled by varying fB and adjusted by an appropriate choice of the lyophilic block (Fig. 3a) and the overall degree of polymerization of the diblock copolymer chains (Fig. 1b). As a result, this optimal window is expected to shift towards higher fB values when increasing the overall block copolymer length and χAB, and also when decreasing χAS (and vice versa).The most important aspect of the design of metamorphic assemblies is to evaluate how χBS depends on the applied stimulus. There are various ways to determine χ parameters36 but many of them are only valid for soluble polymers and are typically time-intensive measurements requiring specific equipment.36 For insoluble homopolymers, there is a relationship between χ and the amount of solvent taken up at equilibrium (φPS), as described by Flory–Huggins solution theory.19 Unfortunately, this relationship cannot be expressed in terms of an exact analytical solution. However, an empirical relation can be derived using numerical analysis or SF-SCF computations (see Methods). Here values of φPS are computed using SF-SCF for a polymer P as a function of the polymer–solvent interaction parameter χSP for various mean degrees of polymerization, NP.
According to Fig. 5, φPS is chain length-independent, and fitting this data set provides the following approximate empirical relationship:
 | (11) |
 | ||
| Fig. 5 SF-SCF results (markers) for the relationship between the polymer–solvent interaction parameter χSP and the solvent volume fraction in the polymer φPS for various homopolymers of differing degrees of polymerization, NP. The full curve represents the empirical fit obtained using eqn (11). | ||
Using (11), a numerical value for χBS and its dependence on the applied stimulus can be readily determined by measuring the solvent uptake (φPS) for a homopolymer with the same composition as the lyophobic block. In principle, this can be achieved simply by gravimetry using a precision microbalance.
It is emphasized that the SF-SCF relative block length fB does not always correspond to the actual experimental block length ratio. Within the lattice-based SF-SCF theory, all segments have the same size and flexibility, which is not necessarily true in reality. For flexible linear diblock copolymers, one strategy is to compute the ratio between the volumes of the B (VB). and A (VA) monomers, ν = VB/VA (the monomer volume can be calculated as the monomer mass divided by the block density). The parameter ν can be multiplied by the experimental block length ratio fB to obtain an effective parameter (feffB = νfB), which is an appropriate and reliable reference for interpreting the SF-SCF predictions. Alternatively, one can map the copolymer onto a lattice by considering the actual chain flexibility of each block, which in principle can be evaluated via scattering experiments.37
Finally, when designing a suitable metamorphic system, it is important to bear in mind that copolymer dispersions might undergo liquid–liquid phase separation under certain conditions.38 Such phase separation can be minimized by ensuring high inter-block segregation (high χAB) and choosing highly soluble (low χAS) lyophilic blocks.38
The principles summarized above can be combined with the SF-SCF results to guide the design of metamorphic assemblies, thus avoiding laborious trial-and-error experimentation.
Conclusions
Scheutjens-Fleer Self-Consistent Field (SF-SCF) numerical lattice computations have been used to systematically study diblock copolymer assemblies that undergo thermally-induced metamorphism, i.e. reversible morphology transitions between spherical micelles, cylindrical micelles, and bilayers (vesicles). It is found that metamorphism is caused by variation in the degree of stretching of the lyophobic blocks in response to changes in solvency. However, such metamorphism is only observed over a relatively narrow block composition interval. The most relevant composition range appears to be 3.5 ≲ fB ≲ 5.5, where fB is the lyophobic/lyophilic block length ratio. The transition from spheres to cylinders and from cylinders to bilayers (and in turn the optimal fB window), can be controlled by varying the overall degree of polymerization of the diblock copolymer chains and also by choosing an appropriate lyophilic block. Empirical relationships are established to connect the SCF–SCF predictions to experimental observations. This study provides a complete theoretical framework for the rational design of AB diblock copolymers that exhibit metamorphic self-assembly behaviour.Conflicts of interest
There are no conflicts to declare.Notes and references
- D. J. Adams, C. Kitchen, S. Adams, S. Furzeland, D. Atkins, P. Schuetz, C. M. Fernyhough, N. Tzokova, J. A. Ryan and M. F. Butler, Soft Matter, 2009, 5, 3086–3096 RSC.
- Z. Zhou, Z. Li, Y. Ren, M. A. Hillmyer and T. P. Lodge, J. Am. Chem. Soc., 2003, 125, 10182–10183 CrossRef CAS PubMed.
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985 RSC.
- F. Leermakers, J. C. Eriksson and H. Lyklema, Fundamentals of Interface and Colloid Science – Vol. V, Academic Press, 2005, pp. 4.1–4.123 Search PubMed.
- S. J. Holder and N. A. J. M. Sommerdijk, Polym. Chem., 2011, 2, 1018–1028 RSC.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef CAS PubMed.
- Q. Zhou, L. Zhang, T. H. Yang and H. Wu, Int. J. Nanomed., 2018, 13, 2921–2942 CrossRef CAS PubMed.
- X. Hu, Y. Zhang, Z. Xie, X. Jing, A. Bellotti and Z. Gu, Biomacromolecules, 2017, 18, 649–673 CrossRef CAS PubMed.
- M. A. Cohen Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef CAS PubMed.
- S. P. Armes, R. Verber, A. Blanazs, C. W. I. Douglas, A. J. Ryan, J. Z. Heath and O. O. Mykhaylyk, J. Am. Chem. Soc., 2012, 134, 9741–9748 CrossRef PubMed.
- E. Blasco, J. L. Serrano, M. Piñol and L. Oriol, Macromolecules, 2013, 46, 5951–5960 CrossRef CAS.
- M. J. Derry, O. O. Mykhaylyk and S. P. Armes, Angew. Chem., Int. Ed., 2017, 56, 1746–1750 CrossRef CAS PubMed.
- Y. Yu, L. Zhang and A. Eisenberg, Macromolecules, 1998, 31, 1144–1154 CrossRef CAS.
- W. Li and W. Jiang, Macromol. Theory Simul., 2009, 18, 434–440 CrossRef CAS.
- A. M. Rumyantsev, F. A. M. Leermakers, E. B. Zhulina, I. I. Potemkin and O. V. Borisov, Langmuir, 2019, 35, 2680–2691 CrossRef CAS PubMed.
- Q. Pan, C. Tong and Y. Zhu, ACS Nano, 2011, 5, 123–128 CrossRef CAS PubMed.
- P. N. Hurter, J. M. H. M. Scheutjens and T. A. Hatton, Macromolecules, 1993, 26, 5592–5601 CrossRef CAS.
- G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Springer, Netherlands, 1993 Search PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, United States, 1953 Search PubMed.
- Y. Zhao, J. Mater. Chem., 2009, 19, 4887–4895 RSC.
- S. F. Edwards, Proc. Phys. Soc., 1965, 85, 613–624 CrossRef CAS.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- G. J. Fleer, Adv. Colloid Interface Sci., 2010, 159, 99–116 CrossRef CAS PubMed.
- G. J. Fleer, A. M. Skvortsov and R. Tuinier, Macromolecules, 2003, 36, 7857–7872 CrossRef CAS.
- S. Choi, F. S. Bates and T. P. Lodge, Macromolecules, 2011, 44, 3594–3604 CrossRef CAS.
- J. Lu, F. S. Bates and T. P. Lodge, Macromolecules, 2015, 48, 2667–2676 CrossRef CAS.
- S. Choi, T. P. Lodge and F. S. Bates, Phys. Rev. Lett., 2010, 104, 047802 CrossRef PubMed.
- T. L. Hill, J. Chem. Phys., 1962, 36, 3182–3197 CrossRef CAS.
- H.-J. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley-VCH Verlag GmbH & Co. KGaA, 2006 Search PubMed.
- J. N. Israelachvili, D. J. Mitchell and W. B. Ninham, J. Chem. Soc., Faraday Trans. 2, 1975, 1525–1568 Search PubMed.
- L. P. D. Ratcliffe, M. J. Derry, A. Ianiro, R. Tuinier and S. P. Armes, Angew. Chem., Int. Ed., 2019, 58, 18964–18970 CrossRef CAS PubMed.
- E. B. Zhulina, M. Adam, I. Larue, S. S. Sheiko and M. Rubinstein, Macromolecules, 2005, 38, 5330–5351 CrossRef CAS.
- E. B. Zhulina and O. V. Borisov, Macromolecules, 2012, 45, 4429–4440 CrossRef CAS.
- J. Lyklema, Fundamentals of Interface and Colloid Science volume V, Elsevier B.V., Amsterdam, 2005 Search PubMed.
- S. J. Byard, C. T. O’Brien, M. J. Derry, M. Williams, O. O. Mykhaylyk, A. Blanazs and S. P. Armes, Chem. Sci., 2020, 11, 396–402 RSC.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer Handbook, ed. A. Abe and D. R. Bloch, John Wiley and Sons, 4th edn, 2005 Search PubMed.
- H. Morawetz, Light scattering from polymer solutions, Academic Press Inc., London, 1973 Search PubMed.
- A. Ianiro, H. Wu, M. M. J. van Rijt, M. P. Vena, A. D. A. Keizer, A. C. C. Esteves, R. Tuinier, H. Friedrich, N. A. J. M. Sommerdijk and J. P. Patterson, Nat. Chem., 2019, 11, 320–328 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |