Filler size effect in an attractive fibrillated network: a structural and rheological perspective

Abstract

The effect of the filler size on the structural and mechanical properties of an attractive fibrillated network composed of oxidised cellulose nanofibrils (OCNF) in water was investigated. Silica nanoparticles with a diameter of ca. 5 nm (SiNp₅) and and ca. 158 nm (SiNp₁₅₈) were chosen as non-interacting fillers of the OCNF network. These filler sizes were chosen, respectively, to have a particle size which was either similar to that of the network mesh size or much larger than it. Contrast matched small angle neutron scattering (SANS) experiments revealed that the presence of the fillers (SiNp₅ and SiNp₁₅₈) did not perturb the structural properties of the OCNF network at the nanometer scale. However, the filler size difference strongly affected the mechanical properties of the hydrogel upon large amplitude oscillatory shear. The presence of the smaller filler, SiNp₅, preserved the mechanical properties of the hydrogels, while the larger filler, SiNp₁₅₈, allowed a smoother breakage of the network and low network recoverability after breakage. This study showed that the filler-to-mesh size ratio, for non-interacting fillers, is pivotal for tailoring the non-linear mechanical properties of the gel, such as yielding and flow.

---

1 Introduction

The growing need for sustainable materials has promoted interest in the use of cellulose nanofibrils (CNF) as building blocks for renewable products. CNF belong to the colloidal domain and are usually characterized by a radius in the order of a few nanometers and a length of 100–1000 nm depending on the preparation method and source.^1,2 TEMPO-mediated oxidation of cellulose has been, for instance, a successful route for the production of oxidised cellulose nanofibrils (OCNF) on a large scale.^2–4 Importantly, the carboxylate groups on the OCNF surface yield a surface negative charge which allows the preparation of stable aqueous dispersions.³ Interfibrillar repulsive/attractive forces have been reported to be strongly dependent on the pH^5,6 and ionic strength^7–9 of the aqueous media.¹⁰ Charge screening due to counterion binding to the carboxylate group has been shown to be an effective gelation mechanism.^7,9 Structural investigation of OCNF dispersions, via small angle X-ray scattering, revealed that, for concentrations above the overlap threshold,¹¹ a clear transition from a repulsive to an attractive fibrillated network occurs upon increasing the ionic strength.⁹ This finding is directly related to the sol–gel transition⁹ and to the theoretical expectations based on the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory for two cylindrical rods.⁷ To broaden the understanding of interfibrillar assembly in systems closer to industrially relevant scenarios, the use of additives, such as surfactants^11,12 and polymers,^13,14 in cellulose nanoparticle-based hydrogels has been explored.¹ Nevertheless, knowledge of the interplay between non-interacting colloidal fillers and a fibrillated network is lacking. The filler surface chemistry, size and volume fraction have been mainly investigated in protein-based hydrogels and are referred to as “active” or “inactive” fillers based on their ability to strengthen or weaken the gel, respectively.^15–17 In principle, fillers could be employed to modulate other mechanical properties such as structural breakage (yielding), flow, structural recoverability and plasticity, which are important parameters to account for in processing operations and/or customer appreciation.¹⁸ Such mechanical properties often occur upon large deformations and high shear rates, where the mechanical response of the material depends on the applied strain and shear rate, identified as non-linear viscoelastic region (NLVR). On this ground, we investigated the filler size effect on the linear and non-linear viscoelastic response of an attractive fibrillated network composed of OCNF. The interfibrillar attractive forces were promoted via addition of 100 mM NaCl, leading to an OCNF network with a mesh size, defined as the average distance between the nearest fibrillar junction zones, of 20–40 nm as recently reported by our group.⁹ Silica nanoparticles (SiNp) with average dimensions similar to the mesh size of the network and SiNp larger (ca. by a factor of 5) than the network mesh size were chosen as non-interacting fillers in the OCNF-based gel. We show that the filler-to-mesh-size ratio, for non-interacting fillers, is of pivotal importance for tailoring non-linear mechanical properties of the gel such as yielding and flow.

2 Experimental

2.1 Materials

An OCNF dispersion was prepared as previously described,¹⁹ using a TEMPO/NaOCl/NaBr oxidation method.²⁰ A 2 wt% OCNF stock was redispersed from freeze-dried OCNF in ultrapure deionised (DI) water (18.2 MΩ cm) and stirred overnight, followed by a mild sonication process (Ultrasonic Processor FB-505, Fisher, 200 W cm⁻², equipped with a 1 cm probe, using a series of 1 s on/1 s off in pulse mode for a net time of 120 s at 30% amplitude on ca. 45 mL dispersion contained in an ice bath). A 10 wt% SiNp₁₅₈ dispersion was prepared by dispersing silica nanopowder (718483 Sigma-Aldrich®) in ultrapure DI water followed by sonication (as for the OCNF indicated above) and used without further treatment. A ca. 9 wt% aqueous SiNp₅ dispersion, provided by Geo40™ (sodium stabilised colloidal silica of geothermal origin), was dialysed using cellulose dialysis tubing (Sigma-Aldrich® cellulose dialysis tubing, molecular weight cut-off of 12 400 Da) against DI water for 3 days, refreshing the DI water twice per day. The dialysed SiNp₅ dispersion was pH adjusted to 7 using HCl (aq) and further dialysed against DI water, as previously described. Larger aggregates were removed using a syringe filter unit with a cut-off size of 0.22 μm (Millex®-GS), and the solid content (wt%) of the filtered dispersion was obtained gravimetrically. Specific OCNF, OCNF–SiNp₅ and OCNF–SiNp₁₅₈ concentrations were obtained via dilution of the stock dispersions described above, except where otherwise stated, followed by the addition of a 2 M NaCl solution to achieve a final NaCl concentration of 100 mM in all samples.

2.2 Methods

Small angle X-ray scattering (SAXS) measurements were performed on an Anton-Paar SAXSpoint 2.0 equipped with a copper source (Cu Kα, λ = 1.542 Å) and a 2D EIGER R series Hybrid Photon Counting (HPC) detector. The sample-to-detector distance was 556 mm covering a range of the scattering vector (q) of about 0.01 < q < 0.4 Å⁻¹. Samples were loaded into 1 mm quartz capillaries, and the scattering intensity (I(q)) was collected in three frames, with 300 s exposure per frame. Temperature was kept at 25 °C via a Peltier unit (±0.1 °C). Small angle neutron scattering (SANS) experiments were conducted at the Institut Laue Langevin (Grenoble, France) on the D22 SANS beamline using a wavelength of 6 Å and a sample-to-detector distance of 2.8 and 17.6 m to yield a q range of 0.003 < q < 0.4 Å⁻¹. Temperature was kept at 25 °C via a Julabo circulating waterbath (±0.5 °C). Particles that have the same scattering length density (SLD) as the continuous phase do not contribute to the scattering intensity (I(q) = 0), and they are said to be contrast matched.²¹ We determined the contrast match point of the SiNp, using different H₂O/D₂O ratios as the continuous phase. This is possible due to the different SLD between H₂O (−0.5 × 10⁻⁶ Å⁻²) and D₂O (6.3 × 10⁻⁶ Å⁻²), which allows tuning of the SLD of the continuous phase upon changing the H₂O/D₂O ratios. Samples were prepared with a continuous phase composed of 60 vol% D₂O (99.9 atom% D, Sigma-Aldrich®) and 40 vol% H₂O (DI water), which was experimentally determined to be the contrast match point for SiNp (Fig. S1, ESI†) in agreement with what was previously reported.²² For this experiment, OCNF, OCNF–SiNp₅ and OCNF–SiNp₁₅₈ concentrations were obtained via dilution of 2 wt% freeze-dried OCNF dispersed in pure D₂O (prepared as previously described) and SiNp stock dispersions described above (SiNp₅ and SiNp₁₅₈ (in H₂O)) with the required H₂O/D₂O ratio, followed by the addition of a 2 M NaCl solution (in H₂O) to achieve a final NaCl concentration of 100 mM in all samples. Samples were measured in 2 cm wide optical quartz cells with 1 mm path length. For SAXS and SANS measurements, background subtraction and data treatment were performed using the Irena package,²³ whilst data analysis was done using the NIST SANS Analysis package (models were used without further modification),²⁴ both within IGOR Pro (Wavemetrics, Inc.). Data are presented as I(q) vs. q and I(q) vs. d, where d is the d-spacing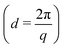 . Details regarding the model of non-interacting flexible cylinders with an elliptical cross-section are described by Schmitt et al.⁹

Dynamic light scattering (DLS) was performed on diluted samples (0.01 wt% in 100 mM NaCl) using a Malvern Zetasizer Nano ZSP® (Malvern, UK). The samples were loaded in disposable polystyrene cells with a path length of 1 cm and measured as an average of 4 measurements of 100 scans each. The values are reported as normalised intensity and obtained from the average of three separate samples. Temperature was kept at 25 °C (±0.1 °C).

The rheological measurements of the OCNF-based hydrogels were performed using a stress-controlled rheometer (Discovery HR3, TA instruments®) equipped with a sandblasted plate-plate geometry (40 mm). To avoid evaporation, the edge of the samples was covered with low viscosity mineral oil and further covered with a solvent trap to ensure constant temperature within the chamber (25 °C ± 0.1 °C via a Peltier unit). After loading, the gel was exposed to (i) a 30 s pre-shear at 300 s⁻¹ to ensure equal sample history, (ii) a time sweep employing small strain amplitudes (γ₀ = 0.05 (%)) at a constant angular frequency (ω = 1 rad s⁻¹) for 50 × 10³ s, (iii) a frequency sweep at a constant strain amplitude, γ₀ = 0.1%, being in the linear viscoelastic region (LVR) (Fig. S2, ESI†) and (iv) a strain sweep at constant frequency, ω = 1 rad s⁻¹. The storage and loss moduli, G′ and G′′, respectively, were computed by the TRIOS software and used to obtain tan δ = G′′/G′. For (iv), raw data were acquired as stress (σ) as a function of intracycle shear rate [small gamma, Greek, dot above] (s⁻¹) and the instantaneous intracycle strain (γ) and presented in the form of Lissajous plots as σ vs. [small gamma, Greek, dot above] and σ vs. γ, known as the viscous and the elastic projection, respectively.

3 Results and discussion

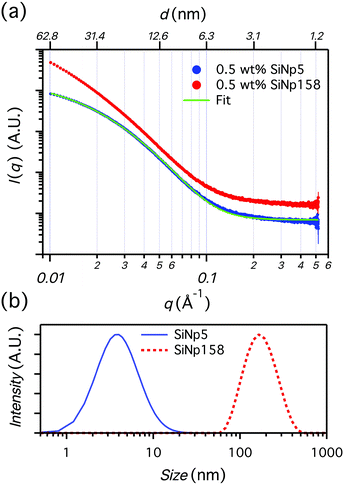
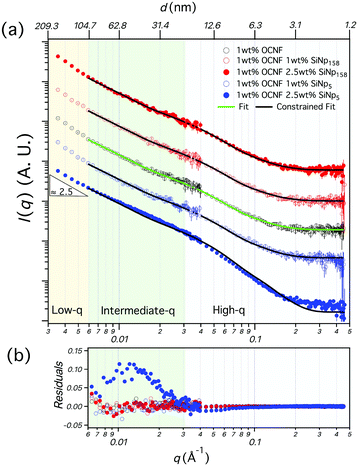
Gelation of the 1 wt% OCNF suspension was achieved upon addition of NaCl (100 mM), resulting in an attractive fibrillated network with a defined mesh size of 20–40 nm.⁹ Silica nanoparticles, with dimensions similar to and greater than the mesh size of the network, were incorporated in the 1 wt% OCNF gel, and their effect on structural and mechanical properties of the OCNF-based gel was investigated. Although silica nanoparticles were chosen to avoid strong interactions with OCNF (e.g. electrostatic, hydrophobic), experimental evidence for this was sought. At first, the filler sizes were evaluated via SAXS using conditions of ionic strength the same as the one employed in this study to induce gelation of OCNF (Fig. 1a). Contrary to SiNp₁₅₈, SiNp₅ displayed an approaching plateau at low q, indicating that the characteristic size of the object is probed (radius of gyration).²⁵ The data of SiNp₅ were fitted to a model of spheres with a log-normal size distribution, yielding a particle mean size of 5.2 ± 0.2 nm and a size distribution as shown in Fig. 1b. Since SAXS measurements did not access the larger size of SiNp₁₅₈, DLS measurements were used to determine the hydrodynamic size of the particles (Fig. 1b). This accounts for the hydration shell of the particles which is expected to be of the order of a few nanometers at this ionic strength.²⁶ Overall, SiNp₁₅₈ displayed a higher mean size (158.0 ± 1.3 nm) and a narrower size distribution compared to SiNp₅. To explore the effect of the filler on the structural properties of the OCNF network, SANS measurements were performed under conditions where the SiNp scattering contribution was matched to that of the solvent. This results in a dominant OCNF scattering intensity, allowing us to probe, solely, the structural properties of the OCNF network in the presence of SiNp. In practice, this was achieved using a continuous phase composed of a mixture of 60 vol% D₂O and 40 vol% H₂O (see Fig. S1 for contrast match point determination for SiNp, ESI†). According to previous reports, the scattering pattern of 1 wt% OCNF at 100 mM NaCl (Fig. 2a) contains information regarding the shape of the fibrils in the high-q and intermediate-q region, which probe the radius and the larger dimensions of the fibril, respectively.^9,19,27 The upturn in the low-q region has been instead associated with the attractive interfibrillar interactions as described by Schmitt et al.⁹ The data were fitted, in the q region where interfibrillar interactions are not detectable (high-q and intermediate-q range), to a model of non-interacting flexible cylinders with an elliptical cross-section from which the minor radius (R_min), major radius (R_maj) and the Kuhn length (b_Kuhn) were obtained, where b_Kuhn is indicative of the OCNF mesh size.⁹ The data fitting was carried out using a fixed and arbitrary contour length (L) of 500 nm as the average length was not accessible in the probed q range, as indicated by the lack of a plateau in the low-q region. In addition, the interfibrillar interactions, in the low-q region, would not allow extrapolation of the OCNF contour length. Since the lower threshold for the data fitting was q_min = 0.06⁻¹, using values of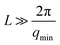 kept the fitting unchanged. The model yielded values of R_min = 1.1 ± 0.1 nm, R_maj = 4.7 ± 0.1 nm and b_Kuhn = 21.4 ± 0.1 nm, in good agreement with previous SAXS measurements^9,19,27 and imaging analysis of OCNF.⁹ Upon SiNp addition, the SANS patterns had a similar trend to that of the pure OCNF gel, indicating that, in the probed q range, neither of these fillers strongly alters the structure of the fibrillated network. As such, the SiNp-containing samples were fitted using fixed values of R_min = 1.1, R_maj = 4.7 and b_Kuhn = 21.4 nm as found for OCNF, allowing only scale and background to vary. The data were satisfactorily fitted using these constrained values with the exception of the sample containing 2.5 wt% SiNp₅, which displayed some difference in the intermediate-q region as shown by the residual plot (Fig. 2b). The poorer fitting in the intermediate-q range could be due to a small residual unmatched scattering contribution from SiNp₅. Analysis of the low-q region revealed a slope of ≈2.5 for all the samples, indicating that neither of the fillers alters the attractive interactions between OCNF at this length scale. Overall, both fillers preserved the architecture of the fibrillated OCNF network at the nanometer length scale, enabling comparison of the rheological properties of the OCNF-based gels under conditions where the network architecture is the same.

Fig. 1 (a) SAXS patterns for the 0.5 wt% SiNp₅ and SiNp₁₅₈ dispersions in 100 mM NaCl. A fit of spheres with log-normal size distribution is shown for SiNp₅. The error bars are the standard error in the data points calculated during radial averaging of the initial 2D images. (b) Size distribution of 0.5 wt% SiNp₅, as obtained by the SAXS fitting in (a), and of 0.01 wt% SiNp₁₅₈ at 100 mM NaCl obtained via DLS.

Fig. 2 (a) SANS patterns of the 1 wt% OCNF-based gels (in 100 mM NaCl). For all the samples, the continuous aqueous phase is composed of 60 vol% D₂O and 40 vol% H₂O. The green line describes the fitting of the variables R_min, R_maj and b_Kuhn from a model of non-interacting flexible cylinders with an elliptical cross-section. The black lines display the fitting for constrained values of R_min, R_maj and b_Kuhn as found from the fitting of 1 wt% OCNF. The error bars are the standard error in the data points calculated during radial averaging of the initial 2D images. (b) Residual plot from the fits in (a).

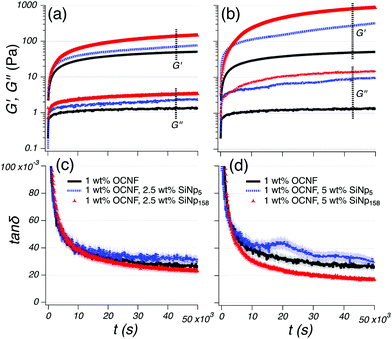
The equilibration of the rheological behaviour of the OCNF-based gels was evaluated after breakage (30 s at [small gamma, Greek, dot above] = 300 s⁻¹) (Fig. 3). After the imposed breakage, both G′ and G′′ of the 1 wt% OCNF gel followed a rapid change (up to ca. 10 × 10³ s) succeeded by a less pronounced evolution, indicating the dynamic nature of the OCNF network. Both filler-loaded gels showed higher values of G′ and G′′ compared to the pure OCNF gel, indicating an overall augmented toughness of the gels (Fig. 3a and b). Nevertheless, it must be noticed that the magnitude of G′ and G′′ does not necessarily describe the elastic/viscous-like balance of materials, but, for instance, its increase may be simply due to the increase in volume fraction upon filler addition. On the other hand, tan δ better correlates with the elastic/viscous-like contributions of materials despite changes in volume fraction (Fig. 3c and d). The tan δ of the 1 wt% OCNF gel containing 2.5 and 5 wt% SiNp₅ displayed a very similar tan δ profile to the 1 wt% OCNF gel up to 10 × 10³ s, whilst, at longer times, it showed higher values, indicating that the addition of SiNp₅ increases the viscous contribution of the gel without evident change of the elasticity. Contrarily, the gel containing 2.5 and 5 wt% of SiNp₁₅₈ had a more pronounced decrease in tan δ compared to the OCNF profile alone, indicating augmented elasticity of the gel.

Fig. 3 Time sweep of the OCNF-based gels, starting after stoppage of the imposed breakage ([small gamma, Greek, dot above] = 300 s⁻¹ for 30 s). G′ and G′′ are displayed in (a) and (b), whilst the tan δ profiles are shown in (c) and (d). The OCNF-based gels containing 2.5 wt% SiNp₅ and SiNp₁₅₈ are shown in (a) and (c), whilst the samples containing 5 wt% SiNp₅ and SiNp₁₅₈ are shown in (b) and (d). The 1 wt% OCNF gel (in black) is shown in both graphs as a reference. G′ and G′′ profiles are indicated by the label and, the legend presented in (c) and (d) applies likewise to (a) and (b), respectively. The displayed data are obtained from a set of duplicate samples; the respective uncertainties are within the size of the symbols for (a) and (b) and are shown by the shaded region in (c) and (d).

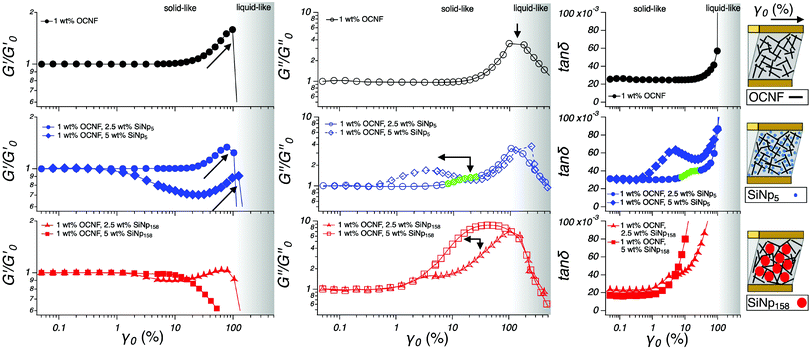
A strain sweep spacing from a small up to large deformation was employed to reveal how the filler size affects the OCNF network (Fig. 4). At small deformations, the 1 wt% OCNF gel showed a clear LVR, whilst at higher deformations, both G′ and G′′ showed a pronounced strain overshoot (signal increase followed by a decrease). Similar G′ and G′′ overshoots have been associated with the balance between breakage and regeneration of the network junctions.²⁸ Specifically, G′ local maxima could arise by the increased connectivity between the fibrils occurring upon deformation, increasing the elastic contribution of the network. However, the presence of local maxima in G′′ would further indicate a co-occurring energy dissipation process, consequent to the network breakage. This is depicted by several network models as the balance between the formation and loss of the network junctions upon large deformations.^29,30 The G′ and G′′ overshoots have been classified by Hyun et al. as a strong strain overshoot.²⁸ The tan δ profile only displayed the upturn corresponding to the onset of yielding due to the higher G′′ overshoot compared to the G′ overshoot. When either 2.5 or 5 wt% SiNp₅ was added into the OCNF gel, G′ overshoots were appreciable, suggesting that SiNp₅ has little influence on the gel mechanics. On the other hand, the G′′ profile of the SiNp₅ containing gel showed a similar overshoot as the pure OCNF gel although with an extra contribution appearing at lower values of γ₀. The G′ overshoot for the OCNF gel containing 2.5 wt% SiNp₁₅₈ was strongly smoothed out and was completely absent for the 5 wt% SiNp₁₅₈ gel. The respective G′′ overshoots became remarkable, indicating a pronounced energy dissipation process upon deformation due to the loss of network junctions. The pronounced dissipative process occurring for the SiNp₁₅₈ containing gel is well captured by tan δ, where the abrupt upturn occurs at lower values of γ₀ compared to the OCNF gel. Differently, for the SiNp₅, the overshoots are still visible in the tan δ profile due to the stronger G′′ overshoot compared to the G′ overshoot. Both fillers, SiNp₅ and SiNp₁₅₈, showed a shift of the G′′ overshoots towards lower values of γ₀ at higher filler concentrations. This can be explained by the higher number of particles which would require lower deformation to cage, allowing an earlier onset of the dissipative energy. SiNp₅ and SiNp₁₅₈ belong, respectively, to a similar and a greater (ca. by a factor 5) length scale compared to the mesh size of the OCNF network.⁹ This information coupled with the herein described rheological measurements indicates that, when strong attractive interactions between the network and the filler could be ruled out (e.g. electrostatic attraction, hydrophobic interactions), the filler-to-mesh-size ratio is of great importance to induce specific rheological responses. Specifically, it is possible to attribute the unchanged elastic fingerprint (G′ profile) of the OCNF–SiNp₅ gels to the possibility of the small filler particles to freely move within the aqueous phase of the OCNF network, only mildly affecting the breakage dynamics of the OCNF network upon oscillatory strain sweep. By contrast, the larger filler, SiNp₁₅₈, would not have available free space, leading to completely different breakage dynamics where the G′ overshoot disappears and the dissipative contribution displayed by G′′ increases substantially (Fig. 4, schematics). Moreover, in agreement with the lack of strong OCNF–SiNp interactions, the addition of SiNp₁₅₈ into the OCNF gel resulted in a transition from a strong strain overshoot (G′ and G′′ increase followed by a decrease) to a weak strain overshoot (only G′′ increase followed by a decrease) due to the weakening of the associative forces between the building blocks of the network, leading to a smoother structural breakage (yielding) upon deformation.²⁸ The dynamic moduli, G′ and G′′, are calculated based on the assumption of the sinusoidal stress response of the material.^31,32 Although G′ and G′′ provide a robust way to obtain structural information in the LVR, this assumption loses rigorous mathematical support in the NLVR, where the stress response deviates from being sinusoidal, as usually the case for large deformations.^31,32

Fig. 4 Strain sweep for the OCNF-based hydrogels. G′ and G′′ normalized by the respective modulus in the LVR (G₀′, G₀′′) as a function of strain (γ₀) are shown in the left and central panels, respectively. Right panels display the tan δ profile as a function of strain (γ₀). The darkening of the background refers to the transition from solid-like (G′ > G′′) to liquid-like (G′ < G′′) for the 1 wt% OCNF gel and is drawn to guide the eye. The green filled symbols are used to highlight the smaller overshoots. On the right are schematics of the OCNF-based hydrogels upon deformation. The displayed data are obtained from a set of duplicate samples; the respective error is within the size of the symbol.

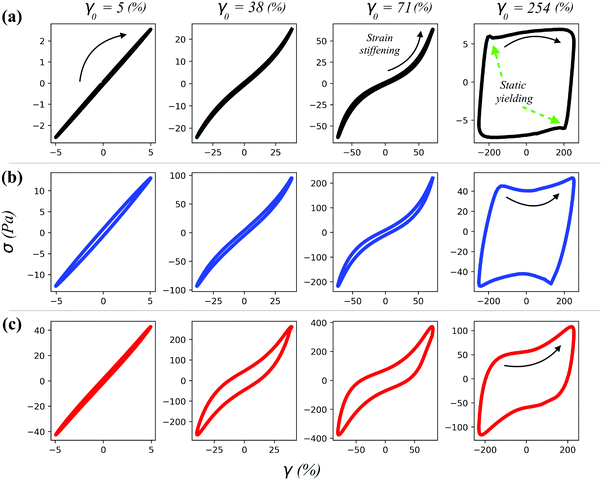
In the case of the herein described gels, the richest rheological behaviour lies in the large deformation range; hence, a waveform inspection was conducted via plotting the stress response (σ) as a function of the instantaneous intracycle strain (γ) (Fig. 5), commonly known as the elastic projection of Lissajous plot (for the viscous projection as σ vs. shear rate ([small gamma, Greek, dot above]) see Fig. S3 (ESI†), whilst for the applied sinusoidal deformation as γ vs. time and the corresponding stress response as σ vs. time see Fig. S4, ESI†).^31,32 At a low deformation (γ₀ = 5%), the Lissajous plots of the gels showed a perfectly elliptical shape which encloses a little portion of area, indicating the dominant linear response and the dominant elastic behaviour of the material, respectively (Fig. 5). By contrast, at higher deformations (γ₀ = 38 and 71%), the Lissajous plots acquired a more distorted shape, indicating the deviation of the stress signal from linearity. At the largest deformation (γ₀ = 254%), the stress response was predominantly viscous and non-linear as indicated by the squared shape of the Lissajous plot. It is important to notice that this trend reflects that displayed by G′ and G′′, indicating that the physical interpretation of G′ and G′′ being proportional to the average energies stored and dissipated per cycle, respectively, is not violated. For γ₀ values of 38 and 71%, the stress response, starting at σ = 0, followed a linear increase with the strain (elastic straining), after which a more pronounced stress increase was observed, indicating strain stiffening at greater intracycle deformations (γ₀ = 71% in Fig. 5), which is in good relation to the G′ overshoot displayed in Fig. 4. Similar strain stiffening phenomena have been reported as ubiquitous in any network composed of semiflexible filamentous proteins³³ although found difficult to mimic using commercially available polymers.³⁴ The origin of strain stiffening in fractal aggregates formed by a diffusion-limited cluster aggregation process, as expected for the OCNF network herein reported, has been proposed to arise from the intrinsic stiffness of the cluster backbone.³⁵ For γ₀ = 38 and 71%, where the solid-like behaviour dominates (G′ > G′′), the shape of the Lissajous plots of the pure OCNF and the 5 wt% SiNp₅ loaded gel showed similar features. In the presence of the 5 wt% SiNp₁₅₈, the Lissajous plots displayed a more opened structure, indicating a pronounced energy dissipation (proportional to the area enclosed in the Lissajous plot in the σ vs. γ₀ projection), and a milder intracycle strain stiffening, underpinning the reorganization of the fibrillar network occurring upon deformation. At higher deformations, γ₀ = 254%, the dominating liquid-like behaviour (G′ < G′′) was underlined by the appearance of the stress shoulder associated with the static yielding prior to flow, where the static yielding is defined as the stress that needs to be overcome to make the material flow.³¹ At γ₀ = 254%, the stress shoulder became broader for both filler loaded gels and, after the static yielding, displayed an abrupt stress decrease followed by an increase (indicated by the arrow). These similarities appeared solely in the Lissajous plots of the filler-loaded gels, suggesting that at higher deformations, after the static yield point, the flow properties are characterised by the filler. To better interpret the non-linear behaviour, we employed the framework of Rogers et al.,³¹ which decomposes the whole amplitude cycle into separate sequences of events. Although different approaches have been developed to analyse Lissajous plots, the one proposed by Rogers et al.³¹ better links rheological events to structural properties.^36,37 In particular, we characterize the linear stress response starting at σ = 0 by the local cage modulus G_cage as follows:

G_cage = dσ/dγ|_σ=0

In the framework proposed by Rogers et al.,³¹ starting at σ = 0, the Lissajous plot at large deformations could be interpreted as a sequence of straining (where G_cage is calculated), static yielding, flowing and structural reformation (labelled 1, 2, 3 and 4, respectively, in Fig. 6b). At small amplitudes, in the LVR, G_cage reduces to G′ as shown in Fig. 6c for the case of 1 wt% OCNF gel (see Fig. S5 for non-normalised values of G′, G′′ and G_cage, ESI†), whilst at higher deformations, G_cage diverges from G′ due to the structural breakage which is not fully recovered upon static yielding (2), flowing (3) and structural reformation (4) imposed by the sinusoidal cycle (Fig. 6a).³⁸ For the pure OCNF gel, a slight decrease in G_cage is displayed at higher deformations as expected by structural breakage which is not fully recovered within the sinusoidal cycle. The presence of SiNp₅ did not substantially affect the rate of change of G_cage upon deformation, confirming that the structural recoverability of the gel is dominated by the OCNF network. However, the presence of SiNp₁₅₈ in the OCNF gel strongly affected the structural recoverability of the gel as displayed by the pronounced G_cage decrease. The onset of G_cage decrease, for the SiNp₁₅₈ containing gel, occurred at lower deformations than for the OCNF gel, indicating that the network undergoes breakage at lower deformations and structural recoverability is not completed within the cycle (Fig. 6b). Although structural properties of the hydrogels, at the nanoscale, are almost unaffected by the different filler size, the mechanical properties of the gel upon breakage change substantially. This indicates that the relationship between mesh size of the network and filler is of great importance to modulate the rheological properties of the hydrogel. Specifically, the presented rheological data point to a mechanism where SiNp₁₅₈, with a larger size compared to the mesh size of the OCNF network, actively dislodges the physical junctions of the network upon large deformations, leading to a smoother yielding (without G′ overshoot). Contrarily, the smaller SiNp₅ does not dislodge the physical junctions of the network due to its ability to be accommodated within the mesh of the network upon large deformations, without disrupting the breakage dynamics of the network.

Fig. 5 Lissajous plots of the (a) 1 wt% OCNF gel, (b) 1 wt% OCNF gel containing 5 wt% SiNp₅ and (c) 1 wt% OCNF gel containing 5 wt% SiNp₁₅₈. The black arrows indicate the direction of σ as a function of the instantaneous intracycle strain, γ. The imposed strain amplitude, γ₀, is indicated at the top of each column. The displayed data are obtained from a set of duplicate samples; the respective error is within the size of the symbol.

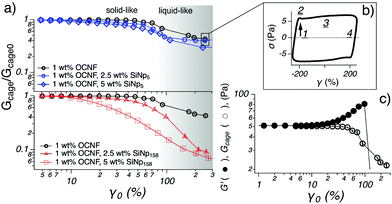Fig. 6 (a) G_cage normalised by the respective modulus in the LVR (G_cage0 = G₀′) as a function of strain (γ₀) for the OCNF-based gels. The 1 wt% OCNF gel is shown in both graphs as a reference. The darkening of the background refers to the transition from solid-like (G′ > G′′) to liquid-like (G′ < G′′) for the 1 wt% OCNF gel and is drawn to guide the eye. (b) The Lissajous plot is drawn to depict the sequence of events which soft materials undergo upon LAOS: straining (1), static yielding (2), flowing (3) and reformation (4), as suggested by Rogers et al.³¹ (c) Strain sweep for the 1 wt% OCNF gel showing non-normalised G′ and G_cage as a function of γ₀. The displayed data are obtained from a set of duplicate samples; the respective error is within the size of the symbol for γ₀ < 100 (%).

4 Conclusions

In this study, we investigated the effect of the filler size on the structural and mechanical properties of an attractive fibrillated network composed of OCNF, under conditions where strong filler–filler and filler–fibril interactions are absent. The two fillers, SiNp₅ and SiNp₁₅₈, were chosen to be of dimensions similar to and greater than the gel network mesh size, respectively. Small angle neutron scattering revealed that the OCNF network preserved its nanoscale architecture in the presence of both fillers, whilst oscillatory shear rheology captured clear rheological differences. Large amplitude oscillatory shear (LAOS) displayed the richest rheological behaviour and allowed to access the impact of the filler-to-mesh-size ratio on the yielding behaviour of the hydrogel. Our findings indicate that the presence of the smaller filler, SiNp₅, in the OCNF network maintains the mechanics of the network almost unvaried. This phenomenon is associated with the ability of SiNp₅ to fit in the mesh size of the gel network without altering the dynamics of the network upon large amplitude oscillatory shear. In contrast, the presence of the larger filler, SiNp₁₅₈, resulted in a gradual structural breakage and a low network recoverability after the breakage induced by large deformations, suggesting that SiNp₁₅₈ could actively dislodge the junctions of the network. The fundamental understanding provided in this study has implications for industrially relevant formulations, where the efficacy of additives in primary matrixes is of main importance towards tunability of specific structural and mechanical properties on demand.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

The authors thank the EPRSC for funding this project (grant number EP/N033310/1). V. Calabrese thanks the University of Bath for funding his PhD studentship. The authors thank Prof. Roger Rothon for the generous donation of SiNp₅ from Geo40™. The authors thank the Institut Laue Langevin for the provision of neutron beam time on D22 instrument provided under the Easy Access System (the data set related to this beam time is archived at DOI: 10.5291/ILL-DATA.EASY-477). Data supporting this work are freely accessible in the Bath Research Data Archive System at DOI: 10.15125/BATH-00762.

Notes and references

1. K. J. De France, T. Hoare and E. D. Cranston, Chem. Mater., 2017, 29, 4609–4631.
2. A. Isogai, T. Saito and H. Fukuzumi, Nanoscale, 2011, 3, 71–85.
3. T. Saito, Y. Nishiyama, J. L. Putaux, M. Vignon and A. Isogai, Biomacromolecules, 2006, 7, 1687–1691.
4. Y. Habibi, H. Chanzy and M. R. Vignon, Cellulose, 2006, 13, 679–687.
5. T. Saito, T. Uematsu, S. Kimura, T. Enomae and A. Isogai, Soft Matter, 2011, 7, 8804–8809.
6. J. Y. Park, C. W. Park, S. Y. Han, G. J. Kwon, N. H. Kim and S. H. Lee, Polymers, 2019, 11, 414.
7. H. Fukuzumi, R. Tanaka, T. Saito and A. Isogai, Cellulose, 2014, 21, 1553–1559.
8. F. Fneich, J. Ville, B. Seantier and T. Aubry, Carbohydr. Polym., 2019, 211, 315–321.
9. J. Schmitt, V. Calabrese, M. A. Da Silva, S. Lindhoud, V. Alfredsson, J. L. Scott and K. J. Edler, Phys. Chem. Chem. Phys., 2018, 20, 16012–16020.
10. L. Mendoza, W. Batchelor, R. F. Tabor and G. Garnier, J. Colloid Interface Sci., 2018, 509, 39–46.
11. R. J. Crawford, K. J. Edler, S. Lindhoud, J. L. Scott and G. Unali, Green Chem., 2012, 14, 300–303.
12. B. L. Tardy, S. Yokota, M. Ago, W. Xiang, T. Kondo, R. Bordes and O. J. Rojas, Curr. Opin. Colloid Interface Sci., 2017, 29, 57–67.
13. K. Chen, Y. Xu, S. Rana, O. R. Miranda, P. L. Dubin, V. M. Rotello, L. Sun and X. Guo, Biomacromolecules, 2011, 12, 2552–2561.
14. H. Oguzlu and Y. Boluk, Cellulose, 2017, 24, 131–146.
15. E. Dickinson and J. Chen, J. Dispersion Sci. Technol., 1999, 20, 197–213.
16. T. Vliet, Colloid Polym. Sci., 1988, 266, 518–524.
17. A. J. Gravelle, S. Barbut and A. G. Marangoni, RSC Adv., 2015, 5, 60723–60735.
18. T. Gillece, R. L. Mcmullen, H. Fares, L. Senak, S. Ozkan and L. Foltis, J. Cosmet. Sci., 2016, 67, 121–159.
19. V. Calabrese, J. C. Muñoz-García, J. Schmitt, M. A. da Silva, J. L. Scott, J. Angulo, Y. Z. Khimyak and K. J. Edler, J. Colloid Interface Sci., 2019, 535, 205–213.
20. T. Saito and A. Isogai, Biomacromolecules, 2004, 5, 1983–1989.
21. I. Grillo, Soft Matter Characterization, Springer, Netherlands, Dordrecht, 2008, pp. 27–30.
22. M. Adamo, A. S. Poulos, R. M. Miller, C. G. Lopez, A. Martel, L. Porcar and J. T. Cabral, Lab Chip, 2017, 17, 1559–1569.
23. J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353.
24. S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900.
25. K. M. Weigandt, D. C. Pozzo and L. Porcar, Soft Matter, 2009, 5, 4321.
26. M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Langmuir, 2005, 21, 5761–5769.
27. M. A. da Silva, V. Calabrese, J. Schmitt, D. Celebi, J. L. Scott and K. J. Edler, Soft Matter, 2018, 14, 9243–9249.
28. K. Hyun, S. H. Kim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2002, 107, 51–65.
29. K. H. Ahn and K. Osaki, J. Non-Newtonian Fluid Mech., 1994, 55, 215–227.
30. H. G. Sim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2003, 112, 237–250.
31. S. A. Rogers, B. M. Erwin, D. Vlassopoulos and M. Cloitre, J. Rheol., 2011, 55, 435–458.
32. K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753.
33. C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194.
34. R. H. Ewoldt, C. Clasen, A. E. Hosoi and G. H. McKinley, Soft Matter, 2007, 3, 634–643.
35. T. Gisler, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 1999, 82, 1064–1067.
36. J. C.-W. Lee, L. Porcar and S. A. Rogers, Polymers, 2019, 11, 1189.
37. C.-W. Lee and S. A. Rogers, Korea-Aust. Rheol. J., 2017, 29, 269–279.
38. K. van der Vaart, Y. Rahmani, R. Zargar, Z. Hu, D. Bonn and P. Schall, J. Rheol., 2013, 57, 1195–1209.

---

Footnotes

† Electronic supplementary information (ESI) available: Contrast match determination for SiNp, frequency sweeps, viscous projection of Lissajous plots, sinusoidal deformation and non-normalised data. See DOI: 10.1039/c9sm02175b

‡ Current address: Micro/Bio/Nanofluidics Unit, Okinawa Institute of Science and Technology, Onna, Okinawa 904-0495, Japan.

---