Steady-state rheology and structure of soft hybrid mixtures of liquid crystals and magnetic nanoparticles

Abstract

Using non-equilibrium molecular dynamics simulations, we study the rheology of a model hybrid mixture of liquid crystals (LCs) and dipolar soft spheres (DSS) representing magnetic nanoparticles. The bulk isotropic LC–DSS mixture is sheared with different shear rates using Lees–Edwards periodic boundary conditions. The steady-state rheological properties and the effect of the shear on the microstructure of the mixture are studied for different strengths of the dipolar coupling, λ, among the DSS. We find that at large shear rates, the mixture shows a shear-thinning behavior for all considered values of λ. At low and intermediate values of λ, a crossover from Newtonian to non-Newtonian behavior is observed as the rate of applied shear is increased. In contrast, for large values of λ, such a crossover is not observed within the range of shear rates considered. Also, the extent of the non-Newtonian regime increases as λ is increased. These features can be understood via the shear-induced changes of the microstructure. In particular, the LCs display a shear-induced isotropic-to-nematic transition at large shear rates with a shear-rate dependent degree of nematic ordering. The DSS show a shear-induced nematic ordering only for large values of λ, where the particles self-assemble into chains. Moreover, at large λ and low shear rates, our simulations indicate that the DSS form ferromagnetic domains.

---

1 Introduction

In recent years, composites of liquid crystals (LCs) and magnetic nanoparticles (MNPs) have been established as an important new class of soft “hybrid” materials. An attractive feature of these systems, which have been originally proposed by Brochard and de Gennes,¹ is that their structural and material properties can be tuned by external fields, such as magnetic, electric and surface fields. This makes them interesting not only from a fundamental perspective, e.g., in the context of spontaneous ferromagnetism² and magnetic field-induced nematic order,³ but also for technical and medical applications.^4–6 For these reasons, mixtures of LCs and MNPs have been extensively studied in experiments^2,7–13 and, more recently, also in particle-based computer simulations.^14–16 Most of these studies have been devoted to systems in thermal equilibrium.

One feature which is particularly accessible for computer simulations is the self-assembly of the MNPs into clusters and chains due to magnetic dipole–dipole interactions. Their impact is typically measured by the dimensionless coupling parameter λ, which is defined by the ratio of the magnetic dipole–dipole energy, when two MNPs are placed in contact (in an antiparallel side-by-side configuration) to each other, to the thermal energy. The unique structure-formation tendency of the MNPs, and its interplay with the LC host matrix, was investigated in detail in several computer simulation studies of Gay–Berne (GB) and dipolar soft spheres (DSS), i.e., spheres with a permanent point dipole moment.^14–17 All of these studies were concerned with equilibrium systems at relatively low densities of MNPs. When the matrix is globally isotropic, the MNPs assemble into randomly distributed chains whose length depends on λ. Interestingly, if these chains are aligned by an external magnetic field, they can induce some degree of nematic ordering in the LC matrix, a feature confirmed by experiments.³ In turn, when the LC matrix undergoes a spontaneous isotropic–nematic (I–N) phase transition, it provides an anisotropic environment already in the absence of a field. The MNP chains then align along the LC director.¹⁵ Moreover, the nematic matrix modifies the equilibrium translational dynamics of the MNPs; they display anomalous diffusion at intermediate timescales, with the extent of the anomalous regime depending again on λ.¹⁷

While the equilibrium structure of LC–MNP mixtures is important and quite intriguing, many applications of such soft hybrid systems, as well as some experiments, actually involve nonequilibrium conditions, particularly shear flow. Taking this as a motivation, we here present results from nonequilibrium Molecular Dynamics (MD) simulations for model mixtures composed of GB and DSS particles in planar Couette shear flow, characterized by the shear rate [small gamma, Greek, dot above]. We investigate both, structural and rheological properties. To unravel the impact of shear, we use the same model potentials and parameters as in earlier simulation studies.^14,15,17 Special interest is devoted to the role of the magnetic coupling parameter λ, which drives the chain formation and has already turned out to be crucial for the equilibrium structure. We thus expect that λ will also crucially affect the rheology (e.g., the shear stress) of the mixtures, which may provide a path to control the flow properties of these hybrid materials even without an external magnetic field.

As a background for the shear-induced behavior of the LC–MNP mixtures we note that already pure LCs show pronounced nonlinear behavior under shear. In particular, one observes shear thinning behavior at large [small gamma, Greek, dot above],^18,19i.e., the apparent viscosity (steady-state shear stress over shear rate) decreases with increasing [small gamma, Greek, dot above]. This shear thinning can be related to the occurrence of a shear-induced I–N transition,^20–22 that is, the LC develops a certain degree of nematic ordering at densities or temperatures where the corresponding equilibrium system ([small gamma, Greek, dot above] = 0) is still globally isotropic. Further, the director of the shear-induced nematic phase includes typically a non-zero angle with the direction of applied shear, commonly called the Leslie angle.^23–25 This term goes back to a phenomenological theory of the shear-induced dynamics of LCs provided by Leslie and Erikson,^18,26,27 which successfully addresses various aspects of the rheological properties of LCs.¹⁹ A more rigorous, statistical mechanics approach was developed by Doi et al.²⁸ and Hess²⁹ who derived continuum equations for the nematic order parameter tensor from a (rotational) Fokker–Planck equation describing the non-equilibrium anisotropic fluid. Several aspects of these continuum theories, such as the resulting anisotropic viscosities, were later confirmed by computer simulations,^30–35 where the LCs are modeled by GB ellipsoids.^36,37

Pure systems of dipolar spheres (which are often used as models of ferrofluids, i.e., suspensions of MNPs) also display shear thinning at large [small gamma, Greek, dot above]^38,39 and sufficiently large λ (in the absence of an external magnetic field). Here, the shear thinning is related to the dipolar self-assembly into chains. At low densities where the equilibrium DSS fluid forms isotropically distributed chains,^40,41 shear flow leads to a breaking of the chains. This is reflected by a reduction of the average size of the chains as function of [small gamma, Greek, dot above].^38,39 Non-equilibrium Brownian dynamics and MD simulations suggest the DSS also show anisotropy in the viscosity under shear.³² A theoretical description to explain the anisotropic viscosity of ferrofluids and the structural changes due to shear was proposed by Ilg et al.^42,43 Also experiments indicate that the shear-induced changes in the viscosity of ferrofluids is strongly correlated with their structure, see, e.g., ref. 44 and 45. In presence of an external magnetic field, the overall viscosity markedly increases due to chain formation in field direction.^46,47 While most of these findings refer to dilute systems of dipolar spheres, there are also simulation studies at high densities.⁴⁸ Here, one observes not only alignment of the chains along the shear direction, but also indications for shear-induced ferromagnetic ordering.

The above overview shows that the shear-induced behavior of LCs, on the one hand, and MNPs, on the other hand, is already quite well understood. This is not the case for hybrid systems containing both components. From a general perspective, a LC matrix in its orientationally ordered state can be viewed as a viscoelastic medium. In a recent study, Ilg et al.⁴⁹ have proposed a mesoscopic model to investigate the dynamics of (individual) MNPs in a viscoelastic medium, focusing on magnetic relaxation phenomena. The findings were found to be consistent with nanorheological experiments.⁵⁰ Still, it is clear that more particle-based investigations are needed to elucidate the behavior of magnetic hybrid systems with complex matrices under shear, especially at larger dipolar coupling strengths.

From this perspective, we consider the model of GB and DSS particles considered in the present study as an archetypal example of a soft magnetic hybrid system. Our focus here is on the steady-state behavior in the absence of a magnetic field, particularly the shear stress and its interplay with chain formation and orientational ordering of the two components. At large λ, we find strongly nonlinear (non-Newtonian) behavior, while the more weakly coupled systems show a crossover from Newtonian to non-Newtonian behavior as functions of [small gamma, Greek, dot above]. Thus, the flow properties of the mixture can indeed be tuned by varying the magnetic coupling.

We restrict our simulation study to a system which, in equilibrium, is in the isotropic state. According to continuum theory (see, e.g., ref. 51–53), the main orientational phenomenon observed upon shearing from the isotropic state is flow alignment (rather than some sort of oscillatory motion); and this is confirmed in our simulations.

The rest of the paper is organized as follows: in Section 2 we present the details of the simulation and methods. Our observations regarding the behavior of the LC–DSS mixture under externally applied shear are discussed in Section 3. Finally, in Section 4, we conclude the paper with a short summary of the present work and an outlook towards future investigations.

2 Simulation details

We consider a binary mixture of LC and DSS with a composition ratio 80 : 20 and perform non-equilibrium MD simulations using the LAMMPS package.^54,55 The LCs are modeled by ellipsoids which interact via a generalized Gay–Berne (GB) potential.^55–57 We consider uniaxial LCs with an aspect ratio of 3 : 1, and the relative energy well depths for side-to-side interaction is considered to be five times stronger than the end-to-end interaction. The DSS interact via a combination of a soft sphere potential and dipolar interactions.^58,59 The diameter of the DSS is considered to be equal to the width of the LCs. Finally, the interaction among the LC and DSS is modeled by a modified GB potential^14,15,17 where the shape and energy parameters chosen for the DSS are appropriate for spheres. We treat the long range dipolar interactions with the three dimensional Ewald sum.^40,59,60 A detailed description of interaction potentials and model parameters is available in ref. 17. The equilibrium phase diagram, self-assembly and dynamics of the LC–DSS mixture considered here are well studied in the literature.^14–17 Therefore, the specific system considered forms an excellent starting point for investigation in non-equilibrium.

The units of length and energy are set by the parameters of the GB potential, σ₀ and ε₀, respectively as defined in ref. 17. The parameters that characterize the structure and phase behavior of the mixture are the reduced temperature T* = k_BT/ε₀, the reduced number density ρ* = Nσ₀³/V (where N and V are the total number of particles and total volume, respectively), and the reduced dipole moment . The Newton's equations of motion for the force and torque acting on a particle (combined with a thermostat, see below) were integrated in the NVT ensemble using a velocity Verlet algorithm and a reduced MD time step . The simulations are performed at fixed ρ* and T* for various values of μ*. Specifically, μ* ranges from 0.0 to 3.0, i.e., the values of dipolar coupling parameter λ = μ²/k_BTσ₀³ ranges from 0.0 to 11.25.

Our simulated system consists of 3200 LC (N_e) and 800 DSS particles (N_s). We start with a mixture equilibrated at ρ* = 0.34 and T* = 0.8. At these parameters, the mixture is in the isotropic phase, however, very close to the equilibrium I–N phase transition line.¹⁷ The state point considered is marked by the red square in the equilibrium phase diagram of the LC–MNP mixture shown in Fig. 1(a) where the blue region represents the isotropic phase while the light green region shows the nematic phase.¹⁷ We obtain this tentative phase diagram by estimating the nematic order parameter at different state points.

Fig. 1 Shearing protocol for a LC–DSS mixture. (a) Tentative equilibrium phase diagram in the ρ*–T* plane obtained via MD simulations¹⁷ (the plot is adapted from the data published in our previous work¹⁷). The red square marks the quiescent state at ρ* = 0.34, T* = 0.8 and μ* = 3.0. (b) Snapshot of the mixture at the equilibrium on which a planar Couette flow is applied in the x–z plane along the x-direction using Lees–Edwards periodic boundary conditions.

We shear the mixture with constant shear rate using Lees–Edwards periodic boundary conditions (see the schematic diagram in Fig. 1(b) where the imposed velocity profile is shown by blue arrows). Specifically, we implement a planar Couette flow in the x–z plane, with x being the direction of flow, and z and y being the gradient and vorticity directions respectively. The range of dimensionless shear rates [small gamma, Greek, dot above]* = (σ²m/ε)^1/2[small gamma, Greek, dot above] is given by 10⁻³–10⁻¹. To maintain the temperature we employ a Langevin thermostat acting in the gradient and vorticity directions.⁶¹

We note that accessing lower shear rates is computationally expensive due to the long-range nature of the interactions among the DSS which complicates the force calculations and as a result a drastic slowdown in the computation occurs. Furthermore, the system size considered in this work is sufficiently large, and finite-size effects are not very significant, see Appendix A.

3 Results

3.1 Stress–strain response

For the understanding of the rheology, the main quantity of interest is the shear stress, σ_xz, which we calculate via the Irving–Kirkwood expression,^22,62In eqn (1), V is the total volume, v_i,(x,z) are the x and z components of the velocity of the ith particle and r_ij,x, F_ij,z are the x-component of the distance vector and z-component of the force between particles i and j, respectively. The angular bracket in eqn (1) represents an average taken over 50 independently prepared samples.

We start by investigating the time evolution of σ_xz as a function of strain, [small gamma, Greek, dot above]*t*, at fixed shear rate. In Fig. 2(a)–(c), we present results for mixtures sheared with [small gamma, Greek, dot above]* = 10⁻¹, 3 × 10⁻² and 10⁻² for λ = 0.0, 5.0 and 11.25, respectively.

Fig. 2 Evolution of σ_xz as a function of strain [small gamma, Greek, dot above]*t* for the LC–DSS mixture at ρ* = 0.34, T* = 0.8 sheared with [small gamma, Greek, dot above]* = 10⁻¹, 3 × 10⁻², 10⁻² for (a) λ = 0.0, (b) λ = 5.0 and (c) λ = 11.25. Here, the shear rate is constant, therefore, the evolution of σ_xz with strain [small gamma, Greek, dot above]*t* is equivalent to evolution with time. Gray curves in all plots represent data averaged over 100 samples. To further improve the statistics, a running average over 10 data points based on the gray curves has been performed.

At the largest shear rate considered ([small gamma, Greek, dot above]* = 10⁻¹), the stress first increases with strain, reaches a maximum and finally settles to a non-zero value. This “overshoot” behavior, which appears for all values of λ, signals a non-linear rheological behavior at high shear rates, it also appears in glassy systems and supercooled liquids.^63,64 As the shear rate is lowered, the height of the stress overshoot decreases and finally disappears for the mixtures with λ = 0.0 and λ = 5.0 (see Fig. 2(a) and (b)). However, in the mixture with λ = 11.25 the stress overshoot persists even at the lowest shear rate considered. These observations already suggest that the degree of dipolar coupling plays a crucial role for the rheology of the mixture. We will come back to this point in the subsequent sections where we focus on the steady-state behavior. The transient behavior, which appears interesting as well, will be discussed in more detail elsewhere.⁶⁵

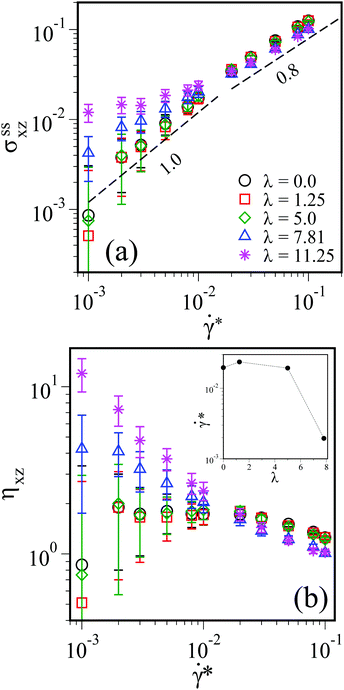
3.2 Steady state flow curve

To proceed, we investigate the behavior of the steady-state stress, σ^ss_xz = lim_t→∞σ_xz, as a function of the shear rate. Fig. 3(a) shows the resulting flow curve of the LC–DSS mixture for various values of λ. For all values of λ except λ = 11.25, we observe a crossover from “Newtonian” behavior, where σ^ss_xz is linearly proportional to [small gamma, Greek, dot above]*, to “non-Newtonian” behavior, where σ^ss_xz varies in a power-law manner as a function of [small gamma, Greek, dot above]*. This transition occurs at a “critical” shear rate, which is approximately given by [small gamma, Greek, dot above]_c* = 0.02.

Fig. 3 (a) The flow-curve for the LC–DSS mixture at ρ* = 0.34, T* = 0.8 and λ = 0.0, 1.25, 5.0, 7.81, 11.25, vertical lines represent error bars. Dashed lines represent slopes 1.0 and 0.8. (b) Average viscosities η_xz, obtained from σ^ss_xz, as a function of [small gamma, Greek, dot above]* for the same λ values as in (a). The inset shows the variation of the critical shear rate [small gamma, Greek, dot above]_c* at which a crossover from Newtonian to non-Newtonian behavior is observed, as function of λ.

At shear rates [small gamma, Greek, dot above]* ≳ [small gamma, Greek, dot above]_c* the stress varies as σ^ss_xz ∝ [small gamma, Greek, dot above]*ⁿ for all values of λ, where the power-law exponent is n ≈ 0.8. This exponent, also called flow index, characterizes the non-Newtonian behavior of the LC–DSS mixture. Specifically, the fact that for [small gamma, Greek, dot above]* ≳ [small gamma, Greek, dot above]_c*, n is smaller than one, indicates a shear thinning. This behavior is also reflected by the average viscosity, defined as η = σ^ss_xz/[small gamma, Greek, dot above]*, which is plotted in Fig. 3(b) as a function of [small gamma, Greek, dot above]*. For a wide range of complex fluids such as microgels, foams, and emulsions, the exponent n is considered to be a “material parameter” that weakly depends on the temperature and density.⁶⁶ Here, we did not study this dependency systematically.

At large λ(= 7.8125, 11.25) both the flow curve and the viscosity as function of [small gamma, Greek, dot above]* reveal two distinct power-law regimes. This feature has also been observed in computer simulations of pure ferrofluids at high dipolar coupling strength.³⁹ Specifically, the steady-state stress grows slowly at low shear rates, before it crosses over to the power-law regime with slope ∼0.8 at high shear rates. This behavior is more evident for λ = 11.25, where the non-Newtonian regime spans the whole range of shear rates considered in the simulations.

In contrast, at small values of λ and low shear rates the stress grows linearly in [small gamma, Greek, dot above]* and the viscosity remains constant, which is characteristic of Newtonian behavior. Shear-thinning behavior occurs only for [small gamma, Greek, dot above]* > [small gamma, Greek, dot above]_c*. We estimated critical shear rates [small gamma, Greek, dot above]_c* for various λ, see the inset of Fig. 3(b). The data reveal a sudden jump in [small gamma, Greek, dot above]_c* when λ increases beyond 5.0. Such a variation of [small gamma, Greek, dot above]_c* with increasing λ has already been observed for pure dipolar fluids, where it has been attributed to the chain forming tendency of the DSS at large λ.³⁹ Similar behavior occurs in the present LC–DSS mixture, as will see below.

3.3 Microstructure under shear

The nonlinear features observed in the flow curves discussed in Section 3.2 already suggest profound structural changes when the LC–DSS mixture is exposed to shear. In the present section we focus, in particular, on the chain formation of magnetic particles. To this end we consider mixtures at λ = 5.0 and λ = 11.25, where the non-Newtonian behavior is particularly pronounced. Before we move ahead with the analysis, it should be noted that here in our LC–DSS mixture, the number density of the DSS is rather small (ρ_DSS* = 0.068). In pure DSS fluids, at such low densities, the DSS form chains with head-to-tail ordering of neighboring particles and the size of the chains depending on λ. These DSS chains are isotropically distributed, that is, there is no long-range orientational order.^41,59,60 In our previous study of a LC–DSS mixture, we have shown that in the isotropic phase (such as one considered here at ρ* = 0.34), the DSS form isotropically distributed chains of significant length if λ ≥ 6.0.¹⁷ Therefore, we expect that in the equilibrium, sizes of the DSS chains should be rather small for λ = 5.0 and relatively larger for λ = 11.25.

We define weak and strong shear rate regimes using the flow curve of the LC–DSS mixture. Shear rates in the Newtonian regime, [small gamma, Greek, dot above]* < [small gamma, Greek, dot above]_c*, are considered as weak shear rates and [small gamma, Greek, dot above]* > [small gamma, Greek, dot above]_c* corresponds to strong shear. To illustrate the effect of shear on the microstructure, we choose two shear rates, [small gamma, Greek, dot above]* = 10⁻¹ and [small gamma, Greek, dot above]* = 5 × 10⁻³, for our analysis. For λ = 5.0, the shear rate [small gamma, Greek, dot above] = 10⁻¹ falls into the non-Newtonian regime, while [small gamma, Greek, dot above]* = 5 × 10⁻³ belongs to the Newtonian regime. For λ = 11.25, both the shear rates fall into the non-Newtonian regime, see Fig. 3.

In Fig. 4(a), we show a snapshot of the LC–DSS mixture for λ = 5.0 in the quiescent state at [small gamma, Greek, dot above]*t* = 0. It is seen that the mixture consists of short DSS chains (shown in Fig. 4(d)) and randomly oriented LCs. At the low shear rate, [small gamma, Greek, dot above]* = 5 × 10⁻³, LCs do not show the shear-induced alignment, see Fig. 4(b). On the contrary, at the high shear rate, [small gamma, Greek, dot above]* = 10⁻¹, the LCs display a shear-induced alignment in the steady-state, see Fig. 4(c). The DSS, plotted in Fig. 4(e) and (f), show no alignment in the direction of the shear at any of the shear rates considered.

Fig. 4 Snapshots of the LC–DSS mixture for λ = 5.0, ρ* = 0.34 and T* = 0.8 in equilibrium and under shear. (a) Initial state ([small gamma, Greek, dot above]*t* = 0.0), which is same for all shear rates considered. (b and c) Illustrate the structure in the steady state ([small gamma, Greek, dot above]*t* = 15.0) for [small gamma, Greek, dot above]* = 5 × 10⁻³ and 10⁻¹, respectively. The snapshots (d), (e) and (f) show the DSS alone at the parameters corresponding to (a), (b), and (c) respectively. All the snapshots are prepared using software OVITO.⁶⁷

In contrast to λ = 5.0, at large λ (= 11.25) the equilibrium configuration is characterized by large DSS chains (see Fig. 5(a) and (d)). In the presence of shear, these DSS chains align with the shear direction at both shear rates considered (see Fig. 5(e) and (f)). The response of the LCs depends on the shear rate: while the LC system at [small gamma, Greek, dot above]* = 5 × 10⁻³ (Fig. 5(b)) displays weak alignment, the ordering at [small gamma, Greek, dot above]* = 10⁻¹ is more significant. We will quantify the degree of shear-induced nematic ordering in Section 3.4. Here we already note that the observed shear-induced ordering of the two species is consistent with previous simulation studies on pure LCs^20,22,31 and pure dipolar fluids.^39,48 The difference in the present case is that the two components strongly influence each other.

Fig. 5 Snapshots of the LC–DSS mixture for λ = 11.25, ρ* = 0.34 and T* = 0.8 in equilibrium and under shear. (a) Initial state ([small gamma, Greek, dot above]*t* = 0.0), which is same for all shear rates considered. (b and c) Illustrate the structure in the steady state ([small gamma, Greek, dot above]*t* = 15.0) for [small gamma, Greek, dot above]* = 10⁻¹ and 5 × 10⁻³, respectively. The snapshots (d), (e) and (f) show the DSS alone at the parameters corresponding to (a), (b), and (c) respectively.

3.4 Nematic order in the steady state

Along with the chain formation, a further interesting issue is the degree of shear-induced nematic ordering in both species of the LC–DSS mixture. To this end, we calculate the nematic order parameters S_e,svia the largest eigenvalues of the ordering tensors Q_e,s for the LCs (e) and the DSS (s) respectively. The instantaneous components of these tensors are given aswhere α, β = x, y, z. Further, for the ith particle, uⁱ_α is one of the components of the orientation unit vector û in the case of LCs, while it is a component of the unit dipole vector [small mu, Greek, circumflex] in the case of DSS. The largest eigenvalue ξ_e,s of the tensors Q_e,s characterizes the extent of the nematic ordering in the two components. The nematic order parameters S_e,s are then obtained by taking the average of ξ_e,s for many samples. Specifically, we have used 100 independent samples for calculation of order parameters and other quantities. Furthermore, the eigenvector corresponding to ξ_e,s defines the nematic directors n̂_e,s for the LCs and DSS respectively. The steady state values of S_e,s are denoted by S^ss_e,s.

Furthermore, at large shear rates where nematic order is present, we analyze the orientation of n̂_e,s with respect to the shear direction (i.e. with the x-axis in our case) by calculating the angle,⁴⁸

Θ_e,s = 〈atan(|n̂_z,(e,s)/n̂_x,(e,s)|)〉, (3)

where n̂_z,(e,s) and n̂_x,(e,s) are the z and x components of the respective nematic directors. This angle defines the orientation of the projection of n̂_e,s in the shear plane (x–z plane) onto the shear direction (x-axis).

We note that in all cases considered, our simulations reveal “flow-aligning” behavior rather than an oscillatory (or otherwise time-dependent) motion of the directors. We believe that this is due to the fact that the equilibrium system is in its isotropic phase, see Fig. 1. The absence of oscillatory motion is consistent with the result from continuum theories⁵² according to which oscillatory motion generally only occurs when shearing from an orientationally ordered state.

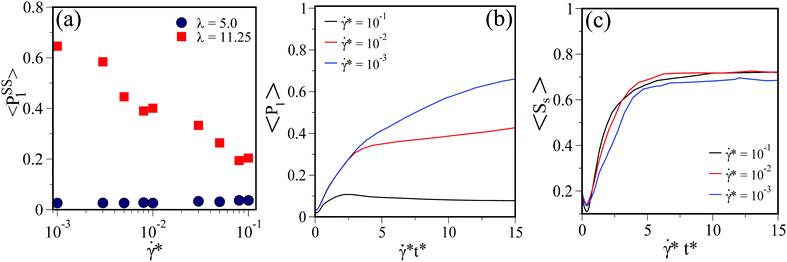
In Fig. 6, we plot the steady-state nematic order parameters S^ss for the LC (S_e black circles) and the DSS (S_s red squares) for λ = 5.0 at different shear rates. We recall that at λ = 5.0, the flow curve reveals both, a Newtonian regime ([small gamma, Greek, dot above]* < [small gamma, Greek, dot above]_c*) and a non-Newtonian regime at high shear rates (see Fig. 3). As seen from Fig. 6, the DSS do not develop any pronounced nematic ordering throughout the range of the shear rates considered. This is different for the LCs. In the Newtonian regime, the LCs do not show shear-induced ordering while at high shear rates, significant (para-)nematic ordering is observed. To this end we note that the value of S_e related to the equilibrium I–N transition is 0.43 according to the Marier–Saupe theory.⁶⁸ This value of S_e (= 0.43) is represented by the horizontal light-blue dashed line in Fig. 6. One sees that this (equilibrium) value is approached and finally exceeded when the shear rate becomes larger than [small gamma, Greek, dot above]_c* (indicated by the grey dashed line). More specifically, from the intersection of the function S^ss_e([small gamma, Greek, dot above]*) and the horizontal blue line we estimate the shear rate of the shear-induced I–N transition as [small gamma, Greek, dot above]_N* ≈ 0.08. We conclude that the non-Newtonian regime of the flow curve at λ = 5.0 is accompanied by orientational ordering of the LCs, but not the DSS.

Fig. 6 Variation of the nematic order parameter in the steady state for λ = 5.0 for the LC (S_e) and the DSS (S_s) as a function of [small gamma, Greek, dot above]*. The horizontal blue dashed line represents the critical value of the nematic order parameter at which I–N transition is observed and the vertical grey dashed line shows the [small gamma, Greek, dot above]_c* for λ = 5.0. The inset shows the birefrigence angle Θ_e (in degrees) for the LCs at λ = 5.0. The three points in the inset correspond to [small gamma, Greek, dot above]* = 10⁻¹, 8 × 10⁻² and 5 × 10⁻².

The appearance of an isotropic–(para)nematic transition at high shear rates is consistent with previous simulation studies of GB ellipsoids,⁶⁹ attractive colloidal rods^20,21 and soft repulsive long ellipsoids.²²

The inset in Fig. 6 shows the angle Θ_e between the director of the LCs and the x-axis (see eqn (3)). Note that, since significant nematic ordering is present only at large shear rates, the relevant points in the inset are those corresponding to [small gamma, Greek, dot above]* = 8 × 10⁻² and 10⁻¹. From these, we observe that the nematic director for LCs does not entirely align with the shear direction, but makes a small angle of approximately 24°. This observation is consistent with previous studies on pure Gay–Berne LCs under shear.^69,70

The situation at large λ, shown in Fig. 7(a), is different. Here, the LC matrix exhibits a significant degree of ordering already at the lowest shear rate, [small gamma, Greek, dot above]* = 10⁻³. Moreover, the nematic order parameter of the DSS is even larger. We understand these properties, which are in marked contrast to those observed at λ = 5.0, as a consequence of the pronounced chain formation of the DSS at λ = 11.25, see Fig. 5(e) and (f).

Fig. 7 (a) Variation of the nematic order parameters for the LC (S_e) and the DSS (S_s) in the steady state for λ = 11.25 as a function of [small gamma, Greek, dot above]*. The horizontal blue dashed line represents the value of the nematic order parameter corresponding to the I–N transition. The vertical grey dashed line indicates [small gamma, Greek, dot above]_c* for λ = 11.25. (b) Birefringence angle Θ (in degrees) as a function of [small gamma, Greek, dot above]* for the LC and the DSS at λ = 11.25. The inset shows the biaxiality parameter, B, (see eqn (4)) as a function of [small gamma, Greek, dot above]*.

Due to the strong correlation within the chains, these form rather stiff and long objects which align in the shear flow. In fact, they align essentially along the shear (x-)direction, as seen from the small values of the angle Θ_s plotted in Fig. 7(b). This is consistent with a result from Leslie theory for elongated particles⁷¹ which states that the angle between the particle and the shear direction decreases with increasing length. The alignment of the chains, in turn, enhances the alignment of the non-magnetic LC particles, leading to relatively large values of S^ss_e.

Upon increase of the shear rate, the nematic order parameter of the DSS remains essentially constant in the range of the shear rates considered. For pure dipolar fluids in the shear flow, it has been observed that the nematic order parameter decreases at high shear rates due to breaking of the chains.^39,43,48 In the present study, we do not observe such a behavior as the maximum shear rate is restricted to [small gamma, Greek, dot above]* = 0.1.

Finally, we consider the birefringence angles Θ_s, defined in eqn (3) and plotted in Fig. 7(b). For all considered shear rates the director of the DSS makes an angle of about 3° from the x-axis, indicating that the DSS chains almost completely align along the shear direction in the steady state.

In contrast, the nematic director of the LCs, makes an angle Θ_e of about 16° at large shear rates with the shear direction. However, Θ_e decreases as the shear rate is lowered. At the same time, the degree of nematic ordering decreases as well, see Fig. 7(a). We suspect that at these low shear rates, the LCs locally align along the DSS chains, that is, along the x-direction, which may lead to the observed reduction in Θ_e. Furthermore, at large shear rates the difference in the angles Θ_e and Θ_s is approximately equal to 12° which indicates that the nematic directors of the two components do not completely align parallel to each other. In order to understand this better, we calculate the biaxiality order parameter which measures the degree of parallel alignment of the two nematic directors, n̂_e and n̂_s, with respect to each other. The biaxiality order parameter, B, is defined as:

where n̂_e,s are the nematic directors for the LCs and DSS respectively. The angular bracket denotes the averaging taken over 50 samples. The value of B equal to 1 corresponds to the parallel alignment of n̂_e and n̂_s and B = −0.5 corresponds to the perpendicular alignment of the two directors. The inset in Fig. 7(b) shows the variation of B as a function of [small gamma, Greek, dot above]*. We observe that at large shear rates, n̂_e and n̂_s slightly deviate from the parallel alignment while at low shear rates the degree of parallel alignment increases which is consistent with the decrease in the difference between the angles Θ_e and Θ_s. We note here that at low shear rates the nematic ordering in the LCs is slightly higher as compared to the nematic ordering at low λ, however, it is not above the critical value. Therefore, we expect that the enhanced alignment of the two nematic directors at low shear rates is the result of the local ordering of LCs near the DSS chains.

3.5 Ferromagnetic ordering

Given the pronounced nematic ordering of the dipolar chains at large values of λ (see Fig. 7a), it is an obvious question whether this nematic ordering is accompanied by ferromagnetic ordering, i.e., parallel orientation of the dipoles in the chains. To this end we consider the polar order parameterwhere [small mu, Greek, circumflex]_i is the unit dipole vector of the ith-particle, and n̂_s is the nematic director of the DSS (the angular brackets denote the average over different samples). Perfect ferromagnetic order corresponds to 〈P₁〉 = 1.

As a background information we note that λ depends upon the distance of contact of two dipoles.⁴⁴ For dipolar particle with soft sphere steric interactions, the definition of contact distance is slightly ambiguous. However, one can safely use Barker–Henderson definition of the hard-sphere diameter⁷² for the present case. Such a choice will not overestimate the value of λ as the contact distance is not much different from the hard-sphere diameter (see the inset in Fig. 9(b), the first peak of the pair correlation function (in equilibrium) appears around 0.98σ). Furthermore, pure DSS fluids do indeed display ferromagnetic ordering (in three dimensions) at large dipolar coupling strengths (λ ≳ 6.67) and large densities (ρσ³ ≳ 0.7).^58,59 Within a mean-field picture,^73–75 the ferromagnetic ordering can be explained via the non-zero average field generated by the neighbors around a dipolar sphere, provided that the boundary conditions are appropriate (i.e., conducting). The relevance of the boundary conditions is a consequence of the long-range character of the dipolar interactions. The mean field is proportional to the density⁷³ and dipolar coupling strength, which allows for ferromagnetic ordering in dense systems and sufficiently low temperatures. From a structural point of view, ferromagnetic ordering is related to a specific configuration of neighboring dipolar chains, where particles are shifted by half a particle diameter.^76,77 In this situation, the interaction between two chains is indeed attractive.⁷⁶

In the present mixture, the number density of the dipolar component is much smaller than in the cases mentioned above, ρσ³ ≈ 0.068. Thus, at least in equilibrium, one would not expect ferromagnetic ordering even at the largest λ considered, and this is confirmed by simulations.¹⁵ The question then is whether such an ordering can be induced by the shear flow. Indeed, shear-induced ferromagnetic ordering has been observed for pure, dense DSS fluids at coupling strength λ ∼ 4.63, where the corresponding unsheared system is still isotropic.^48,78 The density considered in ref. 48 and 78, however, was ρ* = 0.8, that is, far beyond that of the present system.

Numerical results for 〈P₁〉 in the steady state are plotted in Fig. 8(a) as function of the shear rate. For λ = 5.0, the values of the order parameter are negligible throughout the regime considered. However, for λ = 11.25 and the lowest shear rate, [small gamma, Greek, dot above]* = 10⁻³, we observe a quite large value of 〈P₁〉 ≲ 0.7, reflecting a significant degree of ferromagnetic order. This large value decreases upon increase of [small gamma, Greek, dot above]*.

Fig. 8 (a) Ferromagnetic order parameter 〈P₁〉 in the steady state as a function of [small gamma, Greek, dot above]* for λ = 5.0 and 11.25. (b) The evolution of 〈P₁〉 with strain for [small gamma, Greek, dot above]* = 10⁻¹, 10⁻² and 10⁻³ for λ = 11.25. (c) The evolution of the nematic order parameter for the DSS, S_s, as a function of strain, [small gamma, Greek, dot above]*t*, for λ = 11.25 at the same shear rates as in (b).

Given the low density, the large order parameter at [small gamma, Greek, dot above]* = 10⁻³ is indeed quite surprising. To check that the ordering is indeed induced by shear we have also investigated 〈P₁〉 as function of strain [small gamma, Greek, dot above]*t*, see Fig. 8(b). The data clearly reveal the absence of ferromagnetic order at zero shear. The curve for [small gamma, Greek, dot above]* = 10⁻³ also indicates that the ferromagnetic order is gradually “built up” when the strain is increased. Further, the values at the largest strain ([small gamma, Greek, dot above]*t* = 15) reflect what is already seen in Fig. 8(a), namely, that the degree of ferromagnetic order in the steady state decreases with the applied shear rate. Similar to the ferromagnetic ordering, the nematic order in the DSS also increases gradually as the strain is increased, see Fig. 8(c). However, the time evolution of 〈S_s〉 remains almost independent of the shear rate, which is in contrast to the evolution of the ferromagnetic order.

There remains the question as to why the system at low shear rate orders at all, despite of the low density. From a mean-field perspective, one can argue as follows: due to the nematic ordering of the LC host matrix (which, in turn, aligns the dipolar chains), the possible directions of ferromagnetic order of the dipolar component are strongly restricted as compared to the three-dimensional, pure dipolar fluid. Indeed, in the pure case, the director can assume any direction on the unit sphere, whereas in presence of the nematic matrix, the direction of magnetization is essentially restricted to two directions, along the shear and opposite to shear. This corresponds to a change from “XYZ symmetry” to “Ising symmetry”, i.e., a profound reduction of degeneracy. Mean-field theory for a pure dipolar system would then predict a strong reduction of the critical density beyond which ferromagnetic order can occur. Indeed, this critical density is given by ρ_c* = 9/(4πλ) for conventional, three-dimensional dipoles, while it is only ρ_c* = 3/(4πλ) for an “Ising” dipolar system which can order only “up” or “down”.^74,75 Clearly, this line of argumentation assumes an effective equilibrium picture of the system at low shear rates. Still, it describes one important mechanism which could promote ordering at lower densities (even though the theory is known to be strongly incorrect in terms of quantitative predictions).

A further piece of understanding emerges when we consider the structure around a dipolar chain and its dependence on [small gamma, Greek, dot above]*. To this end we have plotted in Fig. 9 various pair correlation functions involving the DSS alone.

Fig. 9 Pair correlation functions between the DSS at λ = 11.25. (a) g(r) as a function of distance in the x-direction for the shear rate [small gamma, Greek, dot above]* = 10⁻³. The inset shows the correlations in y and z-directions for the same shear rate as in the main figure. (b), (c) and (d) correlation function for three different shear rates [small gamma, Greek, dot above]* = 10⁻³, 10⁻² and 10⁻¹ in the x, y and z-directions respectively. The inset in (b) shows the radial distribution function g(r) as a function of r in equilibrium.

Specifically, we have calculated separately the DSS pair correlation functions in directions of shear (x-direction), the shear gradient (z-direction), and vorticity (y-direction) (for a definition of these correlations, see ref. 77). Fig. 9(a) shows all three correlation function at the lowest shear rate, where the order parameter 〈P₁〉 is largest. We observe pronounced, nearly solid-like correlations in shear direction, which corresponds to the direction of the chains. These correlations are, in fact, much stronger than those in the equilibrium system (see inset of Fig. 9(b)), indicating that the shear flow, via the ordering of the LC host matrix, strongly promotes the chain formation. The correlations in the other two directions (see inset of Fig. 9(a)) are much less pronounced (and quite similar). Interestingly, the second peak of these lateral correlation function is much higher than the first one. This strongly differs from the equilibrium situation, where the first peak exceeds by far the other ones. This feature reflects that shear strongly promotes correlations between neighboring chains; in fact, they appear to be more close than in equilibrium. We recall that in the ferromagnetic phase of dense, pure DSS systems, chains are close and are shifted by half a particle diameter, because only then their interaction is attractive.⁷⁶ Therefore, a small chain–chain distance is an important ingredient into the development of ferromagnetic order.

Finally, Fig. 9(b)–(d) illustrate the dependency of the correlation functions on the shear. It is seen that the height of the first peak in lateral directions somewhat increases with increasing shear rate, indicating that shear enhances the correlation. This is somehow surprising in view of the fact that 〈P₂〉 decreases with [small gamma, Greek, dot above]* (see Fig. 8(a)). One possible explanation could be a breakage of chains which is not directly reflected by the correlation functions plotted in Fig. 9. This point remains to be considered in a future study.

4 Summary and outlook

Based on non-equilibrium MD simulations, we have shown that the strength of the dipolar coupling plays a crucial role for the rheological properties of LC–DSS mixtures. In particular, it changes the “critical” shear rate at which the flow curve transforms from Newtonian to non-Newtonian behavior in the steady state.

Further, we find that shear modifies the spatial structure within the mixture and induces an alignment in both components. For low values of λ, the DSS chains are relatively short and do not align with the shear direction. In contrast, for large values of λ, we observe long DSS chains aligning with the shear direction, yielding a nematic ordering of the chains. The degree of this shear-induced nematic ordering is almost independent of the rate of applied shear, and it is significantly higher than the nematic ordering of the LC matrix.

The LC matrix shows a shear-induced nematic transition at high shear rates for all values of λ. This transition occurs at a shear rate which shifts to lower values as λ increases. In particular, at the largest λ considered, nematic ordering of the LC matrix already appears at very low shear rates, although the equilibrium system is isotropic. This is due to the fact that the long DSS chains formed at large values of λ, align with the shear direction already at low shear rates and thereby induce a nematic ordering in the LCs. Similar behavior is also observed in isotropic (unsheared) LC–DSS mixtures in the presence of an external magnetic field, where the alignment of the DSS chains in the field direction leads to a nematic ordering in the LCs.³ Here, the ordering effect of a magnetic field is replaced by shear flow.

Finally, we have found indications that, at very large λ, the sheared mixture displays not only nematic ordering, but also ferromagnetic order of the DSS chains. This is a striking observation in view of the small density of the DSS, which we attempted to explain by mean-field arguments. It seems clear, however, that further investigations are necessary to unravel the underlying structural mechanism.

In conclusion, our results on the steady-state rheological properties of the LC–DSS mixture provide interesting suggestions to design soft hybrid materials with tunable flow properties. To further understand the full rheology of these systems, investigations of the time evolution (that is, the transient structure) of the microstructure under shear and on non-equilibrium flow patterns are in order. Walk in these directions is on the way. A further interesting research direction concerns the rheology of LC–DSS mixtures with non-spherical particles. First results have been reported in ref. 79.

Conflicts of interest

There are no conflicts to declare.

Appendix A: Finite-size effects

To understand the effect of finite sizes, we have performed few simulations with a smaller system size, N = 1000 for λ = 11.25 and investigated the flow curve, nematic order parameters and polar order parameter, see Fig. 10. The open symbols in Fig. 10 correspond to the system size N = 1000 and the solid symbols correspond to the system size N = 4000. The flow curves for the two system sizes, shown in Fig. 10(a), almost fall on the top of each other. Similarly, the nematic order parameters S^ss_e,s for the LCs and DSS, shown in Fig. 10(b), for the two system sizes also do not show much difference. However, the polar order parameter for the two system sizes (shown in Fig. 10(c)) exhibits a slight mismatch at high shear rates. These comparisons indicate that the finite-size effects are not very significant in our case.

Fig. 10 Comparison of (a) the flow curves (b) the nematic order parameters in the steady-state for LCs, S_e, and the DSS, S_s, and (c) the polar order parameter, 〈P^ss₁〉, in the steady state for the LC–DSS mixture with system sizes N = 1000 and N = 4000. In all plots, open symbols represent the system size N = 1000 and solid symbols denote results for N = 4000.

Acknowledgements

We gratefully acknowledge funding support from the Deutsche Forschungsgemainschaft (DFG) via the priority program SPP 1681.

Notes and references

1. P. de Gennes and F. Brochard, J. Phys., 1970, 31, 691.
2. A. Mertelj, D. Lisjak, M. Drofenik and M. Čopič, Nature, 2013, 504, 237.
3. K. May, A. Eremin, R. Stannarius, S. D. Peroukidis, S. H. L. Klapp and S. Klein, Langmuir, 2016, 32, 5085.
4. C. P. Lapointe, T. G. Mason and I. I. Smalyukh, Science, 2009, 326, 1083.
5. C. Scherer and A. M. F. Neto, Braz. J. Phys., 2015, 35, 718.
6. Q. Liu, P. J. Ackerman, T. C. Lubensky and I. I. Smalyukh, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10479.
7. A. M. F. Neto and M. M. F. Saba, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 3483.
8. S.-H. Chen and N. M. Amer, Phys. Rev. Lett., 1983, 51, 2298.
9. P. Kopčanský, N. Tomašovičová, M. Koneracká, V. Závišová, M. Timko, A. Džarová, A. Šprincová, N. Éber, K. Fodor-Csorba, T. Tóth-Katona, A. Vajda and J. Jadzyn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011702.
10. V. Berejnov, J.-C. Bacri, V. Cabuil, R. Perzynski and Y. Raikher, Europhys. Lett., 1998, 41, 507.
11. N. Podoliak, O. Buchnev, O. Buluy, G. D’Alessandro, M. Kaczmarek, Y. Reznikov and T. Sluckin, Soft Matter, 2011, 7, 4742.
12. O. Buluy, S. Nepijko, V. Reshetnyak, E. Ouskova, V. Zadorozhnii, A. Leonhardt, M. Ritschel, G. Schönhense and Y. Reznikov, Soft Matter, 2011, 7, 644.
13. S. Kredentser, O. Buluy, P. Davidson, I. Dozov, S. Malynych, V. Reshetnyak, K. Slyusarenko and Y. Reznikov, Soft Matter, 2013, 9, 5061.
14. S. D. Peroukidis, K. Lichtner and S. H. L. Klapp, Soft Matter, 2015, 11, 5999.
15. S. D. Peroukidis and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 010501(R).
16. S. D. Peroukidis and S. H. L. Klapp, Soft Matter, 2016, 12, 6841.
17. G. P. Shrivastav and S. H. L. Klapp, Soft Matter, 2019, 15, 973.
18. R. G. Larson, Sturcture and rheology of complex fluids, Oxford University Press, Oxford, UK, 1999.
19. K. F. Wissbrun, J. Rheol., 1981, 25, 619.
20. M. Ripoll, P. Holmqvist, R. G. Winkler, G. Gompper, J. K. G. Dhont and M. P. Lettinga, Phys. Rev. Lett., 2008, 101, 168302.
21. M. Ripoll, R. G. Winkler, K. Mussawisade and G. Gompper, J. Phys.: Condens. Matter, 2008, 20, 404209.
22. G. Germano and F. Schmid, J. Chem. Phys., 2005, 123, 214703.
23. F. M. Leslie, Arch. Ration. Mech. Anal., 1968, 28, 265.
24. C. Pujolle-Robic and L. Noirez, Nature, 2001, 409, 167.
25. G. Rienäcker and S. Hess, Phys. A, 1999, 267, 294.
26. F. M. Leslie, Q. J. Mech. Appl. Math., 1966, 19, 357.
27. C. J. Chan and E. M. Terentjev, J. Phys. A: Math. Theor., 2007, 40, R103.
28. N. Kuzuu and M. Doi, J. Phys. Soc. Jpn., 1983, 52, 3486.
29. S. Hess, Z. Naturforsch., A: Phys. Sci., 1976, 31, 1034.
30. S. Sarman, J. Chem. Phys., 1995, 103, 10378.
31. S. Sarman, J. Chem. Phys., 1998, 108, 7909.
32. S. Hess, J. F. Schwarzl and D. Baalss, J. Phys.: Condens. Matter, 1990, 2, SA279.
33. S. Sarman, P. J. Daivis and D. J. Evans, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1784.
34. S. Sarman and D. J. Evans, J. Chem. Phys., 1993, 99, 620.
35. S. Sarman, D. J. Evans and P. T. Cummings, Phys. Rep., 1998, 305, 1.
36. J. G. Gay and B. J. Berne, J. Chem. Phys., 1981, 74, 3316.
37. E. D. Miguel, L. Rull, M. Chalam and K. Gubbins, Mol. Phys., 1991, 74, 405.
38. P. Ilg, E. Coquelle and S. Hess, J. Phys.: Condens. Matter, 2006, 18, S2757.
39. A. Sreekumari and P. Ilg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012306.
40. Z. Wang, C. Holm and H. W. Müller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021405.
41. A. Sreekumari and P. Ilg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042315.
42. P. Ilg and S. Hess, Z. Naturforsch., A: Phys. Sci., 2003, 58, 589.
43. M. Kröger, P. Ilg and S. Hess, J. Phys.: Condens. Matter, 2003, 15, S1403.
44. S. Odenbach, Magnetoviscous Effects in Ferrofluids, Springer, Berlin, Heidelberg, 2003.
45. S. Odenbach, J. Phys.: Condens. Matter, 2004, 16, R1135.
46. L. M. Pop and S. Odenbach, J. Phys.: Condens. Matter, 2006, 18, S2785.
47. H. Shahnazian and S. Odenbach, J. Phys.: Condens. Matter, 2008, 20, 204137.
48. J. L. McWhirter and G. N. Patey, J. Chem. Phys., 2002, 117, 9016.
49. P. Ilg and A. E. A. S. Evangelopoulos, Phys. Rev. E, 2018, 97, 032610.
50. E. Roeben, L. Reder, S. Teusch, M. Effertz, U. K. Deiters and A. M. Schmidt, Colloid Polym. Sci., 2014, 292, 2013.
51. J. Dohnt, in Soft Matter, ed. G. Gompper and M. Schick, Wiley-VCH, 2007, ch. 3, vol. 2, p. 270.
52. D. A. Strehober, H. Engel and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012505.
53. S. Grandner, S. Heidenreich, S. Hess and S. H. L. Klapp, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 353.
54. S. Plimpton, J. Comput. Phys., 1995, 117, 1.
55. W. M. Brown, M. K. Petersen, S. J. Plimpton and G. S. Grest, J. Chem. Phys., 2009, 130, 044901.
56. R. Berardi, A. Costantini, L. Muccioli, S. Orlandi and C. Zannoni, J. Chem. Phys., 2007, 126, 044905.
57. R. Everaers and M. R. Ejtehadi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 8.
58. D. Wei and G. N. Patey, Phys. Rev. Lett., 1992, 68, 2043.
59. J. A. Morenao-Razo, E. Díaz-Herrera and S. H. L. Klapp, Mol. Phys., 2006, 104, 2841.
60. M. Schoen and S. H. L. Klapp, Reviews of Computational Chemistry, John Wiley and Sons, New York, 2007, vol. 24.
61. D. J. Evans and G. P. Morriss, Phys. Rev. Lett., 1986, 56, 2172.
62. M. Allen and D. Tildesley, Computer simulation of liquids, Oxford University Press, Oxford, UK, 2006.
63. F. Varnik, L. Bocquet and J.-L. Barrat, J. Chem. Phys., 2004, 120, 2788.
64. G. P. Shrivastav, P. Chaudhuri and J. Horbach, Phys. Rev. E, 2016, 94, 042605.
65. G. P. Shrivastav and S. H. L. Klapp, in preparation.
66. D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005.
67. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
68. P. G. de Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, Oxford, UK, 2003.
69. N. Mori, R. Semura and K. Nakamura, Mol. Cryst. Liq. Cryst., 2001, 367, 445.
70. C. Wu, T. Qian and P. Zhang, Liq. Cryst., 2007, 34, 1175.
71. D. Baalss and S. Hess, Z. Naturforsch., A: Phys. Sci., 1988, 43, 662.
72. J. A. Barker and D. Henderson, J. Chem. Phys., 1967, 47, 2856.
73. H. Zhang and M. Widom, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 8951.
74. G. Ayton, M. J. P. Gingras and G. N. Patey, Phys. Rev. Lett., 1995, 75, 2360.
75. G. Ayton, M. J. P. Gingras and G. N. Patey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 562.
76. D. Wei and G. N. Patey, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 7783.
77. J. J. Weis and D. Levesque, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3728.
78. J. L. McWhirter and G. N. Patey, J. Chem. Phys., 2002, 117, 2747.
79. N. H. Siboni, G. P. Shrivastav and S. H. L. Klapp, J. Chem. Phys., 2020, 152, 024505.

---