Transient supramolecular assembly of a functional perylene diimide controlled by a programmable pH cycle

Abstract

Self-regulating materials require embedded control systems. Active networks of enzymes fulfill this function in living organisms, and the development of chemical controls for synthetic systems is still in its infancy. While previous work has focused on enzymatic controls, small-molecule networks have unexplored potential. We describe a simple small-molecule network that is able to produce transient pH cycles with tunable lagtimes and lifetimes, based on coupling the acid-to-alkali methylene glycol-sulfite reaction to 1,3-propanesultone, a slow acid generator. Applied to transient pH-driven supramolecular self-assembly of a perylene diimide, our system matches the flexibility of in vitro enzymatic systems, including the ability to perform repeated cycles of assembly and disassembly.

---

Living systems are embedded with active controls that trigger adaptive responses to stimuli. This ability spans length scales from whole organisms to networks of molecules in the cytoplasm. While engineers can readily embed active controls into electro-mechanical systems, embedded control of materials is in its infancy. The control of transient self-assembly is a necessary step in this direction.^1–4

Networks of enzymes are the primary agents of regulation within living cells. Thanks to their evolved selectivity and a vast number of biological networks to inform design, they are the logical starting point for the design of chemical controls. Enzymatic networks in living cells perform an astonishing variety of tasks, including energy transduction, mechanical force generation, sensing, and signalling. Their use in synthetic materials has so far been focused on the control of self-assembly.^5–7 In the case of pH-driven assembly,⁸ networks based on the competition between urease (base-generator) and glucose oxidase (acid-generator), have been applied for the transient pH-driven assembly of micelles,⁹ the formation of peptide-¹⁰ and nucleic acid-based hydrogels¹¹ and the control of polymeric nanoreactors.¹²

These enzymatic networks display a good degree of control over both the lag- and the life-time of the pH change. They can also sustain a number of cycles, each triggered by the external addition of a substrate or “fuel”. Typical disadvantages, however, include a limited range of operating conditions, stability, and scalability. The development of enzyme-free control networks is highly relevant for materials programming.

Control networks based on small molecules have great potential for the design of programmable active materials, but they are still under-explored.^13–15 The best example is given by the Belousov–Zhabotinski (BZ) reaction,^16,17 one of the few batch chemical oscillators known, which has been used to generate autonomous chemo-mechanical oscillations in gels and other polymer systems.¹⁸ Nevertheless, it works in a relatively narrow range of conditions, and additional components can have unpredictable effects on its nonlinear dynamics.¹⁹

Clock reactions²⁰ are a family of relatively simple and robust reaction networks. As in situ generators of pH and redox stimuli, they are useful for the time-control of self-assembly.^15,21–24 Most of the available clocks provide a one-time switch, e.g. from acidic to basic pH, after a lagtime. In presence of a counteracting stimulus, such as an acid generator, the pH change can be made transient i.e. a lifetime can be introduced.

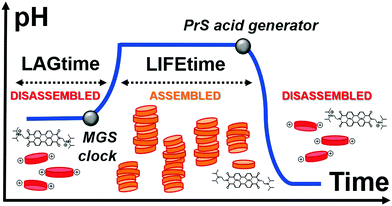
Here, we achieve control over transient supramolecular assembly with a small-molecule network that matches the flexibility of enzymatic analogs (Fig. 1). In particular, we control the lag- and life-time of pH-responsive assemblies, and demonstrate the generation of repeated cycles. To do so, we introduce 1,3-propanesultone (PrS) to counteract the output of the methylene glycol-sulfite (MGS) clock reaction.

Fig. 1 Schematic representation of the transient assembly of a pH-responsive perylene diimide (red and orange disks), triggered by the methylene glycol-sulfite (MGS) clock and reversed by acid generation from 1,3-propanesultone (PrS). From the beginning, the system's components (the MGS clock, the PrS and the perylene diimide building block) are all mixed together.

The methylene glycol-sulfite (MGS) clock reaction generates a sudden, intense change in pH from acidic (pH ∼ 5.5) to alkaline (pH ∼ 10.5). Its mechanism has been investigated in detail²⁵ and can be summarized by eqn (1)–(3). In dilute aqueous solutions, formaldehyde CH₂O is in equilibrium with its hydration product methylene glycol (MG) CH₂(OH)₂ (eqn (1)):

CH₂O + H₂O ⇌ CH₂(OH)₂ (1)

Formaldehyde then reacts with sulfite SO₃²⁻ producing hydroxymethanesulfonate HOCH₂SO₃⁻ and hydroxyl ions OH⁻ (eqn (2)). The latter are rapidly scavenged by bisulfite HSO₃⁻, buffering the pH and generating sulfite at the same time (eqn (3)), thus the reaction is autoaccelerating.

CH₂O + SO₃²⁻ ⇌ HOCH₂SO₃⁻ + OH⁻ (2)

HSO₃⁻ + OH⁻ → SO₃²⁻ + H₂O (3)

For a fixed sulfite–bisulfite ratio, the lagtime can be varied by tuning the initial methylene glycol concentration. This pH change can be made transient by coupling the MGS clock with an in situ acid generator such as a lactone²⁶ (Table S1, ESI†).^14,27 Lactones are the cyclic esters of carboxylic acids, with an enhanced tendency toward hydrolysis driven by the release of ring strain.²⁸ Among lactones, δ-gluconolactone (GL) has risen to the forefront thanks to its non-toxicity, water solubility, availability, and the relatively low pK_a (3.86) of its hydrolysis product, gluconic acid. This approach was recently applied²⁹ to control the reversible assembly and disassembly of micelles and colloids, as well as the swelling/shrinking of a pH-responsive hydrogel. However, so far only one short-lived pH pulse has been demonstrated, due to the fast hydrolysis of GL (Fig. S1, ESI†).

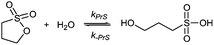
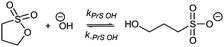
Sultones are the cyclic esters of hydroxysulfonic acids; they are important sulfoalkylating reagents with applications ranging from the synthesis of medicinal compounds to the industrial preparation of surfactants.³⁰ 1,3-Propanesultone dissolves in water (solubility 0.1 g mL⁻¹), with which it slowly reacts (k_PrS = 13.0 × 10⁻⁶ s⁻¹, corresponding to a 14.8 h half-life)^31,32 yielding 1-hydroxypropanesulfonic acid (eqn (4)). Because the product is a strong acid (pK_a 1.53), the hydrolysis of PrS is essentially independent of the hydrogen ion concentration. The reaction at alkaline pH (eqn (5)) is faster but the half-life is still of the order of hours.³³

Conversely, hydrolysis of δ-gluconolactone is fast³⁴ (k_GL = 1 × 10⁻⁴ s⁻¹) and even faster at alkaline pH³⁴ (k_{GL OH} = 4 × 10³ M⁻¹ s⁻¹). Its coupling with the MGS clock produces exceedingly short transient lifetimes (of the order of seconds) and reduces the maximum pH increase (ΔpH) which can be achieved (Fig. S1a, ESI†). Moreover, because GL is quickly consumed, it cannot sustain semi-batch cycles (Fig. S1b, ESI†). These challenges are expected to be even more pronounced for other lactones (Table S1, ESI†). As we will see, these differences in hydrolytic behavior between GL and PrS have dramatic downstream consequences.

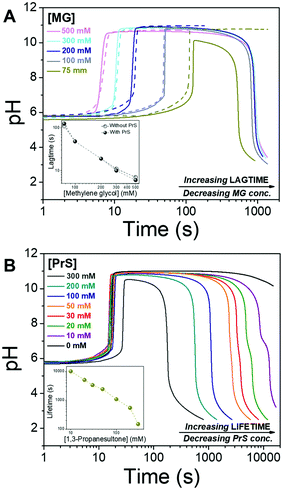
We start the “clock” by adding methylene glycol (MG), together with 1,3-propanesultone (PrS), to a solution containing 50 mM sodium bisulfite NaHSO₃ and 5 mM sodium sulfite Na₂SO₃. The concentration of MG is varied from 75 mM to 500 mM, while that of PrS is between 300 mM and 10 mM. We define the lagtime as the time before the pH increase, and the transient state lifetime as the time spent by the system between the pH increase to above 10 and its decrease back to pH 7.

Lag- and life-time can be tuned independently of each other, as shown in Fig. 2. The lagtime is defined by the MG concentration and can be extended up to 100 s (Fig. 2A), while the lifetime depends on the concentration of PrS and spans a much broader interval, from minutes to hours (Fig. 2B). The pH in the transient state is stable, and the maximum pH is unaffected by all but the highest concentration (300 mM) of PrS.

Fig. 2 Transient pH profiles obtained by coupling the methylene glycol-sulfite (MGS) clock with 1,3-propanesultone (PrS). (A) Lagtime control. The concentration of MG is changed from 75 mM to 500 mM while that of PrS is kept at 100 mM (the dashed lines are the reactions without PrS). (B) Lifetime control. The concentration of MG is kept at 200 mM while that of PrS is varied from 10 mM to 300 mM.

Let us now compare the effects of GL and PrS on the MGS clock (Fig. 2B and Fig. S1a, ESI†). For the same concentration of cyclic ester, e.g. 20 mM, the lifetime is about 1.7 h with PrS while it is only 12 s with GL. Moreover, with PrS the initial pH increase matches the full swing of the bare MGS clock, while with GL the pH increase is reduced to a half.

Lag- and life-time are independent from each other in the MGS–PrS system, and the mechanism for this transient pH cycle can be understood in simple terms. The MGS clock generates a sudden burst of hydroxyl ions OH⁻, which are slowly scavenged by PrS (eqn (5)). The time required to neutralize this base corresponds to the transient lifetime. Then, the pH drops rapidly due to the low pK_a of the acid product of PrS hydrolysis (eqn (4)). However, if the pH is brought back to alkaline by the external addition of sodium hydroxide NaOH, stable and sustained semi-batch cycles can be obtained (Fig. 3). This is because only a small amount of 1,3-propanesultone (ca. 5.5 mM, determined by pH titration) is consumed during each pH cycle. Such results are impossible to achieve with δ-gluconolactone (Fig. S1b, ESI†).

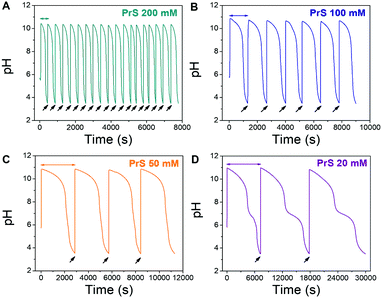Fig. 3 Repeated pH cycles obtained with the MGS–PrS system. The initial pH increase is generated by the MGS clock, the successive ones by external additions (black arrows) of 2 M NaOH. The final volume increase is negligible (<5%). Cycles of 7.5 ± 0.5 min, 21 ± 3 min, 49 ± 1 min and 165 ± 42 min were obtained, respectively with 200, 100, 50 and 20 mM PrS. A kink, associated to the onset of PrS hydrolysis (eqn (4)), becomes apparent at pH 7 for PrS ≤ 20 mM.

In our system, the MGS clock is responsible only for the initial pH increase and the lagtime; it does not influence the lifetime, which depends only on the ring-opening kinetics of PrS. This independence has been confirmed by control experiments, in which 100 mM PrS were added either to the products of the MGS clock (sodium hydroxymethanesulfonate and OH⁻, eqn (2)) or to an inert electrolyte with adjusted pH (sodium perchlorate NaClO₄ and NaOH) (Fig. S2, ESI†). Because the obtained pH-time curves and lifetimes showed no relevant difference compared to those of the MGS–PrS system, we concluded that only the concentrations of PrS and OH⁻ are governing their behavior.

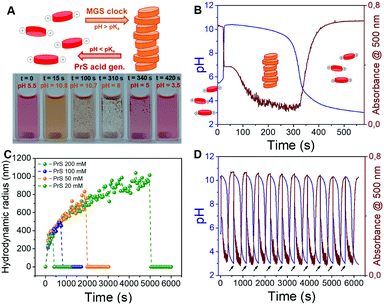
The transient pH features of the above-described MGS–PrS system can be directly applied to control self-assembly. To demonstrate it, we chose the assembly of a pH-responsive perylene diimide, (N,N′-diisopropylethyleneamine)-perylene-3,4:9,10-tetracarboxylic acid diimide or “PDIamine” (eqn (6)). The pH-responsiveness of PDIamine derives from its tertiary amine groups (pK_a 6.5): at pH ≤ 6.5, the electrostatic repulsion introduced by their protonation overcomes the π–π intermolecular attractive forces between the hydrophobic perylene cores,³⁵ while increasing the pH above 6.5 leads to the formation of supramolecular aggregates, which can be redissolved by bringing the pH back to acidic (Fig. 4A).

Fig. 4 Transient assembly of perylene diimide particles enabled by the MGS–PrS system (200 mM MG, 100 mM PrS). (A) Schematic representation and experimental photographic sequence. (B) Evolution of pH and absorbance over time. (C) Evolution of hydrodynamic radius (DLS) over time. (D) Repeated pH and self-assembly cycles fueled by external addition of NaOH (black arrows).

We dissolved PDIamine at a 25 μM concentration in the sulfite–bisulfite solution (pH 5.5). The clock was then started by the coincident addition of methylene glycol and 1,3-propanesultone (final concentrations: 200 mM MG, 100 mM PrS). The pH increase led to PDIamine deprotonation, reflected by a sudden color change from dark pink to yellow (Fig. 4A and Movie S1, ESI†) and the disappearance of the absorption peak at 500 nm in the UV-vis spectrum (Fig. 4B and Fig. S3a, ESI†). Dynamic light scattering (DLS, Fig. 4C) demonstrated that these changes are associated with the formation of micron-sized supramolecular assemblies, which scanning electron microscopy (SEM, Fig. S4, ESI†) revealed to be made of rod-shaped structures, a morphology typical of PDI derivatives. Stirring of the reaction mixture accelerated the precipitation of macroscopic aggregates (Movie S1, ESI†). A more detailed study of this self-assembly process might reveal additional layers of complexity.³⁶

The subsequent disassembly process was controlled by the hydrolysis of PrS. A pH decrease to 4.5 resulted in the sudden dissolution of the supramolecular assemblies (Fig. 4C) and was accompanied by the reappearance of the absorption at 500 nm (Fig. S3b, ESI†). Notably, the overall pH evolution was not affected by the presence of the PDIamine building block, demonstrating that it is possible to obtain macroscopic self-assembly without impacting on the molecular control network.²⁹ Eventually, as showed in Fig. 4D, periodic cycles of assembly and disassembly were obtained under semi-batch conditions by restoring the pH to alkaline with controlled additions of NaOH.

Conclusions

We have demonstrated control over transient and cyclic supramolecular self-assembly with an embedded small-molecule network, based on the coupling of an acid-to-alkaline clock reaction with a slow acid generator. In the short term, our network should be applied to other pH-sensitive systems, including dissipative gel structures with dynamic covalent bonds. Extending the dynamic range of lagtimes of the MGS reaction beyond 100 s remains an open challenge. Also for this reason, it is worth studying the application of PrS to other chemical clocks, such as the bromate-sulfite reaction.²¹ In the long run, we expect that small-molecule networks embedded in synthetic active materials may be able to mimic the complex regulatory functions that enzymatic networks perform within living materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the SNF National Centre of Competence in Research ‘Bio-Inspired Materials’ for partial funding, and the SNSF Grant 200021-172827.

Notes and references

1. J. Boekhoven, W. E. Hendriksen, G. J. M. Koper, R. Eelkema and J. H. Van Esch, Science, 2015, 349, 1075–1079.
2. S. De and R. Klajn, Adv. Mater., 2018, 30, 1706750.
3. B. Rieß and Job Boekhoven, ChemNanoMat, 2018, 4, 710–719.
4. L. Heinen and A. Walther, Soft Matter, 2015, 11, 7857–7866.
5. L. Heinen and A. Walther, Sci. Adv., 2019, 5, eaaw0590.
6. R. J. Williams, A. M. Smith, R. Collins, N. Hodson, A. K. Das and R. V. Ulijn, Nat. Nanotechnol., 2009, 8, 19–24.
7. A. R. Hirst, S. Roy, M. Arora, A. K. Das, N. Hodson, P. Murray, S. Marshall, N. Javid, J. Sefcik, J. Boekhoven, J. H. Van Esch, S. Santabarbara, N. T. Hunt and R. V. Ulijn, Nat. Chem., 2010, 2, 1089–1094.
8. H. Frisch and P. Besenius, Macromol. Rapid Commun., 2015, 36, 346–363.
9. H. E. Cingil, N. C. H. Meertens and I. K. Voets, Small, 2018, 14, 1802089.
10. T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262.
11. L. Heinen, T. Heuser, A. Steinschulte and A. Walther, Nano Lett., 2017, 17, 4989–4995.
12. H. Che, S. Cao and J. C. M. Van Hest, J. Am. Chem. Soc., 2018, 140, 5356–5359.
13. H. W. H. Van Roekel, B. J. H. M. Rosier, L. H. H. Meijer, P. A. J. Hilbers, A. J. Markvoort, W. T. S. Huck and T. F. A. De Greef, Chem. Soc. Rev., 2015, 44, 7465–7483.
14. G. Panzarasa and E. R. Dufresne, Chaos, 2019, 29, 071102.
15. G. Panzarasa, A. Osypova, A. Sicher, A. Bruinink and E. R. Dufresne, Soft Matter, 2018, 14, 6415–6418.
16. B. P. Belousov, Collection of abstracts on radiation medicines, 1959, 147, 145.
17. A. M. Zhabotinsky, Biophysics, 1964, 9, 306–311.
18. R. Yoshida and T. Ueki, NPG Asia Mater., 2014, 6, e107.
19. K. G. Coffman, W. D. McCormick, Z. Noszticzius, R. H. Simoyi and H. L. Swinney, J. Chem. Phys., 1987, 86, 119–129.
20. A. K. Horvath and I. Nagypal, ChemPhysChem, 2015, 16, 588–594.
21. G. Panzarasa, T. Sai, A. L. Torzynski, K. Smith-Mannschott and E. R. Dufresne, Mol. Syst. Des. Eng., 2020 10.1039/C9ME00139E.
22. G. Hu, C. Bounds, J. A. Pojman and A. F. Taylor, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 2955–2959.
23. D. M. Escala, A. P. Muñuzuri, A. De Wit and J. Carballido-Landeira, Phys. Chem. Chem. Phys., 2017, 19, 11914–11919.
24. J. Horváth, Chem. Commun., 2017, 53, 4973–4976.
25. K. Kovacs, R. McIlwaine, K. Gannon, A. F. Taylor and S. K. Scott, J. Phys. Chem. A, 2005, 109, 283–288.
26. K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, J. Phys. Chem. A, 2007, 111, 549–551.
27. T. Bánsági and A. F. Taylor, Tetrahedron, 2017, 73, 5018–5022.
28. Y. Pocker and E. Green, J. Am. Chem. Soc., 1973, 95, 113–119.
29. E. Tóth-Szeles, J. Horváth, G. Holló, R. Szcs, H. Nakanishi and I. Lagzi, Mol. Syst. Des. Eng., 2017, 2, 274–282.
30. S. Mondal, Chem. Rev., 2012, 112, 5339–5355.
31. F. G. Bordwell, C. Edward Osborne and R. D. Chapman, J. Am. Chem. Soc., 1959, 81, 2698–2705.
32. R. F. Fischer, Ind. Eng. Chem., 1964, 56, 41–45.
33. A. Mori, M. Nagayama and H. Mandai, Bull. Chem. Soc. Jpn., 1971, 44, 1669–1672.
34. K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, Phys. Chem. Chem. Phys., 2007, 9, 3711–3716.
35. F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5300.
36. P. A. Korevaar, T. F. A. De Greef and E. W. Meijer, Chem. Mater., 2014, 26, 576–586.

---

Footnote

† Electronic supplementary information (ESI) available: Complete experimental procedures, additional figures and an experiment movie. See DOI: 10.1039/c9sm02026h

---