Open Access Article
Open Access ArticleThe influence of confinement on the structure of colloidal systems with competing interactions
Horacio
Serna
 a,
Eva G.
Noya
a,
Eva G.
Noya
 b and
Wojciech T.
Góźdź
b and
Wojciech T.
Góźdź
 *a
*a
aInstitute of Physical Chemistry Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: wtg@ichf.edu.pl
bInstituto de Química Física Rocasolano, CSIC, C/Serrano 119, 28006 Madrid, Spain
First published on 10th December 2019
Abstract
Colloidal systems with competing interactions have a complex phase diagram with several periodic microphases, in which particles are arranged in lamellae, cylinders or clusters. Using grand canonical Monte Carlo simulations, we investigate how the structure of the colloidal fluid can be modified by confinement in channels with different cross-section geometries and sizes. We pay particular attention to the hexagonal cylindrical phase since it is the most susceptible to form new structures from. In particular, we considered pores with elliptical, triangular, squared, hexagonal, and wedged-cylindrical cross-sections. Our results show that the structure of the confined fluid depends on the commensurability of the bulk periodic structure with the confining cross-section of the channel. We also find that the structure of the confined fluid can be modified by inserting wedges of appropriate geometry and size. These geometrical modifications of the confining pores can be exploited for the controlled assembly of colloidal structures.
1 Introduction
Colloidal particles that attract themselves at short distance and repel at large distance form well defined clusters.1–8 The attraction leads to the formation of clusters and the repulsion prohibits the clusters from merging. The spherical clusters are formed at low or moderate densities. Looesly speaking the cluster radius is of the order of the range of attraction and the inter-cluster distance greater than the range of repulsion to keep the energy low. At intermediate densities, the clusters grow in one dimension and keep the distance between column-like clusters greater than the repulsive range. For even higher densities, the elongated clusters merge with each other and form slabs sufficiently separated to avoid high repulsion.3 Thus, in practice, at small densities the clusters are arranged randomly in a cluster fluid phase, while from intermediate to high densities the clusters self-assemble in periodic structures. Typically, spherical clusters can form a face centered cubic crystal, cylindrical clusters can be arranged into a hexagonal lattice, or layers of colloidal particles can be arranged into lamellar structures. These features of systems with competing interactions are universal and have been documented by theory and simulations in bulk.5,9When a colloidal fluid is confined, both thermodynamic and structural properties are affected. Different types of confinement may be used to promote the formation of structures beyond the well-known ordered phases in bulk.10,11 The process of self-assembling may be highly useful for development of new technologies with applications in different fields like drug delivery, bioelectronics and catalysis.12,13 In particular, colloidal particles confined in channels of different geometries are used to build wave-guide devices with applications in sensing14,15
In this article we investigate, by means of Monte Carlo simulations in the grand canonical ensemble, how the structures stable in bulk can be altered by confinement. We focus on the modifications that the cylindrical phase undergoes due to the effect of the confinement in channels with different cross sections. In particular, we study the influence of elliptical, triangular, hexagonal and square channels. Additionally, we perform a study on cylindrical channels with wedges as obstacles for the colloidal fluid. We investigate three types of wedges to understand how the system is affected by curved and flat walls when both are present at the same time.
The polygons that make up the cross sections of the channels are regular, thus the side length (L) is the control parameter. The shape of the elliptical channels are varied by changing their radii (semi-minor axis (Ry) and semi-major axis (Rx)). The shape of the wedge was changed by varying its angle and radius.
2 The model and the simulation method
We performed Monte Carlo simulations in the grand canonical ensemble, i.e., at fixed chemical potential, temperature and volume (μ, V, T). The interactions between the molecules are modeled by the square-well-linear potential given by,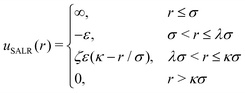 | (1) |
In what follows, all the magnitudes are expressed in reduced units, taking the diameter of the particles, σ, as the unit of length and the value of the potential at the minimum, ε, as the unit of energy. We set the values ζ = 0.05, λ = 1.5, and κ = 4, for which the bulk phase diagram has been recently evaluated in ref. 5. The fluid is confined in channels with different cross-sectional geometries and sizes, which are modeled as hard impenetrable walls. In previous work, we showed that, under cylindrical confinement, the fluid assembles into helical structures, whose morphology depends on the pore radius and boundary conditions. In addition, we found that the length of the channel plays an important role as the helical structures have a preferred pitch about 8.0σ.11 We need to keep the length of the channels as multiples of the optimal pitch to guarantee the proper formation of helical structures when the geometry of the channels allows it. Thus, the channel length was set to Lz = 24σ for all the studied geometries in this work.
With the aim of understanding the effect of the channel geometry, the behavior of the fluid in pores with elliptical, triangular, hexagonal and square cross-sections is now investigated. Additionally, the possibility of modifying the structure of the fluid by inserting wedges in the cavity of cylindrical pores is also explored.
The smallest systems we simulated, i.e., the narrowest channels of each geometry, contained around 150 colloidal particles and the largest systems around 4000. Systems were equilibrated over 1–15 × 109 Monte Carlo steps depending on the system size. Averages were taken over 2 × 109 Monte Carlo steps. A Monte Carlo step consisted of a trial move, that can be a displacement, addition or deletion of a particle. The maximum displacement is adjusted during the equilibration phase of the simulations to obtain 50% of displacement moves acceptance. The addition and deletion moves acceptances have equal values at equilibrium which are around 0.5% for systems with high density and 1.6% for low density. The structures we report here are either cylindrical clusters arranged in a hexagonal lattice, with specific lattice constants, or periodic ordered structures such as helices. The clusters that form such structures change their size and shape during the simulations. These changes are more pronounced for frustrated or disordered configurations than for ordered ones.
3 Results
3.1 Cylindrical hexagonal phase under confinement
In this section, the study is conducted at a thermodynamic state at which the hexagonal cylindrical phase is the most stable phase in bulk. In particular, simulations were performed at T = 0.35, μ = −2.1, which corresponds to a state located at the center of the stability region of the hexagonal phase according to the phase diagram reported in ref. 5. The results presented in this article are universal for a wide range of values of temperature and chemical potential for which the hexagonal phase is stable. We start our study with hexagonal phase since it is the most susceptible to exhibit exotic structures under confinement according to previous works in diblock copolymers.16,17In our former studies we have shown that pores with circular cross-section induce the formation of helical structures.11 It has to be stressed that we have never observed structures composed of straight cylindrical clusters (with the exception of a single cylindrical cluster in the center of the pore for some selected pore diameters).
Let us start by presenting the results for the elliptical channels. We considered three different values for the semi-minor axis, Ry = 3.5, 4.5 and 5σ, and for each of these values, the semi-major axis was given different values within Ry + σ/2 < Rx < (2–3)Ry. As can be seen in Fig. 1, helical structures are still present in some elliptical channels, but straight cylindrical clusters are also observed in some cases. Such structures are often formed when the shape of the ellipse exhibits the largest deviations from the circle (i.e., larger eccentricities).
Neither an ellipse nor a circle reflect perfectly the symmetry of the hexagonal phase. When the hexagonal phase is enclosed in elliptical or circular pores, one may expect that the mismatch between the symmetry of the phase and the shape of the confining walls will cause some frustration that leads to the deformation of the hexagonal phase. This is indeed what happens. At the simulated thermodynamic state, the equilibrium distance between nearest cylindrical clusters in the bulk hexagonal phase is L0 ≈ 6.2σ, and the radius of cylinders is r0 ≈ 1.7σ (as measured from density plots with isosurface ρiso = 0.4). Thus, if one wants to promote the formation of cylindrical clusters, the cross-section of the channels should be chosen such that it can accommodate a number of straight cylindrical clusters of radius r0, preferably separated by the distance L0. Note, however, that the elliptical channels can still accommodate cylindrical clusters if these conditions are not perfectly fulfilled. This is usually attained by either deforming the cylindrical clusters that can adopt also elliptical cross sections and by shortening the distance between nearest clusters.
It is interesting to note that for a circular cross-section, straight cylindrical clusters appear only in the center of the channel. For pores with elliptical cross-section, the system can form cylindrical clusters also close to the pore surface. We attribute this phenomenon to the fact that an ellipse has regions of different curvatures, unlike the circle which has everywhere the same curvature. We may speculate that the straight cylindrical clusters of molecules are stabilized in the regions of high curvature when the cross-section is such that it can accommodate a number of cylindrical clusters separated by a distance close to the equilibrium distance in bulk L0, as can be seen in Fig. 1. However, when the dimensions of the cross-section of the pores are incommensurate with the bulk phase, helical structures are formed instead. In cylindrical pores we have obtained up to three intertwined helical clusters without a cylindrical cluster in the center. In elliptical pores it is possible to obtain more complex structures with up to five intertwined helical clusters. As observed in cylindrical pores, in channels with elliptical cross-section, the formation of right and left-handed helices is equally probable. The behavior of the average density and energy with the radii of the elliptical channels is shown in Fig. 2. In all the studied cases, configurations with straight cylinders are energetically preferred over the helical structures since they usually exhibit lower energies. However, the distorted configurations (for example those for [Rx = 8.5σ, Ry = 4.5σ] and [Rx = 9.0σ, Ry = 3.5σ]) are less favoured than the helices, that often correspond to local minima between two distorted configurations.
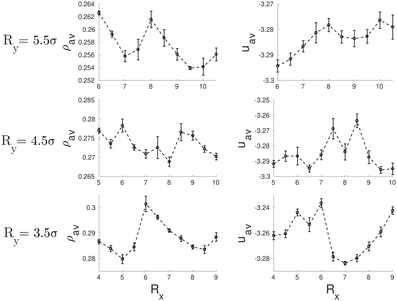 | ||
| Fig. 2 Average density, ρav, (left side) and average energy, uav, (right side) as function of the radii of the elliptical pores. | ||
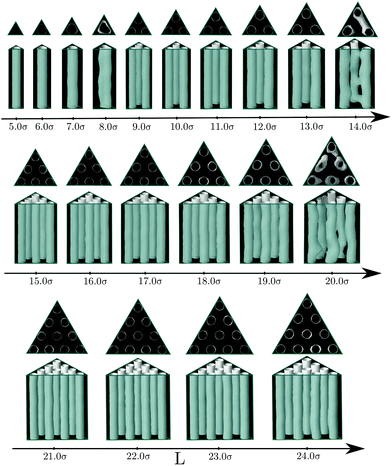
So far we have considered channels whose cross-section exhibit a different symmetry from the bulk fluid. But what happens when the shape of the confining pore is coherent with the symmetry of the bulk phase? Intuitively one expects that the confined phase maintains the same symmetry as the bulk phase for a wide range of pores sizes. To check this hypothesis, we considered channels with triangular and hexagonal cross-sections. In the case of triangular pores, we find that, following intuition, the confined fluid retains the structure of the bulk hexagonal phase for most of the considered pore sizes (see Fig. 3). The bulk phase is only significantly deformed for pore sizes highly incommensurate with its bulk lattice constant, so that the pore cannot accommodate an integer number of cylindrical clusters without a significant distortion of the equilibrium radius and interdistance of the cylindrical clusters in the bulk phase. This behavior is not only favoured by the fact that the confining pore respects the symmetry of the bulk fluid phase; the narrow wedges in the corners of the triangular pore also promote the formation and stabilization of cylindrical clusters. Once these clusters are formed at the corners of the confining triangular pore, they facilitate the growth of additional cylindrical clusters next to them and their ordering in a triangular lattice. The evolution of the average density and energy of the confined fluid as a function of the side length of the triangular pores is shown in Fig. 4. The energy minima correspond to those pore sizes which can accommodate a number of cylindrical clusters whose radius, r0, and interdistance separation, L0, match closely the equilibrium values of the corresponding bulk phase. In particular, the separation distance between two neighbor cylinders is 6.03σ at the second minimum (L ≈ 11σ), 6.00σ at the third minimum (L ≈ 17σ) and 5.99σ at the forth minimum L ≈ 23σ (to be compared to 6.20σ in the bulk phase at the same thermodynamic conditions). Note also that the period from one minimum to the next one is 6σ, which gives further evidence of the correlation between the minimum in energy and the possibility of accommodating the cylindrical clusters with radius and interdistances matching closely those of the bulk phase. Note that, as a consequence of the triangular symmetry of the bulk fluid phase and of the confining pore, the number of cylindrical clusters does not grow continuously; it follows an inverse pyramidal growth, in which the number of clusters goes from one (5.0σ < L < 8.0σ) to three (9.0σ < L < 14.0σ) to six (15.0σ < L < 20.0σ) to ten (21.0σ < L < 24.0σ). Interestingly, the radius of the cylindrical clusters increases periodically with pore size, with sudden drops each time that a new row of cylindrical clusters is formed. Moreover, the maximum packing is achieved when a new row of cylindrical clusters appears (L = 9, L = 15 and L = 21σ), whereas the minima in energy appear at edge lengths somewhat higher. This suggests that the formation of a new row of cylindrical clusters as the edge length increases is first favoured by packing and latter by energetic effects.
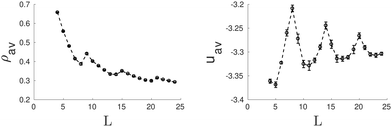 | ||
| Fig. 4 Average density, ρav, (left side) and average energy, uav, (right side) as function of the side length of the triangular pore. | ||
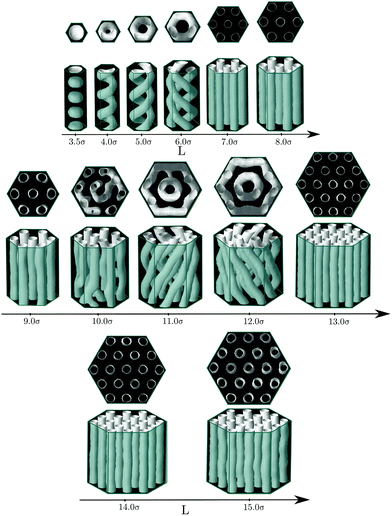
One would expect that confinement effects on the structure of the hexagonal phase in channels with hexagonal cross-sections are similar to those just described for channels with triangular cross-sections. It turns out that this is not true. The behavior of the hexagonal phase in pores with hexagonal sections is, for some sizes, similar to that in pores with triangular cross-section, but, for other pore sizes, the confined fluid adopts structures more similar to those found in channels with circular cross-sections. The bulk hexagonal phase retains its structure for hexagonal channels with edge length within 7.0σ ≤ L ≤ 9.0σ and 13.0σ ≤ L ≤ 15.0σ (see Fig. 5). For the remaining pore sizes, helical structures similar to those observed in cylindrical pores are formed. Given that a hexagon is not so different from a circle, it is not so surprising that for those pore sizes that cannot fit an integer number of cylindrical clusters with values of the cylinder radius and interdistance close to those in bulk, helical structures are instead formed. In particular, we observe intertwined helices for channels with edge lengths within 4.0σ ≤ L ≤ 6.0σ and concentric helices for edge lengths within 11.0σ ≤ L ≤ 12.0σ (see Fig. 5). Even though an hexagon exhibits wedges as a triangle, these are much wider in the hexagon, which might explain why the hexagonal phase is less favoured in hexagonal than in triangular channels. It should be also noticed that clusters formed near the flat boundaries of the pore tend to adopt straight rather than curved cylindrical shapes, at least when clusters adhere to these walls. In Fig. 6 we present the average density and the average energy as functions of the hexagon edge length. We may identify two minima in the energy plot for L = 8.0σ (L0 ≈ 5.97σ, r0 ≈ 1.67σ) and L = 14.0σ (L0 ≈ 6.08σ, r0 ≈ 1.67σ) that correspond to the hexagonal phase. In both cases the radius of the cylindrical clusters and the interdistance separation match closely the equilibrium values of the hexagonal phase in bulk. As in the triangular case, local maxima in packing occur at those sizes just before the energy minima, namely, L = 7.0σ and L = 13.0σ, which are also the first sizes for which the hexagonal phase with a given number of cylindrical clusters is first observed. Again this indicates that the hexagonal phase as a function of the edge length is first stabilized by its efficient packing and latter by its low energy. All the helical structures obtained under hexagonal confinement exhibit a higher energy than the hexagonal phase found at L = 8.0σ and L = 14.0σ, which supports our hypothesis that the helices are formed when the geometrical parameters of the channels are not commensurate with the equilibrium parameters of hexagonal phase in bulk.
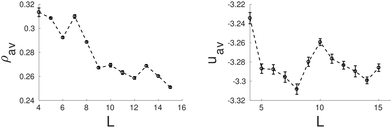 | ||
| Fig. 6 Average density, ρav, (left side) and average energy, uav, (right side) as function of the side length of the hexagonal pore. | ||
Next we present the results for the behavior of the bulk hexagonal phase confined in pores with squared cross-section. In this case, the geometry of the pore is incompatible with the triangular symmetry of the bulk fluid, thus the hexagonal phase will always be frustrated. In this case, cylindrical clusters are still stabilized for a wide range of pore sizes, but they are no longer arranged in a triangular lattice, often they form a square lattice. In particular, we found square lattices with one (8σ ≤ L ≤ 10σ) and with two by two unit cells (15σ ≤ L ≤ 16σ) (see Fig. 7). Interestingly, the energy minima correspond to square lattices as may be observed in Fig. 8. The lattice constant and radius are L0 ≈ 5.74σ and r0 ≈ 1.51σ for L = 9.0σ, and L0 ≈ 5.93σ and r0 ≈ 1.56σ for L = 15σ. As the original hexagonal lattice in bulk has been altered due to the confinement, neither the lattice constants nor the radii of the square lattices are close to their counterparts in bulk which results in relatively high energies. This is evident when the energy plot of the square channel (Fig. 8) is compared to channels which show more coherent symmetries with the bulk such as triangular (Fig. 4) or hexagonal (Fig. 6) channels.
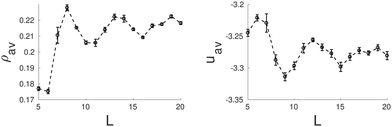 | ||
| Fig. 8 Average density, ρav, (left side) and average energy, uav, (right side) as function of the side length of the square pore. | ||
For the largest considered pores, we observe that the available confined space is sufficient to enable the arrangement of cylinders in the center of pore with the same local environment as in the hexagonal phase.
3.2 Behaviour of other phases under confinement
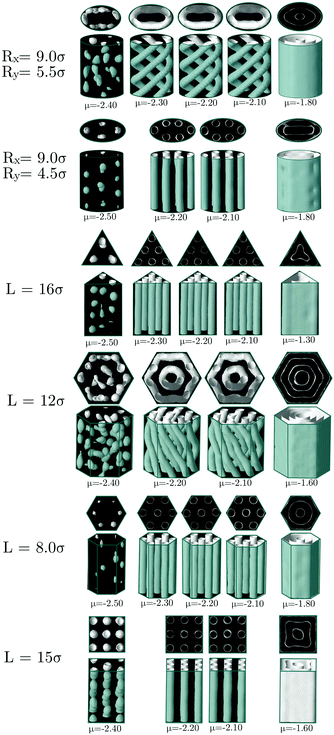
In this section we study the morphological transitions in each sort of channel when the chemical potential is varied. In Fig. 9 we present the most relevant structures obtained for −2.50 ≤ μ ≤ −1.30. Based on the phase diagram reported in ref. 5 and in simulations we performed in bulk, at T = 0.35, the system evolves from a cluster-crystal at −2.60 ≤ μ ≤ −2.35 to a hexagonal cylindrical phase at −2.30 ≤ μ ≤ −1.90 to a lamellar phase at μ > −1.80. For each pore geometry, we chose to study those sizes that yield the lower energies in Fig. 2, 4, 6 and 8, except for the cases of hexagonal and elliptical channels because they stabilize both helical and straight tubes and thus we considered two sizes stabilizing each type of structure. The two top rows in Fig. 9 summarize our results for the elliptical channel. At low chemical potentials, the cluster-crystal phase is completely frustrated and only small clusters with no defined shape are formed randomly, for both pore sizes. Both the helical (top row) and straight cylindrical (second row) phases remain stable in a fairly wide range of intermediate chemical potentials (−2.30 ≤ μ ≤ −2.10 in the helical case and −2.20 ≤ μ ≤ −2.10 for the case of straight tubes). At higher chemical potential (μ > −1.80), the stable phase in bulk is a lamellar phase. Under elliptical confinement, the fluid forms a layered configuration adapted to the shape of the channel cross-section. The largest pore (Rx = 9.0σ, Ry = 5.5σ) holds a layer plus a straight cylinder at the center of the channel, whereas the smaller pore (Rx = 9.0σ, Ry = 4.5σ) is able to host only the layer, as a results of the reduced available space. In the triangular channel (Fig. 9, third row) the situation is not so different from the previous case: random amorphous clusters are formed at low chemical potentials, the triangular arrangement of cylindrical clusters survives in the same range of chemical potentials (−2.30 ≤ μ ≤ −2.10), and the lamellar phase, which is now composed of only one layer, follows a triangular shape. Note, however, that the chemical potential required to favour the formation of the lamellar phase is substantially higher in the triangular pore in comparison to the other channel geometries, which might be a consequence of the triangular pores favouring the cylinder hexagonal phase both due to its commensurability of the pore geometry with the confined phase and the presence of narrow wedges in the pore corners. The behavior of the colloidal fluid inside hexagonal channels (Fig. 9, fourth and fifth rows) is basically the same as we described in the previous cases. The only noticeable difference is that the hexagonal phase is able to survive over a quite broad range of chemical potentials in the small pore (L = 8.0σ), whereas the helical structure formed in the wider pore (L = 12.0σ) is more sensitive to variations in the chemical potential, adopting distorted structures in which the helices start to merge into layers from μ = −2.00. However, this does not mean that the lamellar phase is stabilized at lower chemical potentials in the wider pore, on the contrary, this phase is stabilized first in the channel with L = 8.0σ (μ = −1.80) than in that with L = 12σ (μ = −1.60). Finally, when the fluid is confined into a square channel (Fig. 9, sixth row), at low chemical potentials a cluster crystal is formed. Note that in this case, the square cross-section is compatible with the FCC cluster-crystal stable in the bulk phase, which explains why this phase is observed in this pore but not in the previous considered cases. The hexagonal cylindrical phase is stable at intermediate chemical potentials −2.20 ≤ μ ≤ −2.10, and the lamellar phase, formed now by concentric square layers, is obtained at μ = −1.60.From this study we can draw two conclusions. First, that the boundaries of the stable phases in bulk, namely, the cluster-crystal, the cylindrical hexagonal phase and the lamellar structure are shifted to higher chemical potentials (pressures) by confinement, but the magnitude of the shift depends on the geometry of the confining pore. In particular, the bigger shift to higher chemical potentials is caused by the presence of planar edges in the channels (hexagonal, square and triangular cross-sections). Second, the behaviour of the cluster and lamellar phases is almost independent on the geometry of the channels (with the only exception of the cluster crystal favoured by square confinement), whereas the stability of the hexagonal cylindrical phase is very sensitive to changes in the confining geometry.
3.3 Wedged-cylindrical pores
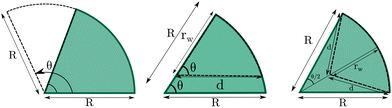
In the previous sections we showed that the bulk phase that adopts more interesting structures under confinement is the cylindrical hexagonal phase. In this section, we explore further how the structure of the confined fluid can be modified by the insertion of wedges in cylindrical channels. Summarizing the main trends observed so far, either the presence of flat walls or the presence of narrow wedges (or regions of high curvature in elliptical pores) promote the formation of straight cylindrical clusters. To find further evidence in support of these conclusions, we now study the hexagonal phase confined in circular pores in which circular wedges are included. This way we may study the effect of curved and flat walls when both are present at the same time. The geometry of the circular wedges is modified in three ways: by changing the angle of the wedge that extends over the whole radius of the circle, by taking a circular wedge with angle π/3 and reducing the radius of the wedge while keeping the angle constant, and by reducing the radius of the wedge while keeping the two planar sides equal to each other and the arc length constant (equilateral wedge). Note that in the two latter cases the wedges are no longer circular sectors (see Fig. 10).Results for a cylinder of R = 8.0σ are presented in Fig. 11. Even though the size of this pore is large enough to host seven cylinders arranged in the hexagonal lattice (six of them distributed along the perimeter of the circular section of the pore plus one at the center), the fluid forms a helical structure with one straight cylindrical cluster at the pore center when confined in a perfect cylindrical pore.
However, this helical structure is no longer stable when a sufficiently large wedge is placed in the inner wall of the pore, as shown in Fig. 11. If the size and shape of the wedge are chosen appropriately, it is possible to recover a structure very similar to that of the bulk phase, consisting of an arrangement of straight cylindrical clusters distributed in the hexagonal lattice. For the first family of wedges (of varying angle, but always extending up to the center of the cylinder), straight cylindrical clusters are obtained for wedges whose angle is an integer multiple of π/3 (that corresponds to the arc length that will be occupied by one straight cylinder of the six cylinders distributed along the cylinder walls). For such wedge angles a number of cylindrical clusters can still be arranged along the perimeter of the cylinder maintaining a separation between them similar to that of the bulk equilibrium phase. Systems exhibiting configurations similar to the equilibrium bulk phase usually exhibit the lower average energies, as can be seen in the top panel of Fig. 12. For other wedge angles, the straight cylindrical clusters are deformed.
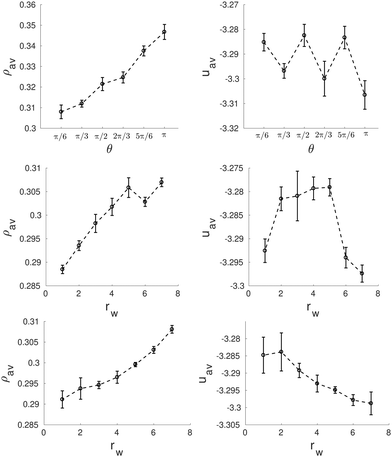 | ||
| Fig. 12 Average density, ρav, (left side) and average energy, uav, (right side) as function of the wedge angle, θ (top row) and the radius, rw, of the asymmetric wedges (central row) and the equilateral wedges (bottom row) for a wedged-cylinder of R = 8.0σ. These results correspond to the structures presented in Fig. 11. | ||
Next we explore the effect of decreasing the wedge radius. This can be done in two ways: maintaining the same angle (thus making the wedge asymmetric and reducing the arc length covered by the wedge, Fig. 11c), or changing the wedge angle (thus keeping the wedge symmetric and the arc length covered by the wedge constant, Fig. 11d). We can observe in Fig. 11c that as long as the arc length of the cylinder surface covered by the wedge is comparable to that of the wedge with angle π/3 (shown in Fig. 11a), the structures are composed of straight cylindrical clusters, despite the smaller radius of the wedge. Once the arc length covered by the wedge is sufficiently small (comparable to the arc length of a wedge of angle π/6), the straight cylinders start to deform. It is interesting to note that for a very tiny wedge, helical clusters are recovered, but the helical pitch is much larger than that of the helices formed in absence of obstacles inside the pore. According to Fig. 12 (central row), the configurations with straight cylinders are energetically favoured over either helical or distorted structures.
The importance of choosing a wedge that covers the appropriate arc length of the confining cylinder is further evidenced by studying symmetric wedges whose radius is shortened but keeping the arc length constant (Fig. 11d). As long as the radius of the wedge is maintained above a given threshold, the confined fluid forms straight cylindrical clusters. Even for very tiny wedges straight cylinders are not significantly distorted. In this case the average energy decreases monotonically up to rw = 7.0σ when an almost perfect hexagonal array of cylindrical clusters is obtained (Fig. 12 bottom row).
One interesting observation is that the presence of wedges leads to the nucleation of two perfect straight cylindrical clusters at each side of the wedge. The size of the wedge also determines the separation distance between those two straight cylinders, which will then affect the rest of the structure.
The same study is also performed for a larger cylindrical pore of radius R = 9.5σ (Fig. 13a). In this case, two concentric single helices are obtained in the pristine cylinder.
Similarly to the previous case, this pore size has the appropriate perimeter length to host an integer number of straight cylinders (eight in this case) distributed along the pore perimeter. This optimal arrangement of the clusters is obtained for the first configuration in Fig. 13b, corresponding to a wedge of angle π/6 (note that at the center of the pore there is a distorted cluster that penalizes energetically the whole structure), as well as for the asymmetric wedges with radius rw = 5.5σ and rw = 3.5σ in Fig. 13c. However, according to the energy plots in Fig. 14, the presence of a deformed cluster at the center of the pore in the wedge of angle π/6 makes this structure less favourable in comparison with the angle 2π/3, when only straight cylinders are obtained (Fig. 14 top row). In contrast, structures obtained for asymmetric wedges with radius rw = 5.5σ and rw = 3.5σ do correspond to low energy configurations since they have helices at the center of the pores (Fig. 14 central row).
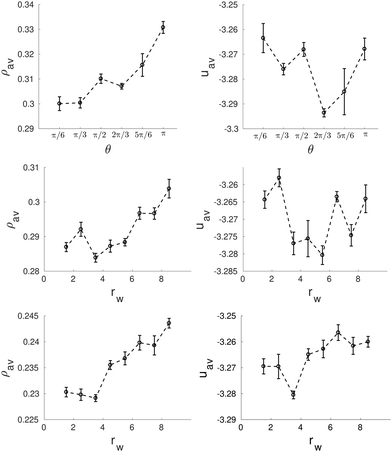 | ||
| Fig. 14 Average density, ρav, (left side) and average energy, uav, (right side) as function of the wedge angle, θ (top row) and the radius, rw, of the asymmetric wedges (central row) and the equilateral wedges (bottom row) for a wedged-cylinder of R = 9.5σ. These results correspond to the structures presented in Fig. 13. | ||
It should be noted that for the above mentioned cases, the arc length of the confining pore covered by the wedge is very similar. As mentioned above, eight straight cylindrical clusters with the preferred distance between them can be accommodated along the walls of the cylinder of the radius R = 9.5σ. If the arc length covered by the wedge is not optimal, the cylindrical clusters are frustrated due to confinement and the system tries to find different solutions for the arrangement of the molecules into the clusters. Usually the clusters are arranged in such a way that they form a combination of cylindrical clusters perpendicular to each other. In some cases these perpendicular cylinders take the form of a ladder, and in some other cases, specially when the wedge is small, distorted helical clusters are formed as shown in Fig. 13d for rw = 3.5σ, 2.5σ, 1.5σ. It is also interesting to note that the presence of a wedge influences the whole structure of the confined fluid, including its structure in the central region of the pore, even when the wedge radius is much smaller than that of the confining pore. Without a wedge in the pore of radius R = 9.5σ the confined fluid is arranged in two concentric single helices. This single helix can be converted into two helices, two or three straight cylindrical clusters or some more irregular shaped clusters.
4 Summary and conclusions
In this work we have carried an extensive simulation study of how the geometry of confined channels affects the structure of a confined fluid with competing interactions. We have demonstrated that confinement can be exploited to tune the structure of the confined fluid. We have identified the conditions that promote different morphologies of the cluster formed as well as their ordering. In particular, we have shown that the helical structures are favoured by cylindrical confinement. Straight cylindrical clusters arranged in a hexagonal lattice can be promoted by using confining pores with narrow edges that favour the nucleation and stabilization of straight cylindrical clusters. Additionally, the preferred symmetry of the arrangement of the cylindrical clusters in bulk can be modified at will by choosing the appropriate confining channel. For example, narrow pores with squared cross-sections stabilize a square lattice of cylinders, as long as the pore size is commensurate with the equilibrium cylinder size and distance separation in the corresponding bulk phase. New structures that are not found in bulk can be produced by confinement.Similar studies have been performed for two dimensional system and spherical cavities.18–26 The computer simulations have been performed for a lattice model25,26 and a model with continuous potential.18,19 Apart from simulations these systems have been studied within the density functional theory.20–24 The phase diagram of a three dimensional systems is richer than that of their two dimensional counterpart. Indeed some phases, such as the cylindrical hexagonal and double gyroid, do not have their analogs in 2D systems. Our study is focused precisely in one of those two structures (the hexagonal phase) and, thus, our investigations significantly broaden the knowledge of the behavior of systems with competing interactions under confinement compared to previous studies. Nevertheless, some behavior is similar for both two and three dimensional systems. Especially, the commensurability of the period of the ordered phases in bulk with the pore geometries and sizes is key to the stabilization of the structure of the confined fluid both in two and three dimensional systems.
Our theoretical predictions are supported by experiments and theoretical calculations in block copolymers, which find similar structures as those presented here for the same confining geometries.16,17,27 This experimental validation for some confining geometries makes credible also the structures found for those confining geometries that have not yet been experimentally studied. In particular, the inclusion of wedges in circular pores can be a versatile option to manipulate at will the structure of the confined fluid. The use of wedges to modify the structure of confined diblock copolymers has also been considered in previous work, although in that case it was used to transform a concentric lamellae into a spiral ones.28,29 All these results suggest that inclusion of wedges in pore cavities are a promising route for tuning the structure of the confined fluids with competing interactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank A. Ciach and A. Meyra for helpful discussion and support of our work. This publication is part of a project that has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 711859 to H. S. and no. 734276 to H. S. and W. G. Additional funding was received from the Ministry of Science and Higher Education of Poland for the project no. 734276 in the years 2017–2020 (agreement no. 3854/H2020/17/2018/2) and for the implementation of the international co-financed project no. 711859 in the years 2017–2021. We would like to acknowledge the support from NCN, Grant No. 2015/19/B/ST3/03122 and from the Agencia Estatal de Investigación and the Fondo Europeo de Desarrollo Regional (FEDER), Grant No. FIS2017-89361-C3-2-P.References
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 11, 432–492 Search PubMed
.
- S. Mossa, F. Sciortino, P. Tartaglia and E. Zaccarelli, Langmuir, 2004, 20, 10756–10763 CrossRef CAS PubMed
.
- A. Ciach and W. Góźdź, Condens. Matter Phys., 2010, 13, 1–12 Search PubMed
.
- M. B. Sweatman, R. Fartaria and L. Lue, J. Chem. Phys., 2014, 140, 124508 CrossRef PubMed
.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef PubMed
.
- M. Edelmann and R. Roth, Phys. Rev. E, 2016, 93, 062146 CrossRef PubMed
.
- D. Pini and A. Parola, Soft Matter, 2017, 13, 9259–9272 RSC
.
- A. Ciach, Soft Matter, 2018, 14, 5497–5508 RSC
.
- A. Ciach, J. Pekalski and W. Góźdź, Soft Matter, 2013, 9, 6301–6308 RSC
.
- E. Lima, P. Pereira, H. Löwen and S. Apolinario, J. Phys.: Condens. Matter, 2018, 30, 325101 CrossRef CAS PubMed
.
- H. Serna, E. G. Noya and W. Góźdź, Langmuir, 2018, 35, 702–708 CrossRef PubMed
.
- S. Mann, Nat. Mater., 2009, 8, 781–792 CrossRef CAS PubMed
.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed
.
- O. Lecarme, T. Pinedo Rivera, L. Arbez, T. Honegger, K. Berton and D. Peyrade, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2010, 28, C6O11–C6O15 CAS
.
- H. Mguez, S. M. Yang and G. A. Ozin, Langmuir, 2003, 19, 3479–3485 CrossRef
.
- A.-C. Shi and B. Li, Soft Matter, 2013, 9, 1398–1413 RSC
.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A.-C. Shi, J. Chem. Phys., 2007, 126, 204903 CrossRef PubMed
.
- A. Imperio and L. Reatto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 040402 CrossRef PubMed
.
- A. Imperio, L. Reatto and S. Zapperi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021402 CrossRef PubMed
.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef PubMed
.
- A. J. Archer, C. Ionescu, D. Pini and L. Reatto, J. Phys.: Condens. Matter, 2008, 20, 415106 CrossRef
.
- R. Roth, Mol. Phys., 2011, 109, 2897–2905 CrossRef CAS
.
- E.-Y. Kim, S.-C. Kim and S.-H. Suh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051203 CrossRef PubMed
.
- S.-C. Kim, S.-H. Suh and B.-S. Seong, J. Chem. Phys., 2012, 137, 114703 CrossRef PubMed
.
- J. Pekalski, N. G. Almarza and A. Ciach, J. Chem. Phys., 2015, 142, 204904 CrossRef PubMed
.
- N. G. Almarza, J. Pekalski and A. Ciach, Soft Matter, 2016, 12, 7551–7563 RSC
.
- G. S. Doerk and K. G. Yager, Mol. Syst. Des. Eng., 2017, 2, 518–538 RSC
.
- H. K. Choi, J.-B. Chang, A. F. Hannon, J. K. W. Yang, K. K. Berggren, A. Alexander-Katz and C. A. Ross, Nano Futures, 2017, 1, 015001 CrossRef
.
- J. Pekalski, E. Bildanau and A. Ciach, Soft Matter, 2019, 15, 7715–7721 RSC
.
| This journal is © The Royal Society of Chemistry 2020 |