Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Flow fields control nanostructural organization in semiflexible networks†
Tomas
Rosén‡
 *ab,
Nitesh
Mittal§
ab,
Stephan V.
Roth
*ab,
Nitesh
Mittal§
ab,
Stephan V.
Roth
 cd,
Peng
Zhang¶
c,
Fredrik
Lundell
cd,
Peng
Zhang¶
c,
Fredrik
Lundell
 ab and
L. Daniel
Söderberg
ab and
L. Daniel
Söderberg
 ab
ab
aWallenberg Wood Science Center, Royal Institute of Technology, SE-100 44 Stockholm, Sweden. E-mail: trosen@kth.se
bLinné FLOW Center, KTH Mechanics, Royal Institute of Technology, Qsquars Backe 18, SE-100 44 Stockholm, Sweden
cDESY, Notkestrasse 85, Hamburg, Germany
dDepartment of Fibre and Polymer Technology, Royal Institute of Technology, Teknikringen 56-58, SE-100 44 Stockholm, Sweden
First published on 29th May 2020
Abstract
Hydrodynamic alignment of proteinaceous or polymeric nanofibrillar building blocks can be utilized for subsequent assembly into intricate three-dimensional macrostructures. The non-equilibrium structure of flowing nanofibrils relies on a complex balance between the imposed flow-field, colloidal interactions and Brownian motion. The understanding of the impact of non-equilibrium dynamics is not only weak, but is also required for structural control. Investigation of underlying dynamics imposed by the flow requires in situ dynamic characterization and is limited by the time-resolution of existing characterization methods, specifically on the nanoscale. Here, we present and demonstrate a flow-stop technique, using polarized optical microscopy (POM) to quantify the anisotropic orientation and diffusivity of nanofibrils in shear and extensional flows. Microscopy results are combined with small-angle X-ray scattering (SAXS) measurements to estimate the orientation of nanofibrils in motion and simultaneous structural changes in a loose network. Diffusivity of polydisperse systems is observed to act on multiple timescales, which is interpreted as an effect of apparent fibril lengths that also include nanoscale entanglements. The origin of the fastest diffusivity is correlated to the strength of velocity gradients, independent of type of deformation (shear or extension). Fibrils in extensional flow results in highly anisotropic systems enhancing interfibrillar contacts, which is evident through a slowing down of diffusive timescales. Our results strongly emphasize the need for careful design of fluidic microsystems for assembling fibrillar building blocks into high-performance macrostructures relying on improved understanding of nanoscale physics.
1 Introduction
Nanofibrillar natural materials are promising candidates for the development of strong, sustainable and biocompatible materials for environmental, energy, optical and biomedical applications.1,2 Nature inspires to engineer fibrillar building blocks into complex hierarchies resulting in materials with exceptional properties that are hard to achieve with synthetic fabrication routes.1,3 To address the challenge of designing high-performance materials via synthetic routes, there is a need for novel processing strategies utilizing enhanced knowledge of physical mechanisms, in particular at the nanoscale. While microfluidics has emerged as a promising tool to regulate the nanofibrils assembly in a controlled manner, it demands scientific understanding of non-equilibrium complex particle dynamics in flow systems, where the fibril dynamics is predominantly controlled through shear or elongation.Dynamic characterization of nanofibrils under flow is thus required for a thorough fundamental understanding of the nanoscale physics. The knowledge will contribute towards the highly uniform spatial organization of building blocks in the three-dimensional macrostructures. The motion of dispersed nanofibrils in flows is due to the translational/rotational advection (the externally forced motion of the nanofibrils due to the deformation of the surrounding medium) and translational/rotational diffusion (the internally forced motion of a collection of nanofibrils together with its solvent towards thermodynamic equilibrium). The translational diffusive motion leads to a uniform spatial distribution of nanofibrils in dispersion that typically remains unaffected by the flow. Although translational diffusion also will affect spatial variations of orientation distributions, the timescales of rotational diffusion is usually much shorter.4 Thus, the diffusive dynamics of nanofibrils is primarily described by their rotational motion.
It is also important to make a distinction between the nanofibrillar systems and typical polymeric systems. Individual polymers are an order of magnitude thinner than typical nanofibrils and are often subject to constant conformational changes due to thermal forcing. The typical crystalline nanofibril remains stiff under thermal forcing with persistence lengths significantly longer than the fibril length.5
Dynamic characterization of nanofibril dispersions to trace the diffusivity is typically achieved with dynamic light scattering (DLS) using a laser light source. By studying the autocorrelation of the scattered light, information on the diffusivity can be obtained.6–10 However, due to problems of multiple scattering in the sample, the dispersions are typically required to be in the dilute regime (<0.1 vol%). Furthermore, the technique can only be used to study the rotational dynamics of anisotropic particles in isotropic and non-flowing systems. Thus, DLS is not suitable to trace the dynamic interactions in material processes where the concentration is high and particles are non-spherical. Another possibility to characterize nanofibrils dynamics is by using X-rays. At isotropic (non-flowing) conditions, SAXS has previously been used to obtain relevant statistics of the individual particle shapes as well as the structure of nanofibril networks.11–13 SAXS has also been widely used to study the orientation of elongated nanoparticles and polymers in flows.14–24 Recently, there has been advances also in X-ray photon correlation spectroscopy (XPCS), which is equivalent to DLS but utilizing X-rays instead of visible light and thus reducing the problem of multiple scattering.25–29 This technique has been used to study the advection and diffusion of dispersed nanoparticles in flowing samples.27 As with all high-flux X-ray techniques, SAXS as well as XPCS requires characterization of the extent of radiation damage as well as suitable strategies to minimize these effects, especially for soft materials. To avoid radiation damage and to possibly increase the scattering contrast, neutron scattering techniques have also been used on nanofibrillar systems in a similar manner as the X-ray techniques.6 However, given the low flux of present spallation sources, such an experiment becomes very time consuming and the availability of such neutron sources is an issue. A potential non-destructive way to thoroughly characterize the dynamics of wet nanofibrillar systems is by using rheo-optical tools including POM as the average alignment of the crystalline fibrils can be correlated to the material birefringence. Such measurements have already been widely used both for nanoparticles/fibrils,5,30–35 polymers,36–40 proteins41,42 and micelles,43 where even more structural information can be extracted by combining with scattering techniques.44,45 An advantage of POM is that visible light can be used as photon source, resulting in negligible damage to the sample. Furthermore, the analysis does not rely on photon correlations, which means that the technique can be used for semi-dilute or concentrated dispersions. Additionally, regular high-speed cameras can be used to detect the transmitted light.
In this study, we demonstrate a flow-stop technique using POM that is easy to operate and is able to obtain a thorough understanding on the nanoscale in situ dynamics of birefringent cellulose nanofibrils (CNFs), which are used as model nanofibrillar systems due to their bio-based origin and abundant availability. Our technique can quantify the non-equilibrium dynamics within a fraction of seconds. We further combined the dynamic characterization with SAXS measurements in a stationary flow to reveal details about the initial (local) orientation distributions of nanofibrils giving rise to the dynamical behavior. The observations from this study can be used to characterize polydisperse fibril systems, paving the way for optimization of the performance of nanostructured materials fabricated via hydrodynamic approaches. This is necessary to realize the true potential of nanoscale building blocks in the macroscopic materials, which is one of the biggest challenges in the field of materials science till date.
2 Experimental
Sample preparation
CNFs were prepared similarly as in the work by Håkansson et al.46 from chemically bleached wood fibers (a mixture of 60% Norwegian spruce and 40% Scots pine, supplied by Domsjö AB, Sweden). The fibrils were prepared by a carboxy methylatation followed by mechanical disintegration, according to a previously reported method.47 In short, carboxy methyl groups were introduced on the surface of the fibrils (degree of substitution of 0.1) to facilitate disintegration of the fiber wall during mechanical treatment. After the chemical pre-treatment, an aqueous dispersion of the fibers was passed through a high-pressure homogenizer. The result is a CNF dispersion with a concentration of 6 g L−1. In an additional step, the un-fibrillated and agglomerated fiber bundles were removed from the CNF dispersion as follows. The gel like dispersion was diluted to 3.3 g L−1 by adding deionized (DI) water, mixed thoroughly using a mechanical mixer (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 min, Ultra Turrax, IKA, Germany) and sonication (10 min, Sonics Vibracell, USA). This diluted dispersion was then centrifuged at 5000 rpm for 60 minutes, precipitate removed and the supernatant used for further studies. The dry content of the final dispersion was determined by gravimetric analysis.
000 rpm for 10 min, Ultra Turrax, IKA, Germany) and sonication (10 min, Sonics Vibracell, USA). This diluted dispersion was then centrifuged at 5000 rpm for 60 minutes, precipitate removed and the supernatant used for further studies. The dry content of the final dispersion was determined by gravimetric analysis.
Length and height of fibrils are characterized with transmission electron microscopy and atomic force microscopy, respectively, with lengths ranging from 100–1600 nm and heights in the range of 1–6 nm (Fig. S1 in ESI†). The lengths and heights of 200 and 100 CNFs were measured using transmission electron microscopy and atomic force microscopy, respectively, by following the same protocol reported elsewhere.22 The CNFs have a surface charge density of ≈600 μmol g−1.
Flow cell and geometries
The flow cell has a sandwich construction (Fig. S2 in ESI†) where a channel plate is placed between two 140 μm thick transparent COC films (Tekni-plex 8007 X-04). The COC films are used because of beneficial optical properties and low birefringence, especially during compression, which makes it ideal for POM-experiments. For the SAXS experiments, these films are replaced by Kapton (DuPont 200HN, 50 μm thickness) to reduce damage to the films made by the high intensity X-ray beam. For mechanical support, two 10 mm aluminum plates are placed outside the films and screws are used to clamp the layers together.Dynamics of nanofibrils under shear and extensional flow is studied using two different channel geometries, creating different deformation states of the dispersion throughout the channels.
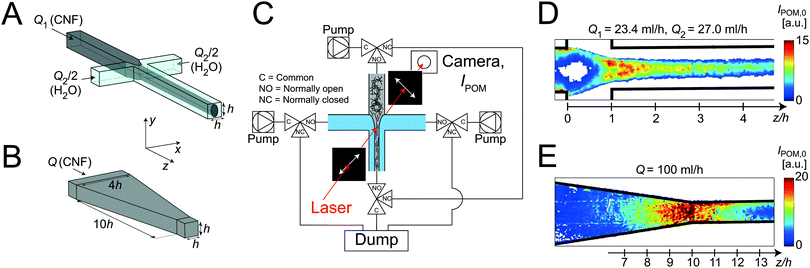
The first geometry is a flow-focusing channel (FFC)46,48 and illustrated in Fig. 1A. It consists of a four channel crossing, where three channels serve as inlets. The core flow of CNF (flow rate Q1) in the center channel is focused by two sheath flows of water (each with flow rate Q2/2) positioned opposite to each other, perpendicular to the center channel. The channels have square cross-sections of 1 × 1 mm2. As characteristic length scale of the flows, we therefore choose h = 1 mm. The flow rates used here are chosen to be Q1 = 23.4 ml h−1 and Q2 = 27 ml h−1, to match the conditions in earlier work.46
The second geometry is a converging channel (CC) as illustrated in Fig. 1B. The flow rate in the CC geometry is denoted as Q and is varied in the range Q = 50–200 ml h−1.
In both channel geometries, the CNF dispersion is accelerated, leading to an increased alignment of the fibrils. However, the fibrils are only aligning due to uni-axial extensional flow in the FFC geometry and in the CC geometry they are aligning as a result of both shear and planar extension (Fig. S3 in ESI†). Further comparisons between the geometries are given in the ESI.†
It is important to note that the local concentration of CNF can safely be assumed to be constant in the FFC core as the translational diffusion is on the order of days over distances of millimeters4 (and of course that incompressibility of the dispersion ensures a divergence free flow field everywhere).
POM flow-stop
The setup of the POM flow-stop experiment is illustrated in Fig. 1C. The flow is distributed to the flow cell using syringe pumps (WPI, Al-4000) and capillary PTFE tubing. The flow cell is placed with the z-direction in the vertical direction between two linear polarization filters, with polarization directions 45° and −45° to the flow (z) direction. A laser module (130 mW and wavelength of ≈660 nm) is used as a light source illuminating a region of around 10 mm in diameter. The intensity of light transmitted through the setup is recorded with a Mako U-029B camera.The intensity IPOM is then directly proportional to the square of the material birefringence B, i.e.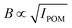 . Furthermore, it is known that
. Furthermore, it is known that 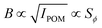 ,49 where
,49 where 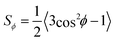 is the order parameter describing flow-alignment of fibrils (ϕ being the angle between fibril major axis and flow direction and the brackets indicate an ensemble average over all fibrils; see Fig. S3 in ESI†). Fig. 1D and E shows example images of the intensity IPOM,0 during stationary flow in the FFC and CC geometries.
is the order parameter describing flow-alignment of fibrils (ϕ being the angle between fibril major axis and flow direction and the brackets indicate an ensemble average over all fibrils; see Fig. S3 in ESI†). Fig. 1D and E shows example images of the intensity IPOM,0 during stationary flow in the FFC and CC geometries.
The flow can be stopped instantly in the flow cell by redirecting the flow with four synchronized three-way Takasago MTV-3SL slider valves. The camera is acquiring images with a rate of 100 frames per second during 15 s. The flow is stopped after more than 5 s of flow, which is sufficient for stationary conditions to have developed.
The exact regions for measurements at different downstream positions z are illustrated in Fig. S4 in ESI.† Further details about the post-processing of the data in the flow-stop experiment as well as a movie illustrating the experiment is given in ESI.†
Given the flow-rates used in this study and switching time of the valves, the time to reach a complete stop of the flow is around 10 ms, with no significant secondary flows due to inertial effects. Further discussion and numerical analysis of the stopping sequence is provided in ESI,† and in Fig. S5–S7.
Since every pixel in the image corresponds to a unique deformation state of the nanofibrils, one single experiment can be used to provide a large amount of data relating to the relaxation towards isotropy from an initially aligned configuration.
In situ SAXS measurements
To verify the relation between the true orientation distributions of CNF with the intensity obtained with POM, in situ SAXS measurements where performed in the FFC geometry during stationary flow.The experiments were performed at the P03 Beamline50 of PETRA III at the Deutsches Elektronen-Synchrotron (DESY) in Hamburg, Germany. The flow cell is mounted on a translation stage in front of the beam, with a detector (Pilatus 1 M, Dectris, with pixel size 172 × 172 μm2) placed at distance D from the sample. This distance was found through calibration with a collagen sample to be D = 7.5 m. The recorded wavelength of the X-rays is λ = 0.95 Å and the beam size is 26 × 22 μm2. The scattered X-rays are recorded on the detector for different scattering vector lengths q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ (where 2ϕ is the angle between incoming and scattered radiation) during 5 s per image and in total more than 20 images per position are acquired. With the flow rates in this study, a fibril stays less than 2 ms inside the beam, which is found to be well below timescales for radiation damage. For the background reference scattering using only DI water in the channel, at least 5 images were recorded. The final analysis was then performed using an average of the images at a given position.
ϕ (where 2ϕ is the angle between incoming and scattered radiation) during 5 s per image and in total more than 20 images per position are acquired. With the flow rates in this study, a fibril stays less than 2 ms inside the beam, which is found to be well below timescales for radiation damage. For the background reference scattering using only DI water in the channel, at least 5 images were recorded. The final analysis was then performed using an average of the images at a given position.
Whereas POM provides a relative measurement of fibril alignment, in situ SAXS can provide the actual orientation distribution function (ODF) of flowing CNF inside the beam.24,46,51 If the dispersion is subject to an axi-symmetric deformation, as is the case in the FFC geometry, the exact 3D-ODF Ψϕ can be obtained and assumed to be constant along the beam path.51 From Ψϕ, the alignment can be quantified through the order parameter 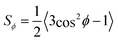 as described earlier.
as described earlier.
Fig. S8 (ESI†) illustrates the experimental setup for the SAXS experiments and Fig. S9 (ESI†) illustrates in detail the steps to post-process the SAXS data. Further details of how the ODF Ψϕ is obtained from the SAXS experiment is provided in ESI.†
Obtaining deformation rates
In order to relate the flow deformations to relaxation rates found in the flow-stop experiment, the velocity fields needs to be known in both geometries. The local velocity gradient tensor is given by: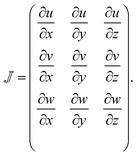 | (1) |
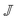 being known given the centerline velocity.
being known given the centerline velocity.
In the CC geometry, the entire velocity field is obtained through computational fluid dynamics (CFD) simulations in Comsol Multiphysics v5.5. More details about the simulations are given in the ESI,† with illustrations in Fig S10.
Given a velocity gradient matrix 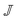 , the strain (deformation) rate
, the strain (deformation) rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ; is the maximum absolute eigenvalue of the strain rate tensor
; is the maximum absolute eigenvalue of the strain rate tensor 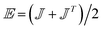 . The major contributions to the strain rate is given by the gradients of the velocity w in the main flow direction z. For discussion, we will therefore define the shear rate as:
. The major contributions to the strain rate is given by the gradients of the velocity w in the main flow direction z. For discussion, we will therefore define the shear rate as:
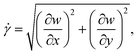 | (2) |
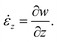 | (3) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) =
= ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) z in a uni-axial extensional flow, and
z in a uni-axial extensional flow, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /2 in a simple shear flow. More details and discussion about obtaining the velocity gradients are given in the ESI.†
/2 in a simple shear flow. More details and discussion about obtaining the velocity gradients are given in the ESI.†
3 Results
Steady state alignment
The initial orientation distributions Ψϕ of the nanofibrils during flow are studied using SAXS (see Methods section for details). In Fig. 2A, the results of the fibril steady state order parameter Sϕ,0(z) are shown as function of downstream position (at centerline). The average of two separate measurements is considered as the true absolute order parameter along the channel. The results are further compared with the SAXS data reported earlier.46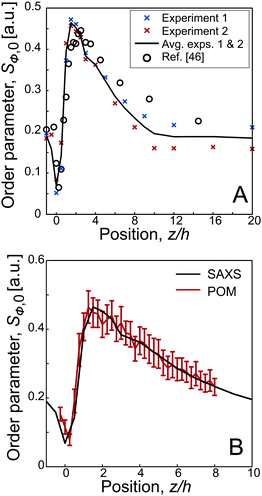 | ||
| Fig. 2 Results of the steady state alignment in the FFC geometry (Q1 = 23.4 ml h−1, Q2 = 27.0 ml h−1): (A) order parameter Sϕ,0versus the downstream position z from the SAXS experiments and compared to the results by Håkansson et al.;46 the black line indicates the average over two separate experiments; (B) results from POM experiments compared with SAXS. | ||
As the birefringence B is linearly proportional to Sϕ,49 the steady state results from SAXS and POM are directly comparable. The POM flow-stop experiments were evaluated at different downstream positions (exact regions are provided in Fig. S4 in ESI†). Using the position of maximum alignment as our reference position, i.e. zref. = 1.5 h, and using the maximum order parameter from the SAXS experiments, we can convert the measured POM intensity IPOM to an order parameter through:49
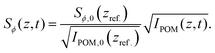 | (4) |
Dynamic characterization
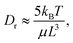 | (5) |
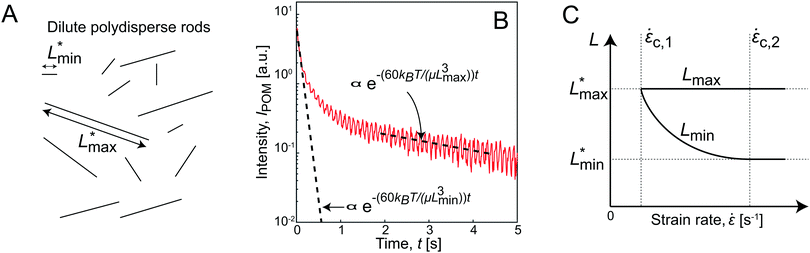
To aid in interpretation, the flow-stop results are related to the behavior of an ideal system of dilute polydisperse rods as illustrated in Fig. 3A, which has a physical real minimum and maximum rod length of Lmin* and Lmax*, respectively. The typical decay of the intensity IPOM after stop is illustrated in Fig. 3B, where the high-frequency oscillations are due to fluctuations of the light source, not due to the oscillations of birefringence. The fastest measurable decay rate (at 0.01 s < t < 0.1 s after stop) is used to extract the minimum apparent length Lmin through eqn (5) (assuming the solvent to be water at T = 293 K). Similarly, the slowest measurable decay rate is used to extract to the maximum apparent length Lmax.
As flow gradients are applied to align this system (Fig. 3C), a critical strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) =
= ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c,1 will be reached, where hydrodynamic forces overcome the Brownian rotary diffusion of the longest rods. A measurement performed at the critical strain rate would yield Lmin ≈ Lmax, since all shorter rods would be dominated by Brownian motion, and thus not part of the aligned fraction. Increasing
c,1 will be reached, where hydrodynamic forces overcome the Brownian rotary diffusion of the longest rods. A measurement performed at the critical strain rate would yield Lmin ≈ Lmax, since all shorter rods would be dominated by Brownian motion, and thus not part of the aligned fraction. Increasing ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) further, the apparent minimum length Lmin will eventually approach Lmin* while Lmax remains constant. Above a second critical strain rate
further, the apparent minimum length Lmin will eventually approach Lmin* while Lmax remains constant. Above a second critical strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c,2, the hydrodynamic forces will be strong enough to align all particles in the dispersion and Lmin = Lmin*.
c,2, the hydrodynamic forces will be strong enough to align all particles in the dispersion and Lmin = Lmin*.
As stated above, in an ideal non-interacting system, the apparent lengths would correspond to the physical lengths. Applying an inverse Laplace transform to the decay from a system aligned with high strain rates, the full length distribution can be extracted as discussed in previous work.34 However, in a semi-dilute system of CNF, the apparent lengths should rather be regarded as an interpretation model of diffusive dynamics. This is in full equivalence to the concept of the hydrodynamic radius used in DLS, with conversion from diffusive timescales to apparent length scales through the Stokes–Einstein relationship.
Any deviation from the ideal behavior in Fig. 3C relating Lmax and Lmin to strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) can be regarded as an effect of fibril–fibril interactions.
can be regarded as an effect of fibril–fibril interactions.
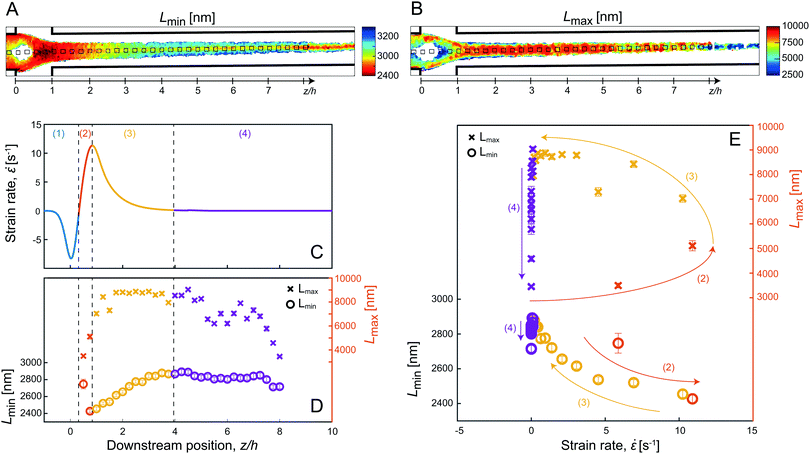 | ||
Fig. 4 Results from the dynamic characterization in the FFC geometry (Q1 = 23.4 ml h−1, Q2 = 27.0 ml h−1): (A) mean values of minimum apparent length Lmin; (B) mean values of maximum apparent length Lmax; (C) strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) as function of downstream position z at centerline from previous work;23 (D) evolution of Lmax and Lmin at centerline as function of z using the pixels indicated with black squares in (A) & (B); (E) Lmax and Lmin with respect to as function of downstream position z at centerline from previous work;23 (D) evolution of Lmax and Lmin at centerline as function of z using the pixels indicated with black squares in (A) & (B); (E) Lmax and Lmin with respect to ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . . | ||
Fig. 4C shows the strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) at the centerline obtained in earlier work.23 Based on
at the centerline obtained in earlier work.23 Based on ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , four regions are defined: (1) region of decelerating flow,
, four regions are defined: (1) region of decelerating flow, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) < 0; (2) region of increasing
< 0; (2) region of increasing ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ; (3) region of decaying
; (3) region of decaying ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) and (4) region of
and (4) region of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ≈ 0.
≈ 0.
In Fig. 4D, the values of Lmax and Lmin along the centerline are illustrated, with the error-bars displaying the standard deviation over the 16 flow-stop experiments, and in Fig. 4E, Lmax and Lmin are shown with respect to the strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) .
.
Before the focusing section (region 1), where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a1.gif) ≲ 0, the intensity (and alignment) is also too low to be evaluated after stop. During the acceleration in the focusing section where
≲ 0, the intensity (and alignment) is also too low to be evaluated after stop. During the acceleration in the focusing section where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) increases (region 2), the system behaves initially very similar to the dilute polydisperse system in Fig. 3C. Both apparent lengths seem to initially be around Lmin ≈ Lmax ≈ 3000 nm and Lmax remains constant while Lmin decreases with increased strain rate.
increases (region 2), the system behaves initially very similar to the dilute polydisperse system in Fig. 3C. Both apparent lengths seem to initially be around Lmin ≈ Lmax ≈ 3000 nm and Lmax remains constant while Lmin decreases with increased strain rate.
In region 3 where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) decreases, Lmin behaves as expected and decreases back to Lmin ≈ 3000 nm. On the other hand, the maximum apparent length increases and remains high at Lmax≈9000 nm as long as
decreases, Lmin behaves as expected and decreases back to Lmin ≈ 3000 nm. On the other hand, the maximum apparent length increases and remains high at Lmax≈9000 nm as long as ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) > 0 as the system is further deformed. This is clearly a sign of increasing interactions during the extensional deformation in the flow and gives rise to three times longer apparent lengths than what is expected in the non-deformed dispersion.
> 0 as the system is further deformed. This is clearly a sign of increasing interactions during the extensional deformation in the flow and gives rise to three times longer apparent lengths than what is expected in the non-deformed dispersion.
In region 4 where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ≈ 0, Lmax decreases and approaches the initial value of Lmax ≈ 3000 nm, which can be interpreted as fibrils becoming disentangled with less interactions. The minimum apparent lengths Lmin also decreases slightly further downstream, but it is clear from Fig. 4A that the lower values of Lmin are found close to the centerline. This is an indication of a non-circular cross-section of the core dispersion where the fibrils at the core/sheath interface experience stronger shear forces close to the walls perpendicular to the viewing direction.
≈ 0, Lmax decreases and approaches the initial value of Lmax ≈ 3000 nm, which can be interpreted as fibrils becoming disentangled with less interactions. The minimum apparent lengths Lmin also decreases slightly further downstream, but it is clear from Fig. 4A that the lower values of Lmin are found close to the centerline. This is an indication of a non-circular cross-section of the core dispersion where the fibrils at the core/sheath interface experience stronger shear forces close to the walls perpendicular to the viewing direction.
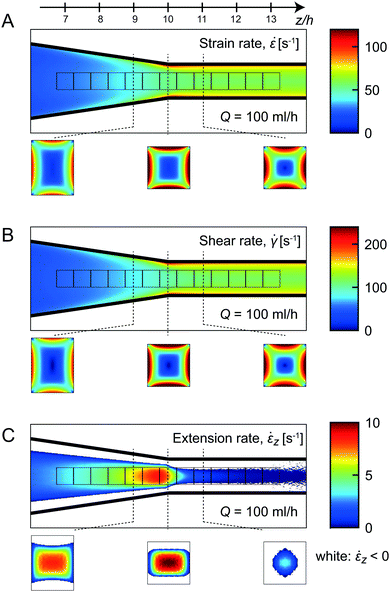
Firstly, the average stationary flow field was obtained through CFD simulations, from which the average velocity gradients could be extracted (more details in the Experimental section and the ESI†). In Fig. 5A–C, the average strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , shear rate
, shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and extension rate
and extension rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) z are averaged in the viewing direction at Q = 100 ml h−1.
z are averaged in the viewing direction at Q = 100 ml h−1.
The extension rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) z increases steadily before the end of the contraction (z/h > 10), and decays rapidly towards zero after the contraction. The highest extension rates are found in the center of the channel, with negligible values close to the walls. It is clear that, even at positions with maximum extension rates, the average strain rate in the channel is dominated by the shear-induced deformation. Since shear rates are also increasing with the accelerating flow, the strain rate
z increases steadily before the end of the contraction (z/h > 10), and decays rapidly towards zero after the contraction. The highest extension rates are found in the center of the channel, with negligible values close to the walls. It is clear that, even at positions with maximum extension rates, the average strain rate in the channel is dominated by the shear-induced deformation. Since shear rates are also increasing with the accelerating flow, the strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is constantly increasing with z throughout the channel. The most rapid increase of the shear rate
is constantly increasing with z throughout the channel. The most rapid increase of the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is occurring shortly after the contraction close to the channel walls.
is occurring shortly after the contraction close to the channel walls.
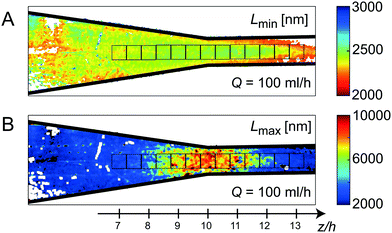
Fig. 6A and B, show the mean values of apparent lengths Lmin and Lmax, respectively at Q = 100 ml h−1. The average values in the measurement locations (black squares in Fig. 6) are plotted versus the normalized strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) max in Fig. 7 for various flow rates Q.
max in Fig. 7 for various flow rates Q.
 | ||
Fig. 7 Apparent lengths Lmin and Lmax with respect to the normalized strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) / /![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) max at various flow rates Q in the CC geometry. max at various flow rates Q in the CC geometry. | ||
Looking at the minimum apparent length Lmin, the similarity to Fig. 5A and B is obvious, with Lmin being fairly constant during the contraction and then increasing rapidly close to the walls similar to the trend of the shear rates. As expected, Lmin further decreases when increasing Q (Fig. 7) given that the velocity gradients are linearly proportional to the change of flow rate. This corresponds well with the observations in the FFC geometry, where Lmin decreases with strain rate.
The apparent length Lmax on the other hand, seems to follow the trend of the extension rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) z in the channel, where Lmax increases as flow accelerates, followed by a rapid decrease after the contraction, with maximum value in the center. Here, the measurement is likely to be related to the dynamics of fibrils close to the centerline where shear rate is negligible and extension rate is maximal. Just like in the FFC geometry, the extensional flow caused more effects of interactions, slowed down the dynamics, and thus appearing as a system of longer fibrils. As soon as the extensional deformation stops, the flow is dominated by shear, and the value of Lmax returns to the original value around 3000 nm. In Fig. 7, it is also clear that the behavior of Lmax in the CC geometry is independent of flow rate Q, emphasizing again the finding in the FFC geometry that the level of fibril interactions is just dependent on the total extensional deformation and not the strain rates.
z in the channel, where Lmax increases as flow accelerates, followed by a rapid decrease after the contraction, with maximum value in the center. Here, the measurement is likely to be related to the dynamics of fibrils close to the centerline where shear rate is negligible and extension rate is maximal. Just like in the FFC geometry, the extensional flow caused more effects of interactions, slowed down the dynamics, and thus appearing as a system of longer fibrils. As soon as the extensional deformation stops, the flow is dominated by shear, and the value of Lmax returns to the original value around 3000 nm. In Fig. 7, it is also clear that the behavior of Lmax in the CC geometry is independent of flow rate Q, emphasizing again the finding in the FFC geometry that the level of fibril interactions is just dependent on the total extensional deformation and not the strain rates.
4 Discussion
Our ultimate goal is to get a complete understanding of the nanoparticles motion in different types of flows. To be able to account for nanoscale network and entanglement effects at different working concentrations in modeling, information on the fibril flexibility, morphology and interfibrillar interactions is needed. At present, quantifying these parameters is impossible due to the limitations of the experimental tools available. Nevertheless, we will discuss the present results in the light of fundamentals regarding rod and fiber motion in shear and extension. It can be argued that from our current and previous efforts, we have managed to obtain a considerable understanding on the nanoscale phenomenon of polydisperse fibrillar systems previously left untouched in the literature due to the number of challenges associated with such systems.The behavior of apparent lengths Lmax and Lmin is understood by comparing with the ideal dilute polydisperse system in Fig. 3. The obvious discrepancy is found when comparing physical lengths to the values of Lmax and Lmin, where the latter quantities typically are about twice as high than expected (physical Lmax* is around 1600 nm from TEM, while the measured value with flow-stop suggests Lmax* ≈ 3000 nm).
One possibility could be that the shortest fibrils cause an increase of the intrinsic solvent viscosity, where only a viscosity modification of the solvent of a factor six, would result in the expected values of Lmax and Lmin, whereas the shear viscosity of low-concentration CNF can be 100–1000 times higher than water depending on shear rate.4
Another plausible reason could be that fibril–fibril interactions in the semi-dilute CNF causes the fibrils of all lengths to have slower rotary diffusion and thus appearing longer (compared to the dilute case). The recent work by Brouzet et al.5 along with the theory of semi-dilute rigid rods by Marrucci and Grizzuti55,56 makes the use of a sample dependent interaction parameter β to adjust the flow-stop results to the physical length distribution from TEM. The theory further suggests that the rotary diffusion coefficient should scale with Dr ∝ L−7 rather than Dr ∝ L−3 used in eqn (5). This would also result in the aligned fraction of fibrils having a very narrow physical length distribution.
Although, the experiments here are not sufficient to understand exactly how the system is slowed down, giving longer apparent lengths, this could probably be assessed by studying more ideal systems of polydisperse nanorods.
In this work, we argue that the apparent length of Lmax ≈ 3000 nm is indeed reflecting the length of the longest fibrils, where the discrepancy with physical length could be explained by either viscosity or interaction effects. The fact that this value still increases with more extensional deformation (independent of rate) is believed to be an indication of the nanoscale entanglements and loose network formation of the longest fibrils as the system is extended. In this particular dispersion, this can lead to a slow-down of dynamics up to an apparent length of Lmax ≈ 9000 nm.
In the CC geometry, the interactions do not reach the same level. Here, the extension rates are more gradually increasing, but the interactions are clearly disturbed by the shear flow, as Lmax rapidly goes back to Lmax ≈ 3000 nm when the extension is removed, even though deformations through shear continues. There is thus a clear preference for extensional flow in order to reach the high degree of interactions that leads to the exceptional values of the maximum apparent length Lmax. To understand the big difference in interactions in shear versus extensional flow, we can take a closer look at the spatial distribution of aligned fibrils. Both shear and extension will cause the fibrils to preferentially align in the flow direction. However, in the extensional system, the average transverse distance d between fibrils is smaller than in the sheared system as illustrated in Fig. 8 and fibrils located perpendicularly will not have any parallel relative motion (as they do in shear). Thus, if there is any potential for stretched and partly aligned fibrils to bind together in a loose network, this is more prone to happen in an extensional flow than in a shear flow. The occasional flipping of fibrils due to the vorticity in the shear flow,53 will increase the interactions with nearby fibrils. This network will however be constantly rotated, ruptured and re-formed and thus obstruct simultaneous alignment and entanglement.
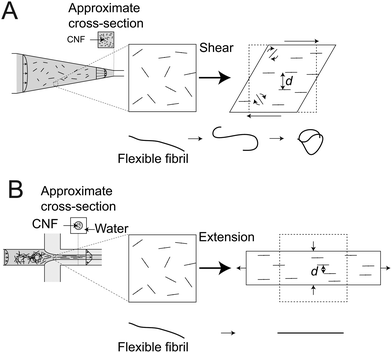 | ||
| Fig. 8 Illustration of the differences between a system of dispersed rods undergoing (A) shear in the CC geometry and (B) extension in the FFC geometry, respectively; although both deformation results in alignment of the particles, the transverse distances d are smaller in extensional flow; in the shear flow, rods also have an intermittent rotational motion;53 lower figures show what happens to a long flexible fiber, where shear causes the fiber to curl and tangle into a bundle while extension will just stretch it out.54 | ||
Apart from length, another contributing factor is the flexibility of an individual fibril (Fig. 8). Long and flexible blocks have a tendency to curl and entangle into semi-spherical (isotropic) bundles that will just rotate with the local vorticity.54,57–59 With respect to the long CNFs in the present system, a natural consequence is that the longest fibrils will not be part of the aligned configuration in shear flow, which could result in apparent maximum lengths Lmax shorter than 3000 nm.
The minimum apparent length Lmin was similar to Lmax at low strain rates and generally was seen to decrease with the strain rate as expected in both geometries, but never going below 2000 nm. A question is if this apparent length is indicative of the shortest fibrils in the dispersion, which have a known physical length of ≈100 nm. We see this as unlikely, since the strain rates in the experiment probably are too weak to overcome Brownian motion. This would also explain the origin of the quite substantial isotropic contribution to the SAXS pattern (see details in ESI†). The fibrils contributing to the shortest apparent lengths here are thus probably also on the higher end of the length distribution, which most likely also are affected by increased entanglement effects in extensional flow, explaining why Lmin is not consistently increasing with total strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) in the CC geometry (see Fig. 7). There are of course also limitations of the experimental flow-stop setup worth mentioning, where a measurement of very short Lmin requires both faster closing times of the valves, less inertia in the flow as well as higher time- and intensity-resolution of the camera.
in the CC geometry (see Fig. 7). There are of course also limitations of the experimental flow-stop setup worth mentioning, where a measurement of very short Lmin requires both faster closing times of the valves, less inertia in the flow as well as higher time- and intensity-resolution of the camera.
As a final discussion point, it has been hypothesized that the rotary diffusion process of CNF could potentially be modeled using only the instantaneous orientation distribution.23 The hypothesis was that higher degree of alignment could result in higher rotary diffusion due to a combination of repulsive electrostatic torques, lower number of immediate fibril–fibril contacts and stretching of potentially non-straight, flexible fibrils. It is already clear from the results in the FFC geometry that neither Lmax nor Lmin (Fig. 4D) follow the general trend of the average steady state alignment (Fig. 2). We find further that differences in apparent lengths cannot be explained by different ODF shapes, which is discussed in greater detail in the ESI,† and Fig. S12. From the results in this work, it is clear that the evolution of the ODF in shear and extensional flow could probably be modeled as a polydisperse system of dilute Brownian rods, with an entanglement term, attributed to the slowing-down of the dynamics specifically in extensional flow.
For the assembly of nanofibrillar building blocks into three dimensional macrostructures, the results in this work strongly emphasize on avoiding shear in the fluidic microsystems. An extruder or spinneret cause significant shear, which result in lower fibril alignment and less interfibrillar contacts. Our observations on the in situ dynamics are very well in agreement with the mechanical properties of nanostructured CNF fibers fabricated using the extensional-flow that resulted in 500% higher strength and stiffness values22 compared to the other shear-dominated approaches typically applied to induce the assembly.60,61
The dynamic characterization demonstrated here clearly provides a unique possibility to study the structural organization of the nanofibrillar network during flow deformations. Even though the exact origin of the apparent lengths is difficult to assess, the flow-stop experiment provides a unique dynamic fingerprint of the nanofibrillar dispersion, which is crucial both to determine if the dispersion is useful in a particular process (e.g. spinning filaments with aligned fibrils) or to determine what process is suitable to promote alignment for a given dispersion.
5 Conclusions
To conclude, we have introduced a technique for dynamic characterization of nanofibrils in situ. The real-time dynamics of fibrils is studied under shear and extension. Rotary diffusion measurements from POM were combined with SAXS to ensure the relation between birefringence and orientation distribution of fibrils. The diffusion of nanofibrils is observed to be a multiple time-scale process where the fastest and slowest diffusion rates are described here in terms of a minimum and maximum apparent fibril lengths Lmin and Lmax, respectively.As expected from an ideal system of polydisperse rods, Lmin is correlated to the strain rate in the flow regardless of type of deformation (shear or extension). The higher strain rate in the shear-dominated regions resulted in lower values of Lmin, as shorter fibrils will be included in the total aligned fraction of the CNF.
However, the maximum apparent length Lmax is not behaving like the ideal system, and is highly dependent on the type of deformation. In extensional flow, with increasing deformation regardless of rate, Lmax is found to increase, most probably due to entanglement of the longest fibrils that slows down their diffusive dynamics. In the shear flow, we do not find the same entanglement effects, thus resulting in much lower values of Lmax.
The demonstrated dynamic characterization methodology is required to understand the complex nanoscale non-equilibrium state and dynamics of polydisperse nanoparticle systems. In a materials fabrication perspective, the entanglements and loose network formation of long fibrils are crucial to the elevated mechanical properties of the nanostructured macroscopic materials fabricated via hydrodynamic approaches.5 A dispersion of mainly long semi-flexible nanofibrils is therefore desirable. However, working with these nanofibrils require that the process has minimal shear and high extension at concentrations that allow for a loose networks to form. If the aim is to align particles that are short and stiff, shear dominated flows might be more suitable, or even necessary, in order to reach high enough rates of deformation. The presented methodology provides fast and easy access to the complex structural dynamics of nanoparticles that are currently accessible only via synchrotron sources, if at all. Our results strongly emphasize the need on a careful selection of microfluidic tools for the assembly of nanoparticles into superstructures, by a thorough fundamental understanding of the hydrodynamics on the nanoscale organization. Moreover, the insights from this study are not only limited to the cellulosic materials but can easily be extended to other non-spherical nanoscale building blocks e.g. DNA-molecules, liquid crystals, inorganic nanoparticles, protein- and polymer-based nanofibrils.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from Wallenberg Wood Science Center (WWSC), the Alf de Ruvo Memorial Foundation and the Hans Werthen Foundation. A special thanks to Dr C. Brouzet and Dr K. Håkansson for the helpful discussions regarding both the POM experiments and the analysis of the SAXS results. T. R. also acknowledges helpful discussions with Prof. B. S. Hsiao. Furthermore, the kind assistance during the SAXS experiments by Krishnegowda V., Dr S. Yu and Dr J. McKenzie is gratefully acknowledged.Notes and references
- S. Ling, D. L. Kaplan and M. J. Buehler, Nat. Rev. Mater., 2018, 3, 18016 CrossRef CAS.
- N. Mittal, R. Jansson, M. Widhe, T. Benselfelt, K. M. Håkansson, F. Lundell, M. Hedhammar and L. D. Söderberg, ACS Nano, 2017, 11, 5148–5159 CrossRef CAS PubMed.
- U. G. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2015, 14, 23–36 CrossRef CAS PubMed.
- K. Gowda, C. Brouzet, T. Lefranc, L. D. Söderberg and F. Lundell, J. Fluid Mech., 2019, 876, 1052–1076 CrossRef.
- C. Brouzet, N. Mittal, F. Lundell and L. D. Söderberg, Macromolecules, 2018, 52, 2286–2295 CrossRef.
- Y. Mao, K. Liu, C. Zhan, L. Geng, B. Chu and B. S. Hsiao, J. Phys. Chem. B, 2017, 121, 1340–1351 CrossRef CAS PubMed.
- S. Chen and T. Kraus, J. Phys. Chem. C, 2012, 116, 16766–16775 CrossRef CAS.
- M. Glidden and M. Muschol, J. Phys. Chem. C, 2012, 116, 8128–8137 CrossRef CAS.
- M. Haghighi, M. N. Tahir, W. Tremel, H.-J. Butt and W. Steffen, J. Chem. Phys., 2013, 139, 064710 CrossRef PubMed.
- S. Balog, L. Rodriguez-Lorenzo, C. A. Monnier, M. Obiols-Rabasa, B. Rothen-Rutishauser, P. Schurtenberger and A. Petri-Fink, Nanoscale, 2015, 7, 5991–5997 RSC.
- B. Chu and T. Liu, J. Nanopart. Res., 2000, 2, 29–41 CrossRef CAS.
- B. Chu and B. S. Hsiao, Chem. Rev., 2001, 101, 1727–1762 CrossRef CAS PubMed.
- N. Stribeck, X-Ray Scattering of Soft Matter, Springer Science & Business Media, Berlin Heidelberg, 2007 Search PubMed.
- R. H. Somani, B. S. Hsiao, A. Nogales, S. Srinivas, A. H. Tsou, I. Sics, F. J. Balta-Calleja and T. A. Ezquerra, Macromolecules, 2000, 33, 9385–9394 CrossRef CAS.
- F. E. Caputo and W. R. Burghardt, Macromolecules, 2001, 34, 6684–6694 CrossRef CAS.
- T. Pfohl, A. Otten, S. Köster, R. Dootz, B. Struth and H. M. Evans, Biomacromolecules, 2007, 8, 2167–2172 CrossRef CAS PubMed.
- Y. Liu, W. Zhou, K. Cui, N. Tian, X. Wang, L. Liu, L. Li and Y. Zhou, Rev. Sci. Instrum., 2011, 82, 045104 CrossRef PubMed.
- M. Trebbin, D. Steinhauser, J. Perlich, A. Buffet, S. V. Roth, W. Zimmermann, J. Thiele and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6706–6711 CrossRef CAS PubMed.
- B. F. Silva, M. Zepeda-Rosales, N. Venkateswaran, B. J. Fletcher, L. G. Carter, T. Matsui, T. M. Weiss, J. Han, Y. Li, U. Olsson and C. R. Safinya, Langmuir, 2015, 31, 4361–4371 CrossRef CAS PubMed.
- V. Lutz-Bueno, J. Zhao, R. Mezzenga, T. Pfohl, P. Fischer and M. Liebi, Lab Chip, 2016, 16, 4028–4035 RSC.
- A. Kamada, N. Mittal, L. D. Söderberg, T. Ingverud, W. Ohm, S. V. Roth, F. Lundell and C. Lendel, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1232–1237 CrossRef CAS PubMed.
- N. Mittal, F. Ansari, K. Gowda, V. C. Brouzet, P. Chen, P. T. Larsson, S. V. Roth, F. Lundell, L. Wågberg, N. A. Kotov and L. D. Söderberg, ACS Nano, 2018, 12, 6378–6388 CrossRef CAS PubMed.
- K. M. O. Håkansson, F. Lundell, L. Prahl-Wittberg and L. D. Söderberg, J. Phys. Chem. B, 2016, 120, 6674–6686 CrossRef PubMed.
- T. Rosén, R. Wang, C. Zhan, H. He, S. Chodankar and B. S. Hsiao, Phys. Rev. E, 2020, 101, 032610 CrossRef PubMed.
- D. O. Riese, W. L. Vos, G. H. Wegdam, F. J. Poelwijk, D. L. Abernathy and G. Grübel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 1676–1680 CrossRef CAS PubMed.
- S. Busch, T. H. Jensen, Y. Chushkin and A. Fluerasu, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 55–62 CrossRef CAS PubMed.
- A. Fluerasu, P. Kwasniewski, C. Caronna, F. Destremaut, J.-B. Salmon and A. Madsen, New J. Phys., 2010, 12, 035023 CrossRef.
- P. Holmqvist, V. Meester, F. Westermeier and D. Kleshchanok, J. Chem. Phys., 2013, 139, 084905 CrossRef CAS PubMed.
- J. Wagner, C. Märkert, B. Fischer and L. Müller, Phys. Lett., 2013, 110, 048301 CrossRef PubMed.
- R. Cerf and H. A. Scheraga, Chem. Rev., 1952, 51, 185–261 CrossRef CAS.
- C. Rosenblatt, R. B. Frankel and R. P. Blakemore, Biophys. J., 1985, 47, 323–325 CrossRef CAS.
- P. L. Frattini and G. G. Fuller, J. Fluid Mech., 1986, 168, 119–150 CrossRef CAS.
- C. Brouzet, N. Mittal, L. D. Söderberg and F. Lundell, ACS Macro Lett., 2018, 7, 1022–1027 CrossRef CAS.
- S. S. Rogers, P. Venema, L. M. Sagis, E. van der Linden and A. M. Donald, Macromolecules, 2005, 38, 2948–2958 CrossRef CAS.
- Q. Liu, M. G. Campbell, J. S. Evans and I. I. Smalyukh, Adv. Mater., 2014, 26, 7178–7184 CrossRef CAS PubMed.
- B. H. Zimm, J. Chem. Phys., 1956, 24, 269–278 CrossRef CAS.
- G. Fuller and L. Leal, Rheol. Acta, 1980, 19, 580–600 CrossRef CAS.
- K. Lim, A. Kapitulnik, R. Zacher and A. Heeger, J. Chem. Phys., 1985, 82, 516 CrossRef CAS.
- S. J. Johnson, P. L. Frattini and G. G. Fuller, J. Colloid Interface Sci., 1985, 104, 440–455 CrossRef CAS.
- F. Del Giudice, S. J. Haward and A. Q. Shen, J. Rheol., 2017, 61, 327–337 CrossRef CAS.
- A. W. Chow and G. G. Fuller, Macromolecules, 1985, 18, 786–793 CrossRef CAS.
- A. W. Chow, G. G. Fuller, D. G. Wallace and J. A. Madri, Macromolecules, 1985, 18, 786–793 CrossRef CAS.
- T. J. Ober, J. Soulages and G. H. McKinley, J. Rheol., 2011, 55, 1127–1159 CrossRef CAS.
- J. Phalakornkul, A. Gast and R. Pecora, Macromolecules, 1999, 32, 3122–3135 CrossRef CAS.
- G. G. Fuller, Annu. Rev. Fluid Mech., 1990, 22, 387–417 CrossRef.
- K. M. Håkansson, A. B. Fall, F. Lundell, S. Yu, C. Krywka, S. V. Roth, G. Santoro, M. Kvick, L. P. Wittberg and L. Wågberg, et al. , Nat. Commun., 2014, 5, 4018 CrossRef PubMed.
- L. Wågberg, G. Decher, M. Norgren, T. Lindström, M. Ankerfors and K. Axnäs, Langmuir, 2008, 24, 784–795 CrossRef PubMed.
- T. Cubaud and S. Notaro, Phys. Fluids, 2014, 26, 122005 CrossRef.
- M. V. Gurp, Colloid Polym. Sci., 1995, 273, 607–625 CrossRef.
- A. Buffet, A. Rothkirch, R. Döhrmann, V. Körstgens, M. M. Abul Kashem, J. Perlich, G. Herzog, M. Schwartzkopf, R. Gehrke and P. Müller-Buschbaum, et al. , J. Synchrotron Radiat., 2012, 19, 647–653 CrossRef CAS PubMed.
- T. Rosén, C. Brouzet, S. V. Roth, F. Lundell and L. D. Söderberg, J. Phys. Chem. C, 2018, 122, 6889–6899 CrossRef.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford university press, New York, 1986 Search PubMed.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- S. B. Lindström and T. Uesaka, Phys. Fluids, 2007, 19, 113307 CrossRef.
- G. Marrucci and N. Grizzuti, J. Polym. Sci., Polym. Lett. Ed., 1983, 21, 83–86 CrossRef CAS.
- G. Marrucci and N. Grizzuti, J. Non-Newtonian Fluid Mech., 1984, 14, 103–119 CrossRef CAS.
- O. Forgacs and S. Mason, J. Colloid Sci., 1959, 14, 473–491 CrossRef CAS.
- D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727 CrossRef CAS PubMed.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS PubMed.
- A. Walther, J. V. Timonen, I. Dez, A. Laukkanen and O. Ikkala, Adv. Mater., 2011, 23, 2924–2928 CrossRef CAS PubMed.
- A. Bentez and A. Walther, J. Mater. Chem. A, 2017, 5, 16003–16024 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01975h |
| ‡ Present address: Treesearch, KTH Royal Institute of Technology, Teknikringen 56-58, SE-100 44 Stockholm, Sweden. |
| § Present address: Department of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. |
| ¶ Present address: School of Materials Science and Engineering, PCFM Lab, Sun Yat-sen University, Guangzhou, 510275, China. |
| This journal is © The Royal Society of Chemistry 2020 |