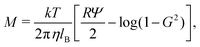DOI:
10.1039/C9SM01938C
(Paper)
Soft Matter, 2020,
16, 238-246
Advective-diffusive spreading of diffusiophoretic colloids under transient solute gradients†
Received
26th September 2019
, Accepted 11th November 2019
First published on 12th November 2019
Abstract
We analytically calculate the one-dimensional advective-diffusive spreading of a point source of diffusiophoretic (DP) colloids, driven by the simultaneous diffusion of a Gaussian solute patch. The spreading of the DP colloids depends critically on the ratio of the DP mobility, M (which can be positive or negative), to the solute diffusivity, Ds. For instance, we demonstrate, for the first time, that solute-repelling colloids (M < 0) undergo long-time super-diffusive transport for M/Ds < −1. In contrast, the spreading of strongly solute-attracting colloids (M/Ds ≫ 1) can be spatially arrested over long periods on the solute diffusion timescale, due to a balance between colloid diffusion and DP under the evolving solute gradient. Further, a patch of the translating solute acts as a “shuttle” that rapidly transports the colloids relative to their diffusive timescale. Finally, we use numerical computations to show that the above behaviors persist for three-dimensional, radially symmetric DP spreading. The results presented here could guide the use of DP colloids for microscale particle sorting, deposition, and delivery.
1 Introduction
Diffusiophoresis (DP) is the deterministic drift of one species induced by the concentration gradient of another species.1–3 A common instance is DP of a colloidal particle in an electrolyte gradient, where the DP colloid velocity uDP is proportional to the gradient of the logarithm of the solute (ion) concentration S; that is, uDP = M∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S.4 Prior studies focused on calculating the DP mobility M with respect to the interactions between the colloid and the surrounding ions, showing that M can be positive or negative, corresponding to DP driving colloids up (solute-attracting) or down (solute-repelling) the solute gradient, respectively.1,2,4–8 Recently, there has been intense interest in utilizing DP to affect microscale colloid transport, including modification of the Batchelor scale for mixing9,10 and chaotic advection;11–13 log-sensing osmotic traps and particle manipulation;14–18 and transport in dead-end pores.19–22 Underlying these applications is the nonlinear relation between the DP colloid velocity and the solute gradient.
S.4 Prior studies focused on calculating the DP mobility M with respect to the interactions between the colloid and the surrounding ions, showing that M can be positive or negative, corresponding to DP driving colloids up (solute-attracting) or down (solute-repelling) the solute gradient, respectively.1,2,4–8 Recently, there has been intense interest in utilizing DP to affect microscale colloid transport, including modification of the Batchelor scale for mixing9,10 and chaotic advection;11–13 log-sensing osmotic traps and particle manipulation;14–18 and transport in dead-end pores.19–22 Underlying these applications is the nonlinear relation between the DP colloid velocity and the solute gradient.
The advective-diffusive spreading of DP colloids is particularly rich precisely due to the nonlinear dependence of uDP on S. For instance, Ault et al.21 calculated similarity solutions for the entrainment (extraction) of DP colloids into (from) a dead-end pore, under the assumption that the transport is one-dimensional along the axis of the pore. The pore initially is filled uniformly with a solute and is devoid of colloids. Colloids continuously enter the pore via a boundary with a prescribed colloid concentration. The same boundary also allows solute exchange by which a solute gradient within the pore is developed to cause colloid DP. In the limit of negligible colloid diffusivity, the method of characteristics was applied to predict the DP colloid motion. This group later extended their analysis to quantify particle focusing under pressure-driven and diffusioosmotic flows.22 Raynal et al.9 analyzed the spreading of a coincident deposition of Gaussian patches of solute and colloids in a two-dimensional linear flow, demonstrating that a patch of solute-attracting colloids first undergoes spatial compression before eventually spreading in the flow. Subsequently, an effective Péclet number for quantifying the mixing of colloids and salt in the same setting as in ref. 9 as well as in a sinusoidal patch under a two-dimensional periodic flow was defined.10
In this article, we analyze the advective-diffusive spreading of a point source of DP colloids, driven by the simultaneous diffusion of a Gaussian solute patch. In Section 2, we calculate the one-dimensional DP spreading of a point source of colloids under the influence of a diffusing solute patch whose centroid is coincident with that of the colloid distribution. Exact solutions of the solute and colloid evolution are derived to demonstrate, for the first time, two novel phenomena: super-diffusion of solute-repelling colloids and arrested spreading (which might be interpreted as “extreme sub-diffusion”) of strongly solute-attracting colloids. An asymptotic analysis is conducted to unify the long-time response for a variety of initial solute profiles. In Section 3, we illustrate how super-diffusion and arrested spreading could enhance the extraction and delivery of DP colloids when coupled with a spatially non-coincident deposition of solute and colloids. In Section 4, we show that a non-coincident deposition of the solute that undergoes advection could shuttle colloids over large distances rapidly compared to their diffusive transport. In Section 5, we use numerical computations to show that the above behaviors persist for three-dimensional DP spreading. We summarize this study and offer ideas for future work in Section 6.
2 One-dimensional coincident DP spreading
We first focus on the simplest physical picture of one-dimensional DP transport, mimicking that in a long, uniform microchannel. This will allow us to derive exact solutions, whose behavior we show persists in higher spatial dimensions. Thus, consider DP of a point source of colloids in an unbounded domain −∞ < x < ∞ in the absence of solvent flow. For a colloid concentration C much less than that of the solute S, the influence of the evolution of C on S is negligible. This approximation originates from Anderson, Prieve, and co-workers,2,4,5,23 who formally derived the relation uDP = M∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S first proposed by Derjaguin and co-workers.1 The chief physical assumption of the relation is based on an ideal solution such that the ionic fluxes are given by the Nernst–Planck equation, which gives very good predictions for electrolyte solutions up to millimolar concentration near moderately charged surfaces of zeta potential ζ ∼ O(kT/e) (k the Boltzmann constant, T the absolute temperature, and e the unit charge). The effects of non-ideal solution such as steric repulsion due to finite ion size, which are important in concentrated electrolytes or nano-confined systems, will generate additional chemical potentials and hence fluxes to the classical Nernst–Planck equation. Relevant discussions and detailed analyses can be found in ref. 6 and 7. Recent experiments13–16,20 have shown excellent agreements with theoretical predictions9,10,12,21,22 of DP colloid transport based on the present approximations. Hence, DP of the colloids is due to a simultaneous, spatially coincident source of the solute whose diffusive transport is governed by
S first proposed by Derjaguin and co-workers.1 The chief physical assumption of the relation is based on an ideal solution such that the ionic fluxes are given by the Nernst–Planck equation, which gives very good predictions for electrolyte solutions up to millimolar concentration near moderately charged surfaces of zeta potential ζ ∼ O(kT/e) (k the Boltzmann constant, T the absolute temperature, and e the unit charge). The effects of non-ideal solution such as steric repulsion due to finite ion size, which are important in concentrated electrolytes or nano-confined systems, will generate additional chemical potentials and hence fluxes to the classical Nernst–Planck equation. Relevant discussions and detailed analyses can be found in ref. 6 and 7. Recent experiments13–16,20 have shown excellent agreements with theoretical predictions9,10,12,21,22 of DP colloid transport based on the present approximations. Hence, DP of the colloids is due to a simultaneous, spatially coincident source of the solute whose diffusive transport is governed by| | 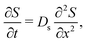 | (1) |
where Ds is the solute diffusivity and t is the time. For a Gaussian distribution of the solute centered at x = 0 and deposited at t = 0,| | 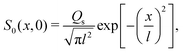 | (2) |
where 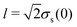 is the lengthscale characterizing the initial solute width [σs2(0) is the initial solute variance], the solution to eqn (1) is
is the lengthscale characterizing the initial solute width [σs2(0) is the initial solute variance], the solution to eqn (1) is| | 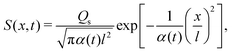 | (3) |
with centroid and variance24| | 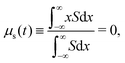 | (4) |
and| | 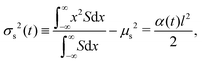 | (5) |
where Qs is the mass of the solute per unit area and α(t) = 1 + 4Dst/l2. Eqn (1) yields the DP velocity uDP = M∂(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S)/∂x = −2Mx/(α(t)l2) in the advection-diffusion equation for the colloids:
S)/∂x = −2Mx/(α(t)l2) in the advection-diffusion equation for the colloids:| | 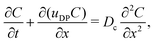 | (6) |
where Dc is the diffusivity of the colloid. Note that uDP is spatially non-uniform and hence represents a “compressible” velocity field. Thus, eqn (6) becomes| | 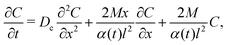 | (7) |
whose solution for a point source of colloids at x = 0 and t = 0, C0(x,0) = Qcδ(x)δ(t), is‡| | 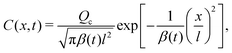 | (8) |
with| | 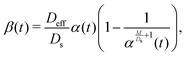 | (9) |
where Qc is the mass of colloids per unit area, δ is the Dirac delta, and Deff = DcDs/(M + Ds) is an effective diffusivity which also appears in the effective Péclet number of previous studies.9,11,12 Consistent with prior work, DP colloid evolution [eqn (8)] is not obtained simply via replacing Ds by Deff in the solute evolution [eqn (3)], due to the compressibility of the DP velocity. In other words, DP spreading cannot be simply treated as pure diffusion with an effective diffusivity. The centroid and the variance of the colloid distribution are given by eqn (4) and (5) with S replaced by C.
We plot the time evolution of S, C, and σc2 in Fig. 1. The variance is
| | 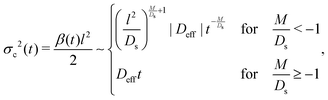 | (10) |
where long-time asymptotics at
t ≫
l2/
Ds are shown on the right of the half bracket. Henceforth we choose an experimentally relevant ratio
Dc/
Ds = 10
−2, which corresponds to colloids of size
O(10
−2–10
−1) μm for small ion solutes of
Ds =
O(10
3–10
2) μm
2 s
−1. All phenomena discussed below persist for
Dc/
Ds ≪ 1. The evolution of the colloids depends critically on
M/
Ds [
Fig. 1(a)], which is typically
O(1) and can be positive or negative.
16,20 For
M/
Ds < −1,
§ the solute-repelling DP leads to super-diffusion of colloids at long times:
σc2 ∼
t−M/Ds, indicating that rapid spreading of colloids can be achieved by DP. The prediction of super-diffusion is the major, original conclusion of our work. For instance, at
t/(
l2/
Ds) = 10
2, the variance for
M/
Ds = −5 is
O(10
10) times larger than that for
M/
Ds = 0. For illustrative purpose in a situation where
Ds =
O(10
3) μm
2 s
−1 and
l =
O(10) μm, DP colloids will spread over a characteristic distance
σc =
O(10
2) μm in 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
s for
M/
Ds = −5 compared to
σc =
O(1) μm for
M/
Ds = 0. For −1 ≤
M/
Ds ≤ 1, DP has a relatively minor impact on the diffusive spreading of colloids. For
M/
Ds = 10
3,
¶ the colloids first undergo regular diffusion at short times [
t/(
l2/
Ds) ≲ 10
−3];
σc2 grows linearly with time. Subsequently, the DP forces that drive the colloids up the solute gradient dominate over diffusion of colloids. Solute-attracting DP inhibits the diffusive spread of colloids such that over a sizable period of time, 5 × 10
−4 ≲
t/(
l2/
Ds) ≲ 5 × 10
−2, the colloid spreading is spatially arrested, which might be interpreted as an extreme sub-diffusion, in contrast to the super-diffusive behavior mentioned above. At
t/(
l2/
Ds) ≳ 10
−1 the solute gradient is sufficiently weak—the arrest is relaxed—and the colloid distribution recovers a diffusive spreading with an effective diffusion coefficient
Deff, highlighting that DP affects the long-time transport. As a general remark, the time interval of arrested spreading increases with
M/
Ds.
Fig. 1(b) illustrates the difference in the broadening of the colloid distribution between different values of
M/
Ds at
t/(
l2/
Ds) = 10
2. For arrested spreading (
M/
Ds = 10
3) the colloid distribution broadens negligibly; the colloids spread more than 10
2 times the width of the initial solute distribution in the presence of super-diffusion (
M/
Ds = −2). The spreading occurs on the solute diffusion time, which is much faster than the colloid diffusion time since
Dc/
Ds is small. The centroids of the colloid distributions remain stationary,
μc = 0.
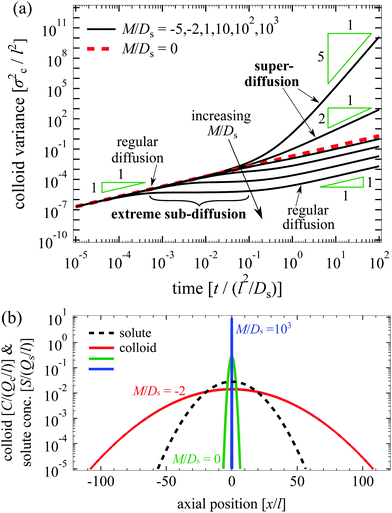 |
| | Fig. 1 (a) Time evolution of σc2/l2 for Dc/Ds = 0.01 and various M/Ds. From top to bottom: M/Ds = −5, −2,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (red dotted), 1, 10, 102, and 103. Super-diffusion of colloids occurs at long times for M/Ds < −1 whereas arrested spreading or “extreme sub-diffusion” occurs at intermediate times for M/Ds ≫ 1. (b) C/(Qc/l) (red solid: M/Ds = −2; green solid: M/Ds = 0; and blue solid: M/Ds = 103) and S/(Qs/l) (black dotted) for Dc/Ds = 0.01 and various M/Ds at t/(l2/Ds) = 102. Colloids undergoing super-diffusion (M/Ds = −2) exhibit significant spreading in contrast to the case with arrested spreading (M/Ds = 103) or without DP (M/Ds = 0). (red dotted), 1, 10, 102, and 103. Super-diffusion of colloids occurs at long times for M/Ds < −1 whereas arrested spreading or “extreme sub-diffusion” occurs at intermediate times for M/Ds ≫ 1. (b) C/(Qc/l) (red solid: M/Ds = −2; green solid: M/Ds = 0; and blue solid: M/Ds = 103) and S/(Qs/l) (black dotted) for Dc/Ds = 0.01 and various M/Ds at t/(l2/Ds) = 102. Colloids undergoing super-diffusion (M/Ds = −2) exhibit significant spreading in contrast to the case with arrested spreading (M/Ds = 103) or without DP (M/Ds = 0). | |
The transition of colloid evolution from regular diffusion for M/Ds ≥ −1 to super-diffusion for M/Ds < −1 at long times is expected for a broad class of initial colloid C0(x,0) and solute S0(x,0) distributions. By the method of steepest descent,26S0(x,0) asymptotes to a Gaussian
| | 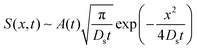 | (11) |
at long times, provided that
| | 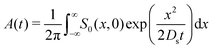 | (12) |
is a convergent integral. All information of the initial solute distribution is encompassed in
A(
t). However,
uDP ∼
Mx/2
Dst at long times because the time-dependent term of
α(
t) dominates; that is
uDP is independent of
A(
t) at long times. Hence, the influence of the initial solute distribution on the DP spreading is lost. Hence, the long-time colloid transport equation is
| | 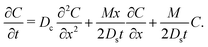 | (13) |
Since eqn (13) is the long-time asymptote of eqn (7), we expect the transition from regular to super-diffusion to be generic for a variety of initial solute profiles. We illustrate this by numerically solving the DP spreading of an initially smoothed point source of colloids subject to a Laplace distribution of the solute [Fig. 2(b)]:
| | 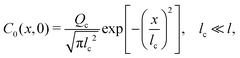 | (14) |
and
| | 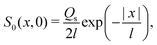 | (15) |
where
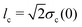
is the lengthscale of the initial colloid distribution. Numerical solutions are obtained by a standard forward-in-time-central-in-space finite-difference scheme.
27 The transition is clearly demonstrated in
Fig. 2(a), which leads to significantly different long-time colloid spreading between the case with and without super-diffusion [
Fig. 2(c)]. Notice too that the solute profile eventually becomes Gaussian.
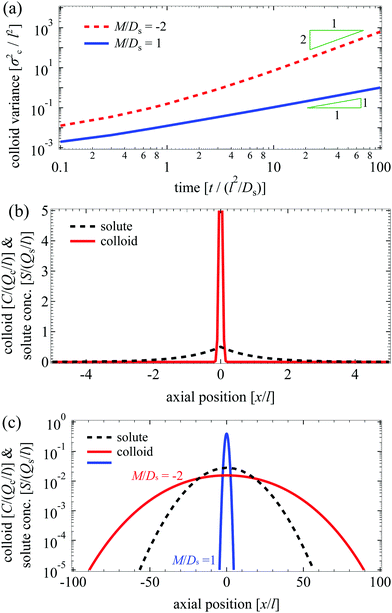 |
| | Fig. 2 (a) Evolution of σc2/l2 for Dc/Ds = 0.01 and various M/Ds for an initial Laplace distribution of the solute. Red dotted: M/Ds = −2; blue solid: M/Ds = 1. (b) Initial colloid and solute distributions, C/(Qc/l) (red solid) and S/(Qs/l) (black dotted), for Dc/Ds = 0.01. (c) C/(Qc/l) (red solid: M/Ds = −2; blue solid: M/Ds = 1) and S/(Qs/l) (black dotted) for Dc/Ds = 0.01 and various M/Ds at t/(l2/Ds) = 102. Transition from regular diffusion for M/Ds ≥ −1 to super-diffusion for M/Ds < −1 at long times is not limited to an initial point source of colloids and a Gaussian solute profile. | |
3 One-dimensional non-coincident DP spreading
Next, we demonstrate how a spatially non-coincident source of solute and colloids can enhance colloid extraction and delivery when coupled with arrested spreading and super-diffusion responses. The diffusion of a Gaussian distribution of the solute centered at x = x0 and deposited at t = 0,| | 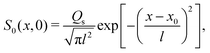 | (16) |
is described by eqn (3) with x being replaced by x − x0. The corresponding colloid transport equation is identical to eqn (7) except that x in the prefactor of the ∂C/∂x term is replaced by x − x0. The solution for a point source of colloids at x = 0 and t = 0 is then||| | 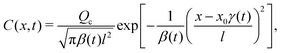 | (17) |
where 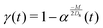 , and the centroid isThe variance is the same as eqn (10).
, and the centroid isThe variance is the same as eqn (10).
The time evolution of S, C, μc, and σc2 are plotted in Fig. 3. First consider the solute-attracting case of M/Ds = 103 [Fig. 3(a) and (b); see supplementary videos, ESI†]. As the solute is deposited at x0/l = 5, colloids are attracted towards the solute centroid—a “soluto-inertial beaconing” effect that has been observed experimentally.14,17 Here, we show that this beaconing can be coupled to arrested spreading to achieve a high recovery of colloids from a remote location: while the colloid distribution broadens slightly at short times [t/(l2/Ds) ≲ 10−3], the spreading of colloids is subsequently arrested and major spreading only occurs upon colloids arrival at the solute centroid. Note that the evolutions of σc2 with t are the same regardless of x0. The evolutions of μc with t for different x0 can be collapsed onto a single curve upon dividing by x0, as apparent from eqn (18).
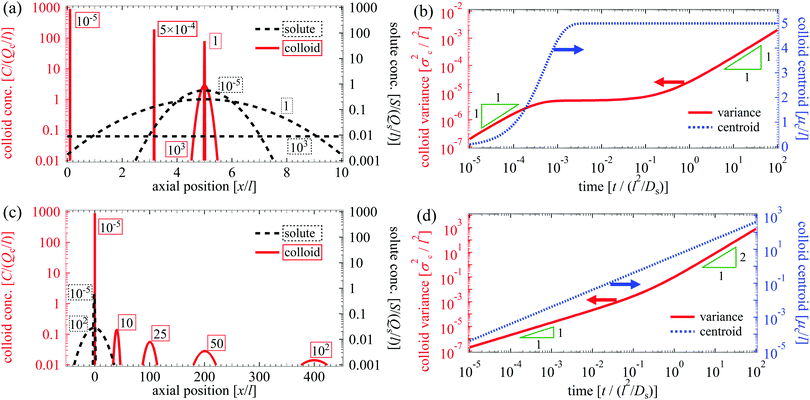 |
| | Fig. 3 Time evolution of (a) C/(Qc/l) (red solid) and S/(Qs/l) (black dotted) and (b) σc2/l2 (red solid) and μc/l (blue dotted) for M/Ds = 103, Dc/Ds = 0.01 and x0/l = 5. By arrested spreading, the majority spreading of colloids occurs upon it being attracted towards the solute centroid, leading to high recovery of colloids. Time evolution of (c) C/(Qc/l) (red solid) and S/(Qs/l) (black dotted) and (d) σc2/l2 (red solid) and μc/l (blue dotted) for M/Ds = −2, Dc/Ds = 0.01 and x0/l = −1. Colloids are transported and spread over a large distance due to repelling solute and super-diffusion, suggesting enhanced colloid delivery. In (a) and (c) the time labels in the dotted and solid boxes refer to the solute and colloid distribution, respectively, for different t/(l2/Ds). In (b) and (d), the arrows point at the y-axes to which the lines refer. These evolutions can be seen clearly in the supplementary videos, (ESI†). | |
Fig. 3(c) and (d) (see supplementary videos, ESI†) show the solute-repelling case of M/Ds = −2. Here, the colloids are driven away from the solute deposited at x0/l = −1. The colloids spread diffusively initially after which super-diffusion takes over at long times. Notice the large distance traveled by the colloids, whose centroid reaches x/l = 400 at t/(l2/Ds) = 102. If DP was absent, the colloids would spread diffusively about x = 0 and a negligible amount would reach x/l = 400 at t/(l2/Ds) = 102. Thus, the present results suggest a means for enhanced colloid delivery via DP. Previous remarks concerning Fig. 3(b) on the evolution of σc2 and μc with t and the collapse of the latter onto a single curve also holds for Fig. 3(d).
4 One-dimensional non-coincident DP spreading under a translating solute
Here, we analyze colloid transport by a spatially non-coincident release of the solute that is undergoing advection upon its deposition. The colloids are free from solvent advection. This case mimics and generalizes a recent laboratory setup: a “soluto-inertial beacon” that emits a long-lasting solute flux.17 Although in ref. 17 the beacon was not translating, this could be realized by a beacon that sediments under gravity while the colloids are neutrally buoyant. Consider a Gaussian distribution of the solute centered at x = x0 and deposited at t = 0 that is now advected with a constant velocity w upon its release. Since w is a spatial and temporal constant, the effect of the solvent flow is simply to advect the centroid of the solute Gaussian, without distortion of its shape into a fore-aft asymmetric form. This statement is valid for one-dimensional advective-diffusive transport. Note, in our suggestion of a sedimenting beacon the (three-dimensional) solvent velocity field around the beacon could lead to a loss of the fore-aft symmetry of solute release. Here, the solute evolution is described by eqn (3) with x being replaced by x − x0 − wt such that the solute centroid μs(t) = x0 + wt. The corresponding colloid DP transport equation is identical to eqn (7) except that x in the prefactor of the ∂C/∂x term is replaced by x − x0 − wt. The solution for a point source of colloids at x = 0 and t = 0 is**| | 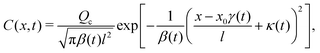 | (19) |
where| | 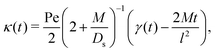 | (20) |
with Pe = wl/Ds, a Péclet number describing the relative importance of solute advection to diffusion. The centroid of the colloids is| | | μc(t) = x0γ(t) − κ(t)l. | (21) |
The variance is the same as eqn (10).
We plot the time evolution of μc, σc2, and μs for Pe = 1 in Fig. 4. With M/Ds = 103 [Fig. 4; see supplementary videos, ESI†], colloids are attracted towards the initial solute centroid regardless of x0. Strongly attractive DP arrests spreading of colloids at early times, and the majority of spreading occurs at long times over which colloids are advected with the solute [μc ∼ μs at t/(l2/Ds) ≫ 1]. Here, the solute acts to guide and shuttle the movement, spreading, and deposition of colloids. Controlled deposition can also be achieved by solute-repelling DP [Fig. 5] where the deposition distance may be much larger than that for solute-attracting DP. However, a slight difference in M/Ds may lead to a qualitatively different colloid spreading with repelling DP. For instance, for M/Ds = −1.5 the solute and colloids travel in the opposite direction, which is in contrast to that for M/Ds = −2.5 despite the same x0/l = −1 [Fig. 5(a)]. This occurs because, with M/Ds = −1.5, solute advection is strong relative to the DP velocity at early times such that the solute centroid overtakes that of the colloids. Regardless of the sign and magnitude of w, such a bi-directional transport of solute and colloids is observed for a spatially coincident deposition with solute advection [Fig. 5(b); M/Ds = −1.5, x0 = 0].
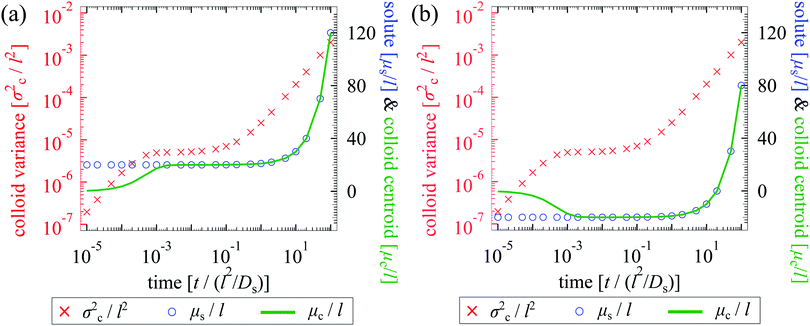 |
| | Fig. 4 Time evolution of σc2/l2 (red crosses), μs/l (blue circles), and μc/l (solid green) for M/Ds = 103, Dc/Ds = 0.01, and Pe = 1. (a) x0/l = 20; (b) x0/l = −20. In both cases, colloids are first attracted towards the solute centroid and then shuttled by the solute. The evolutions in (a) can be seen clearly in the supplementary videos, (ESI†). | |
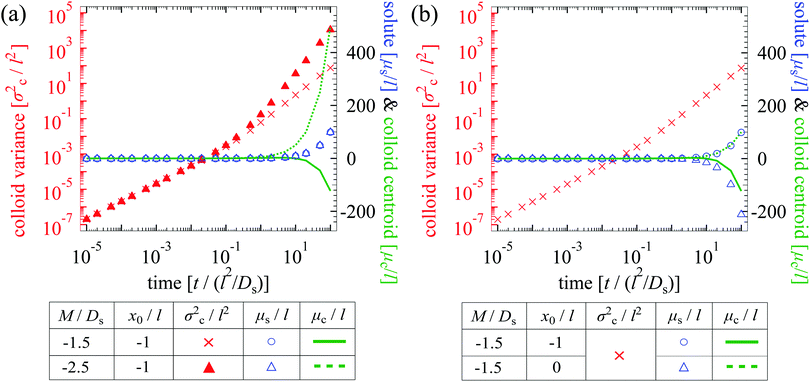 |
| | Fig. 5 Time evolution of σc2/l2 (red crosses and solid triangles), μs/l (blue circles and triangles), and μc/l (green solid and dotted lines) for Dc/Ds = 0.01, and Pe = 1. The two panels share the same set of data for M/Ds = −1.5 and x0/l = −1 for comparison. In (a), changing M/Ds from −1.5 to −2.5 while keeping x0/l fixed causes the solute and colloids to travel in the same direction. In (b), a bi-directional transport of the solute and colloids is always observed for a spatially coincident deposition (x0/l = 0). | |
5 Three-dimensional DP spreading
Lastly, we show that the novel super-diffusion and arrested spreading responses identified in this work persist for DP in higher dimensions. This is done by generalizing the analysis in Section 2 to three dimensions. The equation governing the diffusive transport of the solute in three dimensions is| | 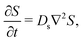 | (22) |
where ∇2 here is the Laplace operator in the spherical coordinate (r,θ,Φ) specifying the radial direction r, the polar angle θ, and the azimuthal angle Φ. For a Gaussian distribution of the solute centered at r = 0 and deposited at t = 0,| | 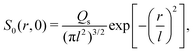 | (23) |
the solution is| | 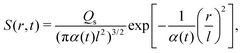 | (24) |
where Qs here is the mass of the solute. Eqn (24) yields the DP velocity uDP = M∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = −2Mr/(α(t)l2)ir (ir is the radial unit vector) in the advection-diffusion equation for the colloids:
S = −2Mr/(α(t)l2)ir (ir is the radial unit vector) in the advection-diffusion equation for the colloids:| | 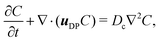 | (25) |
where ∇· is the divergence in spherical coordinates. Thus, eqn (25) becomes, under the assumption of a radially symmetric spreading,| | 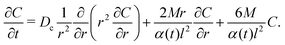 | (26) |
An exact solution of eqn (26) for a point source of colloids at r = 0 and t = 0 is not obtainable by the method employed in the one-dimensional case. Thus, we solve eqn (26) numerically using the built-in partial differential equation solver pdepe in MATLAB and plot the time evolution of σc2 in Fig. 6. As in Fig. 1(a), super-diffusion is observed at long times t ≫ l2/Ds for M/Ds < −1; and the spreading of colloids is spatially arrested—a constant variance over time—at intermediate times for M/Ds ≫ 1. Observations made in Sections 3 and 4, in particular the shuttling response, are also expected to hold in three dimensions.
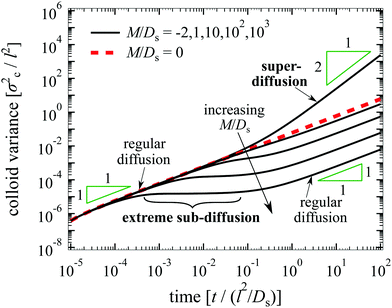 |
| | Fig. 6 Time evolution of σc2/l2 in three dimensions for Dc/Ds = 0.01 and various M/Ds. From top to bottom: M/Ds = −2, 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (red dotted), 1, 10, 102, and 103. Super-diffusion of colloids occurs at long times for M/Ds < −1 whereas arrested spreading or “extreme sub-diffusion” occurs at intermediate times for M/Ds ≫ 1. (red dotted), 1, 10, 102, and 103. Super-diffusion of colloids occurs at long times for M/Ds < −1 whereas arrested spreading or “extreme sub-diffusion” occurs at intermediate times for M/Ds ≫ 1. | |
6 Conclusion
We have analyzed the advective-diffusive spreading of DP colloids under transient solute gradients, revealing three novel phenomena: namely, super-diffusion, arrested spreading (or extreme sub-diffusion), and shuttling. Exact solutions are derived for a one-dimensional point source of colloids in a Gaussian patch of solute for three cases: a spatially coincident and non-coincident deposition, and a non-coincident deposition with a translating solute patch. We have shown that DP radically alters the spreading of colloids, which is critically dependent on the ratio of the DP mobility to solute diffusivity. We have demonstrated that solute-attracting DP can arrest the colloid distribution spreading over a sizable period of time, suggesting a novel mechanism for particle trapping. In contrast, solute-repelling DP leads to super-diffusion of colloids at long times: a means for rapid spreading. An asymptotic analysis indicates that the transition from regular to super-diffusion at long times is generic for a variety of initial solute profiles. For a spatially non-coincident solute and colloid deposition, we have presented two schemes for particle transport: the first to recover a high yield of solute-attracting colloids from a distant location and the second to achieve a long-range, rapid transport of solute-repelling colloids. Further, we have illustrated that a translating solute acts to shuttle the movement of colloids. We closed by demonstrating the generality of the three novel transport phenomena to DP in three spatial dimensions.
As noted in Section 2, we assume that the solute evolution is unaffected by the spreading of the colloid distribution, as is typical in modeling DP colloid transport. Intuitively, or formally from the Onsager reciprocal relation, one may expect that the gradient in the colloid concentration would affect the solute distribution via generation of a cross-flux. However, as demonstrated in experiments on DP transport13–16,20 and recent analyses of multi-component ion transport,28,29 the effect of such a cross-flux, and hence the influence of the colloid motion on the solute distribution, is negligible when the colloid concentration is small compared to that of the solute. This is the relevant limit of our study, in which the colloids are micron-scale and the solute (i.e. ions) is sub-nanometer, and the colloid concentration is orders of magnitude less than the solute concentration. Nevertheless, the effect of cross-fluxes on DP spreading could be relevant to systems where the two species (i.e. the colloid and solute) are of similar size3,30 and concentration.28,29 We will, however, leave this interesting effect for future studies.
The present findings will enable new techniques for colloid transport at microscopic scales, with applications in particle separation, sensing, and deposition. Further modeling work could focus on multiple solute and colloid sources and the stability of the spreading fronts.
Conflicts of interest
There are no conflicts to declare.
Appendix: derivations and solutions for one-dimensional DP spreading
Here, we derive eqn (19) for the colloid concentration in the case of a non-coincident solute deposition, which subsequently undergoes advection with velocity w.31Eqn (19) can readily be simplified to obtain the solution for the other two specific cases, namely coincident [eqn (8)] and non-coincident deposition [eqn (17)], both in the absence of solvent flow.
To obtain eqn (19), we first recall the corresponding advection-diffusion equation
| | 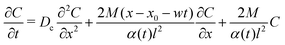 | (27) |
and equate it with the following form
| | 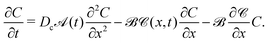 | (28) |
The functions
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
(
t),
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
, and
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
(
x,
t) are identified as
| | ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (t) = 1, (t) = 1, | (29) |
| | 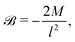 | (30) |
| | 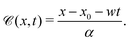 | (31) |
On further equating
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
(
x,
t) =
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) x
x![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
(
t) +
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
t), the functions
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
,
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
(
t), and
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
t) are identified as
| | 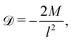 | (32) |
| | ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) = α−1(t), (t) = α−1(t), | (33) |
| | 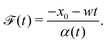 | (34) |
Eqn (27) can then be written as
| | 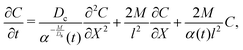 | (35) |
via the transformation
| | 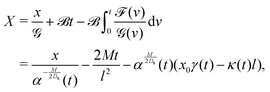 | (36) |
where
| | 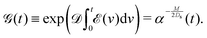 | (37) |
To proceed, an initial condition is assumed
| | C(X,0) = C![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (X), (X), | (38) |
and the following three transformations are invoked
| | 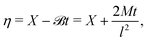 | (39) |
| | 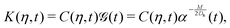 | (40) |
| | 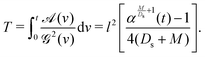 | (41) |
As a result,
eqn (35) can be written as the diffusion equation
| | 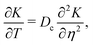 | (42) |
where the initial condition becomes
| | K(η,T = 0) = C![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (η). (η). | (43) |
Thus,
eqn (19) can be obtained from
eqn (42) using the standard method of Green's function.
32
Appendix: a sample physical system showing super-diffusion
Here, we suggest a physical system in which super-diffusion (M/Ds < −1) and arrested spreading (M/Ds ≫ −1) could occur. In the case of charged colloids in a binary electrolyte, the DP mobility M takes the form:23| | 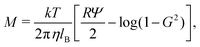 | (44) |
where the first and the second terms on the right-hand side of eqn (44) are the electrophoretic and chemiphoretic contributions to diffusiophoresis, respectively.3,14,23 Here, Ψ = zeζ/kT is the normalized zeta potential of colloids ζ, lB = (ze)2/4πεkT is the Bjerrum length (e the unit charge, z the valence of the ions, k the Boltzmann constant, T the absolute temperature, and ε the dielectric constant of water), and G = tanh(Ψ/4). The factor R ≡ (D+ − D−)/(D+ + D−) is defined using the diffusivity of the cations (D+) and anions (D−). Solute diffusivity is computed by the Nernst–Hartley formula Ds = 2D+D−/(D+ + D−).14,33 For dissociation of phosphoric acid into H+ (D+ = 9.31 × 103 μm2 s−1) and H2PO4− (D− = 0.85 × 103 μm2 s−1),3 the evolution of M/Ds with ζ at T = 363 K (η = 0.32 × 10−3 N s m−2) is shown in Fig. 7. Super-diffusion occurs for ζ < −30 mV whereas weakly arrested spreading [M/Ds ≈ O(10)] is seen for strongly positive ζ. Although strongly arrested spreading is not common in typical settings, it is potentially attainable in some physico-chemical systems21,25 and the present work prompts experiments to seek other systems for exploiting this phenomenon.
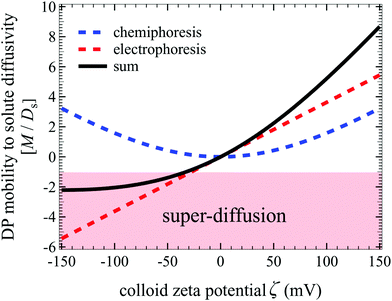 |
| | Fig. 7 Evolution of M/Ds with ζ for D+ = 9.31 × 103 μm2 s−1 and D− = 0.85 × 103 μm2 s−1 at T = 363 K. Blue dotted: normalized chemiporetic mobility; red dotted: normalized electrophoretic mobility; black solid: normalized diffusiophoretic mobility due to the sum of its chemiphoretic and electrophoretic contributions. Super-diffusion is attainable for ζ < −30 mV. | |
Acknowledgements
This work was funded by Procter & Gamble.
References
-
S. S. Dukhin and B. V. Derjaguin, Electrokinetic phenomena, Wiley, New York, 1974 Search PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247–269 CrossRef CAS.
- J. L. Anderson, M. E. Lowell and D. C. Prieve, J. Fluid Mech., 1982, 117, 107–121 CrossRef CAS.
- R. F. Stout and A. S. Khair, Phys. Rev. Fluids, 2017, 2, 014201 CrossRef.
- D. C. Prieve, S. M. Malone, A. S. Khair, R. F. Stout and M. Y. Kanj, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18257–18262 CrossRef CAS.
- A. Gupta, B. Rallabandi and H. A. Stone, Phy. Rev. Fluids, 2019, 4, 043702 CrossRef.
- F. Raynal, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and R. Volk, J. Fluid Mech., 2018, 847, 228–243 CrossRef CAS.
- F. Raynal and R. Volk, J. Fluid Mech., 2019, 876, 818–829 CrossRef.
- J. Deseigne, C. Cottin-Bizonne, A. D. Stroock, L. Bocquet and C. Ybert, Soft Matter, 2014, 10, 4795–4799 RSC.
- R. Volk, C. Mauger, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and F. Raynal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013027 CrossRef CAS.
- C. Mauger, R. Volk, N. Machicoane, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and F. Raynal, Phy. Rev. Fluids, 2016, 1, 034001 CrossRef.
- B. Abecassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, New J. Phys., 2009, 11, 075022 CrossRef.
- J. Palacci, B. Abecassis, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 104, 138302 CrossRef.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Soft Matter, 2012, 8, 980–994 RSC.
- A. Banerjee, I. Williams, R. N. Azevedo, M. E. Helgeson and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8612–8617 CrossRef CAS.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001 CrossRef.
- A. Kar, T. Chiang, I. O. Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS.
- J. T. Ault, P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2017, 13, 9015–9023 RSC.
- J. T. Ault, S. Shin and H. A. Stone, J. Fluid Mech., 2018, 854, 420–448 CrossRef CAS.
- D. C. Prieve and R. Roman, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 1287–1306 RSC.
- R. Aris, Proc. R. Soc. London, Ser. A, 1956, 235, 67–77 CrossRef.
- R. P. Sear and P. B. Warren, Phys. Rev. E, 2017, 96, 062602 CrossRef.
-
C. M. Bender and S. A. Orszag, Advanced mathematics methods for scientists and engineers, Springer-Verlag, New York, 1999 Search PubMed.
-
J. H. Ferziger and M. Peric, Computational methods for fluid dynamics, Springer-Verlag, New York, 2002 Search PubMed.
- J. Peraud, A. J. Nonaka, J. B. Bell, A. Donev and A. L. Garcia, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10829–10833 CrossRef CAS.
- B. Balu and A. S. Khair, Soft Matter, 2018, 14, 8267–8275 RSC.
- J. F. Brady, J. Fluid Mech., 2011, 667, 216–259 CrossRef CAS.
- A. Sanskrityayn and N. Kumar, J. Earth Syst. Sci., 2016, 125, 1713–1723 CrossRef.
-
M. D. Greenberg, Applications of Green's functions in science and engineering, Prentice-Hall, Englewood Cliffs, New Jersey, 1971 Search PubMed.
- J. Josserand, G. Lagger, H. Jensen, R. Ferrigno and H. H. Girault, J. Electroanal. Chem., 2003, 546, 1–13 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The colloid and solute evolutions in Fig. 3(a), (c), and 4(a). See DOI: 10.1039/c9sm01938c |
| ‡ See Appendix for the derivation. |
| § See Appendix for a setting where super-diffusion can be realized. |
| ¶ M/Ds = 103 is admittedly large for colloids in an ionic solution, but potentially attainable in some physico-chemical systems, such as near a liquid–liquid de-mixing critical point.21,25 |
| || See Appendix for the derivation. |
| ** See Appendix for the derivation. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Stephen
Garoff
*a,
Stephen
Garoff
 b,
Robert D.
Tilton
b,
Robert D.
Tilton
 c and
Aditya S.
Khair
c and
Aditya S.
Khair
 *d
*d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S.4 Prior studies focused on calculating the DP mobility M with respect to the interactions between the colloid and the surrounding ions, showing that M can be positive or negative, corresponding to DP driving colloids up (solute-attracting) or down (solute-repelling) the solute gradient, respectively.1,2,4–8 Recently, there has been intense interest in utilizing DP to affect microscale colloid transport, including modification of the Batchelor scale for mixing9,10 and chaotic advection;11–13 log-sensing osmotic traps and particle manipulation;14–18 and transport in dead-end pores.19–22 Underlying these applications is the nonlinear relation between the DP colloid velocity and the solute gradient.
S.4 Prior studies focused on calculating the DP mobility M with respect to the interactions between the colloid and the surrounding ions, showing that M can be positive or negative, corresponding to DP driving colloids up (solute-attracting) or down (solute-repelling) the solute gradient, respectively.1,2,4–8 Recently, there has been intense interest in utilizing DP to affect microscale colloid transport, including modification of the Batchelor scale for mixing9,10 and chaotic advection;11–13 log-sensing osmotic traps and particle manipulation;14–18 and transport in dead-end pores.19–22 Underlying these applications is the nonlinear relation between the DP colloid velocity and the solute gradient.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S first proposed by Derjaguin and co-workers.1 The chief physical assumption of the relation is based on an ideal solution such that the ionic fluxes are given by the Nernst–Planck equation, which gives very good predictions for electrolyte solutions up to millimolar concentration near moderately charged surfaces of zeta potential ζ ∼ O(kT/e) (k the Boltzmann constant, T the absolute temperature, and e the unit charge). The effects of non-ideal solution such as steric repulsion due to finite ion size, which are important in concentrated electrolytes or nano-confined systems, will generate additional chemical potentials and hence fluxes to the classical Nernst–Planck equation. Relevant discussions and detailed analyses can be found in ref. 6 and 7. Recent experiments13–16,20 have shown excellent agreements with theoretical predictions9,10,12,21,22 of DP colloid transport based on the present approximations. Hence, DP of the colloids is due to a simultaneous, spatially coincident source of the solute whose diffusive transport is governed by
S first proposed by Derjaguin and co-workers.1 The chief physical assumption of the relation is based on an ideal solution such that the ionic fluxes are given by the Nernst–Planck equation, which gives very good predictions for electrolyte solutions up to millimolar concentration near moderately charged surfaces of zeta potential ζ ∼ O(kT/e) (k the Boltzmann constant, T the absolute temperature, and e the unit charge). The effects of non-ideal solution such as steric repulsion due to finite ion size, which are important in concentrated electrolytes or nano-confined systems, will generate additional chemical potentials and hence fluxes to the classical Nernst–Planck equation. Relevant discussions and detailed analyses can be found in ref. 6 and 7. Recent experiments13–16,20 have shown excellent agreements with theoretical predictions9,10,12,21,22 of DP colloid transport based on the present approximations. Hence, DP of the colloids is due to a simultaneous, spatially coincident source of the solute whose diffusive transport is governed by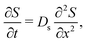
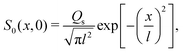
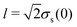 is the lengthscale characterizing the initial solute width [σs2(0) is the initial solute variance], the solution to eqn (1) is
is the lengthscale characterizing the initial solute width [σs2(0) is the initial solute variance], the solution to eqn (1) is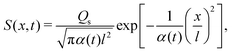
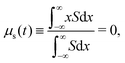
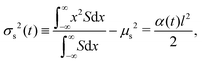
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S)/∂x = −2Mx/(α(t)l2) in the advection-diffusion equation for the colloids:
S)/∂x = −2Mx/(α(t)l2) in the advection-diffusion equation for the colloids: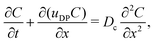
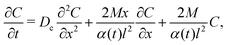
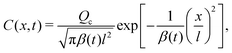
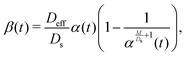
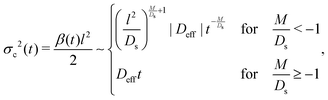
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s for M/Ds = −5 compared to σc = O(1) μm for M/Ds = 0. For −1 ≤ M/Ds ≤ 1, DP has a relatively minor impact on the diffusive spreading of colloids. For M/Ds = 103,¶ the colloids first undergo regular diffusion at short times [t/(l2/Ds) ≲ 10−3]; σc2 grows linearly with time. Subsequently, the DP forces that drive the colloids up the solute gradient dominate over diffusion of colloids. Solute-attracting DP inhibits the diffusive spread of colloids such that over a sizable period of time, 5 × 10−4 ≲ t/(l2/Ds) ≲ 5 × 10−2, the colloid spreading is spatially arrested, which might be interpreted as an extreme sub-diffusion, in contrast to the super-diffusive behavior mentioned above. At t/(l2/Ds) ≳ 10−1 the solute gradient is sufficiently weak—the arrest is relaxed—and the colloid distribution recovers a diffusive spreading with an effective diffusion coefficient Deff, highlighting that DP affects the long-time transport. As a general remark, the time interval of arrested spreading increases with M/Ds. Fig. 1(b) illustrates the difference in the broadening of the colloid distribution between different values of M/Ds at t/(l2/Ds) = 102. For arrested spreading (M/Ds = 103) the colloid distribution broadens negligibly; the colloids spread more than 102 times the width of the initial solute distribution in the presence of super-diffusion (M/Ds = −2). The spreading occurs on the solute diffusion time, which is much faster than the colloid diffusion time since Dc/Ds is small. The centroids of the colloid distributions remain stationary, μc = 0.
s for M/Ds = −5 compared to σc = O(1) μm for M/Ds = 0. For −1 ≤ M/Ds ≤ 1, DP has a relatively minor impact on the diffusive spreading of colloids. For M/Ds = 103,¶ the colloids first undergo regular diffusion at short times [t/(l2/Ds) ≲ 10−3]; σc2 grows linearly with time. Subsequently, the DP forces that drive the colloids up the solute gradient dominate over diffusion of colloids. Solute-attracting DP inhibits the diffusive spread of colloids such that over a sizable period of time, 5 × 10−4 ≲ t/(l2/Ds) ≲ 5 × 10−2, the colloid spreading is spatially arrested, which might be interpreted as an extreme sub-diffusion, in contrast to the super-diffusive behavior mentioned above. At t/(l2/Ds) ≳ 10−1 the solute gradient is sufficiently weak—the arrest is relaxed—and the colloid distribution recovers a diffusive spreading with an effective diffusion coefficient Deff, highlighting that DP affects the long-time transport. As a general remark, the time interval of arrested spreading increases with M/Ds. Fig. 1(b) illustrates the difference in the broadening of the colloid distribution between different values of M/Ds at t/(l2/Ds) = 102. For arrested spreading (M/Ds = 103) the colloid distribution broadens negligibly; the colloids spread more than 102 times the width of the initial solute distribution in the presence of super-diffusion (M/Ds = −2). The spreading occurs on the solute diffusion time, which is much faster than the colloid diffusion time since Dc/Ds is small. The centroids of the colloid distributions remain stationary, μc = 0.
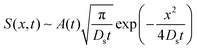
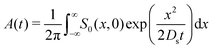
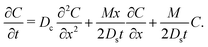
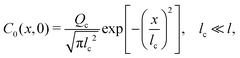
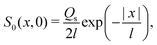
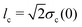 is the lengthscale of the initial colloid distribution. Numerical solutions are obtained by a standard forward-in-time-central-in-space finite-difference scheme.27 The transition is clearly demonstrated in Fig. 2(a), which leads to significantly different long-time colloid spreading between the case with and without super-diffusion [Fig. 2(c)]. Notice too that the solute profile eventually becomes Gaussian.
is the lengthscale of the initial colloid distribution. Numerical solutions are obtained by a standard forward-in-time-central-in-space finite-difference scheme.27 The transition is clearly demonstrated in Fig. 2(a), which leads to significantly different long-time colloid spreading between the case with and without super-diffusion [Fig. 2(c)]. Notice too that the solute profile eventually becomes Gaussian.
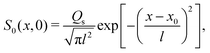
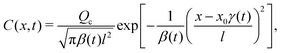
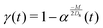 , and the centroid is
, and the centroid is
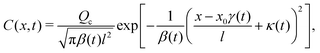
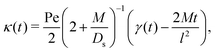

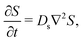
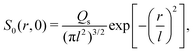
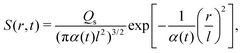
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = −2Mr/(α(t)l2)ir (ir is the radial unit vector) in the advection-diffusion equation for the colloids:
S = −2Mr/(α(t)l2)ir (ir is the radial unit vector) in the advection-diffusion equation for the colloids: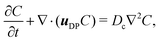
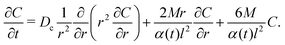
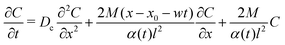
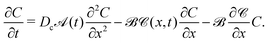
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (t),
(t), ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) , and
, and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (x,t) are identified as
(x,t) are identified as![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (t) = 1,
(t) = 1,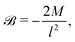
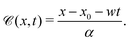
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (x,t) =
(x,t) = ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) x
x![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) +
(t) + ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (t), the functions
(t), the functions ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ,
, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t), and
(t), and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (t) are identified as
(t) are identified as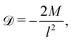
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) = α−1(t),
(t) = α−1(t),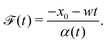
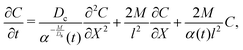
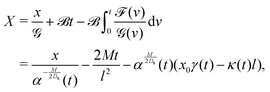
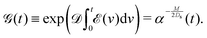
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (X),
(X),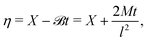
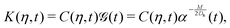
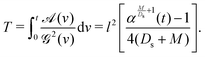
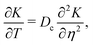
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (η).
(η).