Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of the medium in the effective-sphere interpretation of holographic particle characterization data
Mary Ann
Odete
a,
Fook Chiong
Cheong
a,
Annemarie
Winters
a,
Jesse J.
Elliott
b,
Laura A.
Philips
a and
David G.
Grier
 *c
*c
aSpheryx, Inc., 330 E. 38th Street, #48J, New York, NY 10016, USA
bDepartment of Physics, University of Chicago, 5720 South Ellis Ave., Chicago, IL 60637, USA
cDepartment of Physics and Center for Soft Matter Research, New York University, New York, NY 10003, USA. E-mail: david.grier@nyu.edu
First published on 13th December 2019
Abstract
The in-line hologram of a micrometer-scale colloidal sphere can be analyzed with the Lorenz–Mie theory of light scattering to obtain precise measurements of the sphere's diameter and refractive index. The same technique also can be used to characterize porous and irregularly shaped colloidal particles provided that the extracted parameters are interpreted with effective-medium theory to represent the properties of an equivalent effective sphere. Here, we demonstrate that the effective-sphere model consistently accounts for changes in the refractive index of the medium as it fills the pores of porous particles and therefore yields quantitative information about such particles' structure and composition. In addition to the sample-averaged porosity, holographic perfusion porosimetry gauges the polydispersity of the porosity. We demonstrate these capabilities through measurements on mesoporous spheres, fractal protein aggregates and irregular nanoparticle agglomerates, all of which are noteworthy for their industrial significance.
1 Introduction
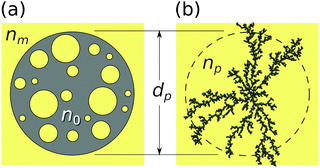
Holographic particle characterization uses in-line holographic video microscopy to measure the diameters and refractive indexes of colloidal particles in their native media while simultaneously tracking their three-dimensional motions.1 The measurement involves fitting a recorded hologram, pixel-by-pixel, to a model based on the Lorenz–Mie theory of light scattering by spheres.2,3 Colloidal particles with more complicated structures can be analyzed by generalizing the light-scattering model4–6 at the cost of additional computational complexity. Alternatively, the Lorenz–Mie model for spheres also can be used to analyze these more general particles.7–10 In this case, the extracted particle characteristics can be interpreted with effective-medium theory11 to describe an effective sphere, shown schematically in Fig. 1, whose boundary encloses the actual particle and whose properties represent contributions from both the particle itself and also the medium filling its pores. This approach has been demonstrated experimentally through measurements on porous colloidal spheres,7 dimpled spheres,8 fractal clusters of silica nanoparticles,9 protein aggregates12,13 and nanoparticle agglomerates.14 It has been validated by analyzing simulated holograms of dimpled spheres8 and fractal clusters.10These previous studies all focused on the relationship between the particle's internal structure and the measured effective-sphere characteristics in a medium of fixed refractive index. The present study provides a complementary experimental test of the medium's role in determining the effective-sphere characteristics of porous particles, specifically mesoporous silica spheres, protein aggregates with branched fractal structure and nanoparticle agglomerates dispersed in chemical–mechanical planarization (CMP) slurries. These model systems were chosen for their relevance to drug delivery and catalysis,15 biopharmaceutical development and manufacturing,16 and semiconductor processing,17 respectively. The results of this study validate the effective sphere model and demonstrate its utility for monitoring molecular perfusion of colloidal particles' pores. Holographic perfusion porosimetry provides precise measurements of both the population-averaged porosity and also the polydispersity of the porosity.
2 Experimental
2.1 Holographic particle characterization
The data for holographic particle characterization are acquired with in-line holographic video microscopy. The microscope, illustrated schematically in Fig. 2(a), illuminates the sample with a collimated laser beam at vacuum wavelength λ. This incident wave can be modeled as a monochromatic plane wave propagating along ẑ with linear polarization along![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) :
:E0(r) = u0eikz![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . . | (1) |
| Es(r) = u0eikzpfs(k(r − rp)), | (2) |
b(r) = |![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + eikzpfs(k(r − rp))|2. + eikzpfs(k(r − rp))|2. | (3) |
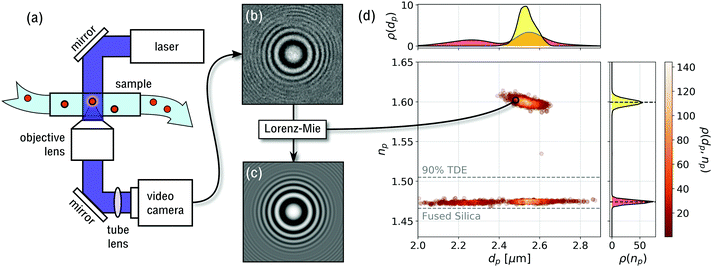 | ||
| Fig. 2 (a) Schematic representation of the holographic video microscope. (b) Typical experimental hologram of a polystyrene sphere. (c) Pixel-by-pixel fit to eqn (3) for optimal values of the particle's position, rp, diameter, dp and refractive index, np. (d) Scatter plot of 2250 particles' diameters and refractive indexes, with each point representing the properties of a single particle. This sample is composed of monodisperse polystyrene spheres (np ≈ 1.6) and mesoporous silica spheres co-dispersed in a mixture of 90% TDE in water. Points are colored by the probability density, ρ(dp,np), of single-particle properties. The two projections, ρ(dp) and ρ(np), show the probability distribution of particle diameters and refractive indexes, respectively, the latter permitting clear differentiation between particle types. Horizontal dashed lines show the refractive indexes of fused silica and 90% TDE solution. | ||
In addition to initial estimates for rp, dp and np, Lorentz–Mie fits require three calibration parameters: the wavelength of the illumination, the magnification of the optical train, and the refractive index of the medium. The first two are fixed instrumental properties. The refractive index of the medium at the imaging wavelength can be measured with a refractometer. Equivalently, nm can be determined by analyzing standard spheres with known optical properties and fitting for nm rather than np.24 Both approaches were used in the present work and yielded consistent values.
In our implementation, data acquisition and analysis are performed with a Spheryx xSight, which is a commercial instrument for holographic particle characterization. Samples are loaded into xSight in disposable xCell microfluidic sample chips, each of whose reservoirs holds 30 μL. xSight mixes the sample and then transfers 3 μL through its holographic microscope using pressure gradients. The chip's observation volume has an optical path length of 50 μm and provides the microscope with a clear 150 μm × 120 μm field of view, given the microscope's magnification of 120 nm per pixel. The instrument records holograms at λ = 447 nm and can analyze particles ranging in size from dp = 400 nm to dp = 10 μm. A typical 15 min measurement can analyze particle concentrations as low as 103 particles per mL and as low as 107 particles per mL. The lower limit is set by counting statistics. The upper limit is set by the need to minimize overlap between holograms of multiple particles in the camera's field of view.
Single-particle characterization measurements are combined into population distributions such as the example in Fig. 2(d). Each point in this scatter plot reflects the measured diameter and refractive index of one particle. The points are colored by the probability density of measurements, ρ(dp,np), computed using a kernel density estimator.25 Clusters of points reflect distinct populations of particles in the colloidal sample. In the case of Fig. 2(d), two populations are clearly distinguishable by their differing refractive indexes even though their size distributions overlap.
2.2 Effective sphere model
The Lorenz–Mie function, fs(kr), describes light scattering by an isotropic homogeneous sphere and is not inherently suitable for describing light scattering by porous, irregularly shaped or otherwise inhomogeneous particles. Generalizing fs(kr) to accommodate more general particle shapes and compositions is feasible,4,5,26 but is computationally costly. We retain the efficiency of the standard Lorenz–Mie implementation by treating irregular and inhomogeneous particles as if they were homogeneous spheres whose measured properties then can be interpreted as averages over the media contained within their least bounding spheres, as suggested schematically in Fig. 1.7–10,12The basis for this effective-sphere model is provided by Maxwell Garnett effective medium theory,11 according to which a particle composed of N different phases dispersed in a medium of refractive index nm, has an effective refractive index, np, that satisfies the condition
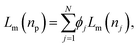 | (4a) |
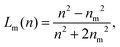 | (4b) |
Porous spheres and colloidal aggregates may be modeled as two-phase systems composed of a host material of refractive index n0 at volume fraction ϕ whose pores are filled with the surrounding fluid medium, as shown schematically in Fig. 1. Such a particle's porosity is related to its volume fraction by p = 1 − ϕ. Noting that Lm(nm) = 0, the effective-sphere model then predicts
| Lm(np) = ϕLm(n0) | (5) |
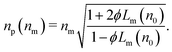 | (6) |
3 Results & discussion
3.1 Effective-sphere characterization of mesoporous silica spheres
We test the effective-sphere model's predictions by measuring the properties of well-characterized porous particles dispersed in media with a range of refractive indexes. The particles used for this study are nominally 2.5 μm-diameter mesoporous silica spheres with 4 nm-diameter pores (Sigma-Aldrich, catalog number 806951). These test particles are codispersed with crosslinked polystyrene spheres (Spherotech, catalog number PP10-20-10), which serve as control particles because they are not porous7 and should not respond in any way to changes in the properties of the medium. Polystyrene has a refractive index around np = 1.6 at λ = 447 nm and the manufacturer specifies that these particles' diameters fall in the range dp = (2.5 ± 0.1) μm.Mesoporous silica spheres and polystyrene controls are dispersed at a total concentration of 106 particles per mL in mixtures of deionized water and 2,2′-thiodiethanol (TDE, Sigma-Aldrich catalog number 166782, CAS No. 111-48-8). TDE is miscible with water and has a refractive index of 1.520 at the imaging wavelength, which substantially exceeds the value for fully dense fused silica, n0 = 1.466.27
The data in Fig. 2(d) were obtained with this system at 90% TDE by volume, whose refractive index is measured to be nm = 1.505 ± 0.007. The scatter plot shows results for 894 polystyrene spheres and 352 silica spheres. Fig. 3 summarizes results from ten such data sets over the range from pure water (nm = 1.339 ± 0.001) to 90% TDE. As anticipated, the measured properties of the polystyrene control particles (yellow squares) do not depend on the refractive index of the medium. Both the mean diameter of these spheres, dp = (2.55 ± 0.04) μm, and the refractive index, np = 1.603 ± 0.005, are consistent with the manufacturer's specification over the entire range of nm.
 | ||
| Fig. 3 (a) Dependence of the population-averaged diameter, dp(nm), and (b) refractive index, np(nm), of the polystyrene and mesoporous silica spheres as a function of the refractive index of the medium, nm. Neither the particles’ diameters nor the measured refractive indexes of the polystyrene reference particles vary significantly with nm. The refractive index of the mesoporous silica spheres depends on nm in agreement with eqn (6). Error bars reflect population standard deviations for the two types of particles. Shaded boxes identify data from Fig. 2. | ||
The measured diameter of the mesoporous silica spheres also is insensitive to changes in nm. The mean refractive index, by contrast, increases from np = 1.393 ± 0.001 in deionized water to np = 1.482 ± 0.001 in 90% TDE. The dashed curve through the refractive index data in Fig. 3(b) is a fit to eqn (6) that tracks this trend and yields n0 = 1.457 ± 0.001 and ϕ = 0.47 ± 0.01.
The 0.7% discrepancy between n0 and the refractive index of fused silica may be ascribed in part to the well-documented difference in density between emulsion-polymerized silica and fused silica.28–31 The discrepancy also is likely to depend on the molecules' sizes and their affinity for silica, both of which affect their ability to access the particles' pores. Pores that are inaccessible to the high-index species in solution will tend to reduce a sphere's apparent porosity. The inaccessible volume being filled with low-index solvent, this effect also will tend to reduce the apparent refractive index of the silica matrix.
Differences in accessibility may explain the subtle species-dependent variations in n0 and porosity reported in Table 1. In addition to the results obtained with TDE, this table summarizes two additional series of measurements using glycerol (Sigma-Aldrich, catalog number G9012, CAS 56-81-5, refractive index 1.526 ± 0.002) and saturated sucrose solution (Sigma-Aldrich, catalog number S8501, CAS 57-50-1, refractive index 1.501 ± 0.002) to tune the refractive index of the aqueous medium. Both yield slightly smaller values for n0 and p than TDE, and in both cases the differences are statistically significant. Sucrose is substantially bulkier than TDE, which suggests that the difference might be attributed to steric exclusion. Glycerol is comparable in size to TDE but nevertheless yields smaller values for n0 and p. The difference in this case might reflect differences in the solute molecules' interactions with silica.
| High-index species | n 0 | p |
|---|---|---|
| 2,2′-Thiodiethanol | 1.457 ± 0.001 | 0.53 ± 0.01 |
| Glycerol | 1.448 ± 0.001 | 0.51 ± 0.01 |
| Sucrose | 1.441 ± 0.002 | 0.51 ± 0.02 |
All three results suggest that the mesoporous silica spheres have a mean porosity exceeding 50% in a matrix whose optical properties are consistent with low-density silica. Consistency among these results serves to validate the effective-sphere model's predictions for porous spheres. The subtle but significant differences in results obtained with different high-index species suggest that holographic porosimetry based on solvent perfusion may provide useful insights into pore structure and functionality.
3.2 Effective sphere analysis of protein aggregates and nanoparticle agglomerates
Having successfully applied the effective-sphere model to mesoporous spheres, we now use it to interpret holographic characterization data for irregularly shaped particles. Fig. 4(a) presents holographic characterization data for a mixture of protein aggregates and silicone oil emulsion droplets. The two populations cannot be distinguished by size, but are clearly differentiated by refractive index. | ||
| Fig. 4 (a) Joint distribution of particle diameter and refractive index for a mixture of IgG aggregates and silicone oil emulsion droplets in a sucrose solution at refractive index nm = 1.429. Each analyzed particle is represented by a plot symbol, colored by the density of measurements, ρ(dp,np). The horizontal dashed line represents nm. The two types of particles cannot be distinguished in the projected distribution of particle diameters, ρ(dp), but are clearly resolved in the distribution of refractive indexes, ρ(np). (b) Projected refractive index distributions as a function of the medium's refractive index, nm. Curves are offset by steps of 0.020 for clarity. (c) Dependence of the mode refractive indexes for IgG and silicone particles as a function of nm. The horizontal dashed line represents the bulk refractive index of silicone oil, 1.404 ± 0.002. The diagonal curve is a fit to eqn (6). | ||
The aggregates in this sample are composed of human immunoglobulin G (IgG, Sigma-Aldrich catalog number 12511, MDL number MFCD00163923), dissolved in Tris buffer (Sigma-Aldrich, catalog number 648314, CAS number 77-86-1) at a concentration of 5 mg mL−1. IgG is a protein that naturally tends to aggregate into branched fractal clusters.13,32 Holograms created by such clusters can be analyzed with the effective sphere model, as indicated schematically in Fig. 1(b), to obtain estimates for each cluster's effective diameter and refractive index.9,10,12
Emulsion droplets are created by manually agitating silicone oil (Sigma-Aldrich, product number 378399, CAS number 63148-62-9) in water. The emulsion then is blended into the protein solution at a concentration of 105 droplets per mL. Silicone oil droplets are common contaminants in biopharmaceutical products.33 In the present application, they serve as non-porous reference spheres.
Adding saturated sucrose solution to the buffer increases its refractive index. The data in Fig. 4(a) were obtained for a sample at nm = 1.429 ± 0.002. Two populations of particles are clearly resolved in the scatter plot of single-particle properties and can be distinguished by refractive index alone in the projected distribution, ρ(np). Fig. 4(b) shows how ρ(np) depends on sucrose concentration through its influence on nm. One peak in the bimodal distribution remains centered at refractive index of 1.404 ± 0.002, which is consistent with the refractive index of bulk silicone oil. The other peak tracks changes in nm as anticipated by the effective sphere model. We identify the former as the contribution of silicone oil droplets and the latter as reflecting the properties of protein aggregates.
The data in Fig. 4(c) show how the position of the aggregate peak, np(nm), depends on the refractive index of the medium. If we further assume that the aggregates' structure is not affected substantially by changes in the solvent, we may invoke the effective-sphere model to interpret the observed dependence. The diagonal dashed curve is a fit to eqn (6) that yields a effective volume fraction of ϕ = 0.03 ± 0.03, which corresponds to a porosity of p = 0.97 ± 0.03. Such a high porosity is expected for fractal aggregates that have grown to many times the size of their monomers.9,32 Because ϕ is so small for these aggregates, eqn (6) does not effectively constrain n0.
The effective-sphere model implicitly treats the aggregates as homogeneously porous particles whose internal structure is independent of size and buffer composition. Accounting for the fractal aggregates' size-dependent porosity9 does not change the magnitude of the observed porosity in the experimentally accessible size range. More importantly, the results presented in Fig. 4 offer insights into the particles' composition without requiring a priori knowledge of their detailed structure. Even if their structure were to vary with changes in the solvent composition, the observed dependence of np on nm still would indicate greater than 90% porosity over the entire range of solvent compositions.
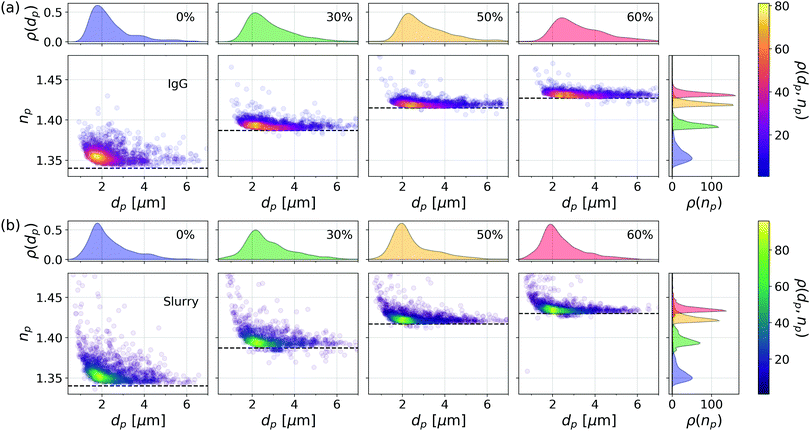
Fig. 5(a) shows comparable characterization data for IgG aggregates when glycerol is used to adjust nm instead of sucrose. Results are presented for glycerol at 0%, 30%, 50% and 60% by volume. The buffer's refractive index at each concentration is indicated by a horizontal dashed line. As with the sucrose data, the aggregates' measured refractive indexes track nm. The mean porosity inferred from the mode values of np(nm) is p = 0.96 ± 0.03, which also is consistent with results obtained with sucrose. This is not to say that the aggregates have the same structure in the different media but that any structural changes are not apparent in the aggregates' overall porosity.
Analogous results are plotted in Fig. 5(b) for nanoparticle agglomerates in a slurry of silica nanoparticles (General Engineering & Research 80 nm, SIO2-743). Unless stabilized by added surfactants, nanoparticles in this slurry tend to agglomerate into fractal clusters.34 This system also is noteworthy because the high concentration of dispersed nanoparticles renders the slurry turbid. Provided the optical pathlength is not too long, multiple scattering by dispersed nanoparticles contributes speckle to the recorded holograms' background, thereby reducing the measurement's signal-to-noise ratio, but not otherwise impeding holographic characterization in the remaining singly-scattered light.14,34
The effective refractive index of nanoparticle agglomerates tracks the refractive index of the medium, as anticipated by the effective sphere model. Also as expected, the size distribution of nanoparticle agglomerates appears not to vary appreciably with the addition of glycerol. We conclude that these agglomerates also are highly porous and that their pores are perfused by the fluid medium. Reproducing these trends in such physically distinct systems as protein aggregates and nanoparticle agglomerates lends further credibility to the effective-sphere interpretation of irregular clusters' light-scattering properties.
3.3 Polydispersity of porosity
So far, we have focused on how a porous particle's effective refractive index depends on its porosity and the refractive index of the medium. The projected refractive index distributions in Fig. 5 not only shift upward as nm increases, but also become more narrow. The range, Δnp, of apparent refractive indexes for clusters of a given size presumably reflects variations in the clusters' structures and therefore the spread, Δϕ, in values of ϕ. Eqn (6) accounts for the dependence of Δnp on Δϕ through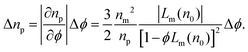 | (7) |
Fig. 6(a) shows the result of applying this analysis to the data for mesoporous silica spheres dispersed in TDE. The width of the refractive index distribution at each value of nm is estimated with robust principal component analysis, as is the uncertainty of the width. The dashed curve in a one-parameter fit to eqn (7) for Δϕ using the value of n0 = 1.455 obtained from np(nm). The result, Δϕ = 0.023 ± 0.001, is consistent with a 4% polydispersity in these particles' porosity.
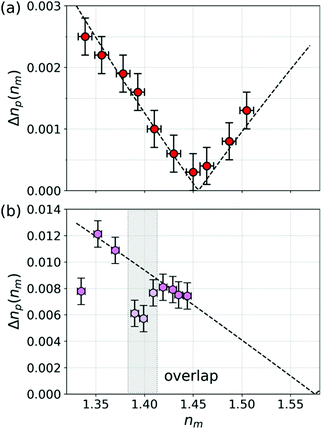 | ||
| Fig. 6 (a) Width of the refractive index distribution, Δnp(nm), for mesoporous silica spheres dispersed in aqueous TDE solution spheres as a function of the medium's refractive index, nm. (b) Δnp(nm) for protein aggregates in buffer with added sucrose, from Fig. 4. Widths are unreliable in the shaded region where the distribution of protein aggregates overlaps with the distribution of silicone oil droplets. Dashed curves in (a) and (b) are fits to eqn (7). | ||
Applying the same analysis to the data for protein aggregates in sucrose solution yields the results in Fig. 6(b). The widths of the distributions cannot be assessed reliably in the range of nm for which the silicone oil distribution overlaps with the aggregate distribution, which is indicated by the shaded region. The first point, which is obtained in pure buffer without sucrose, similarly shows less variability in np than the others. We speculate that adding sucrose may influence aggregate morphology, possibly favoring more highly branched structures.35 Fitting the remainder of the data to eqn (7) yields Δϕ = 0.05 ± 0.02 and n0 = 1.575 ± 0.008. This value for the monomer refractive index is consistent with expectations for proteins such as IgG.36 This interpretation must be viewed cautiously, however, because the protein aggregates might adopt different structures in different media and such changes might not be reflected in the effective-sphere characterization data.
4 Conclusions
The experimental studies presented here demonstrate that the effective-sphere model usefully accounts for the properties of porous spheres and irregularly shaped colloidal particles as reported by Lorenz–Mie analysis of holographic microscopy data. Specifically, these studies validate the predicted role of the medium in establishing a porous particle's effective refractive index. This dependence is characteristic of porous particles and can be used to differentiate them from non-porous particles, such as the polystyrene spheres and silicone oil droplets used as references in this study.Fitting measurements of np(nm) to eqn (6) yields estimates for the particles' porosity and the refractive index of their matrix. These characterization results are found to depend on the choice of compounds used to adjust the medium's refractive index. Tracking this dependence may be useful for probing the size distribution, connectivity and surface functionality of the pores within porous particles.
Changes in the medium that affect the refractive index also influence other physical properties. The viscosity of the samples in Fig. 3, for example, increases from 1 × 10−3 Pa s in pure water to 6 × 10−3 Pa s in 90% TDE. Consistent characterization results for polystyrene standards demonstrate that the approach to holographic particle characterization implemented in xSight is insensitive to such ancillary effects.
The ability of holographic particle characterization to differentiate porous colloidal particles from non-porous particles has immediate applications for assessing the quality of protein-based biopharmaceutical products12,13,37 and nanoparticle-based CMP slurries used for semiconductor manufacturing.14,34 Monitoring solute perfusion in mesoporous particles may provide an approach to porosimetry that complements mercury intrusion, helium isotherms, and electron microscopy, with particular benefits for analyzing the pore structure of colloidal materials.
Conflicts of interest
M. A. O., F. C. C., A. W. and L. A. P. are employees of Spheryx, Inc., which manufactures the xSight instruments used for this study. D. G. G., F. C. C. and L. A. P. are founders of Spheryx.Acknowledgements
We are grateful to Prof. Andrew Hollingsworth for guidance on handling and characterizing the mesoporous silica spheres. Research reported in this publication was supported by the National Science Foundation under Award Number 1631815, and the National Center For Advancing Translational Sciences of the National Institutes of Health under Award Number R44TR001590. Additional support was provided by the MRSEC program of the National Science Foundation under award number DMR-1420073. The Spheryx xSight used for the work at NYU was made available by the NYU MRSEC as shared instrumentation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the National Science Foundation.Notes and references
- S.-H. Lee, Y. Roichman, G.-R. Yi, S.-H. Kim, S.-M. Yang, A. van Blaaderen, P. van Oostrum and D. G. Grier, Opt. Express, 2007, 15, 18275–18282 CrossRef PubMed
.
-
C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley Interscience, New York, 1983 Search PubMed
.
-
M. I. Mishchenko, L. D. Travis and A. A. Lacis, Scattering, Absorption and Emission of Light by Small Particles, Cambridge University Press, Cambridge, 2001 Search PubMed
.
- R. W. Perry, G. N. Meng, T. G. Dimiduk, J. Fung and V. N. Manoharan, Faraday Discuss., 2012, 159, 211–234 RSC
.
- A. Wang, T. G. Dimiduk, J. Fung, S. Razavi, I. Kretzschmar, K. Chaudhary and V. N. Manoharan, J. Quant. Spectrosc. Radiat. Transfer, 2014, 146, 499–509 CrossRef CAS
.
-
T. G. Dimiduk, J. Fung, R. W. Perry and V. N. Manoharan, HoloPy – Hologram processing and light scattering in python, 2016, https://github.com/manoharan-lab/holopy Search PubMed
.
- F. C. Cheong, K. Xiao, D. J. Pine and D. G. Grier, Soft Matter, 2011, 7, 6816–6819 RSC
.
- M. Hannel, C. Middleton and D. G. Grier, Appl. Phys. Lett., 2015, 107, 141905 CrossRef
.
- C. Wang, F. C. Cheong, D. B. Ruffner, X. Zhong, M. D. Ward and D. G. Grier, Soft Matter, 2016, 12, 8774–8780 RSC
.
-
J. Fung and S. Hoang, Novel Techniques in Microscopy, 2019, p. JT4A.19 Search PubMed
.
- V. Markel, J. Opt. Soc. Am. A, 2016, 33, 1244–1256 CrossRef PubMed
.
- C. Wang, X. Zhong, D. B. Ruffner, A. Stutt, L. A. Philips, M. D. Ward and D. G. Grier, J. Pharm. Sci., 2016, 105, 1074–1085 CrossRef CAS PubMed
.
- P. N. Kasimbeg, F. C. Cheong, D. B. Ruffner, J. M. Blusewicz and L. A. Philips, J. Pharm. Sci., 2019, 108, 155–161 CrossRef CAS PubMed
.
- F. C. Cheong, P. Kasimbeg, D. B. Ruffner, E. H. Hlaing, J. M. Blusewicz, L. A. Philips and D. G. Grier, Appl. Phys. Lett., 2017, 111, 153702 CrossRef
.
- S.-H. Wu, C.-Y. Mou and H.-P. Lin, Chem. Soc. Rev., 2013, 42, 3862–3875 RSC
.
- W. Wang, Int. J. Pharm., 2005, 289, 1–30 CrossRef CAS PubMed
.
- G. B. Basim and B. M. Moudgil, J. Colloid Interface Sci., 2002, 256, 137–142 CrossRef CAS
.
- D. B. Ruffner, F. C. Cheong, J. M. Blusewicz and L. A. Philips, Opt. Express, 2018, 26, 13239–13251 CrossRef CAS PubMed
.
- F. C. Cheong, B. Sun, R. Dreyfus, J. Amato-Grill, K. Xiao, L. Dixon and D. G. Grier, Opt. Express, 2009, 17, 13071–13079 CrossRef CAS PubMed
.
- B. J. Krishnatreya and D. G. Grier, Opt. Express, 2014, 22, 12773–12778 CrossRef CAS PubMed
.
- M. D. Hannel, A. Abdulali, M. O'Brien and D. G. Grier, Opt. Express, 2018, 26, 15221–15231 CrossRef CAS PubMed
.
- A. Yevick, M. Hannel and D. G. Grier, Opt. Express, 2014, 22, 26884–26890 CrossRef PubMed
.
- B. J. Krishnatreya, A. Colen-Landy, P. Hasebe, B. A. Bell, J. R. Jones, A. Sunda-Meya and D. G. Grier, Am. J. Phys., 2014, 82, 23–31 CrossRef CAS
.
- H. Shpaisman, B. J. Krishnatreya and D. G. Grier, Appl. Phys. Lett., 2012, 101, 091102 CrossRef
.
-
B. W. Silverman, Density Estimation for Statistics and Data Analysis, Chapman & Hall, New York, 1992 Search PubMed
.
- J. Fung and V. N. Manoharan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 020302 CrossRef PubMed
.
- I. H. Malitson, J. Opt. Soc. Am., 1965, 55, 1205–1208 CrossRef CAS
.
- S. Li, Q. Wan, Z. Qin, Y. Fu and Y. Gu, Langmuir, 2015, 31, 824–832 CrossRef CAS PubMed
.
- S. Parnell, A. Washington, A. Parnell, A. Walsh, R. Dalgliesh, F. Li, W. Hamilton, S. Prevost, J. Fairclough and R. Pynn, Soft Matter, 2016, 12, 4709–4714 RSC
.
- J. Farrando-Pérez, C. López, J. Silvestre-Albero and F. Gallego-Gómez, J. Phys. Chem. C, 2018, 122, 22008–22017 CrossRef
.
- C. P. Blakemore, A. D. Rider, S. Roy, A. Fieguth, A. Kawasaki, N. Priel and G. Gratta, Phys. Rev. Appl., 2019, 12, 024037 CrossRef CAS
.
- J. Feder, T. Jøssang and E. Rosenqvist, Phys. Rev. Lett., 1984, 53, 1403 CrossRef CAS
.
- L. S. Jones, A. Kaufmann and C. R. Middaugh, J. Pharm. Sci., 2005, 94, 918–927 CrossRef CAS PubMed
.
-
F. C. Cheong, P. Kasimbeg, A. Winters, J. M. Blusewicz, E.-H. Hlaing, D. B. Ruffner, R. V. Ihnfeldt, D. G. Grier and L. A. Philips, Proceedings of the International Conference on Planarization/CMP Technology, ICPT, Seoul, Korea, 2018, pp. 126–131 Search PubMed
.
- C. Marasini, V. Foderà and B. Vestergaard, RSC Adv., 2017, 7, 10487–10493 RSC
.
- J. Vörös, Biophys. J., 2004, 87, 553–561 CrossRef PubMed
.
- D. C. Ripple and M. N. Dimitrova, J. Pharm. Sci., 2012, 101, 3568–3579 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2020 |