Numerical exploration on buckling instability for directional control in flagellar propulsion†
Abstract
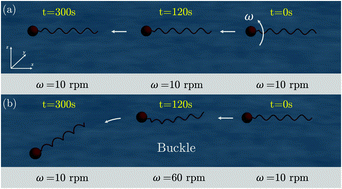
We report a numerical method to control the swimming direction by exploiting buckling instability in uniflagellar bacteria and bio-inspired soft robots. Our model system is comprised of a spherical rigid head and a helical elastic flagellum. The rotation of the flagellum in low Reynolds environment generates a propulsive force that allows the system to swim in fluid. The locomotion is an intricate interplay between the elasticity of the flagellum, the hydrodynamic loading, and the flow generated by the moving head. We use the Discrete Elastic Rods algorithm to capture the geometrically nonlinear deformation in the flagellum, Lighthills Slender Body Theory to simulate the hydrodynamics, and Higdons model for the spherical head in motion within viscous fluid. This flagellated system follows a straight path if the angular velocity of the flagellum is below a critical threshold. Buckling ensues in the flagellum beyond this threshold angular velocity and the system takes a nonlinear trajectory. We consider the angular velocity as the control parameter and solve the inverse problem of computing the angular velocity, that varies with time, given a desired nonlinear trajectory. Our results indicate that bacteria can exploit buckling in flagellum to precisely control their swimming direction.


 Please wait while we load your content...
Please wait while we load your content...