Open Access Article
Open Access ArticleStructural characterization of fibrous synthetic hydrogels using fluorescence microscopy†
Johannes
Vandaele
 a,
Boris
Louis
a,
Boris
Louis
 ab,
Kaizheng
Liu
ab,
Kaizheng
Liu
 c,
Rafael
Camacho
c,
Rafael
Camacho
 a,
Paul H. J.
Kouwer
a,
Paul H. J.
Kouwer
 c and
Susana
Rocha
c and
Susana
Rocha
 *a
*a
aMolecular Imaging and Photonics, KU Leuven, 3001 Leuven, Belgium. E-mail: susana.rocha@kuleuven.be
bDivision of Chemical Physics and NanoLund, Lund University, 22100 Lund, Sweden
cInstitute for Molecules and Materials, Radboud University, 6525 AJ Nijmegen, The Netherlands
First published on 15th April 2020
Abstract
The structural features of the matrix surrounding the cells play a crucial role in regulating their behavior. Here, we used fluorescence microscopy and customized analysis algorithms to characterize the architecture of fibrous hydrogel networks. As a model system, we investigated a new class of synthetic biomimetic material, hydrogels prepared from polyisocyanides. Our results show that these synthetic gels present a highly heterogeneous fibrous network, with pores reaching a few micrometers in diameter. By encapsulating HeLa cells in different hydrogels, we show that a more porous structure is linked to a higher proliferation rate. The approach described here, for the characterization of the network of fibrous hydrogels, can be easily applied to other polymer-based materials and provide new insights into the influence of structural features in cell behavior. This knowledge is crucial to develop the next generation of biomimetic materials for 3D cell models and tissue engineering applications.
1. Introduction
The physical properties of the cell environment have a significant impact on its fate in terms of survival, proliferation and differentiation.1–6 A major component of the cellular environment is the extracellular matrix (ECM). This porous 3D network of proteoglycans, polysaccharides and fibrous proteins provides a physical scaffold for the cells and initiates important mechano-transduction pathways. While the most well-studied physical cue is the stiffness (or elasticity) of the matrix,7–9 other properties such as surface and structural characteristics also influence cellular behavior.10–12 Results on the role of topological characteristics of 2D surfaces show that topographic features in the nanometer range alter the subcellular sensing mechanisms, and that features larger than 10 μm (the length-scale of a mammalian cell) mainly affect the whole cell morphology.13 For instance, osteogenic differentiation of mesenchymal stem cells was promoted when the cells were cultured in substrates containing topographic features of ridges and grooves ranging from 0.7 to 2 μm (1.4–4 μm in pitch).14In vivo and in 3D cultures, where cells are completely surrounded by ECM, the effects of physical cues are similarly important, but certainly not identical to the 2D experiments,15–17 hence, studies in 3D cultures are of paramount importance. Moreover, recent works have demonstrated that cell behavior is influenced by the parameters associated with the 3D fibrous network, including pore size and pore connectivity of the extracellular matrix.18,19 For example, highly interconnected pores enable better vascularization throughout the scaffold, thereby enhancing bone regeneration.12,13
Hydrogels with natural or synthetic origins serve as the primary used scaffold for 3D cell cultures. Their architectures are commonly studied using scanning or transmission electron microscopies (SEM/TEM), atomic force microscopy (AFM) or small angle scattering techniques (SAXS/SANS). Despite the high spatial resolution achieved with these techniques, they present important limitations. Both AFM and SEM/TEM provide a 2D view of a 3D structure while scattering techniques give only average values for structural parameters. In addition, sample requirements restrict imaging in native conditions and these methods are therefore unable to measure dynamics in situ.
In contrast to the aforementioned methods, optical microscopy can unravel the structure and dynamics of complex heterogeneous materials with nano- to micrometer resolution, in 3D, over a wide range of time scales. This makes optical microscopy an ideal tool to study the complex ECM. Indeed, despite the lower spatial resolution, conventional fluorescence microscopy is perfectly suited to image the structure of biopolymer gels, for instance, gels based on collagen or fibrin.20–23 The majority of reports, however, merely concentrate on imaging the polymer network and lack subsequent network analysis and quantification.
In this work, we present automated software to analyse the 3D structure of hydrogels, using fluorescence images. Compared to existing algorithms,24–27 our approach yields more accurate results for highly porous networks which tend to yield highly complex distance maps often resulting in over-segmented pores.
As a model system, we used a fully synthetic fibrillar hydrogel based on oligo(ethylene glycol)-grafted polyisocyanides (PICs),16,17 which provides a reproducible fibrous matrix that is tunable with preparation conditions. While the mechanical properties of the PIC hydrogels are well documented,17 it remains unclear how synthesis and experimental conditions (e.g. molecular structure and polymer concentration) impact the gel architecture and, with that, cell behavior. So far, studies of the PIC hydrogels’ structure focussed on the nanometer scale: AFM analysis showed that the formation of fibrils or (∼7 chains per bundle) is independent of the polymer concentration.16 SAXS measurements confirmed bundle dimensions and showed that a decrease in the polymer concentration resulted in an increase of the pore size of the network, with minimal changes on the bundle diameter.18 However, data at micrometer length scale is still lacking.
For our analysis, we prepared and analysed PIC hydrogels of different molecular weight polymers and at different concentrations. With fluorescence microscopy and our improved network analysis tool, we show how the architecture of these different gels changes. Lastly, from the proliferation rates of the HeLa cells encapsulated in these hydrogels we demonstrate that, indeed, the hydrogel architecture greatly affects cell behavior. The approach depicted in this work can be easily applied to investigate the structure of other (bio)materials.
2. Materials & methods
2.1. Polymer synthesis
PIC polymers were synthesized by a nickel(II)-catalyzed co-polymerization of tri(ethylene glycol)-functionalized isocyano-(D)-alanyl-(L)-alanine (monomer 1, Chiralix) and the azide-appended equivalent (monomer 2, molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 is 29
2 is 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), following the synthesis procedure as published elsewhere.28 Briefly, both monomers were dissolved in freshly distilled toluene (50 mg mL−1) and the appropriate amount of catalyst Ni(ClO4)2 was added (ratios given in Table 1). The reaction mixture was stirred at room temperature (20 °C) for 24–48 h until IR spectroscopy indicated full consumption of the monomer. The synthesized polymers were precipitated three times from dichloromethane in diisopropyl ether and dried overnight in air. Molecular weights were determined through viscosity measurements in acetonitrile following an earlier reported protocol.29
1), following the synthesis procedure as published elsewhere.28 Briefly, both monomers were dissolved in freshly distilled toluene (50 mg mL−1) and the appropriate amount of catalyst Ni(ClO4)2 was added (ratios given in Table 1). The reaction mixture was stirred at room temperature (20 °C) for 24–48 h until IR spectroscopy indicated full consumption of the monomer. The synthesized polymers were precipitated three times from dichloromethane in diisopropyl ether and dried overnight in air. Molecular weights were determined through viscosity measurements in acetonitrile following an earlier reported protocol.29
| Polymer | [Ni2+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [M] ratio [M] ratio |
M v (kg mol−1) | Polymer lengthb (nm) | Hydrogel | c (g L−1) | G′ (Pa) | σ c (Pa) |
|---|---|---|---|---|---|---|---|
| a The molecular weight of the polymer is calculated based on viscosity measurements.29 b The polymer length is calculated from the estimated Mv. | |||||||
| Sshort | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000 |
363 | 145 | S025 | 0.25 | 0.8 | 0.2 |
| S05 | 0.5 | 4.8 | 0.6 | ||||
| S1 | 1 | 34.0 | 3.9 | ||||
| Llong | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5000 5000 |
572 | 229 | L025 | 0.25 | 10.3 | 1.2 |
| L05 | 0.5 | 52.6 | 7.6 | ||||
| L1 | 1 | 96.3 | 13.4 | ||||
2.2. Rheology analysis
For the mechanical analysis of the gels, a stress-controlled rheometer (Discovery HR-2, TA Instruments) with an aluminum or steel parallel plate geometry was used (diameter = 40 mm, gap = 500 μm). All samples were loaded onto the rheometer plate in the liquid state at T = 5 °C followed by a temperature ramp to T = 37 °C at a rate of 1.0 °C min−1. The moduli were measured in the linear viscoelastic regime at amplitude of γ = 0.02 or 0.04 and a frequency of ω = 1.0 Hz. The sample was allowed to equilibrate at 37 °C prior to the nonlinear measurements. Here, the gel was subjected to a constant prestress of σ0 = 0.5 to 200 Pa, and the differential modulus K′ was probed with a small superposed oscillatory stress at frequencies of ω = 10 to 0.1 Hz (reported data at ω = 1 Hz). The oscillatory stress was at least 10 times smaller than the applied prestress.2.3. Polymer labelling and sample preparation
Before each measurement a fresh stock solution of 2 mg mL−1 of PIC polymers was prepared by mixing the polymers with Milli-Q water overnight at 5 °C. To fluorescently label the polymer molecules, carboxy tetramethyl-rhodamine (TAMRA) with a covalently attached DBCO linker (Sigma Aldrich) was added to the polymer solution in a ratio of 1 mg polymer: 2–5 μM of dye. Considering the molecular weight of the polymer, this resulted in a final density of 6–12 fluorophores every 100 nm of polymer bundle (considering that a polymer bundle contains 7 polymer chains). The solution was incubated for at least 5 minutes on ice.For imaging, the PIC solution was loaded into a perfusion chamber (CoverWell™ Perfusion Chambers 9 mm, Grace Bio-Labs) glued on a clean cover slide (Menzel-Gläser). Once loaded, the chamber was sealed with tape to avoid evaporation and kept at room temperature for 2–3 h to ensure complete labelling and gel formation.
2.4. Confocal fluorescence imaging
Fluorescence imaging was done with a Leica TCS SP8 X confocal microscope. The images were acquired using a water objective (HC PL APO 63×/1.20, motCORR, Leica), a hybrid photomultiplier tube as detector (HYD-SMD, Leica) and a field-of-view scanner (200 Hz, bidirectional). As an excitation source, a supercontinuum white light laser (470–670 nm, pulsed, 80 MHz, NKT Photonics) was used. PIC polymers labelled with TAMRA were excited at 553 nm. The fluorescence was collected between 560 nm and 750 nm. All measurements were performed in a temperature controlled environment (25 °C).At least five different areas in the perfusion chamber were randomly selected and imaged for each sample in duplicate. Data was acquired with Leica Application Suite X software and ImageJ was then used for data visualization. The images were acquired with a pixel size of 180 nm in XY and a z-step of 200 nm.
2.5. Polymer network analysis
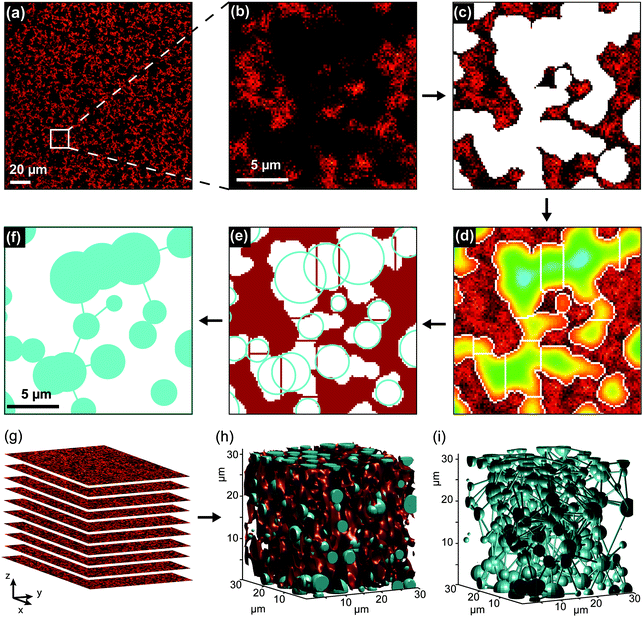
Image segmentation and analysis of the network were performed using a software developed in-house, written in MATLAB® (Fig. 1). The software is freely available at https://github.com/BorisLouis/Segmentation or https://borislouis.github.io/Codes/.The software is composed of different parts, namely loading, pre-processing, segmentation, post-processing and calculations. The different parts are explained in detail in the link provided above. Briefly, after a 3D Gaussian filtering (pre-processing), the smoothed images are segmented using an adaptive or global threshold (Fig. 1c). In the majority of the applications appropriate segmentation can be achieved using a global threshold. In the fluorescence images where the background signal is not uniform, the adaptive threshold provides better results. To minimize the differences in the illumination or local background we use an adaptive threshold in all the analysed images. This implies that the threshold in a given pixel is chosen in 3D, based on the mean of N neighbouring pixels and a sensitivity value. For the images here presented, we used a 6 × 6 × 6 pixel window (N = 216) and a sensitivity value of 0.6. This sensitivity was chosen after the comparison between images segmented using different sensitivities with data manually segmented (see Supporting Note, ESI†). After segmentation, a binary image is generated, where each pixel (2D) or voxel (3D) is classified as belonging to a pore (value 0) or to a polymer fiber (value 1), depending on its intensity (below or above a chosen intensity threshold). The binary volume created is cleaned from small artefacts as a post-processing step. This segmentation step leads to the detection of the pores (Fig. 1c). It is important to mention that pores with a volume smaller than 0.0065 μm3 (diameter of approx. 0.12 μm) will be removed from the analysis. This is a result of the optical diffraction limit of the confocal microscope used, combined with the post-processing step to remove small artefacts. Following Gostick's workflow, the segmented images were used to calculate an Euclidean distance map (Fig. 1d). For each pixel/voxel in the pore, the software calculated the distance to the closest ‘fiber pixel/voxel’. The distance map was used as input for a watershed transformation (Fig. 1e). This algorithm identifies local maxima within the pore region and divides the pore into segments containing a single local maximum. In other words, the pores detected in the segmentation step are divided into sections in the region where the pores show a (local) minimum in the diameter. This local minimum in the diameter of the pore is designated by the throat and is represented by the white/red lines in Fig. 1d and e, respectively. For each section in the pores, we calculated several parameters, namely maximum pore diameter, throat diameter and pore connectivity (Fig. S1, ESI†). The cyan circles in Fig. 1e represent the maximum diameter in each section of the pore. In addition to the local pore properties, the porosity of the 3D volume image was determined by calculating the percentage of ‘pore pixels/voxels’ in all intensity-based segmented images. The software provided in the link above allows for analysis of 2D and/or 3D datasets. Our software package also includes the possibility to visualize the calculated parameters in different forms (histogram, CCDF, violin distribution) and rendering the 3D models of the polymer network.
2.6. Cell proliferation
HeLa cells cultured in Dulbecco's Modified Eagle's Medium (DMEM, Merck) with 10% fetal bovine serum (Merckx), 1% GlutaMAX™ (Thermo Fisher, Gibco®) and 0.1% Gentamicin (Carl Roth GMBH). The cells were kept in a controlled atmosphere (humidified, 5% CO2) at 37 °C.For cell passage and sample preparation, HeLa cells were resuspended using 0.05% trypsin (Thermo Fisher, Gibco®) for 5–10 minutes at 37 °C. Cells were encapsulated in PIC-based hydrogels by mixing freshly made PIC solution in DMEM with suspended HeLa cells, to a final density of 105 cells per mL. All manipulations were conducted on ice to prevent gel formation. After mixing, the PIC/cells solution was pipetted into a 96 well plate (Thermo Scientific™) and left at 37 °C for 15 minutes to ensure gel formation. After gelation, pre-warmed DMEM was gently added on top of the hydrogel and the cells were incubated for 7 days at 37 °C (humidified atmosphere, 5% CO2).
Cell proliferation was determined using a methylthiazolyldiphenyl-tetrazolium bromide (MTT) colorimetric assay (Acros Organics), according to the manufacturer's instructions. Briefly, a fresh stock solution of MTT (4 mg mL−1) was prepared using 1× Hanks’ Balanced Salt Solution (HBSS). MTT was added to each well to a final concentration of 1 mg mL−1. After the addition of MTT, the plate was incubated for 1 hour in a controlled atmosphere, at 37 °C (humidified, 5% CO2). Before measuring, 50 μL of the media was removed and replaced with dimethyl sulfoxide (DMSO, Merckx) to induce cell lysis. After 15 minutes of incubation, the absorbance was read at 570 nm using a plate reader (Tecan). All conditions were prepared and measured in triplicate.
3. Results and discussion
3.1. Polymer synthesis and mechanical characterization
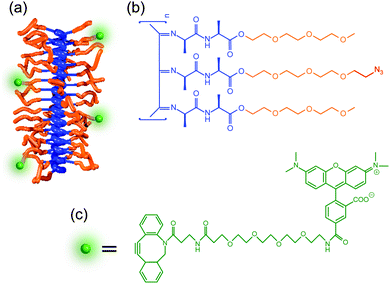
PIC polymers were synthesized using a nickel(II)-catalyzed polymerization reaction following well-established protocols.28,29 The polymer was functionalized to incorporate a fluorescent dye by introducing a small fraction of azide (N3) containing monomers (3.3% ratio, see Fig. 2). PIC polymers of different molecular weights were prepared to study the influence of the polymer length on the hydrogel architecture. The mechanical properties of the hydrogels formed using different concentrations were evaluated using standard rheometry (Fig. S2, ESI†, data summarized in Table S1). In line with earlier results,29 we find that increasing the polymer concentration or the polymer length increases both the stiffness (storage modulus G′) of the gel as well as the critical stress σc. The latter parameter is defined as the stress onset for strain-stiffening, where the gel stiffness can increase many times upon further deformation, a process typically found in semi-flexible fibrous hydrogels.30 Independent variation of polymer length and concentrations allows us to make hydrogels of different composition, but similar mechanical properties (e.g. S1 and L05).3.2. Structural characterization using fluorescence microscopy
To image the structure of PIC-based hydrogels with fluorescence microscopy, the polymer chains were labelled with a fluorescent marker using copper-free click chemistry. More specifically, the N3-functionalized polymers were labelled using 5-carboxytetramethylrhodamine (TAMRA) conjugated to dibenzocyclooctyne-amine (DBCO, Fig. 1c) in Milli-Q water. After conjugation, the polymer solution was heated to 25 °C to form the TAMRA-PIC hydrogel and its fibrous architecture was visualized using confocal fluorescence microscopy (more details in the Methods section). As depicted in Fig. 3 and 4, PIC-based hydrogels displayed a highly heterogeneous structure, where PIC fibers were interconnected in a branched 3D network. This resulted in a very porous structure, with pores reaching sizes in the micrometer range. While similar fiber architectures have been observed in collagen- or fibrin-based gels,31,32 most synthetic polymers display a more uniform and dense network. Using fluorescence imaging we were able to show that PIC-based gels, albeit synthetic, mimic the architecture of naturally occurring hydrogels. Most likely, this is related to the fibrous nature and high persistence length of PIC polymers, unique when compared to other synthetic polymers.28To provide a quantitative description of the fiber architecture, the fluorescence images acquired were analysed using customized software developed in-house (details in the Experimental section). Briefly, the fluorescence images were segmented into ‘pores’ and ‘polymer fibers’. Following Gostick's workflow,33 the segmented images were used to calculate an Euclidean distance map which was used as input for a watershed transformation (Fig. 1e).
Previous algorithms have determined the pore size by maximizing the coverage of the pores region with circles or spheres (bubble analysis).24–27 From the distribution of the radii, it is possible to retrieve the average radius of the pores. In our analysis, the pore diameter is obtained directly from the calculated distance map after the watershed transformation. This makes the algorithm very time efficient and yields more accurate results. For porous networks, the bubble analysis algorithms includes several circles/spheres in the same pore while using the watershed-method the elongated pores are not oversampled (comparison of the methods in the Supporting Note on image analysis, ESI†). Furthermore, in addition to the pore diameter, the algorithm we developed calculates the pore connectivity and throat diameter, which cannot be obtained with other methods. In this manuscript, our quantitative hydrogel architecture analysis was used to investigate the influence of polymer concentration and molecular structure on the fiber architecture of the resulting hydrogels, allowing us to link changes in architecture directly to changes in cell behaviour.
3.3. Influence of polymer concentration
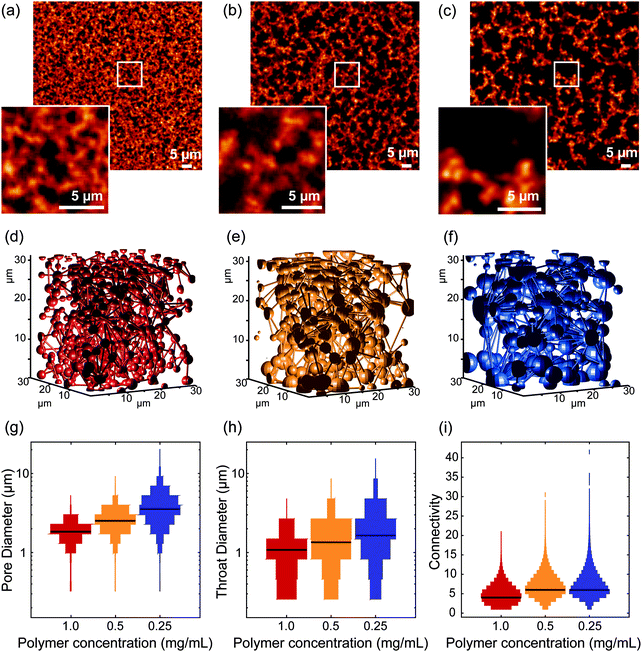
In the first set of experiments, we investigated the influence of polymer concentration on the architecture of the 3D network. We compared three different concentrations: 0.25 mg mL−1, 0.5 mg mL−1 and 1 mg mL−1, for both short and long polymers (samples designated by S025/S05/S1 and L025/L05/L1, for short and long polymers, respectively). Note that at higher PIC concentrations (2 mg mL−1), it was not possible to distinguish the polymer fibers from the pores due to the limited spatial resolution of optical microscopy (Fig. S3, ESI†).Fig. 3 shows the results obtained from the gels of the long polymers. The fluorescence images exhibited a clear difference between the different concentrations. Segmentation of the acquired images revealed a porosity of 68 ± 4%, 56 ± 4% and 41 ± 6%, for L025, L05 and L1, respectively (mean ± std, data shown in Fig. S4, ESI†). The porosity of polymer architecture affects the growth and penetration of cells in hydrogels,34–37 which explains the increasing efforts to generate such porous materials, based on techniques like solvent casting/particle leaching, freeze-drying, gas foaming and electrospinning.37 PIC-based hydrogels are intrinsically very porous, which makes them very attractive for application in 3D cell culture.
A quantitative analysis of the fiber architecture in the different gels show that with decreasing concentration, the pore diameter increases (mean ± std, 1.8 ± 0.5 μm, 2.6 ± 0.5 μm and 3.7 ± 1.6 μm, for L1, L05 and L025, respectively) as does the mean diameter of the throat (1.0 ± 0.6 μm, 1.4 ± 0.7 μm and 1.9 ± 1.2 μm, for L1, L05 and L025, respectively). The broad distribution of both parameters is a result of the high heterogeneity of the fiber architecture.
Earlier obtained cryoSEM images showed pores with a more uniform size and overall a less heterogeneous architecture on a sub-diffraction scale.38 This imaging method provides an image of the surface of a material. However, for porous materials, the subsurface region is also imaged. The cryoSEM images of PIC-based hydrogels show the polymer bundles presented at the surface and subsurface of the material, and quantification of the pore size is not possible. The difference in results between the electron and fluorescence microscopy data highlights the challenges associated with characterizing these highly porous materials and that it is crucial to study them in situ and to develop efficient software for parameter extraction.
While the mean pore diameter only shows a twofold increase, the overall architecture of the PIC-polymer fibers in L1, L05 and L025 is very distinct (Fig. 3a–c). To further quantify the differences observed in the fiber architecture of the different hydrogels, we analyzed the pore connectivity of the polymer network. Here, the connectivity of a given pore is defined by the number of pores in contact in this pore. The network connectivity is described by the distribution of the connectivity of each pore. For unconnected, isolated pores, the mean network connectivity is 0; higher connectivity values indicated a more branched network (Fig. S1, ESI†).
For the gels with a polymer concentration of 1 mg mL−1, 7.9% of the pores were isolated, i.e., surrounded by polymer fibers in all directions and presented an almost spherical shape. This number decreased to 0.7% for the lowest concentration (0.25 mg mL−1). From 1 to 0.5 mg mL−1, the median connectivity increases from 3 to 5. From 0.5 to 0.25 mg mL−1, the median connectivity remains 5, but there are some pores with very high connectivity (>20 connections). As the concentration decreases, the higher porosity of the network is translated into a higher connectivity of the calculated pores. The data acquired with the short polymers yields similar results (Fig. S5 and Table S1, ESI†). The decrease in the overall diameter of the pores indicates that increasing the concentration of PIC polymers leads to an increase in density of polymer bundles instead of an increase of polymer chains per bundle. This is in agreement with previous SAXS experiments,26 where changing the polymer concentration did not change the thickness of the polymer bundles.
The high connectivity and pore diameter make PIC-based hydrogels an interesting candidate for tissue engineering applications, for instance for bone regeneration, where interconnected micropores with 1–10 μm diameter were found to stimulate the formation of cell-rich mineralized tissue.39
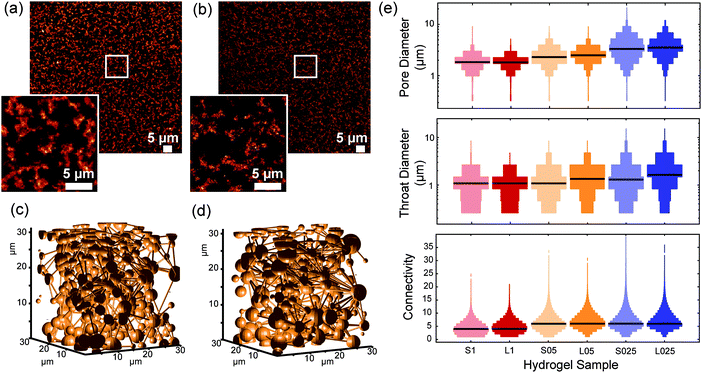
3.4. Influence of polymer length
When comparing the architectures of gels that were prepared from polymer of different lengths but at the same concentration (Fig. 4 and Fig. S5, ESI†), we find remarkably small differences in pore size, throat diameter and connectivity, certainly much smaller than the effects that we observed after changing the concentration. This result comes as a surprise, since the mechanical properties of gels from different length PICs strongly depend on the molecular weight/polymer length. In fact, earlier work showed that the shear modulus G′ scales with L2 where L is the contour length of a single polymer.29 Also in this work, we found much higher stiffnesses for the long polymer hydrogels. How can such large differences in mechanics be consistent with such similar architectures?The answer must lie in the architectural differences at the nanometer scale. Since the length of the polymers used in this study is between 145–229 nm, the rheological properties of the hydrogels are most likely determined by the bundle structures at this length scale. SAXS experiments of gels of shorter polymers revealed that they form bigger bundles that are less effective in carrying mechanical load, thereby reducing the modulus. These structures, however, seem to assemble analogously at the micrometer length scale, which accidently opens up a unique opportunity to truly study the mechanical effects of cell cultures in gels that are compositionally as well as architecturally virtually identical.
Recently, Kouwer's group has shown that the mechanical properties of PIC-based gels influence the spreading of adipose derived stem cells.40 In that report, gels of the same concentration but different composition, i.e., formed using polymers with different length, were used. The authors concluded that nonlinear mechanics influence cell proliferation: gels with a higher critical stress induce cell growth. However, the effects of the structural parameters were not investigated.
3.5. Influence of fiber architecture on cell proliferation
To study the influence of structural properties on cellular proliferation, HeLa cells were encapsulated in PIC hydrogels. Previous studies have shown that HeLa cells can proliferate in PIC hydrogels and that the proliferation rate is similar for gels with and without arginylglycylaspartic acid (RGD), an adhesive peptide that binds to integrin molecules present in the plasma membrane.40Cell proliferation in RGD-free PIC-based hydrogels was measured using the MTT assay (details in the Experimental section). As shown in Fig. 5, proliferation of HeLa cells in PIC hydrogels was lower than on plastic, for all samples. This result is in agreement with previous reports which indicate that softer materials lead to an decrease in cell proliferation.41–43
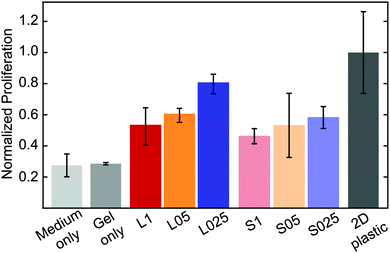 | ||
| Fig. 5 Proliferation of HeLa cells in RGD-free PIC-based hydrogels. Cell proliferation was measured using the MTT assay, 7 days after encapsulation (initial cell density: 105 cells per mL). | ||
For gels with the same composition (short or long polymers), the proliferation is higher at lower concentrations (L025 > L05 > L01 and S025 > S05 > S1). This indicates that the higher porosity of the hydrogel at lower concentrations, i.e., larger pores and higher connectivity, enhances cell proliferation. It is worth mentioning that encapsulation of HeLa cells results in a reduction of the pore size. While the median value of the pore size in PIC-based gels was found to be 1.8, 2.6 and 3.7 μm, in PIC gels with encapsulated HeLa cells the median values of the pore diameter decreased (1.55, 2.0 and 2.9 μm, for 1.0 mg mL−1, 0.5 mg mL−1 and 0.25 mg mL−1, respectively – see Fig. S9, ESI†). The volume occupied by the cells decreases the available volume of the polymer solution, and consequently leads to a decrease in the pore size. Furthermore, the presence of salts and other molecules in the cell medium might also affect the formation of the polymer bundles and consequently alter the architecture of the hydrogels.
Other trends on cell proliferation can be observed. In hydrogels with a similar initial stiffness, the proliferation rate is higher in a more porous network – for instance, cells encapsulated in S1 hydrogels grow slower than those in L025 hydrogels (cell-free G′ = 34.0 Pa, c = 1 mg mL−1 and cell-free G′ = 10.8 Pa, c = 0.25 mg mL−1, respectively). In addition, in gels with the same concentration, i.e., similar structure, proliferation seems to be higher in gels with a higher initial stiffness – for instance, cell proliferation is higher in L025 when compared with S025 (cell-free G′ = 10.3 Pa and cell-free G′ = 0.8 Pa, respectively). When evaluating the possible effect of stiffness in cell proliferation it should be noted that cell encapsulation might affect the bulk mechanical properties of the hydrogel. More important, cellular growth and proliferation might change these properties locally, in the network surrounding the cells. The relation between cells and the mechanical properties of their surrounding matrix is highly complex and not the goal of this study. Apart from the influence of the mechanical properties, the results presented here show that structural features play an important role in guiding cellular behavior.
4. Conclusions
Fluorescence microscopy offers the possibility to image structural properties of (biomimetic) hydrogels at the subcellular length scale. Moreover, as optical imaging techniques can be performed at environmental conditions, these methods are compatible with live cell imaging. Characterization of the structural properties however requires suitable analysis algorithms. Here, we developed custom analysis software to perform a network analysis of 3D fluorescence images. Our analysis approach can be broadly used to map out the architectural features of other fibrillar hydrogels.As a model system, we used PIC-based hydrogels, a new class of biomimetic materials that forms fibrous hydrogels. Our analysis revealed that PIC-based hydrogels present a highly heterogeneous structure, with pores an average pore diameter of 1.8 to 3.7 μm. Furthermore, our results show that a decrease in the concentration of the polymer led to an increase in the diameter or the pores and a higher connectivity, in particular for low concentrations (c = 0.25 mg mL−1). The polymer length, which contributes strongly to the gel stiffness has a negligible effect on the micrometer-scale fiber architecture of the hydrogel. This implies that PIC-based hydrogels with different polymers but the same polymer concentration will have different mechanical properties but similar structure. Consequently, these hydrogels can be used to investigate the influence of mechanical properties, independently of structural features, and vice versa.
The decoupling of physical cues that influence cell behavior is extremely difficult. In the example of this manuscript, we find that in gels with larger, more connected pores (but with a similar cell-free stiffness), HeLa cell proliferation is enhanced. Our freely available software is an excellent tool to provide good quality architectural properties that, together with analysis of other physical other cues (stiffness, relaxation, strain-stiffening, etc.) provides a comprehensive overview of the ECM properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Johan Hofkens for the valuable discussions and careful reading of this manuscript, Ami de Weerdt and Rik Nuyts for technical assistance, Guillermo Solis and Ovia Thirukkumaran for their support on the cell proliferation studies. This work was supported by the Research Foundation – Flanders (FWO, onderzoeksproject G0A5817N and 1529418N) and by KU Leuven (C14/16/053). J. V., B. L. and S. R. acknowledge FWO for their personal grants (1186220N, 11B1119N and 12J2616N). K. L. acknowledges the EMBO Short-Term Fellowship (7427) for his research stay in KU Leuven. This project has received funding from the European Union's Horizon 2020 research and innovation Programme under the Marie Skłodowska-Curie grant agreement no. 642687 (BIOGEL).References
- M. G. Haugh and S. C. Heilshorn, Integrating Concepts of Material Mechanics, Ligand Chemistry, Dimensionality and Degradation to Control Differentiation of Mesenchymal Stem Cells, Curr. Opin. Solid State Mater. Sci., 2016, 20(4), 171–179, DOI:10.1016/j.cossms.2016.04.001.
- S. Di Cio and J. E. Gautrot, Cell Sensing of Physical Properties at the Nanoscale: Mechanisms and Control of Cell Adhesion and Phenotype, Acta Biomater., 2016, 30, 26–48, DOI:10.1016/j.actbio.2015.11.027.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Matrix Elasticity Directs Stem Cell Lineage Specification, Cell, 2006, 126(4), 677–689, DOI:10.1016/j.cell.2006.06.044.
- R. O. Hynes, The Extracellular Matrix: Not Just Pretty Fibrils, Science, 2009, 326(5957), 1216–1219, DOI:10.1126/science.1176009.
- B. Geiger, J. P. Spatz and A. D. Bershadsky, Environmental Sensing through Focal Adhesions, Nat. Rev. Mol. Cell Biol., 2009, 10(1), 21–33, DOI:10.1038/nrm2593.
- C. Frantz, K. M. Stewart and V. M. Weaver, The Extracellular Matrix at a Glance, J. Cell Sci., 2010, 123(24), 4195–4200, DOI:10.1242/jcs.023820.
- K. A. Jansen, D. M. Donato, H. E. Balcioglu, T. Schmidt, E. H. J. Danen and G. H. Koenderink, A Guide to Mechanobiology: Where Biology and Physics Meet, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853(11, Part B), 3043–3052, DOI:10.1016/j.bbamcr.2015.05.007.
- P. A. Janmey, J. P. Winer, M. E. Murray and Q. Wen, The Hard Life of Soft Cells, Cell Motil., 2009, 66(8), 597–605, DOI:10.1002/cm.20382.
- C. S. Chen, Mechanotransduction – a Field Pulling Together?, J. Cell Sci., 2008, 121(20), 3285–3292, DOI:10.1242/jcs.023507.
- K. Metavarayuth, P. Sitasuwan, X. Zhao, Y. Lin and Q. Wang, Influence of Surface Topographical Cues on the Differentiation of Mesenchymal Stem Cells in Vitro, ACS Biomater. Sci. Eng., 2016, 2(2), 142–151, DOI:10.1021/acsbiomaterials.5b00377.
- Y. Li, Y. Xiao and C. Liu, The Horizon of Materiobiology: A Perspective on Material-Guided Cell Behaviors and Tissue Engineering, Chem. Rev., 2017, 117(5), 4376–4421, DOI:10.1021/acs.chemrev.6b00654.
- I. A. Janson and A. J. Putnam, Extracellular Matrix Elasticity and Topography: Material-Based Cues That Affect Cell Function via Conserved Mechanisms, J. Biomed. Mater. Res., Part A, 2015, 103(3), 1246–1258, DOI:10.1002/jbm.a.35254.
- A. T. Nguyen, S. R. Sathe and E. K. F. Yim, From Nano to Micro: Topographical Scale and Its Impact on Cell Adhesion, Morphology and Contact Guidance, J. Phys.: Condens. Matter, 2016, 28(18), 183001, DOI:10.1088/0953-8984/28/18/183001.
- S. Watari, K. Hayashi, J. A. Wood, P. Russell, P. F. Nealey, C. J. Murphy and D. C. Genetos, Modulation of Osteogenic Differentiation in HMSCs Cells by Submicron Topographically-Patterned Ridges and Grooves, Biomaterials, 2012, 33(1), 128–136, DOI:10.1016/j.biomaterials.2011.09.058.
- B. M. Baker and C. S. Chen, Deconstructing the Third Dimension – How 3D Culture Microenvironments Alter Cellular Cues, J. Cell Sci., 2012, 125(13), 3015–3024, DOI:10.1242/jcs.079509.
- K. Duval, H. Grover, L.-H. Han, Y. Mou, A. F. Pegoraro, J. Fredberg and Z. Chen, Modeling Physiological Events in 2D vs. 3D Cell Culture, Physiology, 2017, 32(4), 266–277, DOI:10.1152/physiol.00036.2016.
- K. Bott, Z. Upton, K. Schrobback, M. Ehrbar, J. A. Hubbell, M. P. Lutolf and S. C. Rizzi, The Effect of Matrix Characteristics on Fibroblast Proliferation in 3D Gels, Biomaterials, 2010, 31(32), 8454–8464, DOI:10.1016/j.biomaterials.2010.07.046.
- A. Pathak and S. Kumar, Biophysical Regulation of Tumor Cell Invasion: Moving beyond Matrix Stiffness, Integr. Biol., 2011, 3(4), 267–278, 10.1039/c0ib00095g.
- E. Prince and E. Kumacheva, Design and Applications of Man-Made Biomimetic Fibrillar Hydrogels, Nat. Rev. Mater., 2019, 4(2), 99, DOI:10.1038/s41578-018-0077-9.
- A. Zoumi, A. Yeh and B. J. Tromberg, Imaging Cells and Extracellular Matrix in Vivo by Using Second-Harmonic Generation and Two-Photon Excited Fluorescence, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(17), 11014–11019, DOI:10.1073/pnas.172368799.
- V. L. Cross, Y. Zheng, N. Won Choi, S. S. Verbridge, B. A. Sutermaster, L. J. Bonassar, C. Fischbach and A. D. Stroock, Dense Type I Collagen Matrices That Support Cellular Remodeling and Microfabrication for Studies of Tumor Angiogenesis and Vasculogenesis in Vitro, Biomaterials, 2010, 31(33), 8596–8607, DOI:10.1016/j.biomaterials.2010.07.072.
- K. A. Leonidakis, P. Bhattacharya, J. Patterson, B. E. Vos, G. H. Koenderink, J. Vermant, D. Lambrechts, M. Roeffaers and H. Van Oosterwyck, Fibrin Structural and Diffusional Analysis Suggests That Fibers Are Permeable to Solute Transport, Acta Biomater., 2017, 47, 25–39, DOI:10.1016/j.actbio.2016.09.044.
- P. Amadio, B. Porro, L. Sandrini, S. Fiorelli, A. Bonomi, V. Cavalca, M. Brambilla, M. Camera, F. Veglia and E. Tremoli, et al., Patho-Physiological Role of BDNF in Fibrin Clotting, Sci. Rep., 2019, 9(1), 1–11, DOI:10.1038/s41598-018-37117-1.
- W. Mickel, S. Münster, L. M. Jawerth, D. A. Vader, D. A. Weitz, A. P. Sheppard, K. Mecke, B. Fabry and G. E. Schröder-Turk, Robust Pore Size Analysis of Filamentous Networks from Three-Dimensional Confocal Microscopy, Biophys. J., 2008, 95(12), 6072–6080, DOI:10.1529/biophysj.108.135939.
- M. Molteni, D. Magatti, B. Cardinali, M. Rocco and F. Ferri, Fast Two-Dimensional Bubble Analysis of Biopolymer Filamentous Networks Pore Size from Confocal Microscopy Thin Data Stacks, Biophys. J., 2013, 104(5), 1160–1169, DOI:10.1016/j.bpj.2013.01.016.
- S. Münster and B. Fabry, A Simplified Implementation of the Bubble Analysis of Biopolymer Network Pores, Biophys. J., 2013, 104(12), 2774–2775, DOI:10.1016/j.bpj.2013.05.016.
- M. Molteni, D. Magatti, B. Cardinali, M. Rocco and F. Ferri, Response to “a Simplified Implementation of the Bubble Analysis of Biopolymer Networks Pores, Biophys. J., 2013, 104(12), 2776–2777, DOI:10.1016/j.bpj.2013.05.015.
- P. H. J. Kouwer, M. Koepf, V. A. A. Le Sage, M. Jaspers, A. M. van Buul, Z. H. Eksteen-Akeroyd, T. Woltinge, E. Schwartz, H. J. Kitto and R. Hoogenboom, et al., Responsive Biomimetic Networks from Polyisocyanopeptide Hydrogels, Nature, 2013, 493(7434), 651–655, DOI:10.1038/nature11839.
- M. Jaspers, M. Dennison, M. F. J. Mabesoone, F. C. MacKintosh, A. E. Rowan and P. H. J. Kouwer, Ultra-Responsive Soft Matter from Strain-Stiffening Hydrogels, Nat. Commun., 2014, 5, 5808, DOI:10.1038/ncomms6808.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nonlinear Elasticity in Biological Gels, Nature, 2005, 435(7039), 191–194, DOI:10.1038/nature03521.
- S. R. Caliari and J. A. Burdick, A Practical Guide to Hydrogels for Cell Culture, Nat. Methods, 2016, 13(5), 405–414, DOI:10.1038/nmeth.3839.
- G. Huang, F. Li, X. Zhao, Y. Ma, Y. Li, M. Lin, G. Jin, T. J. Lu, G. M. Genin and F. Xu, Functional and Biomimetic Materials for Engineering of the Three-Dimensional Cell Microenvironment, Chem. Rev., 2017, 117(20), 12764–12850, DOI:10.1021/acs.chemrev.7b00094.
- J. T. Gostick, Versatile and Efficient Pore Network Extraction Method Using Marker-Based Watershed Segmentation, Phys. Rev. E, 2017, 96(2), 023307, DOI:10.1103/PhysRevE.96.023307.
- K. Zhang, Y. Fan, N. Dunne and X. Li, Effect of Microporosity on Scaffolds for Bone Tissue Engineering, Regener. Biomater., 2018, 5(2), 115–124, DOI:10.1093/rb/rby001.
- F. J. O’Brien, Biomaterials & Scaffolds for Tissue Engineering, Mater. Today, 2011, 14(3), 88–95, DOI:10.1016/S1369-7021(11)70058-X.
- I. Bružauskaitė, D. Bironaitė, E. Bagdonas and E. Bernotienė, Scaffolds and Cells for Tissue Regeneration: Different Scaffold Pore Sizes-Different Cell Effects, Cytotechnology, 2016, 68(3), 355–369, DOI:10.1007/s10616-015-9895-4.
- N. Annabi, J. W. Nichol, X. Zhong, C. Ji, S. Koshy, A. Khademhosseini and F. Dehghani, Controlling the Porosity and Microarchitecture of Hydrogels for Tissue Engineering, Tissue Eng., Part B, 2010, 16(4), 371–383, DOI:10.1089/ten.teb.2009.0639.
- D. C. Schoenmakers, A. E. Rowan and P. H. J. Kouwer, Crosslinking of Fibrous Hydrogels, Nat. Commun., 2018, 9(1), 2172, DOI:10.1038/s41467-018-04508-x.
- M. Bohner, G. Baroud, A. Bernstein, N. Döbelin, L. Galea, B. Hesse, R. Heuberger, S. Meille, P. Michel and B. von Rechenberg, et al., Characterization and Distribution of Mechanically Competent Mineralized Tissue in Micropores of β-Tricalcium Phosphate Bone Substitutes, Mater. Today, 2017, 20(3), 106–115, DOI:10.1016/j.mattod.2017.02.002.
- K. Liu, S. M. Mihaila, A. Rowan, E. Oosterwijk and P. H. J. Kouwer, Synthetic Extracellular Matrices with Nonlinear Elasticity Regulate Cellular Organization, Biomacromolecules, 2019, 20(2), 826–834, DOI:10.1021/acs.biomac.8b01445.
- R. Kaukonen, A. Mai, M. Georgiadou, M. Saari, N. De Franceschi, T. Betz, H. Sihto, S. Ventelä, L. Elo and E. Jokitalo, et al., Normal Stroma Suppresses Cancer Cell Proliferation via Mechanosensitive Regulation of JMJD1a-Mediated Transcription, Nat. Commun., 2016, 7, DOI:10.1038/ncomms12237.
- Y.-T. Yeh, S. S. Hur, J. Chang, K.-C. Wang, J.-J. Chiu, Y.-S. Li and S. Chien, Matrix Stiffness Regulates Endothelial Cell Proliferation through Septin 9, PLoS One, 2012, 7(10), e46889, DOI:10.1371/journal.pone.0046889.
- F. Ataollahi, S. Pramanik, A. Moradi, A. Dalilottojari, B. Pingguan-Murphy, W. A. B. W. Abas and N. A. Abu Osman, Endothelial Cell Responses in Terms of Adhesion, Proliferation, and Morphology to Stiffness of Polydimethylsiloxane Elastomer Substrates, J. Biomed. Mater. Res., Part A, 2015, 103(7), 2203–2213, DOI:10.1002/jbm.a.35186.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01828j |
| This journal is © The Royal Society of Chemistry 2020 |