Open Access Article
Open Access Article(Homo)polymer-mediated colloidal stability of micellar solutions
Álvaro
González García†
 ab,
Alessandro
Ianiro†
ab,
Alessandro
Ianiro†
 b,
Roos
Beljon
b,
Frans A. M.
Leermakers
b,
Roos
Beljon
b,
Frans A. M.
Leermakers
 c and
Remco
Tuinier
c and
Remco
Tuinier
 *ab
*ab
aVan’t Hoff Laboratory for Physical and Colloid Chemistry, Department of Chemistry & Debye Institute, Utrecht University, Padualaan 8, 3584 CH, The Netherlands. E-mail: r.tuinier@tue.nl
bLaboratory of Physical Chemistry, Department of Chemical Engineering and Chemistry & Institute for Complex Molecular Systems (ICMS), Eindhoven University of Technology, PO Box 513, 5600 MB, Eindhoven, The Netherlands
cPhysical Chemistry and Soft Matter, Wageningen University, Stippeneng 4, 6708 WE Wageningen, The Netherlands
First published on 8th January 2020
Abstract
Despite their wide range of applications, there is a remarkable lack of fundamental understanding about how micelles respond to other components in solution. The colloidal stability of micellar solutions in presence of (homo)polymers is investigated here following a theoretical bottom-up approach. A polymer-mediated micelle–micelle interaction is extracted from changes in the micelle–unimer equilibrium as a function of the inter-micelle distance. The homopolymer-mediated diblock copolymer micelle–micelle interaction is studied both for depletion and adsorption of the homopolymer. The fluffy nature of the solvophilic domain (corona) of the micelle weakens the depletion-induced destabilization. Accumulation of polymers into the corona induces bridging attraction between micelles. In fact, both depletion and adsorption phenomena are regulated by the coronal thickness relative to the size of the added polymer. Penetration of guest compounds into the coronal domain of crew-cut micelles, with a narrower yet denser corona, is less pronounced as for starlike micelles (with a more diffuse corona). Therefore, crew-cut micelles are less sensitive to the effect of added compounds, and hence more suitable for applications in multicomponent systems, such as industrial formulations or biological fluids. The trends observed for the colloidal stability of crew-cut micelles qualitatively match with our experimental observations on aqueous dispersions of polycaprolactone–polyethylene glycol (PCL–PEO) micellar suspensions with added PEO chains.
1 Introduction
Spherical micelles formed from amphiphilic block copolymers in solution have received ample interest for multiple applications, including drug delivery,1–4 coatings5 and are present in foodstuffs.6,7 Diblock copolymers are constituted by a solvophilic and a solvophobic block, consisting of n-solvophilic and m-solvophobic units respectively. The solvophobic blocks drive the micelle formation, as the solvophobic segments (B) tend to minimize their contact with the solvent by forming a compact, solvent-depleted core.8 The solvophilic blocks (A) concentrate in the well-solvated corona. From both fundamental and application perspectives, biocompatible neutral block copolymers are appealing as their self-assembly is regulated by a small set of system parameters: the length, nature, and sequence of the blocks. Even though block copolymer micelles are mainly applied in multi-component systems, there is a remarkable lack of fundamental understanding regarding how micelles respond to other components in solution,9,10 and most investigations have focused on highly concentrated micellar solutions.11,12 Significant attention has been paid to understanding how homopolymers affect the self-organization of block copolymers in bulk13–15 but little investigations have focused on block copolymer–homopolymer–solvent ternary mixtures. Here, we study how added free homopolymers affect both the self-assembly of block copolymers in solution and the colloidal interactions between the resulting self-assembled structures. The latter may be of relevance to understand conformational changes in biological systems.16 For instance, crowding with free polymers can tune the assembly of structures in cells,17 and polymer-mediated forces affect several properties of biological membranes.18Micelles made of neutral block copolymers may be considered as sterically-stabilized colloids19 and are qualitatively similar to polymer-grafted hard colloids, but their associative nature yields some important differences.20 The colloidal stability of sterically-stabilized colloids generally increases with increasing the number of polymers per unit area (grafting density) and the length of the stabilizing chains.21 For polymer-grafted hard colloids these parameters can be controlled independently and are not affected by the environmental conditions. Conversely, the effective grafting density of block copolymer micelles depends on the equilibrium aggregation number of the micelles, which is controlled by the absolute and the relative length of the blocks, by their solubility and by the solution conditions (including the presence of dispersed additives).22 For a given lyophobic block length the aggregation number of the micelles, and hence the grafting density of the lyophilic brushes at the micelle's core, decreases with increasing the length of the lyophilic blocks.22 This mutual dependence between grafting density and lyophilic block length makes it very difficult to predict whether micelles with long lyophilic blocks (star-like micelles) are more stable from a colloidal perspective than micelles with short lyophilic blocks (crew-cut micelles) in multicomponent mixtures.22 In fact, the presence of dispersed polymeric additives might compromise the colloidal stability of the micelles via the depletion-induced attraction or bridging flocculation mechanisms observed for hard colloids.21 Being able to predict such phenomena is of key importance for reliable application of block copolymer micelles in multi-component systems, such as industrial formulations and biological fluids. For instance, a micellar drug delivery system acts in the presence of a myriad of components that may alter the micellar properties23 and affect their colloidal stability,24 resulting in a reduction or suppression of their therapeutic efficiency.
The effective interaction between multi-arm star polymers is frequently used as a model for interactions between soft colloidal particles.25 The phase stability of dispersions containing soft colloidal particles mixed with linear polymers has been reported both theoretically25,26 and experimentally.27,28 Furthermore, micelle–micelle interactions have been compared to those between star polymers.29,30 In contrast with other theoretical approaches, here we explicitly account for the associative nature of the micelles within self-consistent mean-field theory.
We use the Scheutjens–Fleer Self-Consistent Field Theory21,31 (SCFT) to investigate the colloidal stability of crew-cut and star-like micelles with a fixed lyophobic block length in the presence of dispersed (soluble) (homo)polymers. Using this theory we recently studied the solubilization of small added compounds into a block copolymer micelle32 and the interaction between block copolymer micelles20 (in the absence of additives). We showed that both phenomena are highly affected by the associative nature of the micelles. The SCFT method previously presented for the micelle–micelle interactions20 is extended here to account for the addition of homopolymers to the micellar suspension. We investigate how the presence of homopolymer in solution affects the micelle–unimer equilibrium, as this is directly related to the micelle free energy.
Therefore, by monitoring changes in the micelle–unimer equilibrium (i.e. the variation on the critical micelle concentration) as a function of the inter-micelle distance, it is possible to collect polymer-mediated micelle–micelle interactions. By allowing variations on the micelle's aggregation number, we also take into account their stability with respect to dissolution. Micelle morphology transitions are not investigated, as we focus on the interaction between spherical micelles in the dilute regime. Eventual morphology transitions can however be expected at high micelle concentrations.33 Furthermore, homopolymer addition may change the preferred spatial organization of concentrated micelles.12 From the collected potentials, we calculated the second osmotic virial coefficient (B2)34,35 to assess the phase stability of association colloid–polymer mixtures (ACPMs). Consider a dilute micelle suspension at a fixed diblock concentration (above the critical micelle concentration, CMC) to which guest compounds are added. If such a mixture has a B2-value near or above the hard sphere limit,36 it is expected to remain optically transparent (B2* ≡ B2/vc = 4, with vc the considered colloidal particle volume). If instead micelles (strongly) attract each other, B2* < 4 and the micelle suspension may get turbid. In case of B2* ≤ −6, the Vliegenthart–Lekkerkerker (VL) criterion37 states that colloidal gas–liquid phase separation of the micellar dispersion is expected. Even though this B2-value is in principle experimentally resolvable,38–42 there are many practical difficulties related to measuring B2. Thus, direct visual observation of the (in)stability of the ACPM serve here as a pragmatic confirmation of theoretical predictions made. Trends found based on our theoretical model are compared with the stability of polycaprolactone–polyethylene glycol (PCL–PEO) micelles in water in the presence of added PEO chains.
Contrary to more computationally expensive approaches,10 SCFT computations allow us to systematically asses the effect of added homopolymers with different affinity to the corona. This allows us to study both adsorption and depletion phenomena. Whilst a lot is known about the polymer-mediate phase stability of non-associative colloids, the results presented here constitute the first systematic investigation on the colloidal stability of association colloids as far as we are aware.
2 Methods
In this section we summarise the theoretical and numerical methods used to study the diblock copolymer micelles.2.1 SCFT for micelle–micelle interactions
We used the Scheutjens–Fleer self-consistent field theory (SCFT)21,31 to perform numerical calculations. We use the sfbox software in our numerical computations. In this method, the mean field approximation is implemented for a liquid mixture which is composed of lattice sites organised in ‘layers’ numbered as z = 1,…,Nlat, similar to the Flory–Huggins theory,43 with Nlat the number of lattice layers. Volume fraction profile variations between layers are allowed. On such a lattice, the Edwards equation is implemented which basically results in the discrete freely jointed chain model for the chain statistics.44 The incompressibility condition (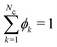 , with Nc the number of components) is applied to the volume fractions ϕk(z) at each lattice layer, and at each lattice site z a segment potential uk(z) is defined. The geometry of the lattice and the boundary conditions further define the system of interest. Micelles are modelled in a spherical lattice geometry wherein the number of lattice sites increases basically quadratically with z: the lattice is defined as shells from the centre of the lattice z = 0 up to z = Nlat. For such a system one can write down a mean field free energy F ≡ F(ϕ,u,α), where α is a Lagrange field that is coupled to the incompressibility constraint. Nearest-neighbour segment–segment interactions are captured via Flory–Huggins interaction parameters between species i and j, χij. Note that within the Flory–Huggins approach all self-interactions are athermal: χii = 0. We choose the self-interactions as zero, which sets the reference for the other interactions present. Extremisation of the mean-field free energy leads to the self-consistent field relation:
, with Nc the number of components) is applied to the volume fractions ϕk(z) at each lattice layer, and at each lattice site z a segment potential uk(z) is defined. The geometry of the lattice and the boundary conditions further define the system of interest. Micelles are modelled in a spherical lattice geometry wherein the number of lattice sites increases basically quadratically with z: the lattice is defined as shells from the centre of the lattice z = 0 up to z = Nlat. For such a system one can write down a mean field free energy F ≡ F(ϕ,u,α), where α is a Lagrange field that is coupled to the incompressibility constraint. Nearest-neighbour segment–segment interactions are captured via Flory–Huggins interaction parameters between species i and j, χij. Note that within the Flory–Huggins approach all self-interactions are athermal: χii = 0. We choose the self-interactions as zero, which sets the reference for the other interactions present. Extremisation of the mean-field free energy leads to the self-consistent field relation:| ϕk(uk) ↔ uk(ϕk), |
The SCFT approach accurately resolves the equilibrium properties of the system of interest. From the free energy, one can derive other thermodynamic functions such as the grand potential Ω, which is a central quantity in the small system thermodynamics approach.45Via Ω, the conditions under which the diblock copolymers form self-assembled morphologies can be resolved. To find the equilibrium configuration, we compute the grand potential Ω of the system for a specific diblock copolymer as a function of the aggregation number gp, which is the number of diblocks per micelle. This grand potential relates to the inhomogeneities in the system (i.e., for any homogeneous bulk phase such as a pure solvent or a polymer solution Ω = 0). As diblock copolymers are added to the solution, Ω increases due to the unfavourable contacts present between solvent molecules and solvophobic blocks. The appearance of the first thermodynamically stable micelle is marked by a maximum in Ω. If a micelle can form, Ω decreases with gp, and at a given diblock concentration the condition Ωgp≠0 = 0 is met (with ∂Ω/∂gp<0). At this condition, the most probable micelle (ignoring translational entropy effects) is found. Following the thermodynamics of micelle formation, the micelle is in equilibrium with free block copolymers in the bulk. Hence, the chemical potential μp of one copolymer in the micelle μmicellep is equal to that in the bulk μbulkp:
μbulkp = μmicellep ≡ μp ≈ cnst + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lnϕbulkp, lnϕbulkp, | (1) |
| ω(r) = gp(r)μp(r) + gs(r)μs(r) + gG(r)μG(r), | (2) |
 | (3) |
From the micelle–micelle interactions, the second (osmotic) virial coefficient (B2) can be extracted to assess the stability of the colloidal suspension.34,35 For any form of the pair interaction W(r), the second virial coefficient follows as:
 | (4) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ≡ r/(2Roh) the normalised inter-micelle distance with Roh the undistorted (homopolymer-free) micelle size. As the micelle–micelle interactions are not resolvable for
≡ r/(2Roh) the normalised inter-micelle distance with Roh the undistorted (homopolymer-free) micelle size. As the micelle–micelle interactions are not resolvable for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ≪ 1, interpolation of the SCFT-generated results at the smallest resolved
≪ 1, interpolation of the SCFT-generated results at the smallest resolved ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) are used.
are used.
2.2 System parameters
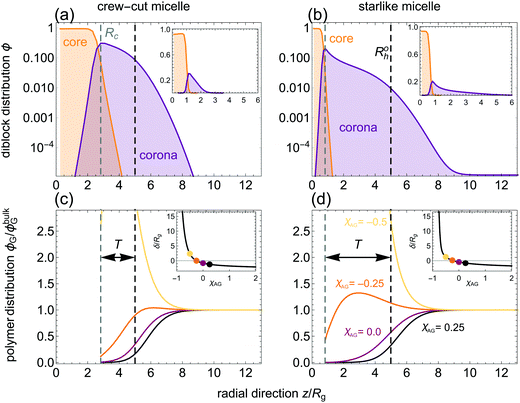
We followed the approach outlined in the previous section to collect (homo)polymer-mediated micelle–micelle interactions. When considering diblock copolymer micelles in the presence of polymers in a common solvent, the key variables are those reported in Fig. 1. Specifically, these variables are: (i) the different segment–segment and segment–solvent interactions; (ii) the equilibrium micelle properties, and (iii) the relative size of homopolymer to micelle and its bulk concentration. Contrary to more computationally expensive methods,10 in the SCFT approach followed one can easily scan this parameter space. Micelles are constituted of gp (the aggregation number) diblock copolymers with composition B24An, where B is the solvophobic block (χBW = 2), A is the solvophilic block (χAW = 0.4), and χAB = 1. Here, W stands for the solvent molecule. These parameters are selected to meet typical solvencies for industrially-relevant systems such as pluronics in water,53,54 and are based on previous investigations.55 At fixed solvophobic block length (m = 24) we consider a crew-cut and a starlike micelle with n = 45 and n = 450, respectively. This enables us to study simultaneously the effects of very different bulk unimer concentrations and peripheral micelle regions on the micelle–homopolymer mixture: to compare crew-cut and starlike micelles. In Table 1 the parameters that define the architecture of the diblocks and guest polymers are specified. | ||
| Fig. 1 Representation of micelle–unimer equilibrium of a micelle (left) composed of gp unimers (purple and orange) in the presence of added homopolymer (green). Addition of a second component in the bulk (potentially) affects this equilibrium. The top-right quadrant corresponds to the segment–segment and segment–solvent interactions considered (values given in Table 1), with A the solvophilic block, B the solvophobic block, G the homopolymer block, and W the solvent. Further specified are the hydrodynamic micelle radius Rh, the corona thickness T, the core radius Rc, and the radius of gyration of the homopolymer Rg. We highlight the parameter χAG which determines whether homopolymers are depleted or adsorbed. | ||
| m | n | N | χ BW | χ AW ≡ χGW | χ AB ≡ χGB | χ AG |
|---|---|---|---|---|---|---|
| 24 | 45, 450 | Var | 2 | 0.4 | 1 | var |
To assess the effects of the homopolymer-mediated micelle–micelle interactions, we introduce the size ratio of the (guest) homopolymer to the undistorted micelle size:
 | (5) |
 | (6) |
 | (7) |
 | (8) |
We identify whether the homopolymer is adsorbed onto or depleted from the micelle in terms of the adsorption thickness δ, defined here from the discrete SCFT density profile ϕG(z) as:
 | (9) |
2.3 Experimental methods
Block copolymers PCL12PEO45 have been synthesized and purified, and the micelle dispersions have been prepared as in previous works.55 The undistorted hydrodynamic radius of the resulting micelles (Ro,exph = 9 nm) was measured using dynamic light scattering (DLS). DLS experiments were performed by means of an ALV CGS-3 equipped with a 532 nm green laser. The polymers used as depletants, namely PEO45, PEO136 and PEO227, were purchased from Sigma-Aldrich and have been used as received. The Rg value of these copolymers (Rg = 1.4, 2.6 and 3.4 nm respectively) have been calculated using eqn (6) assuming b = 0.4 nm.55 The overlap concentrations of these polymers have been estimated upon applying eqn (7), while the polymer volume fraction in solution have been calculated dividing the polymer mass concentration by the polymer density ρ = 1.125 g × cm−3.583 Results and discussion
We first discuss the equilibrium properties of micelles and the concentration distribution of diluted homopolymers as a function of the homopolymer-corona effective affinity. Subsequently, homopolymer concentration effects on the micelle equilibrium are studied for different guest polymer–micelle combinations (crew cut, starlike, depleted, adsorbed). Additionally, the stability of association colloid–polymer mixtures (ACPMs) is investigated, and results are discussed in terms of the second virial coefficient B2. Representative homopolymer-mediated micelle–micelle interactions are rationalised in Appendix A.3.1 Homopolymer depletion and adsorption in spherical micelles
Some SCFT-computed characteristics of isolated crew-cut and starlike micelles are presented in Table 2. The different architectures of the unimers leads to distinct properties of the micelle, reflected in the aggregation number gp, undistorted hydrodynamic size Roh, critical micelle concentration (CMC), and sharpness of the corona (expressed through the maximum concentration of solvophilic blocks ϕmaxA). Due to the (much) lower gp-value but larger Roh-value of the starlike micelle compared to the crew-cut one, the available surface area per diblock of a starlike micelle is significantly larger than for a crew-cut one.20 Hence, the peripheral region of the starlike micelle is more diffuse than for the crew-cut one. The CMC is controlled at first order by the solvophobic block length.59 However, due to the larger solvophilic to solvophobic block size ratio of the starlike micelle, its CMC (expressed here via the diblock bulk volume fraction ϕbulkp) is about 500 times larger. Consequently, the unimer-micelle equilibrium upon addition of guest homopolymer is expected to be more affected for a starlike micelle than for a crewcut one.| Unimer | g p | ϕ bulkp ≈ CMC | ϕ maxA | R oh | R c | T |
|---|---|---|---|---|---|---|
| B24A45 | 134 | 3.6 × 10−8 | 0.31 | 19.5 | 11 | 8.5 |
| B24A450 | 37 | 1.3 × 10−5 | 0.20 | 48.3 | 8 | 40.3 |
Equilibrium radial volume fraction profiles are shown in Fig. 2(a) and (b) as a function of the distance from the centre of the micelle z. The maximum concentration of solvophilic blocks ϕmaxA roughly coincides with the position of the core–corona interface, used here as estimated core radius [Rc ≡ z(ϕmaxA)]. The corona thickness (defined as T = Roh − Rc) is obviously larger for the starlike micelle, which has a smaller Rc due to the much lower value of gp. The lower ϕmaxA-value also indicates that the outer region of the starlike micelle is overall less dense than for the crew-cut assembly.
Not only the relative size of the homopolymer and its concentration modulate the effective micelle–micelle interactions, but also the affinity between the homopolymer and the outer micelle region (i.e., the corona).60 Homopolymers in solution are either depleted from or adsorbed to the corona domain, depending on the affinity between the corona blocks and the homopolymer. In Fig. 2(c) and (d), the normalised homopolymer volume fraction (ϕG/ϕbulkG) is plotted as a function of z at fixed ϕbulkG/ϕG* = 10−4. For χAG ≥ 0 homopolymers are depleted (ϕG < ϕbulkG) from the micelle, with ϕG(z = Rc) ≈ 0. Due to the entropic penalty of homopolymers being near or within the micelle, ϕG decreases with respect to ϕbulkG if χAG attains a sufficiently large (repulsive) value.
For χAG = −0.25 adsorption occurs and ϕG(z ≲ Roh) is larger than for χAG = 0.25 or χAG = 0, see Fig. 2(c) and (d). For the crew-cut micelle the homopolymer practically does not adsorb at z > Roh for χAG = −0.25, and is still partially depleted from Rc (note there is a finite homopolymer concentration at Rc). For the starlike micelle, ϕG reaches a pronounced maximum value above ϕbulkG within the corona; yet it is also partially depleted close to the core (z → Rc). This suggests that the degree of penetration of the added polymer into the coronal domains modulates the stability of ACPMs. For χAG = −0.5, ϕG is always greater than ϕbulkG for z-values within the corona: homopolymer adsorption to the corona occurs. The adsorption thickness δ (see Methods) indicates whether depletion (δ < 0) or adsorption (δ > 0) takes place. The transition from homopolymer depletion to adsorption is observed in the insets of Fig. 2(c) and (d) in terms of δ as a function of χAG. Near χAG = −0.25, the sign of δ switches from negative (depletion) to positive (adsorption). The thickness of the depletion layer |δ| increases with increasing χAG until it reaches a plateau, in concordance with what is expected for depletion from a hard surface. The dramatic increase in δ upon homopolymer adsorption upon lowering χAG is also in line with observations of homopolymer adsorption at a hard surface.21
3.2 Addition of homopolymer modulates the micelle–unimer equilibrium
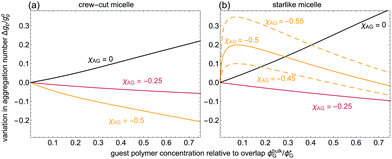
The homopolymer concentration considered in the previous section was in the dilute regime to study adherence to the micelles. Here, the focus is on elevated homopolymer concentrations at which the micelle–unimer equilibrium is affected. Firstly, we focus on cases where depletion of the homopolymer is observed in Fig. 2. Particularly, we study the effect of homopolymer concentration (ϕbulkG) on the equilibrium local density profiles near and within an isolated micelle. In Fig. 3 the influence of homopolymer depletion on the aggregation number, expressed in terms of Δgp = gp(ϕbulkG) − gp(ϕbulkG = 0) is shown. It follows that the aggregation number of both kinds of micelles increases with increasing ϕbulkG. This agrees with previously reported experimental observations.9 The increase in gp is weaker when the homopolymer size is larger (i.e., increasing q). For large homopolymers it is more difficult to penetrate the corona. Interestingly, the micelle size is hardly affected by these changes in gp. In fact, upon averaging over all considered q-values and ϕbulkG concentrations in Fig. 3, we find for the crew cut micelle 〈Rh〉 = 19.8 ± 0.2 [l.u.] and for the starlike micelle 〈Rh〉 = 48.0 ± 0.9 [l.u.]. These values are fairly close to the depletant-free, undistorted micelle sizes presented (see Table 2). The addition of homopolymer to the bulk reduces the effective volume available for the free block copolymers, as they cannot access the portion of the solvent within the solvated (homo)polymer coils. Consequently, the micelle–unimer equilibria shifts towards the micelle, thus increasing gp. This is confirmed by the fact that for q = 0.2 and χAG = 0.5, gp is larger than for χAG = 0 at the same ϕbulkG. The steeper increase of gp for the starlike micelle follows from its (much) higher ϕbulkp (see Table 2).Next, we study the effect of corona-adsorbing homopolymers on the equilibrium micelle properties at fixed (homo)poloymer-to-micelle size ratio q. In Fig. 4, the variation on gp due to polymers with an enthalpic preference for the corona is reported (χAG < 0), and compared to guest polymers with athermal interaction with the corona (χAG = 0). For isolated micelles and low guest polymer concentrations, adsorption to the corona of the starlike micelle is much higher than to the crew-cut one (detailed profile in Appendix B). Contrary to the depletion case, the micelle–unimer equilibria shifts towards the unimer side due to favourable diblock–homopolymer interactions in the bulk (i.e., the addition of (homo)polymers effectively increases the solvent quality). For a sufficiently strong solvophilic block–homopolymer affinity, homopolymers adsorbed at the core–corona interface screen the solvophobic core.32 These two arguments suffice for explaining the decrease in gp with increasing ϕbulkG observed for crew-cut micelles, shown in Fig. 4.
The effect of adsorption onto the corona of starlike micelles is more intricate due to the more diffuse peripheral domain. A polymer with a strong affinity for the (large) corona may actually stick solvophilic brushes together, hence overcompensating the entropic penalty associated with the interpenetration of the homopolymers in the corona. This leads to the observed increase of gp at very low ϕbulkG. Saturation of the corona with homopolymers then leads to a decrease of gp at higher ϕbulkG: homopolymer-diblock contacts in the bulk become, again, more favourable than in the saturated micelle. The curves for χAG = −0.45 and χAG = −0.55 for the starlike micelle corroborate this explanation. The same effect on gp could be observed for stronger attractions (χAG ≈ −0.7) of the homopolymer with the coronal domain of the crew-cut micelle. From our theoretical investigations [see also32 for encapsulation of small (q ≪ 0.1) guest compounds], it is clear that the changes on gp and Rh can be used to experimentally assess the distribution of adsorbing homopolymers over the micelles.
3.3 On the stability of ACPMs: crew-cut vs. star-like
In this last Results section, the colloidal stability of association colloid–polymer mixtures (ACPMs) is assessed in terms of the second osmotic virial coefficient B2, calculated from the polymer-mediated micelle–micelle interactions (see Appendix A). We consider the colloidal particle volume as the one of an isolated micelle and without any added homopolymers, vc ≡ voh = (4π/3)(Roh)3. In Fig. 5, B2* ≡ B2/vc is shown for q = 0.2 as a function of the homopolymer concentration ϕbulkG/ϕG* at fixed homopolymer-to-micelle size q = 0.2. These B2*-values follow from interactions as those presented in Fig. 8–10. We focus first on homopolymers which only interact via excluded volume with the coronal domain, χAG = 0. Both for crew-cut and starlike micelles, B2 decreases only weakly upon addition of homopolymer: the depletion zone spans through the coronal domains and hardly on the outside of the micelles, rendering depletion effects weak. The colloidal stability decreases dramatically from ϕbulkG/ϕG* ≈ 0.1 when depletion effects arise via a corona-homopolymer effective affinity with an enthalpic repulsion beyond the excluded volume (χAG = 0.25). Hence, it is expected that a suspension of micelles gets unstable at high homopolymer concentrations. Due to the wider coronal region, depletion-induced destabilisation of a starlike micelle-depletant mixture occurs at slightly higher homopolymer bulk concentration. For starlike micelles, the depletion effects are weaker due to the deeper penetration of homopolymer into the corona.Adding weakly-adsorbing homopolymers (χAG = −0.25) to a crew-cut micelle suspension leads to a mostly ϕbulkG-independent micelle–micelle interaction. For stronger homopolymer-solvophilic block attraction (χAG = −0.5), bridging attraction and restabilisation is observed in terms of B2. The trends observed considering (weakly) adsorbing homopolymers show that starlike micelles destabilize more easily than the crew-cut analogues. For adsorbing polymers at high ϕbulkG, starlike micelles are more easily destabilized. In micelle applications (such as drug-delivery systems), components with different affinities for the corona blocks may be present. In virtue of their shorter relative hydrophilic block length, we expect that crew-cut micelles are overall more stable in multicomponent systems due to, in essence, a denser and narrower coronal region.
To verify the reliability of our approach, we compared the SCFT predictions with experimental observations on crew-cut micelles. The set of interaction parameters used in this study is suitable to describe polycaprolactone–polyethylene glycol (PCL–PEO) diblock copolymer micelles55 in water. An aqueous suspension of such spherical micelles was prepared (the block copolymer composition was CL12EO45, see Methods for details), and mixed with free PEO homopolymers of different molar masses at different concentrations. A CL monomer is roughly twice as large as an EO monomer,55 therefore, CL12EO45 may be mapped onto our B24A45 model crew-cut micelle. In Fig. 6(a) we show photographs of mixtures of micelles (diblock copolymer concentration is 5 mg ml−1) mixed together pure PEO at fixed concentration φ/φ*, where φ denotes experimentally-resolved PEO concentrations for various (weight-averaged) molar masses: I, Mw = 2 kDa; II, Mw = 6 kDa; and III, Mw = 10 kDa. Photographs IV, II, and VI refer to a single type of PEO (Mw = 6 kDa, corresponding to N = 136) for various PEO concentrations. In Fig. 6(b) and (c) we plot the SCFT-predicted B2 values as a function of the relative polymer size (b) and polymer concentration (c). As experimentally observed, for theoretically-calculated B2* ≲ −6 gets unstable. Sample II is stable but clearly more turbid than Samples I and IV. This can be explained by a significant free PEO-induced micelle–micelle attraction (B2* ≲ 0), although the attractions not yet sufficiently strong to induce demixing.
4 Conclusions
In this paper, homopolymer-meditated micelle–micelle interactions were studied using numerical lattice computations based on the Scheutjens–Fleer self-consistent field theory, which explicitly considers the associative nature of the micelles. We quantified how the addition of soluble homopolymer in bulk shifts the unimer-micelle equilibria and study the effect of different affinities between the homopolymer and the outer coronal blocks on the structure of the micelle. The resulting changes of the bulk unimer concentration determine the micelle properties, particularly the aggregation number (gp). In line with previous experimental observations, homopolymer depletion leads to an increase of the aggregation number which can be rationalised in terms of the micelle–unimer equilibria. For added homopolymers which are attracted to the solvophilic blocks, weak adsorption leads to a decrease of the aggregation number with increasing homopolymer bulk concentrations. Above a certain affinity threshold, the aggregation number first increases and then decreases with increasing homopolymer bulk concentration.In case of non-adsorbing homopolymers, the diffuse micellar outer region leads to small effective depletion layers because they penetrate into the coronas. Despite the broader depletion profile as compared to near hard spheres, depletion effects are weaker as the overlap of depletion layers is screened by the presence of the fluffy corona. Even at intermicelle distances in the order of their (undistorted) diameter, full homopolymer depletion may not be observed. Not surprisingly, an added enthalpic repulsion between the corona-forming blocks and the guest homopolymer enhances depletion effects. A strong enough guest polymer affinity to the corona leads to an almost classical polymer-mediated interaction between crew-cut micelles: bridging flocculation at low concentrations, and restabilisation upon saturation of the corona. Remarkably, weakly-adsorbing polymers may not affect the stability of the micellar suspension if the enthalpic and entropic effects of homopolymers in the coronal domain are balanced. For starlike micelles, bridging within the coronal domains leads to attractions which only increases with increasing polymer bulk concentration (up to the near-overlap concentrations studied). The packing of the homopolymer in the corona determines whether the micelle–micelle steric repulsion vanishes at high enough homopolymer concentrations. If the corona thickness is of the order of the added homopolymer diameter, a repulsive contribution to the micelle–micelle interaction is expected to be present.
From the second virial coefficient (B2) we observe that both crew-cut and starlike micelles are destabilized at high enough non-adsorbing homopolymer concentration due to a (weak) depletion attraction. In case of added adsorbing homopolymer, the B2-value of the crew-cut micelle–homopolymer mixture is less sensitive than for the starlike case. The trends predicted by our SCFT computations for the crew-cut micelles are qualitatively confirmed experimentally using biocompatible PCL–PEO diblock copolymer micelles in water and added free PEO homopolymer. We deduce from our investigation that a narrower coronal domain makes spherical micelles more suitable for applications, such as drug-delivery systems, where multiple macromolecular components are present. We encourage experimentalists to compare their results to our SCFT predictions. Requests for the SFbox program can be submitted to F. A. M. Leermakers, Wageningen University.
Conflicts of interest
There are no conflicts to declare.Appendix
A Micelle–micelle interactions
In this Appendix some example pair-potentials calculated are presented and discussed.A.1 Depletion in ACPMs
Homopolymer volume fraction distributions for selected ϕbulkG-values are shown in Fig. 7. The observed partial penetration of homopolymers in the coronal domain has been previously reported,11 and such interpenetration also occurs between polymer brushes and free homopolymer,61,62 and in polymer-grafted spheres in a polymeric matrix.63 With increasing homopolymer bulk concentration, |δ| decreases due to the increasing osmotic pressure that bulk homopolymers exert onto those in the vicinity or within the diffuse micelle's peripheral region. This effect is well-known for non-adsorbing polymers near a hard surface.56,64 As depletants penetrate through the coronal region, this compression of the depletion layer is weaker for a micelle than for a hard colloidal surface. As can be observed, the shape of the depletion profile resembles that of non-adsorbing homopolymers in Θ-solvent around a hard sphere56 [ ]. However, in this case the depletion density profile extents in between the limits of a ‘classical’ depletion profile from hard spheres with radii Roh and Rc (dashed vertical lines in Fig. 7). A broader coronal thickness leads to a wider depletion profile for the star-like micelles.
]. However, in this case the depletion density profile extents in between the limits of a ‘classical’ depletion profile from hard spheres with radii Roh and Rc (dashed vertical lines in Fig. 7). A broader coronal thickness leads to a wider depletion profile for the star-like micelles.
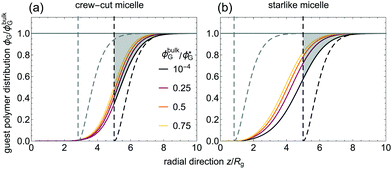 | ||
| Fig. 7 Homopolymer (depletant) segment radial volume fraction profiles as a function of the distance from the centre of a micelle z as computed using SCFT in a spherical lattice considering crew-cut (a) and star-like (b) micelles. The homopolymer considered is of the same nature as the corona (χAG = 0). Dashed curves correspond to the depletion profiles of polymers in Θ-solvent condition from a hard sphere,56 considering the hard sphere radius either as the core radius (Rc, grey) or the hydrodynamic radius of the undistorted micelle (Roh, black). The relative polymer size is q ≡ Rg/Roh = 0.2. Results are given for a few homopolymer concentrations, indicated in the plot. The coloured grey areas are used to illustrate the depletion thickness (δ) from z0 ≈ Roh for the lowest homopolymer concentration. | ||
In Fig. 8 the micelle–micelle interactions in presence of depleted homopolymers are presented. At low depletant concentrations (ϕbulkG/ϕG* = 0.01), the micelle–micelle interactions can be described as a hard-core Yukawa repulsion.20 At higher ϕbulkG, pure excluded volume interactions of the homopolymer with the coronal blocks (χAG = 0) induce a shallow minimum in the micelle–micelle interaction between crew-cut micelles. This minimum is due to the homopolymer-induced depletion attraction between micelles. The position of this minimum shifts towards r = 2Roh with increasing ϕbulkG due to the compression of the depletion layer [inset of Fig. 8(a)]. For the starlike micelle considered, χAG = 0 is insufficiently repulsive to induce an attractive minimum in the interaction potential between the micelles [inset of Fig. 8(b)]; the micelle–micelle interaction is only repulsive. This weakening of the steric repulsion between micelles upon adding free non-adsorbing homopolymers has also been reported for the interaction between star polymers.25 This micelle–micelle repulsion significantly weakens in r < 2Roh with increasing ϕbulkG. These effects are further rationalised in Appendix A.3. For χAG = 0.25, a minimum in the homopolymer-mediated micelle–micelle interactions is present for the two kinds of micelles as a result of more repulsive hydrophilic block–homopolymer interactions, which effectively shifts the depletion zone towards the outer micelle region: there is not only an entropic, but also an enthalpic penalty whenever depletants penetrate into the coronal domain. The trends observed in the micelle–micelle interactions in case of homopolymer depletion match with expectations based upon the interactions between soft colloids:25,27 the interaction weakens as the outer coronas get more fluffy.
Experimentally, depletion effects decrease the effective (hard-sphere equivalent) colloidal size of the micelle, which may relate to the lack of a repulsive contribution to the micelle–micelle interaction observed for the starlike micelle at high enough homopolymer concentrations.9 We note here that whereas |δ| decreases with ϕbulkG, this decrease is not enough (in hard colloidal suspensions) to re-stabilize the depletion attraction, whose strength increases with ϕbulkG. The overlap of depletion zones when micelles get closer does not lead to full depletion of the guest homopolymer, even if an added enthalpic penalty is considered (profile details in Appendix B). From the trends of the depletion profiles and of the micelle–micelle interactions, we conclude that the depletion attraction is weaker in micellar suspensions than in hard colloidal systems due to the inherent steric repulsion and the penetration of the depletants into the micellar domain. Insights into micelle–micelle interactions may be of relevance for further understanding the effects of depletion phenomena in systems where micelles are present, such as drug-delivery4 or foodstuffs.6
A.2 Coronal physisorption in ACPMs
In Fig. 9, example micelle–micelle interactions mediated by corona-adsorbing homopolymers are shown. For crew cut-micelles, a slight preference for the coronal blocks (χAG = −0.25) hardly affects the pair interactions upon increasing ϕbulkG; even close to ϕG*, the micelle–micelle interaction mostly remains unaffected. For a stronger homopolymer–coronal affinity (χAG = −0.5), a shallow attraction at low ϕbulkG appears, which then weakens with increasing ϕbulkG (inset of Fig. 9). This can be explained by a bridging attraction mechanism:21 at low concentration homopolymers simultaneously adsorb onto the coronas of different micelles, which leads to attraction between them. This trend of the bridging attraction between micelles with increasing ϕbulkG is similar to that observed between hard colloids.21 With increasing ϕbulkG, the coronal domains may get saturated with homopolymer, leading to a restabilisation of the micelle suspension. The homopolyer-mediated micelle–micelle bridging attraction results from the intricate combination of homopolymer configuration changes (loop-to-bridge) and micelle–unimer equilibria. Perhaps, fewer loops transform intro bridges as compared to the attraction between hard spheres due to the fluffy and diffuse nature of the interface. This leads to a weaker bridging attraction between micelles as between hard spheres.As for the depletion cases, the effect of adsorbing polymer is more convoluted for starlike micelles due to their broader corona. For the q-value considered (q = 0.2), the relative volume of the (undistorted) homopolymer per coronal block is about four times larger for the starlike micelle than for the crew-cut one (see Appendix B). Note that at fixed q and χAG, adsorption is much higher for the starlike micelle than for the crewcut one (see profiles in Appendix B). Hence, bridging effects are strong for starlike micelles as they get closer. The large and fluffy corona prevents saturation of the peripheral ‘colloidal domain’, at least within the considered ϕG-values. Thus, contrary to the crew-cut micelle, re-stabilisation of the bridging flocculation is not observed in the micelle–micelle interactions even at high ϕG. The steric micelle–micelle repulsion gets screened due to the presence of adsorbing homopolymer, leading to a transition from repulsive to attractive micelle–micelle interaction. The larger coronal domain may favour the loop-to-bridge transition, which becomes dominant over the steric repulsion. In the next section, the relevance of the relative size of the added homopolymer to the coronal thickness is addressed: penetration of homopolymer is rationalised not in terms of q ≡ Rg/Roh, but in terms of Rg/T.
A.3 Corona thickness and colloidal stability
It is clear from the computed micelle–micelle interactions that a high degree of interpenetration of either adsorbing or depleted compounds into the coronal domain leads to destabilisation of the micelle suspension with increasing the guest homopolymer concentration ϕbulkG. In block copolymer/homopolymer blends, the degree of homopolymer penetration in the corona is related to its length relative to the corona-forming block length.13 For the relative size q = 0.2, the starlike micelle–micelle steric repulsion practically vanishes at ϕbulkG/ϕG* = 0.75 [see Fig. 8(b)]. Within the model here considered, the strongest repulsive contribution to the (homopolymer-free) micelle–micelle interaction arises from the expel of diblocks.20 Independently of the value of χAG, the presence of homopolymers in the corona may screen this strongly-repulsive core compression. For the crew-cut micelle considered, q ≈ 0.2 corresponds to the situation where the diameter of the added homopolymer roughly equals the coronal thickness (2Rg = T). For a starlike micelle, this situation is retained for q ≈ 0.4.We present in Fig. 10 the homopolymer-meditated starlike micelle–micelle interaction for q = 0.4 and χAG = 0. This micelle–micelle interactions are similar to those between crew-cut micelles at q = 0.2 (for which Rg = T/2): for larger q, fewer polymer chains fit into the corona, and a repulsive contribution to the homopolymer-mediated micelle–micelle interaction remains. The much higher ϕbulkG-value for the starlike micelle renders all guest homopolymer effects on the micelle equilibria stronger due to the lower energy required to remove a diblock from the starlike micelle as compared to the crew-cut one. This leads to a clear decrease of the repulsive contribution to the micelle–micelle interaction, which decreases from W(r = 2Roh) ≈ 10kBT in absence of homopolymer to W(r = 2Roh) ≈ 5kBT at ϕbulkG/ϕG* = 0.75. It follows from this short section that it is the ratio of the corona thickness to the diameter of the added homopolymer which determines whether a repulsive contribution to the micelle–micelle interaction is present upon addition of homopolymer. Therefore, the ratio T/Rg might be of relevance in the design of controlled experiments. In fact, it has been experimentally shown that this ratio controls the homopolymer-induced aggregation of vesicles in water upon homopolymer addition.65
B Packing arguments and concentration profiles
The relative volume of a corona block in the micelle per undistorted homopolymer volume Q can be derived from geometrical arguments: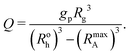 | (10) |
Acknowledgements
Á. G. G. acknowledges NWO, DSM and SymoChem for funding NWO-TA project 731.015.205. Á. G. G. and A. I. thank K. Poschl for inspiring discussions.References
- L. Yang, X. Qi, P. Liu, A. El Ghzaoui and S. Li, Int. J. Pharm., 2010, 394, 43–49 CrossRef CAS.
- W. Li, J. Li, J. Gao, B. Li, Y. Xia, Y. Meng, Y. Yu, H. Chen, J. Dai, H. Wang and Y. Guo, Biomaterials, 2011, 32, 3832–3844 CrossRef CAS PubMed.
- J. Wang, X. Xing, X. Fang, C. Zhou, F. Huang, Z. Wu, J. Lou and W. Liang, Philos. Trans. R. Soc., A, 2013, 371, 20120309 CrossRef PubMed.
- D. Lombardo, P. Calandra, D. Barreca, S. Magazú and M. A. Kiselev, Nanomaterials, 2016, 6, 125 CrossRef PubMed.
- A. Muñoz-Bonilla, S. I. Ali, A. del Campo, M. Fernández-García, A. M. van Herk and J. P. A. Heuts, Macromolecules, 2011, 44, 4282–4290 CrossRef.
- A. Syrbe, W. J. Bauer and H. Klostermeyer, Int. Dairy J., 1998, 8, 179–193 CrossRef CAS.
- J. O’Connell, V. Grinberg and C. G. De Kruif, J. Colloid Interface Sci., 2003, 258, 33–39 CrossRef.
- C. B. E. Guerin and I. Szleifer, Langmuir, 1999, 15, 7901–7911 CrossRef CAS.
- S. Abbas and T. P. Lodge, Phys. Rev. Lett., 2007, 99, 137802 CrossRef PubMed.
- T. Yang, Z. Lei, S. Yang and E.-Q. Chen, Phys. Chem. Chem. Phys., 2019, 21, 2121–2127 RSC.
- R. Yamazaki, N. Numasawa and T. Nose, Polymer, 2004, 45, 6227–6234 CrossRef CAS.
- S. Abbas and T. P. Lodge, Macromolecules, 2008, 41, 8895–8902 CrossRef CAS.
- K. Gohr, W. Schärtl, L. Willner and W. Pyckhout-Hintzen, Macromolecules, 2002, 35, 9110–9116 CrossRef CAS.
- R. W. Sandoval, D. E. Williams, J. Kim, C. B. Roth and J. M. Torkelson, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 2672–2682 CrossRef CAS.
- M. J. Greenall, D. M. A. Buzza and T. C. B. McLeish, Macromolecules, 2009, 42, 5873–5880 CrossRef CAS.
- D. Otzen, Biochim. Biophys. Acta, Proteins Proteomics, 1814, 2011, 562–591 Search PubMed.
- R. Hancock, J. Struct. Biol., 2004, 146, 281–290 CrossRef CAS PubMed.
- R. N. Frese, J. C. Pámies, J. D. Olsen, S. Bahatyrova, C. D. van der Weij-de Wit, T. J. Aartsma, C. Otto, C. N. Hunter, D. Frenkel and R. van Grondelle, Biophys. J., 2008, 94, 640–647 CrossRef CAS PubMed.
- I. Hamley, Block Copolymers in Solution: Fundamentals and Applications, John Wiley and Sons, Ltd, 2005 Search PubMed.
- Á. González García, A. Ianiro and R. Tuinier, ACS Omega, 2018, 3, 17976–17985 CrossRef PubMed.
- G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at interfaces, Springer, Netherlands, 1998 Search PubMed.
- E. B. Zhulina and O. V. Borisov, Macromolecules, 2012, 45, 4429–4440 CrossRef CAS.
- R. Savić, T. Azzam, A. Eisenberg and D. Maysinger, Langmuir, 2006, 22, 3570–3578 CrossRef PubMed.
- T. Riley, T. Govender, S. Stolnik, C. D. Xiong, M. C. Garnett, L. Illum and S. S. Davis, Colloids Surf., B, 1999, 16, 147–159 CrossRef CAS.
- E. Stiakakis, D. Vlassopoulos, C. N. Likos, J. Roovers and G. Meier, Phys. Rev. Lett., 2002, 89, 208302 CrossRef CAS PubMed.
- B. Lonetti, M. Camargo, J. Stellbrink, C. N. Likos, E. Zaccarelli, L. Willner, P. Lindner and D. Richter, Phys. Rev. Lett., 2011, 106, 228301 CrossRef CAS.
- E. Stiakakis, G. Petekidis, D. Vlassopoulos, C. N. Likos, H. Iatrou, N. Hadjichristidis and J. Roovers, Europhys. Lett., 2005, 72, 664–670 CrossRef CAS.
- D. Truzzolillo, D. Vlassopoulos, M. Gauthier and A. Munam, Soft Matter, 2013, 9, 9088–9093 RSC.
- M. Laurati, J. Stellbrink, R. Lund, L. Willner, D. Richter and E. Zaccarelli, Phys. Rev. Lett., 2005, 94, 195504 CrossRef CAS PubMed.
- S. Gupta, M. Camargo, J. Stellbrink, J. Allgaier, A. Radulescu, P. Lindner, E. Zaccarelli, C. N. Likos and D. Richter, Nanoscale, 2015, 7, 13924–13934 RSC.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Chem. Phys., 1979, 83, 1619–1635 CrossRef CAS.
- A. Ianiro, A. González García, S. Wijker, J. P. Patterson, A. C. C. Esteves and R. Tuinier, Langmuir, 2019, 35, 4776–4786 CrossRef CAS PubMed.
- E. B. Zhulina, M. Adam, I. LaRue, S. S. Sheiko and M. Rubinstein, Macromolecules, 2005, 38, 5330–5351 CrossRef CAS.
- M. L. Kurnaz and J. V. Maher, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 572 CrossRef CAS.
- A. Quigley and D. Williams, Eur. J. Pharm. Biopharm., 2015, 96, 282–290 CrossRef CAS.
- A. Mulero, Theory and simulations of Hard-Sphere Fluids and Related Sytem, Springer, Heidelberg, 2008 Search PubMed.
- G. A. Vliegenthart and H. N. W. Lekkerkerker, J. Chem. Phys., 2000, 112, 5364–5369 CrossRef CAS.
- Č. Koňák, Z. Tuzar, P. Štěpánek, B. Sedláček and P. Kratochvíl, Frontiers in Polymer Science, Darmstadt, 1985, pp. 15–19 Search PubMed.
- M. Villacampa, E. Diaz de Apodaca, J. R. Quintana and I. Katime, Macromolecules, 1995, 28, 4144–4149 CrossRef CAS.
- T. Yoshimura and K. Esumi, J. Colloid Interface Sci., 2004, 276, 450–455 CrossRef CAS PubMed.
- W. Li, M. Nakayama, J. Akimoto and T. Okano, Polymer, 2011, 52, 3783–3790 CrossRef CAS.
- T. Zinn, L. Willner, R. Lund, V. Pipich, M.-S. Appavou and D. Richter, Soft Matter, 2014, 10, 5212–5220 RSC.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- G. J. Fleer, Adv. Colloid Interface Sci., 2010, 159, 99–116 CrossRef CAS.
- T. L. Hill, Thermodynamics of Small Systems, Parts I & II, WILEY-VCH Verlag, 1965, vol. 3 Search PubMed.
- R. Feynman, R. Leighton and M. Sands, The Feynman Lectures on Physics, 1965, vol. I, ch. 14, http://www.feynmanlectures.caltech.edu/I_14.html Search PubMed.
- J. Sprakel, N. A. M. Besseling, M. A. Cohen Stuart and F. A. M. Leermakers, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 25, 163–173 CrossRef CAS.
- J. Bergsma, F. A. M. Leermakers and J. van der Gucht, Phys. Chem. Chem. Phys., 2015, 17, 9001–9014 RSC.
- A. Kelarakis, V. Havredaki, X.-F. Yuan, Y.-W. Yang and C. Booth, J. Mater. Chem., 2003, 13, 2779–2784 RSC.
- R. Lund, L. Willner, J. Stellbrink, A. Radulescu and D. Richter, Macromolecules, 2004, 37, 9984–9993 CrossRef CAS.
- A. P. Philipse, Brownian Motion: Elements of Colloid Dynamics, Springer International Publishing, 2018 Search PubMed.
- M. Camargo and C. N. Likos, Phys. Rev. Lett., 2010, 104, 078301 CrossRef PubMed.
- K. Mortensen, Europhys. Lett., 1992, 19, 599–604 CrossRef CAS.
- K. Mortensen, J. Phys.: Condens. Matter, 1996, 8, A103–A124 CrossRef CAS.
- A. Ianiro, J. Patterson, Á. González García, M. M. J. van Rijt, M. M. R. M. Hendrix, N. A. J. M. Sommerdijk, I. K. Voets, A. C. C. Esteves and R. Tuinier, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 330–339 CrossRef CAS.
- H. N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction, Springer, Heidelberg, 2011 Search PubMed.
- C. Guerrero-Sanchez, D. Wouters, C.-A. Fustin, J.-F. Gohy, B. G. G. Lohmeijer and U. S. Schubert, Macromolecules, 2005, 38, 10185–10191 CrossRef CAS.
- F. J. Bailey, Poly(Ethylene Oxide), Academic Press, Amsterdam, 1st edn, 1976 Search PubMed.
- F. A. M. Leermakers, J. C. Eriksson and J. Lyklema, Association Colloids and their Equilibrium Modelling, in Fundamentals of Colloid and Interface Science, ed. J. Lyklema, Academic Press, 2005, vol. 5, ch. 4 Search PubMed.
- R. Tuinier, S. Ouhajji and P. Linse, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 115 CrossRef CAS.
- B. Vincent, J. Edwards, S. Emmett and A. Jones, Colloids Surf., 1986, 18, 261–281 CrossRef CAS.
- A. Jones and B. Vincent, Colloids Surf., 1989, 42, 113–138 CrossRef CAS.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Soft Matter, 2012, 8, 5002 RSC.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- T. P. Smart, A. J. Ryan, J. R. Howse and G. Battaglia, Langmuir, 2010, 26, 7425–7430 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |