Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cohesive self-organization of mobile microrobotic swarms†
Berk
Yigit‡
 ,
Yunus
Alapan‡
,
Yunus
Alapan‡
 and
Metin
Sitti
and
Metin
Sitti
 *
*
Physical Intelligence Department, Max Planck Institute for Intelligent Systems, 70569 Stuttgart, Germany. E-mail: sitti@is.mpg.de
First published on 23rd January 2020
Abstract
Mobile microrobots are envisioned to be useful in a wide range of high-impact applications, many of which require cohesive group formation to maintain self-bounded swarms in the absence of confining boundaries. Cohesive group formation relies on a balance between attractive and repulsive interactions between agents. We found that a balance of magnetic dipolar attraction and multipolar repulsion between self-assembled particle chain microrobots enables their self-organization into cohesive clusters. Self-organized microrobotic clusters move above a solid substrate via a hydrodynamic self-propulsion mechanism. Cluster velocity increases with cluster size, resulting from collective hydrodynamic effects. Clustering is promoted by the strength of cohesive interactions and is hindered by the heterogeneities of individual microrobots. The scalability of cohesive interactions allows the formation of larger groups, whose internal spatiotemporal organization undergoes a transition from solid-like ordering to a liquid-like behavior with increasing cluster size. Our work elucidates the dynamics of clustering under cohesive interactions, and presents an approach for addressing the operation of microrobots as localized collectives.
Introduction
Untethered mobile microrobotic systems are envisioned to revolutionize our ability to manipulate the microscopic world with unprecedented flexibility. Mobile microrobots, actuated with external magnetic and acoustic fields, light, chemical reactions, and biological propellers, have been developed recently for precision micromanipulation, minimally invasive medical operations, and environmental applications.1–8 However, translation of microrobots to most of these applications requires large numbers of microrobots (in the order of 101–105 microrobots per mm2, for microrobot sizes smaller than 50 μm) to work together to manipulate their macroscopic targets in much larger millimeter and centimeter scales.Microrobot swarms have been introduced to address the need for collective functions and navigation of large numbers of microrobots in complex environments. Microrobot swarms of magnetic micro/nanoparticles have been utilized for enhancing functional output, their reconfigurability, multifunctionality and adaptability to dynamic environments.9–13 For enhanced mobility and imaging, previous approaches relied on attractive interactions to keep the particles aggregated. However, in the absence of balancing attractive and repulsive interactions, these swarms are limited to disordered formations, lacking cohesive self-organization inherent in natural swarms.14–16 Cohesive self-organization facilitates group formation in open spaces via attraction at large separations, and prevents jamming, overcrowding, and clumping at high densities via repulsion at small separations between agents.17,18
To emulate the bio-inspired self-organized cohesion in synthetic swarms, distance-dependent interactions between microrobotic agents need to be controlled via physical forces. Here, we demonstrate the self-organization of cohesive microrobotic collectives emerging from their magnetic multipolar interactions in a liquid environment (Fig. 1). Formation, propulsion, and interactions of microrobots were controlled by a global precessing magnetic field. Microrobots were formed by the dynamic self-assembly of paramagnetic microparticles into anisotropic linear chains. The interactions between the microrobotic chains were controlled via their induced magnetic moments. At specific opening angles of the precessing field, magnetic interactions between chains carry a slow decaying dipolar attraction and a rapid decaying multipolar repulsion. These counteracting effects give rise to a steady-state distance between pairs, where the sum of dipolar and multipolar forces equates to zero. Under cohesive interactions, chains self-organize into clusters by arranging themselves at steady-state distances from their neighbors. These clusters leverage collective synergies to move faster as the cluster size increases, which is promoted by hydrodynamic interactions. Group formation and dissolution were mainly determined by the competition between cohesive interactions and intragroup heterogeneities. The internal organization of clusters ranged from solid-like ordering to liquid-like dynamic behavior, which depended on the group size. Our approach addresses the operation of microrobots as localized collectives, which will inspire researchers interested in active matter and microrobotics applications for designing advanced collective systems.
Results
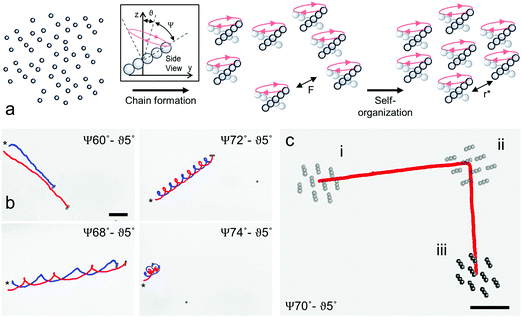
Cohesive interactions of chain microrobots
Microrobots were formed by the dynamic self-assembly of superparamagnetic particles into linear chains under a global precessing magnetic field. Initially, a low concentration of monodisperse superparamagnetic particles (particle radius a was approximately 2.5 μm) in deionized water was dispersed in a microchannel and sedimented on the planar glass substrate. The particles were actuated with a precessing magnetic field (B0 = 10 mT, Ω = 18.8 rad s−1, 3 Hz) (Supplementary note 1, ESI†). The precessing magnetic field is defined by two parameters: the precession angle Ψ, which is the angle between the instantaneous magnetic field vector B(t) and the axis of precession, and the tilt angle θ, which is the angle between the precession axis and the normal vector to the substrate plane (Fig. 1a). Under the magnetic field, particles interact with their induced magnetic dipoles and form chains by the head-to-toe alignment of their induced dipoles. Formation of chains is a dynamic self-assembly process, which depends on the magnetic field strength, the field frequency, the fluid viscosity, and the size and magnetic susceptibility of particles.8 Once assembled, chains synchronously rotate with B(t). By tilting the precession axis by θ, chains self-propel over the substrate, orthogonal to the direction of the tilt. Self-propulsion results from the hydrodynamic symmetry breaking mechanism due to the rotation of chains near the solid boundary, which has been described in detail elsewhere.8,19,20We first investigated the pairwise dynamics of a homogeneous pair of chains for varying field parameters: 60° ≤ Ψ ≤ 76° at θ = 5° (Fig. 1b, S1, Video S1, ESI†). For Ψ < 65°, the trajectories of the pairs diverged, during which the distance between the pairs steadily grew until there was no discernible pairwise interaction (Fig. 1b and Fig. S1b, ESI†). For 65° ≤ Ψ ≤ 72°, the pairwise distance converged to and oscillated around a steady-state value that persisted during the experiment duration. In this regime, pairs translated and rotated around their center, which led to the trochoidal trajectories (Fig. 1b and Fig. S1b, ESI†). By increasing Ψ further, the steady-state distance between the chains decreased until the pairs collapsed at Ψ = 74° (Fig. 1b and Fig. S1b, ESI†). By increasing the number of chains, the chains self-organized into a cluster with a discernible order in their spatial organization, where each chain was distanced at an approximately equal steady-state distance from their nearest neighbors (Fig. 1c, Video S1, ESI†). Clusters could be steered by changing the orientation of the precession axis in the x–y plane without changing Ψ and θ (Fig. 1c). Furthermore, chain microrobots and clusters could be reversibly assembled, disassembled, clustered, and de-clustered, respectively (Video S2, ESI†).
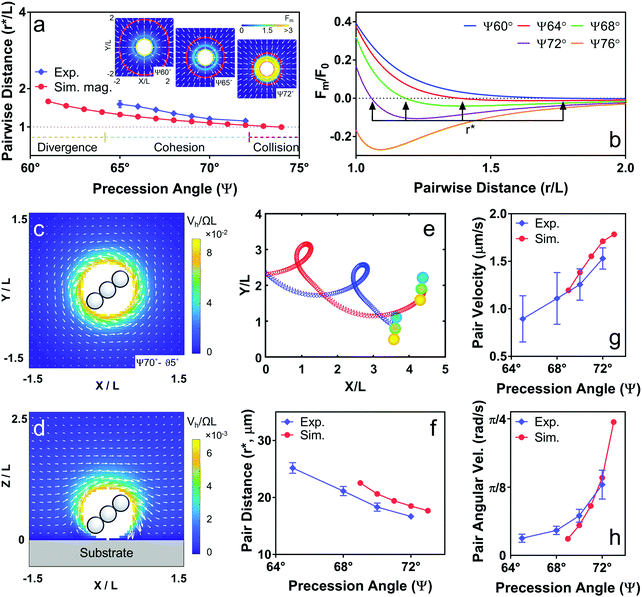
Pairwise magnetic and hydrodynamic interactions
Pairwise steady-state distances obtained from experiments are reported for different Ψ values and categorized under “divergence”, “cohesion”, and “collision” states based on their pairwise behavior (Fig. 2a). We attribute the emergence of a pairwise steady-state distance to dipolar and multipolar magnetic interactions between chains caused by their anisotropic shape magnetization. The magnetic interaction forces between chains were calculated numerically for all combinations of Ψ and θ, and for different number of microparticles per chain, n (Fig. 2a, b, Fig. S2, see Supplementary note 2, ESI†). Particles that have isotropic magnetizations, such as spherical paramagnetic particles (n = 1), interact solely with their dipoles. For θ = 0°, time-averaged dipolar interactions are repulsive when Ψ is smaller than the magic angle 54.7°,21,22 and are attractive when Ψ > 54.7°. In contrast, chains (n > 1) additionally have higher-order magnetic moments due to spatially separated dipoles positioned at centers of particles that form the chains.21,23,24 For doublets (n = 2), the dominant repulsive multipolar interaction is the hexapole-dipole for Ψ < 61.5°, which decays rapidly with r−6 compared to the r−4 decay rate of the attractive dipolar interaction forces.21 Similar multipolar interactions are also in play for chains with n > 2 (Fig. S2e–g, ESI†). Due to the different decay rates of attractive dipolar and repulsive multipolar interactions, chains attract each other at large separations, and repel at small separations. The cross-over distance between the dipolar attraction and multipolar repulsion defines a dynamic steady-state distance r* between a pair of chains, and this distance depends on Ψ and n (i.e., the length of the chain L = 2an) (Fig. 2b and Fig. S2d–g, ESI†). For θ = 0°, pairwise magnetic interaction is axisymmetric about the precession axis, with a negligible anisotropy produced by a small tilt of θ < 5° (Fig. S2d, ESI†).The pairwise motion of chains is mainly determined by the hydrodynamic interactions, especially when they are in the cohesive regime. Precessing chains generate fluid flows, which lead to their self-propulsion and to hydrodynamic interactions influencing the motion of their neighbors. Simulations were used for calculating the velocity field around precessing chains (Supplementary note 3, ESI†). The chain rotation in a plane perpendicular to the substrate leads to a rotational flow in the x–y plane, leading to the rotation of pairs about their center (Fig. 2c and Fig. S3a, ESI†). For θ > 0°, rotation has a component parallel to the substrate, leading to the self-propulsion of chains and the generation of a secondary flow field that increases the velocity of neighboring chains via advection (Fig. 2d and Fig. S3b, c, ESI†).
Simulations combining magnetic and hydrodynamic interactions of chains qualitatively captured the dynamics of pair motion (Fig. 2e–h and Video S3, Supplementary note 4, ESI†). In the experiments, translational and rotational velocities of pairs increased while pair distance decreased with Ψ, which was supported by simulations (Fig. 2f–h). Furthermore, our model also captured pair dynamics for chains of different lengths. For increasing n, pair distance and translational velocity increased and rotational velocity decreased (Fig. S4, ESI†). The differences between the model and the experiments, especially at low precession angles, could be due to a mismatch of material properties, such as magnetic susceptibility of particles.
Dynamics and organization of homogeneous and heterogeneous clusters
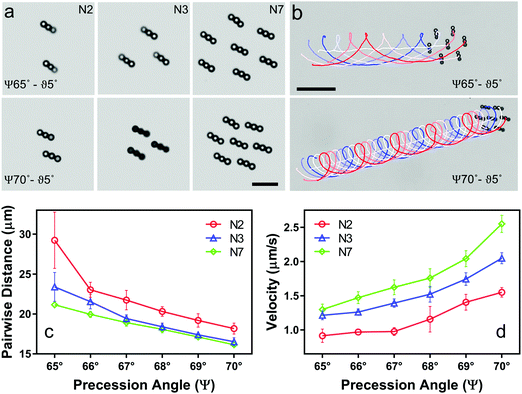
Upon increasing the number of chains N, we observed their self-organization into clusters (Fig. 3a and b). For homogeneous clusters, each chain was distanced evenly from their nearest neighbors (Fig. 3c Video S4, ESI†). The pairwise distance decreased with Ψ (Fig. 3c). The pairwise distance also decreased from N = 2 to N = 3, but remained relatively unchanged with further increases in N (Fig. 3c). We ascribe this to the increased mutual dipolar attraction when multiple chains are present, which compacts the cluster. Cluster velocity increased with Ψ and N (Fig. 3d, Video S4, ESI†). The latter effect can be attributed to the enhancement of collective hydrodynamic advection resulting from the superposition of flows generated by N chains.To understand the effects of intragroup variations on the collective dynamics, we investigated the clusters formed by heterogeneous members (Fig. 4). Dynamic self-assembly enabled the assembly and disassembly of members of the cluster until the desired chain length distribution was achieved, enabling systematic investigation of heterogeneity (N = 7). Group stability was evaluated based on two order metrics: rotational order parameter, R, and connectivity (Supplementary note 6, ESI†). R measures the degree of coherence of rotational motion of chains around the cluster center. R → 1 for perfectly coherent rotational motion, and R → 0 for no rotation.25 Connectivity is based on total magnetic interaction potential; thus, it quantifies the strength of cohesive interactions that hold the chains together.
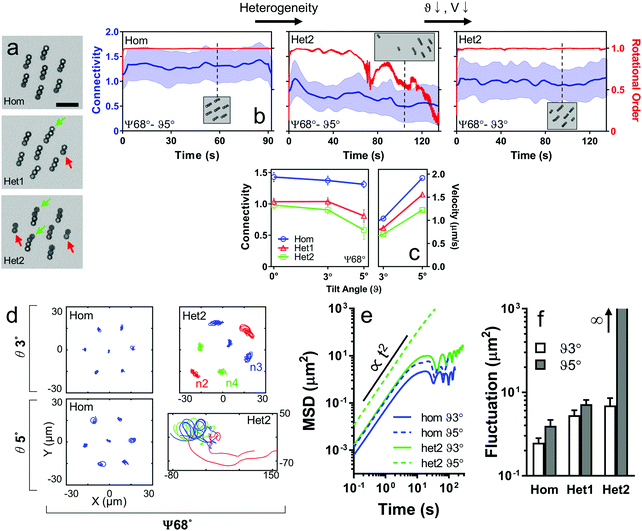
Three clusters of varying degrees of heterogeneity were formed (Fig. 4a). Cluster heterogeneity was measured by taking the the standard deviation of the number of particles in chains (σn), with the average ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) fixed at 3. Homogeneous clusters actuated at Ψ = 68° and θ = 5° remained as a single cluster, in which chains preserved their ordered spatial organization over time with R ∼ 1 (Fig. 4b and c). However, when heterogeneities were introduced, clusters were more likely to break down, with decreasing R and connectivity over time as the chain interactions weakened (Fig. 4b and c, Video S4, ESI†). Decreasing θ to 3° reduced the cluster velocity and re-established the R and connectivity of the heterogeneous clusters (Fig. 4b and c, Video S5, ESI†). For single chains, velocity increases with chain length (Fig. S5, ESI†). In a heterogeneous group, variance in velocities causes the distance between chains to increase over time, which leads to cluster dissolution. On the other hand, cohesive magnetic forces act to keep chains together. By decreasing the chain velocities, the balance of these competing effects is shifted from heterogeneity-induced dissolution to cohesion.
fixed at 3. Homogeneous clusters actuated at Ψ = 68° and θ = 5° remained as a single cluster, in which chains preserved their ordered spatial organization over time with R ∼ 1 (Fig. 4b and c). However, when heterogeneities were introduced, clusters were more likely to break down, with decreasing R and connectivity over time as the chain interactions weakened (Fig. 4b and c, Video S4, ESI†). Decreasing θ to 3° reduced the cluster velocity and re-established the R and connectivity of the heterogeneous clusters (Fig. 4b and c, Video S5, ESI†). For single chains, velocity increases with chain length (Fig. S5, ESI†). In a heterogeneous group, variance in velocities causes the distance between chains to increase over time, which leads to cluster dissolution. On the other hand, cohesive magnetic forces act to keep chains together. By decreasing the chain velocities, the balance of these competing effects is shifted from heterogeneity-induced dissolution to cohesion.
To elucidate the group formation and dissolution dynamics, we investigated the chain trajectories after subtracting the mean cluster translation and rotation, revealing the internal motion of individual chains (Fig. 4d, Video S5, Supplementary note 6, ESI†). For stable clusters, chain displacements were constrained around their mean internal positions, where they perform small oscillations, as quantified by their mean-squared displacement (MSD) curves (Fig. 4e). We observed that the amplitude of these positional fluctuations increased with increasing heterogeneity and θ (Fig. 4f). Positional fluctuations were bound to a finite amplitude when clusters exhibited structural ordering. However, when the clusters were disintegrating into smaller groups and individual chains (i.e., Het2, Ψ68°–θ5°), MSD and positional fluctuations grew indefinitely (∝t2) as the distance between the chains increased (Fig. 4e and f).
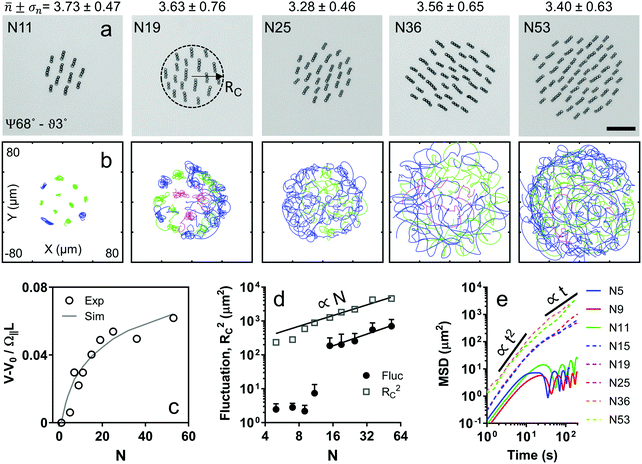
Formation of large clusters
Scalability of cohesive interactions enabled the formation of large clusters (up to N = 53), which were formed by introducing more particles during the cluster formation (Fig. 5, Video S6, ESI†). Global motion and internal fluctuations of such clusters were measured experimentally (Fig. 5a and b, Video S7, ESI†). We observed that the mean neighbor distance did not vary considerably with N (Fig. S6, ESI†). On the other hand, the cluster velocity increased (Fig. 5c, Video S7, ESI†), continuing the trend observed for smaller clusters (Fig. 3d). We ascribe this observation to scaling effects associated with the collective hydrodynamic interactions with increasing cluster size. To assess this argument, we developed a reduced-order model that captures magnetic and hydrodynamic interactions in large clusters (Video S8, Supplementary note 5, ESI†). Briefly, we model the attractive-repulsive magnetic interactions with an effective pair interaction force, and the hydrodynamic interactions with rotlet singularities located above a solid wall (Fig. S7, ESI†). The flow generated by chain rotation parallel to the substrate has a positive contribution to the propulsion velocity of neighboring chains, thus increases cluster velocity with increasing number of chains (Fig. 2d and Fig. S7a, ESI†). The reduced-order model captures the qualitative features of the cluster motion, including trochoidal motion (Fig. S7c, ESI†), and the changes in the cluster velocity with increasing number of chains (Fig. 5c and Fig. S7d, e, ESI†).The internal motion of clusters reveals a tendency towards large positional fluctuations of chains with increasing N (Fig. 5b and Video S7, ESI†). In small clusters (N ≤ 11), chains perform small fluctuations around their mean internal positions, which remain relatively fixed over long times, indicative of a solid-like order (Fig. 5b and d). As the cluster size grew (N ≥ 15), the chains started moving inside the cluster, while remaining confined within the cluster radius RC (Fig. 5b and d). As such, the amplitude of positional fluctuations grew proportional to RC when N ≥ 15 (Fig. 5d). MSD data showed that the chain motion exhibits ballistic ∼t2 behavior at short times (Fig. 5e). For t > 10 s, chain motion varied from small bounded oscillations evidenced in solid-like structuring in clusters for N ≤ 11, to liquid-like diffusive ∼t behavior confined to the cluster radius for N ≥ 15 (Fig. 5e).
We ascribe the tendency towards larger fluctuations with increasing N to the different distance-dependent decay rates of magnetic and hydrodynamic interactions. Magnetic dipolar interactions decay with r−4, whereas the far-field of rotlet flow parallel to the wall decays with r−2.26,27 Being short-ranged, magnetic forces holding chains together in a solid-like order rapidly reach saturation as the number of neighboring chains increases. On the other hand, the hydrodynamic forces displacing chains keep increasing due to their longer range. It can be expected that hydrodynamic effects compete with magnetic effects at a certain cluster size, and the cluster transforms to a liquid-like internal state.
Discussion
Collective motion manifests itself at all length scales relevant to biology.28 Examples range from cytoplasmic transport in plant cells,29 maze-solving slime moulds,30 cooperative foraging in social ant groups,31 migratory flocking of white storks,32 and human motion in crowded environments.33 Inspired from natural systems, robotic swarm systems are being developed to address complex tasks such as collective construction and search operations.34,35 A similar trend is prevalent in the microscale robotic swarms, with the aim of enhancing functional throughput, multitasking capabilities, and to impart microrobots with reconfigurability to enhance their adaptability to environmental constraints. However, a direct transfer of algorithmic approaches designed for swarms of macroscale robots (>1 cm) to microrobotic swarms is not feasible due to the challenges in miniaturization and powering of analogous components.1,36 Instead, microrobotic systems currently need to rely on micron-scale physical interactions for local coupling that generate global collective behaviors. Here, we demonstrated a microrobotic system where pairwise magnetic interactions can guide the self-organization of cohesive clusters, which leads to a synergistic enhancement of the collective mobility over individual microrobots via hydrodynamic interactions.Cohesive interactions play an important role in biological swarms (imagine a herd of sheep), where the group formation needs to be maintained without confining boundaries.15–17 As opposed to the purely attractive interactions that lead to the collapse of agents into tightly packed clusters, inclusion of short-range repulsive interactions can promote inter-agent spacing. In microrobotic swarms, several works have achieved cohesive organization in non-propulsive systems by combining repulsive capillary/hydrodynamic and attractive magnetic forces, however only at the liquid–air interfaces.37,38 There is a great interest to form self-organizing swarms in fully liquid environments, due to their relevance to biomedical applications. In this work, we have achieved cohesive self-organization of microrobotic swarms in a fully immersed liquid environment by taking advantage of multipolar interactions resulting from anisotropic shape-magnetization of chains actuated with time-varying fields. Programming multipolar interactions by incorporating complex magnetization profiles into the microrobot structure is promising for the design of advanced collective motion and manipulation of microrobotic swarm systems,6,8,23,24,39,40 as we have shown here.
Swarm heterogeneity can enhance the resilience of social collectives against random noise,41 or can allow collaborative task division in robotic collectives.42 On the other hand, the introduction of large variances in population characteristics (e.g., velocity, interaction strength) may have deleterious effects on the order and cohesiveness of flocking swarms that interact locally, which can be regulated or alleviated by self-sorting and mixing mechanisms.43–45 Despite its importance, the heterogeneity has remained relatively unexplored in the field of synthetic active matter swarms. In the present system, heterogeneities mainly contribute to the disordering of cohesive clusters due to the variance of individual mobilities. However, collective ordering can be restored by slowing down the swarm, which re-adjusts the competing effects of cohesiveness and individuality.
Self-organized cohesion can be further scaled to form large swarms. In our system, we observed that increasing group size enhances swarm mobility, akin to the hydrodynamic cooperation observed in collectives of sperm cells46 and of active colloidal rollers.27,47,48 On the other hand, different scalings of magnetic (decaying with r−4, short range) and hydrodynamic (decaying with r−2, long range) interactions affect the spatiotemporal organization of chains as swarms grow larger. We observed a solid-like spatial organization in small clusters, where magnetic cohesion is dominant over hydrodynamics. The two effects became comparable in larger groups, resulting in liquid-like dynamics, where chains displaced with respect to their neighbors. These states are highly similar to the flying crystal and the moving droplet formations in flocks interacting with cohesive alignment rules.16 Although fixed in this work, the magnetic field magnitude and frequency can be used for tuning the ratio of hydrodynamic forces to magnetic forces (∝Ω/B02), which has a direct influence on dynamic assembly and collective behaviors.49 When magnetic forces are dominant, longer chains and stronger magnetic interactions would be expected. On the other hand, strong hydrodynamic forces overwhelming the magnetic cohesion might result in short chains and cluster dissolution.
In conclusion, we have presented mobile microrobots interacting with each other to generate a cohesive organization much larger than an individual microrobotic unit, which introduce synergistic advantages and display rich spatiotemporal organizations arising from collective dynamics. Our approach addresses the operation of microrobots as localized collectives, which could inspire researchers in active matter and microrobotics fields for designing advanced collective systems for future applications in biomedicine, precision manipulation and manufacturing, and environmental sensing and remediation.
Materials and methods
Experimental setup
External magnetic fields required for self-assembly and actuation of chain microrobots were generated using a custom five-coil magnetic setup integrated on an inverted optical microscope (Axio Observer A1, Carl Zeiss) (Fig. S8, ESI†). The magnetic coil system was arranged to generate up to 20 mT in in-plane directions and 10 mT in out of plane z-direction.7 All experiments were performed in closed microfluidic channels (75 μm height × 6 mm width × 10 mm length) composed of poly(methyl methacrylate) (PMMA) tops with inlet and outlet ports, double sided tape defining the channel outline and height, and a cover glass (Fig. S9, ESI†).50 PMMA tops and double sided tapes were laser micromachined and then assembled with a cover glass, forming the microchannels. Superparamagnetic polystyrene microparticles (5 μm in diameter, Sigma Aldrich) were used in the self-assembly of chain microrobots. The microparticles were suspended in a 0.1% Tween 20 (Sigma Aldrich, St Louis, MO) solution in deionized water and injected into the microchannel. A precessing magnetic field with pre-determined tilt and precession angles is applied to assemble and actuate chain microrobots, which is detailed in Supplementary note 1 (ESI†).Dynamic model and simulations
Magnetic interactions between two chains were calculated by averaging dipolar interaction forces between particles over a cycle of magnetic field precession. We defined a characteristic magnetic interaction force,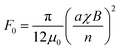 , for two chains separated by a distance L = 2an. Detailed methods for calculating magnetic interactions are described in Supplementary note 2 (ESI†).
, for two chains separated by a distance L = 2an. Detailed methods for calculating magnetic interactions are described in Supplementary note 2 (ESI†).
Hydrodynamic simulations were used for calculating the fluid flow induced by the motion of a precessing chain. For given particle kinematics, flow velocity at an arbitrary point in space can be calculated via a hydrodynamic Blake tensor, which accounts for the no-slip boundary condition at the wall surface.26 The method for calculating the flow fields is detailed in Supplementary note 3 (ESI†).
Pairwise dynamics of chains were simulated by modeling the motion of individual particles constituting the chains. The model takes into account magnetic, hydrodynamic, and excluded volume interactions between particles that are driven by a precessing magnetic field. The equation of motion for particles is given by:
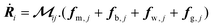 | (1) |
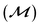 is used for calculating velocities (Ṙi) of hydrodynamically interacting particles near a no-slip boundary, for a set of forces acting on the ensemble of particles.51 Details of the dynamic model are described in Supplementary note 4 (ESI†).
is used for calculating velocities (Ṙi) of hydrodynamically interacting particles near a no-slip boundary, for a set of forces acting on the ensemble of particles.51 Details of the dynamic model are described in Supplementary note 4 (ESI†).
A reduced-order discrete chain model was developed for simulating the dynamics of ensembles of chains that self-organize into mobile clusters. Briefly, the model considers each chain as a discrete agent, and uses time-averaged force functions for calculating their magnetic and hydrodynamic interactions. Details of the model are described in Supplementary note 5 (ESI†).
Data analysis
Acquired microscopy images were processed using Fiji52 to identify individual chains and their midpoints, marking their position. Tracking software53 was used to generate the trajectories of the chains and to determine their velocities. All data analyses were performed on MATLAB (MathWorks, Inc.). Methods to analyze cluster translation, rotation and internal motion of chains are described in Supplementary note 6 (ESI†).Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
Y. A. thanks Alexander von Humboldt Foundation for the Humboldt Postdoctoral Research Fellowship. This work is funded by the Max Planck Society. Open Access funding provided by the Max Planck Society.References
- M. Sitti, Mobile Microrobotics, MIT Press, 2017 Search PubMed.
- Y. Alapan, O. Yasa, B. Yigit, I. C. Yasa, P. Erkoc and M. Sitti, Microrobotics and Microorganisms: Biohybrid Autonomous Cellular Robots, Annual Review of Control, Robotics, and Autonomous Systems, 2019, 205–230 Search PubMed.
- P. Erkoc, I. C. Yasa, H. Ceylan, O. Yasa, Y. Alapan and M. Sitti, Mobile microrobots for active therapeutic delivery, Adv. Ther., 2019, 2, 1800064 CrossRef.
- Z. Zhang, X. Wang, J. Liu, C. Dai and Y. Sun, Robotic Micromanipulation: Fundamentals and Applications, Annual Review of Control, Robotics, and Autonomous Systems, 2019, 2, 181–203 CrossRef.
- L. Soler and S. Sánchez, Catalytic nanomotors for environmental monitoring and water remediation, Nanoscale, 2014, 6, 7175–7182 RSC.
- Y. Alapan, B. Yigit, O. Beker, A. F. Demirors and M. Sitti, Shape-encoded dynamic assembly of mobile micromachines, Nat. Mater., 2019, 1244–1251 CrossRef CAS.
- Y. Alapan, et al., Soft erythrocyte-based bacterial microswimmers for cargo delivery, Science Robotics, 2018, 3, eaar4423 CrossRef.
- B. Yigit, Y. Alapan and M. Sitti, Programmable Collective Behavior in Dynamically Self-Assembled Mobile Microrobotic Swarms, Adv. Sci., 2019, 6, 1801837 CrossRef.
- S. Martel and M. Mohammadi, Using a swarm of self-propelled natural microrobots in the form of flagellated bacteria to perform complex micro-assembly tasks. In: 2010 IEEE International Conference on Robotics and Automation, IEEE (2010).
- A. Servant, F. Qiu, M. Mazza, K. Kostarelos and B. J. Nelson, Controlled In Vivo Swimming of a Swarm of Bacteria-Like Microrobotic Flagella, Adv. Mater., 2015, 27, 2981–2988 CrossRef CAS.
- J. Yu, B. Wang, X. Du, Q. Wang and L. Zhang, Ultra-extensible ribbon-like magnetic microswarm, Nat. Commun., 2018, 9, 3260 CrossRef.
- B. Wang, et al., Reconfigurable Swarms of Ferromagnetic Colloids for Enhanced Local Hyperthermia, Adv. Funct. Mater., 2018, 28, 1705701 CrossRef.
- H. Xie, et al., Reconfigurable magnetic microrobot swarm: Multimode transformation, locomotion, and manipulation, Science Robotics, 2019, 4, eaav8006 CrossRef.
- J. K. Parrish and L. Edelstein-Keshet, Complexity, Pattern, and Evolutionary Trade-Offs in Animal Aggregation, Science, 1999, 284, 99–101 CrossRef CAS PubMed.
- I. D. Couzin, J. Krause, R. James, G. D. Ruxton and N. R. Franks, Collective memory and spatial sorting in animal groups, J. Theor. Biol., 2002, 218, 1–11 CrossRef PubMed.
- G. Grégoire, H. Chaté and Y. Tu, Moving and staying together without a leader, Phys. D, 2003, 181, 157–170 CrossRef.
- F. A. Lavergne, H. Wendehenne, T. Bauerle and C. Bechinger, Group formation and cohesion of active particles with visual perception-dependent motility, Science, 2019, 364, 70–74 CrossRef CAS.
- F. Mou, et al., Phototactic flocking of photochemical micromotors, iScience, 2019, 19, 415–424 CrossRef PubMed.
- C. E. Sing, L. Schmid, M. F. Schneider, T. Franke and A. Alexander-Katz, Controlled surface-induced flows from the motion of self-assembled colloidal walkers, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 535–540 CrossRef CAS PubMed.
- L. Zhang, et al., Controlled Propulsion and Cargo Transport of Rotating Nickel Nanowires near a Patterned Solid Surface, ACS Nano, 2010, 4, 6228–6234 CrossRef CAS PubMed.
- P. Tierno, S. Schreiber, W. Zimmermann and T. M. Fischer, Shape Discrimination with Hexapole−Dipole Interactions in Magic Angle Spinning Colloidal Magnetic Resonance, J. Am. Chem. Soc., 2009, 131, 5366–5367 CrossRef CAS PubMed.
- M. Salehizadeh and E. Diller, Two-agent formation control of magnetic microrobots in two dimensions, Journal of Micro-Bio Robotics, 2017, 12, 9–19 CrossRef.
- P. Tierno, Recent advances in anisotropic magnetic colloids: realization, assembly and applications, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- S. H. Klapp, Collective dynamics of dipolar and multipolar colloids: From passive to active systems, Curr. Opin. Colloid Interface Sci., 2016, 21, 76–85 CrossRef CAS.
- A. Attanasi, et al., Collective behaviour without collective order in wild swarms of midges, PLoS Comput. Biol., 2014, 10, e1003697 CrossRef.
- J. R. Blake and A. T. Chwang, Fundamental singularities of viscous flow, J. Eng. Math., 1974, 8, 23–29 CrossRef.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Unstable fronts and motile structures formed by microrollers, Nat. Phys., 2017, 13, 375 Search PubMed.
- T. Vicsek and A. Zafeiris, Collective motion, Phys. Rep., 2012, 517, 71–140 CrossRef.
- F. G. Woodhouse and R. E. Goldstein, Cytoplasmic streaming in plant cells emerges naturally by microfilament self-organization, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 14132–14137 CrossRef CAS PubMed.
- T. Nakagaki, H. Yamada and Á. Tóth, Intelligence: Maze-solving by an amoeboid organism, Nature, 2000, 407, 470 CrossRef CAS PubMed.
- O. Feinerman, I. Pinkoviezky, A. Gelblum, E. Fonio and N. S. Gov, The physics of cooperative transport in groups of ants, Nat. Phys., 2018, 1, 683–693 Search PubMed.
- A. Flack, M. Nagy, W. Fiedler, I. D. Couzin and M. Wikelski, From local collective behavior to global migratory patterns in white storks, Science, 2018, 360, 911–914 CrossRef CAS PubMed.
- J. L. Silverberg, M. Bierbaum, J. P. Sethna and I. Cohen, Collective motion of humans in mosh and circle pits at heavy metal concerts, Phys. Rev. Lett., 2013, 110, 228701 CrossRef PubMed.
- J. Werfel, K. Petersen and R. Nagpal, Designing collective behavior in a termite-inspired robot construction team, Science, 2014, 343, 754–758 CrossRef CAS PubMed.
- T. Stirling, S. Wischmann and D. Floreano, Energy-efficient indoor search by swarms of simulated flying robots without global information, Swarm Intell., 2010, 4, 117–143 CrossRef.
- S. Palagi and P. Fischer, Bioinspired microrobots, Nat. Rev. Mater., 2018, 3, 113–124 CrossRef CAS.
- W. Wang, J. Giltinan, S. Zakharchenko and M. Sitti, Dynamic and programmable self-assembly of micro-rafts at the air–water interface, Sci. Adv., 2017, 3, e1602522 CrossRef.
- Q. Wang, L. Yang, B. Wang, E. Yu, J. Yu and L. Zhang, Collective Behavior of Reconfigurable Magnetic Droplets via Dynamic Self-Assembly, ACS Appl. Mater. Interfaces, 2019, 11, 1630–1637 CrossRef CAS PubMed.
- S. Miyashita, E. Diller and M. Sitti, Two-dimensional magnetic micro-module reconfigurations based on inter-modular interactions, Int. J. Robot. Res., 2013, 32, 591–613 CrossRef.
- E. Diller, C. Pawashe, S. Floyd and M. Sitti, Assembly and disassembly of magnetic mobile micro-robots towards deterministic 2-D reconfigurable micro-systems, Int. J. Robot. Res., 2011, 30, 1667–1680 CrossRef.
- M. C. Miguel, J. T. Parley and R. Pastor-Satorras, Effects of heterogeneous social interactions on flocking dynamics, Phys. Rev. Lett., 2018, 120, 068303 CrossRef CAS PubMed.
- F. Ducatelle, G. A. Di Caro, C. Pinciroli and L. M. Gambardella, Self-organized cooperation between robotic swarms, Swarm Intell., 2011, 5, 73 CrossRef.
- K. Copenhagen, D. A. Quint and A. Gopinathan, Self-organized sorting limits behavioral variability in swarms, Sci. Rep., 2016, 6, 31808 CrossRef CAS PubMed.
- D. Yllanes, M. Leoni and M. Marchetti, How many dissenters does it take to disorder a flock?, New J. Phys., 2017, 19, 103026 CrossRef.
- X. Fu, et al., Spatial self-organization resolves conflicts between individuality and collective migration, Nat. Commun., 2018, 9, 2177 CrossRef CAS PubMed.
- Y. Yang, J. Elgeti and G. Gompper, Cooperation of sperm in two dimensions: Synchronization, attraction, and aggregation through hydrodynamic interactions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061903 CrossRef PubMed.
- F. Martinez-Pedrero, A. Ortiz-Ambriz, I. Pagonabarraga and P. Tierno, Colloidal Microworms Propelling via a Cooperative Hydrodynamic Conveyor Belt, Phys. Rev. Lett., 2015, 115, 138301 CrossRef PubMed.
- M. Driscoll and B. Delmotte, Leveraging collective effects in externally driven colloidal suspensions: Experiments and simulations, Curr. Opin. Colloid Interface Sci., 2018, 42–57 Search PubMed.
- S. Melle and J. E. Martin, Chain model of a magnetorheological suspension in a rotating field, J. Chem. Phys., 2003, 118, 9875–9881 CrossRef CAS.
- Y. Alapan, Y. Matsuyama, J. A. Little and U. A. Gurkan, Dynamic deformability of sickle red blood cells in microphysiological flow, Technology, 2016, 4, 71–79 CrossRef CAS PubMed.
- J. W. Swan and J. F. Brady, Simulation of hydrodynamically interacting particles near a no-slip boundary, Phys. Fluids, 2007, 19, 113306 CrossRef.
- J. Schindelin, et al., Fiji: an open-source platform for biological-image analysis, Nat. Methods, 2012, 9, 676 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, Methods of Digital Video Microscopy for Colloidal Studies, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01284b |
| ‡ These authors contributed equally and share the first authorship. |
| This journal is © The Royal Society of Chemistry 2020 |