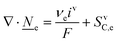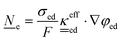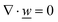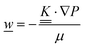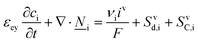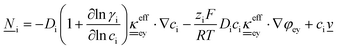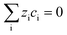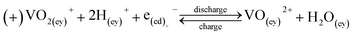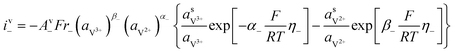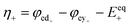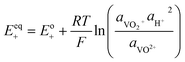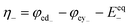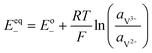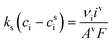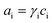Modelling of redox flow battery electrode processes at a range of length scales: a review

Abstract

In this article, the different approaches reported in the literature for modelling electrode processes in redox flow batteries (RFBs) are reviewed. RFB models vary widely in terms of computational complexity, research scalability and accuracy of predictions. Development of RFB models have been quite slow in the past, but in recent years researchers have reported on a range of modelling approaches for RFB system optimisation. Flow and transport processes, and their influence on electron transfer kinetics, play an important role in the performance of RFBs. Macro-scale modelling, typically based on a continuum approach for porous electrode modelling, have been used to investigate current distribution, to optimise cell design and to support techno-economic analyses. Microscale models have also been developed to investigate the transport properties within porous electrode materials. These microscale models exploit experimental tomographic techniques to characterise three-dimensional structures of different electrode materials. New insights into the effect of the electrode structure on transport processes are being provided from these new approaches. Modelling flow, transport, electrical and electrochemical processes within the electrode structure is a developing area of research, and there are significant variations in the model requirements for different redox systems, in particular for multiphase chemistries (gas–liquid, solid–liquid, etc.) and for aqueous and non-aqueous solvents. Further development is essential to better understand the kinetic and mass transport phenomena in the porous electrodes, and multiscale approaches are also needed to enable optimisation across the relevent length scales.

---

Evangelos Kalamaras

Evangelos is currently working as project engineer in battery characterization and testing for WMG at University of Warwick. He received his BSc degree in Physics (2011) and MSc in Energy and Environment (2013) from University of Patras, Greece. After that, he earned his PhD in Engineering from Heriot-Watt University, Edinburgh, and worked as a research engineer in the field of redox flow batteries. He has co-authored more than 14 papers in refereed journals focusing on electrochemical and photo-electrochemical systems for energy conversion and storage.

Antonio Bertei

Antonio Bertei obtained his MSc and PhD in Chemical Engineering from the University of Pisa, Italy. After a brief period at the Massachusetts Institute of Technology, he moved to Imperial College London for two years thanks to a Marie Skłodowska-Curie Fellowship. He is currently a Lecturer at the University of Pisa. His research interests include the physically-based modelling of batteries and fuel cells, three-dimensional characterization of porous media and phase field simulation of phase-separating materials.

J. Rubio-Garcia

Javier Rubio Garcia is a Research Associate at the Department of Chemistry at Imperial College London (UK). He did a PhD in Nanotechnology at the Centre National de la Recherche Scientifique (CNRS, France) and Université Paul Sabatier (France) before moving in 2010 to a postdoctoral position at the Energy Research Institute of Catalonia (IREC, Spain). In 2014 he joined Imperial College London to work under the supervision of Prof Anthony Kucernak. His research interests focus on materials and catalysis for electrochemical devices with a particular emphasis on redox flow batteries and low temperature fuel cells.

Kevin M. Tenny

Kevin M. Tenny received his B.S. in chemical engineering from the University of Kansas in 2017 and his M.S. in chemical engineering practice from the Massachusetts Institute of Technology (MIT) in 2019. He is currently a PhD candidate at MIT under the supervision of Prof. Fikile R. Brushett and Prof. Yet-Ming Chiang and is supported by an NSF Graduate Research Fellowship. His research interests leverage experimental techniques and computational tools to engineer electrode microstructures for redox flow batteries.

Chee Tong John Low

John Low works as an Associate Professor in WMG (University of Warwick). He leads a team applying the discovery and understanding in electrochemical science through to application-driven technology programmes. He collaborates with UK businesses across power devices supply chain, delivering technology into market and exploiting the rich history of electrochemical engineering. He received BEng (2004), PhD (2007) and postdoctoral experience (2007 to 2013). Current activities study the use of electrochemical materials, cell manufacture prototyping devices, solid-state battery manufacture, electrochemical flow reactors, developments in lithium-ion capacitor and lithium-ion recycling processes.

Edward P. L. Roberts

Edward (Ted) Roberts is a Professor in the Department of Chemical and Petroleum Engineering at the University of Calgary. He completed his PhD in Chemical Engineering at the University of Cambridge, UK. After 16 years at UMIST and the University of Manchester he moved to the University of Calgary in 2012. He has studied a wide range of electrochemical technologies for energy and environmental applications. His current research focuses on redox flow batteries, electrocoagulation, electrochemical regeneration of graphite adsorbents, and electrochemical exfoliation of graphene.

1. Introduction

Energy storage research is undergoing a steady increase over the years in response to the need for deploying renewable energy sources for mitigating climate change issues.^1,2 Several nations,³ such as the USA,⁴ UK,^5,6 Europe,⁷ China,⁸ Japan⁹ and others, have taken positive steps forward by allocating significant public funds for this purpose.^10,11 Amongst several energy storage technologies available, redox flow batteries (RFBs) are considered viable for future renewable energy and grid-scale load levelling applications^12,13 due to favorable qualities, such as independent power/energy sizing, high efficiency, ambient or near ambient temperature operation and projected long charge/discharge cycle life.¹⁴ Despite these benefits, cost and irreversible crossover of active species in asymmetric chemistries (e.g., iron/chromium redox flow battery, or ICFB for short) have limited widespread RFB adoption into the storage market necessitating further research activities.¹²

Despite having been in development since 1970s, RFBs have had limited penetration into the energy storage market.^15,16 Since the initial RFB chemistry, several different redox systems have been studied, including aqueousand non-aqueous electrolytic systems,^17–19 metallic or non-metallic electrodes and/or current collectors, membranes as well as means for scaling-up.^20,21 The most widely studied aqueous inorganic systems include the all–vanadium redox flow battery (VRFB), the zinc–bromine redox flow battery (ZFB), ICFB and the polysulfide–bromine redox flow battery (PSB). The redox reactions and standard potentials for these battery systems are shown in eqn (1)–(7) below.

VRFB:

V³⁺ + e⁻ ⇌ V²⁺, E^o = −0.255 V (1)

VO₂⁺ + +2H⁺ + e⁻ ⇌ VO²⁺ + H₂O, E^o = +1.004 V (2)

ZFB:

Zn²⁺ + 2e⁻ ⇌ Zn(s), E^o = −0.76 V (3)

Br₃⁻ + 2e⁻ ⇌ 3Br⁻, E^o = +1.087 V (4)

ICFB:

Cr³⁺ + e⁻ ⇌ Cr²⁺, E^o = −0.42 V (5)

Fe³⁺ + e⁻ ⇌ Fe²⁺, E^o = +0.77 V (6)

PSB (positive redox reaction is shown in eqn (4)):

S₄²⁻ + 2e⁻ ⇌ 2S₂²⁻, E^o = −0.48 V (7)

RFBs suffer from issues of cross-contamination between electrolytes of both half-cells,²² poor electrochemical kinetics of some redox couples, shunt current losses²³ and poor energy and power densities. In addition, the growth of non-aqueous RFBs is still in development phase and considerable research is required to match the performance of such systems with their aqueous counterparts.²⁴ Due to such challenges, only the VRFB and ZFB²⁵ have seen some commercial success. Moreover, the VRFB is the only system that has been developed to commercial scales as large as 5 MW/10 MW h (this system has been installed to combine with a 50 MW wind farm in Liaoning Province in China).²⁶ Despite significant research advances in China and other parts of the world^27–37 (including attempts to increase energy density by introducing polyhalide redox couples in the positive half-cell electrolyte),³⁸ VRFBs still suffer from several issues related to capacity fading, material degradation, precipitation of active species and others as detailed elsewhere.^6,39–47 Hence, the technology requires further optimisation.

The need to address the optimisation and commercialisation of both VRFBs and other RFB systems raises several important issues for developers of this technology, particularly improvements in flow distribution and operating conditions, enhancement in electrolyte stability as well as enhancement of electrode materials' resistivity towards oxidation.⁴⁸ For such cases, it is useful to implement modelling and simulation across multiple length scales in order to optimise the number of laboratory tests required for performance evaluation, to scale this performance to larger form factor cells and to conduct simulations that better inform experimental investigations in this regard.^49–52

Most key mathematical modelling aspects of VRFBs have been reviewed in depth by Zhang et al.⁴⁹ In brief, the models were classified into three types: (i) macro, (ii) micro and (iii) molecular/atomic approaches. Similarly, the applications of such models were also classified into four types: (i) market level, (ii) stack and system level, (iii) cell level and (iv) material level (Fig. 1). In a VRFB, the utilization of electrolyte is strongly related to its distribution inside an electrode.⁴⁹ If the electrolyte flow is not homogeneous, then the rate of the electrochemical reaction is relatively slow, which tends to lead to poor concentration and current distribution,⁵³ low power density, high overpotential and increased temperatures inside the cell. Although increased electrolyte flow rate may smooth out these effects, this comes at the expense of system efficiency due to the increased parasitic pumping load.⁵⁴ Therefore, understanding and controlling the distribution of flowing electrolyte within a VRFB is essential for maximizing battery performance and longevity.

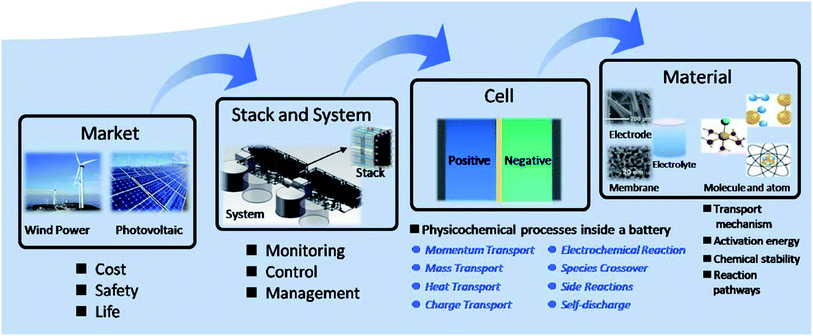Fig. 1 Classification of VRFB model applications into four types as reported by Zhang and co-workers. Reproduced with permission from Elsevier.⁴⁹

Hence, this work builds upon an idea proposed by Zhang and co-workers to determine the effects of redox active species in the porous electrodes at different length scales to effectively analyse and optimise the RFB further.⁴⁹ Current research work is thus briefly presented and a short perspective on the development of the RFB technology—not solely limited to the VRFB—is discussed. Specifically, this review article is divided into seven parts. This introduction is followed by Section 2, which summarises the key results from the mathematical modelling of various flow battery chemistries (excluding VRFBs, which are covered in Section 4). Section 3 highlights major issues related with electrolyte flow and its interaction with porous electrodes inside the RFB, while Section 4 discusses the progress made on the macro-scale modelling of VRFBs. Section 5 considers the progress of research on micro-scale modelling in VRFBs, while Section 6 tackles the development made on the modelling of reaction and transport processes in RFB porous electrodes. Section 7 discusses key aspects involved in the system integration of RFBs from a modelling perspective. Finally, Section 8 concludes this article and provides a fresh perspective and future directions on modelling of electrodes for RFBs.

2. Various flow battery chemistries and developments

Since their inception, RFBs have branched from their genesis redox chemistry (iron–chromium⁶⁵) to a diverse range of redox couples. Thus, to demonstrate the broad applicability of the governing fundamental equations and to present the popular redox couples hitherto, we briefly summarise the academic works on these systems. Note, VRFB models are discussed at length in Section 4 and thus are not included in this section.

2.1 Brief history

One of the first models reported on flow cells was by Danckwerts and Hulburt in the 1950s,^55,56 whose work was also adapted to develop boundary conditions,⁵⁷ while other models were advanced for flow-through porous electrodes by the 1980s.⁵⁸ It was shown that the flow-by porous electrodes provided an improved performance relative to the flow-through counterpart when used in RFBs.⁵⁹ Consequently, most subsequent studies employed flow-by electrodes;^60–64 however, Fedkiw and Watts observed that additional enhancements were possible to the model if the effect of geometrical and operational parameters on faradaic efficiency and cell performance was also examined.⁶⁵

2.2 Zinc–bromine modelling

Mathematical modelling of the zinc/bromine flow battery (ZFB) in a parallel plate configuration took off in the 1980s,⁶⁶ with the models by Lee and Selman^67,68 and Evans and White^69,70 providing predictions for many aspects of the ZFB cell of interest to designers. Microscopic models, which focused on zinc dendrite initiation and growth during electrodeposition, were also studied⁷¹ with a macroscopic model of the ZFB flow reactor in combination with a microscopic one describing dendrite growth.⁶⁷ These predictions included the current density distributions along the electrode surfaces, the overall battery efficiency and the round trip cell efficiencies.⁷⁰ Such work established many of the independent design parameters for an individual cell and showed how to improve cell efficiency via changes in these design criteria.^72–74

2.3 Iron–chromium systems

Iron–chromium (ICFB) RFB systems have also attracted industrial attention due to the potential low cost of the electrolytes. However, commercialization has yet to be realised due to issues around electrolyte crossover and hydrogen evolution, which results in accelerated capacity decay.⁷⁵ However, many models often make simplifying assumptions that disregard this process⁷⁶ even though the importance of hydrogen evolution on device lifetime is frequently highlighted. Scale-up investigations of ICFBs using shunt current modelling analysis were performed in the early 1990s⁷⁷ resulting in an enhanced energy efficiency of ca. 80% for a 0.7 kW battery. This was an improvement over the results reported by Fedkiw and Watts, who showed that membrane resistance contributed significantly to performance loss⁶⁵ albeit not sufficiently enough to warrant further investigations for almost two decades.^39,78 Another investigation described the experimental and numerical modelling applied to a particular Iron Flow Cell prototype.⁷⁹ The experimental validation showed numerical errors < 2.25% suggesting this methodological research provided a powerful calibration tool to help engineers in optimisation procedures.

2.4 Reversible solid oxide fuel cell

Another class of rechargeable battery composed of a reversible solid oxide fuel cell (RSOFC) and a metal–metal oxide redox cycle unit (RCU), termed solid oxide metal–air redox battery or SOMARB, has been reported.⁸⁰ Its high energy-density, high rate-capacity and easy system integration has drawn an increasing interest from the energy community.⁸¹ Since its debut in 2011, significant progress has been made in the areas of electrical performance,^82,83 new metal–air chemistries⁸⁴ and operation optimisation.^85–87

2.5 Polysulfide–bromine flow battery

Another potentially low cost redox flow cell couple of interest is the polysulfide–bromine battery (PSB, as shown in Fig. 4).⁸⁸ An investigation of the bromide half-cell found that multiple reaction mechanisms could account for observed behaviour,⁸⁹ leading to the mathematical modelling of the PSB system. For the conditions studied, mass transport overpotentials at the bromide electrode were found to limit the performance during discharge.⁹⁰ The model showed that significant drift in conditions could occur due to self-discharge and electro-osmotic effects. For the PSB system using the composite activated carbon electrodes developed by Regenesys,⁹⁰ bromide and sulfide kinetics rate constants of 4 × 10⁻⁷ and 3 × 10⁻⁸ m s⁻¹ were obtained. This model was followed by an investigation on the technical performance of a 15 MW, 120 MW h utility-scale PSB system⁹¹ and was later combined with a simple economic model including the main capital and operating costs to optimise the design and evaluate its commercial viability. Based on 2006 prices, the system was predicted to make a net loss of 0.45 pence per kW h at an optimum current density of 500 A m⁻² and an energy efficiency of 64%. The system was predicted to become economically-viable for arbitrage (assuming no further costs were incurred) if the kinetic rate constants of both electrolytes could be increased to 10⁻⁵ m s⁻¹, for example, by using a suitable (low cost) electro-catalyst. The economic viability was found to be strongly sensitive to the costs of the electrochemical cells and the electrical energy price differential.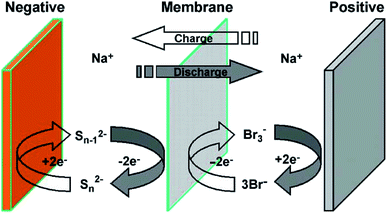

Fig. 2 The principle of sodium polysulfide–bromine redox flow battery as portrayed by Zhou and co-workers. Reproduced with permission from Elsevier.⁸⁸

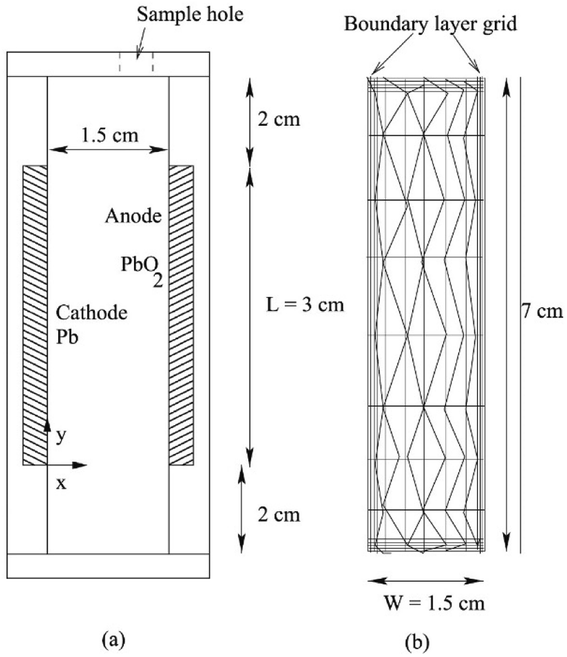Fig. 3 Schematic of (a) closed rectangular flowing Pb cell with electrodes mounted on walls used to carry out experiments, and (b) the computational grid used to carry out simulations. Reproduced with permission from Elsevier.⁹⁸

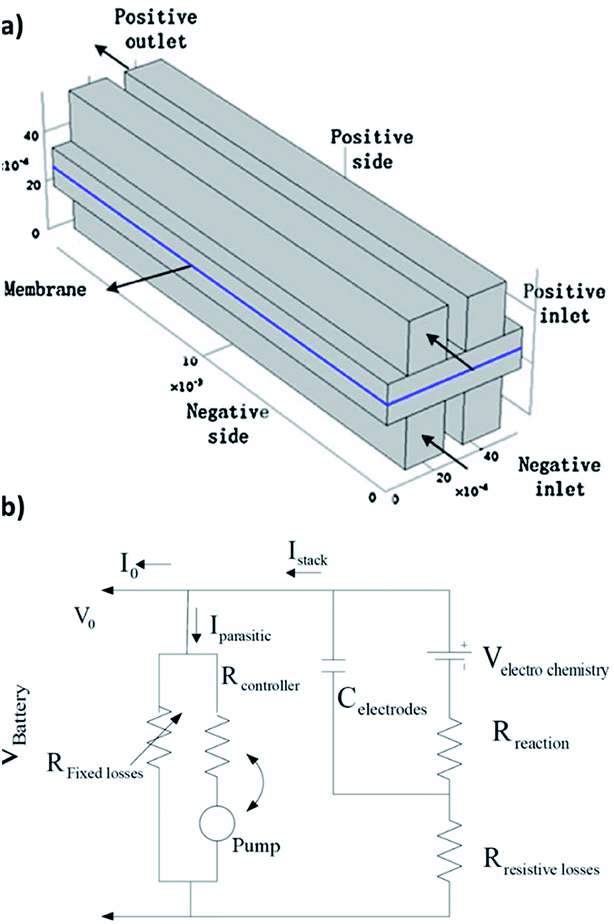Fig. 4 (a) Schematic of the quinone–bromide flow cell modelling domains. Reproduced with permission from Elsevier.¹³⁰ (b) Equivalent circuit modelling formulation for a flow battery in terms of resistances, flow of currents and potentials. Reproduced with permission from IEEE.¹³¹

2.6 Soluble lead redox battery

With regards to the soluble lead RFB (SLRFB), a number of issues have to be addressed before it can be commercialised,⁹² such as low charge efficiency⁵³ and incomplete dissolution of active solids (Pb on the cathode and PbO₂ on the anode), which can accumulate during charge–discharge cycling. After a few charge–discharge cycles, the accumulated residue on the electrodes begins to disintegrate and PbO₂/PbO particles entrain in the electrolyte, resulting in an irreversible loss of the active material that leads to the formation of an insulating layer deep inside the PbO₂ deposits at high acid concentrations. Consequently, this can cause premature capacity loss thereby yielding a very low cycle life of the SLRFB.⁹³ Increases in electrolyte flow rates to match the rise in battery efficiency only provide a marginal gain,⁹³ and attempts to increase battery capacity by enhancing deposit thickness are met with accelerated disintegration of the residue.⁹⁴ A resolution of these and other issues requires an understanding of residue build-up on the electrodes. Hence, the previous modelling studies on SLRFB have provided insights into two step charging⁹⁵ and effects of temperature, species concentrations⁹⁶ and electrode morphology⁹⁷ on battery performance.⁵³

One of these models accounts for ion transport resistance for electron transfer reactions using Butler–Volmer kinetics with fitted values of rate constants and non-uniform deposition on electrodes by simulating non-uniform current densities on the electrodes.⁵³ The model is simulated using COMSOL® for a SLRFB with planar electrodes using fast reaction kinetics, slow reaction kinetics and low transport resistance in the concentration boundary layer. The results suggest that resistance for ion transport in the bulk and concentration boundary layers and resistance for electron transfer at the anode control battery performance. There is a good fit with the model and the reported voltage vs. time measurements during charging, relaxation and discharging stages. The model also predicts that increasing the thickness of the concentration boundary layer in the flow direction leads to a significantly non-uniform distribution of deposit thickness. In the discharge cycle, the deposits near the trailing edge are dissolved completely, which is in agreement with the experimental observations. As time proceeds, the contact line separating the bare portion of the electrode from the active portion recedes into the active region rapidly. This ultimately manifests as a sharp decrease in cell voltage, leading to the cutoff value and termination of the discharge cycle. The incomplete dissolution of the deposited material leaves residues behind, which become thicker with successive charge–discharge cycles.

The model correctly captures the experimentally observed marginal effects of an increase in flow rate on voltage vs. time profiles.⁵³ The simulations show that a change in flow rate and velocity profile have a profound effect on the distribution of the deposits. The simulations carried out with alternating flow directions also show significantly reduced rate of residue buildup. Replacing the planar electrodes with annular cylindrical electrodes, where the anode is outside, leads to a substantial increase in energy efficiency and also decreases the rate of residue buildup.

Nandanwar and Kumar found that natural convection induced by difference in concentration of Pb²⁺ ions near the electrode surface and the bulk of the electrolyte plays a dominant role in the performance of a soluble lead battery with no external circulation.⁹⁸ This was later modeled by using a concentration difference driven body force term in the equations of motion. The augmented model,⁹⁸ with all the parameter values same as those reported by the same authors elsewhere,⁵³ very well explains the experimental data obtained in a narrow rectangular cell with no external flow as shown schematically in Fig. 5.⁹⁸

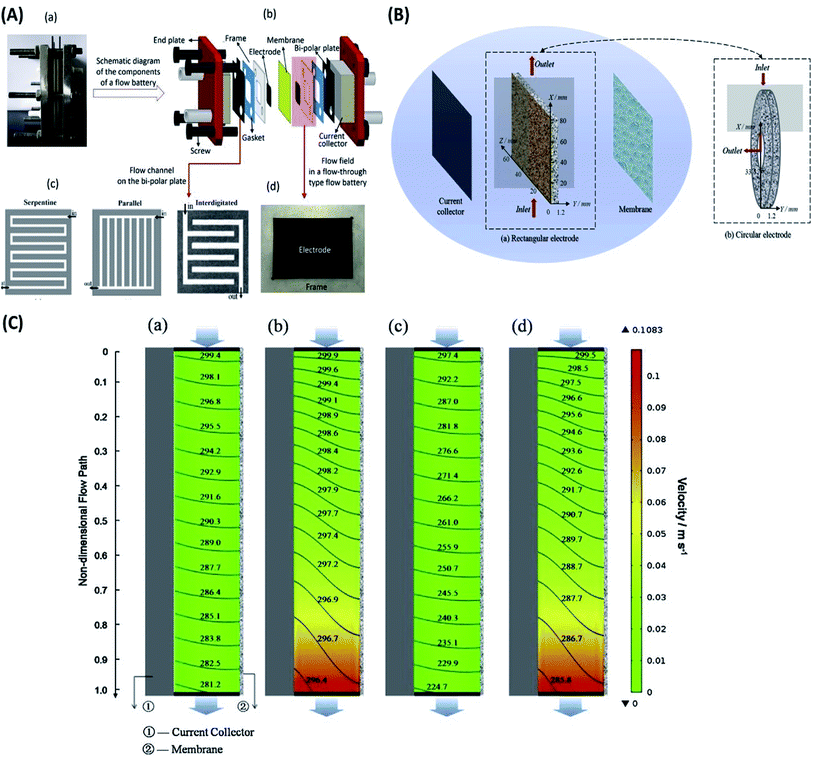Fig. 5 (A) Details of a redox flow battery set up as used in the Dalian Institute of Chemical Physics. (a) Digital picture of a single flow battery. (b) Schematic diagram of the components of a flow battery. (c) Flow channels on the bipolar plate. (d) Digital picture of the flow field in a flow-through type flow battery. Reproduced with permission from Elsevier;¹⁵⁷ (B) vanadium flow battery with (a) rectangular electrode and (b) circular electrode. Reproduced with permission from Elsevier;¹⁵⁸ (C) the spatial distribution of the velocity (color chart, m s⁻¹) and reactant (V³⁺) concentration (contour line, mol m⁻³) for (a) RFB at 40 mA cm⁻², (b) CFB at 40 mA cm⁻², (c) RFB at 160 mA cm⁻² and (d) CFB at 160 mA cm⁻² (P_in = 4.25 × 10⁴ Pa, P_out = 0). Reproduced with permission from Elsevier.¹⁵⁸

The electrode and deposit conductivities in most of the SLRFB models are considered to be infinitely large compared to that of the electrolyte.⁹⁸ Therefore, these models do not require the potential distribution in the solid phase to be determined. On a microscopic level, the assumption of high conductivity of deposits holds well for the cathode as current passes either through Pb deposits or graphite electrode, both of which are highly conducting. The situation at the anode is different though as the assumption of high conductivity holds for the first charge cycle as the deposit consists of only PbO₂. In the first discharge cycle, some PbO₂ is electro-dissolved and some is converted into insulating PbO solid. Oury and co-workers monitored the change in cycle mass at the anode during discharge using quartz crystal micro-balance and impedance spectra.⁹⁹ Their studies confirmed PbO₂ to PbO conversion and formation of an insulating layer that eventually stops the discharge process altogether.

The assumption of highly conducting deposits on the anode irrespective of the fractional content of non-conducting PbO appears unfounded. Oury et al. introduced a revised model that incorporates changes occurring in deposit conductivity on the anode and studied its impact on charge–discharge profiles, particularly in the context of charge coup de fouet (the voltage dip shortly after charging of a fully discharged battery begins), which cannot be explained by previously reported models.⁹⁷ Specifically, the updated model varied deposit conductivity with compositional changes, from highly conducting to non-conducting when conducting pathways cease to percolate beyond a critical volume fraction of the non-conducting phase. The change in conductivity of a thin layer of deposit on conducting graphite electrodes was used to develop an approximation that permits model predictions to be obtained without determining voltage profiles in the composite solid phase. The model effectively explains the observed charge coup de fouet phenomenon and its variation with depth-of-discharge.

2.7 Hydrogen–bromine flow battery

For the gas-phase Br₂–H₂ flow battery, which is again attractive due to the potential low cost, several mathematical models exist.^100–103 For instance, a mathematical model has been compared to experimental data¹⁰¹ and predicts the operating conditions of the cell in both fuel-cell (i.e., discharge) and electrolysis (i.e., charge) modes as a function of current, inlet gas composition, flow rate and pressure differential across the membrane. The analysis reveals that gas-phase Br₂/HBr reactants significantly enhance mass transfer, which enable higher current densities to be achieved in comparison to a liquid-fed system. A key feature of the model is in accounting for water transport across the membrane, which determines membrane conductivity, reactant concentration and undesired condensation. The model is then used to provide insights into cell operation, including operating conditions needed to avoid water condensation. For example, operating at pressure differentials where condensation is avoided, the model predicts current densities of 1.4 A cm⁻² on both charge and discharge states with round-trip efficiencies of approximately 63% and 37% at current densities of 0.5 and 1.4 A cm⁻², respectively.¹⁰¹

2.8 Iron–vanadium chemistry

In the past decade, scientists at the Pacific Northwest National Laboratory (PNNL) introduced a new iron–vanadium (Fe/V) RFB.^104,105 The flow cell performance was demonstrated using a small single cell (active area ca. 10 cm²) operable in a wide range of operating temperatures (0–50 °C) with negligible capacity fade over cycles. In addition, this new chemistry ensured reliable and safe operation as a result of negligible hydrogen evolution without any catalysts on the electrode, which was a concern with the previous ICFB chemistry.^106,107

The Fe/V chemistry was validated using a small-scale, single cell at a high flow rate (2 cm min⁻¹), although performance validation at the kW-scale at a more reasonable flow rate (<0.3 cm min⁻¹) is needed to demonstrate the potential of the technology for large-scale applications. The application of deep eutectic solvents for this chemistry has also been reported.^108–110 Further optimisation of both aqueous and non-aqueous Fe/V systems including electrode geometry, electrode design and flow rate are needed to enhance performance. Mathematical models can assist in cell scale-up as well as the optimisation of RFBs by simulating the effects of various cell geometries, varied electrolyte compositions and membranes on cell performance.¹¹¹ Furthermore, models aid in cost analysis and optimisation of system control.¹⁰⁶

A zero-dimensional electrochemical model of the aqueous Fe/V RFB has been presented that can model performance at low flow rates (<0.5 cm min⁻¹) and varied temperatures. The electrochemical model is appropriate for practical RFBs and shows good agreement with experimental data.¹⁰⁶ In addition, a proposed non-ideal electrode model is introduced that accounts for higher voltage losses at low flow rates. Semi-quantitative operational strategies and electrode design guidelines can be obtained from the model. The authors found that ohmic losses associated with the electrolyte were dominating the electrode losses, which meant operating the cell at higher temperatures could reduce electrolyte ohmic losses and viscosity, thus leading to a higher system efficiency. Using thinner electrodes (4.5 mm-thick felt electrodes were used in this study) can reduce ohmic and pumping losses if the same space velocity‡ is maintained. This electrochemical model could be easily incorporated into system-level and cost models, which could help in system optimisation, system control and pump selection to avoid potential risks that may be involved during large scale RFB system development.¹⁰⁶

2.9 Flowable semi-solid lithium-ion battery

In the work of Brunini et al.,¹¹² a porous electrode theory based approach was used and extended from the work of Fuller, Doyle and Newman¹¹³ to incorporate convection of both dissolved ions and active intercalation particles in a system based semi-solid electrodes. They utilised flowable mixtures of solid Li-ion storage compound particles suspended in a liquid non-aqueous electrolyte. The semi-solid electrode suspension was made electronically conductive by co-suspending nanoscale conductive particles (e.g., carbon black) along with storage compound particles in the electrolyte. In such semi solid flow cells, conductive particle networks replaced the static current collectors (e.g., carbon felt) used in conventional flow batteries.¹¹⁴ Additionally, due to the modelling of low flow rate operation added to the fact that the equilibrium voltage functions of Li-ion intercalation compounds vary, the non-uniform current density was modelled by applying potentiostatic boundary conditions while adjusting the voltage with time to match the desired current.¹¹² As in prior porous electrode models,^{113,115–118} the transport properties in the solid and electrolyte phases, the equilibrium voltage functions of the intercalation particles and the Butler–Volmer exchange current were employed as model parameters.¹¹² Of these, the shape of the equilibrium voltage function and the electronic conductivity of the suspension are observed to have the greatest effect on the current density and state of charge distributions in the matched charge and flow rate limit.

An evolved version of this concept has been developed in recent years to mitigate some of the fluid dynamics issues.¹¹⁹ The concept relies on placing the Li-intercalation material in an independent reservoir and employing dissolved species with the ability to mediate the lithiation reaction.¹²⁰ Since the mediator can undergo a reversible redox reaction in a flow battery configuration, the reaction overpotential is reduced when compared to the semisolid counterpart. The solid, storing reservoir enables higher volumetric energy density than conventional RFBs.¹¹⁹ This concept, which has been named redox targeting-RFB or redox solid energy boosters for flow batteries, has been successfully applied for different Li-intercalation materials.^121–123 Moreover, this redox targeting approach has been demonstrated beyond aprotic Li-based chemistries and aqueous configurations with excellent reported performance, including Prussian blue/ferrocyanide/ferricyanide mediated system,¹²⁴ vanadium chemistries,¹²⁵ Na-ion intercalation materials¹²⁶ and polyaniline solid charge storage material applied at both the negative and positive sides of the battery.¹²⁷ While no examples of mathematical modelling are available in the literature, charge-diffusion mechanisms within the solid material have been considered in different studies.^128,129

2.10 Quinone-based flow battery

A 3D model, including full coupling of the mass balances, momentum balances, ionic current balance, and electronic current balance, was developed for an organic–inorganic aqueous flow cell based on quinone chemistry.¹³⁰Fig. 6(a) is a schematic representation of the flow-through electrode model, which includes five domains: positive channel, positive electrode, ion exchange membrane, negative electrode and negative channel. From simulations, which were in good agreement with the experimental data it was concluded that six layers of carbon paper was the most appropriate electrode thickness. More than six layers of carbon paper provide more surface area at the expense of ohmic resistance, but less carbon paper cannot provide adequate specific active area. The flow fields in the x and z directions are analysed to account for the electric current density distribution where the high current density at the junction of the land and channel for the flow-through electrode cell is related to the flow field in the z direction.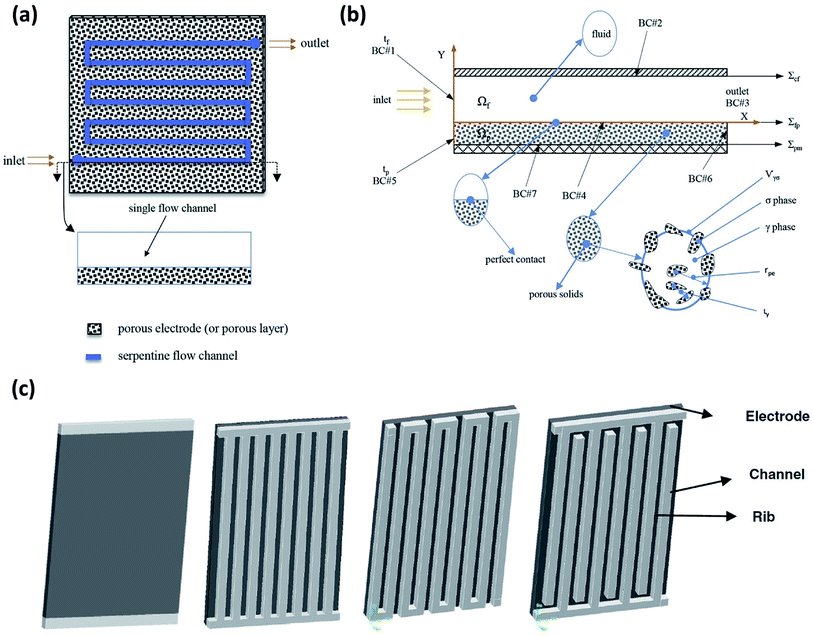

Fig. 6 (a) Flow segment modelled on a serpentine flow channel with a porous electrode. (b) 2D schematic showing a macroscopic diagram of flow through a flow channel and over the porous electrode, including a representative porous element: σ for solid phase, γ for liquid phase, r_pe denotes the average radius and ι_γ represents the characteristic length for γ phase within V_γσ. (c) Other flow configurations commonly being employed for RFB experimental and simulations studies are shown – from left to right: no flow field, parallel flow field, serpentine flow field and interdigitated flow field. Reproduced with permission from Elsevier⁵⁰ and Springer.¹⁵⁶

2.11 Single flow zinc–nickel system

In another paper, the primary characteristics of a single flow zinc–nickel battery is illustrated and based on that, the electrical equivalent circuit model (see Fig. 6(b))¹³¹ is established for the first time.¹³² The parameters in the battery model are identified by means of a variety of experiments, carried out on a small-capacity battery in the lab. According to the simulation and experimental verifications, the model can properly estimate the performance of the batteries under different conditions. The model is also validated for large-scale single-flow, zinc–nickel batteries.

2.12 Summary of flow battery chemistries

Despite the progress reported above, most of the published literature is based on experimental studies while only a few experimental studies on RFBs take into account mathematical modelling to design more efficient flow cells based upon electrolyte interaction with porous electrodes. The next section therefore discusses this important topic and surveys some of the modelling aspects involved.

3. Electrolyte flow and its interaction with porous electrodes

3.1 Introduction

In the last decade, a number of technical advances made in polymer-electrolyte fuel cells (PEFCs) field have been introduced in the flow battery technology, leading to dramatic performance improvements through enhanced mass transport and reduced area specific resistance (ASR).¹³³ Indeed, many of the constituent components and designs engineered for PEFCs are directly applicable to RFBs. Consequently, most redox flow cells (especially microfluidic designs¹³⁴) have advanced from lower power densities (ca. 200 mW cm⁻²) to higher, operational values.¹¹ For example, VRFB power densities greater than 700 mW cm⁻² have been reported, despite an operating limiting current density of ca. 1 A cm⁻² and requiring relatively high temperatures,³⁰ which also augment the cost due to the necessary thermal management and/or sequestration. Workers in Dalian achieved doubled power densities for their VRFB system (1.45 W cm⁻²)¹³⁵ in comparison to those achieved in Tennessee (0.76 W cm⁻²).¹³⁶ Similar high, peak power densities were reported from experiments on quinone-bromide systems conducted in Harvard University (1.00 W cm⁻²).^137–139 Despite such improvements, continued advancement of power performance is necessary to support further cost reduction, motivating research and development in the engineering science of RFBs.¹³³

There are several stimulating features in the engineering of the cell: construction materials, electrode and membrane.¹⁴⁰ VRFBs have been the subject of significant research efforts, with in-depth analyses being reported by Ma et al.¹⁴¹ and Secanell and co-workers.¹⁴² The uniformity of the electrolyte flow has a substantial effect upon the effective area of the electrode (fiber area of the porous electrode where the actual charge-transfer reaction occurs),¹⁴³ the depth, efficacy and lifetime of the battery as well as the electrochemical overpotentials, particularly when the current density varies significantly.

Miyabayashi et al. showed that a uniform electrolyte flow rate resulted in higher energy efficiencies for RFBs¹⁴⁴—specifically, even if the flow was homogeneous, there were, among other factors, significant local changes on the electrode surfaces resulting in high pH variations.¹⁴⁵ The significance of such a velocity study has also been confirmed in works by Bengoa and co-workers¹⁴⁶ and Wragg and Leontaritis.¹⁴⁷

Unfortunately, flow distribution within the battery is a difficult parameter to measure; it is influenced by several factors, including electrode micro-structure, surface chemistry, compression and electrolyte composition. Most articles to date imply the need of improved flow distribution for enhancing the entire system's efficiency;^148,149 for example, Escudero-González suggested a factor in order to evaluate the flow disorder in a three-dimensional analysis.¹⁵⁰ This involved a fraction of the volume en-route, the foremost flow, and in the reverse course to estimate the fluidic dead zones and membrane recirculation, which improved the estimation capability compared to other studies.⁷⁹

The factor suggested by Escudero-González and co-workers should allow the modeler to associate geometries by considering flow uniformity through computational fluid dynamic (CFD) methods.¹⁵⁰ This validation of the numerical model is of an extra benefit, since the real electrolyte is strongly acidic and corrosive that can impair experimental accuracy. The simplified model, however, does not consider these chemical facets and only models the fluid hydrodynamic performance.¹⁴⁵ Uniform flow is important for the performance factors in the RFB cell: the electrode effective area; the robustness and efficacy; the useful battery life; and the electrochemical polarization.^63,151 As a result, the effect of various geometries, the flow conditions and the membrane position and configuration¹⁵² on several cells have been studied with the goal of understanding and enhancing RFB operation.^{34,146,147,153}

3.2. Electrolyte flow field effects

The electrolyte velocity distribution from the flow field has been an active area of RFB research.¹⁵⁴ A rigorous analysis of flow fields needs two important numerical tools, namely CFD and statistical techniques. As mentioned, CFD aids in the simulation of pressure and velocity distribution providing simple performance indicators and enabling comparisons between different configurations. Statistical techniques can be applied to analyse a large range of individual velocity profiles in an accurate manner. The employment of hypothesis tests on data generated by means of CFD enables a quantitative analysis of several features on the velocity fields.^145,155

Even though a broad range of flow fields are possible for fuel cell applications, four patterns are chiefly employed in RFB applications. These include the serpentine, flow-through, interdigitated and parallel flow fields.¹⁵⁶ Besides the conventional RFB set-up that includes two, flow-through electrodes (usually carbon or graphite felts) separated by an ion-exchange membrane or separator (non-zero-gap assembly), over the past decade, a PEFC-based design has been increasingly adopted (Fig. 2 – this displays a zero-gap membrane–electrode-assembly that has been extensively tested in the Dalian Institute of Chemical Physics, China).^157,158 In brief, this system usually employs structured flow fields that act as the current collector and compress carbon electrodes (usually felts) against a membrane to yield a zero-gap assembly that dramatically reduces ohmic drop in the cell,¹⁵⁹ thereby yielding high current and power densities.^34,136,160

Flow fields vary with regards to their ability to transport the electrolyte to the reaction zone and the pressure drop necessary to maintain uniform flow. In the flow-through system, the electrolyte is introduced directly through the carbon felt electrode at one end of the cell and is allowed to disperse throughout the electrode before flowing out of the opposite end to the outlet channel (flow-through design). This generates a high pressure drop as all the fluid is forced through the entire length of porous media and potentially results in hydraulic short-circuiting⁷⁷ that hinders cell performance.^15,17,64,161 Thus, uniform distribution of electrolyte over the electrode surface is necessary to minimise pressure losses over the entire surface.¹⁵⁶ Therefore, it is essential to operate at optimal electrolyte flow rates established for balanced system efficiency and capacity.¹⁶²

Beyond the simplistic design of the flow-through flow field, other architectured flow fields have been investigated. The parallel flow field has been found to exhibit low pressure drops but can present severe flow non-uniformity especially within the channels¹⁶³ as well as poor convection under the ribs of the channels that slow mass transport.^164,165 Chen et al.¹⁴⁸ investigated a parallel flow configuration along with CFD analysis for flow allocations in the VRFB and achieved a rather low power density of 15.9 mW cm⁻², which they attributed to non-uniform flow rates throughout the cell. Xu et al.¹⁶⁶ compared the output parameters of different VRFBs with flow-through, serpentine and parallel flow configurations and revealed that the serpentine flow channels elicited the highest round-trip efficiencies. Latha and co-workers¹⁶⁷ also studied the serpentine flow field of a VRFB by investigating the effect of rib convection and porous electrode compression on flow dissemination and pressure drops.⁵⁰ The pressure drop in two, geometrically different serpentine flow fields was also determined over a range of Reynolds numbers, which, combined with CFD simulations, demonstrated the significance of the compression of the porous medium as an effective parameter for estimating the flow distribution and pressure drop in such flow fields.

It is known from fuel cell studies that the porous electrode can experience uneven compression under the ribs and channels of the flow field,¹⁶⁸ and this has also been observed in RFBs. In fuel cells, this uneven compression can affect the flow, ohmic resistance and pressure drop.¹⁶⁹ Similarly, uneven compression has also been observed in RFBs.^170–174 Numerical simulations indicate that the uneven compression and intrusion of the porous electrode into the flow channel increased the flow velocity in the channel, enhancing transport processes and electrochemical performance.^172,173

Harper et al.¹⁷⁵ recommended a flow channel design for the bipolar plate in order to reduce pressure drops and to maintain a distributed flow arrangement consistently. The authors also suggested the use of an interdigitated channel design for the flow cell asserting this could improve the cell operation without escalating the pressure drop and promote uniform electrolyte flow through the porous electrode. Tian and co-workers⁵⁴ numerically analysed several flow configurations with a single flow inlet and outlet, multiple inlets and outlets, a wide single inlet and outlet as well as a wide single inlet and outlet with branched/staggered interdigitated hollow channels in the porous electrode. They determined that unlike conventional designs, the introduction of flow distribution channels could enable enhanced flow uniformity throughout the electrode, while the introduction of channels inside the porous electrode could decrease pressure drop adversely impacting power output.¹⁵⁶

Tsushima and co-workers¹⁷⁶ studied the influence of cell geometry and operating parameters on the performance of a RFB with serpentine and interdigitated flow fields. They also observed better performance with an interdigitated flow field in the VRFB in comparison to the former flow configuration. Several experimental and numerical studies have also been reported for laminar flow fuel cells, which are effectively RFBs with laminar electrolyte flow in single channel flow-through electrodes without an ion-exchange membrane. Kjeang et al.¹⁷⁷ designed a simple microfluidic vanadium redox flow cell with a high aspect ratio Y-shaped micro-flow channel over a porous carbon substrate to obtain a peak power density of 70 mW cm⁻², which was lower than membrane-based systems. Zawodzinski and co-workers^34,136,160 adjusted PEFC cell configurations for RFB applications to improve current and power densities. In these designs the electrolyte flowed through serpentine channels behind a porous electrode sandwiched to a membrane and counter-electrode (membrane–electrode-assembly).

Further niche flow field designs have also been explored. Originating in PEFCs, Guo et al.¹⁷⁸ created leaf-like flow fields emulating the venous, biological structure found in plants and blood vessels. Employing a topological optimisation, Behrou et al.¹⁷⁹ proposed a depth-averaging model to maximise power density in PEFCs. The topological optimisation procedure has taken root in RFBs as a numerical study;¹⁸⁰ however, the performance of many of these flow field designs has yet to be experimentally validated.¹⁸¹

In summary, numerous studies have shown direct flow field influence on cell power performance of the cell, energy requirements and round-trip efficiency. Generally, serpentine and interdigitated flow fields appear superior to the flow-through and parallel flow fields, stemming from the significant and uniform cross-flow or under-the-rib convection inherent to these designs.¹⁸² While these phenomena have been well-studied in the fuel cell context,^164,183,184 the results are different for RFB applications. Specifically, while interdigitated flow fields have not found favor in PEFC applications—presumably due to the much higher pressure drop compared to the serpentine flow field^164,183,185—they appear to be the flow field of choice for RFBs. To resolve this discrepancy, Latha performed an in-depth, experimental and numerical investigation of the hydrodynamics of serpentine and interdigitated flow fields in typical RFB operating conditions and found that, at the same flow rate, the pressure drop in interdigitated flow field was lower than its serpentine counterpart.¹⁵⁶ CFD studies further show that strong under-the-rib convection in the reaction zone exists in both flow fields but with a shorter residence time in the case of the interdigitated configurations. These findings appear to explain the superior performance of interdigitated flow fields in RFB cells;¹⁵⁶ however, there is still considerable research needed to tailor flow field structure to improve uniformity of electrolyte flow and, consequently, power density.

3.3. General mathematical modelling of porous electrodes and their interaction with electrolyte flow

The modelling of RFBs seeks to enhance fundamental understanding and enable high-performing, economical designs of these systems through the development of mathematical equations implemented for numerical simulation of electrochemically reactive flow. One aspect of these models involves predicting the effect of flow distribution and the flow rate schedule on electrochemical performances at porous electrode surfaces. A few dynamic lumped models have been proposed in the literature to address this issue.^186–189 Nevertheless, given the need to represent the fluid dynamics within the flow field channels and the porous media, higher order models are needed to capture these phenomena. Ke et al. established a two-dimensional (2D) macroscopic mathematical model to simulate the dynamic flow patterns in RFBs represented by a single passage of a serpentine flow channel over a porous electrode as shown in Fig. 3(a)⁵⁰ with a 2D cross-section of the flow pattern represented in Fig. 3(b) and other general RFB flow configurations shown in Fig. 3(c). The non-dimensional average flow velocity (normalised with respect to the inlet flow velocity) in the flow channel decreased from the entrance to the fully developed flow region while an opposite trend was found in the porous layer. The volumetric flow rate in the porous layer increased as the thickness of this layer rose from 0.041 to 0.287 cm (the number of porous layers ranged from one to seven) for the carbon fiber paper electrodes.

Moreover, the authors also developed a description of the maximum current density that estimates the stoichiometric availability of reactant in the porous layer for reaction.⁴⁷ Under the inlet condition (Q_in = 20 mL min⁻¹ or u_in = 33.3 cm s⁻¹), the volumetric flow in the electrode layer, Q_p increased from 7.81 × 10⁻⁴ to 1.5 × 10⁻³ cm³ s⁻¹ when the electrode thickness increased from one to three layers of carbon paper. Under such conditions, the maximum current density increased from 377 to 724 mA cm⁻² as the electrode thickness increased. The predicted maximum current densities were found to be in good agreement with experimentally measured limiting current densities, and the same was observed for estimated values of porous layer permeability (377 mA cm⁻² predicted vs. ca. 400 mA cm⁻² measured for one layer, and 724 mA cm⁻² predicted vs. ca. 750 mA cm⁻² measured for three layers).

Other work on mathematical modelling and experimental validation shows minimum electrolyte recirculation in the membrane area, which improves the overall interchange efficiency of the cell (ionic interchange). To compare the experimental and computational models for a flow of 50 L h⁻¹, a methodology is proposed by Escudero-González.¹⁵⁰ Differential pressure and velocity fields are compared in both models with an acceptable convergence that leads to an improved design and key geometric parameters for creating and comparing new cell architectures.

Kee and Zhu performed a study to optimise the flow uniformity and the pressure drop for the interdigitated design via a simple fluid dynamics model.¹⁹⁰ The study provides dimensionless charts and analytic representations to estimate the pressure drop and the flux uniformity in a wide range of conditions, providing a rapid assessment of the channel layout as well as design guidelines for its optimisation.

A number of ex situ and in situ studies of flow field designs have been reported in the literature on RFBs. Hoberecht¹⁹¹ proposed a conventional flow field with inlet and outlet manifolds so that the fluid can spread out evenly before moving upward through the electrode. This work studied the influence of cell geometry and design parameters such as cavity thickness, inlet and outlet flow port width, and depth and flow rates on pressure drop. Hoberecht found that the compression of the porous electrode is a major contributing factor and accounts for nearly half of the pressure drop. Miyabayashi et al.¹⁴⁴ have since proposed a cell design with multiple slits in inlet and outlet manifolds to provide a uniform flow distribution pattern and reduce pressure drop while Inoue and Kobayashi¹⁹² proposed a porous electrode with convex, semi-circle, and v-shaped grooves.

In situ studies of flow fields and flow distribution effects in VRFBs have also been reported. Chen et al. performed experimental and numerical investigations of electrolyte flow distribution using a parallel flow field for a VRFB.¹⁴⁹ Their results showed a highly non-uniform electrolyte distribution over the entire surface with concentrated distribution in the central area of the flow field and a vortex flow in the inlet and the outlet regions. Simulated results, in agreement with experimental data, suggested that an optimised inner flow field structure should be designed. Xu and co-workers performed a study on serpentine and parallel flow fields along with a historical configuration (flow through a porous electrode in which the membrane is separate from the electrodes and is not in direct contact with them) using a three-dimensional (3D) numerical model.⁸⁴ At optimal flow rates, higher energy and round-trip efficiencies were observed with a serpentine flow field. Zhu et al. experimentally investigated the effects of flow fields with flow-through and flow-pass (serpentine, interdigitated or parallel flow as shown in Fig. 3) patterns finding that the flow-through pattern increases the electrolyte flow uniformity and the electrode effective area thereby increasing the efficiency.¹⁹³ Koeppel et al.¹⁹⁴ redesigned a VRFB for reduced pressure loss using an interdigitated flow field which Gerhardt et al.¹⁹⁵ further investigated by adjusting the land and channel dimensions to identify an optimal configuration. Other modelling and simulation studies described and accounted for all the relevant phenomena. Escudero-González introduced a methodology comprising three performance indicators (namely the symmetry coefficient, the uniformity coefficient, and the variability range coefficient of velocity front) using CFD simulations to determine the flow distribution in a particular VRFB geometry.¹⁴⁵ Finally, recent numerical and DFT simulations confirmed an experimental study on enhanced VRFB performance due to nitrogen doping of carbon granular electrodes,¹⁹⁶ thereby validating the efficacy of using both experimental and numerical techniques to guide a realizable and cost-effective solution for high-power VRFBs. In this regard, the next section follows up on a survey of macro length-scale modelling of VRFBs.

4. Macro length-scale modelling of VRFBs

A range of processes may influence the operational limitations in VRFBs.¹⁹⁷ At the cell level, reaction kinetics, ionic transport through electrodes, electronic contact resistance and mass-transfer resistance into and out of the electrodes are expected to impact the power output. Polarization curve analysis is typically implemented to assess the relative magnitude of these resistive contributions over a range of operating currents.¹⁶⁰ Depending on the region of the polarization curve, different losses can dominate cell performance, for example at low currents kinetic limitations are most important (Fig. 7).¹⁹⁷ Extracting all aforementioned parameters from experimental measurements may not be feasible unless coupled with pore-scale resolved kinetic and mass transport models.¹¹¹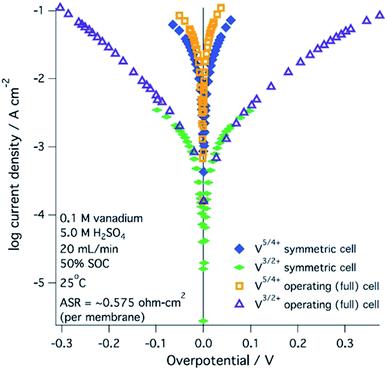

Fig. 7 Kinetic region polarization data for VRFB charging and discharging behaviour (ASR = area specific resistance). The electrolyte was 0.1 M vanadium in 5.0 M H₂SO₄. Reproduced with permission from ECS and IOP Science.¹⁹⁷

Here, we survey macro length-scale models for VRFBs due to their widespread investigation in literature. The fundamental equations described are applicable to other single-phase chemistries that follow Butler–Volmer kinetics by changing the parameters and stoichiometric coefficients of reacting species.

4.1 Background and literature survey on VRFB models

Macro length-scale models of VRFBs can be generally categorised into two groups: (1) lumped models, which mainly serve as control and monitoring tools, and (2) distributed models, which capture the spatial variations of field variables within the cell and can be employed for cell design and optimisation.^49,198 Lumped models on the system level address the prediction of stack voltage, state-of-charge (SOC), state-of-power (SOP), flow rate and system efficiency in different SOCs by using global mass and energy balances.^{49,52,199,200} These models are suitable to simulate transient characteristics such as mechanical (pumping) and electrochemical performance often based on a unit cell.^70,168 Similarly, equivalent circuits, which combine various elements, such as capacitors, resistances and voltage sources, have been used to represent the characteristics of the battery. These models are simple and straightforward without considering the inner structure of the battery, but do require experimental data to obtain various operational parameters.^{151,201–203} Due to their simplicity, lumped models are widely implemented for practical battery control and for the development of monitoring strategies. Table 1 summarises the main assumptions of typical zero-dimensional lumped models. Conversely, distributed models aim to describe the physical and chemical processes occurring within the cells in greater detail. These models are used to enhance the design of the electrodes, membranes, flow fields and to determine the optimal operating conditions such as temperature and current density.

Table 1 Key assumptions for zero-dimensional VRFB models

Model type & target	Software	Key assumptions	Ref.
Dynamic	In-house code	• Isothermal conditions	151
		• Proton concentration is neglected in tank and cells
		• No time delay in electrolyte flow and mixing in cells and tanks
		• Same chemical reaction rate during charge and discharge
		• Concentration changes driven by linear chemical reactions and concentration difference between cells and tanks
		• Flow rates in both electrodes are balanced and constant
		• Concentration of V^2+ is same as VO2^+
		• Voltage calculated with Nernst equation and unitary activity coefficients
System-level oriented (iron/vanadium flow cell)	In-house code	• Isothermal conditions	106
		• Incompressible fluid flow
		• Uniform redox species concentration across the electrode thickness, linear concentration changes along convective flow direction
		• Isotropic and homogeneous electrode, electrolyte and membrane properties
		• Electrode Nernst potentials related to electrolytes state of charge
		• No cross-over, no side reactions
		• Butler–Volmer kinetics
		• Negligible volume change of each electrolyte reservoir
		• An averaged current density is used
Control-oriented	In-house code	• Dilute solution approximation	213
		• Isothermal conditions
		• Complete dissociation of sulfuric acid
		• Constant liquid density
		• Equal charge transfer coefficients
		• Constant charge/discharge current
		• No side reactions or self-discharge of V species
		• Electrolyte conductivities, specific surface area and rate constant in negative electrode used as free fitting parameters

---

The mathematical description of reaction kinetics represents the first step of the mechanistic modelling of VRFBs. Nonetheless, kinetic models alone are not suitable for describing the complete electrochemical behaviour of the VRFB system due to the coupled transport phenomena in RFBs. Moreover, the appropriateness of different kinetic formalisms are dependent on the reactions in question as well as detailed information of the system unless ab initio calculations, which are seldom applied for VRFBs, are employed to support reaction pathways or species' stability.⁴³ Additionally, flow models simulate only the momentum transport while the species, charge transport and electrochemical reactions are neglected.^204–206 Thus, these flow models are only valid for a limited range of conditions. Higher accuracy can be obtained if the models include detailed physicochemical processes related to the active species concentration, potential drop and current density within the battery.⁴⁹ Abu-Sharkh and Doerffel²⁰⁷ as well as Dees et al.²⁰⁸ suggest that complete electrochemical models are best suited for optimisation of the physical design aspects²⁰⁹ of electrodes and electrolytes.

The complete distributed electrochemical models are based on the mathematical description of electrochemical reactions and conservation laws of mass, charge, energy and momentum of electrolyte in the stack and tanks.^210–218 These models involve detailed considerations of the dynamic processes of vanadium species, the structure of individual cells and the stack as well as a large number of selected parameters. With the higher order models, the accuracy of the physical domain can be improved but at the cost of computational times. However, depending on the model application, lower dimensional models and other simplifications may be acceptable at the discretion of the researcher. The key assumptions for some of these distributed continuum electrochemical models are summarised in Tables 2–4 for 1D, 2D and 3D models, respectively.

Table 2 Key assumptions for one-dimensional VRFB models

Model type & target	Software	Key assumptions	Ref.
Continuum (reduced from a 2D model)	COMSOL Multiphysics®	• Dilute solution approximation	211
		• Pseudo steady-state isothermal operation
		• Incompressible fluid with constant density and viscosity
		• Plug-flow for the circulating electrolyte
		• Electroneutrality in electrolyte bulk
		• Fully humidified membrane, permeable to protons only
		• Concentration-dependent Butler–Volmer kinetics
		• Neglected sulfuric acid dissociation reaction
		• No side reactions
Continuum	MATLAB	• Same as reported by Vynnycky^211	221
		• Donnan potential considered
		• Mass transfer between electrolyte bulk and electrode surface considered

---

Table 3 Key assumptions for two-dimensional VRFB models

Model type	Software	Key assumptions	Ref.
Dynamic continuum model at cell level	COMSOL Multiphysics®	• Dilute solution approximation	210
		• Isothermal condition
		• Incompressible laminar flow with constant viscosity
		• Electroneutrality in electrolyte bulk
		• Isotropic and homogeneous electrode, electrolyte and membrane properties
		• Concentration-dependent Butler–Volmer kinetics with mass transfer between electrolyte bulk and electrode surface
		• Water transport in membrane driven by concentration, potential and pressure gradients (but volume change neglected in electrodes)
		• No side reactions
		• Neglected Donnan potential
		• Neglected sulfuric acid dissociation reaction
Stationary continuum model at cell level	COMSOL Multiphysics®	• Same as reported by Shah et al.^210	214
		• Steady-state operation
		• Considered dispersion along cell length
		• Water permeation or drag through membrane neglected
		• Ignored migration term in species flux
Dynamic continuum model at cell level (non-isothermal)	COMSOL Multiphysics®	• Same as reported by Shah et al.^210	212
		• Heat balance included (assumed same temperature locally between electrode and electrolyte)
Dynamic continuum model at cell level (non-isothermal, side reaction considered)	COMSOL Multiphysics®	• Same as reported by Al-Fetlawi et al.^212 and Shah et al.,^216 but considering O2 evolution at positive electrode	215
Dynamic continuum model at cell level (side reaction considered)	COMSOL Multiphysics®	• Same as reported by Shah et al.^210	216
		• Considered H2 evolution at negative electrode assuming formation of spherical gas bubbles that do not coalesce
		• Overall momentum equation (for the gas bubbles and liquid) approximated by that of the liquid phase
Stationary continuum model at cell level (parametric study on compression)	COMSOL Multiphysics®	• Same as reported by Shah et al.^210	171
		• Only the first proton dissociation of the sulfuric acid is considered
		• Proton concentration considered in Nernst potential but no Donnan potential considered
		• Electrode surface area and solid volume assumed constant under compression
Dynamic continuum model at cell level (cross-over of species)	COMSOL Multiphysics®	• Similar to that reported by Shah et al.^210	228
		• Donnan potential and proton concentration in Nernst potential are considered
		• Kinetics of second dissociation of sulfuric acid considered
		• Considered cross-over of species across membrane through a simplified Nernst–Planck equation and assumed fast kinetics of associated chemical reactions
Stationary continuum model at electrode level (not specific for VRFBs)	COMSOL Multiphysics®	• Similar to that reported by Shah et al.^210	229
		• Steady-state condition
		• Neglected electric resistance of solid matrix
		• Neglected ionic migration in electrolyte
		• Plug flow
		• Tafel-regime

---

Table 4 Key assumptions for three-dimensional VRFB models

Model type & target	Software	Key assumptions		Ref.
Stationary continuum model at electrode level with channels (isothermal)	COMSOL Multiphysics®	• Similar to that reported by Shah et al.^210		141
		• Considered negative electrode only
		• Neglected ionic migration in the electrolyte
Stationary continuum model at cell level (flow field study)	ANSYS® 13.0 package	• Similar to that reported by Shah et al.^210		166
		• Only proton transport across membrane (Ohm's law)
Dynamic continuum model at cell level (non-isothermal)	Finite volume method (in-house FORTRAN code)	• Similar to that reported by Al-Fetlawi et al.^212		230
		• Kinetics of second dissociation of sulfuric acid considered
		• Cross-over of species across membrane considered
Pore-scale resolved model	Lattice Boltzmann and finite volume methods	• For electrolyte flow	∘ Incompressible and Newtonian laminar flow with uniform viscosity	231
			∘ Fluid flow independent from ionic species
			∘ No-slip boundary condition at the carbon fibre surface
			∘ Flow is driven by a constant pressure gradient along Z-axis;
			∘ Isolated pores do not contribute
		• For ionic species	∘ Nernst–Plank equation under dilute solution approximation
			∘ Electroneutrality in electrolyte bulk
			∘ Sulfuric acid completely dissociated in SO4^2− and H^+
		• Electrochemical reaction	∘ Concentration-dependent Butler–Volmer kinetics
		• Additional	∘ Steady-state and isothermal condition
			∘ No side reactions or cross-over
			∘ Migration of H^+ and H2O across membrane is neglected
Pore-scale resolved model	Same as reported by Qiu et al.^231	• Same as reported by Qiu et al.^231		232

---

Despite the coupled nature of the transport and reaction phenomena, in some cases the solution of the mathematical formulation is performed in three stages (Fig. 8):¹⁹⁸

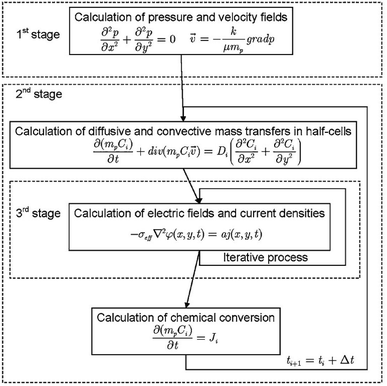Fig. 8 Flow chart showing how VRFB models are usually solved numerically as detailed in the literature. Reproduced with permission from Springer.¹⁹⁸

• Distribution of pressure and of flow in the cell;

• Distribution of chemical species, considering electrochemical interaction; and

• Distribution of the electric field and the current density.

Following this approach, Bayanov and Vanhaelst¹⁹⁸ solve the fluid dynamic and electrochemistry equations by means of the coarse particles method combined with an iteration process. The post-processing of simulation results combined with experimental data enables the determination of the main characteristics of the VRFB—the voltage, the current and the internal resistances. The study of the electrolyte flow in a VRFB is a relatively recent research topic compared to the evaluation of other key parameters of the system.²¹⁹ The flow structure is formed by means of a system of inlet and outlet channels as well as porous electrodes. The theoretical models used to simulate the flow behaviour are based on mass and charge conservation. Rudolph et al.²¹⁹ analysed the electrolyte flow on the basis of three theoretical models: (1) total flow, depending on the electric current; (2) flow distribution in the inlet/outlet channel system; and (3) flow distribution in a half-cell. For a test RFB, the capacity availability is calculated and measured for a wide range of flow rates and electric currents. The flow distribution in the porous electrode is calculated and the efficiency (affected by the different flow configurations in the half-cells) is measured. The parameters and the configuration of the electrolyte inlet/outlet channels are optimised to obtain a uniform distribution of the electrolyte flow to each half-cell. The results, comprising the SOC of electrolytes, electric current, maximum voltage by charge, power, charge/discharge duration and capacity, correlate with the measured data within an accuracy of ±2%. It is shown that the simple flow design in the electrodes with single inlet and outlet channels allows for an effective use of more than 89% of the electrode surface.

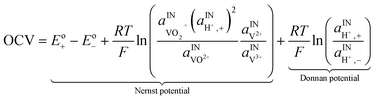
A major issue with the existing VRFB models is the inaccurate prediction of the open circuit voltage (OCV), which results in a discrepancy of 131 to 140 mV in predicted cell voltages when compared to experimental data.²²⁰ This deviation is shown to be caused by the incomplete description of the electrochemical double layers within the cell when calculating the OCV using the Nernst equation adopted from fuel cell literature. A more complete description of the Nernst equation has been provided by a couple of authors^220,221 which accounts for two additional electrochemical mechanisms that exist in a VRFB, namely: (1) the proton activity at the positive electrode (V^4+/5+) due to the involvement of the protons in the redox reaction, and (2) the Donnan potential due to the proton concentration differences across the membrane (Fig. 9).²²⁰ The more complete form of the Nernst equation closely matches reported experimental data with an average error of 1.2%, and is a significant improvement over the incomplete Nernst equation (8.1% average error).

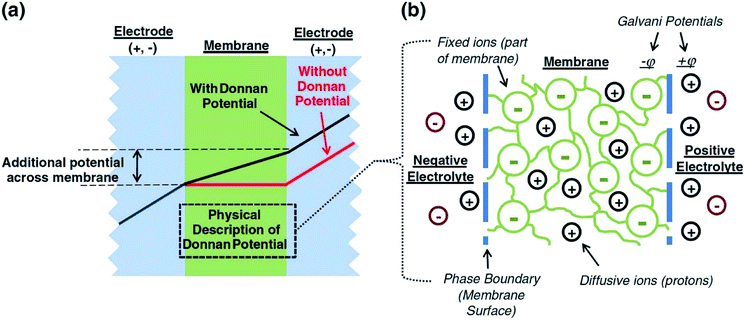Fig. 9 (a) OCV with and without the membrane potential, (b) physical representation of the electrolytic double layers on both sides of the ion exchange membrane. Reproduced with permission from Elsevier.²²⁰

Various models take into account capacity losses due to crossover,^51,222,223 side reactions^215,216 and consider different thermal effects^{52,162,224,225} as a function of time, for different operating conditions and cell designs. These models assist in understanding the change in electrolyte concentration over long-term operation. Thus, the models can be used for the development of battery control systems that can automatically restore VRFB capacity by periodic electrolyte rebalancing.^171,226,227

Several groups have attempted to investigate mass transport effects through porous materials using experimental techniques to complement model predictions. For example, thermal visualization methods have extensively been exploited for PEFCs and were also extended to investigate the electrolyte convective velocity and distribution in the electrode.^233,234 The detailed data on flow velocity and distribution enabled accurate simulation of mass transport effects using computational models for both serpentine and interdigitated flow field designs.

While this imaging method provides valuable information regarding liquid reactant distribution, it does not provide any information concerning electrochemical reactions. Aligned with previous experience in PEFCs, Gandomi et al. successfully implemented reference electrodes as probes within the layered porous carbon electrode to map reaction locations associated with potential distribution at the positive electrode of the VRFB.²³⁵ This approach allowed for the identification of regions operating under mass transport limitation (i.e., reactant V(IV) or V(V) starvation) when the system was operated at high current densities. Following a similar approach, Clement et al. implemented a segmented cell with reference electrodes to study the 2D current distribution for a VRFB.²³⁶ The authors correlated the influence of local electrolyte velocity in the electrode and electrolyte concentration with mass transport limiting conditions. In addition, the authors identified electrode microstructure and wettability as major factors to be considered to successfully understand RFB performance.

4.2 Fundamental equations for VRFB macro length-scale electrode modelling

This section summarises the modelling approach for VRFB electrodes, for which the governing equations are provided in Table 5. VRFBs are considered here, but the fundamental equations can be adapted also to other similar chemistries by changing a few specific parameters and stoichiometric coefficients. Going beyond what is currently reviewed in the literature,⁷⁶ alternative approaches used in other fields, such as in battery modelling, are also discussed and incorporated in the model in order to improve the mathematical description at the macro-length scale.

Table 5 Governing equations for the continuum modelling of VRFB electrodes. The nomenclature used in this table is reported in the ESI (Table S1)

Type and phase	Balance equation		Transport equation
Electrons (ed)		(8a)		(8b)
Continuity (ey)		(9a)		(9b)
Species (ey)		(10a)		(10b)
Electroneutrality (ey)				(11)

---

Thermodynamics and kinetics
Reactions		(12a)
		(12b)
Open circuit voltage		(13)
Current density		(14a)
		(14b)
Overpotential	with	(15a)
	with	(15b)
Mass transfer in stagnant layer		(16)
Activity definition		(17)

---

The core of a macro length-scale model of VRFB electrodes consists of a set of conservation equations of mass, charge and chemical species in both electrode and electrolyte as reported in eqn (8a)–(10a). For simplicity, only the faradaic contributions to molar balances are reported in explicit form in the right-hand side of eqn (8a) and (10a). The source term due to the kinetics of sulphuric acid dissociation (S^v_d,i)²²⁸ are not explicitly reported, while the source terms due to electric double-layer contributions (S^v_C,i), normally neglected in VRFB models,^76,210,221 are briefly discussed later in this section. The conservation equations are coupled with transport equations (eqn (8b)–(10b)), which express the fluxes as a function of field variables. Typically, the transport of electrons in the solid phase is described according to Ohm's law (eqn (8b)). The multicomponent transport of chemical species within the electrolyte is based on the generalised Nernst–Planck equation (eqn (10b)),²³⁷ which considers diffusion, migration and convection. The electrolyte is a concentrated solution, thus (i) the mass average velocity w̲ in eqn (9) differs from the molar average velocity v̲ in eqn (10a)^210,211 (the conversion between w̲ and v̲ has been reported by Bird et al.²³⁸); and (ii) the diffusion of species is affected by ionic interactions, which are considered using the thermodynamic correction factor ∂ln γ_i/∂ln c_i in eqn (10b). Alternatively, the generalised Maxwell–Stefan approach proposed by Krishna and co-workers²³⁹ can be used to model mass transport. The difficulty of modelling mass transport in concentrated solutions stems from the complex dependence of diffusion coefficients on species concentrations, which requires experimental characterization. Moreover, when the mass transport is modelled in 1D or 2D, the diffusion coefficient should be corrected for the dispersion as a function of the Péclet number.⁷⁶

The electroneutrality equation (eqn (11) (Table 5)) is typically enforced instead of the Poisson equation to simplify the mathematical treatment.²³⁷ As such, the formation of electric double-layers is not explicitly modeled. Normally the double-layer contribution, S^v_C,i, is neglected because its dynamics are faster than the other transport processes. However, this contribution must be taken into account when analysing impedance spectra, either by introducing a phenomenological capacitance into model equations or by properly incorporating diffuse charge in porous electrode theory and Frumkin correction to the Butler–Volmer kinetic expression^240,241 as presented by Bazant and co-workers.^242,243

The transport of electrons and chemical species is affected by the microstructural properties of the electrode, that is, by the effective conductivity factors, 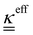, and the permeability, 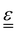. However, commonly these tensors are replaced by scalar quantities through the adoption of semi-empirical correlations, such as the Bruggeman correlation,^76,210,244 the Carman–Kozeny relation²³⁹ or more sophisticated relationships.²⁴⁵ However, these correlations, whose reciprocal consistency should be assessed,^246,247 may be too generic for the specific electrode under consideration, and their evaluation through the micro length-scale modelling of the electrode is recommended (vide infra).

The kinetics of the faradaic reactions is typically described by using global Butler–Volmer expressions (Table 5, eqn (14)), although elementary reaction mechanisms dependent on the electrode surface functional groups have been proposed.²⁴⁸ Notably, all the reacting species must be included in the kinetic expression, in particular the proton activity in the local equilibrium potential of the positive electrode, E^eq₊ (eqn (15a)), and in the Nernst potential (eqn (13)), as discussed in the previous section. In addition, the Donnan potential is added to the Nernst potential in eqn (13) to accurately compute the OCV as discussed by Knehr and Kumbur.²²⁰

The mass-transport resistance due to the stagnant layer between the concentration in the electrolyte bulk c_i and the concentration at the electrode/electrolyte interface, c^s_i, is considered in eqn (16). Generally, the mass-transfer resistance of protons is negligible through the assumption that the surface concentration of protons, 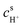equals the bulk concentration, c_H⁺,²²¹ which additionally simplifies the kinetic expression in eqn (14a). In such a case, by rearranging eqn (14) and (16) the surface concentrations can be eliminated in favor of the bulk values.^210,221 Finally, the mass-transfer coefficient, k_s, can be estimated through a variety of correlations involving the Sherwood number as a function of Reynolds and Schmidt numbers, according to the electrode micro-structure and flow conditions.²⁴⁹ Numerical simulations at the micro length-scale can potentially be used in such regard.²⁵⁰ Although these simulations are computationally expensive, they provide the governing equation with information that would not be available otherwise.

5. Quantification and modelling of electrode properties at micro-length scale of VRFBs

Quite often, the available properties for electrochemical reactions are not based on the geometry of actual materials, especially for the electrode, the membrane and the electrolyte.^49,251 Therefore, the continuum models implementing surface or volume averaging (i.e., eqn (10) (Table 5)) at the cell level cannot be employed to evaluate the local effects of the materials' nano- and micro-structure on the VRFB performance. In order to develop a more precise comprehension of these structural effects on the performance and operation of VRFBs, it is crucial to employ methods that can probe electrode structure at various length scales.²⁵² Methods such as 3D X-ray tomography and radiography (Fig. 10)²⁵³ can be used to reveal the internal structure of electrodes over a range of length scales (tens of cm to sub-nm).^254,255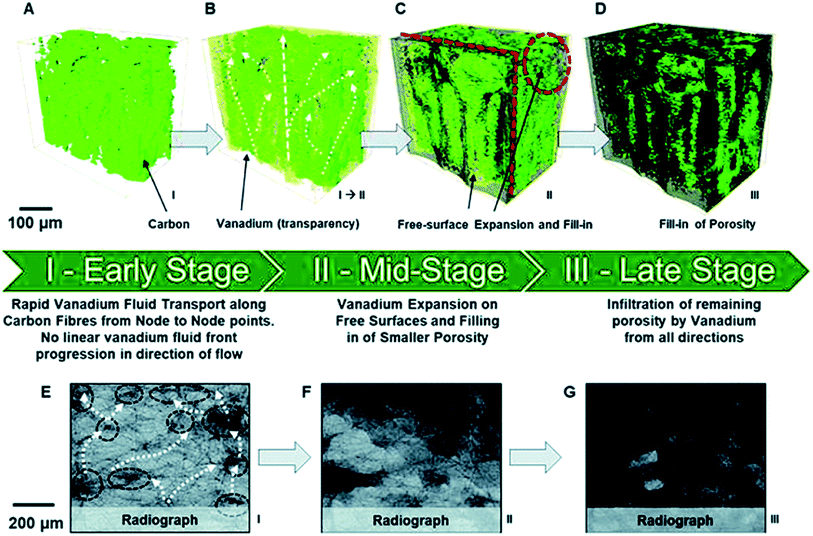

Fig. 10 Mechanisms of vanadium permeation following stages from (A) dry carbon paper electrode, (B) rapid node-to-node electrolyte infiltration, (C) then fill in of free surfaces and (D) fill in of final remaining porosity (determined via X-ray computed tomographic reconstructions of SGL 10AA carbon paper electrodes). Radiographs (E) illustrate the nodal transport, (F) fill in of free surfaces bypassed earlier and (G) full fill in of outstanding porosity. Using this mechanism, the vanadium electrolyte permeates across the carbon electrode without requiring filling of the whole porous volume at the first step, leaving air pockets which are filled in later. Reproduced with permission from RSC.²⁵³

The application of tomography to carbon-based materials for energy storage application has been slowly growing. Traditionally, the relatively low Z number of carbon stymies the rendering of electrode images using X-ray computed tomography (XCT). Similarly, preferential sputtering of carbon materials makes it difficult to image using focused ion beam (FIBSEM) tomography.^42,256–258 In other words, the imaging of carbon fibers and particles at sub-micron resolution in 3D has been challenging due to (i) the low X-ray attenuation coefficient of graphite and (ii) the interaction of graphite with focused ion beams that may lead to highly non-uniform nano-scale milling.²⁵⁹ Thus, the precise nano-structure of graphite-based anodes at high resolution remains poorly understood.²⁶⁰

However, innovations in 3D imaging techniques has meant that the tomography of challenging carbon-based materials is becoming increasingly common in a wide range of studies and numerous metrics, such as specific surface areas, effective conductivity/tortuosity factors, permeability tensors, pore/particle size distributions, etc., which can now be quantified at high resolutions of the order of sub-100 nm.^261,262 For example, using phase contrast XCT and high-Z compound epoxy-impregnation techniques for FIBSEM, it is possible to achieve good contrast for carbon materials.^263,264 Another technique being utilized is to study the effects of mechanical compression on carbon-based electrodes.¹⁷⁰Table 6 summarises the range of materials and compression conditions previously reported in the literature (non XCT-based).²⁶⁵ It can be seen that the nature of the gas diffusion layer (GDL) and the compression range has a significant effect on the contact resistance measured. The bipolar plate (BPP as labelled in Table 6) material is also known to affect the contact resistance.²⁶⁶

Table 6 Comparison of compression ranges and resistances reported in the literature for different bipolar plate (BPP) and gas diffusion layer (GDL) materials. Reproduced with permission from Elsevier²⁶⁵

GDL material	BPP material	Compression range (MPa)	Resistance (mΩ cm^2)
Toray H060	Plexiglas	0.48–2.41	N/A
Paper type	Graphite	0.25–3.5	45–23
SGL-10	—	0.15–3	6–2
Toray H series	—	0.45–3.6	160–0.06
ELAT	Stainless steel	0.42–0.92	28–14
ELAT	Graphite	3	10
ELAT	Graphite	0.4	13
Carbel CL	Poco graphite	0.5–3	30–10

---

Weyland and Midgley²⁶⁷ report, in a review of electron tomography (sub-10 nm resolution), the use of bright field and energy filtered electron tomography (by means of the Yamauchi et al.²⁶⁸ stain) to identify complex structural details of a different three-phase polymer. Similarly, Yoshizawa and co-workers have employed electron tomography (3D TEM) to observe the internal structure and connectivity of carbon nanospheres.²⁶⁹ Thorat and co-workers²⁷⁰ have developed a method to determine electrode and separator tortuosity, in contrast to its more mundane treatment as an adjustable parameter.¹¹⁵

Recently, the modification of carbon paper electrodes by reduced graphene oxide for improved battery performance has been studied by means of XCT and correlated with other methods.^271,272 It was demonstrated for the first time that XCT can resolve between carbon paper and carbon-based deposited layers. Fig. 10 shows tomographic reconstructions of the carbon paper electrodes (SGL 10AA) using results obtained from a separate investigation.²⁵³ Particularly, Fig. 10(a) shows the solid phase (fibers) of the electrode itself that may be modelled via Ohm's law (eqn (8) (Table 5)), thereby determining the conduction properties of the material; Fig. 10(b) shows the fiber-pore interfacial surface that could be used for modelling electrochemical reactions using Butler–Volmer kinetics (eqn (14)); and Fig. 10(c) shows the region of pores filled with electrolyte that may be modelled using equations related to diffusion (Fick's law, Nernst–Planck, etc.) and forced convection (Navier–Stokes). Fig. 10(d) shows tomographic re-constructions of the permeation of 1 M VOSO₄ + 5 M H₂SO₄ (VRFB electrolyte as reported for zero-gap flow cell) through a carbon paper substrate demonstrating how real-time XCT may be used to evaluate and model flow mechanisms in situ for flow batteries.²⁵³

The 3D imaging work on carbon-based materials can capture structures that may be used as geometric inputs to model the behaviour of electrodes and electrolytes. Interestingly, until extensive investigations were performed by Shearing and co-workers,²⁷³ there have been relatively few reports of 3D reconstructions of carbonaceous RFB electrodes in the literature.²³⁵ Qiu et al. have utilised XCT to simulate the effect of concentration, overpotential and charge density within an RFB with a pore-scale resolved model²³¹ and later demonstrated the effects of real pore/electrode morphology acquired using XCT on electrochemical performance showing that the cell voltage increases with greater electrolyte flow rate as a result of decreasing concentration gradients.²³² Their simulations also suggest that a detrimental effect of performance may occur in the RFB in the event of fuel starvation/low flow rates/low electrolytic concentrations for fresh carbon felt materials. As such, there has been at least one additional study on the tomography of voltage-cycled cells to better understand this behaviour.²⁷⁴

Reconstructed 3D images of the VRFB electrodes show fiber agglomeration and carbon electrochemical oxidation during continuous battery functioning. Key geometric features of the graphite felt samples can also be obtained from these 3D images allowing the estimation of porosity and volume-specific surface area and the changes from operation for each sample. In one study, a significant decrease (ca. 37%) in the volume-specific surface area of voltage-cycled graphite felts is seen after only 65 h of continuous VRFB testing, indicating its structural alteration due to carbon oxidation/fiber agglomeration.²⁷⁴ SEM and XPS are employed to verify the structural and surface changes observed by micro-computed tomography. SEM displays fibers with a bundle structure commencing to agglomerate after VRFB cycling and XPS confirms the electrochemical oxidation of graphite fibers, demonstrating the formation of an intermediate carbon oxidation product (COOH) on the electrode surface.

The pore-level mass-transfer coefficient is related to the morphology of pore surfaces, electrolyte properties and the local velocity of the electrolyte.²⁷⁵ The lattice-Boltzmann method (LBM) may be employed to simulate the flow across the pore space.^231,232 The acquired correlation equation for the effective diffusivity of vanadium ions through the porous electrode includes the effects of both the porous electrode structure and flow dispersion (Fig. 11).²³¹ It was found that the influence of flow dispersion becomes more significant with an increase in flow rates and the pore-level mass-transfer coefficient is independent of current density.

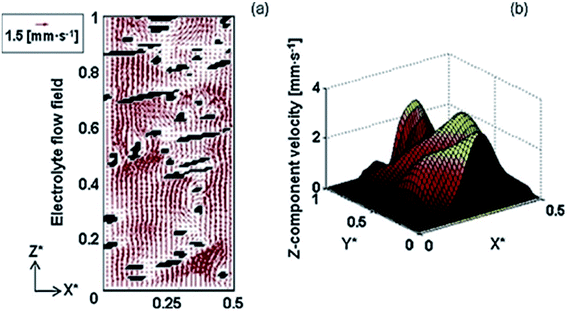Fig. 11 LBM simulation of electrolyte flow through a porous carbon-felt electrode. (a) Velocity field in the negative half-cell shown in a cross section about the mid-plane in Y. (b) Vertical component of the fluid velocity in an XY plane at the inlet. Reproduced with permission from Elsevier.²³¹

Based on the obtained structural information, 3D pore scale models have been developed to explore the effect of electrolyte flow rate, vanadium ion concentration and electrode morphology on VRFB performance. It has been found that overall cell voltage can be improved by increasing flow rate and by using denser electrode structures. In addition, an electrochemical model using the Butler–Volmer equation is employed to provide species flux boundary conditions at the surface of the carbon fibers and to deliver the necessary coupling to the local concentration of these species available in the pore space.

One caveat to using 3D imaging of carbon electrodes for electrochemical transport modelling is the large computational expense. One numerical simplification is afforded through pore network modelling (PNM), which converts 3D tomographic images into a connection of pores and throats that are approximated as spheres and cylinders, respectively (Fig. 12).^276–278 Recently, PNMs have been used to model the electrochemical transport in electrodes and determine physical characteristics, such as the pore size distribution, permeability, porosity and electroactive surface area.²⁷⁹ The robustness of PNM has afforded a platform for rapid parametric studies to determine physical insights into electrode microstructure on RFB performance.^278,280 However, further work is necessary to quantify and understand the effects of micro/nano structure on RFB electrode performance and durability.

Fig. 12 A rendering of a PNM for a hydrogen–bromine fuel cell. Reproduced with permission from ECS and IOP Science.²⁷⁸

6. Progress on the modelling of reaction and transport processes in RFB porous electrodes

6.1 Modelling for VRFB and similar aqueous-based systems

To enable numerical models to give physically meaningful results of RFB operational parameters, precise transport properties are needed, in addition to a sound formulation.²⁸¹ An important transport property is the effective diffusivity, which is necessary to model the mass transport at the representative elementary volume level of porous electrodes in the context of Darcy's law. The widely-used effective diffusivity^210,214,282 is a simple association equation with the inherent diffusivity and the material porosity using a Bruggemann correction;²¹¹ a concern with this correlation, however, is that the influence of the pore morphology of various porous structures is missed. In parallel, efforts have also been made to experimentally measure the effective diffusivity. A customary approach is to position a porous sample structure between two reservoirs, one of which contains an electrolyte solution, while the other contains de-ionised water, respectively. UV-visible spectroscopic measurements are performed to quantify the change in ion concentration of DI water over a time period. This will enable the extraction of an effective diffusivity value for the ions through the media as a function of porous structural area, thickness and overall solution volume.^283–285 A limitation of this approach is the unaccounted inhomogeneous flow distribution that exists in a functional RFB.²⁷⁵ In addition, there may be other effects not taken into consideration, such as different ionic strengths of two solutions, that may cause a concentration polarization across the porous media.²⁷⁵

Based on the theoretical context of mass transport within RFB electrodes, diagnostic experimental arrangements have been developed to establish the two, transport properties: the effective diffusivity and the pore-level mass-transport coefficient. The properties were evaluated at a range of electrolyte flow rates through a graphite felt,²⁸⁶ and the relationship for the effective diffusivity of vanadium ions through the porous electrode includes the contributions of both the porous electrode structure and flow dispersion with the influence of flow dispersion increasing with greater flow rates. The pore-level, mass-transport coefficient was found to be independent of the current density. In addition, it is worth mentioning that several modelling efforts were dedicated to addressing the effects of compression and other mechanical conditions on effective transport properties,^287–290 even via the development of coupled electrochemical–mechanical models.²⁹¹

Xu et al. developed a 2D mass-transport and electrochemical model for a VRFB that accounted for the effect of SOC-dependent electrolyte viscosity.²⁹² The model was used to explore the distributions of vanadium ions concentration, overpotential and local current density for a single VRFB cell. Compared with the outcomes from a constant-electrolyte-viscosity model, the results from this model display higher pressure drop (particularly in the positive half-cell) and sharper distributions of overpotential and local current density in the electrodes. The comparison of modelling results shows that the consideration of the SOC-dependent electrolyte viscosity allows more accurate simulations and estimations of pumping energy and system efficiency of VRFBs. A table providing a detailed summary of the governing equations and key findings of mathematical models on VRFB porous electrodes is given in the ESI (Table S2).†

Yu and Chen point out the importance of mass-transfer effects on the overpotential or crossover effects on charge/discharge efficiency and cycle life.²⁹³ As the current density increases, mass-transfer effects must be considered as depicted in the full Butler–Volmer equation (eqn (14)). However, for small current densities, mass-transfer effects do not play a significant role and can be removed from eqn (14) (Table 5), thus reducing the computational cost. The conditions in which the effects of mass transfer may be considered negligible depending on the SOC and other electrochemical parameters.

Fig. 13(a) compares the Butler–Volmer equation including the effects of mass transfer (using a mass-transfer limit [MTL] approximation) to the entire current–overpotential equation (as displayed in eqn (14)) at 50% SOC for two dissimilar flow rates as a function of the current density normalised by the limiting current density (the outcome is balanced for anodic currents so it is removed).²⁹³ The Butler–Volmer equation (without mass-transfer effects) is fairly accurate at low current densities but slowly deviates as current density rises and mass-transfer effects become significant. The point at which the two plots intersect is where the MTL approximation becomes more accurate, and at higher current the full Butler–Volmer equation is employed (eqn (14) in Table 5).²⁴¹ The overpotential curve is also displayed in the case where flow rate is increased from 1 mL s⁻¹ to 5 mL s⁻¹. Note, Fig. 13(b) is at 20% SOC and displays an enhancement in the absolute estimation error as compared to the 50% SOC case.²⁹³

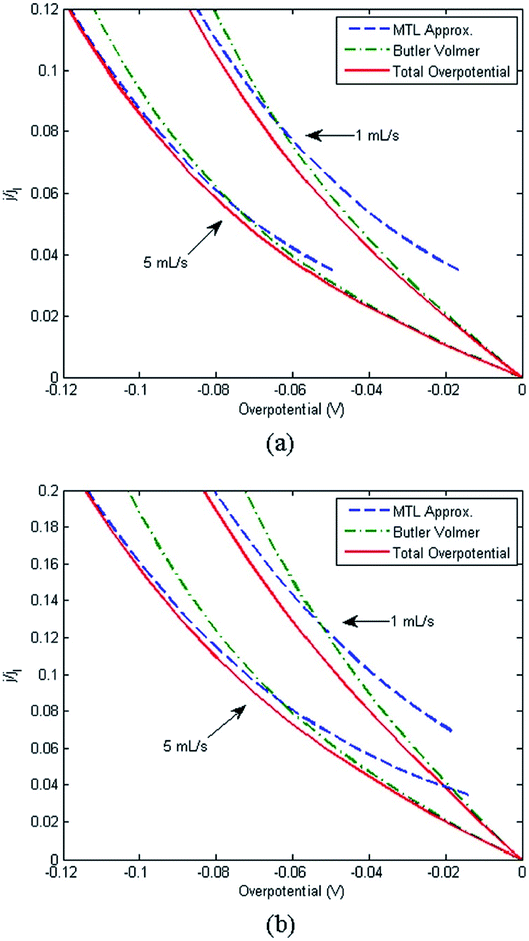Fig. 13 A comparison of the MTL approximation and Butler–Volmer equation (without mass-transfer effects) to the total overpotential (which can be estimated from eqn (14) as it accounts for both kinetic and mass-transfer effects) for flow rates of 1 mL s⁻¹ and 5 mL s⁻¹ at (a) 50% SOC and (b) 20% SOC. Reproduced with permission of the American Society for Mechanical Engineers.²⁹³

Fig. 14(a) compares the voltage output with and without the inclusion of mass-transport effects in the overpotential computation for a 40 min discharge at 600 A m⁻² with 80% original capacity.²⁹³ The divergence of ca. 0.05 V after 40 min of discharge is significant and will continue to grow as the SOC decreases. When the flow rate is increased by a factor of five (to 5 mL s⁻¹) as in Fig. 14(b), the overpotential losses reduce because of higher mass-transfer effects. In summary, the simulation results reveal that the mass transfer of active species to the porous electrode surface has a significant impact on the voltage response.^151,213,222

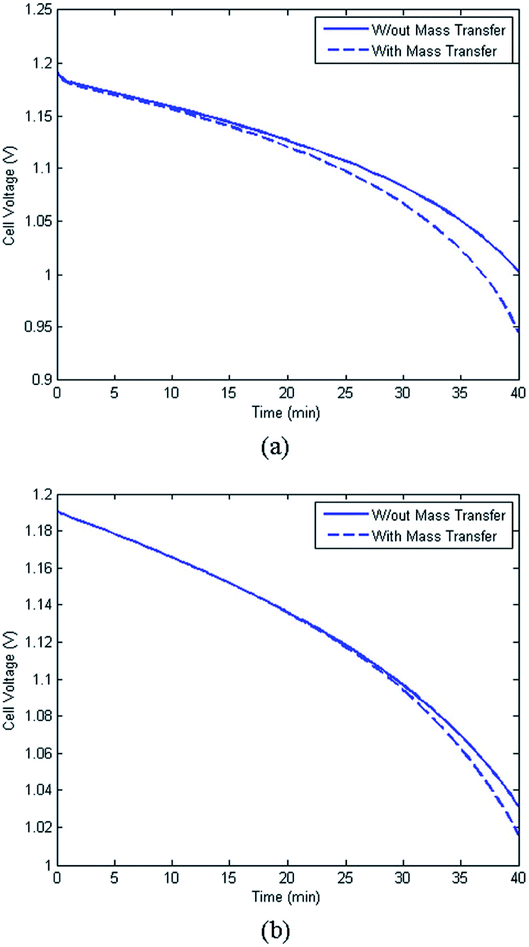Fig. 14 Discharge voltage response with and without mass-transfer effects at 750 A m⁻² current density and 80% initial SOC for flow rates of (a) 1 mL s⁻¹ and (b) 5 mL s⁻¹. Reproduced with permission from the American Society for Mechanical Engineers.²⁹³

Another simulation paper by Wang and Cho provides: (1) a 3D model outline of dynamic VRFBs; (2) a meticulous elucidation of pore-level transfer resistance and pumping power; and (3) timescale and dimensionless parameter evaluation.²³⁰ At the pore scale, the diffusion time span, which is the approximate timescale for the concentration variation due to diffusion to reach a steady-state, and Péclet number are functions of pore dimensions and are estimated to be ca. 1 s and 1000, respectively. The evaluation also shows that electrolyte pumping accounts for a small part of the VRFB power output (<0.1% for the conditions studied). The model was successfully employed for 3D simulation and was validated with experimental results of charging, idling and discharging. Local working states, such as temperature contours, ion concentration distribution, flow field and reaction rate, were also evaluated. It was found that the peak temperature occurs near the separator at first and is cooled by the electrolyte flow as well as the surface of the current collector for both charging and discharging processes. It took ca. 60 s for a steady-state temperature to be achieved. The V(V) concentration at the outlet displays a rapid alteration in the first few seconds when switching operation. Most transfer current generation was found to occur near the electrode–separator interface; the transfer current represents the local charge transfer rate and is representative of the local electrochemical reaction activity. The Damköhler (Da) number, which relates the chemical reaction and mass transport rates, shows that the macroscopic mass transport rate is higher in the transverse direction, relative to the reaction kinetics. The transfer current fluctuates slightly from upstream to downstream of the reaction zone during the early phases of charging and discharging, demonstrating the usefulness of the multi-dimensional method for fundamental analysis of RFBs.²³⁰ Future investigations to further enhance such RFB models include: (1) more accurately assessing multiphase flows, side reaction, heat-flow in electrodes, especially as they pertain to local degradation mechanisms; (2) attaining rigorous experimental data for both material selection, such as electrochemical kinetics and thorough validation (e.g., local distributions); and (3) advancing numerical methods to effectively simulate practical system operation.

A few modelling studies have evaluated the effect of mechanical compression on vanadium redox flow battery performance.^{170,173,290,291} Two dimensional models have been used to investigate the effect of changes in the porosity, permeability and ohmic resistance of the porous electrode with compression. In most cases the models have relied on experimental data for the properties of the porous electrode under compression with a notable exception of Xiong et al.,²⁹¹ who used a multiphysics approach combining mechanical, mass transport and electrochemical processes. All of these studies show that increasing compression leads to a trade-off between increased electrochemical performance (due to reduced ohmic losses) and higher pressure drop, and, consequently, an optimal compression typically exists. In addition, Wang et al.¹⁷³ modelled the effect of non-uniform compression (under the ribs and channels of a flow field) on the electrochemical performance, based on experimental observations of the electrode intrusion into the channels. Further modelling efforts are needed on the effect of compression, especially the non-uniform compression expected with complex rib/channel flow field designs, in order to enable improved flow field design, optimisation and scalability.

Finally, the application of mathematical modelling on vanadium-based microfluidic cells provides an interesting discussion on the reaction phenomena at the porous electrode and electrolyte interface.²⁹⁴ The model is dimensionless and is applied to flow-through porous carbon fiber electrodes to explore different designs.²⁹⁵ The working mechanisms of porous electrodes under different operational and geometric parameters were studied. Increasing velocity from the ‘insufficient flow’ to the ‘overflow’ regime (based on Péclet number as shown in Fig. 15(b) for laminar flow conditions) shows that the electrochemical reaction zone moves from the reactant inlet to the electrode/channel interface. In the operational region (Fig. 15(b)), the electrochemical reaction zone mainly distributes in the region close to the electrode/channel interface (Fig. 15). These reaction distribution characteristics are generally applicable for cells with microfluidic channels, which is in contrast to the situation in a flow-through VRFB modelled separately, in which the reaction was found to occur at the electrode–membrane interface.²³⁰ Accordingly, an optimised dimensional parameter for the electrode length and partially modified porous electrode can be obtained.²⁹⁵

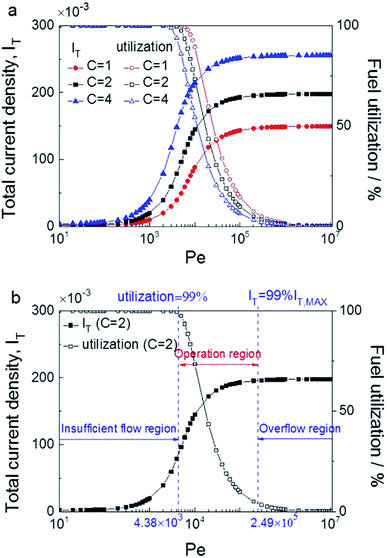Fig. 15 (a) Dependence of dimensionless total current density I_T and fuel utilization with dimensionless parameter Pe at different dimensionless concentration C and (b) three different flow regimes distinguished (V_cell = 0.6 V). Reproduced with permission from Elsevier.²⁹⁵

Most of the studies discussed above account for membrane transport phenomena in greater detail than the influence of the electrodes for VRFBs.^26,296,297 It is thus necessary for future investigations to focus on the modelling of electrode phenomena, especially considering cases where electrodes are modified with catalysts or physicochemical treatment (e.g. thermal activation) to understand why VRFB performance improves as a result of such electrode treatments.

Other RFB chemistries have been modelled with respect to mass-transfer effects in porous electrodes, which are briefly discussed below. The number of studies of modelling that focus on other RFB chemistries is much less than the number that consider VRFBs.

6.2 Modelling for non-aqueous and similar flow cell systems

In 2011, Duduta et al. demonstrated a non-aqueous, semisolid, lithium-ion RFB, a hybrid between a traditional flow battery configuration and a rechargeable Li-ion battery.¹¹⁴ The charge transfer mechanism occurs via dilute yet percolating networks of nanoscale conductors and suspended solid storage compounds. While this mechanism was originally explored by Kastening et al. in 1985 in fluidised-bed carbon-based suspensions in sulfuric acid and potassium hydroxide electrodes,²⁹⁸ such an approach did not receive much attention until the beginning of the last decade when flowable semisolid supercapacitors and flow batteries were reported.²⁹⁹ One of the main advantages of a semisolid electrode formulation is the high concentration of electroactive species (10–20 M) in suspended solid phase and system energy densities that can be achieved when compared to metal redox species in aqueous/nonaqueous solutions (<2 M concentrations and <35 W h L⁻¹).²⁹⁹

Carter et al. modelled the fluidics and the electrochemical performance for non-aqueous and aqueous semisolid RFBs using both 1D and 3D models. Their investigation revealed performance issues associated to the use of highly viscous and non-Newtonian flowable electrodes.¹¹² For example, the semi-solid configuration necessitates a low resistance interface between stationary current collector and the flowable electrode, which is only achievable via intermittent flow. In contrast, a continuous flow mode leads to battery self-discharge processes associated to charge gradients within the fluid.³⁰⁰ Moreover, other capacity degradation issues known for Li-ion intercalation chemistries such as the formation and growth of the solid electrolyte interphase (SEI), are completely linked to cell voltage variations for different SOC. Indeed, the utilization of electroactive materials presenting flat potential profiles during charge and discharge contribute to the improvement of the battery efficiency. Similar conclusions were experimentally achieved by Tarascon and co-workers.³⁰¹

Other electrochemical energy storage devices, such as zinc–nickel RFBs,^19,302 flowable supercapacitors, and Li–polysulfide hybrid chemistries, have been demonstrated in recent years.²⁹⁹ However, few efforts have been devoted to device analysis using mathematical models. In this context, an all-iron aqueous RFB was operated and modelled by Savinell and co-workers³⁰⁰ who used slurry electrodes to enable separate optimisation of the energy storage capacity and the power delivery capability. However, the negative electrode reaction would need to occur on the slurry particles at high current densities for this electrode to be effective. Thus, mathematical modelling was performed to understand the current distribution in the slurry electrode as a function of the slurry specific area and electrical conductivity. The aim was to obtain >95% plating in the slurry electrode in comparison to that on the flat plate at a high current density in excess of 200 mA cm⁻². The model helped in selecting multi-walled carbon nanotubes (MWCNTs) as the most effective slurry material. With the MWCNTs, experimental studies enabled the performance objectives to be achieved.³⁰⁰

In 2013, Grätzel proposed an alternative lithium-ion, non-aqueous RFB based on redox mediators targeting reactions at both electrodes.³⁰³ A mathematical model based on the conservation of charge and species was later developed by Sharma and co-workers.³⁰⁴ The reaction and transport processes at the anodic side were of interest, whilst mass and charge transfer at the porous electrode were assumed to be isotropic and the electrode kinetics and regeneration in the storage tank were also considered. In addition, reactions occurring at the positive electrode were assumed first-order reversible, as confirmed from cyclic voltammetry in a separate study.³⁰⁵ The model was able to capture the performance of the experimental setup with reasonable accuracy; however, the model did not include temperature effects,³⁰⁶ detailed reaction mechanisms, effects of electrode compression¹⁷¹ or shunt currents.

The effect of electrode thickness on the quinone-bromide aqueous RFB was studied in 2015.¹³⁰ Polarization experiments on several layers of carbon paper electrodes showed that cells with six to eight layers of electrode thickness gave best overall performance in terms of minimising losses. It was concluded that the variation of the electrode thickness led to a change of both the active surface area and the electrode resistance, thereby enhancing performance. Similar conclusions were obtained by Mench and co-workers for vanadium RFB with serpentine and interdigitated flow field configurations.³⁰⁷ They simulated average electrolyte velocity in the electrode domain for increasing layers of carbon paper taking into account the non-uniformity of the distribution in both the in-plane and through-plane directions. Correlations between computational and experimental results for polarization and discharge curves showed how the combination of electrolyte residence time and available electrochemical surface area contributed to alleviate mass-transport limitations regardless of the flow field design.

A specific, non-isothermal, transient model has also been reported for the quinone-bromide RFB.³⁰⁸ In this enhanced geometric model, the authors accounted for the influence of the graphite plate and channel on the cell performance. The interface between the porous carbon electrode and the flow channels were modeled by means of the Brinkman equation. Energy transport was also considered while the temporal effect on voltage and overpotential changes were discussed. At a low applied current density, the flow rate was found to have little effect on cell performance.

A 2D transient, non-isothermal, simulation model for a non-aqueous, hybrid, lithium–oxygen RFB was developed to study the heat and mass-transfer effects within the battery and validate the proposed design.³⁰⁹ Experiments employed 1 M lithium-based electrolytes in a solvent mixture of propylene carbonate (PC), ethylene carbonate (EC), 1,2-dimethoxyethane (DME), diethyl carbonate (DEC), dimethyl carbonate (DMC), γ-butyrolactone (γ-BL), tetrahydrofuran, and tetrahydropyran.³¹⁰ During operation, the electrolyte was saturated with oxygen in a tank outside of the electrochemical reactor and then pumped into the positive electrode end plate embedded with interdigitated flow channels. Simulation results showed that the convection effect significantly enhanced oxygen supply in the positive electrode and hence increased battery capacity. However, the model assumed constant positive electrode activation overpotential, and the potential distribution in the electrolyte was neglected. The mass-transport equations for lithium cations and molecular oxygen were based on dilute solution theory. The pressure, the electrolyte velocities, the oxygen concentration, the electrolyte concentration, the electrolyte potential, the electrode potential, the reaction rate, the volume fraction of the solid product and the porosity change caused by Li₂O₂ precipitation were solved in the computation domain as shown in Fig. 16.³¹¹ An improved model was proposed based upon the porous electrode method and a concentration solution theory was developed by the Newman group.^{59,113,115,117,312}

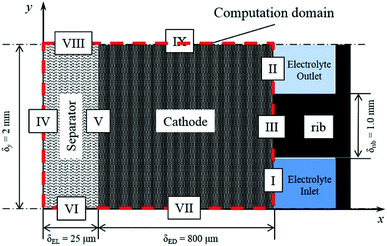Fig. 16 Computational domain of an aprotic Li–O₂ flow battery. Reproduced with permission from Elsevier.³¹¹

Compared to those for traditional RFBs, the improved model considers the effects of the insoluble discharge product deposition in the electrode.³¹¹ In contrast to conventional Li–O₂ battery models, this model includes the effect of convection in species transport. A parametric study was performed to find the influence of modelling parameters on the prediction of positive electrode specific capacity and energy. Based on the analysis of the results, two methods: (1) a dual porosity positive electrode structure, and (2) an alternating electrolytic flow method were proposed to further increase the capacity of the aprotic Li–O₂ flow battery. Efforts were made to keep the property data consistent for the same electrolyte type. The model also accounted for organic electrolyte recirculation through the positive electrode to enhance oxygen supply and also incorporated convection effects. Results showed that contrary to conventional static Li–O₂ cells, the electrolyte with a lower conductivity could increase the specific capacity of the Li–O₂ flow cell. The results also revealed that the dual layer positive electrode led to higher capacity than a single layer positive electrode at a current density of 1.5 mA cm⁻² and alternating electrolyte flow increased the cathodic capacity by 3.7% at a current density of 0.2 mA cm⁻².

In the past decade, several regenerative fuel cells using a combination of the hydrogen oxidation reaction or the oxygen reduction reaction coupled with soluble redox couples have been reported.^313–316 Some modelling studies have been performed that have been limited to vanadium–oxygen,³¹⁷ hydrogen–vanadium³¹⁸ and hydrogen–bromine³¹⁹ systems. Considering the versatility of such regenerative fuel cells, especially when employing economically sourced quinone-based couples,²⁹⁶ there is a need for increased effort in simulation of these systems.

As discussed above, aqueous RFBs have been more thoroughly investigated than non-aqueous RFBs;^{24,108,320,321} therefore, a brief summary on how non-aqueous RFBs may be harnessed for practical and commercial applications³²² follows to conclude this section.

(1) Redox molecules for non-aqueous RFB applications should be very soluble (resulting in enhanced capacity and energy density), possess highly positive or negative redox potentials in the electrolyte (causing an increased voltage, energy density, and power density), have fast kinetics (increasing voltage and power density), have stable oxidation states (increasing cycling lifetime), and be economically sourced. High-throughput density functional theory (DFT) computation, physical organic studies, and molecular engineering are effective strategies for molecular design.^323,324 Similarly, redox-active molecular melts,³²⁵ ionic liquids⁴¹ or deep eutectic solvents^61,326 are an alternative to redox molecules dissolved in aqueous or non-aqueous solvents and should possess similar properties.³²²

(2) In-depth understanding of the solution chemistry and electrochemistry of redox-active molecules^24,327 and their electrolytes are necessary^328,329 in conjunction with DFT computation for exploring the physicochemical information on redox-active molecules.^323,324,330 Furthermore, computational chemistry can play a role in predicting and mitigating the effect on the degradation of redox active molecules.^322,331

(3) Finally, the effect of ion-transport across ion-exchange membranes on the performance of non-aqueous RFBs needs further evaluation.³²²

The subsequent section discusses practical examples of system integration involving mainly aqueous RFBs, although some limited work has been demonstrated with non-aqueous RFBs.

7. System integration of redox flow batteries

The high energy storage density, quick response time, modularity and long cycle life of RFBs have sparked research interest in developing these systems for various applications, such as grid-scale load leveling/peak shaving, emergency power and renewable energy integration.³⁵ RFBs have potential integration with wind farms; for example, Turker et al.³³³ developed a model for the integration of VRFBs and a medium sized (10 MW) wind farm.³³² In this study, they used the real wind power data, synthetic wind power forecasting tools, and a VRFB software. The market structure was taken from the Spanish electricity market as they employ deviation penalties. The model demonstrated that VRFBs can be used for the compensation of deviations resulting from the forecast errors in an electricity market bidding structure. The developed model aimed to respond to the deviations between the actual wind farm output and the forecasted electricity demand by varying the battery size and level of deviation penalty. The study showed that a significant amount of power deviations could be mitigated by utilizing a 2 MW/6 MW h VRFB for the investigated 10 MW wind farm.

RFBs have also found potential integration with various other renewable energy applications. Li et al. integrated an RFB with a photocatalytic, two-step Z-scheme water splitting system for enhancing the solar energy conversion efficiency of the system.³³³ The authors experimentally showed the successful integration of these systems and achieved around 0.13% overall solar-to-fuel conversion efficiency.

Liao et al. proposed to integrate solar rechargeable flow cells (SRFCs) with RFBs.³³⁴ SRFCs are electricity generation devices which capture and store the intermittent solar energy via photoelectrochemical reactions.³³⁵ In the study reported by Liao and co-workers, they demonstrated an SRFC integrating a dual-silicon photoelectrochemical (PEC) cell into a quinone/bromine RFB for in situ solar energy conversion and storage.³³⁴

Yu et al. demonstrated the combination of PEC-conversion and energy-storage functions into one device (aqueous lithium–iodine [Li–I] solar flow battery [SFB]) for efficient utilization of solar energy.³³⁶ For this integration, they incorporated a dye-sensitised TiO₂ photoelectrode in a Li–I redox flow battery for simultaneous conversion and storage of solar energy. The photoelectrode and Li–I are linked via an I³⁻/I⁻ based positive electrolyte. In this device, iodide anions are photo electrochemically oxidised to I³⁻, thereby collecting solar energy and storing it in the chemical form. During the experiments, the device is charged at an input voltage of 2.90 V under 1 sun illumination (AM1.5 G, 100 mW cm⁻²) and discharged at an output voltage of 3.30 V (current density ca. 0.50 mA cm⁻²).³³⁶ Due to this voltage reduction during charging, this device can save up to 20% energy efficiency as compared to traditional Li–I batteries. This work showed that PEC storage using redox species led to higher levels of photon absorption and more effective charge separation, which has been seen in the development of an all vanadium photoelectrochemical storage cell as reported by Wei et al.³³⁷ In this work, a PEC energy storage was combined with a vanadium flow battery, which took advantage of the good round-trip efficiency of the aqueous vanadium redox couples (VO²⁺/VO₂⁺ and V³⁺/V²⁺). The system reported enhanced photocurrent and energy conversion efficiencies along with reduced photo corrosion of the photocatalysts. The authors experimentally demonstrated this device and achieved a faradaic efficiency of 95% and the incident photon-to-current efficiency of 12% under 350 nm light.³³⁷

In another effort, Li et al. integrated a regenerated photoelectrochemical solar cell with an organic redox flow battery.³³⁸ They used regenerative silicon solar cells and 9,10-anthra-quinone-2,7-disulfonic acid (AQDS)/1,2-benzoquinone-3,5-disulfonic acid (BQDS) RFB for this integration, highlighting how organic redox flow batteries have a relative ease with which their properties may be adjusted via target functionalization.²⁹⁶ These RFBs can also have relatively high energy density exceeding 50 W h L⁻¹ due to a high aqueous solubility (>1 M) of functionalised quinones. In this study, the authors demonstrated the direct charging of the device using solar light without external bias and the discharging of the device was similar to a typical RFB.³³⁸ They achieved solar-to-electricity efficiency of ca. 1.7% and an energy storage density of 1.15 W h L⁻¹.

Baumann and Boggasch integrated an alkaline electrolyser, PEM-fuel cell and a VRFB in a building automation system.³³⁹ The built system is constructed as a grid-connected hybrid storage with the sole purpose of self-utilization of power produced by photovoltaics. The main components of the integrated systems are the PV arrays, a wind turbine, a micro-combined heat and power system, a fuel cell, an alkaline electrolyser, a VRFB, a lead-acid battery, three programmable electronic AC loads and a charging station for electric vehicles (electric vehicle supply equipment). The demonstration of the hybrid system shows how the transient variation of the hydrogen system (electrolyser and fuel cell) and a VRFB integrated into a building automation system affects the performance of the combined system. The results show that such a type of integrated system has limitations in terms of following a load profile.³³⁹ This limitation arises mainly because of the communication amongst the energy management unit, the energy meters, and the local control units. This communication issue can delay the response to high fluctuations within a very short timescale and limits their practical use. More research is required to find possible pathways to mitigate this issue for any successful implementation of such types of system integration.

In short, a lot has been done to enhance the technical feasibility of RFBs for a range of integrated applications.³⁴⁰Fig. 17 shows an advanced RFB developed by Sumitomo and New Energy and Industrial Technology Development Organization (NEDO) being applied for system integration in San Diego.³⁴¹ As presented, the high energy efficient RFB can achieve simultaneous energy conversion and storage, which further distributes electricity to different end uses.³⁴⁰ In addition to controlling and regulating the residential energy consumption at home scales, RFBs may even be used for portable electronics with greatly improved energy density comparable with alkali-ion batteries, and the liquid-state electrodes are especially applicable for flexible devices.³⁴² Finally, RFBs can be almost instantly recharged by replacing the discharged electrolytes while simultaneously recovering the exhausted electroactive materials separately, providing beneficial flexibility for electric vehicle applications. However, further investigations on system delay responses are necessary before such benefits are fully realised at practical-scales of applications.

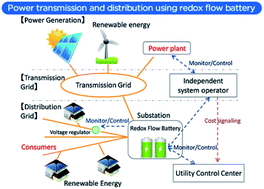Fig. 17 One of the largest RFB systems (2 MW/8 MW h) developed by Sumitomo and NEDO for systems integration in the US. Reproduced with permission from Green Car Congress, SEI.³⁴¹

8. Summary and perspective

RFB models are being developed at the cell- and fundamental-level to address the issues that are important for battery enhancement at the stack/system level, enabling optimisation, reduced cost and improved commercial viability. To attain a more accurate prediction of the battery performance, the models at the cell- and fundamental-level may be improved by including additional physical phenomena, such as water transfer and the electrode microstructure, along with rational simplifications. In addition to the optimisation of battery structure and operating conditions, the uniform distribution (electrolyte concentration, current density, overpotential, etc.) inside a device can be achieved via relevant material modification. Significant variations in local current at the flow channel length-scale suggest that RFBs could operate at much higher current (and hence power) densities if a more uniform current distribution is achieved. Accordingly, modelling work should focus on optimizing electrode structures (3D microscale) based on the objective function of current density, overpotential or electrolyte concentration. In addition, investigation into the molecular/atomic structure and nature of the vanadium electrolyte, leading on to the analogous understanding of other relevant electrolytes (both aqueous and non-aqueous) for RFBs, is of great significance for achieving a higher energy density via improving the solubility and stability of the electrolytes.

In order to simulate battery operation, multiscale models of VRFB stack/system are needed. Such combination of modelling approaches will enable the integration of phenomena occurring at the wide range of relevant lengths scales in VRFBs. Multiscale models may be derived at the cell- or fundamental-level by considering multiple cells arranged in a VRFB stack/system. In other words, such models should have the capability of connecting microscale processes to cell/stack performance and optimisation levels.

Another topic to be addressed is the roles of micropores and adsorption on RFB performance (depending on the chemistry). Many experimental studies have shown “activation” of the carbon electrode enhances performance,^272,343,344 and this is normally explained in terms of changes in the functional groups on the electrode surface. However, this activation may also generate micropores and increase the surface area, and there are few modelling studies to investigate if the micropores play a role in the enhancement of battery performance or not.

From the system integration perspective, many new configurations have been proposed and tested for the grid-scale power balancing, peak power and integration with other renewable energy technologies.^333,338 Most of these demonstrations have provided promising, initial results for such types of integrations. However, more work is needed to find the economic feasibility of these configurations. Another important area that requires more attention is the mitigation of delay in the response of these combined systems against the high fluctuations in a short duration. Any such delay in the response time decreases the reliability of these systems, thereby limiting their future implementation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has received financial support from EPSRC ISCF Wave 1: 3D electrodes from 2D materials (EP/R023034/1), EPSRC Lower Cost and Longer Life Flow Batteries for Grid Scale Energy Storage project (EP/L014289/1), EPSRC Zinc–Nickel Redox Flow Battery for Energy Storage (EP/P003494/1), Natural Sciences and Engineering Research Council of Canada (grant reference RGPIN-2018-03725), Joint Center for Energy Storage Research as an Energy Innovation Hub funded by the U.S. Department of Energy (De-AC02-06CH11357) and U.S. National Science Foundation Graduate Research Fellowship (1122374). Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation. We would also like to thank Yas Ashraf Gandomi, McLain E. Leonard, Katharine V. Greco, Alexis M. Fenton, Jr, Kara E. Rodby, Charles T. C. Wan, Lauren E. Clarke, Weiran Gao, Bertand J. Neyhouse, and Alexander H. Quinn of the Brushett lab at MIT for their constructive feedback in reviewing this work.

References

1. J. W. Tester, Energy Environ. Sci., 2011, 4, 3729–3730.
2. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
3. J. Baxter, Z. Bian, G. Chen, D. Danielson, M. S. Dresselhaus, A. G. Fedorov, T. S. Fisher, C. W. Jones, E. Maginn, U. Kortshagen, A. Manthiram, A. Nozik, D. R. Rolison, T. Sands, L. Shi, D. Sholl and Y. Wu, Energy Environ. Sci., 2009, 2, 559–588.
4. V. Brummer, Renewable Sustainable Energy Rev., 2018, 94, 187–196.
5. N. P. Brandon, J. S. Edge, M. Aunedi, P. G. Bruce, B. K. Chakrabarti, T. Esterle, J. W. Somerville, Y. L. Ding, C. Fu, P. S. Grant, P. J. Hall, C. Huang, G. H. Leng, Y. L. Li, V. L. Martins, M. E. Navarro, G. J. O. Posada, A. J. R. Rennie, D. J. Rogers and D. A. Worsley, UK research needs in grid scale energy storage technologies, Energy Storage Research Network, 2016.
6. P. Leung, X. Li, C. Ponce de León, L. Berlouis, C. T. J. Low and F. C. Walsh, RSC Adv., 2012, 2, 10125–10156.
7. P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120(14), 6490–6557.
8. Z. Ming, L. Ximei, L. Yulong and P. Lilin, Renewable Sustainable Energy Rev., 2014, 31, 23–37.
9. M. Esteban, J. Portugal-Pereira, B. C. McLellan, J. Bricker, H. Farzaneh, N. Djalilova, K. N. Ishihara, H. Takagi and V. Roeber, Appl. Energy, 2018, 224, 698–707.
10. P. G. Taylor, R. Bolton, D. Stone and P. Upham, Energy Policy, 2013, 63, 230–243.
11. M. L. Perry and A. Z. Weber, J. Electrochem. Soc., 2016, 163, A5064–A5067.
12. M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55–R79.
13. G. Strbac, M. Aunedi, D. Pudjianto, P. Djapic, F. Teng, A. Sturt, D. Jackravut, R. Sansom, V. Yufit, N. Brandon, Strategic Assessment of the Role and Value of Energy Storage Systems in the UK Low Carbon Energy Future, http://https://www.imperial.ac.uk/media/imperial-college/energy-futures-lab/research/Strategic-Assessment-of-the-Role-and-Value-of-Energy-Storage-in-the-UK.pdf, 2012, accessed December 18, 2019.
14. P. Alotto, M. Guarnieri and F. Moro, Renewable Sustainable Energy Rev., 2014, 29, 325–335.
15. C. Bae, E. P. L. Roberts, M. H. Chakrabarti and M. Saleem, Int. J. Green Energy, 2011, 8, 248–264.
16. M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli, M. Saleem and I. Mustafa, Arabian J. Sci. Eng., 2013, 38, 723–739.
17. M. H. Chakrabarti, E. P. L. Roberts, C. Bae and M. Saleem, Energy Convers. Manage., 2011, 52, 2501–2508.
18. S.-H. Shin, S.-H. Yun and S.-H. Moon, RSC Adv., 2013, 3, 9095–9116.
19. D. P. Trudgeon, K. Qiu, X. Li, T. Mallick, O. O. Taiwo, B. Chakrabarti, V. Yufit, N. P. Brandon, D. Crevillen-Garcia and A. Shah, J. Power Sources, 2019, 412, 44–54.
20. G. Nikiforidis, L. Berlouis, D. Hall and D. Hodgson, J. Power Sources, 2013, 243, 691–698.
21. M.-S. Park, N.-J. Lee, S.-W. Lee, K. J. Kim, D.-J. Oh and Y.-J. Kim, ACS Appl. Mater. Interfaces, 2014, 6, 10729–10735.
22. L. Su, R. M. Darling, K. G. Gallagher, W. Xie, J. L. Thelen, A. F. Badel, J. L. Barton, K. J. Cheng, N. P. Balsara, J. S. Moore and F. R. Brushett, J. Electrochem. Soc., 2016, 163, A5253–A5262.
23. Y.-S. Chen, S.-Y. Ho, H.-W. Chou and H.-J. Wei, J. Power Sources, 2018, 390, 168–175.
24. L. Bahadori, M. A. Hashim, N. S. A. Manan, F. S. Mjalli, I. M. AlNashef, N. P. Brandon and M. H. Chakrabarti, J. Electrochem. Soc., 2016, 163, A632–A638.
25. J. Choe, Y. Cho and G. Choe, In Standalone ESS modeling and dual-loop control using Zn–Br Redox flow battery, 2014 IEEE Energy Conversion Congress and Exposition (ECCE), 2014, pp. 5317–5322.
26. X. Li, H. Zhang, Z. Mai, H. Zhang and I. Vankelecom, Energy Environ. Sci., 2011, 4, 1147–1160.
27. P. Zhao, H. Zhang, H. Zhou, J. Chen, S. Gao and B. Yi, J. Power Sources, 2006, 162, 1416–1420.
28. P. Qian, H. Zhang, J. Chen, Y. Wen, Q. Luo, Z. Liu, D. You and B. Yi, J. Power Sources, 2008, 175, 613–620.
29. C. Sun, J. Chen, H. Zhang, X. Han and Q. Luo, J. Power Sources, 2010, 195, 890–897.
30. M. Skyllas-Kazacos, G. Kazacos, G. Poon and H. Verseema, Int. J. Energy Res., 2010, 34, 182–189.
31. Z. Mai, H. Zhang, X. Li, C. Bi and H. Dai, J. Power Sources, 2011, 196, 482–487.
32. M. Vijayakumar, M. S. Bhuvaneswari, P. Nachimuthu, B. Schwenzer, S. Kim, Z. Yang, J. Liu, G. L. Graff, S. Thevuthasan and J. Hu, J. Membr. Sci., 2011, 366, 325–334.
33. L. X. Wu Xiong-Wei, H. Ke-Long, Z.-P. Ding, Z.-C. Jiang, L. Su-Qin and L. Xiao-Gang, Acta Chim. Sin., 2011, 69, 1858–1864.
34. D. S. Aaron, Q. Liu, Z. Tang, G. M. Grim, A. B. Papandrew, A. Turhan, T. A. Zawodzinski and M. M. Mench, J. Power Sources, 2012, 206, 450–453.
35. R. M. C. M. Moore, J. S. Watson, T. A. Zawodzinski and H. Kamath, Chem. Eng. Educ., 2012, 46, 239–250.
36. Q. Liu, A. Turhan, T. A. Zawodzinski and M. M. Mench, Chem. Commun., 2013, 49, 6292–6294.
37. C.-N. Sun, F. M. Delnick, D. S. Aaron, A. B. Papandrew, M. M. Mench and T. A. Zawodzinski, J. Electrochem. Soc., 2014, 161, A981–A988.
38. M. Skyllas-Kazacos, J. Power Sources, 2003, 124, 299–302.
39. A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137.
40. G. Kear, A. A. Shah and F. C. Walsh, Int. J. Energy Res., 2012, 36, 1105–1120.
41. M. H. Chakrabarti, F. S. Mjalli, I. M. AlNashef, M. A. Hashim, M. A. Hussain, L. Bahadori and C. T. J. Low, Renewable Sustainable Energy Rev., 2014, 30, 254–270.
42. M. H. Chakrabarti, N. P. Brandon, S. A. Hajimolana, F. Tariq, V. Yufit, M. A. Hashim, M. A. Hussain, C. T. J. Low and P. V. Aravind, J. Power Sources, 2014, 253, 150–166.
43. M. Vijayakumar, L. Li, G. Graff, J. Liu, H. Zhang, Z. Yang and J. Z. Hu, J. Power Sources, 2011, 196, 3669–3672.
44. P. Han, Y. Yue, Z. Liu, W. Xu, L. Zhang, H. Xu, S. Dong and G. Cui, Energy Environ. Sci., 2011, 4, 4710–4717.
45. J. E. Halls, A. Hawthornthwaite, R. J. Hepworth, N. A. Roberts, K. J. Wright, Y. Zhou, S. J. Haswell, S. K. Haywood, S. M. Kelly, N. S. Lawrence and J. D. Wadhawan, Energy Environ. Sci., 2013, 6, 1026–1041.
46. H. Zhang, H. Zhang, F. Zhang, X. Li, Y. Li and I. Vankelecom, Energy Environ. Sci., 2013, 6, 776–781.
47. S. Gu, K. Gong, E. Z. Yan and Y. Yan, Energy Environ. Sci., 2014, 7, 2986–2998.
48. H. A.-F. A. A.-K. Omran and F. K. Matlub, Int. J. Adv. Res. Technol., 2015, 7, 1630–1641.
49. Q. Zheng, X. Li, Y. Cheng, G. Ning, F. Xing and H. Zhang, Appl. Energy, 2014, 132, 254–266.
50. X. Ke, J. I. D. Alexander, J. M. Prahl and R. F. Savinell, J. Power Sources, 2014, 270, 646–657.
51. D. You, H. Zhang, C. Sun and X. Ma, J. Power Sources, 2011, 196, 1578–1585.
52. A. Tang, J. Bao and M. Skyllas-Kazacos, J. Power Sources, 2012, 216, 489–501.
53. M. N. Nandanwar and S. Kumar, J. Electrochem. Soc., 2014, 161, A1602–A1610.
54. C.-H. Tian, R. Chein, K.-L. Hsueh, C.-H. Wu and F.-H. Tsau, Rare Met., 2011, 30, 16–21.
55. P. V. Danckwerts, Chem. Eng. Sci., 1953, 2, 1–13.
56. H. M. Hulburt, Ind. Eng. Chem., 1944, 36, 1012–1017.
57. J. F. Wehner and R. H. Wilhelm, Chem. Eng. Sci., 1956, 6, 89–93.
58. J. A. Trainham and J. Newman, J. Electrochem. Soc., 1978, 125, 58–68.
59. J. A. Trainham and J. Newman, Electrochim. Acta, 1981, 26, 455–469.
60. A. Parasuraman, T. M. Lim, C. Menictas and M. Skyllas-Kazacos, Electrochim. Acta, 2013, 101, 27–40.
61. M. H. Chakrabarti, N. P. Brandon, M. A. Hashim, F. S. Mjalli, I. M. AlNashef, L. Bahadori, N. Abdul Manan, M. Hussain and V. Yufit, Int. J. Electrochem. Sci., 2013, 8, 9652–9676.
62. H. Prifti, A. Parasuraman, S. Winardi, T. M. Lim and M. Skyllas-Kazacos, Membranes, 2012, 2, 275–306.
63. M. H. Chakrabarti, R. A. W. Dryfe and E. P. L. Roberts, Electrochim. Acta, 2007, 52, 2189–2195.
64. M. H. Chakrabarti, E. P. Lindfield Roberts and M. Saleem, Int. J. Green Energy, 2010, 7, 445–460.
65. P. S. Fedkiw and R. W. Watts, J. Electrochem. Soc., 1984, 131, 701–709.
66. M. J. Mader and R. E. White, J. Electrochem. Soc., 1986, 133, 1297–1307.
67. J. Lee and J. R. Selman, J. Electrochem. Soc., 1982, 129, 1670–1678.
68. J. Lee and J. R. Selman, J. Electrochem. Soc., 1983, 130, 1237–1242.
69. T. I. Evans and R. E. White, J. Electrochem. Soc., 1987, 134, 866–874.
70. T. I. Evans and R. E. White, J. Electrochem. Soc., 1987, 134, 2725–2733.
71. J. W. Diggle, A. R. Despic and J. O. M. Bockris, J. Electrochem. Soc., 1969, 116, 1503–1514.
72. G. D. Simpson and R. E. White, J. Electrochem. Soc., 1990, 137, 1843–1846.
73. G. D. Simpson and R. E. White, J. Electrochem. Soc., 1989, 136, 2137–2144.
74. Z. Xu, J. Wang, S. C. Yan, Q. Fan and P. D. Lund, J. Power Sources, 2020, 450, 227436.
75. Y. K. Zeng, T. S. Zhao, L. An, X. L. Zhou and L. Wei, J. Power Sources, 2015, 300, 438–443.
76. Q. Xu and T. S. Zhao, Prog. Energy Combust. Sci., 2015, 49, 40–58.
77. G. Codina and A. Aldaz, J. Appl. Electrochem., 1992, 22, 668–674.
78. R. D. McKerracher, C. Ponce de Leon, R. G. A. Wills, A. A. Shah and F. C. Walsh, ChemPlusChem, 2015, 80, 323–335.
79. J. Escudero González, A. Alberola and P. Amparo López Jiménez, Eng. Appl. Comput. Fluid Mech., 2013, 7, 168–181.
80. N. Xu, X. Li, X. Zhao, J. B. Goodenough and K. Huang, Energy Environ. Sci., 2011, 4, 4942–4946.
81. X. Jin, X. Zhao and K. Huang, J. Power Sources, 2015, 280, 195–204.
82. X. Zhao, N. Xu, X. Li, Y. Gong and K. Huang, RSC Adv., 2012, 2, 10163–10166.
83. X. Zhao, N. Xu, X. Li, Y. Gong and K. Huang, ECS Trans., 2013, 50, 115–123.
84. X. Zhao, X. Li, Y. Gong, N. Xu, K. Romito and K. Huang, Chem. Commun., 2013, 49, 5357–5359.
85. X. Zhao, X. Li, Y. Gong and K. Huang, Chem. Commun., 2014, 50, 623–625.
86. X. Zhao, Y. Gong, X. Li, N. Xu and K. Huang, J. Electrochem. Soc., 2013, 160, A1716–A1719.
87. X. Zhao, Y. Gong, X. Li, N. Xu and K. Huang, J. Electrochem. Soc., 2013, 160, A1241–A1247.
88. H. Zhou, H. Zhang, P. Zhao and B. Yi, Electrochim. Acta, 2006, 51, 6304–6312.
89. R. E. White and S. E. Lorimer, J. Electrochem. Soc., 1983, 130, 1096–1103.
90. D. P. Scamman, G. W. Reade and E. P. L. Roberts, J. Power Sources, 2009, 189, 1220–1230.
91. D. P. Scamman, G. W. Reade and E. P. L. Roberts, J. Power Sources, 2009, 189, 1231–1239.
92. M. N. Nandanwar, K. S. Kumar, S. S. Srinivas and D. M. Dinesh, J. Power Sources, 2020, 454, 227918.
93. J. Collins, G. Kear, X. Li, C. T. J. Low, D. Pletcher, R. Tangirala, D. Stratton-Campbell, F. C. Walsh and C. Zhang, J. Power Sources, 2010, 195, 1731–1738.
94. X. Li, D. Pletcher and F. C. Walsh, Electrochim. Acta, 2009, 54, 4688–4695.
95. A. A. Shah, X. Li, R. G. A. Wills and F. C. Walsh, J. Electrochem. Soc., 2010, 157, A589–A599.
96. A. Bates, S. Mukerjee, S. C. Lee, D.-H. Lee and S. Park, J. Power Sources, 2014, 249, 207–218.
97. A. Oury, A. Kirchev and Y. Bultel, J. Power Sources, 2014, 246, 703–718.
98. M. Nandanwar and S. Kumar, Chem. Eng. Sci., 2016, 154, 61–71.
99. A. Oury, A. Kirchev, Y. Bultel and E. Chainet, Electrochim. Acta, 2012, 71, 140–149.
100. X. You, Q. Ye, T. Van Nguyen and P. Cheng, J. Electrochem. Soc., 2016, 163, A447–A457.
101. R. Zhang and J. W. Weidner, J. Appl. Electrochem., 2011, 41, 1245–1252.
102. K. Oh, A. Z. Weber and H. Ju, Int. J. Hydrogen Energy, 2017, 42, 3753–3766.
103. K. Oh, T. J. Kang, S. Park, M. C. Tucker, A. Z. Weber and H. Ju, Electrochim. Acta, 2017, 230, 160–173.
104. W. Wang, S. Kim, B. Chen, Z. Nie, J. Zhang, G.-G. Xia, L. Li and Z. Yang, Energy Environ. Sci., 2011, 4, 4068–4073.
105. W. Wang, Z. Nie, B. Chen, F. Chen, Q. Luo, X. Wei, G.-G. Xia, M. Skyllas-Kazacos, L. Li and Z. Yang, Adv. Energy Mater., 2012, 2, 487–493.
106. D. Stephenson, S. Kim, F. Chen, E. Thomsen, V. Viswanathan, W. Wang and V. Sprenkle, J. Electrochem. Soc., 2012, 159, A1993–A2000.
107. M. Lopez-Atalaya, G. Codina, J. R. Perez, J. L. Vazquez and A. Aldaz, J. Power Sources, 1992, 39, 147–154.
108. L. Bahadori, M. H. Chakrabarti, M. A. Hashim, N. S. A. Manan, F. S. Mjalli, I. M. AlNashef and N. P. Brandon, J. Electrochem. Soc., 2015, 162, H617–H624.
109. M. H. Chakrabarti, N. S. A. Manan, N. P. Brandon, R. C. Maher, F. S. Mjalli, I. M. AlNashef, S. A. Hajimolana, M. A. Hashim, M. A. Hussain and D. Nir, Chem. Eng. J., 2015, 274, 213–223.
110. Q. Xu, L. Y. Qin, Y. N. Ji, P. K. Leung, H. N. Su, F. Qiao, W. W. Yang, A. A. Shah and H. M. Li, Electrochim. Acta, 2019, 293, 426–431.
111. Q. Ma, L. Zhao, J. Xu, H. Su, W. Zhang, W. Yang and Q. Xu, Electrochim. Acta, 2020, 353, 136486.
112. V. E. Brunini, Y.-M. Chiang and W. C. Carter, Electrochim. Acta, 2012, 69, 301–307.
113. M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533.
114. M. Duduta, B. Ho, V. C. Wood, P. Limthongkul, V. E. Brunini, W. C. Carter and Y.-M. Chiang, Adv. Energy Mater., 2011, 1, 511–516.
115. M. Doyle, J. Newman, A. S. Gozdz, C. N. Schmutz and J. M. Tarascon, J. Electrochem. Soc., 1996, 143, 1890–1903.
116. M. Doyle and Y. Fuentes, J. Electrochem. Soc., 2003, 150, A706–A713.
117. J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41.
118. Q. Zhang, Q. Guo and R. E. White, J. Power Sources, 2007, 165, 427–435.
119. S. Gentil, D. Reynard and H. H. Girault, Curr. Opin. Electrochem., 2020, 21, 7–13.
120. Q. Wang, S. M. Zakeeruddin, D. Wang, I. Exnar and M. Grätzel, Angew. Chem., Int. Ed., 2006, 45, 8197–8200.
121. Y. G. Zhu, Q. Liu, Y. Rong, H. Chen, J. Yang, C. Jia, L.-J. Yu, A. Karton, Y. Ren, X. Xu, S. Adams and Q. Wang, Nat. Commun., 2017, 8, 14308.
122. Q. Huang, J. Yang, C. B. Ng, C. Jia and Q. Wang, Energy Environ. Sci., 2016, 9, 917–921.
123. C. Jia, F. Pan, Y. G. Zhu, Q. Huang, L. Lu and Q. Wang, Sci. Adv., 2015, 1, e1500886.
124. Y. Chen, M. Zhou, Y. Xia, X. Wang, Y. Liu, Y. Yao, H. Zhang, Y. Li, S. Lu, W. Qin, X. Wu and Q. Wang, Joule, 2019, 3, 2255–2267.
125. Y. Cheng, X. Wang, S. Huang, W. Samarakoon, S. Xi, Y. Ji, H. Zhang, F. Zhang, Y. Du, Z. Feng, S. Adams and Q. Wang, ACS Energy Lett., 2019, 4, 3028–3035.
126. Y. Xu, S. Zheng, H. Tang, X. Guo, H. Xue and H. Pang, Energy Storage Mater., 2017, 9, 11–30.
127. E. Zanzola, C. R. Dennison, A. Battistel, P. Peljo, H. Vrubel, V. Amstutz and H. H. Girault, Electrochim. Acta, 2017, 235, 664–671.
128. S. Gentil, N. Lalaoui, A. Dutta, Y. Nedellec, S. Cosnier, W. J. Shaw, V. Artero and A. Le Goff, Angew. Chem., Int. Ed., 2017, 56, 1845–1849.
129. S. Gentil, S. M. Che Mansor, H. Jamet, S. Cosnier, C. Cavazza and A. Le Goff, ACS Catal., 2018, 8, 3957–3964.
130. X. Li, Electrochim. Acta, 2015, 170, 98–109.
131. W. Bingying, Z. Buhan, M. Biao and Z. Jiajun, presented in part at the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), 6–9 July 2011.
132. Y. Li, M. Wong, W. Ip, P. Zhao, C. Wong, J. Cheng and Z. You, 2014 9th IEEE Conference on Industrial Electronics and Applications, 2014, pp. 1621–1626,  DOI:10.1109/ICIEA.2014.6931427.
133. K. T. Cho, P. Albertus, V. Battaglia, A. Kojic, V. Srinivasan and A. Z. Weber, Energy Technol., 2013, 1, 596–608.
134. E. Kjeang, R. Michel, D. A. Harrington, N. Djilali and D. Sinton, J. Am. Chem. Soc., 2008, 130, 4000–4006.
135. Q. Zheng, F. Xing, X. Li, T. Liu, Q. Lai, G. Ning and H. Zhang, J. Power Sources, 2014, 266, 145–149.
136. Q. H. Liu, G. M. Grim, A. B. Papandrew, A. Turhan, T. A. Zawodzinski and M. M. Mench, J. Electrochem. Soc., 2012, 159, A1246–A1252.
137. Q. Chen, M. R. Gerhardt, L. Hartle and M. J. Aziz, J. Electrochem. Soc., 2016, 163, A5010–A5013.
138. Q. Chen, L. Eisenach and M. J. Aziz, J. Electrochem. Soc., 2016, 163, A5057–A5063.
139. M. R. Gerhardt, E. S. Beh, L. Tong, R. G. Gordon and M. J. Aziz, MRS Adv., 2017, 2, 431–438.
140. V. Esfahanian, H. M. Darian, H. Babazadeh, M. Aghvami, R. Pasandeh, F. Torabi and G. Ahmadi, J. Power Sources, 2009, 191, 139–143.
141. X. Ma, H. Zhang and F. Xing, Electrochim. Acta, 2011, 58, 238–246.
142. M. Secanell, J. Wishart and P. Dobson, J. Power Sources, 2011, 196, 3690–3704.
143. X. L. Zhou, Y. K. Zeng, X. B. Zhu, L. Wei and T. S. Zhao, J. Power Sources, 2016, 325, 329–336.
144. M. Miyabayashi, K. Sato, T. Tayama, Y. Kageyama and H. Oyama, US Pat. US5851694A, 1998.
145. P. A. L.-J. Juan Escudero-González, J. Power Sources, 2014, 251, 243–253.
146. C. Bengoa, A. Montillet, P. Legentilhomme and J. Legrand, J. Appl. Electrochem., 1997, 27, 1313–1322.
147. A. A. Wragg and A. A. Leontaritis, Chem. Eng. J., 1997, 66, 1–10.
148. J. Q. Chen, B. G. Wang and H. L. Lv, Adv. Mater. Res., 2011, 236–238, 604–607.
149. J. Q. Chen, B. G. Wang and J. E. Yang, Solvent Extr. Ion Exch., 2009, 27, 312–327.
150. J. Escudero-González and P. Amparo López-Jiménez, Eng. Appl. Comput. Fluid Mech., 2014, 8, 435–446.
151. M. Li and T. Hikihara, IEICE Trans. Fund. Electron. Comm Comput. Sci., 2008, E91-A, 1741–1747.
152. C. Jia, J. Liu and C. Yan, J. Power Sources, 2010, 195, 4380–4383.
153. J. Collins, X. Li, D. Pletcher, R. Tangirala, D. Stratton-Campbell, F. C. Walsh and C. Zhang, J. Power Sources, 2010, 195, 2975–2978.
154. M. Lopez-Atalaya, G. Codina, J. R. Perez, J. L. Vazquez, A. Aldaz and M. A. Climent, J. Power Sources, 1991, 35, 225–234.
155. G. Aparicio-Mauricio, F. A. Rodríguez, J. J. H. Pijpers, M. R. Cruz-Díaz and E. P. Rivero, J. Energy Storage, 2020, 29, 101337.
156. T. Jyothi Latha and S. Jayanti, J. Appl. Electrochem., 2014, 44, 995–1006.
157. Q. Zheng, F. Xing, X. Li, G. Ning and H. Zhang, J. Power Sources, 2016, 324, 402–411.
158. Q. Zheng, F. Xing, X. Li, T. Liu, Q. Lai, G. Ning and H. Zhang, J. Power Sources, 2015, 277, 104–109.
159. J. Houser, A. Pezeshki, J. T. Clement, D. Aaron and M. M. Mench, J. Power Sources, 2017, 351, 96–105.
160. D. Aaron, Z. Tang, A. B. Papandrew and T. A. Zawodzinski, J. Appl. Electrochem., 2011, 41, 1175–1182.
161. C. Bae, H. Chakrabarti and E. Roberts, J. Appl. Electrochem., 2008, 38, 637–644.
162. B. Xiong, J. Zhao, K. J. Tseng, M. Skyllas-Kazacos, T. M. Lim and Y. Zhang, J. Power Sources, 2013, 242, 314–324.
163. R. J. Kee, P. Korada, K. Walters and M. Pavol, J. Power Sources, 2002, 109, 148–159.
164. K. B. S. Prasad and S. Jayanti, J. Power Sources, 2008, 180, 227–231.
165. P. V. Suresh, S. Jayanti, A. P. Deshpande and P. Haridoss, Int. J. Hydrogen Energy, 2011, 36, 6067–6072.
166. Q. Xu, T. S. Zhao and P. K. Leung, Appl. Energy, 2013, 105, 47–56.
167. T. Jyothi Latha and S. Jayanti, J. Power Sources, 2014, 248, 140–146.
168. I. Nitta, T. Hottinen, O. Himanen and M. Mikkola, J. Power Sources, 2007, 171, 26–36.
169. N. Kulkarni, M. D. R. Kok, R. Jervis, F. Iacoviello, Q. Meyer, P. R. Shearing and D. J. L. Brett, J. Power Sources, 2019, 426, 97–110.
170. J. P. James, H. W. Choi and J. G. Pharoah, Int. J. Hydrogen Energy, 2012, 37, 18216–18230.
171. K. Bromberger, J. Kaunert and T. Smolinka, Energy Technol., 2014, 2, 64–76.
172. J. Millichamp, T. J. Mason, T. P. Neville, N. Rajalakshmi, R. Jervis, P. R. Shearing and D. J. L. Brett, J. Power Sources, 2015, 284, 305–320.
173. Q. Wang, Z. G. Qu, Z. Y. Jiang and W. W. Yang, Appl. Energy, 2018, 220, 106–116.
174. T.-C. Chang, J.-P. Zhang and Y.-K. Fuh, J. Power Sources, 2014, 245, 66–75.
175. M. A. M. Harper, Electrochemical Battery Incorporating Internal Manifolds, US Pat., US7687193B2, 2017.
176. S. Tsushima, S. Sasaki and S. Hirai, ECS Meeting Abstracts, 2013, MA2013-02, 1664.
177. E. Kjeang, B. T. Proctor, A. G. Brolo, D. A. Harrington, N. Djilali and D. Sinton, Electrochim. Acta, 2007, 52, 4942–4946.
178. N. Guo, M. C. Leu and U. O. Koylu, Int. J. Hydrogen Energy, 2014, 39, 21185–21195.
179. R. Behrou, A. Pizzolato and A. Forner-Cuenca, Int. J. Heat Mass Transfer, 2019, 135, 72–92.
180. K. Yaji, S. Yamasaki, S. Tsushima, T. Suzuki and K. Fujita, Struct. Multidiscip. Optim., 2018, 57, 535–546.
181. K. M. Lisboa and R. M. Cotta, Appl. Math. Model., 2020, 77, 1512–1530.
182. B. W. Zhang, Y. Lei, B. F. Bai and T. S. Zhao, Int. J. Heat Mass Transfer, 2019, 135, 460–469.
183. K. B. Shyam Prasad, P. V. Suresh and S. Jayanti, Int. J. Hydrogen Energy, 2009, 34, 8289–8301.
184. S.-S. Hsieh, S.-H. Yang, J.-K. Kuo, C.-F. Huang and H.-H. Tsai, Energy Convers. Manage., 2006, 47, 1868–1878.
185. X. Li and I. Sabir, Int. J. Hydrogen Energy, 2005, 30, 359–371.
186. A. Tang, J. Bao and M. Skyllas-Kazacos, J. Power Sources, 2014, 248, 154–162.
187. S. König, M. R. Suriyah and T. Leibfried, J. Power Sources, 2016, 333, 134–144.
188. T. Wang, J. Fu, M. Zheng and Z. Yu, Appl. Energy, 2018, 227, 613–623.
189. D. K. Kim, S. J. Yoon, J. Lee and S. Kim, Appl. Energy, 2018, 228, 891–901.
190. R. J. Kee and H. Zhu, J. Power Sources, 2015, 299, 509–518.
191. M. A. Hoberecht, Pumping power considerations in the designs of NASA-Redox flow cells, https://ntrs.nasa.gov/search.jsp?R=19810019981.
192. M. Inoue and M. Kobayashi, US Pat. US5648184A, 1995.
193. S.-Q. Zhu, J.-Q. Chen, Q. Wang and B.-G. Wang, Battery Bimon., 2008, 5.
194. B. J. Koeppel, K. P. Recknagle, D. E. Stephenson, D. Reed, E. Thomsen and V. Sprenkle, ECS Meeting Abstracts, 2013, MA2013-02, 1660.
195. M. R. Gerhardt, A. A. Wong and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A2625–A2643.
196. Q. Ma, X.-X. Zeng, C. Zhou, Q. Deng, P.-F. Wang, T.-T. Zuo, X.-D. Zhang, Y.-X. Yin, X. Wu, L.-Y. Chai and Y.-G. Guo, ACS Appl. Mater. Interfaces, 2018, 10, 22381–22388.
197. D. Aaron, C.-N. Sun, M. Bright, A. B. Papandrew, M. M. Mench and T. A. Zawodzinski, ECS Electrochem. Lett., 2013, 2, A29–A31.
198. I. M. Bayanov and R. Vanhaelst, J. Math. Chem., 2011, 49, 2013–2031.
199. M. Pugach, S. Parsegov, E. Gryazina and A. Bischi, J. Power Sources, 2020, 455, 227916.
200. M. Pugach, M. Kondratenko, S. Briola and A. Bischi, Appl. Energy, 2018, 226, 560–569.
201. B. Xiong, J. Zhao and J. Li, presented in part at the 2013 IEEE Power & Energy Society General Meeting, 21–25 July 2013.
202. G. Merei, S. Adler, D. Magnor, M. Leuthold and D. U. Sauer, Energy Procedia, 2014, 46, 194–203.
203. Z. Chen, M. Ding and J. Su, presented in part at the 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), 6–9 July 2011.
204. Q. Ze-jing, Chin. J. Power Sources, 2012, 11, 25.
205. B. Xu, L. Qi, K. Yao and X. Xie, Chem. Ind. Eng. Prog., 2013, 32, 313–314.
206. X. Ma, H. Zhang, F. Xing and C. Sun, Chin. J. Power Sources, 2012, 36, 1647–1650.
207. S. Abu-Sharkh and D. Doerffel, J. Power Sources, 2004, 130, 266–274.
208. D. W. Dees, V. S. Battaglia and A. Bélanger, J. Power Sources, 2002, 110, 310–320.
209. M. R. Mohamed, H. Ahmad, M. N. A. Seman, S. Razali and M. S. Najib, J. Power Sources, 2013, 239, 284–293.
210. A. A. Shah, M. J. Watt-Smith and F. C. Walsh, Electrochim. Acta, 2008, 53, 8087–8100.
211. M. Vynnycky, Energy, 2011, 36, 2242–2256.
212. H. Al-Fetlawi, A. A. Shah and F. C. Walsh, Electrochim. Acta, 2009, 55, 78–89.
213. A. A. Shah, R. Tangirala, R. Singh, R. G. A. Wills and F. C. Walsh, J. Electrochem. Soc., 2011, 158, A671–A677.
214. D. You, H. Zhang and J. Chen, Electrochim. Acta, 2009, 54, 6827–6836.
215. H. Al-Fetlawi, A. A. Shah and F. C. Walsh, Electrochim. Acta, 2010, 55, 3192–3205.
216. A. A. Shah, H. Al-Fetlawi and F. C. Walsh, Electrochim. Acta, 2010, 55, 1125–1139.
217. Y. Y. Choi, S. Kim, S. Kim and J.-I. Choi, J. Power Sources, 2020, 450, 227684.
218. B. W. Zhang, Y. Lei, B. F. Bai, A. Xu and T. S. Zhao, Appl. Therm. Eng., 2019, 151, 495–505.
219. S. Rudolph, U. Schröder, R. I. Bayanov, K. Blenke and I. M. Bayanov, J. Electroanal. Chem., 2015, 736, 117–126.
220. K. W. Knehr and E. C. Kumbur, Electrochem. Commun., 2011, 13, 342–345.
221. C. L. Chen, H. K. Yeoh and M. H. Chakrabarti, Electrochim. Acta, 2014, 120, 167–179.
222. A. Tang, J. Bao and M. Skyllas-Kazacos, J. Power Sources, 2011, 196, 10737–10747.
223. M. Skyllas-Kazacos and L. Goh, J. Membr. Sci., 2012, 399–400, 43–48.
224. A. Tang, S. Ting, J. Bao and M. Skyllas-Kazacos, J. Power Sources, 2012, 203, 165–176.
225. A. Tang, J. McCann, J. Bao and M. Skyllas-Kazacos, J. Power Sources, 2013, 242, 349–356.
226. K. Schafner, M. Becker and T. Turek, J. Appl. Electrochem., 2018, 48, 639–649.
227. M. Lu, W. Yang, Y. Deng and Q. Xu, Int. J. Energy Res., 2020, 44, 2604–2616.
228. K. W. Knehr, E. Agar, C. R. Dennison, A. R. Kalidindi and E. C. Kumbur, J. Electrochem. Soc., 2012, 159, A1446–A1459.
229. D. You, H. Zhang and J. Chen, J. Electroanal. Chem., 2009, 625, 165–171.
230. Y. Wang and S. C. Cho, J. Electrochem. Soc., 2014, 161, A1200–A1212.
231. G. Qiu, A. S. Joshi, C. R. Dennison, K. W. Knehr, E. C. Kumbur and Y. Sun, Electrochim. Acta, 2012, 64, 46–64.
232. G. Qiu, C. R. Dennison, K. W. Knehr, E. C. Kumbur and Y. Sun, J. Power Sources, 2012, 219, 223–234.
233. E. Engebretsen, J. B. Robinson, O. Obeisun, T. Mason, D. Finegan, G. Hinds, P. R. Shearing and D. J. L. Brett, J. Power Sources, 2016, 302, 210–214.
234. Q. Meyer, S. Ashton, S. Torija, C. Gurney, P. Boillat, M. Cochet, E. Engebretsen, D. P. Finegan, P. Adcock, P. R. Shearing and D. J. L. Brett, Electrochim. Acta, 2016, 203, 198–205.
235. Y. A. Gandomi, D. S. Aaron, T. A. Zawodzinski and M. M. Mench, J. Electrochem. Soc., 2016, 163, A5188–A5201.
236. J. T. Clement, D. S. Aaron and M. M. Mench, J. Electrochem. Soc., 2016, 163, A5220–A5228.
237. W. Lai and F. Ciucci, Electrochim. Acta, 2011, 56, 4369–4377.
238. W. E. S. R. Byron Bird and E. N. Lightfoot, Transport Phenomena, John Wiley & Sons, Revised 2nd edn, 2007.
239. R. Krishna and J. A. Wesselingh, Chem. Eng. Sci., 1997, 52, 861–911.
240. A. Frumkin, Z. Phys. Chem., 1933, 164, 121–133.
241. L. R. F. A. J. Bard, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001.
242. P. M. Biesheuvel, Y. Fu and M. Z. Bazant, Phys. Rev. E, 2011, 83, 061507.
243. P. M. Biesheuvel, Y. Fu and M. Z. Bazant, Russ. J. Electrochem., 2012, 48, 580–592.
244. C. C. Chueh, A. Bertei, J. G. Pharoah and C. Nicolella, Int. J. Heat Mass Transfer, 2014, 71, 183–188.
245. M. M. Tomadakis and T. J. Robertson, J. Compos. Mater., 2005, 39, 163–188.
246. M. Avellaneda and S. Torquato, Phys. Fluids A, 1991, 3, 2529–2540.
247. S. Torquato, Appl. Mech. Rev., 1991, 44, 37–76.
248. K. J. Kim, M.-S. Park, Y.-J. Kim, J. H. Kim, S. X. Dou and M. Skyllas-Kazacos, J. Mater. Chem. A, 2015, 3, 16913–16933.
249. D. Schmal, J. Van Erkel and P. J. Van Duin, J. Appl. Electrochem., 1986, 16, 422–430.
250. M. Quintard, M. Kaviany and S. Whitaker, Adv. Water Resour., 1997, 20, 77–94.
251. L. D. Brown, T. P. Neville, R. Jervis, T. J. Mason, P. R. Shearing and D. J. L. Brett, J. Energy Storage, 2016, 8, 91–98.
252. B. Tjaden, D. J. L. Brett and P. R. Shearing, Int. Mater. Rev., 2018, 63, 47–67.
253. F. Tariq, J. Rubio-Garcia, V. Yufit, A. Bertei, B. K. Chakrabarti, A. Kucernak and N. Brandon, Sustainable Energy Fuels, 2018, 2, 2068–2080.
254. M. D. Uchic, L. Holzer, B. J. Inkson, E. L. Principe and P. Munroe, MRS Bull., 2007, 32, 408–416.
255. R. Jervis, L. D. Brown, T. P. Neville, J. Millichamp, D. P. Finegan, T. M. M. Heenan, D. J. L. Brett and P. R. Shearing, J. Phys. D: Appl. Phys., 2016, 49, 434002.
256. J. R. Izzo, A. S. Joshi, K. N. Grew, W. K. S. Chiu, A. Tkachuk, S. H. Wang and W. Yun, J. Electrochem. Soc., 2008, 155, B504–B508.
257. P. R. Shearing, J. Golbert, R. J. Chater and N. P. Brandon, Chem. Eng. Sci., 2009, 64, 3928–3933.
258. J. R. Wilson, W. Kobsiriphat, R. Mendoza, H.-Y. Chen, J. M. Hiller, D. J. Miller, K. Thornton, P. W. Voorhees, S. B. Adler and S. A. Barnett, Nat. Mater., 2006, 5, 541–544.
259. V. Yufit, P. Shearing, R. W. Hamilton, P. D. Lee, M. Wu and N. P. Brandon, Electrochem. Commun., 2011, 13, 608–610.
260. F. Tariq, R. Haswell, P. D. Lee and D. W. McComb, Acta Mater., 2011, 59, 2109–2120.
261. O. Coindreau, G. Vignoles and P. Cloetens, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 200, 308–314.
262. F. Tariq, V. Yufit, M. Kishimoto, P. R. Shearing, S. Menkin, D. Golodnitsky, J. Gelb, E. Peled and N. P. Brandon, J. Power Sources, 2014, 248, 1014–1020.
263. M. Biton, V. Yufit, F. Tariq, M. Kishimoto and N. Brandon, J. Electrochem. Soc., 2017, 164, A6032–A6038.
264. F. Cosmi, A. Bernasconi and N. Sodini, Compos. Sci. Technol., 2011, 71, 23–30.
265. T. J. Mason, J. Millichamp, T. P. Neville, A. El-kharouf, B. G. Pollet and D. J. L. Brett, J. Power Sources, 2012, 219, 52–59.
266. D. J. L. Brett and N. P. Brandon, J. Fuel Cell Sci. Technol., 2006, 4, 29–44.
267. M. Weyland and P. A. Midgley, Mater. Today, 2004, 7, 32–40.
268. K. Yamauchi, K. Takahashi, H. Hasegawa, H. Iatrou, N. Hadjichristidis, T. Kaneko, Y. Nishikawa, H. Jinnai, T. Matsui, H. Nishioka, M. Shimizu and H. Furukawa, Macromolecules, 2003, 36, 6962–6966.
269. N. Yoshizawa, O. Tanaike, H. Hatori, K. Yoshikawa, A. Kondo and T. Abe, Carbon, 2006, 44, 2558–2564.
270. I. V. Thorat, D. E. Stephenson, N. A. Zacharias, K. Zaghib, J. N. Harb and D. R. Wheeler, J. Power Sources, 2009, 188, 592–600.
271. B. Chakrabarti, D. Nir, V. Yufit, F. Tariq, J. Rubio-Garcia, R. Maher, A. Kucernak, P. V. Aravind and N. Brandon, ChemElectroChem, 2017, 4, 194–200.
272. B. Chakrabarti, V. Yufit, A. Kavei, Y. Xia, G. Stevenson, E. Kalamaras, H. Luo, J. Feng, F. Tariq, O. Taiwo, M.-M. Titirici and N. Brandon, Int. J. Hydrogen Energy, 2019, 44, 30093–30107.
273. M. D. R. Kok, R. Jervis, T. G. Tranter, M. A. Sadeghi, D. J. L. Brett, P. R. Shearing and J. T. Gostick, Chem. Eng. Sci., 2019, 196, 104–115.
274. P. Trogadas, O. O. Taiwo, B. Tjaden, T. P. Neville, S. Yun, J. Parrondo, V. Ramani, M.-O. Coppens, D. J. L. Brett and P. R. Shearing, Electrochem. Commun., 2014, 48, 155–159.
275. Q. Xu and T. S. Zhao, Phys. Chem. Chem. Phys., 2013, 15, 10841–10848.
276. Y. Mehmani and H. A. Tchelepi, Adv. Water Resour., 2017, 108, 83–98.
277. Q. Xiong, T. G. Baychev and A. P. Jivkov, J. Contam. Hydrol., 2016, 192, 101–117.
278. M. A. Sadeghi, M. Aganou, M. Kok, M. Aghighi, G. Merle, J. Barralet and J. Gostick, J. Electrochem. Soc., 2019, 166, A2121–A2130.
279. A. Gayon Lombardo, B. A. Simon, O. Taiwo, S. J. Neethling and N. P. Brandon, J. Energy Storage, 2019, 24, 100736.
280. Q. Ma, Q. Xu, Q. Chen, Z. Chen, H. Su and W. Zhang, Appl. Therm. Eng., 2019, 160, 114015.
281. L. F. Arenas, C. Ponce de León and F. C. Walsh, Curr. Opin. Electrochem., 2019, 16, 117–126.
282. M. W. Verbrugge and R. F. Hill, J. Electrochem. Soc., 1990, 137, 886–893.
283. X. Luo, Z. Lu, J. Xi, Z. Wu, W. Zhu, L. Chen and X. Qiu, J. Phys. Chem. B, 2005, 109, 20310–20314.
284. J. Qiu, M. Li, J. Ni, M. Zhai, J. Peng, L. Xu, H. Zhou, J. Li and G. Wei, J. Membr. Sci., 2007, 297, 174–180.
285. C. Jia, J. Liu and C. Yan, J. Power Sources, 2012, 203, 190–194.
286. W. Lu, X. Li and H. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 23–35.
287. R. Banerjee, N. Bevilacqua, A. Mohseninia, B. Wiedemann, F. Wilhelm, J. Scholta and R. Zeis, J. Energy Storage, 2019, 26, 100997.
288. N. Bevilacqua, L. Eifert, R. Banerjee, K. Köble, T. Faragó, M. Zuber, A. Bazylak and R. Zeis, J. Power Sources, 2019, 439, 227071.
289. R. Jervis, M. D. R. Kok, T. P. Neville, Q. Meyer, L. D. Brown, F. Iacoviello, J. T. Gostick, D. J. L. Brett and P. R. Shearing, J. Energy Chem., 2018, 27, 1353–1361.
290. K. Oh, S. Won and H. Ju, Electrochim. Acta, 2015, 181, 13–23.
291. J. Xiong, Y. Song, S. Wang, X. Li, J. Liu, C. Yan and A. Tang, J. Power Sources, 2019, 431, 170–181.
292. Q. Xu, T. S. Zhao and C. Zhang, Appl. Energy, 2014, 130, 139–147.
293. V. Yu and D. Chen, J. Sol. Energy Eng., 2013, 136, 021005.
294. L. Li, G. Nikiforidis, M. K. H. Leung and W. A. Daoud, Appl. Energy, 2016, 177, 729–739.
295. L. Li, K. Zheng, M. Ni, M. K. H. Leung and J. Xuan, Energy, 2015, 88, 563–571.
296. S. Yun, J. Parrondo and V. Ramani, J. Mater. Chem. A, 2014, 2, 6605–6615.
297. M.-s. J. Jung, J. Parrondo, C. G. Arges and V. Ramani, J. Mater. Chem. A, 2013, 1, 10458–10464.
298. B. Kastening, W. Schiel and M. Henschel, J. Electroanal. Chem. Interfacial Electrochem., 1985, 191, 311–328.
299. K. B. Hatzell, M. Boota and Y. Gogotsi, Chem. Soc. Rev., 2015, 44, 8664–8687.
300. T. J. Petek, N. C. Hoyt, R. F. Savinell and J. S. Wainright, J. Power Sources, 2015, 294, 620–626.
301. S. Hamelet, D. Larcher, L. Dupont and J. M. Tarascon, J. Electrochem. Soc., 2013, 160, A516–A520.
302. S. Li, K. Li, E. Xiao, R. Xiong, J. Zhang and P. Fischer, J. Power Sources, 2020, 445, 227282.
303. Q. Huang, H. Li, M. Grätzel and Q. Wang, Phys. Chem. Chem. Phys., 2013, 15, 1793–1797.
304. A. K. Sharma, E. Birgersson, F. Pan and Q. Wang, Electrochim. Acta, 2016, 204, 1–8.
305. F. Pan, J. Yang, Q. Huang, X. Wang, H. Huang and Q. Wang, Adv. Energy Mater., 2014, 4, 1400567.
306. K. Oh, H. Yoo, J. Ko, S. Won and H. Ju, Energy, 2015, 81, 3–14.
307. J. Houser, J. Clement, A. Pezeshki and M. M. Mench, J. Power Sources, 2016, 302, 369–377.
308. D. Chu, X. Li and S. Zhang, Electrochim. Acta, 2016, 190, 434–445.
309. X. Li, J. Huang and A. Faghri, Energy, 2015, 81, 489–500.
310. J. Read, J. Electrochem. Soc., 2002, 149, A1190–A1195.
311. J. Huang and A. Faghri, Electrochim. Acta, 2015, 174, 908–918.
312. J. Newman, K. E. Thomas, H. Hafezi and D. R. Wheeler, J. Power Sources, 2003, 119–121, 838–843.
313. Z. Li, M. S. Pan, L. Su, P.-C. Tsai, A. F. Badel, J. M. Valle, S. L. Eiler, K. Xiang, F. R. Brushett and Y.-M. Chiang, Joule, 2017, 1, 306–327.
314. V. Yufit, F. Tariq, D. S. Eastwood, M. Biton, B. Wu, P. D. Lee and N. P. Brandon, Joule, 2019, 3, 485–502.
315. H. Hewa Dewage, B. Wu, A. Tsoi, V. Yufit, G. Offer and N. Brandon, J. Mater. Chem. A, 2015, 3, 9446–9450.
316. M. C. Tucker, K. T. Cho, A. Z. Weber, G. Lin and T. Van Nguyen, J. Appl. Electrochem., 2015, 45, 11–19.
317. C. L. Chen, H. K. Yeoh and M. H. Chakrabarti, ECS Trans., 2015, 66, 1–23.
318. C. A. Pino-Muñoz, B. K. Chakrabarti, V. Yufit and N. P. Brandon, J. Electrochem. Soc., 2019, 166, A3511–A3524.
319. W. A. Braff, M. Z. Bazant and C. R. Buie, Nat. Commun., 2013, 4, 2346.
320. F. R. Brushett, M. J. Aziz and K. E. Rodby, ACS Energy Lett., 2020, 5, 879–884.
321. D. G. Kwabi, Y. Ji and M. J. Aziz, Chem. Rev., 2020, 120(14), 6467–6489.
322. J. Luo, B. Hu, M. Hu, Y. Zhao and T. L. Liu, ACS Energy Lett., 2019, 4, 2220–2240.
323. S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Chem. Sci., 2015, 6, 885–893.
324. J. Rubio-Garcia, A. Kucernak, A. Parra-Puerto, R. Liu and B. Chakrabarti, J. Mater. Chem. A, 2020, 8, 3933–3941.
325. G. Kwon, S. Lee, J. Hwang, H.-S. Shim, B. Lee, M. H. Lee, Y. Ko, S.-K. Jung, K. Ku, J. Hong and K. Kang, Joule, 2018, 2, 1771–1782.
326. M. H. Chakrabarti, N. P. Brandon, F. S. Mjalli, L. Bahadori, I. M. Al Nashef, M. A. Hashim, M. A. Hussain, C. T. J. Low and V. Yufit, J. Solution Chem., 2013, 42, 2329–2341.
327. L. Bahadori, M. H. Chakrabarti, N. S. A. Manan, M. A. Hashim, F. S. Mjalli, I. M. AlNashef and N. Brandon, PLoS One, 2015, 10, e0144235.
328. P. Leung, D. Aili, Q. Xu, A. Rodchanarowan and A. A. Shah, Sustainable Energy Fuels, 2018, 2, 2252–2259.
329. M.-A. Goulet and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A1466–A1477.
330. S. D. Pineda Flores, G. C. Martin-Noble, R. L. Phillips and J. Schrier, J. Phys. Chem. C, 2015, 119, 21800–21809.
331. X. Wei, W. Pan, W. Duan, A. Hollas, Z. Yang, B. Li, Z. Nie, J. Liu, D. Reed, W. Wang and V. Sprenkle, ACS Energy Lett., 2017, 2, 2187–2204.
332. B. Turker, S. Arroyo Klein, L. Komsiyska, J. J. Trujillo, L. von Bremen, M. Kühn and M. Busse, Energy Convers. Manage., 2013, 76, 1150–1157.
333. Z. Li, W. Wang, S. Liao, M. Liu, Y. Qi, C. Ding and C. Li, Energy Environ. Sci., 2019, 12, 631–639.
334. S. Liao, X. Zong, B. Seger, T. Pedersen, T. Yao, C. Ding, J. Shi, J. Chen and C. Li, Nat. Commun., 2016, 7, 11474.
335. L. Fan, C. Jia, Y. G. Zhu and Q. Wang, ACS Energy Lett., 2017, 2, 615–621.
336. M. Yu, W. D. McCulloch, D. R. Beauchamp, Z. Huang, X. Ren and Y. Wu, J. Am. Chem. Soc., 2015, 137, 8332–8335.
337. Z. Wei, D. Liu, C. Hsu and F. Liu, Electrochem. Commun., 2014, 45, 79–82.
338. W. Li, H.-C. Fu, L. Li, M. Cabán-Acevedo, J.-H. He and S. Jin, Angew. Chem., Int. Ed., 2016, 55, 13104–13108.
339. L. Baumann and E. Boggasch, Int. J. Hydrogen Energy, 2016, 41, 740–751.
340. Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Chem, 2019, 5, 1964–1987.
341. Green Car Congress, https://www.greencarcongress.com/2017/03/20170317-sei.html, accessed July 2020.
342. T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767.
343. C. Flox, M. Skoumal, J. Rubio-Garcia, T. Andreu and J. R. Morante, Appl. Energy, 2013, 109, 344–351.
344. C. Flox, C. Fàbrega, T. Andreu, A. Morata, M. Skoumal, J. Rubio-Garcia and J. R. Morante, RSC Adv., 2013, 3, 12056–12059.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0se00667j

‡ In chemical engineering and reactor engineering, space velocity, refers to the quotient of the entering volumetric flow rate of the reactants divided by the reactor volume or the catalyst bed volume, which indicates how many reactor volumes of feed can be treated in a unit time.

---