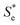Open Access Article
Open Access ArticleA fundamental study of the thermoelectrochemistry of ferricyanide/ferrocyanide: cation, concentration, ratio, and heterogeneous and homogeneous electrocatalysis effects in thermogalvanic cells†
Mark A.
Buckingham‡
 a,
Samer
Hammoud‡
a,
Huanxin
Li
ab,
Conor J.
Beale
a,
Jason T.
Sengel
a and
Leigh
Aldous
a,
Samer
Hammoud‡
a,
Huanxin
Li
ab,
Conor J.
Beale
a,
Jason T.
Sengel
a and
Leigh
Aldous
 *a
*a
aDepartment of Chemistry, Britannia House, King's College London, London, SE1 1DB, UK. E-mail: leigh.aldous@kcl.ac.uk
bState Key Laboratory for Chemo/Biosensing and Chemometrics, College of Chemistry and Chemical Engineering, Hunan University, Changsha, Hunan 410082, China
First published on 18th May 2020
Abstract
Thermogalvanic cells typically utilise equimolar concentrations of the oxidised and reduced states of a redox couple in solution, sandwiched between two electrodes at dissimilar temperatures; entropy drives redox processes to occur at these electrodes, generating a potential difference and a current. However, significant gaps still exist in fundamental data and understanding of these ‘thermocells’. In this study, thermocells based upon potassium ferricyanide, K3[Fe(CN)6], and potassium ferrocyanide, K4[Fe(CN)6], were investigated. The ratio of the oxidised and reduced states were systematically varied, and this had a significant effect upon the power produced; notably maximum power did not correspond to the equimolar ratio. A concentration study using equimolar ratios was also performed. Trends in the potential generated as a function of temperature (or ‘Seebeck coefficient’) were rationalised by the Nernst equation and Debye–Hückel theory. The trends in the current and the electrical power produced were successfully modelled using the Butler–Volmer equation. The effects of heterogeneous electrocatalysis were also explored (using platinum and two types of graphite) as well as homogeneous electrocatalysis, by the direct addition of alkali metal salts (as lithium, sodium, potassium, rubidium and caesium chlorides and sulphates). Clear trends were observed, and homogeneous and heterogeneous electrocatalysis had an additive effect when combined. Addition of CsCl was able to boost the maximum power output by upto ca. 80%, via both an increased Seebeck coefficient (through altered solvation) and through increased current (via homogeneous electrocatalysis of electron transfer). Finally, a limited economic comparison was performed, which highlights how the use of non-stoichiometric ratios of the redox couple could improve the cost-per-power value of the systems.
1. Introduction
There is currently extensive interest in thermoelectrochemistry, or temperature-dependent electrochemistry.1 A primary application of this is for thermogalvanic processes;2–5 here two electrodes at dissimilar temperatures sharing a common redox active electrolyte can convert the temperature gradient directly into electrical current.2,6 This comes about due to the temperature dependence of the electrode potential, which is directly related to the entropy difference, as expressed in eqn (1);7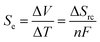 | (1) |
Several thermogalvanic cells (or ‘thermocells’) have been reported, using a range of organic solvents,11 ionic liquids,12 aqueous electrolytes7,13 or their mixtures.12 Numerous redox couples have been investigated, including metal-based iron,7,13 cobalt,11 copper14,15 and lithium systems,16,17 and a wide variety of other systems including, but not limited to, ferrocene/ferrocenium18,19 and I−/I3−.19–21 However, arguably the most extensively reported thermogalvanic system is aqueous [Fe(CN)6]3−/4−, or the ferricyanide/ferrocyanide redox couple.6,13 This system has a relatively high Se of ca. −1.4 mV K−1,6 typically exhibiting fast, reversible electrode kinetics (as a pseudo-outer sphere redox couple),22,23 and its potassium salts are relatively stable, soluble and commercially available.
The redox entropy of the [Fe(CN)6]3−/4− redox couple has been reported to have an equivalent Seebeck of −1.8 mV K−1, at low ionic strength values (<0.2 M).24 However, typically the [Fe(CN)6]3−/4−-based thermogalvanic cells are formed by dissolving 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6] in water, since this is near the solubility limits of the mixed system in water. At this higher ionic strength (3.2 M), a lower Se value of ca. −1.4 mV K−1 is expected.6 Higher concentrations have been reported, either where the cations are substituted for another cation such as [NH4]+ (up to 0.45 M of each redox state),25 or for specialised high-temperature cells (up to 0.8 M of each redox state).26 Typically the reduced and oxidised species are dissolved at matching concentrations, for obvious reasons; only one non-stoichiometric example for the thermoelectrochemistry of [Fe(CN)6]3−/4− was found in the literature (employing 0.85 M K3[Fe(CN)6] and 0.13 M K4[Fe(CN)6]) but the impact of using non-stoichiometric ratios was not discussed.27
Extensive work has explored the effect of altering the electrode, using the 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6] system in water as a ‘standard system’. Many of these systems have focussed upon modified carbon electrodes, mainly utilising carbon nanotubes,25,28–32 where changes in the geometry and surface area are likely dominant. Others have used planar electrodes, including platinum,6,33 stainless steel,13 gold34 and a range of carbon materials25,35 such as carbon nanotubes,36,37 reduced graphene oxide (rGO)38 and carbon aerogels.29 This has been observed to have significant electrocatalytic effects, with for example platinum-sputtered stainless steel generating orders of magnitude higher power than that of bare stainless steel.33,39 Poisoning effects also need to be considered, e.g. a short term electrocatalytic effect was observed by introducing gold nanoparticles upon a carbon electrode, but over longer times this resulted in lower power output due to [Fe(CN)6]3−/4−-induced corrosion of the gold nanoparticles.34 Stainless steel electrodes can have their electrocatalytic performance with respect to [Fe(CN)6]3−/4−-based thermogalvanic cells enhanced by acid treatment, or decreased by extended exposure to the [Fe(CN)6]3−/4−.39
Others have explored [Fe(CN)6]3−/4−-based thermogalvanic cells mixing water with organic solvents (such as methanol), and observed changes in the Se associated with altered solvation spheres around the two redox states; early reports indicated it significantly increased the Se,40 whereas subsequent comprehensive work has demonstrated the opposite.41 This was expanded by using 24 M urea and 2.6 M guanidine chloride as additives to 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6] in water, to also improve the Se to −4.2 mV K−1.42 Recently, the effect upon the ΔSrc of the [Fe(CN)6]3−/4− redox couple of a large excess of electrolyte has also been investigated.43 It was observed that ‘structure breaking ions’ such as Cs+ were found to increase the entropy change in the system, whereas ‘structure-making ions’ such as Li+ were found to decrease the entropy change in the system.43 Gelled aqueous electrolytes have also been investigated for [Fe(CN)6]3−/4−-based thermogalvanic cells, using cellulose,44 sodium polyacrylate,39 poly(vinyl alcohol)45 and agar agar39 as gelling systems.
As such, the addition of alkali metal cations to [Fe(CN)6]3−/4−-based systems can alter entropy changes in the system,43 but this has not been explored in thermogalvanic cells. Additionally, no fundamental investigation has explored the effect of using non-stoichiometric ratios of the redox couple in thermogalvanic cells. Limited fundamental electrocatalytic work has also been performed. As such, here we report an in-depth study of the [Fe(CN)6]3−/4− redox system in a thermoelectrochemical context, where the effect of [Fe(CN)6]3−/4− concentration, the concentration ratio of [Fe(CN)6]3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe(CN)6]4− ions and altering the counter-cation have been investigated with respect to the Seebeck coefficient, current density and power density in thermogalvanic cells. Significant trends were observed in the Se and power output upon altering the ratio; this was rationalised and modelled based upon a combination of Nernstian and Butler–Volmer behaviour. Ultimately, a non-stoichiometric ratio (0.15 M K3[Fe(CN)6] + 0.25 M K4[Fe(CN)6]) displayed slightly higher power output than the stoichiometric ratio (0.20 M K3[Fe(CN)6] + 0.20 M K4[Fe(CN)6]). The effect of added alkali metal cations was also capable of boosting the thermogalvanic cells power output, representing a means of ‘homogeneous electrocatalysis’. This was compared with conventional ‘heterogeneous electrocatalysis’ by varying the electrode material. Finally, a preliminary cost comparison of the [Fe(CN)6]3−/4− thermocell demonstrated that although ‘homogeneous electrocatalysis’ using caesium chloride afforded the most powerful thermogalvanic cell, it was 7-fold higher on a cost of electrolyte-per-power output basis. Non-stoichiometric cells were in fact found to be the most economically favourable systems, demonstrating how a ‘less is more’ approach can be effective in thermogalvanic cells.
[Fe(CN)6]4− ions and altering the counter-cation have been investigated with respect to the Seebeck coefficient, current density and power density in thermogalvanic cells. Significant trends were observed in the Se and power output upon altering the ratio; this was rationalised and modelled based upon a combination of Nernstian and Butler–Volmer behaviour. Ultimately, a non-stoichiometric ratio (0.15 M K3[Fe(CN)6] + 0.25 M K4[Fe(CN)6]) displayed slightly higher power output than the stoichiometric ratio (0.20 M K3[Fe(CN)6] + 0.20 M K4[Fe(CN)6]). The effect of added alkali metal cations was also capable of boosting the thermogalvanic cells power output, representing a means of ‘homogeneous electrocatalysis’. This was compared with conventional ‘heterogeneous electrocatalysis’ by varying the electrode material. Finally, a preliminary cost comparison of the [Fe(CN)6]3−/4− thermocell demonstrated that although ‘homogeneous electrocatalysis’ using caesium chloride afforded the most powerful thermogalvanic cell, it was 7-fold higher on a cost of electrolyte-per-power output basis. Non-stoichiometric cells were in fact found to be the most economically favourable systems, demonstrating how a ‘less is more’ approach can be effective in thermogalvanic cells.
2. Experimental
2.1. Chemicals
All reagents were purchased from UK suppliers and were used as received, unless otherwise specified. These were potassium ferrocyanide (K4[Fe(CN)6], potassium hexacyanoferrate(II) trihydrate, ≥99.5%, Sigma Aldrich), potassium ferricyanide (K3[Fe(CN)6], potassium hexacyanoferrate(III), ≥99.0%, Sigma Aldrich), lithium chloride (Fluorochem), lithium sulphate (99%+, Acros Organics), sodium chloride (≥99.5%, Sigma Aldrich), sodium sulphate (≥99.0%, Sigma Aldrich), potassium chloride (≥99.0%, Sigma Aldrich), potassium sulphate (≥99.0%, Sigma Aldrich), rubidium chloride (Fluorochem), rubidium sulphate (99.8%, Sigma Aldrich), caesium chloride (Fluorochem) and caesium sulphate (99%, Alfa Aesar). All water used was ultra-purified, with a resistivity of 18.2 MΩ cm.2.2. Thermoelectrochemical setup
One thermoelectrochemistry set-up was employed, employing two different thermoelectrochemical cells. Broadly, all electrodes were placed in thermal contact with copper-based CPU cooling blocks (purchased from eBay.co.uk). These CPU copper heat exchangers had their temperature controlled by flowing water from two TX150-R2 heated/refrigerated thermostatic circulator baths (Grant Instruments Ltd, UK), to within <0.1 °C accuracy.Two distinct cells were employed, as described below. During measurements the cell and electrodes were arranged horizontally, and vertically with respect to gravity.14
Throughout this study, a temperature difference (ΔT) of 20 °C was applied. This was achieved with ‘hot’ and ‘cold’ temperatures, Thot and Tcold, of 35.0 °C and 15.0 °C, respectively. However, careful analysis revealed that although a ΔT of 20 °C was applied via the water, the electrodes experienced a ΔT value of ca. 18 °C. The lab was ca. 24 °C, and much of the temperature gradient was lost at the cold electrode, such that Tcold was actually ca. 17 °C. All reported Se values have been corrected to reflect this.
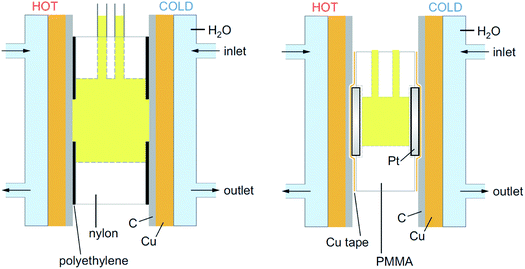
All graphite electrode measurements were performed using a thermoelectrochemical cell (shown in Fig. 1) that consisted of a nylon 6,6 cylinder with an outer diameter of 18 mm, an inner diameter of 8 mm and a length of 8 mm (RS Components Ltd, UK). This was placed between two graphite electrodes, which were held in contact with the copper heat exchangers via silicone heat transfer compound (Pro-Power, RS Components Ltd, UK). The contact area between the solution and the electrode was fixed by covering the graphite with an adhesive polyethylene label (P12/64 R MWPE, Label Planet, UK) into which a 6 mm diameter hole had been punched; this gave a consistent geometric electrode surface area of 28 mm2, with an inter-electrode spacing of 8 mm.
2.3. Thermogalvanic concentration and ratio study of K3[Fe(CN)6] and K4[Fe(CN)6]
These thermogalvanic measurements were performed using the graphite thermoelectrochemical cell mentioned above, using the amorphous graphite electrodes. The concentration study used a series of concentrations comprising equimolar amounts of both K3[Fe(CN)6] and K4[Fe(CN)6] in water, using 0.05 M, 0.1 M, 0.15 M, 0.2 M or 0.25 M of each. The latter solution was essentially super-saturated; all were prepared freshly prior to measurement.The ratio study used a series of concentrations with different ratios of K3[Fe(CN)6] and K4[Fe(CN)6] in water, where the sum of the concentrations of K3[Fe(CN)6] and K4[Fe(CN)6] always added up to 0.4 M. Therefore solutions were prepared which contained K3[Fe(CN)6] at concentrations of 0 M, 0.025 M, 0.05 M, 0.1 M, 0.15 M, 0.2 M, 0.25 M, 0.3 M, 0.35 M, 0.375 M and 0.4 M, with the concentration of K4[Fe(CN)6] in the system following the reverse order.
2.4. Alkali metal cation effect upon the thermoelectrochemical properties of [Fe(CN)6]3−/4−
Studies were performed with added alkali metal salts. The Seebeck coefficients were initially determined in the platinum thermoelectrochemical cell mentioned above, using 5 mM K3[Fe(CN)6] and 5 mM K4[Fe(CN)6] and either 0.4 M X2SO4 or 1 M XCl, where X represents either the Li, Na, K, Rb or Cs salt. The ratio of X+ to K+ for X2SO4 and XCl was 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 29
1 and 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. The power density measurements were determined using the platinum cell, using 25 mM K3[Fe(CN)6] and 25 mM K4[Fe(CN)6] in the presence of 1.5 M XCl, where X represents either the Li, K or Cs salt. The ratio of X+ to K+ for these power measurements was 9
1, respectively. The power density measurements were determined using the platinum cell, using 25 mM K3[Fe(CN)6] and 25 mM K4[Fe(CN)6] in the presence of 1.5 M XCl, where X represents either the Li, K or Cs salt. The ratio of X+ to K+ for these power measurements was 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Finally, 200 mM K3[Fe(CN)6] and 200 mM K4[Fe(CN)6] were studied in both the graphite and the platinum cells, in the presence and absence of 0.7 M CsCl; here the ratio of Cs+ to K+ was 1
1. Finally, 200 mM K3[Fe(CN)6] and 200 mM K4[Fe(CN)6] were studied in both the graphite and the platinum cells, in the presence and absence of 0.7 M CsCl; here the ratio of Cs+ to K+ was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
2.5. Cyclic voltammetric study of alkali metal cation effect upon [Fe(CN)6]3−/4−
Cyclic voltammetric experiments were carried out using a PGSTAT204 potentiostat and NOVA 2.0 software (Metrohm Autolab, the Netherlands). The three-electrode experimental setup was a 1.6 mm diameter Pt disc electrode, a Pt wire counter electrode and an Ag/AgCl (3 M NaCl) reference electrode (all BASi, USA). All data was recorded at a scan rate of 50 mV s−1. All solutions contained 5 mM K3[Fe(CN)6] and 5 mM K4[Fe(CN)6], with 0.4 M X2SO4 as supporting electrolyte, where X represents either Li, Na, K, Rb or Cs salt. The ratio of X+ to K+ was 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
3. Results and discussion
3.1. Fundamental aspects of the thermogalvanic cell: concentration and ratio effects
Here, an amorphous graphite electrode-based thermogalvanic cell was utilised, and the concentration of K3[Fe(CN)6] and K4[Fe(CN)6] were varied from a total concentration of 0.1 M (0.05 M of each) to 0.5 M (0.25 M of each). Fig. 2 displays the effect of altering concentration upon the (a) Se, (b) jsc and (c) Pmax. The expected trends were observed, i.e. jsc and Pmax increased in an essentially linear manner with concentration, and the Seebeck coefficient decreased with increasing concentration; the latter observation is rationalised in terms of increasing ionic strength, and discussed further below. The relatively large uncertainties in the 0.25 M samples correspond to these solutions being essentially super-saturated, resulting in limited stability and relatively variable performance.
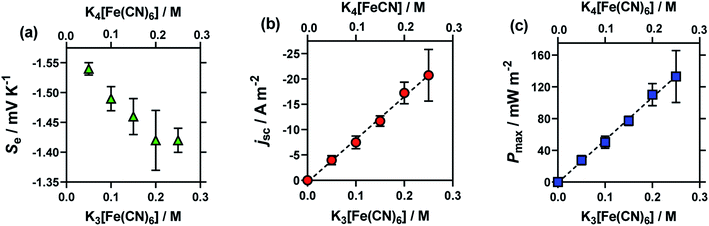 | ||
| Fig. 2 Plots (a)–(c) showing the effect of the total concentration of equimolar K3[Fe(CN)6]|K4[Fe(CN)6] upon (a) the Se coefficient (green triangles), (b) the jsc (orange circles) and (c) the Pmax (blue square) of the thermocell. Obtained using the graphite thermocell using amorphous graphite electrodes, with applied ΔT = 18 °C (Tcold = 17 °C; Thot = 35 °C), where error bars represent 1 SD from triplicate measurements. All values shown in these figures and other figures are tabulated in the ESI.† | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) K4[Fe(CN)6] ratio upon the thermogalvanic cell.
To the best of our knowledge, a systematic study of the effect of the ratio of K3[Fe(CN)6] to K4[Fe(CN)6] in a thermogalvanic cell has not been reported. Overwhelmingly, studies simply use them in an equimolar ratio. Ikeshoji investigated 0.85 M K3[Fe(CN)6] and 0.13 M K4[Fe(CN)6] (a ratio of 6.5
K4[Fe(CN)6] ratio upon the thermogalvanic cell.
To the best of our knowledge, a systematic study of the effect of the ratio of K3[Fe(CN)6] to K4[Fe(CN)6] in a thermogalvanic cell has not been reported. Overwhelmingly, studies simply use them in an equimolar ratio. Ikeshoji investigated 0.85 M K3[Fe(CN)6] and 0.13 M K4[Fe(CN)6] (a ratio of 6.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), likely on account of the significantly higher solubility of the former, but the effect of using a non-stoichiometric ratio was not discussed.27 The motivation for this study was two-fold; (i) the relative prices of K3[Fe(CN)6] to K4[Fe(CN)6] can vary significantly, and (ii) curiosity.
1), likely on account of the significantly higher solubility of the former, but the effect of using a non-stoichiometric ratio was not discussed.27 The motivation for this study was two-fold; (i) the relative prices of K3[Fe(CN)6] to K4[Fe(CN)6] can vary significantly, and (ii) curiosity.
This study was performed by ensuring that the concentration of K3[Fe(CN)6] plus that of K4[Fe(CN)6] equalled 0.4 M, then varying the ratio of [Fe(CN)6]3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
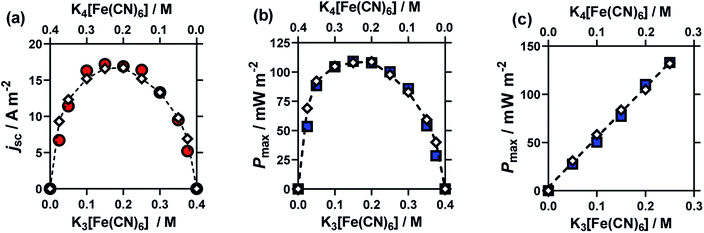
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe(CN)6]4−. The results from these cells are summarised in Fig. 3, for (a) Se, (b) jsc and (c) Pmax. Notably, here the Se value varied significantly (between −1.65 mV K−1 and −1.22 mV K−1).
[Fe(CN)6]4−. The results from these cells are summarised in Fig. 3, for (a) Se, (b) jsc and (c) Pmax. Notably, here the Se value varied significantly (between −1.65 mV K−1 and −1.22 mV K−1).
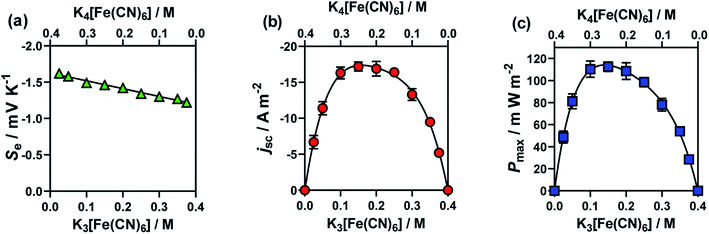 | ||
| Fig. 3 Plots (a)–(c) showing the effect of changing the ratio of [Fe(CN)6]3− to [Fe(CN)6]4− upon (a) the Se coefficient (green triangles); (b) the jsc (orange circles) and (c) the Pmax (blue squares). The concentrations of the redox couples were varied whilst maintaining a summed concentration of 0.4 M, where error bars represent 1 SD (not shown if bars smaller than symbol). All other experimental conditions as per Fig. 1. | ||
The jsc (Fig. 3(b)) displayed a polynomial-like relationship, with the highest current, in the region of 0.1–0.2 M [Fe(CN)6]3− and 0.3–0.2 M [Fe(CN)6]4−. Notably, if this system was exclusively limited by the least abundant redox couple then an inverted V shape, Λ, would be expected, based upon the above concentration study. This more complex trend is quantitatively modelled and explained below.
The Se was significantly higher in systems with more [Fe(CN)6]4− than [Fe(CN)6]3− (Fig. 3(a)); since a larger Se typically results in a higher current, there is a slight asymmetry in the jsc curve (Fig. 3(b)) towards the [Fe(CN)6]4−-rich systems. As the Pmax is achieved at 0.5Se and 0.5jsc, this asymmetry is even more significant in the power output (Fig. 3(c)), so much so that the cell containing 0.15 M [Fe(CN)6]3− (a [Fe(CN)6]3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe(CN)6]4− ratio of 3
[Fe(CN)6]4− ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) generated the highest average Pmax value. While this represents only a modest 4% increase, prior to now the general convention has been to always use a ratio of 1
5) generated the highest average Pmax value. While this represents only a modest 4% increase, prior to now the general convention has been to always use a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, or even the opposite ratio (significantly more [Fe(CN)6]3−).
1, or even the opposite ratio (significantly more [Fe(CN)6]3−).
| ln(γ) = −Azi2I0.5 | (2) |
| ln|Se| ∝ −I0.5 | (3) |
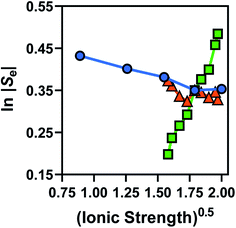
Broadly, such a relationship can be observed for the Se trend vs. equimolar [Fe(CN)6]3−/4− shown in Fig. 2(a); Fig. 4 displays this data re-plotted as ln(|Se|) vs. I0.5, and clearly demonstrated a linear correlation between the measured ln(|Se|) and the I0.5 of the relevant solution (●). Kang et al.30 have previously varied the concentration of equimolar K3/4[Fe(CN)6], applied ‘Debye–Hückel treatment’ and demonstrated a linear relationship between the Se and the square root of concentration, C0.5, but this only applied at extremely dilute concentrations; notably, they used Se rather than ln|Se|, which likely explains this observation.
Fig. 4 also displays the data from the ratio study (■). The non-equimolar ratio system covers a systematic range of I0.5 values, from 0.4 M K3[Fe(CN)6] with an ionic strength of ca. 2.4 M, to 0.4 M K4[Fe(CN)6] with an ionic strength of ca. 4 M. However, the trend of ln|Se| vs. −I0.5 from the ratio study (■) is clearly the opposite of that demonstrated by the concentration-study (●), intersecting only at the equimolar ratio. Therefore the Debye–Hückel relationship does not dominate in these systems. The electrochemical behaviour of non-equimolar concentrations of reduced and oxidised systems relative to equimolar systems is instead well described by the Nernst equation;
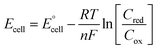 | (4) |
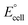 is the standard cell potential, n is the number of electrons transferred, R is the universal gas constant, T is the temperature, F is Faraday's constant, and Cred and Cox are the concentrations of the reduced and oxidised species, respectively. By substituting E for ΔE, and T for ΔT then dividing by ΔT to obtain Se rather than E, eqn (5) is obtained:
is the standard cell potential, n is the number of electrons transferred, R is the universal gas constant, T is the temperature, F is Faraday's constant, and Cred and Cox are the concentrations of the reduced and oxidised species, respectively. By substituting E for ΔE, and T for ΔT then dividing by ΔT to obtain Se rather than E, eqn (5) is obtained: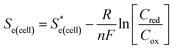 | (5) |
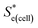 represents the Se when the concentrations of both redox species are equal (i.e.
represents the Se when the concentrations of both redox species are equal (i.e.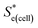 = −1.43 mV K−1 when [[Fe(CN)6]3−] + [[Fe(CN)6]4−] = 0.4 M and [[Fe(CN)6]3−] = [[Fe(CN)6]4−]).25,30 Thus Se(cell) represents the Se when the concentrations of the reduced and oxidised species are not equal.
= −1.43 mV K−1 when [[Fe(CN)6]3−] + [[Fe(CN)6]4−] = 0.4 M and [[Fe(CN)6]3−] = [[Fe(CN)6]4−]).25,30 Thus Se(cell) represents the Se when the concentrations of the reduced and oxidised species are not equal.
Using eqn (5), the recorded Se values for the non-stoichiometric systems shown in Fig. 3(a) were given a ‘Nernstian correction’ (i.e. converted from Se(cell) into 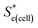 using the known Cred and Cox values). The Nernstian-corrected
using the known Cred and Cox values). The Nernstian-corrected 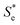 values are also shown in Fig. 4 (▲), and the resulting
values are also shown in Fig. 4 (▲), and the resulting 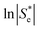 vs. I0.5 displays the same Debye–Hückel-like relationship as that demonstrated by the concentration study (●). Therefore, the concentration imbalance is the main factor dictating the variation in Se in the non-stoichiometric ratio study, in line with the Nernst equation, with the Debye–Hückel effect being a minor and opposite factor.
vs. I0.5 displays the same Debye–Hückel-like relationship as that demonstrated by the concentration study (●). Therefore, the concentration imbalance is the main factor dictating the variation in Se in the non-stoichiometric ratio study, in line with the Nernst equation, with the Debye–Hückel effect being a minor and opposite factor.
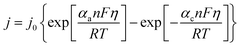 | (6) |
| j0 = Fk0(CoxαCredα) | (7) |
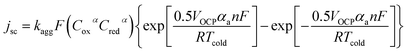 | (8) |
| Pmax = 0.25jscVOCP | (9) |
Fig. 5 displays the original jsc and Pmax data from the non-stoichiometric ratio study (from Fig. 3(b) and (c), respectively), but now overlaid with data generated from eqn (8) and (9), respectively, where the single unknown in the equation, kagg, has been set as 1.68 × 10−4 cm s−1. As can be observed, excellent correlation is observed between the experimental and modelled data, given that only a single parameter was varied.
A range of k0 values are available in the literature for the [Fe(CN)6]3−/4− redox couple, and typically range from ca. 0.020–0.25 cm s−1.22,49,50 However, this means the observed rate constant, kagg of 1.68 × 10−4 cm s−1 is ca. 2 to 3 orders of magnitude lower than k0 values; this is despite the amorphous graphite electrode material demonstrating excellent electrocatalytic ability, on par with platinum (discussed later). Here it must be recalled that the jsc value is the steady state current achieved after the cell has been generating maximum current and therefore the concentration of redox active species at the electrode surface no longer matches that in the bulk. Modifications to the Butler–Volmer equation can introduce a ratio C*/Co, where C* is the concentration at the electrode surface and Co is the bulk concentration.48 The C* was therefore estimated using the Nernst equation, but when this correction was applied to the above model, it predicted that the cell would proceed in the opposite direction. The fact that this is not the case reflects that as the concentration ratio of the redox species varies, so does the overpotential (by virtue of the Se changing). Therefore, a significantly more complicated system is required to model the cell when thermogalvanic current is generated; all forms of mass transport (diffusion, migration and convection) would need to be considered to determine concentration gradients, and then this needs to be used to account for how the overpotential is then changed as local concentration ratios and ionic strengths are altered at the electrode surface via redox processes.
Previously, Hornut and Storck stated that a Butler–Volmer equation-based model was in excellent agreement with experimental results from an equimolar K3/4[Fe(CN)6] thermogalvanic cell (in 1 M NaOH); the Butler–Volmer equation was merged with a global mass transfer coefficient, and treated for ohmic drop.51 However, comparison between experimental and modelled values appear to have been limited to a single experimental data point, and the values of the numerous specific parameters used in the substantial equation were unfortunately not stated. At present, we are not able to confidently formulate a complete model. However, it is remarkable that one of the simplest versions of the Butler–Volmer equation can be applied, and all kinetic, mass transport, overpotential and ohmic issues appear to be incorporated within a single constant, kagg, as shown in eqn (8). While this kagg cannot be taken as a universal constant (e.g. it is expected to include significant aspects of the cell geometry, including inter-electrode spacing, convection and be extremely ΔT sensitive) this could be utilised to compare different systems in the same cell. It also fully rationalises the observed polynomial-like dependence of the thermogalvanic output as a function of the ratio of [reduced]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [oxidised].
[oxidised].
Finally, if this model is valid, it should be able to mirror the equimolar concentration results presented previously (cf.Fig. 2). Therefore the values from this study were applied to eqn (8), and the modelled data generated; the experimental data is overlaid vs. the experimental data in Fig. 5(c). As can be seen, excellent correlation is observed, using the same value of kagg = 1.68 × 10−4 cm s−1, as for the ratio study.
3.2. Homogeneous electrocatalysis effects in the thermogalvanic cell using cations
The rate constant of the [Fe(CN)6]3−/4− redox system is known to be sensitive to both the electrode material23,33,39 and to the cations43,52,53 present in the system. Following on from the concentration and ratio study, the cation effect upon the thermogalvanic properties of the [Fe(CN)6]3−/4− redox couple was explored. This was largely inspired by a recent publication by Huang et al.,43 where they investigated the cation effect upon the (thermo)electrochemical properties (i.e. E°, Se, k0), but did not investigate the effect upon the thermogalvanic power (e.g. jsc and Pmax).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
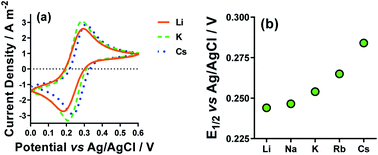
The CVs for Li+, K+ and Cs+ are displayed in Fig. 6(a), and the shift in E1/2 for [Fe(CN)6]3−/4−vs. the various M2SO4 salts are plotted in Fig. 6(b). Clearly, the different M+ employed had a significant effect upon the E1/2 values for the [Fe(CN)6]3−/4− couple. This could potentially correspond to a junction potential between the electrolyte and the Ag/AgCl reference electrode; however, these observations are consistent with several other electrochemical studies, which have observed the strong effect that alkali metal cations have upon the properties of the [Fe(CN)6]3−/4− redox couple.43,52,53 This effect is also prevalent in solution, such as the homogeneous electron exchange reactions between [Fe(CN)6]3− and [Fe(CN)6]4−; these are catalysed by additional M+, or the effect completely removed by the addition of suitable crown ethers.54 The source of this effect is attributed to the collision or association of the [Fe(CN)6]3−/4− anions with the M+ cations, opening M+-catalysed reaction pathways.52 It is also sensitive to a number of other factors, such as viscosity, light, etc.55,56
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K+ is ca. 23
K+ is ca. 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Additionally, M2SO4 was also substituted with 1 M MCl (where M+
1). Additionally, M2SO4 was also substituted with 1 M MCl (where M+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K+ is ca. 29
K+ is ca. 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).
1).
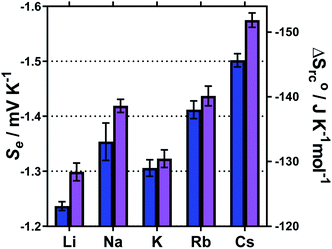
The Se values were determined by the gradient of the measured ΔE vs. ΔT (5 °C, 10 °C, 15 °C and 20 °C) for each of these systems; the corresponding ΔSrc were then calculated using eqn (1). These results are summarised in Fig. 7, and show a general trend of increasing Se values from Li+ < Na+ < Rb+ < Cs+, and also consistently higher Se values in the MCl systems relative to the M2SO4 systems. The K+ system was a notable outlier from the periodic trend, falling in the order: Li+ < K+ < Na+ < Rb+ < Cs+.
Recently, Huang et al. investigated similar systems but using isothermal cyclic voltammetry (hence reported dE°/dT rather than ΔE/ΔT) and observed the same trend as observed here for the E1/2 (Fig. 6), namely that the Se increased following the trend Li+ < Na+ < K+ < Rb+ < Cs+.43 In our case, the K+ system did not fit into this trend, but K+ is the only system to not contain a mixture of alkali metal cations; solutions containing two or more alkali metal cations are known to have significant effects upon the solvation dynamics of [Fe(CN)6]4−.57
Regarding the increase in Se upon going from Li+ to Cs+, Huang et al. attributed this to the structure breaking and structure making nature of these cations, respectively.43 However, observed variations in the Se have more frequently been attributed to changes in the activity coefficients in line with Debye–Hückel electrostatic interactions.16,30,46 This is consistent with the trend in activity coefficients, since M+ systems are known to mirror the trend Li+ < Na+ < K+ < Rb+ < Cs+.58 Arguably, the structure making/breaking nature of the cations and extended Debye–Hückel theory reflects the same solvation dynamics, and therefore explains the same observations but from different perspectives.
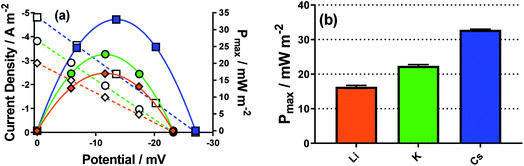
Here Li+, K+ and Cs+ were investigated, using 25 mM K3[Fe(CN)6] and 25 mM K4[Fe(CN)6] in the presence of 1.5 M of MCl; this had to be changed from the more dilute systems used above since the current in the dilute systems suffered from background noise and were therefore not suitably reproducible. The same trend in Se was observed, and the jsc increased going from Li+ to K+ to Cs+ (shown by the linear I–V plots in Fig. 8(a)), and therefore Pmax also followed the same trend (power curves in Fig. 8(a), and bar chart in Fig. 8(b)). Notably, going from Li+ to Cs+ the power doubled, indicating a significant electrocatalytic factor is introduced into the thermogalvanic cell by the nature of the alkali metal cation. This mirrors the reported investigations into the effect of these cations upon the apparent k0 of the [Fe(CN)6]3−/4− couple.43,52,53
3.3. Thermogalvanic power via heterogeneous electrocatalysis
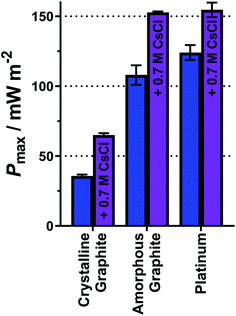
As demonstrated above, a homogeneous electrocatalytic effect was observed via added cations. It is also well established that the nature of the electrode material is highly influential upon the power generated by thermogalvanic cells (i.e. heterogeneous electrocatalysis).33,39,59 Three electrode materials were therefore tested, as shown in Fig. 9(a), using equimolar 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6]. These were two forms of graphite, and platinum metal. Gold electrodes are known to experience passivation and dissolution issues with the [Fe(CN)6]3−/4− redox couple,34 and when tested here we were unable to obtain Pmax values of sufficient reproducibility.The platinum electrodes generated the highest average Pmax value of 124 mW m−2 (Fig. 9), in line with expectations and previous reports.33,39 Carbon electrodes have variable surface functionality and therefore variable electrocatalytic ability;4 the two graphite electrodes tested here displayed significantly different Pmax values (Fig. 9). One form of graphite, highly crystalline pyrolytic graphite (sold as a thermal interface sheet), gave a Pmax of 36 mW m−2, whereas amorphous graphite pressed into a sheet (sold as a gasket material) gave a Pmax nearly 3 times higher, of 108 mW m−2. This difference likely relates to the different forms of graphite at the surface; amorphous graphite is expected to have numerous edge-sites facing the solution, relative to the highly crystalline pyrolytic graphite, and such edge-sites are known to be more electrocatalytically active than basal planes for redox couples such as [Fe(CN)6]3−/4−.60 These results were modelled using the modified Butler–Volmer equation (eqn (8) and (9)) and yielded the expected kagg values, ranging from 0.58 × 10−4 cm s−1 for the crystalline graphite though to 1.93 × 10−4 cm s−1 for platinum (full values in Table S7 in the ESI†).
Finally, having investigated both homogeneous and heterogeneous electrocatalysis separately, they were also compared when combined. Fig. 9 displays the Pmax values for the three electrode materials for just 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6] (blue bars) as well as Pmax after the addition of 0.7 M CsCl (purple bars). This system only had a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for Cs+
2 for Cs+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K+, but could not be increased further due to solubility limitations. However, even this modest amount of Cs+ significantly increased Pmax, and this homogeneous electrocatalytic effect was observed across the three electrode materials; the Pmax was boosted by ca. 80% at the highly crystalline pyrolytic graphite, and Pmax increased by ca. 40% at the two (more heterogeneous electrocatalytic) electrodes. This was a result of more modest increases in the kagg values, e.g. by 38% on the highly crystalline pyrolytic graphite, and by 25% on platinum.
K+, but could not be increased further due to solubility limitations. However, even this modest amount of Cs+ significantly increased Pmax, and this homogeneous electrocatalytic effect was observed across the three electrode materials; the Pmax was boosted by ca. 80% at the highly crystalline pyrolytic graphite, and Pmax increased by ca. 40% at the two (more heterogeneous electrocatalytic) electrodes. This was a result of more modest increases in the kagg values, e.g. by 38% on the highly crystalline pyrolytic graphite, and by 25% on platinum.
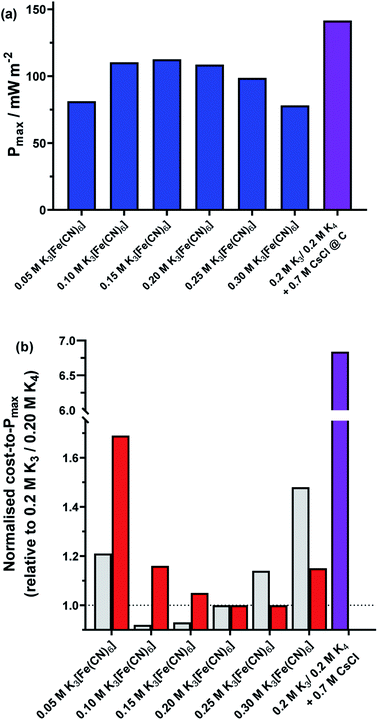
3.4. A relative cost comparison of the different homogeneous systems
Finally, a preliminary economic assessment was made of the various homogeneous routes presented here as ways to increase thermogalvanic power output. The heterogeneous electrocatalytic aspects (i.e. platinum vs. graphite) were not considered because bulk materials were employed, but numerous other approaches could be employed to minimise the amount of material utilised (e.g. sputtering of a thin film of platinum).13Fig. 10(a) summarises the maximum power density outputs from the equimolar 0.2 M K3[Fe(CN)6] and 0.2 M K4[Fe(CN)6] amorphous graphite cell, against the same cell but with non-equimolar ratios, and the same cell with 0.7 M CsCl. Fig. 10(b) (grey bars) displays the power normalised with respect to the cost of the salt dissolved in the solution (assuming Sigma Aldrich ReagentPlus grade materials utilised; full details in ESI†), whereby the equimolar cell has been set to a cost per W m−2 of 1. What is clearly observed is that while the addition of CsCl increased the overall power (Fig. 10(a)), the significantly higher cost of CsCl resulted in an 685% increase in cost per W m−2 (Fig. 10(b), purple bar). Conversely, because ReagentPlus K4[Fe(CN)6] was ca. 22% cheaper per mol than ReagentPlus K3[Fe(CN)6], and having more K4[Fe(CN)6] generated more power, moving away from the 0.2 M stoichiometric ratio commonly employed by others can actually result in a decrease in cost per W m−2; this reaches an optimum at 0.10 M K3[Fe(CN)6] and 0.30 M K4[Fe(CN)6], at only 92% of the cost per W m−2 of the equimolar system. However, an important caveat is that this only applies at current prices and using 0.5 kg bottles of ReagentPlus grade materials; the relative cost of K4[Fe(CN)6] and K3[Fe(CN)6] actually invert for ACS grade material (Fig. 10(b), red bars), thereby making the 0.25 M K3[Fe(CN)6] and 0.15 M K4[Fe(CN)6] cell have the lowest cost per W m−2, by a modest 1% relative to the equimolar cell.
While the reductions in cost per W m−2 are modest, both nevertheless demonstrate that a ‘less is more’, non-stoichiometric approach can be viable for thermogalvanic cells from a technoeconomic perspective. Clearly both good heterogeneous and homogeneous electrocatalysts are required to achieve the highest power cells, but what is demonstrated here is that the deliberate addition of additives that are significantly more costly than the redox active species themselves are hard to justify economically, unless even more significant increases in Pmax can be achieved.
4. Conclusions
This research set out to explore some fundamental aspects of thermogalvanic cells, using ferricyanide/ferrocyanide as a ‘standard’ redox couple. By comparing a standard concentration study using equimolar ratios with apparently the first systematic study of non-equimolar ratios, significant insight was generated. This demonstrated how the Seebeck coefficient is concentration dependent (via Debye–Hückel theory, in line with prior observations) and is even more significantly sensitive to the ratio of ferricyanide to ferrocyanide (via the Nernst equation); it also allowed us to apply a slightly modified Butler–Volmer equation to quantitatively model the current and electrical power generated by the various systems. This Butler–Volmer model generated just one variable as an aggregated rate constant, kagg.Homogeneous electrocatalysis (the deliberate addition of an alkali metal salt to the electrolyte solution) was also explored alongside a more conventional heterogeneous electrocatalytic (electrode material) study. Both had significant effects upon the overall current produced by the thermocells, but homogeneous electrocatalysis could also boost the potential difference, by virtue of altered thermodynamics. Combining both optimal heterogeneous and homogeneous electrocatalysis generated the highest power thermocells. However, while addition of the alkali metal salt CsCl significantly boosted power (up to +80%), it increased the relative cost of the electrolyte by an even more significant margin (+685%). It was also demonstrated that moving from a standard equimolar system to a non-equimolar system could yield a higher maximum power (+4%), and could decrease the cost-per-unit-power of the thermocell electrolyte even more significantly (−8%).
These results help rationalise variations in thermocell performance as a function of concentration and ratio. It also introduces a means to quantitatively model the resulting performance to yield a single value as a performance metric, the kagg.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MAB acknowledges the EPSRC for funding (Standard Research Studentship (DTP), EP/N509498/1). LA and CJB acknowledges the PLuS Alliance for funding (PLuS Alliance Seed Grant, project code PA17046). HXL acknowledges the Chinese Scholarship Council for funding (CSC No. 201806130204).References
- P. Gründler, In-situ Thermoelectrochemistry: Working with Heated Electrodes, Springer, Berlin, 1st edn, 2015 Search PubMed.
- T. I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3985–3994 CrossRef CAS.
- A. Gunawan, C. H. Lin, D. A. Buttry, V. Mujica, R. A. Taylor, R. S. Prasher and P. E. Phelan, Nanoscale Microscale Thermophys. Eng., 2013, 17, 304–323 CrossRef CAS.
- M. S. Romano, J. M. Razal, D. Antiohos, G. G. Wallace and J. Chen, J. Nanosci. Nanotechnol., 2015, 15, 1–14 CrossRef CAS PubMed.
- M. Dupont, D. R. MacFarlane and J. M. Pringle, Chem. Commun., 2017, 53, 6288–6302 RSC.
- B. Burrows, J. Electrochem. Soc., 1976, 123, 154–159 CrossRef CAS.
- M. A. Buckingham, F. Marken and L. Aldous, Sustainable Energy Fuels, 2018, 2, 2717–2726 Search PubMed.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639 CrossRef CAS PubMed.
- H. Julian Goldmid, Introduction to Thermoelectricity, Springer Berlin Heidelberg, 2nd edn, 2016 Search PubMed.
- M. A. Buckingham and L. Aldous, J. Electroanal. Chem., 2020 DOI:10.1016/j.jelechem.2020.114280.
- T. J. Abraham, D. R. Macfarlane and J. M. Pringle, Energy Environ. Sci., 2013, 6, 2639–2645 RSC.
- T. J. Abraham, D. R. MacFarlane, R. H. Baughman, N. Li, Y. Chen and J. M. Pringle, Mater. Res. Soc. Symp. Proc., 2019, 53, 1689–1699 Search PubMed.
- M. Al Maimani, J. J. Black and L. Aldous, Electrochem. Commun., 2016, 72, 181–185 CrossRef CAS.
- C. Lin, A. Gunawan, P. E. Phelan, D. A. Buttry, V. Mujica, R. A. Taylor and R. S. Prasher, Proc. ASME 2012 Int. Mech. Eng. Congr. Expo., 2012, vol. 1, pp. 1–7 Search PubMed.
- H. Li, A. Gunawan, P. E. Phelan, D. A. Buttry, V. Mujica, R. A. Taylor and R. S. Prasher, Proc. ASME 2013 Int. Mech. Eng. Congr. Expo., 2013, vol. 1, pp. 1–2 Search PubMed.
- J. J. Black, T. Murphy, R. Atkin, A. Dolan and L. Aldous, Phys. Chem. Chem. Phys., 2016, 18, 20768–20777 RSC.
- J. J. Black, A. Dolan, J. B. Harper and L. Aldous, Phys. Chem. Chem. Phys., 2018, 20, 16558–16567 RSC.
- L. Aldous, J. J. Black, M. C. Elias, B. Gélinas and D. Rochefort, Phys. Chem. Chem. Phys., 2017, 19, 24255–24263 RSC.
- E. H. B. Anari, M. Romano, W. X. Teh, J. J. Black, E. Jiang, J. Chen, T. Q. To, J. Panchompoo and L. Aldous, Chem. Commun., 2016, 52, 745–748 RSC.
- H. Zhou, T. Yamada and N. Kimizuka, J. Am. Chem. Soc., 2016, 138, 10502–10507 CrossRef CAS PubMed.
- T. J. Abraham, D. R. MacFarlane and J. M. Pringle, Chem. Commun., 2011, 47, 6260–6262 RSC.
- P. H. Daum and C. G. Enke, Anal. Chem., 1969, 41, 653–656 Search PubMed.
- R. L. McCreery, Chem. Rev., 2008, 108, 2646–2687 CrossRef CAS PubMed.
- E. L. Yee and M. J. Weaver, Inorg. Chem., 1980, 19, 1077–1079 CrossRef CAS.
- L. Zhang, T. Kim, N. Li, T. J. Kang, J. Chen, J. M. Pringle, M. Zhang, A. H. Kazim, S. Fang, C. Haines, D. Al-Masri, B. A. Cola, J. M. Razal, J. Di, S. Beirne, D. R. MacFarlane, A. Gonzalez-Martin, S. Mathew, Y. H. Kim, G. Wallace and R. H. Baughman, Adv. Mater., 2017, 29, 1605652 CrossRef PubMed.
- T. Ikeshoji and R. S. Gonçalves, J. Appl. Electrochem., 1993, 23, 516–519 CAS.
- T. Ikeshoji, Bull. Chem. Soc. Jpn., 1987, 60, 1505–1514 Search PubMed.
- R. Hu, B. A. Cola, N. Haram, J. N. Barisci, S. Lee, S. Stoughton, G. Wallace, C. Too, M. Thomas, A. Gestos, M. E. Dela Cruz, J. P. Ferraris, A. A. Zakhidov and R. H. Baughman, Nano Lett., 2010, 10, 838–846 CrossRef CAS PubMed.
- H. Im, T. Kim, H. Song, J. Choi, J. S. Park, R. Ovalle-Robles, H. D. Yang, K. D. Kihm, R. H. Baughman, H. H. Lee, T. J. Kang and Y. H. Kim, Nat. Commun., 2016, 7, 10600 CrossRef CAS PubMed.
- T. J. Kang, S. Fang, M. E. Kozlov, C. S. Haines, N. Li, Y. H. Kim, Y. Chen and R. H. Baughman, Adv. Funct. Mater., 2012, 22, 477–489 CrossRef CAS.
- M. S. Romano, N. Li, D. Antiohos, J. M. Razal, A. Nattestad, S. Beirne, S. Fang, Y. Chen, R. Jalili, G. G. Wallace, R. Baughman and J. Chen, Adv. Mater., 2013, 25, 6602–6606 CrossRef CAS PubMed.
- F. Zhao, W. Qian, M. Li, W. Li, L. Chen, F. Zhong, W. Huang and C. Dong, RSC Adv., 2017, 7, 23890–23895 RSC.
- H. A. H. Alzahrani, J. J. Black, D. Goonetilleke, J. Panchompoo and L. Aldous, Electrochem. Commun., 2015, 58, 76–79 Search PubMed.
- H. A. H. Alzahrani, M. A. Buckingham, F. Marken and L. Aldous, Electrochem. Commun., 2019, 102, 41–45 CrossRef CAS.
- H. Im, H. G. Moon, J. S. Lee, I. Y. Chung, T. J. Kang and Y. H. Kim, Nano Res., 2014, 7, 443–452 CrossRef CAS.
- W. Huang, J. Xu, K. He, Z. Li, W. Qian and C. Dong, IOP Conf. Ser. Earth Environ. Sci., 2018, 121, 042027 CrossRef.
- N. E. Holubowitch, J. Landon, C. A. Lippert, J. D. Craddock, M. C. Weisenberger and K. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 22159–22167 CrossRef CAS PubMed.
- M. S. Romano, S. Gambhir, J. M. Razal, A. Gestos, G. G. Wallace and J. Chen, J. Therm. Anal. Calorim., 2012, 109, 1229–1235 CrossRef CAS.
- J. Wu, J. J. Black and L. Aldous, Electrochim. Acta, 2017, 225, 482–492 Search PubMed.
- T. Kim, J. S. Lee, G. Lee, H. Yoon, J. Yoon, T. J. Kang and Y. H. Kim, Nano Energy, 2017, 31, 160–167 CrossRef CAS.
- D. Inoue, Y. Fukuzumi and Y. Moritomo, Jpn. J. Appl. Phys., 2020, 59, 037001 Search PubMed.
- J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Nat. Commun., 2018, 9, 1–8 CrossRef PubMed.
- B. Huang, S. Muy, S. Feng, Y. Katayama, Y. C. Lu, G. Chen and Y. Shao-Horn, Phys. Chem. Chem. Phys., 2018, 20, 15680–15686 Search PubMed.
- L. Jin, G. W. Greene, D. R. MacFarlane and J. M. Pringle, ACS Energy Lett., 2016, 1, 654–658 Search PubMed.
- P. Yang, K. Liu, Q. Chen, X. Mo, Y. Zhou, S. Li, G. Feng and J. Zhou, Angew. Chem., Int. Ed., 2016, 55, 12050–12053 CrossRef CAS PubMed.
- M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, J. Chem. Phys., 2011, 134, 114513–114518 CrossRef CAS PubMed.
- P. Blanc and C. Madic, Inorg. Chim. Acta, 1984, 94, 134–136 CrossRef.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, Inc., 2nd edn, 2001 Search PubMed.
- K. Winkler, J. Electroanal. Chem., 1995, 388, 151–159 CrossRef.
- D. H. Angell and T. Dickinson, J. Electroanal. Chem., 1972, 35, 55–72 CrossRef CAS.
- J. M. Hornut and A. Storck, J. Appl. Electrochem., 1991, 21, 1103–1113 CrossRef CAS.
- L. M. Peter, W. Dürr, P. Bindra and H. Gerischer, J. Electroanal. Chem., 1976, 71, 31–50 CrossRef CAS.
- S. A. Campbell and L. M. Peter, J. Electroanal. Chem., 1994, 364, 257–260 CrossRef CAS.
- A. Zahl, R. Van Eldik and T. W. Swaddle, Inorg. Chem., 2002, 41, 757–764 CrossRef CAS PubMed.
- D. E. Khoshtariya, T. D. Dolidze, A. Neubrand and R. Van Eldik, J. Mol. Liq., 2000, 89, 127–146 CrossRef CAS.
- D. E. Khoshtariya, T. D. Dolidze, D. Krulic, N. Fatouros and D. Devilliers, J. Phys. Chem. B, 1998, 102, 7800–7806 CrossRef CAS.
- A. J. Esswein, J. Goeltz, D. Amadeo, High solubility iron hexacyanides, US 2014/0051003 A1, 2014, p. 14.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC.
- T. J. Abraham, N. Tachikawa, D. R. MacFarlane and J. M. Pringle, Phys. Chem. Chem. Phys., 2014, 16, 2527–2532 RSC.
- C. E. Banks, M. R. Moore, T. J. Davies and R. G. Compton, Chem. Commun., 2004, 10, 1804–1805 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0se00440e |
| ‡ These authors contributed equally to this work. |
| § This relationship can break down at higher I values, such that the γ can actually begin to increase with I; however, literature values for [Fe(CN)6]3− and [Fe(CN)6]4− do not demonstrate this characteristic change, which would require use of the extended Debye–Hückel law. |
| This journal is © The Royal Society of Chemistry 2020 |