Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hidden figures of photo-charging: a thermo-electrochemical approach for a solar-rechargeable redox flow cell system†
Dowon
Bae‡
 *a,
Gerrit M.
Faasse‡
a and
Wilson A.
Smith
*a,
Gerrit M.
Faasse‡
a and
Wilson A.
Smith
 abc
abc
aDelft University of Technology, Department of Chemical Engineering – Materials for Energy Conversion and Storage (MECS), Van der Maasweg 9, 2629 HZ Delft, The Netherlands. E-mail: d.bae@tudelft.nl
bNational Renewable Energy Laboratory (NREL), 15013 Denver West Parkway, Golden, CO 80401, USA
cRenewable & Sustainable Energy Institute, University of Colorado Boulder, 4001 Discovery Dr Suite N321, Boulder, CO 80303, USA
First published on 27th March 2020
Abstract
Achieving high current densities without thermal performance degradation at high temperatures is one of the main challenges for enhancing the competitiveness of photo-electrochemical energy storage systems. We describe a system that overcomes this challenge by incorporating an integrated photoelectrode with a redox flow cell, which functions as a coolant for the excess heat from the photo-absorber. We perform quantitative analyses to theoretically validate and highlight the merit of the system. Practical operation parameters, including daily temperature and redox reaction kinetics, are modeled with respect to heat and charge transfer mechanisms. Our analyses show a profound impact on the resulting solar-to-chemical efficiencies and stored power, which are 21.8% higher than that of a conventional photovoltaic-assisted energy storage system. This paves the way for reassessing the merit of photovoltaic-integrated systems, which have hitherto been underrated as renewable energy storage systems.
Direct conversion of solar energy into a chemical fuel such as hydrogen using photo-electrochemical (PEC) approaches has been considered to be a promising solution for a sustainable energy economy.1,2 However, previous reports have claimed that the sluggish reaction kinetics of water oxidation significantly hamper the wide implementation of solar water splitting.3–5 So far, Li-based batteries are the dominant technology in the energy storage market. But, Li-based batteries suffer from severe safety issues, including thermal runaway.6,7 In this context, photoelectrochemically rechargeable redox flow batteries (RFB) have come to be regarded as particularly attractive in recent years.8,9 Redox flow batteries are known to be stable in a wide operational range, and they have the additional advantage of a long discharging time.10 Moreover, unlike conventional PEC chemical conversion processes, solar redox flow batteries (SRFB) offer flexibility in terms of redox potential and solubility in a wide pH range.8 Most recently, SRFB systems with tandem photovoltaic (PV) devices have shown solar-to-chemical conversion efficiencies (STC%) of 12.3% and 14.1% using monolithic tandem a-Si and III–V devices, respectively.9,11 A single-junction-based SRFB with c-Si and WSe2 photoelectrodes also recently demonstrated a meaningful STC%.12,13
Despite the above-mentioned progress, the view is pessimistic with regard to the practical application of SRFBs due to their inherent thermal resistance under heat, which leads to photovoltage loss from the PEC charging device. For instance, the c-Si device shows a power loss rate of 0.45%/°C (around 200 mV loss at 70 °C).14 Specifically, photovoltage loss could eliminate the driving force for the redox chemical reactions. However, no thorough quantitative analysis has been conducted on the thermal effect on the photo-charging performance of the RFB. The unique working principle of the SRFB is that the electrolyte flow gives rise to a pathway that can remedy thermal losses using heat transfer from the photo-electrode to the liquid flow, which is placed directly behind the photo-device, as illustrated in Fig. 1a. This means that the electrolyte effectively functions as a coolant.
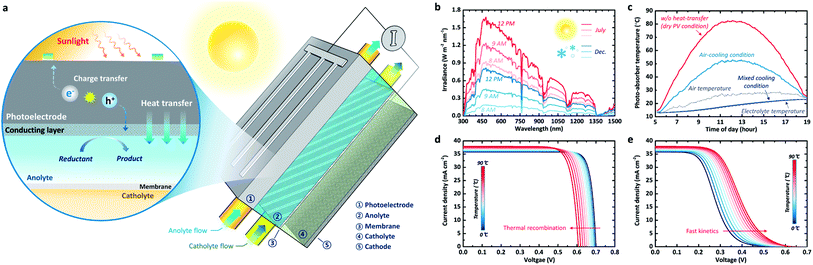 | ||
| Fig. 1 (a) Illustration of the PEC-device-integrated redox flow system. This flow system includes electrolyte flow, which is charged by photoelectrodes under illumination. (b) Time-dependent solar spectra in summer (July) and winter (December). (c) Absorber temperature over the course of a summer day (31/07/2018) for the three different heat-transfer scenarios. (d) Temperature-dependent J–V characteristics of a c-Si PV modeled for the case of fast kinetics (i.e. no overpotential) using its real temperature-dependent absorption spectrum21 and the recombination rate calculated based on the absorption spectrum.23 (e) Temperature-dependent J–V characteristics of a c-Si photoelectrode with highly dominant kinetic overpotential losses. The equation for the temperature-dependant kinetic overpotential used for (e) can be found in the ESI.† | ||
Here, we address the thermo-electrochemical behaviour of photo-charging performance for the redox flow cell applications and unravel the synergic effect of the PEC-device-integrated system using a combined model based on our previously verified study12 and heat transfer theory.15 For effective content delivery, we developed an innovative multi-functional photo-charging cell concept (Fig. 1a). We used real solar spectral data from a typical winter day and a typical summer day obtained from the National Renewable Energy Laboratory (NREL) in Colorado16 (Fig. 1b). The suggested design uses active thermal management, employing heat transfer and forced convection to cool the photoelectrode (e.g. photoanode in Fig. 1a) and heat (via heat transfer phenomena) the electrolyte, thus stabilizing the temperature of the photoelectrode. This thermo-electrochemical approach is critical for enhancing the overall energy storage (i.e. photo-charged electrolyte). Furthermore, we quantify its potential for enhancing the theoretical maximum photo-charging, compared with the conventional approaches of an SRFB without cooling and a system without an integrated PEC device. In fact, this architecture whereby the electrolyte is isolated from sunlight has been actively used in recent reports9,11,17 since the parasitic optical loss by the electrolyte and its photodegradation cannot be avoided.12 However, no in-depth quantitative analysis of photo-charging performance has been reported so far. Simple mechanical integration of a water-cooling line with the PV panel, such as III-V PV module with concentrator,18 also can be considered as an alternative scenario. However, this approach may require an additional pumping system, which generally results in an overall efficiency loss of approximately 8–15%,19 and thus, it has not been dealt with in this work.
Our photo-charging component model consists of a single-junction photoelectrode directly integrated onto an electrolyte flow slab, which function as a cooling channel to remove excess heat from the photoelectrode. Because crystalline silicon is the dominant player in the solar PV market (∼90% share), the suggested SRFB model has a c-Si device with material properties obtained from previous reports.20,21 One lesson learned from previous photo-chemistry studies is that the photo-redox effect of certain redox couples, such as anthraquinones, can lead to a shift in the redox potential, thus benefitting the PEC junction under direct light irradiation.22 We emphasize that this theoretical estimation was made without considering a possible photo-redox effect (i.e. electrolytes are completely isolated from light by the photo-absorber) or an energy-level mismatch between the PEC device surface and the redox couples. Furthermore, we assume that the flux of the electrolyte is sufficient for the current output not to be limited by mass transport. We show that our SRFB model has excellent photo-charging stability over time. We also argue that heat flow management reduces photovoltage loss, allowing effective solar energy conversion and storage even at peak daytime temperatures.
The time-dependent solar spectra and ambient air temperature for both a typical summer and a typical winter day in Colorado (Lakewood), displayed in Fig. 1b, show major variations in the visible part of the spectrum (380 to 780 nm). We note that the absorption peaks do not change significantly with time but that the total integrated irradiance and the air temperature change, causing the photo-absorber temperature to vary. The heat balance method enables us to calculate the photo-absorber temperature using three separate scenarios to highlight the impact of the electrolyte on both the temperature and the solar-to-chemical conversion efficiency (STC%). The first scenario is extreme: no convective heat transfer with either the ambient air or the electrolyte is assumed. In the second case, convective heat transfer with the air is included, which is comparable to the first scenario. In the third case, the impact of cooling owing to heat transfer to the electrolyte is also shown.
Fig. 1c shows the photo-absorber temperature for the three proposed scenarios over the course of a day in July (31st July 2018), calculated using the experimentally measured solar spectrum data (Fig. 1b). It can be observed that, as expected, the photo-absorber temperature varies with time and reaches around 82 °C in the ‘no convection scenario’. The modeled current–voltage (J–V) behaviour for dry PV c-Si cells (Fig. 1d) reveals that the photovoltage is reduced by more than 90 mV at temperatures over 80 °C, compared to the standard condition at room temperature. This photovoltage reduction is attributed to the increased recombination rate based on the generally accepted Shockley–Read–Hall (SRH) model23–25 and the temperature-dependent model simplified by Green et al.26 It should be noted that the real absorption spectrum of silicon is used for these simulations.20
Previous studies have established that this increased temperature leads to a slight increase in the photocurrent caused by the thermal decrease in the band gap.27 When considering convective heat transfer with the air (a heat transfer coefficient of 10 W m−2 K−1), which is calculated using a heat balance model (see ESI method 1†), the photo-absorber temperature, as expected, follows the air temperature more closely. It can be observed that the electrolyte temperature follows the air temperature with a delay, due to its high specific heat (1.15 and 1.08 W h kg−1 K−1 at 25 °C and 80 °C, respectively). It should be noted that we assumed the specific heat of the electrolyte to be similar to that of water for the calculation. The temperature-dependent specific heat data used in this work can be found in the ESI (Table 1†). Interestingly, the absorber temperature almost perfectly follows the electrolyte temperature when the convective heat transfer between the absorber and the electrolyte (∼1000 W m−2 K−1) is also considered. The heat transfer coefficients for air and electrolyte used in this work are typical values for common fluid flow problems, which correspond to wind speed of 3–7 m s−1 under atmospheric environment and approximately 80 mL min−1 of water flux through the 1 mm-thick channels, respectively.28–30
Unlike the J–V curves for the dry PV conditions, as shown in Fig. 1e, the PEC model exhibits opposite behaviour with respect to temperature; the onset potential increases with the temperature owing to improved electrochemical kinetics (i.e. reduced overpotential). The reference exchange current and the activation energy used in this analysis for the sluggish kinetics case are 4.62 A cm−2 and 48.6 kJ mol−1 (which are identical to the water oxidation with high overpotential), respectively.31,32 Since the activation energy and the exchange current are poorly documented for specific redox species and reactions, the effect of increasing temperature on the reaction kinetics in Fig. 1e is mainly considered for these well-documented values,31 which would show a drastic shift under the temperature variation. Based on the equations derived by Haussener et al.31 (see also ESI method 2†), overpotential is a highly dominant loss factor in this case, which decreases with increasing temperature. Actually, Tembhurne et al. demonstrated improved water electrolysis for hydrogen production under concentrated solar irradiation.31 Such sluggish kinetics do not always apply to the redox flow cell. Generally, RFBs present facile kinetics, which, as described elsewhere,33 are several orders of magnitudes faster than water splitting. Due to this inherent property of RFBs, the stabilized temperature condition produced by the electrolyte should have a positive effect on the overall STC%. Naturally, the STC% trend towards the dynamic temperature conditions varies with the type of redox chemicals and the consequent kinetics, as will be addressed later in this paper.
The STC% plotted with respect to time differs for the three convection cases, as shown in Fig. 2a. The efficiency landscape change in the scenario for the fast kinetic cases without any heat transfer from the photo-absorber (dark solid) is particularly noteworthy as it reflects the above-mentioned effect of the photo-absorber temperature (Fig. 1c) on the J–V behaviour in the dry PV device case. In the early morning, the STC% increased relatively quickly (at the same rate as in the other scenarios) and then dropped slowly from around 18.5% to 9.6% at about noon, after which the efficiency appeared to increase again at a slow rate. This trend clearly shows the impact of the thermal photovoltage loss on the overall energy storage. The other scenarios, in which the convective heat transfer cooled down the operating temperature of the photo-absorber, exhibit high STC% without the U-shaped valley at peak temperature (i.e. at noon). Specifically, the last scenario with heat transfer to both air and electrolyte showed a high STC% of over 34% in the morning (7–8 am). Once the STC% was saturated, the model showed a stable output with a maximum STC% of 35.4% until the 17th hour (5 pm) without any significant change or degradation. The system with mixed cooling conditions appears to have had 63.2% and 21.8% more storable energy than the system without any heat-transfer (red curve in Fig. 2a) and the system with air-cooling (light blue curve), respectively.
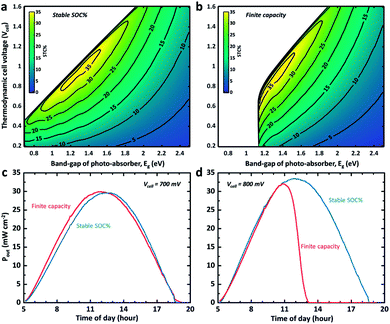
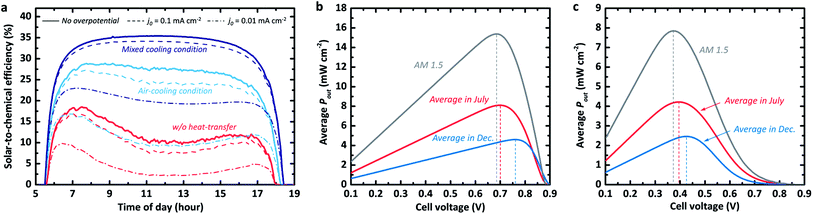 | ||
| Fig. 2 (a) Time-dependant STC% curves of the SRFB system with a Vcell of 0.83 V for various reaction kinetics and heat-transfer scenarios. (b) and (c) Averaged output power density (Pout) versus cell voltage in the fast kinetics (i.e. no overpotential) and sluggish kinetics cases, respectively. The grey curves in (b) and (c) correspond to the averaged Pout under the standard AM 1.5 solar spectrum for the same period during the day (5 am to 7:30 pm). Note that the temperature profiles are based on the NREL database measures for 31/07/2018 and 04/12/2018.16 | ||
We emphasize that the trend in the STC% landscape towards the various scenarios appears to be similar for the cases with slow kinetics. As shown in Fig. 2a, the systems for relatively sluggish kinetics (dashed and dash-dotted lines) with exchange current densities (j0) reaching 10−1 mA cm−2 (e.g., Ti3+/4+ and Cr2+/3+)34 and j0 of 10−2 mA cm−2 (e.g., Sn2+/4+),34 still show their highest STC% under the mixed heat-transfer condition, but we observe a decrease in STC% values with diminishing j0. We also note that this thermos-electrochemical advantage could be diminished for the significantly poor kinetic cases, where the sensitivity to temperature is significant. For the severely poor kinetic case with a j0 of 10−3 mA cm−2, which is equivalent to the OER, the trend is opposite to the fast RFB kinetics (Fig. S1†). It showed the highest STC% without any cooling condition, implying that the kinetic advantage at high-temperature conditions would be significant for the stand-alone solar-to-chemical system with high overpotential kinetics. The outcome of the analysis is strongly coupled to the parameter assumed in the simulation. For instance, variation in wind speed, electrolyte flow rate, and its thickness directly influence the heat transfer coefficients. It is noteworthy that the results in Fig. 2a were simulated using the records (e.g., solar spectrum and temperature profile) experimentally measured by NREL.16 The dynamic change of the measured data over time of the day is also reflected in the model, whereas the heat transfer coefficients for the air and electrolyte are fixed during the course of the day.
Moving on to seasonal dependence, the model is used to determine whether there are variations in optimal cell voltage (i.e. optimal redox couples). The output power density (Pout; i.e. converted power density) for both July and December under the measured time-dependent ambient air temperature of the respective month with respect to the cell voltage for a silicon-based system is shown in Fig. 2b. As a reference, the converted power density from the standard AM 1.5 spectral (without daily variation) is also plotted (grey curve). The optimal cell voltage (depicted as dashed vertical lines) appears to vary seasonally. This can be attributed to the seasonal incoming solar radiation variation and the consequential temperature variation at the measurement station (see Fig. 1b). The lower temperature in December results in higher open-circuit voltages (as demonstrated in Fig. 1d) when no significant temperature-dependency of the electrochemical reaction kinetics is assumed. This allows quite high optimum cell voltage (∼0.77 V). For the high-temperature season (i.e. July), the optimum cell voltage shifts negatively to around 0.7 V due to reduced photovoltage and the consequent maximum power point, as estimated above in Fig. 1d.
In the case with sluggish reaction kinetics (Fig. 2c), the difference between the optimum cell voltages for July and December is smaller than in the case with fast kinetics (i.e. there is no kinetic overpotential contribution), implying lowered sensitivity to the redox couple selection. However, this seasonal variation seems to be of minor importance for the cell voltage management as the average Pout of the warm season surpasses the maximum Pout in December by a factor of 2. Furthermore, the system with cell voltage at the Pout,max in summer (i.e. July) still yields an average power density that is nearly 95% of the Pout,max in December. Nevertheless, having a high cell voltage is an important parameter together with a sufficient electrolyte concentration for the energy storage capacity of the system with a limited electrolyte volume. As highlighted in other studies,9,11,35 a low discharge capacity would limit the potential of the redox flow cell for practical applications, such as RFBs for mobilities.
Although addressing cell voltage and electrolyte volume optimization for high storage capacity is beyond the scope of this work, the dynamic STC% landscape change with respect to the cell voltage and the band gap of the photo-absorber due to a change in the electrolyte volume is visualized in Fig. 3. This provides further insights into the flow cell operation. As shown in Fig. 3a, it is expected that an STC% of over 35% can be obtained if the band gap of the photo-absorber is within 1.2–1.4 eV and the thermodynamic cell voltage is around 0.8–1.0 V at noon. The silicon-based system (1.12 eV) is expected to exhibit a slightly lower but still relatively high theoretical maximum STC% of close to 33%. However, this estimation is applicable only if the state-of-charge (SOC) is a constant value (i.e. fixed SOC). The same STC% landscape is plotted in Fig. 3b, but under the assumption that the system has a finite storage volume (i.e. the conventional SRFB concept). As expected, no meaningful STC% output can be found for the conditions with a band gap and cell voltage of below ∼1.3 eV and 0.9 V, respectively. This landscape change is due to the high SOC, which, based on the Nernst equation, results in a cell voltage barrier shift,8,12 which, in turn, hampers the ability of the low band gap materials (i.e. low photo-voltage) to drive the redox chemical reaction.
In Fig. 3c and d, the output power for two different cell voltage systems with a c-Si photoelectrode is plotted over the course of a day charging from 5% to 85% of SOC under the same light illumination condition used for Fig. 1c and 2a. The dynamic SOC is implemented as described above. It can be observed that even a slight change in cell voltage (from 0.7 to 0.8 V) significantly changes the mean power converted into chemical energy when a dynamic SOC effect (like that of a conventional battery system) is considered, while the overall performance and trend for the continuous electrolyte flow with the steady SOC (50% in Fig. 3c and d) are preserved. This problem can be mitigated by careful redox-couple selection to secure a certain level of voltage margin between the thermodynamic cell voltage and the photovoltage of the system. We previously demonstrated this with a 95% SOC using a 0.51 V c-Si photocathode with a 0.35 V TEMPO-sulphate/ferricyanide SRFB system.36 At the same time, the results shown in Fig. 3c and d indicate that the SRFB system shows promise as a high power-rating system where the continuous flow of the electrolyte results in simultaneous charging and discharging.
Conclusions
After conducting a series of theoretical studies of the thermo-electrochemical effect on photo-charging performance, we came to understand that the management of excess thermal energy from the photo-absorber is a crucial factor for avoiding thermal loss during the course of a day. The proposed solar redox system, in which an electrolyte functions simultaneously as both an energy storage medium and a coolant, can enhance photo-charging efficiency owing to the thermally stabilized current–voltage behaviour of the photo-device and the improved redox reaction kinetics. The system we model in the present study has the potential to store a maximum of 21.8% more solar energy than the system with only air cooling (i.e. a conventional PV + redox flow system) under the mixed heat-transfer condition with a direct contact between the photo-absorber and the electrolyte, which has been applied in PEC redox systems reported in recent years.9,11,12 This implies that our findings would bring insights for unravelling hidden value (e.g. extra storable solar energy) and shed light on underrated PV-integrated energy storage systems. At the same time, the analysis implies that the kinetic advantage under the high-temperature conditions also would be impactful for the stand-alone system with high overpotential. Based on our results, we believe that our thermo-electrochemical approach contributes to the development of solid pathways for the broad implementation of solar redox technologies, including SRFBs and similar redox flow cells.Conflicts of interest
The authors declare no competing interests.Acknowledgements
We thank the financial supports provided by the LEaDing Fellowship from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 707404.Notes and references
- Q. Ding, F. Meng, C. R. English, M. Cabán-Acevedo, M. J. Shearer, D. Liang, A. S. Daniel, R. J. Hamers and S. Jin, J. Am. Chem. Soc., 2014, 136, 8504–8507 CrossRef PubMed.
- Z. Chen, T. F. Jaramillo, T. G. Deutsch, A. Kleiman-Shwarsctein, A. J. Forman, N. Gaillard, R. Garland, K. Takanabe, C. Heske, M. Sunkara, E. W. McFarland, K. Domen, E. L. Miller, J. a. Turner and H. N. Dinh, J. Mater. Res., 2010, 25, 3–16 CrossRef.
- H. M. Chen, C. K. Chen, R.-S. Liu, L. Zhang, J. Zhang and D. P. Wilkinson, Chem. Soc. Rev., 2012, 41, 5654 RSC.
- W. A. Smith, I. D. Sharp, N. C. Strandwitz and J. Bisquert, Energy Environ. Sci., 2015, 8, 2851–2862 RSC.
- D. Bae, B. Seger, P. C. K. Vesborg, O. Hansen and I. Chorkendorff, Chem. Soc. Rev., 2017, 46, 1933–1954 RSC.
- X. Feng, M. Ouyang, X. Liu, L. Lu, Y. Xia and X. He, Energy Storage Mater., 2018, 10, 246–267 CrossRef.
- X. Liu, D. Ren, H. Hsu, X. Feng, G. L. Xu, M. Zhuang, H. Gao, L. Lu, X. Han, Z. Chu, J. Li, X. He, K. Amine and M. Ouyang, Joule, 2018, 2, 2047–2064 CrossRef.
- K. Wedege, D. Bae, W. A. Smith, A. Mendes and A. Bentien, J. Phys. Chem. C, 2018, 122, 25729–25740 CrossRef.
- W. Li, H. C. Fu, Y. Zhao, J. H. He and S. Jin, Chem, 2018, 4, 2644–2657 Search PubMed.
- J. Wang, K. Lu, L. Ma, J. Wang, M. Dooner, S. Miao, J. Li and D. Wang, Energies, 2017, 10, 991 CrossRef.
- F. Urbain, S. Murcia-López, N. Nembhard, J. Vázquez-Galván, C. Flox, V. Smirnov, K. Welter, T. Andreu, F. Finger and J. R. J. R. Morante, J. Phys. D: Appl. Phys., 2019, 52, 044001 CrossRef.
- D. Bae, G. M. Faasse, G. Kanellos and W. A. Smith, Sustainable Energy Fuels, 2019, 3, 2399–2408 RSC.
- J. R. McKone, F. J. DiSalvo and H. D. Abruña, J. Mater. Chem. A, 2017, 5, 5362–5372 RSC.
- M. J. Adinoyi and S. A. M. Said, Renewable Energy, 2013, 60, 633–636 CrossRef.
- A. Trovò, A. Saccardo, M. Giomo and M. Guarnieri, J. Power Sources, 2019, 424, 204–214 CrossRef.
- A. Andreas and T. Stoffel, MIDC: NREL Solar Radiation Research Laboratory (BMS); NREL Report No. DA-5500-56488, Golden, CO, 1981 Search PubMed.
- D. Bae, G. Kanellos, G. M. Faasse, E. Dražević, A. Venugopal and W. A. Smith, Design principles for efficient photoelectrodes in solar rechargeable redox flow cell applications, Communications Materials, 2020 Search PubMed , in press.
- N. Ahmad, A. Khandakar, A. El-Tayeb, K. Benhmed, A. Iqbal and F. Touati, Energies, 2018, 11, 3231 CrossRef CAS.
- E. Garc, I. Almonacid, Á. Maria, C. Mart, V. Miroslavov, E. Serrano, J. Pedro and A. Salmer, Batteries, 2019, 5, 52 CrossRef.
- M. A. Green, J. Appl. Phys., 1990, 67, 2944–2954 CrossRef CAS.
- D. Bae, B. Seger, M. Malizia, I. Chorkendorff, P. C. K. Vesborg, T. Pedersen, O. Hansen and A. Kuznetsov, Energy Environ. Sci., 2015, 8, 650–660 RSC.
- E. A. Gibson, L. Le Pleux, J. Fortage, Y. Pellegrin, E. Blart, F. Odobel, A. Hagfeldt and G. Boschloo, Langmuir, 2012, 28, 6485–6493 CrossRef PubMed.
- C. H. Henry, Phys. Rev., 1952, 87, 387 CrossRef.
- W. Shockley and W. T. Read, Phys. Rev., 1952, 87, 835–842 CrossRef.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef.
- M. A. Green, Third Generation Photovoltaics - Advanced Solar Energy Conversion, Springer, Heidelberg, 2008 Search PubMed.
- C. Berthod, R. Strandberg, G. H. Yordanov, H. G. Beyer and J. O. Odden, Energy Procedia, 2016, 92, 2–9 CrossRef CAS.
- J. H. Lienhard IV and J. H. Lienhard V, A Heat Transfer Textbook, J. H.Lienhard V, Cambridge, 3rd edn, 2001 Search PubMed.
- J. C. Roy, T. Boulard, C. Kittas and S. Wang, Biosyst. Eng., 2002, 83, 1–20 CrossRef.
- A. J. Robinson, IEEE Trans. Compon. Packag. Technol., 2009, 32, 347–357 CAS.
- S. Tembhurne, F. Nandjou and S. Haussener, Nat. Energy, 2019, 4, 399–407 CrossRef CAS.
- Y. Fang, X. Li and X. Wang, ChemSusChem, 2019, 12, 2605–2608 CrossRef CAS.
- E. H. Calderon, A. Katsaounis, R. Wüthrich, P. Mandin, G. Foti and C. Comninellis, J. Appl. Electrochem., 2009, 39, 1827–1833 CrossRef CAS.
- J. Giner, L. Swette and K. Cahill, Screening of redox couples and electrode materials, Waltham, MA, 1976 Search PubMed.
- W. Li, H.-C. Fu, L. Li, M. Cabán-Acevedo, J.-H. He and S. Jin, Angew. Chem., Int. Ed., 2016, 55, 13104–13108 CrossRef CAS PubMed.
- K. Wedege, D. Bae, E. Dražević, A. Mendes, P. C. K. Vesborg and A. Bentien, RSC Adv., 2018, 8, 6331–6340 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: A description on the detailed calculation methods and specific heat data table used in this work. See DOI: 10.1039/d0se00348d |
| ‡ These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |