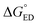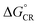Open Access Article
Open Access ArticleCharge transfer characteristics of fullerene-free polymer solar cells via multi-state electronic coupling treatment†
Tuuva
Kastinen
 * and
Terttu I.
Hukka
* and
Terttu I.
Hukka
 *
*
Chemistry and Advanced Materials, Faculty of Engineering and Natural Sciences, Tampere University, P.O. Box 541, FI-33014 Tampere, Finland. E-mail: tuuva.kastinen@tuni.fi; terttu.hukka@tuni.fi; Tel: +358 40 198 1133
First published on 8th June 2020
Abstract
Recently, non-fullerene (NF) polymer solar cells (PSCs), where new electron acceptor (eA) materials are blended with a donor–acceptor (D–A) copolymer as an electron donor (eD), have shown promising power conversion efficiencies up to 18%. Some of the best-performing NF PSCs use the eD copolymers PBDT-TzBI, PDTB-EF-T, and PBDB-T-2F, and either a D–A copolymer P(NDI2OD-T2) or small molecule acceptors (SMAs) ITIC-4F and ITIC-2Cl as the NF eA compounds. Here we investigate these systems with density functional theory methods and extend our previous study of the multi-state fragment charge difference (FCD) electronic coupling scheme by applying it to the calculations of charge transfer (CT) rates for exciton dissociation and charge recombination (CR) processes at local eD–eA interfaces. Despite similar backbone structures and optical properties, the studied eD copolymers have different conformational, ionization, excitation, and CT characteristics. The electronic couplings and CT rates depend strongly on the relative positioning of the eD and eA compounds in the eD–eA complexes. While the main CT path is from eD to the eA compound, CT from eA to the eD compound is also predicted in the polymer–polymer PBDT-TzBI–P(NDI2OD-T2) system. The multi-state FCD electronic couplings are independent of the number of the excited states included in the calculations when using a dispersion-corrected optimally tuned long-range corrected functional. The calculated CR rates are slower in the polymer–SMA systems than in the polymer–polymer system, which could partly account for their higher experimentally observed efficiencies in devices.
Introduction
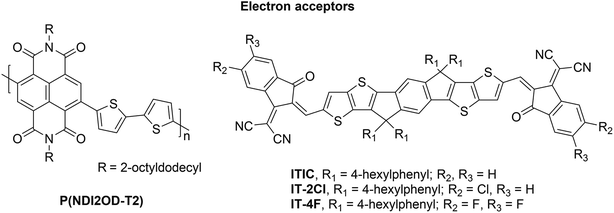
Polymer solar cells (PSCs) have a great potential as a low-cost, lightweight, flexible, and scalable technology for light conversion.1,2 So far, the most studied systems have included fullerene derivatives as the electron acceptor (eA) materials with conjugated donor–acceptor (D–A) copolymers as the electron donor (eD) materials. Although these fullerene-based PSCs have achieved promising power conversion efficiencies (PCEs) of ca. 12%,3,4 they possess several hindrances, such as limited possibilities to tune the chemical structures and energy levels of fullerene derivatives, high synthesis cost, poor light absorption in the visible and infrared spectral regions, and morphological instabilities.5,6 To overcome these limitations, the researchers have developed alternative eA materials with tunable structural and optoelectronic features, which can be matched with a wider range of eD copolymers. As a consequence, a rapid and encouraging progress has been made in designing fullerene-free, i.e. non-fullerene (NF) PSCs during the past few years.5,7In all-polymer solar cells (APSCs), D–A copolymers composed of electron-rich donor and electron-deficient acceptor units in the constitutional repeating unit (CRU) are employed as both the eD and eA materials. This type of a design strategy8,9 has enabled fine-tuning of the structural and optoelectronic properties, e.g. ionization energies (IE), electron affinities (EA), and optical gaps, of the D–A copolymers by selecting the backbone donor and acceptor units with the desirable characteristics.10 Controlling these features for the eA compounds can yield APSC devices with improved light absorption, higher open-circuit voltage, and enhanced long-term stability compared to the conventional, fullerene-based PSCs.5 Especially, naphthalene diimide (NDI) based copolymers have been popular eA materials in APSCs due to their large EAs, high electron mobilities, and good thermal and oxidative stabilities.11,12 The highest PCEs have been ca. 12%13,14 for APSCs using poly[(N,N′-bis(2-octyldodecyl)naphthalene-1,4,5,8-bis(dicarboximide)-2,6-diyl)-alt-5,5′-(2,2′-bithiophene)] (P(NDI2OD-T2), also referred to as N2200) as the eA material15 (Fig. 1). These efficiencies have been surpassed recently with a new eA copolymer (PJ1), which is based on a small molecule acceptor (SMA) building block leading to the PCE of 14.4%.16
Another emerging type of the efficient NF PSCs makes use of π-conjugated SMAs as the eA materials, whose acceptor–donor–acceptor (A–D–A) structure leads to strong intramolecular electron push–pull effects similar to the ones in D–A copolymers. For example, in a successful ITIC,17 an electron-donating, bulky seven-ring indacenodithieno[3,2-b]thiophene (IT) core is end-capped with electron-withdrawing 2-(3-oxo-2,3-dihydroinden-1-ylidene)malononitrile (INCN) groups. This type of a rigid A–D–A structured backbone results in the extended conjugation and reduces reorganization energy, which is beneficial for charge transport.17,18 However, on the downside, planar backbones with the extended conjugation may lead to the undesired aggregation behavior for ITIC (and other SMAs) and consequently decreased efficiencies of PSCs. Thus, four 4-hexylphenyl have been substituted to the IT core to restrict the planarity and consequently aggregation of ITIC in blend films. The advantages of ITIC derivatives are strong light absorption and good electron mobility. Furthermore, their properties can be easily tuned via molecular modifications, while simultaneously maintaining their key aspects of efficient eAs.19,20 For example, NF-SMA PSCs based on ITIC derivatives with halogenated (e.g. fluorinated or chlorinated) end groups have some of the highest PCEs (ca. 15%) for PSCs.21–23 The record PCEs (ca. 18%24) for the NF PSCs have been achieved recently with a SMA25 (Y6) consisting of dithienothiophen[3.2-b]-pyrrolobenzothiadiazole core and 2-(5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile side groups.
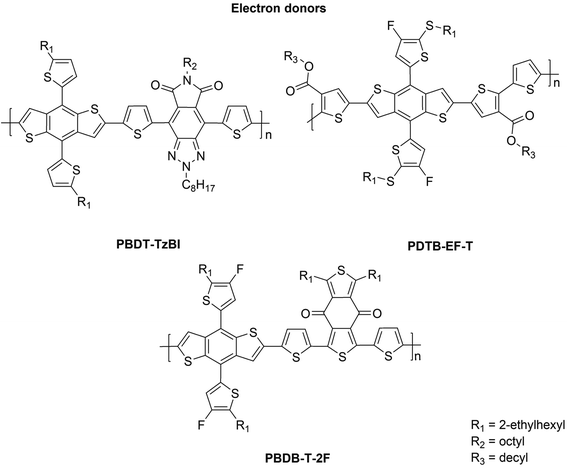
The NF eA materials discussed above have either small (i.e. below 1.50 eV; ca. 1.48 eV for P(NDI2OD-T2)) or medium (i.e. 1.50–1.90 eV; ca. 1.60 eV for ITIC) bandgaps.26 Thus, to achieve a wide absorption of the solar spectrum and efficient NF PSCs, they are typically combined with medium- or wide-bandgap (>1.9 eV) copolymers as the eD compounds. These kinds of copolymers (Fig. 2) include poly[4,8-bis(5-(2-ethylhexyl)thiophen-2-yl)benzo[1,2-b:4,5-b′]dithiophene-co-4,8-di(thien-2-yl)-6-octyl-2-octyl-5H-pyrrolo[3,4-f]benzotriazole-5,7(6H)-dione] (referred to as PBDT-TzBI in this work; known also as PTzBI27 or PTZBIBDT28), PDTB-EF-T,29 and poly[(2,6-(4,8-bis(5-(2-ethylhexyl)-4-fluorothiophen-2-yl)benzo[1,2-b:4,5-b′]dithiophene))-alt-(5,5-(1′,3′-bis(thiophen-2-yl)-5′,7′-bis(2-ethylhexyl)benzo[1′,2′-c:4′,5′-c′]dithiophene-4,8-dione))],30,31 see the ref. 32 for the alternative naming (referred to as PBDB-T-2F![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 in this work; known also as PBDB-TF21 or PM6
33 in this work; known also as PBDB-TF21 or PM6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31). Among these eDs, PBDT-TzBI28 and PBDB-T-2F31 have been originally developed for fullerene-based PSCs.
31). Among these eDs, PBDT-TzBI28 and PBDB-T-2F31 have been originally developed for fullerene-based PSCs.
All of the aforementioned copolymers have the same weak, electron-rich donor unit, benzo[1,2-b:4,5-b′]dithiophene (BDT), but different electron-deficient acceptor units, TzBI in PBDT-TzBI28 and 1,3-bis(thiophen-2-yl)-5,7-bis(2-ethylhexyl)benzo[1,2-c:4,5-c′]dithiophene-4,8-dione (BDD)34,35 in PBDB-T-2F. In addition, there are thiophene spacers between the donor and acceptor units, which have a role in controlling planarity, and accordingly, aggregation.36 The introduction of thiophenes in the copolymer backbone also weakens the intramolecular charge transfer (CT) character between the donor and acceptor units, which leads to the medium or wide band gaps in these copolymers.37 In PDTB-EF-T, the thiophenes with the electron-withdrawing ester groups have been used instead of a strong electron-deficient unit.29 Additionally, the desired IEs, EAs and structural characteristics of these copolymers have been achieved by attaching different functional groups, such as aromatic rings (e.g. thiophene) and electronegative atoms, e.g. fluorine,29,31,33,38 to their backbones.
Theoretical quantum chemical calculations provide means for determining intrinsic structure–property relationships of π-conjugated PSC materials. Moreover, they can provide insight into the CT processes taking place at local interfaces of the eD and eA compounds. So far, there have been a number of studies on structural and optoelectronic properties of individual NF PSC compounds with density functional theory (DFT) methods.25,39–42 For example, Wang et al. have investigated both the electronic and optical properties of two NF SMAs (IDIC and IDTBR) and five D–A copolymers and their interfacial characteristics.41 The effect of fluorination on the characteristics of the eD copolymers and ITIC has been examined by Benatto et al.43 Local interfaces in the NF devices have been exploited, as well.23,41,44–49 Han et al. have studied the impact of different eD molecular architectures on the interfacial arrangements and electronic properties of the NF organic solar cells based on small-molecule eDs and the SMA ITIC-4F with the multiscale simulations combining molecular dynamics (MD) and DFT calculations.45 Moreover, they have compared the interfacial complexes consisting of PBDB-T-2F as the eD copolymer and either PC71BM or ITIC as the eA compound with both MD and DFT.44 The NF PSC systems of PBDB-T-2F and different ITIC derivatives have been the subject of other MD simulations, as well.46–49 Han et al. have also compared the packing of the ITIC and PC71BM acceptor thin films with MD simulations.50 While these studies have included electronic structure calculations of some of the aforementioned efficient NF PSC compounds, they have mostly concentrated on the MD simulations of the blend morphologies, and thus a deeper understanding of the electronic structure–function relations and CT characteristics of these compounds is still required.
For the efficient charge generation in PSCs, the rates of exciton dissociation (ED) should be maximized, whereas the rates of charge recombination (CR) should be minimized.51 In the previous theoretical studies of the NF PSCs systems, the ED and CR rates have also been evaluated to gain deeper understanding of these CT pathways.47–49 The electronic coupling (Hif) between the initial (i) and final (f) charge-localized, i.e. diabatic states is one of the key parameters defining the CT rates.52 Number of different theoretical approaches have been developed for calculating the couplings.53–55 In the studies of polymer–fullerene-based PSC systems, the two-state fragment charge difference (FCD)56 and generalized Mulliken–Hush (GMH)57,58 schemes have been popular choices.59–62 However, if a component of the local excitation is mixing with the CT state of interest, multiple adiabatic states should be included to obtain a more accurate description of the diabatic states.63,64 In our previous studies,65,66 we have observed the tendency of the long-range-corrected (LRC) functionals to predict mixed CT states for the polymer–fullerene systems. Our latest study66 showed that use of the multi-state FCD and GMH schemes64 with both the non-tuned and optimally-tuned (OT) LRC functionals reduces this mixing. In the previous studies of the NF PSC systems, the GMH scheme has been applied in conjunction with the (non-tuned) LRC functional CAM-B3LYP for PBDB-T–ITIC47,48 and with the OT-ωB97X-D functional for PBDB-T–IT-OM.49 However, the FCD scheme, which we observed66 to be less sensitive to the number of states and the choice of the calculation method compared to GMH, does not seem to have been applied for the NF PSC systems yet. Furthermore, it is beneficial to investigate, whether the inclusion of multiple states effects the electronic couplings of the NF PSC systems. Information regarding the effect of the dispersion corrections included in the DFT functional on the multi-state coupling calculations is still missing, as well.
In this work, we will investigate via DFT and time-dependent DFT (TDDFT) methods a selected set of eD (Fig. 2) and eA (Fig. 1) compounds, which have been recently employed in some of the most efficient NF PSCs.6,27,29,33,67 The selected eD compounds include D–A copolymers PBDT-TzBI, PDTB-EF-T, and PBDB-T-2F, whereas for the eA compounds, the D–A copolymer P(NDI2OD-T2), the SMA ITIC, and its fluorinated and chlorinated counterparts, ITIC-4F and ITIC-2Cl, respectively, have been chosen. We use theory to shed light on those characteristics that make the selected compounds successful and on the CT processes that take place at their local eD–eA interfaces. The first part of the work will explore the structural, ionization, excitation, and optoelectronic properties of the individual eD and eA compounds. In the second part, we will examine the local interfacial configurations, CT characteristics, and CT rates for the ED (eD*–eA → eD+–eA−) and CR (eD+–eA− → eD–eA) processes of the corresponding eD–eA complexes. For obtaining the CT rates, we utilize the multi-state FCD scheme to calculate the electronic couplings. This work extends our previous study66 of the effects of the two- versus multi-state treatments on electronic couplings in fullerene-based PSC systems by exploring the influence of multiple states and dispersion corrections on coupling values of the studied NF PSCs. Based on our65 and other's findings68,69 on organic solar cell systems, dispersion corrections are important for describing weak dispersion interactions at their local eD–eA interfaces. Furthermore, tuned LRC functionals have performed well in calculations of both the individual PSC compounds70,71 and local interfaces.65,66 Thus, the OT version of the dispersion corrected LRC functional ωB97X-D72 was selected to investigate the effects of both the tuning of a LRC functional and dispersion corrections on the electronic coupling values. In some of the TDDFT calculations, we employ also the global hybrid PBE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73–75 functional for comparison.
73–75 functional for comparison.
Computational details
Models
The eD and eA compounds studied here (see Fig. 1 and 2) comprise both of the D–A copolymers (PBDT-TzBI, PDTB-EF-T, PBDB-T-2F, and P(NDI2OD-T2)) and the A–D–A-type SMAs (ITIC, ITIC-2Cl, and ITIC-4F). In most calculations, the full-length side chains of the compounds were replaced by methyl groups to reduce the computational cost, except for some of the relaxed potential energy surface (PES) scans of the side groups to check the dihedral angles within the side groups and between the side groups and the backbone donor or acceptor units. We note, however, that long alkyl side chains affect the solid-state packing and resulting optoelectronic characteristics,76 and they should be included, e.g. when the atomistic simulations of blends are carried out.The eD and eA copolymer models are defined by their CRUs (i.e. the repeating units, n). A CRU consists of donor and acceptor units and additional thiophene spacers. The monomer and oligomer models of the copolymers consist of 1–4 CRUs and will be referred to as BDT-TzBI, DTB-EF-T, BDB-T-2F, and NDI2OD-T2 (without P in front). The relative orientations of their backbone units were selected based on the relaxed PES scans (see Methods below and Fig. S1–S3† for the studied dihedrals). Within the CRU of a D–A copolymer, neighboring donor and acceptor units can be either anti to each other, i.e. the neighboring heteroatoms of the units are on the opposite sides, or syn to each other, i.e. the neighboring heteroatoms are on the same side. Similarly, the neighboring CRUs can be either anti or syn with respect to each other. In the text, the conformations are referred to as: anti/anti or anti–anti/anti, where the first word (or words) refers to the conformation(s) within one CRU and the second word to the conformation between two CRUs. Here, we have considered only the energetically most stable conformations for each copolymer.
Monomer models (i.e. hydrogen-terminated CRUs, n = 1) of the D–A copolymers were used in the PES calculations to determine the optimal dihedral angles within the backbone. Furthermore, the monomers were employed in the eD–eA complexes (see below). In the studies of the structural, ionization, and excitation characteristics of the individual eD and eA compounds, trimers (n = 3) were used as the oligomeric models of the D–A copolymers. As an exception, P(NDI2OD-T2) was modeled using a tetramer (n = 4) to keep the relative conjugation lengths (i.e. the number of the double bonds, N, within the shortest path between the terminal carbon atoms of the backbone) in the copolymer models consistent with each other.
The eD–eA complexes were constructed using the optimized GS geometries of the monomer models of the eD and eA copolymers and the ITIC-based eA compounds. In addition, dimer models of both the eD copolymer PBDT-TzBI and eA copolymer P(NDI2OD-T2) were used in one complex configuration to study the effect of a longer oligomer on the local structure and CT characteristics at the eD–eA interface. In all complexes, the eD models were oriented in the xy plane along the x axis. Three configurations of each complex were studied: the eA model was positioned above the donor, thiophene, and acceptor unit of the eD model along the x axis by superposing the centroids of the specific heterocyclic aromatic rings with the initial intermolecular distance of 4 Å (see the ESI† for further information of construction of different configurations). After this, the complexes were fully optimized without any constraints (see Methods).
Methods
All the calculations were carried out with the Gaussian 16 Rev.B01 suite of programs,77 except for the electronic coupling calculations of the complexes, which were carried out with the Q-Chem 4.2 software.78 The LRC ωB97X-D functional72 was selected, as it includes the dispersion corrections and is recommended for studying systems with extended π-conjugated structures.68To determine the relative orientations of the backbone units in the eD and eA compounds for the further calculations, the torsional potentials between the adjacent units within the monomer models of the eD and eA copolymers and the eA compound ITIC in their neutral GS geometries were determined with the relaxed PES scans at the ωB97X-D/6-31G** level of theory in vacuum (with the default range-separation parameter, ω, of 0.2 bohr−1). The PES scans were carried out also for the dihedral angles between the BDT donor unit and the full-length alkyl thiophene side groups of the eD models (BDT-TzBI, DTB-EF-T, and BDB-T-2F) in addition to those between the BDD acceptor unit and alkyl side chains of BDB-T-2F to check their relative orientations (Fig. S3†). The constrained geometry optimizations were carried out at 5° intervals, i.e. the studied dihedral angle was kept fixed while fully optimizing the geometry of the rest of the compound.
For all the other DFT and TDDFT calculations, the optimally tuned dispersion corrected functional, OT-ωB97X-D, was used with the 6-31G** basis set, unless stated otherwise (see the next paragraph). For this purpose, the ω value in ωB97X-D was optimally tuned in vacuum with the gap tuning procedures for the individual eD and eA compounds79,80 (eqn (S1) in ESI†) and the eD–eA complexes65,66,80,81 (eqn (S2) in ESI†). The OT ω values were determined with an accuracy of 0.01 bohr−1 using the 6-31G** basis set. The GS geometries of the neutral eD and eA compounds and their radicals, i.e. cations and anions, were fully optimized with DFT. In the characterization of the individual compounds, calculations were carried out in vacuum, solvent, and blend environments, unless stated otherwise. Solvation effects were included by means of the conductor-like polarizable continuum model (CPCM)82,83 using the static (εs) and dynamic (i.e. optical, εop) dielectric constants of 4.7113 and 2.090627, respectively, for CHCl3. For the blend environment, the εs and εop of 4.00 and 2.25 were used, respectively, which are approximate values employed in previous studies for different organic semiconductors.84,85 For studying ionization of the eD and eA compounds, their vertical and adiabatic ionization energies (IEs, VIE and AIE) and electron affinities (EAs, VEA and AEA) were calculated with eqn (S3)–(S6) (ESI†). The intramolecular reorganization energies for the hole (λh) and electron (λe) transfer of the eD and eA compounds were calculated with eqn (S7) and (S8).†
For examining the intramolecular CT character of the NF PSC compounds and determining their UV-vis absorption spectra, the vertical excitation energies for the 10 lowest excited singlet states of the isolated eD and eA compounds were carried out with TDDFT. For the ITIC derivatives, the vertical excitations for the 20 lowest excited singlet states were required to yield the best description of the UV-vis spectra. Additionally, the TDDFT calculations of the individual eD and eA compounds were carried out in CHCl3 at the PBE0/6-31G** level of theory using the OT-ωB97X-D-optimized geometries for comparing with the OT-ωB97X-D calculated spectra. The graphical illustrations of the UV-vis absorption spectra were created via convolution of the calculated singlet vertical transition energies and oscillator strengths using a Gaussian-shape broadening with a full width at half-maximum (FWHM) of 0.30 eV.
The nature of the excited states for both the individual NF PSC compounds and their complexes was described using natural transition orbitals (NTOs)86 as a representation for the transition density matrix. The NTOs for the complexes were obtained from the TDDFT calculations carried out with Q-Chem, whereas the NTOs of the individual compounds were generated from the TDDFT calculations using Gaussian. Only the dominant pairs of the NTOs, i.e. those with the largest eigenvalues (λNTO) indicating the fraction of a particular hole–electron excitation to the overall transition,86,87 were considered. In the case of the individual compounds, the contributions of the backbone units to the NTOs were determined using the C-Squared Population Analysis (C-SPA)88 as implemented in Multiwfn 3.6.89–91 For the eD–eA complexes, the nature of the states was determined from the pictorial presentations of the NTOs and calculating the contributions of the eD and eA compounds to the NTOs by using the C-SPA within a self-made code. Pictorial presentations of the geometries and NTOs were generated using ChemCraft 1.8.92
The CT rates for the ED and CR processes taking place at the local interfacial complexes were calculated with the semi-classical Marcus theory:93–95
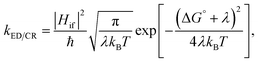 | (1) |
Results and discussion
Ground-state structural properties of the eD and eA compounds
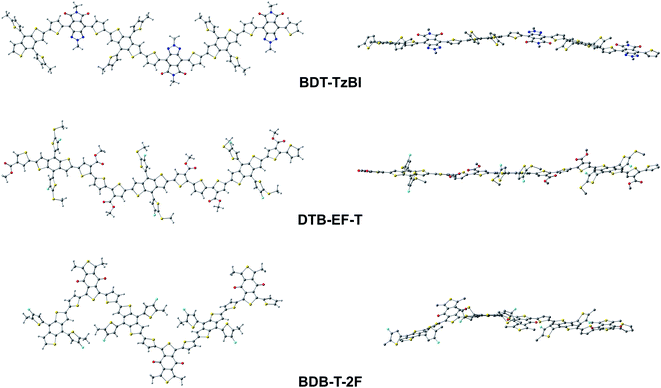
To better understand the characteristics of the studied NF PSC compounds, we begin by exploring the geometrical structures of the individual eD oligomers and eA compounds. The shapes and sizes of the π-conjugated donor and acceptor units and the inclusions of the additional spacer units between them are among the factors defining the shapes of the backbones of both the D–A copolymers97 and SMAs.98 In addition, conformational preferences and resulting torsions induced by weak non-bonding interactions99 between heteroatoms and between heteroatoms and hydrogens in the adjacent electron-rich and electron-deficient units affect the shape of the backbone.44,100First, we will consider the eD copolymers. Based on their OT-ωB97X-D-optimized (see Tables S1 and S2† for the OT ω values) GS trimer geometries, BDT-TzBI, DTB-EF-T, and BDB-T-2F have twisted backbones with different curvatures (Table 1 and Fig. 3). The backbones of BDT-TzBI and BDB-T-2F have sine wave patterns, whereas that of DTB-EF-T has a zigzag pattern.101 Furthermore, the curvature of the backbone increases in the order of DTB-EF-T < BDT-TzBI < BDB-T-2F, which can impact the degrees of ordering and folding of the copolymer chains and the mixing of the eD and eA compounds in the blends.97 The backbones of the eD trimers are predicted to have similar torsional twists of 2–49° from planarity regardless of the surrounding medium (Table 1 and Fig. 3; see also Table S3 and Fig. S1† for the PES curves). In all cases, each BDT donor unit and its neighboring thiophene spacers are anti to each other in the eD trimer models due to the repulsive S⋯S interactions.99 The thiophenes and acceptor units are syn to each other in BDT-TzBI and BDB-T-2F because of the possible nontraditional hydrogen bonding99 between the carbonyl oxygen of the acceptor unit and the C–H hydrogen of the neighboring thiophene. In DTB-EF-T, the thiophenes are anti to each other, except for those between the adjacent CRUs that are syn to each other due to a possible hydrogen bonding between the hydrogen of the unsubstituted thiophene and the carbonyl oxygen of the ester group in the thiophene of the next CRU. The same conformation has been also predicted for the dimer model of PDTB-EF-T in the original study of Li et al.29
| Type | Compound | n | N | Conformation | Backbone type | Planarity | Dihedral angleb (°) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| α 1 | α 2 | α 3 | θ CRU–CRU | |||||||
| a The neutral GS geometries. b See Fig. S1 and S2 for the definition of the dihedral angles. The dihedral angles of the eD and eA compounds determined in vacuum and CHCl3 are presented in Table S3. c Number of the CRUs in the studied oligomer. d Number of the double bonds in the studied oligomer. e Between the CRUs in the oligomers. | ||||||||||
| eD | BDT-TzBI | 3 | 30 | Anti–syn/anti | Sine wave | Twisted | 157–159 | 41–42 | 43–44 | 159–162 |
| DTB-EF-T | 3 | 30 | Anti/syn | Zigzag | Twisted | 159–162 | 159–160 | 131–152 | 45 | |
| BDB-T-2F | 3 | 30 | Anti–syn/anti | Sine wave | Twisted | 156–162 | 39–44 | 43–44 | 175–178 | |
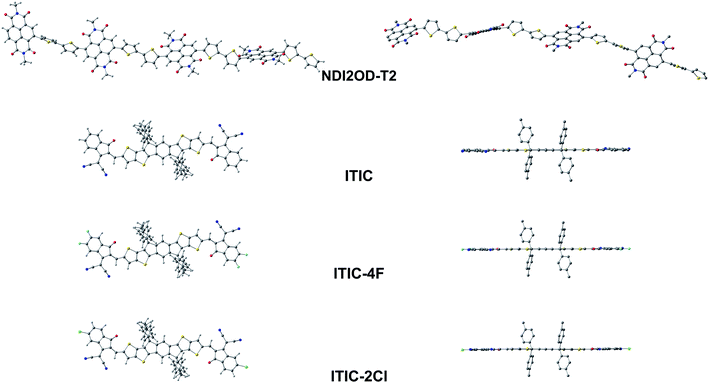
| eA | NDI2OD-T2 | 4 | 28 | Syn–anti/syn | Helical | Twisted | 56–57 | 152–153 | — | 60–61 |
| ITIC | — | — | Anti | Linear | Planar | 180 | — | — | — | |
| ITIC-4F | — | — | Anti | Linear | Planar | 180 | — | — | — | |
| ITIC-2Cl | — | — | Anti | Linear | Planar | 180 | — | — | — | |
Next, we will turn our attention to the eA compounds. The OT-ωB97X-D functional predicts that the eA tetramer NDI2OD-T2 has a slightly helical backbone with a small curvature most probably due to the syn–anti/syn conformation (see below). The thiophene donors are predicted to be anti to each other with the torsion from planarity of ca. 27–28° between them (see Tables 1 and S3†), which is in line with, although somewhat smaller than the previous findings (the torsion of 32° from planarity by B3LYP/6-311G**102). The thiophene donor and NDI acceptor units of NDI2OD-T2 are not in the same plane due to the relatively large dihedral angles (ca. 60°) between them (Tables 1, S3, Fig. 4 and S2†). Similar, although somewhat smaller dihedrals have been predicted previously theoretically (syn-conformation: 42° and anti-conformation: 138°) using the global hybrid functional B3LYP (with the 6-311G** basis set) and experimentally (syn: 37° and anti: 142°) with the IR and reflection–absorption IR spectroscopy measurements.102 Here, the use of a LRC functional and truncated side groups could explain, respectively, the differences compared to the previous theoretical and experimental results.102 Larger (ca. 65°) than the experimental dihedrals have been obtained previously also with a (non-tuned) LRC CAM-B3LYP functional.103 Here, the adjacent NDI acceptor and thiophene donor units in NDI2OD-T2 are predicted to be syn to each other, i.e. the sulfur atoms of the thiophene donors and the closest carbonyl oxygens of the neighboring acceptor units are on the same side. Previous theoretical studies have predicted varying results for the preferred orientation between the NDI and thiophenes depending on the copolymer model and functional: (i) equally stable anti and syn conformations (for the dimer model, B3LYP/6-31G*),104 (ii) more favorable anti (for the monomer and pentamer models, B3LYP/6-311G**),102 or (iii) more favorable syn conformation (for the dimer model, CAM-B3LYP/6-31G*).103 Furthermore, the inclusion of full-length side chains and presence of the other NDI2OD-T2 chains play a role in defining the more favorable conformation in the real blend environment.105
The OT-LRC functional OT-ωB97X-D predicts that the backbones of the SMA compounds ITIC, ITIC-4F, and ITIC-2Cl are completely planar (Table 1, Fig. 4 and S2†). In the experimental X-ray diffraction analysis of ITIC and fluorinated ITIC derivatives, somewhat larger torsions (4–16°) between the IT core and the INCN end-groups have been observed for their single-crystal structures.106 Based on our calculations, ITIC prefers the syn-conformation, where the sulfurs of the IT donor core and the carbonyl oxygens of electron-deficient INCN end-groups are on the same side. This finding is consistent with both the previous theoretical calculations carried out at the B3LYP/6-31G** level of theory107 and experimental X-ray diffraction analysis.106 Based on these modeling results on ITIC compounds, both the extended π-conjugation and planarity have been gained via fused sp2-hybridized rings, which agree with the experimental goals for SMAs to pursue strong light absorption and good charge mobility, respectively.17,18
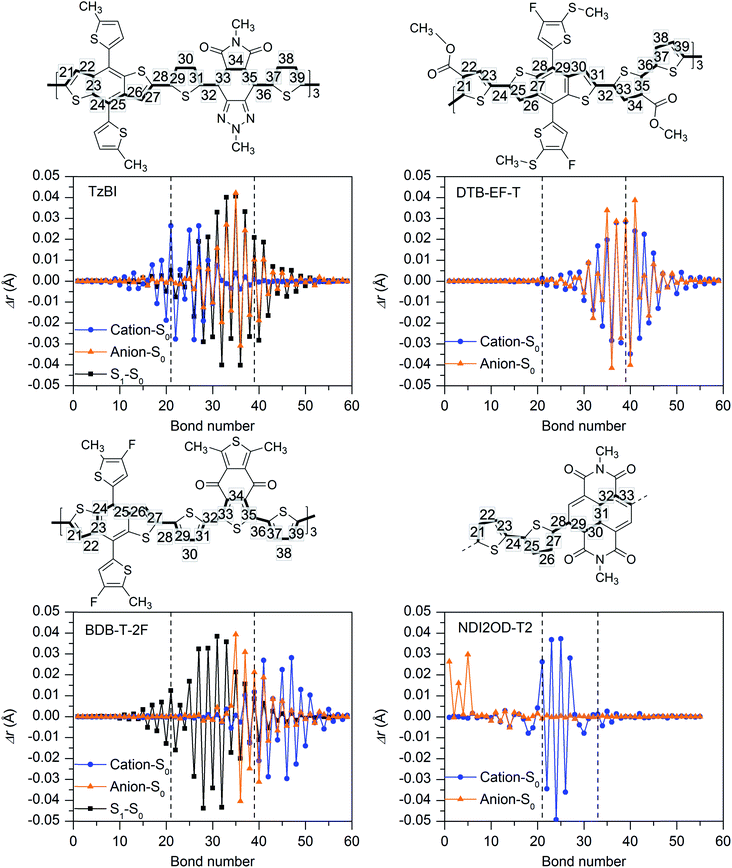
The degree of the aromaticity and delocalization of the π-electrons in the polymers, i.e. π-conjugation, is described by the bond length alternation (BLA) parameter, which is defined here as the average value of the differences between adjacent single and double C–C bonds. Greater delocalization leads to equalized bond lengths and thus to the lower BLA values.108,109 The BLA values calculated for the centermost CRUs (BLAmiddle) of the (neutral) GS geometries of the eD trimers BDT-TzBI, DTB-EF-T, and BDB-T-2F are very similar (Table 2, see Table S4† for the total BLA values) indicating similar delocalization along their conjugation paths (see Fig. 5). Moreover, the BLAmiddle of the eA tetramer NDI2OD-2T, which has been calculated for the innermost donor and acceptor units, is only slightly larger than those of the eD trimers. If two innermost CRUs of NDI2OD-2T are considered instead, the BLAmiddle values increase somewhat. Based on the positive BLAmiddle, these eD and eA copolymers have highly alternated single and double C–C bond patterns in their backbones (also referred to as an “aromatic” character in literature sometimes109,110). The environment does not seem to have strong effect on the BLAmiddle values, as they are very similar in blend, CHCl3, and vacuum. Here we note that for molecules with a large degree of conjugation (i.e. long polyene and cyanine chains), the tuning of ω may lead to incorrect BLA values, which may originate from the lack of size-consistency and an unbalanced description of σ and π orbitals in the tuned LRC functionals.111 However, as we are merely interested in the relative results between different compounds and not the absolute values, we expect the OT-LRC functional to be suitable for this case.
| Compound | BLAmiddle | Intramolecular reorganization energies | ||||
|---|---|---|---|---|---|---|
| S0 (GS) | S1 | Cation | Anion | λ h (eV) | λ e (eV) | |
| a Calculated for the conjugation paths presented in Fig. 5. b For the hole (λh) and electron transfer (λe). Calculated with eqn (S7) and (S8). c In the case of the copolymers, n = 3 for BDT-TzBI, DTB-EF-T, and BDB-T-2F and n = 4 for NDI2OD-2T. d The S1 geometries of DTB-EF-T did not converge in either CHCl3 or blend. e For the (three) innermost donor and acceptor units. f For the two innermost CRUs. | ||||||
| BDT-TzBI | 0.046 | 0.006 | 0.016 | 0.017 | 0.30 | 0.42 |
| (0.047) | (0.000) | (0.025) | (0.021) | (0.30) | (0.44) | |
| [0.047] | [0.001] | [0.025] | [0.022] | [0.31] | [0.46] | |
| DTB-EF-T | 0.044 | 0.012d | 0.010 | 0.019 | 0.30 | 0.50 |
| (0.045) | (0.022) | (0.023) | (0.38) | (0.60) | ||
| [0.045] | [0.021] | [0.023] | [0.38] | [0.60] | ||
| BDB-T-2F | 0.046 | 0.005 | 0.018 | 0.039 | 0.27 | 0.18 |
| (0.047) | (0.000) | (0.023) | (0.030) | (0.38) | (0.43) | |
| [0.047] | [0.000] | [0.041] | [0.030] | [0.42] | [0.46] | |
| NDI2OD-T2 | 0.048e/0.051f | — | 0.039e/0.029f | 0.031e/0.038f | 0.75 | 0.43 |
| (0.049e/0.052f) | (0.011e/0.033f) | (0.037e/0.046f) | (0.64) | (0.42) | ||
| [0.049e/0.052f] | [0.010e/0.032f] | [0.049e/0.052f] | [0.65] | [0.34] | ||
| ITIC | — | — | — | — | 0.24 | 0.26 |
| (0.22) | (0.24) | |||||
| [0.22] | [0.25] | |||||
| ITIC-4F | — | — | — | — | 0.25 | 0.27 |
| (0.22) | (0.25) | |||||
| [0.22] | [0.25] | |||||
| ITIC-2Cl | — | — | — | — | 0.24 | 0.26 |
| (0.22) | (0.24) | |||||
| [0.22] | [0.24] | |||||
In conclusion, while some similar features are observed for the studied eD and eA compounds, they have distinguished features in the shapes of their backbones, degrees of the planarity, and conformational preferences, which may have impact on their packing and mixing behavior in the photoactive blends. However, we note that in the case of the copolymers, more than one backbone conformation can coexist in real solvent and solid-state environments.105,112 Moreover, the polymer chains may adopt conformations in blends other than those predicted for single chains due to the stabilizing effects of the bulk interchain interactions.113 The inclusion of the full-length side chains can also lead to somewhat different results compared to our models with truncated CH3 side groups. For example, DFT PES scans of several D–A copolymers have been noted to yield more planar structures for the monomer models of CRUs than in aggregates given by MD simulations.114 Nevertheless, these results shed more light on the intrinsic properties that may impact the interactions between the studied eD and eA compounds at their eD–eA interfaces.
Ionization of the eD and eA compounds
In the next paragraphs, we compare the ionization (both the oxidation and reduction) characteristics of the studied eD and eA compounds. In general, oxidation and reduction cause notable changes in the geometries of the eD and eA oligomers, as is observed from the bond length differences (Fig. 5 for blend and Fig. S4† for vacuum and CHCl3) and the BLA values (Tables 2 and S4†) of the radicals (cation and anion) with respect to the corresponding neutral compounds. The largest changes in the eD and eA oligomers caused by oxidation and reduction occur mainly in their middle regions, i.e. the centermost CRUs, although there are some variations depending on the surrounding medium. Moreover, larger intramolecular reorganization energies for the hole (λh) and electron (λe) transfer, which correspond to the relaxation energies of the compounds upon oxidation and reduction, respectively, are predicted in blend and CHCl3 indicating somewhat larger geometrical changes in these environments compared to vacuum (Table 2). Ionization of the neutral oligomers mainly shortens the single bonds and lengthens the double bonds resulting in an inverse single–double C–C bond pattern compared to the neutral GS geometries. Decreased bond length alternation between single and double bonds and thus increased delocalization can be observed also from smaller BLAmiddle values of the most radicals compared to the neutral compounds (Table 2).Oxidation induces rather similar geometrical changes to all three eD trimer models, as can be observed from their bond length difference patterns (Fig. 5 and S4†). However, the backbone regions, which are affected the most by oxidation, are somewhat different for them. In BDT-TzBI and BDB-T-2F, the largest changes are observed in both the BDT donor and thiophene spacer units, whereas in DTB-EF-T, the largest changes caused by oxidation take place in both the unsubstituted electron-rich and ester-substituted electron-deficient thiophenes (see ‘Excited-state characteristics of the isolated eD and eA compounds’ below), while the BDT donor units are mainly unaffected. The λh values (Table 2) and IEs (both VIEs and AIEs, Fig. S5 and Table S5 in ESI†) of the eD trimers increase slightly in the order of BDT-TzBI < DTB-EF-T ≤ BDB-T-2F in both blend and CHCl3, which indicates the smallest changes for BDT-TzBI making it the easiest to oxidize among the studied eD trimers (in vacuum, the trends in the λh and IE values vary more). The calculated λh values suggest that the hole mobilities of the eD compounds increase in the order of BDB-T-2F < DTB-EF-T < BDT-TzBI, which is in line with the experimental hole mobilities predicted for the corresponding copolymers.28,29,115
Reduction of the eD trimers takes mainly place in different backbone regions than oxidation, namely in the acceptor units and neighboring thiophenes for BDT-TzBI and BDB-T-2F. The surrounding medium has some effect on these regions, as reduction of BDB-T-2F affects mostly its thiophene spacers in vacuum instead of the BDD acceptor unit. In DTB-EF-T, reduction takes place in the same units as oxidation, i.e. the unsubstituted electron-rich and substituted electron-deficient thiophenes. The λe values of the eD trimers increase in the order of BDB-T-2F < BDT-TzBI < DTB-EF-T (in all media) following the same trend as their λh values in vacuum (Table 2). Overall, the λh values are predicted to be smaller than the λe values for the eD compounds indicating faster hole mobilities,43 as can be expected from their nature as the hole-transporting materials.103
Similar trends in ionization are observed for the eA tetramer NDI2OD-T2 as for the eD trimers BDT-TzBI and BDB-T-2F in all media, namely the oxidation of NDI2OD-T2 takes place in the electron-rich thiophene donor units, whereas the reduction affects mostly the NDI acceptor unit and some of the thiophenes. However, larger geometrical changes take place in NDI2OD-2T upon oxidation compared to the other eD and eA compounds, as can be concluded from the bond length difference patterns (Fig. 5 and S4†) and the larger λh values of NDI2OD-2T (Table 2). This is most probably due to the two neighboring, unsubstituted thiophene donor units within the CRU of NDI2OD-2T, which introduce more flexibility and degrees of freedom to the backbone compared to the more conjugated donor units in the other eD and eA compounds. On the contrary, reduction induces only small changes to the more rigid NDI acceptor unit of NDI2OD-T2, as can be observed from the bond length differences (predicted in all media) and the λe value (predicted in blend). Overall, the calculated reorganization energies are consistent with the previously predicted λh (0.38–0.56 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103,116) and λe (0.30 eV
103,116) and λe (0.30 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103) values for the oligomers (n = 1–5) of P(NDI2OD-2T) with the (non-tuned) LRC CAM-B3LYP functional. The smaller λe values of NDI2OD-2T compared to its λh values indicate faster electron mobility than the hole mobility, as expected from its electron-transporting nature.
103) values for the oligomers (n = 1–5) of P(NDI2OD-2T) with the (non-tuned) LRC CAM-B3LYP functional. The smaller λe values of NDI2OD-2T compared to its λh values indicate faster electron mobility than the hole mobility, as expected from its electron-transporting nature.
Based on their somewhat smaller λh and λe values, the geometrical changes upon oxidation and reduction in the eA ITIC derivatives are not as large as in the eD and eA copolymer models. In addition, the λh and λe values of ITIC derivatives are almost identical with each other despite the different substituents in their electron-withdrawing INCN end-groups. The smaller λh and λe values are not surprising,43,117 as one aim of the rigid A–D–A type backbones of the ITIC-based compounds has been to reduce their reorganization energies for improved charge transport. In comparison, the studied eD and eA oligomers have more flexibility and degrees of freedom between their backbone units, which lead to the larger reorganization energies for the hole and electron transfer.
Excited-state characteristics of the isolated eD and eA compounds
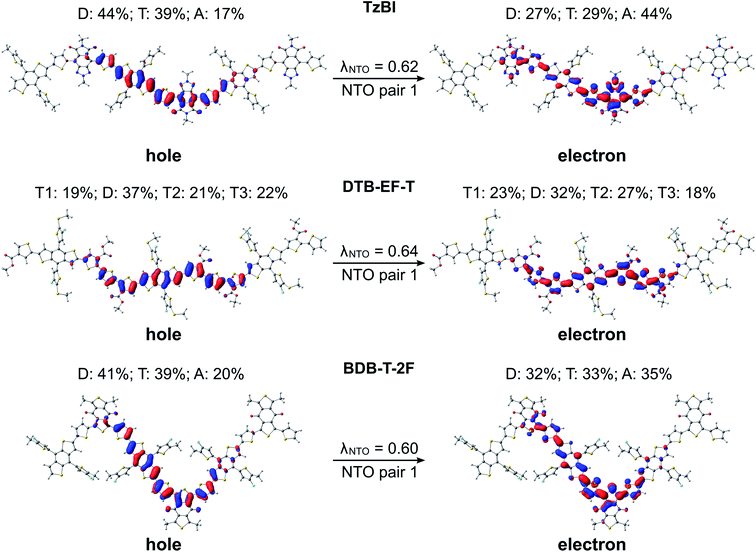
Next, we turn our attention to the excitation characteristics of the studied NF PSC compounds. First, the intramolecular CT characters of the eD and eA compounds will be compared by examing the NTOs of their main transitions, i.e. those with the largest oscillator strengths corresponding to the absorption maxima in their calculated UV-vis spectra (Fig. S6 and Table S6†). In the eD and eA oligomers (i.e. trimers for eDs and tetramer for the eA copolymer), both the hole and electron NTO determined in blend are mainly localized in the middle CRU (or CRUs, see Fig. 6 and 7). The surrounding medium does not have much effect on the charge distribution, and the NTOs predicted in vacuum and CHCl3 are almost the same (see Table S7†) and thus are not presented here.In all compounds, a partial intramolecular CT is observed from the electron-rich donor units to the electron-deficient acceptor units, as expected.17,18,65,100,118 In the eD trimers, charge transfers also from the thiophene spacers to the acceptor units, namely the hole NTOs are more localized on the donor and thiophene units, whereas the electron NTOs are more localized on the acceptor units. This contribution of the thiophenes to the CT is in line with their known, weakening effect on the push–pull interaction between the donor and acceptor units.37 The nature of CT is rather similar in BDT-TzBI and BDB-T-2F, which have the same electron-rich units, i.e. the BDT donor and thiophene spacer units, but different acceptor units. However, a somewhat larger amount of charge density moves from the electron-rich units to the acceptor unit in the case of BDT-TzBI compared to BDB-T-2F (TzBI: 31 percentage points, i.e. pp, vs.BDB-T-2F: 16 pp, see Table S7†). We predicted also in our previous study65 a similar kind of CT character for a copolymer with a similar backbone structure, where the BDT donor unit and the quinoxaline acceptor unit were separated by the thiophene spacers. As the corresponding eD copolymers have been incorporated in the efficient fullerene-based and NF PSCs, this kind of a backbone structure and resulting CT character can be concluded to be beneficial for the performance of the PSCs. However, no exact conclusion on the efficiencies can be drawn merely based on these factors. Namely, DTB-EF-T, whose corresponding copolymer has been employed in the highly efficient NF PSC, has somewhat different backbone structure and intramolecular CT characteristics. In DTB-EF-T, both the hole and electron NTOs are quite evenly distributed along the BDT donor and thiophene units and only a small amount of charge (ca. 9 pp) is transferred from the BDT donor units and unsubstituted thiophenes to the electron-deficient thiophenes with the ester side groups.
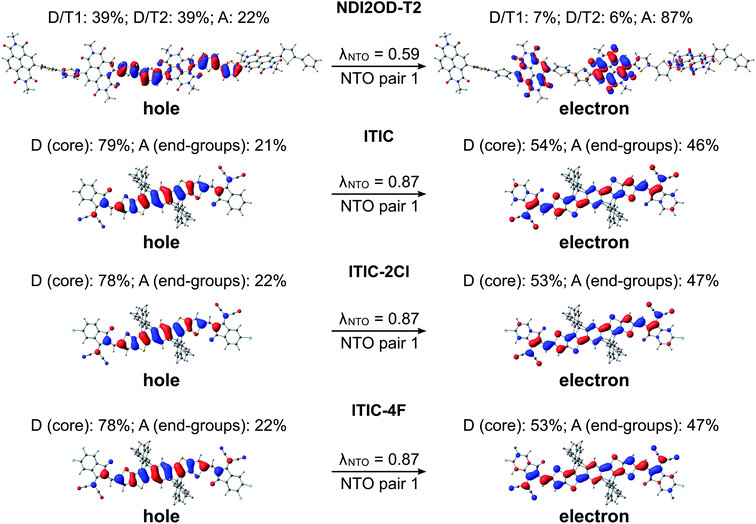
In the eA tetramer NDI2OD-T2 (Fig. 7), the hole NTOs are more clearly localized on the thiophene donor units and the electron NTOs on the NDI acceptor units compared to the NTOs in the eD trimers, which are more delocalized along several donor and acceptor units (see Fig. 6). This is most probably due to the larger twists between the donor and acceptor units in NDI2OD-T2 compared to the eD trimers (see Table 1) hindering the delocalization along the backbone.
For all three ITIC-based SMAs, the hole NTO is more localized on the electron-donating IT core group, whereas the electron NTO is quite evenly distributed on both the core and electron-withdrawing INCN end-groups (Fig. 7). Fluorination and chlorination of the INCN end-groups have been stated to enhance the intramolecular CT nature of ITIC, as based on the larger dipole moments predicted for the halogenated regional parts.33 However, the introduction of either F or Cl atoms did not affect the electron density distributions of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). The same is observed here with the NTOs, which are also very similar to each other indicating that the fluorination and chlorination does not affect the electron density distribution much in these models. However, slightly smaller vertical excitation energies of the main, S0 → S1 transition (Table S6†) and consequently red-shifted UV-vis spectra of ITIC-4F and ITIC-2Cl (Fig. S6†) indicate some enhancement in their intramolecular CT character with respect to ITIC, which is in line with the experimentally predicted UV-vis absorption spectra.33
Next, we compare the GS and S1 state geometries of the eD trimers to display the structural changes taking place upon the excitation and resulting vibrational relaxation. The S1 relaxation energies increase from those calculated for BDT-TzBI (210 kJ mol−1 in vacuum; 204 kJ mol−1 in CHCl3; 205 kJ mol−1 in blend) and DTB-EF-T (217 kJ mol−1 in vacuum) to those for BDB-T-2F (221 kJ mol−1 in vacuum; 213 kJ mol−1 in CHCl3; 214 kJ mol−1 in blend). Smaller relaxation energies indicate smaller geometrical changes in BDT-TzBI than in the other two eD trimers upon excitation. These trends are similar as those of the λh values calculated in CHCl3 and blend (see above, Table 2). The BLAmiddle values for the optimized S1 geometries of the eD BDT-TzBI and BDB-T-2F trimers are practically zero in all media indicating highly delocalized structures (Table 2). The BLAmiddle value of DTB-EF-T (in vacuum) is also notable smaller due to more delocalized backbone compared to the neutral GS geometry. The largest differences in the bond lengths between the GS and S1 state geometries of the eD trimers are mainly in the acceptor and neighboring thiophene units of the middle CRU, i.e. in the same regions as for reduction (Fig. 5 and S4†). However, small structural changes occur in the BDT donor of BTB-T-2F, as well, which might explain its larger S1 relaxation energies.
Local interfacial eD–eA configurations
After establishing the structural and optoelectronic features of the individual eD and eA compounds, we will focus next on the eD–eA complexes and their structural and CT characteristics to better understand the interactions at their local eD–eA interfaces. In the case of the polymer–polymer system BDT-TzBI–NDI2OD-T2, the most stable configuration is predicted to form when the NDI acceptor units of NDI2OD-T2 (n = 1) and BDT-TzBI (n = 1) are face-to-face, while their donor units are also face-to-face (the AA(1) configuration, see Tables S8–S10† and Fig. 8 and S7†). In another possible configuration (i.e. the DA(2) configuration with the energy difference of 0.9 kJ mol−1 compared to the most stable one), the acceptor unit of NDI2OD-T2 and the donor units of BDT-TzBI are face-to-face, while the donor units of NDI2OD-T2 and the acceptor unit of BDT-TzBI are face-to-face. This agrees with the experimental evidence119 for the face-to-face stacking between the similar PTzBI-Si copolymer and P(NDI2OD-T2). These kinds of face-to-face orientations are essential for forming strong π-orbital overlap at the polymer–polymer interfaces, reducing the binding energy of the excitons, and promoting the formation of free charge carriers.37 The calculated distances between the backbones of BDT-TzBI and NDI2OD-T2 are ca. 3.4–4.0 Å with the average of 3.7 Å, which is consistent with the experimental π–π distance (3.7 Å).120 Based on the electrostatic potential energy surface maps (Table S11†) calculated for the different configurations of BDT-TzBI–NDI2OD-T2, there are subtle differences in the electronegative and electropositive regions, which could have roles in defining the energetically favorable positioning of BDT-TzBI and NDI2OD-T2 observed in the studied set of configurations.In the case of the polymer–SMA systems, energetically favored placement of the eA SMA compound above the eD copolymer compounds depends on the system. Namely, for DTB-EF-T–ITIC-4F, the most stable configuration is predicted to be the one where the electron-withdrawing end-group of ITIC-4F is on the top of the BDT donor unit of DTB-EF-T (the DA configuration, see Table S9†). Even in the model, where the end-group of ITIC-4F has been initially positioned on the top of the acceptor (the AA configuration) ITIC-4F has shifted so that the end-group is located above the bond connecting the acceptor and donor units of DTB-EF-T. However, in BDB-T-2F–ITIC-2Cl, energetically the most favorable configuration is the one where the end-group of ITIC-2Cl is on the top of the BDD acceptor unit of BDB-T-2F (the AA configuration, see Table S10†). This is consistent with the previous atomistic simulations of the BDB-T-2F–ITIC systems,49,121 where the end-groups of ITIC are observed to locate more probably on the top of the acceptor unit than the donor unit of BDB-T-2F.
We note that our models of the monomers with the truncated side groups cannot entirely describe the best possible arrangements of the studied compounds, as the full side chains will most likely set steric hindrances in some configurations and prevent the compounds getting as close as in the monomer-based complexes studied here. Additionally, the single CRU models (monomers) do not take the effects that the additional CRUs might have on the preferred relative positioning in the copolymer backbone into account. Thus, we optimized the geometry of BDT-TzBI–NDI2OD-T2 also by using the dimers of PBDT-TzBI and P(NDI2OD-T2) for the DA(2) configuration, for comparison (see Table S8† and Fig. 8). The relative positions of BDT-TzBI and NDI2OD-T2 in the dimer configuration are rather similar as in the monomer configuration, indicating that the sizes of the D–A oligomers do not seem to have a significant effect at least not for this system. More importantly, the predicted CT characteristics in complexes are very similar for both the monomer and dimer models (see ‘Charge transfer characteristics in the local interfacial eD–eA complexes’ below). Unfortunately, the geometry optimization of the DA(2) dimer configuration was computationally so demanding that we were unable to verify the effect of size for the other systems. Thus, even though our truncated models may introduce some inaccuracies to the results, our models can give some insight into the relative placements of the studied eD and eA compounds and the CT characteristics at their local interfaces.
Charge transfer characteristics in the local interfacial eD–eA complexes
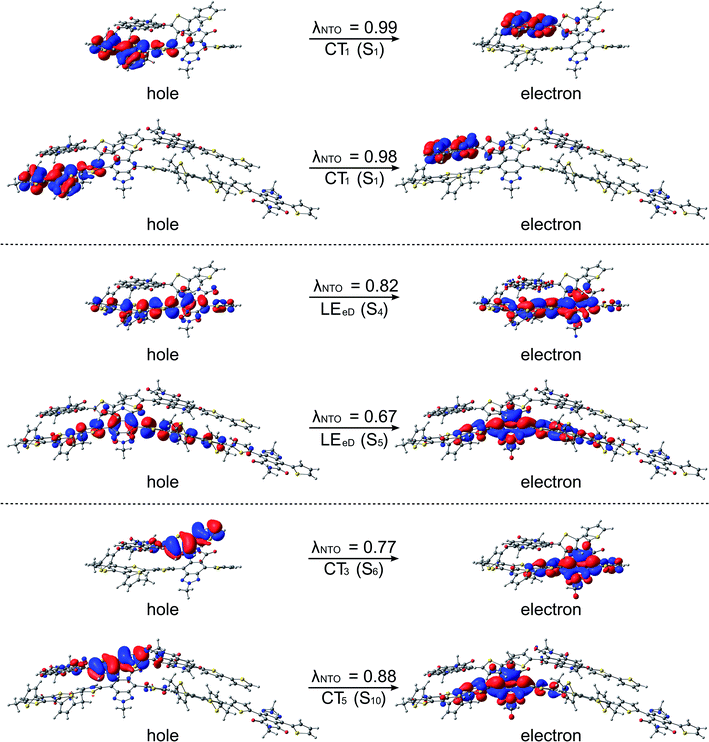
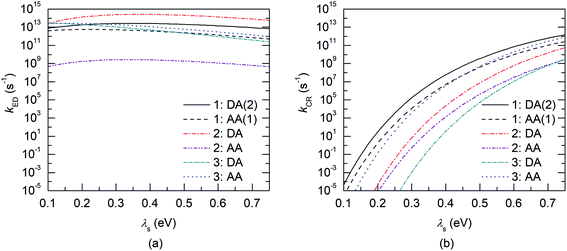
Next, the nature of the excited states relevant to the ED and CR processes of the eD–eA complexes will be examined. The most stable configurations of the interfacial eD–eA complexes will be investigated in the case of the polymer–SMA systems. For the polymer–polymer BDT-TzBI–NDI2OD-T2 system, the DA(2) configuration will be discussed instead due to its larger electronic couplings and CT rates compared to the most stable AA(1) configuration (see “Calculating the CT rates for the local interfacial eD–eA complexes” below). In the DA(2) configuration of BDT-TzBI–NDI2OD-T2, the S1 state is the CT1 state, where the hole NTO is delocalized on the BDT donor and thiophene units of BDT-TzBI and the electron NTO is localized on the NDI acceptor unit of NDI2OD-T2 (Fig. 8). In other words, the charge transfers from the electron-rich units of BDT-TzBI to the electron-deficient unit of NDI2OD-T2. The LE state, which is the local excitation of the eD compound, BDT-TzBI, is predicted to be higher in energy (i.e. the S4 state here) than the CT1 state. An opposite ordering of the LE and CT1 states is sometimes detected for the copolymer–PC71BM complexes with both the non-tuned LRC and OT LRC functionals.65,66 Interestingly, in the third lowest CT state, i.e. CT3, CT is observed from the eA compound NDI2OD-T2 to the eD compound BDT-TzBI. Namely, the charge transfers from the thiophene donor units of NDI2OD-T2 to several units of BDT-TzBI, the largest amount of the electron NTO being on the TzBI acceptor unit. This kind of a CT could originate from the hole transfer from the eA compound to eD, also referred to as the “Channel II” CT process, which may participate in the regular electron transfer process from the eD compound to eA in charge generation of APSCs.37,122As mentioned above (see “Local interfacial eD–eA configurations“), the use of longer oligomers for constructing the complexes would have been more ideal instead of the truncated monomer models. However, when comparing the NTOs of the monomer and dimer models of the DA(2) configuration of BDT-TzBI–NDI2OD-T2, it can be observed that the nature of the CT processes is rather similar in both models (Fig. 8). Moreover, the ordering of the states is the same, namely the CT1 state is below both the LE state and the CT state (CT5 for the dimer model, CT3 for the monomer model), where the CT occurs from the eA compound to the eD compound. For both the monomer and dimer configurations, the hole and electron NTOs of the CT states are localized in the equally large regions regardless the sizes of the eD and eA models. The LE state, while having the same shape in both the monomer and dimer configurations, is not distributed only on a single CRU but on the both CRUs in the dimer configuration. To conclude, as both the monomer and dimer models have very similar charge distributions, the smaller monomer models can be expected to provide sufficiently good description of the nature of the states for this NF PSC system.
The relative positioning of BDT-TzBI and NDI2OD-T2 has some effect on the nature of the states, although the overall shapes of the NTOs are rather similar. Namely, in the AA(1) configuration (Fig. S7†), the hole NTO of CT1 and the electron NTO of CT3 are more delocalized along the whole backbone of BDT-TzBI compared to the DA(2) configuration (Fig. 8). Moreover, a small amount of a local excitation of the eA compound NDI2OD-T2 is mixed with the CT1 state in the AA(1) configuration. We have observed the similar mixing of the local and CT states also for different copolymer–PC71BM complexes in our previous theoretical studies.65,66 This is due to the tendency of the LRC functionals to predict the mixed states for these kinds of photoactive systems. The absence of the local excitations in the CT state of the DA(2) configuration might explain its faster ED and CR rates compared to the AA(1) configuration (see Table 3 and Fig. 11). However, previous experimental123 and theoretical51,123 studies have also speculated that the delocalized CT states at the eD–eA interfaces of organic solar cells could be beneficial for decreasing the Coulomb binding energy as a result of reduced electrostatic attraction between the hole and electron.
| Complex | Configuration | H if,ED (meV) | H if,CR (meV) | λ i,ED (eV) | λ i,CR (eV) | (eV) | (eV) | k ED (s−1) | k CR (s−1) |
|---|---|---|---|---|---|---|---|---|---|
| a Electronic couplings (Hif) calculated with the multi-state (11 states) FCD scheme (eqn (S22)–(S24)), inner (intermolecular) reorganization energies (λi, eqn (S10)–(S15)), Gibbs free energies (ΔG°, eqn (S16)–(S19)), and CT rates (k, eqn (1)). The Coulomb energies (eqn (S17) and (S19)) are presented in Table S15. b See Table S16 for the parameters and rates for the other configurations of BDT-TzBI–NDI2OD-T2. c The rates presented in this table were calculated using the external reorganization energy of 0.53 eV, chosen from the range of the possible values shown in Fig. 11. | |||||||||
| BDT-TzBI–NDI2OD-T2 | DA(2) | 37.54 | 72.74 | 0.43 | 0.30 | −0.81 | −1.70 | 1.92 × 1013 | 9.78 × 109 |
| AA(1) | 16.55 | 47.76 | 0.43 | 0.32 | −0.68 | −1.81 | 2.12 × 1012 | 1.13 × 109 | |
| DTB-EF-T–ITIC-4F | DA | 110.91 | 99.80 | 0.22 | 0.30 | −0.56 | −2.03 | 1.52 × 1014 | 5.83 × 106 |
| AA | 0.35 | 24.38 | 0.23 | 0.32 | −0.59 | −2.01 | 1.65 × 109 | 1.70 × 106 | |
| BDB-T-2F–ITIC-2Cl | DA | 6.87 | 70.37 | 0.28 | 0.24 | −0.36 | −2.00 | 1.77 × 1012 | 3.18 × 105 |
| AA | 33.82 | 131.83 | 0.32 | 0.30 | −0.50 | −1.83 | 5.05 × 1012 | 1.72 × 109 | |
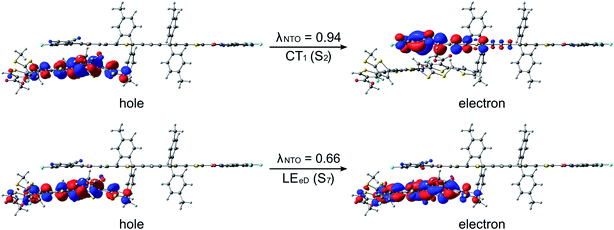
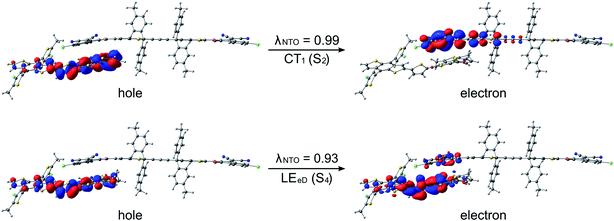
The studied polymer–SMA systems exhibit the same ordering of the states as the polymer–polymer system BDT-TzBI–NDI2OD-T2, i.e. the CT1 (S2) is at a lower energy than the LE state (S7 for DTB-EF-T–ITIC-4F and S4 for BDB-T-2F–ITIC-2Cl, Fig. 9 and 10). In both DTB-EF-T–ITIC-4F and BDB-T-2F–ITIC-2Cl, the natures of the CT1 states are quite similar and CT occurs from the eD compound, i.e.DTB-EF-T and BDB-T-2F, to the end-group of the ITIC-based eA compound, i.e.ITIC-4F and ITIC-2Cl, respectively. In the both polymer–SMA systems, the hole NTO of the CT1 state is distributed over several backbone units of the eD compounds, although in DTB-EF-T, the charge density is more localized on the donor unit, whereas in BDB-T-2F, it mainly localizes on the acceptor unit. Here, no CT from the eA ITIC compounds to the eD monomers were observed for the polymer–SMA systems, although there have been experimental evidence for the “Channel II” process also in several polymer–SMA systems.124 However, only the 10 lowest excited singlet states have been considered here, so it is possible that this type of a “Channel II” CT could be observed at higher-energy states.
Calculating the CT rates for the local interfacial eD–eA complexes
Finally, we have calculated the CT rate parameters and rates for the ED and CR processes (Tables 3 and S12–S16). First, we will consider the electronic couplings, which, as expected, are highly sensitive to the relative positions of the eD and eA compounds.66,125–128 Overall, the largest couplings are predicted mainly for the most stable polymer–SMA systems, i.e. the DA and AA configurations of DTB-EF-T–ITIC-4F and BDB-T-2F–ITIC-2Cl, respectively (see Tables 3, S12, and S13†). In the BDT-TzBI–NDI2OD-T2 polymer–polymer system, the second most stable DA(2) configuration has somewhat stronger couplings than the most stable AA(1) configuration; the energy difference between the configurations is 0.9 kJ mol−1. The CR couplings are predicted to be larger than the ED couplings in all the other systems, except in the DA configuration of DTB-EF-T–ITIC-4F. We observed larger CR couplings compared to ED couplings also previously in our study of the copolymer–fullerene system.66Next, we will discuss the effect of the dispersion corrected OT-LRC functional on calculating the electronic couplings for different NF PSC systems with the two- and multi-state FCD schemes in complement to our previous study66 of the multi-state electronic couplings of polymer–fullerene PSC system. In that case, both the non-tuned CAM-B3LYP and OT-BNL LRC functionals predicted oscillating coupling values especially for the CR couplings of the TQ–PC71BM complexes with the increasing number of the states.66 On the contrary, both the ED and CR couplings predicted here for the polymer–polymer BDT-TzBI–NDI2OD-T2 are relatively constant with different number of states (2–26, Table S12†). Similar trends, i.e. consistent two- and multi (11)-state electronic couplings, are also predicted for the polymer–SMA systems (Table S13†), although in their case the effect of the larger number of states could not be confirmed due to the convergence problems in computations. Here, we have only carried out the calculations with the dispersion corrections and with tuning the default value of ω (i.e. using the optimally tuned OT-ωB97X-D functional) so we cannot determine, whether the constant couplings result from the dispersion corrections or from the tuning of the ω. Moreover, the studied system may affect the couplings, as well. However, as the dispersion corrections are important for the correct description of the local interfacial eD-eA complexes,65,68,69 their inclusion can be expected to be beneficial also for calculating electronic couplings in these PSC systems. Thus, while final conclusions cannot be drawn merely from these results, they are still encouraging in a sense that dispersion corrections seem to stabilize the coupling values when employed with the OT-LRC functionals.
The second important CT rate parameter is the inner (intermolecular) reorganization energy, λi, which describes the structural changes in the geometries of the eD and eA compounds upon CT.126 For the efficient ED process and fast ED rates, the reorganization energy of the system should be minimized. In most cases, the λi (and consequently the total λ, i.e. λi + λs) values are larger for the ED process than for the CR process (Table 3) indicating that the faster ED rates with respect to the CR rates are due to the other CT parameters (see below). The λi values predicted for BDB-T-2F–ITIC-2Cl agree with those (λi,ED of ca. 0.20 eV and λi,CR of ca. 0.25–0.29 eV) calculated previously for the similar system of BDB-T-2F and methoxy-substituted ITIC (ITIC-OM) by Wang and Brédas.49 A closer look at the contributions of the eD and eA compounds to the inner reorganization energies reveals the differences in their geometrical changes during the ED and CR processes (Table S14†). The eD trimers BDT-TzBI and BDB-T-2F are predicted to undergo larger geometric changes upon ED (i.e. eD* → eD+) than CR (i.e. eD+ → eD), whereas the geometrical changes in DTB-EF-T are larger during CR than ED. In other words, for BDT-TzBI and BDB-T-2F, the geometries of the S1 state and cation differ more than those of the cation and neutral species. The contribution of the eA compound is the same for both ED and CR, i.e. when going from the GS geometry to that of the radical anion (eA → eA−) and vice versa (eA− → eA). Overall, the λi,CR values for the studied NF PSC systems are close to each other, whereas the λi,ED values increase somewhat in the order of DTB-EF-T–ITIC-4F < BDB-T-2F–ITIC-2Cl < BDT-TzBI–NDI2OD-T2. This ordering indicates smaller geometrical relaxation upon ED for the polymer–SMA systems compared to the polymer–polymer system, which may be one factor explaining the higher efficiencies predicted for these SMA containing NF PSCs.27,29,129
Next, we will consider the third CT parameter, i.e. the Gibbs free energy for the CT reaction that is the energy difference (i.e. driving force) between the LE and CT1 states for the ED process and between the CT1 state and GS for the CR process. For the efficient ED process, the 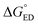 value should be maximized. Based on the negative values of ΔG°, both the ED and CR processes are predicted to be spontaneous in all the complexes (Table 3). The
value should be maximized. Based on the negative values of ΔG°, both the ED and CR processes are predicted to be spontaneous in all the complexes (Table 3). The 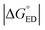 values of BDB-T-2F–ITIC-2Cl are consistent with those (0.11–0.45 eV) predicted previously for the similar BDB-T-2F–ITIC-OM systems at the OT-ωB97XD/6-31G* level of theory.49 The value of the external reorganization energy defines (the range of 0.10–0.75 eV has been considered here for λs, see ESI† for the justification), whether the ED processes of the studied systems take place in the Marcus normal region (
values of BDB-T-2F–ITIC-2Cl are consistent with those (0.11–0.45 eV) predicted previously for the similar BDB-T-2F–ITIC-OM systems at the OT-ωB97XD/6-31G* level of theory.49 The value of the external reorganization energy defines (the range of 0.10–0.75 eV has been considered here for λs, see ESI† for the justification), whether the ED processes of the studied systems take place in the Marcus normal region (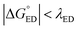 , where λED = λi,ED + λs). The CR processes of all the systems are predicted to occur deep in the Marcus inverted region (
, where λED = λi,ED + λs). The CR processes of all the systems are predicted to occur deep in the Marcus inverted region (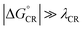 , where λCR = λi,CR + λs), which will have consequences on the predicted CR rates (see below). The
, where λCR = λi,CR + λs), which will have consequences on the predicted CR rates (see below). The 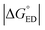 values of the polymer–SMA systems are smaller than those of the polymer–polymer system BDT-TzBI–NDI2OD-T2, but because their λi,ED values are also smaller and the electronic couplings larger (for the most stable configurations) their ED rates are relatively similar with the polymer–polymer BDT-TzBI–NDI2OD-T2 system (see above). The larger
values of the polymer–SMA systems are smaller than those of the polymer–polymer system BDT-TzBI–NDI2OD-T2, but because their λi,ED values are also smaller and the electronic couplings larger (for the most stable configurations) their ED rates are relatively similar with the polymer–polymer BDT-TzBI–NDI2OD-T2 system (see above). The larger 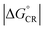 of the polymer–SMA systems, in turn, will lead to the slower CR rates with respect to BDT-TzBI–NDI2OD-T2 (see below).
of the polymer–SMA systems, in turn, will lead to the slower CR rates with respect to BDT-TzBI–NDI2OD-T2 (see below).
After examining the individual CT parameters, the rates for the ED and CR processes of the studied NF PSC systems are presented as a function of λs (0.10–0.75 eV) in Fig. 11 and S8.† For all the systems, the ED rates are larger than the CR rates (1012 to 1014 s−1 and below 1012 s−1, respectively). Even though no irrevocable conclusions regarding the relative efficiencies of the studied NF PSC systems can be drawn based on their ED rates, which depend highly on the relative orientations of the eD and eA compounds (see below), we can conclude the following. The CR rates of the polymer–SMA systems are predicted to be slower compared to those of the polymer–polymer system, which could be one factor defining the higher efficiencies of the polymer–SMA systems PDTB-EF-T–ITIC-4F and PBDB-T-2F–ITIC-2Cl compared to those of the polymer–polymer system PBDT-TzBI–P(NDI2OD-T2). The calculated ED rates are consistent with those (∼108 to 1012 s−1) predicted for the systems consisting of BDB-T-2F and different derivatives of ITIC by using the Marcus theory.47–49 Similarly, the CR rates calculated here are mostly in line with those (102–1010 s−1) predicted for the complexes of BDB-T-2F and ITIC derivatives.47–49 However, vanishingly small CR rates are observed here with the smaller values of λs, which could be due to that the CR processes of all the systems occur deep into the Marcus inverted region 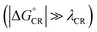 .130 As the Marcus theory may predict underestimated rates in such a case,49,131 another, e.g. the Marcus–Levich–Jortner rate model132 could be more suitable for calculating the CR rates in these PSC systems.
.130 As the Marcus theory may predict underestimated rates in such a case,49,131 another, e.g. the Marcus–Levich–Jortner rate model132 could be more suitable for calculating the CR rates in these PSC systems.
The relative orientations of the eD and eA compounds (see Tables S8–S10† for the optimized configurations) have a significant influence on the calculated rates, and the different configurations of the same system can have completely different rates. As an example, the DA configuration of the copolymer–SMA system DTB-EF-T–ITIC-4F, where the electron-withdrawing end-group of ITIC-4F is on the top of the BDT donor unit of DTB-EF-T, is predicted to have the fastest ED rate among the studied PSC systems. However, DTB-EF-T–ITIC-4F has the slowest ED rate among the studied systems, when the end-group of ITIC-4F is on the top of the acceptor unit of DTB-EF-T (i.e. ester-substituted thiophene; the AA configuration). As other CT parameters of these two configurations are relatively similar (Table 3), the smaller ED rates of the AA configuration can be attributed to its significantly smaller electronic couplings compared to those of the DA configuration.
For the polymer–SMA systems, the energetically more stable configurations have faster ED and CR rates following the same trends as their electronic couplings. However, for the polymer–polymer BDT-TzBI–NDI2OD-T2 system, the most stable configuration, i.e. the AA(1) configuration, has generally the slowest ED and CR rates among the studied complex configurations of BDT-TzBI–NDI2OD-T2 (Fig. S8†) due to its smaller 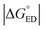 value and moderate ED electronic couplings. Moreover, based on the larger
value and moderate ED electronic couplings. Moreover, based on the larger 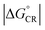 value of the AA(1) configuration with respect to the other configurations of BDT-TzBI–NDI2OD-T2, the CR process of AA(1) takes place deeper in the Marcus inverted region leading to the slower CR rates. While we have not included the full-length side groups, which also impact the interfacial orientations and stacking distances of the compounds, our findings complement the experimental findings for the importance of the optimal molecular orientation at the eD–eA interfaces.37
value of the AA(1) configuration with respect to the other configurations of BDT-TzBI–NDI2OD-T2, the CR process of AA(1) takes place deeper in the Marcus inverted region leading to the slower CR rates. While we have not included the full-length side groups, which also impact the interfacial orientations and stacking distances of the compounds, our findings complement the experimental findings for the importance of the optimal molecular orientation at the eD–eA interfaces.37
Conclusions
In this work, the structural, optoelectronic, and CT characteristics of several eD and eA compounds and their local interfacial eD–eA complexes have been examined with the DFT and TDDFT methods. The chosen compounds are based on some of the most efficient NF PSC systems to date, including both the APSC system and those containing eD copolymers and NF SMAs. We have extended our previous study of multi-state electronic couplings by comparing the two- and multi-state couplings for the ED and CR processes of these systems and exploring the effects of both the tuning of a LRC functional and the inclusion of the dispersion corrections on the electronic coupling values. Finally, the CT rates for the ED and CR processes in the studied NF PSC systems have been calculated using the semi-classical Marcus theory.The results indicate that the studied eD copolymers PBDT-TzBI, PDTB-EF-T, and PBDB-T-2F have some similar features, such as similar torsions in their backbones and UV-vis absorption profiles. However, the conformational preferences and varying backbone curvatures of these eD copolymers may lead to significant differences in their packing behavior in the blend environment. Moreover, a closer look at the structural deformations caused by ionization and excitation reveal subtle differences in the regions of their backbones, which are affected most by these processes. While all the studied eD copolymer models show a partial intramolecular CT character, the amount of transferred charge density is smaller in DTB-EF-T than in BDT-TzBI and BDB-T-2F. In general, both the twisted backbone structures, which originate from the additional degrees of freedom caused by the thiophene spacers between the donor and acceptor units of the modelled eD copolymers, and the predicted intramolecular CT characteristics are concluded to be beneficial for the performance of the PSCs.
Based on our computational studies of the CT characteristics in various possible face-to-face orientations between the eD and eA compounds in the eD–eA complexes of the NF PSC systems, the following conclusions were reached. In addition to the conventional CT from the eD compound to the eA compound, which is prominent in all NF PSC systems, the CT process is also observed from the eA compound NDI2OD-T2 to the eD compound, which indicates that NDI2OD-T2 could contribute to the charge generation in the studied polymer–polymer system. In the polymer–SMA systems, the energetically most favorable configurations have the strongest electronic couplings and the fastest CT rates. However, the positioning of the eA with respect to the eD is predicted to be different in DTB-EF-T–ITIC-4F and BDB-T-2F–ITIC-2Cl. In the case of the polymer–polymer system, the most stable configuration leads to smaller electronic couplings and slower CT rates compared to the second most stable configuration. Our results agree with the reports in the literature that the electronic couplings are highly dependent on the relative positioning of the eD and eA compounds which should be carefully controlled to ensure the fast ED rates, but slow CR rates.
The present FCD electronic coupling calculations complement our previous results on the effects of the two- versus multi-state treatment on the PSC systems. In this work we observed, that the multi-state FCD electronic couplings seem to be stabilized by including the dispersion corrections in the OT-LRC functional, i.e. relatively constant ED and CR couplings are predicted with both the two- and multi-state treatments. While more work would be required to confirm the effect of dispersion corrections on the electronic couplings in other NF PSC systems, these findings complement our and other's previous statements for the importance of the combined effect of the dispersion corrections and tuned LRC functional when describing the local interfacial characteristics of PSC systems.
The polymer–SMA systems are predicted to have smaller inner reorganization energies for the ED process, which could be one factor explaining their higher efficiencies with respect to the polymer–polymer system. However, the Gibbs free energies for ED are smaller for the polymer–SMA systems than for the polymer–polymer system, which could explain, why no clear trends in ED rates are observed between the studied NF PSC systems. Nevertheless, the calculated ED rates are faster than the CR rates in all systems, which is desirable for working devices. In addition, the CR rates in the polymer–SMA systems are generally slower than in the polymer–polymer system, which could contribute to the higher power conversion efficiencies in the SMA containing systems. The magnitudes of the ED rates are rather constant regardless of the external reorganization energy, which affects the CR rates more pronouncedly. The vanishingly small CR rates associated with the smaller external reorganization energies indicate that comparing the applicability of an alternative CT rate model, e.g. the Marcus–Levich–Jortner, could be beneficial, when calculating the CR rates for these types of NF PSC systems.
This work provides more insight into the interplay between the structural, optoelectronic, and CT characteristics of the NF PSC compounds with high PCEs demonstrated in devices. Furthermore, important information about the structural and CT characteristics in both the APC and polymer-SMA type NF PSC systems has been revealed. Overall, the dispersion corrected OT-LRC functional is concluded to be a suitable choice for modeling of the NF PSC systems, especially for calculating the FCD electronic couplings. The findings of this work are beneficial for understanding the working principles of the studied systems and can help in designing and developing more efficient NF PSCs.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Computing resources provided by the CSC – IT Center for Science Ltd, administrated by the Finnish Ministry of Education, are acknowledged. Financing of this research by the Graduate School of Tampere University of Technology (TUT), the Finnish Cultural Foundation, and the Faculty of Engineering and Natural Sciences of Tampere University is greatly appreciated. Professor Demetrio da Silva Filho and Assistant Professor Lassi Paunonen are acknowledged for allowing a continued use of the codes for analyzing the NTO contributions of the complexes and calculating the multi-state electronic couplings, respectively. We also thank M.Sc. Tech. Maria Pullinen for the information from her calculations of DTB-EF-T in her Master's thesis.References
- Z. He, C. Zhong, S. Su, M. Xu, H. Wu and Y. Cao, Nat. Photonics, 2012, 6, 591–595 CrossRef.
- G. Li, R. Zhu and Y. Yang, Nat. Photonics, 2012, 6, 153–161 CrossRef CAS.
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 15027 CrossRef CAS.
- Y. Jin, Z. Chen, M. Xiao, J. Peng, B. Fan, L. Ying, G. Zhang, X.-F. Jiang, Q. Yin, Z. Liang, F. Huang and Y. Cao, Adv. Energy Mater., 2017, 7, 1700944 CrossRef.
- H. Kang, W. Lee, J. Oh, T. Kim, C. Lee and B. J. Kim, Acc. Chem. Res., 2016, 49, 2424–2434 CrossRef CAS PubMed.
- S. Chen, Y. An, G. K. Dutta, Y. Kim, Z.-G. Zhang, Y. Li and C. Yang, Adv. Funct. Mater., 2017, 27, 1603564 CrossRef.
- F. Shen, J. Xu, X. Li and C. Zhan, J. Mater. Chem. A, 2018, 6, 15433–15455 RSC.
- Z.-H. Zhou, T. Maruyama, T. Kanbara, T. Ikeda, K. Ichimura, T. Yamamoto and K. Tokuda, J. Chem. Soc., Chem. Commun., 1991, 1210–1212 RSC.
- E. E. Havinga, W. ten Hoeve and H. Wynberg, Polym. Bull., 1992, 29, 119–126 CrossRef CAS.
- H. Zhou, L. Yang and W. You, Macromolecules, 2012, 45, 607–632 CrossRef CAS.
- F. Würthner and M. Stolte, Chem. Commun., 2011, 47, 5109–5115 RSC.
- G. Wang, F. S. Melkonyan, A. Facchetti and T. J. Marks, Angew. Chem., Int. Ed., 2019, 58, 4129–4142 CrossRef CAS PubMed.
- Z. Li, L. Ying, P. Zhu, W. Zhong, N. Li, F. Liu, F. Huang and Y. Cao, Energy Environ. Sci., 2019, 12, 157–163 RSC.
- L. Zhu, W. Zhong, C. Qiu, B. Lyu, Z. Zhou, M. Zhang, J. Song, J. Xu, J. Wang, J. Ali, W. Feng, Z. Shi, X. Gu, L. Ying, Y. Zhang and F. Liu, Adv. Mater., 2019, 31, 1902899 CrossRef CAS PubMed.
- X. Guo and M. D. Watson, Org. Lett., 2008, 10, 5333–5336 CrossRef CAS PubMed.
- T. Jia, J. Zhang, W. Zhong, Y. Liang, K. Zhang, S. Dong, L. Ying, F. Liu, X. Wang, F. Huang and Y. Cao, Nano Energy, 2020, 72, 104718 CrossRef CAS.
- Y. Lin, J. Wang, Z.-G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174 CrossRef CAS PubMed.
- G. Zhang, J. Zhao, P. C. Y. Chow, K. Jiang, J. Zhang, Z. Zhu, J. Zhang, F. Huang and H. Yan, Chem. Rev., 2018, 118, 3447–3507 CrossRef CAS PubMed.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed.
- H. Sun, F. Chen and Z. K. Chen, Mater. Today, 2019, 24, 94–118 CrossRef CAS.
- Z. Zheng, Q. Hu, S. Zhang, D. Zhang, J. Wang, S. Xie, R. Wang, Y. Qin, W. Li, L. Hong, N. Liang, F. Liu, Y. Zhang, Z. Wei, Z. Tang, T. P. Russell, J. Hou and H. Zhou, Adv. Mater., 2018, 30, 1801801 CrossRef PubMed.
- Y. Cui, H. Yao, L. Hong, T. Zhang, Y. Xu, K. Xian, B. Gao, J. Qin, J. Zhang, Z. Wei and J. Hou, Adv. Mater., 2019, 31, 1808356 CrossRef PubMed.
- H. Yao, Y. Cui, D. Qian, C. S. Ponseca, A. Honarfar, Y. Xu, J. Xin, Z. Chen, L. Hong, B. Gao, R. Yu, Y. Zu, W. Ma, P. Chabera, T. Pullerits, A. Yartsev, F. Gao and J. Hou, J. Am. Chem. Soc., 2019, 141, 7743–7750 CrossRef CAS PubMed.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275 CrossRef CAS.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H. L. Yip, T. K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- B. Fan, L. Ying, Z. Wang, B. He, X. F. Jiang, F. Huang and Y. Cao, Energy Environ. Sci., 2017, 10, 1243–1251 RSC.
- L. Lan, Z. Chen, Q. Hu, L. Ying, R. Zhu, F. Liu, T. P. Russell, F. Huang and Y. Cao, Adv. Sci., 2016, 3, 1600032 CrossRef PubMed.
- S. Li, L. Ye, W. Zhao, H. Yan, B. Yang, D. Liu, W. Li, H. Ade and J. Hou, J. Am. Chem. Soc., 2018, 140, 7159–7167 CrossRef CAS PubMed.
- L. Zhan, S. Li, S. Zhang, X. Chen, T. K. Lau, X. Lu, M. Shi, C. Z. Li and H. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 42444–42452 CrossRef CAS PubMed.
- M. Zhang, X. Guo, W. Ma, H. Ade and J. Hou, Adv. Mater., 2015, 27, 4655–4660 CrossRef CAS PubMed.
- Poly[(4,8-bis[5-(2-ethylhexyl)-4-fluoro-2-thienyl)benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl]-2,5-thiophenediyl(5,7-bis(2-ethylhexyl)-4,8-dioxo-4H,8H-benzo[1,2-c:4,5-c′]dithiophene-1,3-diyl)-2,5-thiophenediyl], PBDB-T-2F at Sigma-Aldrich, available at: https://www.sigmaaldrich.com/catalog/product/aldrich/906336?lang=fi%26region=FI, accessed 20/05/2020.
- H. Zhang, H. Yao, J. Hou, J. Zhu, J. Zhang, W. Li, R. Yu, B. Gao, S. Zhang and J. Hou, Adv. Mater., 2018, 30, 1800613 CrossRef PubMed.
- Y. Ie, J. Huang, Y. Uetani, M. Karakawa and Y. Aso, Macromolecules, 2012, 45, 4564–4571 CrossRef CAS.
- D. Qian, L. Ye, M. Zhang, Y. Liang, L. Li, Y. Huang, X. Guo, S. Zhang, Z. Tan and J. Hou, Macromolecules, 2012, 45, 9611–9617 CrossRef CAS.
- D. Gedefaw, M. Tessarolo, W. Zhuang, R. Kroon, E. Wang, M. Bolognesi, M. Seri, M. Muccini and M. R. Andersson, Polym. Chem., 2014, 5, 2083–2093 RSC.
- C. Lee, S. Lee, G.-U. Kim, W. Lee and B. J. Kim, Chem. Rev., 2019, 119, 8028–8086 CrossRef CAS PubMed.
- Q. Zhang, M. A. Kelly, N. Bauer and W. You, Acc. Chem. Res., 2017, 50, 2401–2409 CrossRef CAS PubMed.
- L. Benatto and M. Koehler, J. Phys. Chem. C, 2019, 123, 6395–6406 CrossRef CAS.
- L. Benatto, C. F. N. Marchiori, C. Moyses Araujo and M. Koehler, J. Mater. Chem. C, 2019, 7, 12180–12193 RSC.
- Q. Wang, Y. Li, P. Song, R. Su, F. Ma, Y. Yang, Q. Wang, Y. Li, P. Song, R. Su, F. Ma and Y. Yang, Polymers, 2017, 9, 692 CrossRef PubMed.
- Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- L. Benatto and M. Koehler, J. Phys. Chem. C, 2019, 123, 6395–6406 CrossRef CAS.
- G. Han, Y. Guo, X. Ma and Y. Yi, Sol. RRL, 2018, 2, 1800190 CrossRef.
- G. Han and Y. Yi, Adv. Theory Simul., 2018, 1, 1800091 CrossRef.
- J. Lee, E. M. Go, S. Dharmapurikar, J. Xu, S. M. Lee, M. Jeong, K. C. Lee, J. Oh, Y. Cho, C. Zhang, M. Xiao, S. K. Kwak and C. Yang, J. Mater. Chem. A, 2019, 7, 18468–18479 RSC.
- Q.-Q. Pan, S.-B. Li, Y.-C. Duan, Y. Wu, J. Zhang, Y. Geng, L. Zhao and Z.-M. Su, Phys. Chem. Chem. Phys., 2017, 19, 31227–31235 RSC.
- Q.-Q. Pan, S.-B. Li, Y. Wu, Y. Geng, M. Zhang and Z.-M. Su, Org. Electron., 2018, 53, 308–314 CrossRef CAS.
- T. Wang and J.-L. Brédas, Matter, 2020, 2, 119–135 CrossRef.
- G. Han, Y. Guo, X. Song, Y. Wang and Y. Yi, J. Mater. Chem. C, 2017, 5, 4852–4857 RSC.
- J.-L. Brédas, V. Coropceanu, C. Doiron, Y. T. Fu, T. Körzdörfer, L. Pandey, C. Risko, J. Sears, B. Yang, Y. Yi and C. Zhang, Modeling the electronic and optical processes in organic solar cells: density functional theory and beyond, in Organic Solar Cells: Fundamentals, Devices, and Upscaling, ed. B. P. Rand and H. Richter, CRC Press, Taylor & Francis Group, LLC, Boca Raton, 2014, pp. 537–588 Search PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- C.-P. Hsu, Acc. Chem. Res., 2009, 42, 509–518 CrossRef CAS PubMed.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- P. Song, Y. Li, F. Ma, T. Pullerits and M. Sun, Chem. Rec., 2016, 16, 734–753 CrossRef CAS PubMed.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS.
- Y. Li, T. Pullerits, M. Zhao and M. Sun, J. Phys. Chem. C, 2011, 115, 21865–21873 CrossRef CAS.
- Y. Li, Y. Feng and M. Sun, Sci. Rep., 2015, 5, 13970 CrossRef PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Brédas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- T. Wang, X.-K. Chen, A. Ashokan, Z. Zheng, M. K. Ravva and J.-L. Brédas, Adv. Funct. Mater., 2018, 28, 1705868 CrossRef.
- M. Rust, J. Lappe and R. J. Cave, J. Phys. Chem. A, 2002, 106, 3930–3940 CrossRef CAS.
- C.-H. Yang and C.-P. Hsu, J. Chem. Phys., 2013, 139, 154104 CrossRef PubMed.
- T. Kastinen, M. Niskanen, C. Risko, O. Cramariuc and T. I. Hukka, Phys. Chem. Chem. Phys., 2016, 18, 27654–27670 RSC.
- T. Kastinen, D. A. Da Silva Filho, L. Paunonen, M. Linares, L. A. Ribeiro Junior, O. Cramariuc and T. I. Hukka, Phys. Chem. Chem. Phys., 2019, 21, 25606–25625 RSC.
- T. Kim, J. H. Kim, T. E. Kang, C. Lee, H. Kang, M. Shin, C. Wang, B. Ma, U. Jeong, T. S. Kim and B. J. Kim, Nat. Commun., 2015, 6, 8547 CrossRef CAS PubMed.
- K. Do, M. K. Ravva, T. Wang and J.-L. Brédas, Chem. Mater., 2017, 29, 346–354 CrossRef CAS.
- C.-R. Zhang, J. S. Sears, B. Yang, S. G. Aziz, V. Coropceanu and J.-L. Brédas, J. Chem. Theory Comput., 2014, 10, 2379–2388 CrossRef CAS PubMed.
- L. Pandey, C. Doiron, J. S. Sears and J.-L. Brédas, Phys. Chem. Chem. Phys., 2012, 14, 14243–14248 RSC.
- M. Niskanen and T. I. Hukka, Phys. Chem. Chem. Phys., 2014, 16, 13294–13305 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- D. Niedzialek, I. Duchemin, T. B. De Queiroz, S. Osella, A. Rao, R. Friend, X. Blase, S. Kümmel and D. Beljonne, Adv. Funct. Mater., 2015, 25, 1972–1984 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531 CrossRef CAS PubMed.
- T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820 CrossRef CAS PubMed.
- B. Yang, Y. Yi, C.-R. Zhang, S. G. Aziz, V. Coropceanu and J.-L. Brédas, J. Phys. Chem. C, 2014, 118, 27648–27656 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- X.-K. Chen, M. K. Ravva, H. Li, S. M. Ryno and J.-L. Brédas, Adv. Energy Mater., 2016, 6, 1601325 CrossRef.
- G. Han and Y. Yi, J. Phys. Chem. Lett., 2019, 10, 2911–2918 CrossRef CAS PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- P. Ros and G. C. A. Schuit, Theor. Chim. Acta, 1966, 4, 1–12 CrossRef CAS.
- Multiwfn 3.6, available at: http://sobereva.com/multiwfn/, accessed 05/01/2020.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and F. Chen, Acta Chim. Sin., 2011, 69, 2393–2406 CAS.
- G. A. Zhurko, Chemcraft - graphical program for visualization of quantum chemistry computations, Ivanovo, Russia, 2005, available at: http://www.chemcraftprog.com, accessed 24/05/2020.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- C. F. Huang, S. L. Wu, Y. F. Huang, Y. C. Chen, S. T. Chang, T. Y. Wu, K. Y. Wu, W. T. Chuang and C. L. Wang, Chem. Mater., 2016, 28, 5175–5190 CrossRef CAS.
- A. Wadsworth, M. Moser, A. Marks, M. S. Little, N. Gasparini, C. J. Brabec, D. Baran and I. McCulloch, Chem. Soc. Rev., 2019, 48, 1596–1625 RSC.
- N. E. Jackson, B. M. Savoie, K. L. Kohlstedt, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2013, 135, 10475–10483 CrossRef CAS PubMed.
- T. Kastinen, M. Niskanen, C. Risko, O. Cramariuc and T. I. Hukka, J. Phys. Chem. A, 2016, 120, 1051–1064 CrossRef CAS PubMed.
- I. Osaka, T. Abe, S. Shinamura and K. Takimiya, J. Am. Chem. Soc., 2011, 133, 6852–6860 CrossRef CAS PubMed.
- E. Giussani, D. Fazzi, L. Brambilla, M. Caironi and C. Castiglioni, Macromolecules, 2013, 46, 2658–2670 CrossRef CAS.
- D. Fazzi, M. Caironi and C. Castiglioni, J. Am. Chem. Soc., 2011, 133, 19056–19059 CrossRef CAS PubMed.
- T. Schuettfort, S. Huettner, S. Lilliu, J. E. MacDonald, L. Thomsen and C. R. McNeill, Macromolecules, 2011, 44, 1530–1539 CrossRef CAS.
- V. Lemaur, L. Muccioli, C. Zannoni, D. Beljonne, R. Lazzaroni, J. Cornil and Y. Olivier, Macromolecules, 2013, 46, 8171–8178 CrossRef CAS.
- T. J. Aldrich, M. Matta, W. Zhu, S. M. Swick, C. L. Stern, G. C. Schatz, A. Facchetti, F. S. Melkonyan and T. J. Marks, J. Am. Chem. Soc., 2019, 141, 3274–3287 CrossRef CAS PubMed.
- Z. Zhang, J. Yu, X. Yin, Z. Hu, Y. Jiang, J. Sun, J. Zhou, F. Zhang, T. P. Russell, F. Liu and W. Tang, Adv. Funct. Mater., 2018, 28, 1705095 CrossRef.
- C. Van Dyck, T. J. Marks and M. A. Ratner, ACS Nano, 2017, 11, 5970–5981 CrossRef CAS PubMed.
- J. Casado, Top. Curr. Chem., 2017, 375, 1–40 CrossRef CAS PubMed.
- S. Suramitr, W. Meeto, P. Wolschann and S. Hannongbua, Theor. Chem. Acc., 2010, 125, 35–44 Search PubMed.
- T. Körzdörfer, R. M. Parrish, J. S. Sears, C. D. Sherrill and J.-L. Brédas, J. Chem. Phys., 2012, 137, 124305 CrossRef PubMed.
- W. Porzio, G. Scavia, L. Barba, G. Arrighetti and C. R. McNeill, Eur. Polym. J., 2014, 61, 172–185 CrossRef CAS.
- Y. Olivier, D. Niedzialek, V. Lemaur, W. Pisula, K. Müllen, U. Koldemir, J. R. Reynolds, R. Lazzaroni, J. Cornil and D. Beljonne, Adv. Mater., 2014, 26, 2119–2136 CrossRef CAS PubMed.
- N. E. Jackson, K. L. Kohlstedt, B. M. Savoie, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2015, 137, 6254–6262 CrossRef CAS PubMed.
- W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, J. Am. Chem. Soc., 2017, 139, 7148–7151 CrossRef CAS PubMed.
- M. Caironi, M. Bird, D. Fazzi, Z. Chen, R. Di Pietro, C. Newman, A. Facchetti and H. Sirringhaus, Adv. Funct. Mater., 2011, 21, 3371–3381 CrossRef CAS.
- E. F. Oliveira and F. C. Lavarda, Polymer, 2016, 99, 105–111 CrossRef CAS.
- C. Risko, M. D. McGehee and J.-L. Brédas, Chem. Sci., 2011, 2, 1200–1218 RSC.
- B. Fan, L. Ying, P. Zhu, F. Pan, F. Liu, J. Chen, F. Huang and Y. Cao, Adv. Mater., 2017, 29, 1703906 CrossRef PubMed.
- A. Yin, D. Zhang, S. H. Cheung, S. K. So, Z. Fu, L. Ying, F. Huang, H. Zhou and Y. Zhang, J. Mater. Chem. C, 2018, 6, 7855–7863 RSC.
- G. Han, Y. Guo, X. Ma and Y. Yi, Sol. RRL, 2018, 2, 1800190 CrossRef.
- D. M. Stoltzfus, J. E. Donaghey, A. Armin, P. E. Shaw, P. L. Burn and P. Meredith, Chem. Rev., 2016, 116, 12920–12955 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. Van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- S. Chen, S. M. Lee, J. Xu, J. Lee, K. C. Lee, T. Hou, Y. Yang, M. Jeong, B. Lee, Y. Cho, S. Jung, J. Oh, Z. G. Zhang, C. Zhang, M. Xiao, Y. Li and C. Yang, Energy Environ. Sci., 2018, 11, 2569–2580 RSC.
- L. Pandey, PhD thesis, Georgia Institute of Technology, 2013.
- J. L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003 CrossRef PubMed.
- X.-K. Chen, M. K. Ravva, H. Li, S. M. Ryno and J.-L. Brédas, Adv. Energy Mater., 2016, 6, 1601325 CrossRef.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Mater. Chem., 2011, 21, 1479–1486 RSC.
- W. Li, L. Ye, S. Li, H. Yao, H. Ade and J. Hou, Adv. Mater., 2018, 30, 1707170 CrossRef PubMed.
- V. Lemaur, M. Steel, D. Beljonne, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2005, 127, 6077–6086 CrossRef CAS PubMed.
- T. Unger, S. Wedler, F.-J. Kahle, U. Scherf, H. Bässler and A. Köhler, J. Phys. Chem. C, 2017, 121, 22739–22752 CrossRef CAS.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: More details on the construction of the eD–eA complexes. Additional information regarding the methods. The following details on the results: the OT ω for the individual eD and eA compounds and the eD–eA complexes. Relaxed PES scans of the selected dihedrals in the monomer models of the eD and eA copolymers and ITIC. The BLAtotal values of the eD and eA compounds and bond length differences between the geometries of the charged (radical and S1) and neutral (GS) eD and eA compounds in vacuum and CHCl3. Additional optoelectronic properties (HOMO, LUMO, and HOMO–LUMO gap energies, IEs, EAs, vertical excitation energies, oscillator strengths, and UV-vis absorption spectra) of the eD and eA compounds. The optimized geometries and relative energies of the eD–eA complexes. The multi-state FCD electronic couplings, additional CT parameters, and rates of the eD–eA complexes. See DOI: 10.1039/d0se00306a |
| This journal is © The Royal Society of Chemistry 2020 |