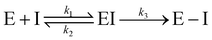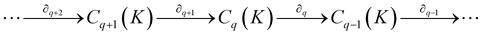Open Access Article
Open Access ArticleUnveiling the molecular mechanism of SARS-CoV-2 main protease inhibition from 137 crystal structures using algebraic topology and deep learning†
Duc Duy
Nguyen
a,
Kaifu
Gao
b,
Jiahui
Chen
b,
Rui
Wang
b and
Guo-Wei
Wei
 *bcd
*bcd
aDepartment of Mathematics, University of Kentucky, KY 40506, USA
bDepartment of Mathematics, Michigan State University, MI 48824, USA. E-mail: weig@msu.edu
cDepartment of Biochemistry and Molecular Biology, Michigan State University, MI 48824, USA
dDepartment of Electrical and Computer Engineering, Michigan State University, MI 48824, USA
First published on 30th September 2020
Abstract
Currently, there is neither effective antiviral drugs nor vaccine for coronavirus disease 2019 (COVID-19) caused by acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Due to its high conservativeness and low similarity with human genes, SARS-CoV-2 main protease (Mpro) is one of the most favorable drug targets. However, the current understanding of the molecular mechanism of Mpro inhibition is limited by the lack of reliable binding affinity ranking and prediction of existing structures of Mpro–inhibitor complexes. This work integrates mathematics (i.e., algebraic topology) and deep learning (MathDL) to provide a reliable ranking of the binding affinities of 137 SARS-CoV-2 Mpro inhibitor structures. We reveal that Gly143 residue in Mpro is the most attractive site to form hydrogen bonds, followed by Glu166, Cys145, and His163. We also identify 71 targeted covalent bonding inhibitors. MathDL was validated on the PDBbind v2016 core set benchmark and a carefully curated SARS-CoV-2 inhibitor dataset to ensure the reliability of the present binding affinity prediction. The present binding affinity ranking, interaction analysis, and fragment decomposition offer a foundation for future drug discovery efforts.
1 Introduction
Starting in late Dec, 2019, the COVID-19 pandemic caused by new severe acute respiratory syndrome coronavirus (SARS-CoV-2) has infected more than 22 million individuals and has caused more than 777![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fatalities in all of the continents and over 213 countries and territories by August 19th, 2020. Under the current global health emergency, researchers around the world have engaged in the investigation of the different drug targets of SARS-CoV-2, such as the main protease (Mpro, also called 3CLpro), papain-Like protease (PLpro), RNA-dependent RNA polymerase (RdRp), 5′-to-3′ helicase protein (Nsp13) to seek potential cures for this serious pandemic. To date, although there are some vaccines undergoing the Phase III trials,1 their safety and efficacy are still unclear.2
000 fatalities in all of the continents and over 213 countries and territories by August 19th, 2020. Under the current global health emergency, researchers around the world have engaged in the investigation of the different drug targets of SARS-CoV-2, such as the main protease (Mpro, also called 3CLpro), papain-Like protease (PLpro), RNA-dependent RNA polymerase (RdRp), 5′-to-3′ helicase protein (Nsp13) to seek potential cures for this serious pandemic. To date, although there are some vaccines undergoing the Phase III trials,1 their safety and efficacy are still unclear.2
The main protease, one of the best-characterized targets for coronaviruses, attracts lots of research attention because it is very conservative and distinguished from any human gene. A recent study shows that although the overall sequence identity between SARS-CoV and SARS-CoV-2 is just 80%, the Mpro of SARS-CoV-2 shares 96.08% sequence identity to that of SARS-CoV.3 Therefore, we hypothesize that a potent SARS Mpro inhibitor is also a potent SARA-CoV-2 Mpro inhibitor.
At this moment, more than 300 potential SARS-CoV Mpro inhibitors with its binding affinities are available in ChEMBL database4 which can be considered as the potential SARS-CoV-2 Mpro inhibitors. Recently, total 146 crystal structures of SARS-CoV-2 Mpro with its ligand complexes are released on the Protein Data Bank (PDB).5 Among them, 137 crystal structures have no available binding affinities reported for various reasons. However, the central dogma of drug design and discovery concerns the molecular mechanism and binding affinity of drug target interactions. Knowing the binding affinities and their ranking of 137 SARS-CoV-2 Mpro inhibitors is of great significance to the future design of anti SARS-CoV-2 drugs.
In this work, for the first time, we predict the binding affinities of these 137 Mpro–inhibitor complexes by reformulating algebraic topology-based mathematics-deep learning (MathDL) models, which have been the top competitor in D3R Grand Challenges, a worldwide competition series in computer aided drug design in the past three years.6 We generate reliable poses for 141 Mpro inhibitors with binding affinities but without complex structures. Together with 44 other complexes, we compose a set of 185 Mpro–inhibitor complexes, which is paired with 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 protein–ligand complexes in PDBbind 2019 general set. These datasets are utilized to construct 11 MathDL models in single-task and multitask settings.6 One of these 11 MathDL models has been validated by using the PDBbind v2016 core set benchmark, achieving the top performance over all exiting scoring functions. The other ten MathDL models have cross-validated on a set of 185 Mpro–nhibitor complexes, showing an averaged Pearson's correlation coefficient of 0.73.
382 protein–ligand complexes in PDBbind 2019 general set. These datasets are utilized to construct 11 MathDL models in single-task and multitask settings.6 One of these 11 MathDL models has been validated by using the PDBbind v2016 core set benchmark, achieving the top performance over all exiting scoring functions. The other ten MathDL models have cross-validated on a set of 185 Mpro–nhibitor complexes, showing an averaged Pearson's correlation coefficient of 0.73.
Notably, for covalent inhibitors, the scheme of covalent irreversible inhibition of SARS-CoV/SARS-CoV-2 Mpro is presented below:
The inhibitor first binds to the protease noncovalently, then a nucleophilic attacking by Cys145 leads to the formation of a stable covalent bond between the protease and the inhibitor.7,8 The interaction depends on both the equilibrium-binding constant Ki (designated as k1/k2) and the inactivation rate constant for covalent bond formation k3. In this work, the binding affinity/IC50 assesses the first step to form noncovalent binding.
In a nutshell, the present work provides reliable binding affinity predictions and ranking of 137 SARS-CoV-2 inhibitors that have crystal structures. It also offers data curation and validated models for exploring potential SARS-CoV-2 Mpro inhibitors. Furthermore, this work explores different possible binding regions on the SARS-CoV-2 main protease and decode the most favorable molecular fragments for the inhibitor design.
2 Results and discussions
2.1 Results
This section is devoted to the utilization of our MathDL models developed in Section 3.3 to predict the binding affinities and their ranking of SARS-CoV-2 inhibitors that do not have reported experimental affinities. To reduce the role of 3D pose prediction errors in our model, we use the SARS-CoV-2 inhibitors with X-ray structures available in the PDB for our study. We manually search these ligands on the PDB and arrive at a set consisting of 137 SARS-CoV-2 Mpro inhibitors having X-ray crystal structures but lacking of experimental binding affinities. We name this set SARS-CoV PDB-noBA (see Table 3). In this experiment, we develop a MathDL model optimized from PDBbind v2016 core set (see Section 3.3.1), five MathDL-ALL and five MathDL-MT models obtained from 5-fold study on the SARS-CoV BA set (see Section 3.3.2). The final predicted binding affinity is the consensus of these 11 models. The top ten inhibitors indicated by our models are shown in Table 1.| PDBID | Pred. BA | Pred. IC50 | PDBID | Pred. BA | Pred. IC50 |
|---|---|---|---|---|---|
| 7c8t | −8.90 | 0.30 | 6z2e | −8.43 | 0.66 |
| 5rgl | −8.50 | 0.58 | 6xbi | −8.34 | 0.76 |
| 6xhm | −8.50 | 0.58 | 6xmk | −8.33 | 0.78 |
| 7bqy | −8.49 | 0.59 | 5rh7 | −8.32 | 0.79 |
| 5rfr | −8.45 | 0.63 | 6xbh | −8.27 | 0.86 |
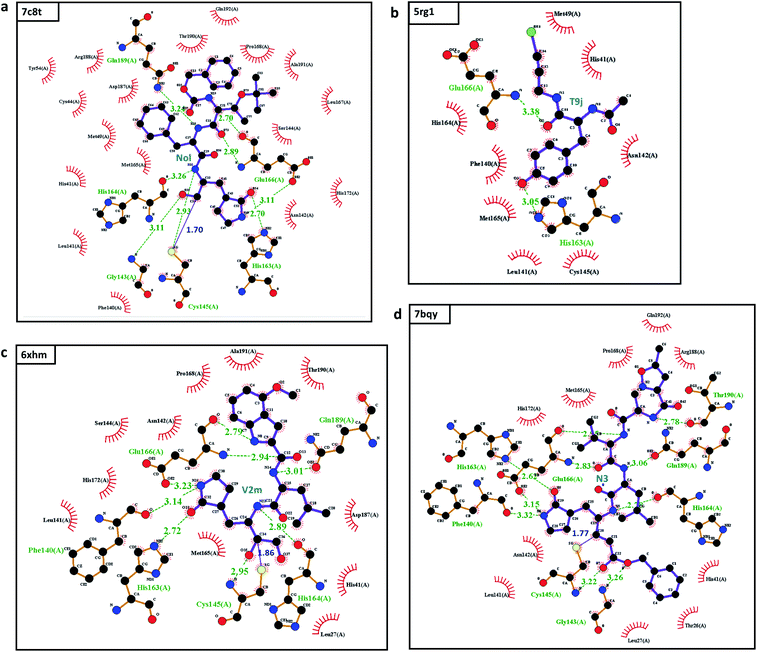
The most potent SARS-CoV-2 inhibitor found by our MathDL models is the inhibitor Nol in complex 7c8t. Nol was synthesized by Yang and his colleagues,9 Nol is found remarkable activities against SARS-CoV and HCoV.9 Specifically, the dissociation constant Ki of Nol was found to be 0.053 μM against SARS-CoV.9 Our MathDL reveals that Nol still inhibits SARS-CoV-2 main protease with a potent affinity at 0.30 μM.
Another important top potent SARS-CoV-2 inhibitor found by our models is the Michael acceptor inhibitor N3 in complex 7bqy. Designed by Yang and his colleagues,8 N3 was found to have viral activities against different coronavirus Mpro such as SARS-CoV and MERS-CoV.8,10 Specifically, the dissociation constant Ki of N3 was found to be 9.0 μM against SARS-CoV.8 Our MathDL reveals that N3 still inhibits SARS-CoV-2 main protease with an even better affinity at 0.59 μM. This finding is consistent with the literature work11 showing that N3 is a potent inhibitor of COVID-19 virus Mpro.
The inhibitor Qys in the complex 6xmk is also noticeable. Our predicted IC50 is 0.78 μM. Soon after we made the prediction, on August 12th, 2020, Rathnayake et al.12 released another Qys-main protease complex with PDB ID 6w2a and also reported the IC50 of Qys to SARS-CoV-2 is 0.45 μM, which is close to our prediction.
It is worth pointing out, except for the inhibitor T9j in the complex 5rg1, the rest of inhibitors reported in Table 1 are covalent inhibitors, which irreversibly form covalent bonds with Cys145 of the main protease (see discussion in Section 2.2.2). However, our models only predict the non-covalent binding affinity which is measured before the enzyme deactivation. The predicted binding affinities of all 137 complexes in SARS-CoV PBD-noBA dataset from various MathDL models are presented in Table S8 in ESI.† In this table, we also supply the synthetic accessibility score (SAS), partition coefficient log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, and solubility log
P, and solubility log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S for each small molecule. Except for SAS obtained via RDKit,13 log
S for each small molecule. Except for SAS obtained via RDKit,13 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and log
P and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S are evaluated by our TopP-S model.14
S are evaluated by our TopP-S model.14
2.2 Discussion
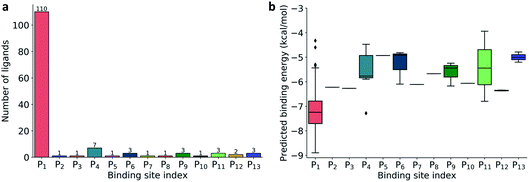 | ||
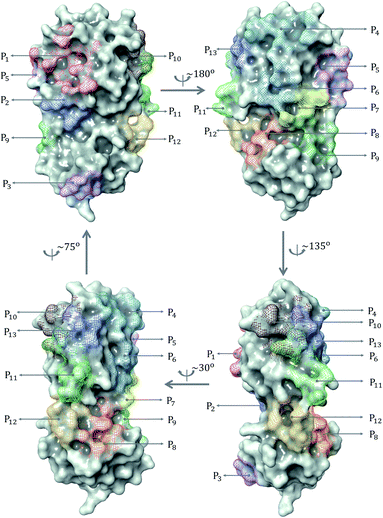
| Fig. 2 (a) Distribution of 137 ligands across 13 distinct binding sites; (b) Box plot of predicted binding energies (kcal mol−1) of all inhibitors in each binding site. | ||
The prevailing binding pocket P1 is the best region on the SARS-CoV-2 Mpro for inhibitor design with the median binding energy being −7.22 kcal mol−1. Nol is the best inhibitor candidate for the binding site P1 with predicted affinity found to be −8.90 kcal mol−1. Other binding regions such as P4, and P11 are less common but show their adequate effects on the binding mechanism with their best energy binding affinities calculated at −7.28 kcal mol−1 and −6.80 kcal mol−1, respectively. These potential binding sites can guide drug combination to inhibit coronavirus Mpro effectively.
This examination manifests how well our models preserve and capture the physical and chemical properties described in intermolecular bonding interactions. Furthermore, the ligand T9J that binds to Mpro in complex 5rg1 with a quite close binding energy at −8.50 kcal mol−1 forms different hydrogen bonds in comparison to three previously mentioned inhibitors (see Table 2). Since our models only concern the non-covalent binding affinity, the lack of covalent bond in 5rg1's interactions does not downgrade its binding strength. With two relatively large hydrogen bonding distances (O2-His163: 3.05 Å, O3-Glu166: 3.38 Å (see Fig. 3d)), the binding affinity of 5rg1 is still comparable to the top inhibitors indicating the important roles in acquiring the hydrogen bonds to these residues in the main protease's binding process.
In the top 10 inhibitors as listed in Table 1, T9J in the complex 5rg1 is only one non-covalent inhibitor. The rest belongs to the class of targeted covalent inhibitors (TCI) in which they interacts with the protein residues, i.e., cysteine, to form a covalent complex strongly neutralizing target's function. However, the major disadvantage of TCIs is the association with the high toxicity risks.16 TCIs' strong covalent bond can irreversibly modify the unintended protein targets in the human body. As a result, the top covalent inhibitors in SARS-CoV PBD-noBA dataset may have little chance to become approved market drugs in comparison to their non-covalent counterparts such as T9J in 5rg1.
Due to the popularity of the binding site P1 among 137 interested inhibitors, we mainly analyze the interaction network around the residues in that region. Out of 110 molecules binding to P1, there are 103 inhibitors forming at least one hydrogen bond to the nearby amino acid in the SARS-CoV-2 main protease. We have identified 20 different residues in the binding pocket P1 composing hydrogen bonds to these small molecules. Fig. 4 illustrates the frequency of these 20 residues across 110 inhibitors. Based on Fig. 4, Gly143 residue is the most attractive site to form the hydrogen bond. It appears in 53.6% of 110 intermolecular bonding interactions, followed by Glu166 residue with a frequency of 39.1%; residue Cys145 and His163 also occupy 38.2% and 30.9%, respectively. It is worth noting when these molecules form a hydrogen bond with Cys145, they also constitute another hydrogen bond with Gly143. In all cases, both these residues share the same hydrogen-bond acceptor. Besides the hydrogen bond network, 71 ligands in the SARS-CoV PDB-noBA dataset form a covalent bond to γ-sulfur of Cys145. Except the second one, all the others in the top 10 inhibitors are equipped with that covalent bond (see Table S8 in ESI†).
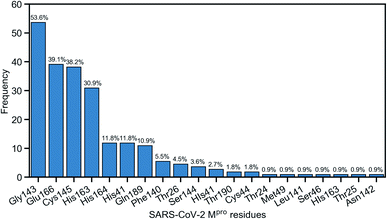 | ||
| Fig. 4 Popularity of amino acids in the binding site P1 constituting the hydrogen bonds with ligands. | ||
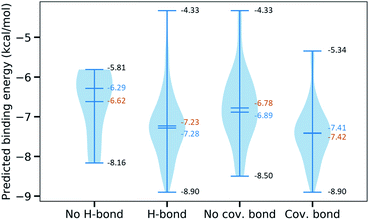
Furthermore, we are interested in the binding energy distribution associated with the interaction network. Fig. 5 depicts the violin plot of that distribution across four categories, namely no H-bond (no hydrogen bond), H-bond (at least one hydrogen bond), no cov. bond (no covalent bond), and cov. bond (at least one covalent bond). Hydrogen bond interactions that are expected to play an important role in the binding mechanism are well captured in our MathDL models. Specifically, while the average energy of inhibitors having no hydrogen bond is −6.62 kcal mol−1, the average energy of ones with hydrogen bond is as low as −7.23 kcal mol−1.
It is noted that our MathDLs only measure the non-covalent binding affinity. The covalent bond appearing at the final covalent complex is not properly accounted for in our framework. Therefore, it is expected that our models sometimes overestimate the covalent-bond inhibitors over the non-covalent-bond candidates. Fig. 5 reveals molecules in the group of covalent bonds generally are predicted with lower binding energy with an average being −7.42 kcal mol−1 in comparison to −6.89 kcal mol−1 averagely measured on ones without covalent bonds.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, often constitutes a hydrogen bond with Gly143 and in many cases forms a covalent bond with Cys145.
O, often constitutes a hydrogen bond with Gly143 and in many cases forms a covalent bond with Cys145.
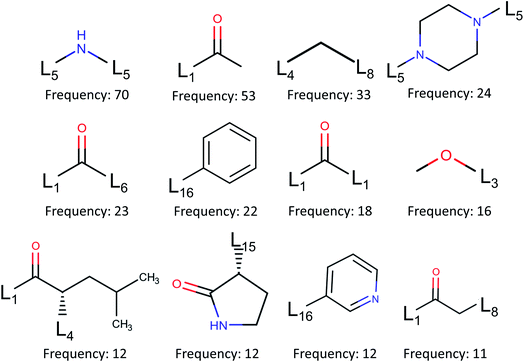 | ||
| Fig. 6 Fragment frequencies based on BRICS decomposition of 110 inhibitors of binding site pocket P1. Li is the link atom of a certain type described in ref. 17. | ||
3 Materials and methods
3.1 Datasets
Our deep learning-based scoring function, MathDL, was trained on public databases including PDBbind18 and ChEMBL.4 The PDBbind sets contain all complexes with crystal structures deposited in the PDB with the binding affinities not limited to Kd, Ki, and IC50 reported in the literature. In this work, we employ the PDBbind v2019, the latest version of its generation. The v2019 version of the PDBbind consists of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 protein–ligand complexes. However, the data preprocessing of the MathDL32 only retains 17
679 protein–ligand complexes. However, the data preprocessing of the MathDL32 only retains 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 complexes. Among them, there are 10
382 complexes. Among them, there are 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 ligands measured in Kd/Ki and 6537 ligands measured in IC50.
485 ligands measured in Kd/Ki and 6537 ligands measured in IC50.
ChEMBL is another manually curated database of bioactive molecules. Currently, ChEMBL contains more than 2 million compounds in the SMILES string format. Excluding 30 main protease inhibitors in PDBbind data, we have found other 277 small molecules on ChEMBL with reported Kd/IC50. Additionally, we have found more than 300 other SARS-CoV main protease inhibitors from literatures.18–20,25–31 In total, there are more than 600 ligands bound to SARS-CoV/SARS-CoV-2 main protease having the experimental binding affinities; among them, there are 44 crystal structures. For compounds without the crystal structures, MathPose6 is utilized to generate their 3D conformations. The predicted 3D coordinates of these structures are presented in the SDF format and available in ESI.† Currently, there are roughly 137 ligands forming crystal complexes with the SARS-CoV-2 main protease on PDB without the report of the experimental inhibitor activities. Most of them are deposited by the PanDDA analysis group (https://pandda.bitbucket.io/#).
To serve model validation purposes, we classify the selected data into five different groups as listed in Table 3. Specifically, PDBbind v2019 is the biggest set in this compilation with its PDB IDs and experimental binding affinities listed in Table S1 in ESI.† PDBbind v2016 core set is a subset of PDBbind v2019 and is formed by 290 complexes representing all protein classes in the refined set of PDBbind v2016.18,33 The PDB IDs of all complexes in the PDBbind v2016 core set are provided in Table S2.† We also collect all Mpro complexes of SARS-CoV/SARS-CoV-2 on the PDB, denoted by SARS-CoV PDB, which results in a total of 192 structures (see Table S3†). Among them, there are 44 ligands with the report of experimental binding affinities denoted by SARS-CoV PDB-BA (see Table S4†). Furthermore, we are interested in the set of SARS-CoV-2 Mpro complexes in the aforementioned SARS-CoV PDB set but their affinities are not presented or undisclosed. We call this set SARS-CoV PDB-noBA with PDB IDs listed in Table S5.† To enrich our training data targeting SARS-CoV/SARS-CoV-2 main protease inhibitors, we gather some inhibitors reported on the literature.4,25 For those compounds with only 2D information, we limit ourselves to ones having the similarity score based on the path-based fingerprint FP2 no lower than 0.6 to at least one inhibitor in the SARS-CoV PDB set. As a result, we arrive at a set of 141 structures named SARS-CoV 2D (see Table S6†). Combining SARS-CoV PDB-BA and SARS-CoV 2D data sets, we finalize a reliable database focusing on SARS-CoV/SARS-CoV-2 main protease inhibitors. Notice that the binding affinities in this set are all reported in IC50. Table S7 in ESI† presents the PDB IDs as well as the experimental binding energies of these ligands.
| Data name | Data size | Descriptions | References |
|---|---|---|---|
| PDBbind v2019 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 382 |
Partial PDBbind general set v2019 | 18 |
| PDBbind v2016 core set | 290 | PDBbind v2016 core set | 18 |
| SARS-CoV PDB | 192 | Inhibitors of SARS-CoV/SARS-CoV-2 Mpro having X-ray crystal structures | 5, 19 and 20 |
| SARS-CoV PDB-BA | 44 | Inhibitors of SARS-CoV/SARS-CoV-2 Mpro having X-ray crystal structures and experimental binding affinities | 5, 18–23 |
| SARS-CoV PDB-noBA | 137 | Inhibitors of SARS-CoV-2 Mpro having X-ray crystal structures but lacking of experimental binding affinities | 5, 18–20, 24 |
| SARS-CoV 2D | 141 | Inhibitors of SARS-CoV/SARS-CoV-2 Mpro having only 2D structures | 4, 19, 20, 25–31 |
| SARS-CoV BA | 185 | Inhibitors of SARS-CoV/SARS-CoV-2 Mpro having experimental binding affinities | 5, 18–20, 26–31 |
3.2 Methods
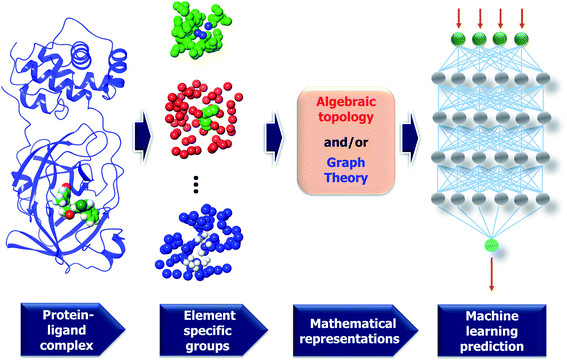 | ||
| Fig. 7 A framework of MathDL energy prediction model which integrates advanced mathematical representations with sophisticated CNN architectures. | ||
3.2.1.1 Algebraic topology-based representations. Algebraic topology studies the topological spaces with the use of abstract algebra, which can dramatically simplify the geometric complexity. Persistent homology (PH) is one of the algebraic topology approaches which has the capacity to track the multiscale topological information over different scales along with filtration by characterizing independent components, rings, and higher dimensional voids in space.34 In this section, we will briefly review the algebraic topology-based representations. Additionally, since we are dealing with the protein–ligand system, therefore, the biological considerations will take into account as well.
Simplex. The q-simplex denoted as σq is the convex hull of q + 1 affinely independent points in
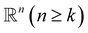 . For example, the 0, 1, 2, and 3-simplex is considered as a vertex, an edge, a triangle, and a tetrahedron, respectively. We call the convex hull of each non-empty subset of q + 1 points the face of σq, and each points are also called the vertices.
. For example, the 0, 1, 2, and 3-simplex is considered as a vertex, an edge, a triangle, and a tetrahedron, respectively. We call the convex hull of each non-empty subset of q + 1 points the face of σq, and each points are also called the vertices.
Simplicial complex. A set of simplices is a simplicial complex denote K which satisfies that every face of a simplex σq ∈ K is also in K and the non-empty intersection of any two simplices in K is the common face for both.
Chain complex. A formal sum of q-simplices in simplicial complex K with coefficients in an algebraic field (typically
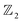 ) is a q-chain. A set of all q-chains of the simplicial complex K equipped with an algebraic field is called a chain group and denoted as Cq(K). The boundary operator is defined by ∂q: Cq(K) → Cq−1(K) to relate the chain groups. More specifically, we denote σq = [v0, v1, …, vq] for the q-simplex spanned by its vertices, and then the boundary operator can be represented as:
) is a q-chain. A set of all q-chains of the simplicial complex K equipped with an algebraic field is called a chain group and denoted as Cq(K). The boundary operator is defined by ∂q: Cq(K) → Cq−1(K) to relate the chain groups. More specifically, we denote σq = [v0, v1, …, vq] for the q-simplex spanned by its vertices, and then the boundary operator can be represented as: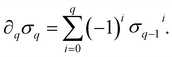 | (1) |
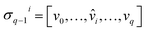 is the (q − 1)-simplex with vi being omitted. The sequence of chain groups connected by boundary operators is called the chain complex and expressed as:
is the (q − 1)-simplex with vi being omitted. The sequence of chain groups connected by boundary operators is called the chain complex and expressed as:The q-cycle group Zq(K) and the q-boundary group Bq(K) are defined as Zq(K) = ker(∂q) = {c ∈ Cq(K)|∂qc = ∅} and Bq(K) = im(∂q+1) = {∂q+1c|c ∈ Cq+1(K)}. The q-th homology group is the quotient group Hq(K) = Zq(K)/Bq(K). Moreover, the rank of q-th homology group can be computed as rankHq(K) = rankZq(K) − rankBq(K), which is denoted as the q-th Betti number βq. To be notice that the q-th Betti number count the number of q-dimensional holes that can not be continuously deformed to each other.
Persistent homology. A filtration of a simplicial complex K is a nested sequence of subcomplexes of K such that ∅ = K0 ⊆ K1 ⊆ K2⋯⊆ Km = K. Then the p-persistent qth homology group of Kt is defined as:
| Hqp(Kt) = Zq(Kt)/(Bq(Kt+p) ∩ Zq(Kt)). | (2) |
3.2.1.2 Element specific considerations. The protein–ligand complex is structural and also biological. The persistent homology provides a theoretical approach to encode high-dimensional spatial data of protein–ligand complexes into algebraic topological representations. In this section, we address the biological considerations for biomolecular complexity. There are many kinds of interactions that exist in the protein–ligand complex, such as electrostatics, hydrogen bonds, and hydrophobic effects. Although persistent homology can capture the interactions among the nearest neighbors, the long-range interactions will be hindered. This difficulty can be avoided via the deployment of the element-specific attention.32 There are 4 commonly atom types in protein, namely C, N, O, S, and there are 11 commonly atom types in ligand, including C, N, O, S, P, F, Cl, Br, I, H, B. We include Boron in the ligand atom type consideration since it appears in more than 200 small compounds in our training data. The general framework of MathDL is depicted in Fig. 7 under exemplified steps. In addition, the details of the deep learning architecture of the current MathDL is offered in Fig. S1.† For the details of feature descriptions as well as the deep learning architecture, interested readers are referred to our previous work.32
3.3 Validations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 complexes. MathDL with the architecture described in Section 3.2.1 is trained on those complexes. The resulting model is utilized to predict the binding affinity of 290 structures in the PDBbind v2016 core set.
211 complexes. MathDL with the architecture described in Section 3.2.1 is trained on those complexes. The resulting model is utilized to predict the binding affinity of 290 structures in the PDBbind v2016 core set.
With the purpose of exploring the most optimal model for this benchmark, MathDL is trained for 1000 epochs. Then, we pick the epoch based on the root-mean-squared error (RMSE) of the PDBbind v2016 core set prediction. We have found that MathDL achieves the smallest RMSE in this experiment at 140 epochs. Specifically RMSE, Rp, and τ metrics on the v2016 core set are 1.56 kcal mol−1, 0.858, and 0.671, respectively. Meanwhile, the training accuracy is 0.387 kcal mol−1 in terms of RMSE and its Pearson's correlation coefficient is Rp = 0.994. These performances reveal that our MathDL converges very fast and with only 140 epochs and maintains a good balance between training and testing accuracies. This is a state-of-the-art performance since our MathDL is ranked in the second place in comparison to 33 other scoring functions (see Fig. 8). It is noted that the top model is TopBPcon. published in our previous work32 with Rp = 0.861. TopBPcon. is the consensus of gradient boosted tree and deep learning-based models. If only the deep learning framework is considered, the performance of TopBP (denoted by TopBP-DL) on the core set of PDBbind v2016 is Rp = 0.848.
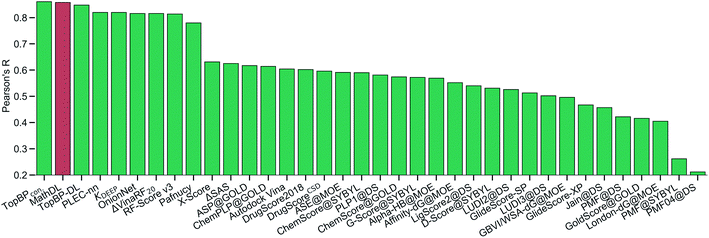 | ||
Fig. 8 The Pearson correlation coefficient of various scoring functions on PDBbind v2016 core set benchmark. Our MathDL is in red. The performances of other models that are in green are taken from ref. 18, 32, 38–41. TopBPcon., the consensus model in our published work,32 attains the highest Rp at 0.861. The current MathDL is followed with the second highest Rp at 0.858 and RMSE = 1.56 kcal mol−1. The third place in the list is another TopBP model, TopBP-DL, solely based on the deep learning architectures and its reported Rp is 0.848.32 It is noted that all of the machine learning based scoring functions in this comparison were trained on the PDBbind v2016 refined set of 3767 complexes except for our MathDL. Explicitly, MathDL is trained on a much larger training set consisting of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 complexes picked out from the PDBbind v2019 set and SARS-CoV BA set. 211 complexes picked out from the PDBbind v2019 set and SARS-CoV BA set. | ||
It is worth mentioning that except for our MathDL, all machine learning-based scoring functions listed in Fig. 8 were trained on the PDBbind v2016 refined set of 3767 complexes. As mentioned above, the current MathDL is compiled on a much larger training set comprised of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 complexes selected from PDBbind v2019 and SARS-CoV BA data. Even the present MathDL has not outperformed its predecessor, i.e., TopBPcon., MathDL is still a preference model since it is trained on a diverse data set covering various protein families and different binding energy ranges. As a result, it is expected to deliver more reliable predictions on the SARS-CoV-2 inhibitor, especially when this main protease family is not included in the training data of previous TopDL models. The resulting MathDL model is labeled as MathDL-Core2016 and is utilized to predict affinities of complexes in SARS-CoV PDB-noBA in Section 2.1.
211 complexes selected from PDBbind v2019 and SARS-CoV BA data. Even the present MathDL has not outperformed its predecessor, i.e., TopBPcon., MathDL is still a preference model since it is trained on a diverse data set covering various protein families and different binding energy ranges. As a result, it is expected to deliver more reliable predictions on the SARS-CoV-2 inhibitor, especially when this main protease family is not included in the training data of previous TopDL models. The resulting MathDL model is labeled as MathDL-Core2016 and is utilized to predict affinities of complexes in SARS-CoV PDB-noBA in Section 2.1.
Table 4 reveals that MathDL-All models are well trained with the averaged accuracy RMSE = 0.286 kcal mol−1, Pearson's correlation coefficient Rp = 0.994, and Kendall's tau τ = 0.934. Their averaged performances on test data across 5-fold of the SARS-CoV BA set are found to be Rp = 0.729, τ = 0.540, and RMSE = 0.789 kcal mol−1. These results endorse the reliability of these models in the binding affinity prediction of SARS-CoV/SARS-CoV-2 inhibitors. Table 4 also lists the training and testing performances of five multi-task learning models. The averaged training performance of the MathDL-MT model is Rp = 0.995, τ = 0.941 and RMSE = 0.275 kcal mol−1. The accuracy of the multi-task architecture on the test sets is similar to MathDL-All with Rp = 0.727, τ = 0.532, and RMSE = 0.822 kcal mol−1. With these promising results, it is encouraging to carry out MathDL models to predict unknown binding affinities of SARS-CoV/SARS-CoV-2 inhibitors. It is worth noting that if the 5-fold cross-validation is conducted purely on the SARS-CoV BA set, the average Rp and τ are as low as 0.561 and 0.388, respectively. These results strongly support the inclusion of diverse information such as PDBbind v2019 in conjunction with sophisticated deep learning architectures to achieve the accurate binding energy prediction of Mpro inhibitors.
| MathDL-ALL | MathDL-MT | |||||
|---|---|---|---|---|---|---|
| R p | τ | RMSE | R p | τ | RMSE | |
| Fold 1 (train) | 0.992 | 0.923 | 0.327 | 0.996 | 0.949 | 0.253 |
| Fold 1 (test) | 0.792 | 0.534 | 0.682 | 0.818 | 0.534 | 0.680 |
| Fold 2 (train) | 0.995 | 0.943 | 0.266 | 0.996 | 9.948 | 0.236 |
| Fold 2 (test) | 0.625 | 0.498 | 0.866 | 0.689 | 0.538 | 0.826 |
| Fold 3 (train) | 0.991 | 0.917 | 0.367 | 0.994 | 0.934 | 0.327 |
| Fold 3 (test) | 0.771 | 0.572 | 0.758 | 0.767 | 0.593 | 0.802 |
| Fold 4 (train) | 0.996 | 0.948 | 0.240 | 0.997 | 0.951 | 0.177 |
| Fold 4 (test) | 0.618 | 0.397 | 0.874 | 0.642 | 0.472 | 0.901 |
| Fold 5 (train) | 0.995 | 0.941 | 0.231 | 0.991 | 0.921 | 0.380 |
| Fold 5 (test) | 0.838 | 0.699 | 0.767 | 0.719 | 0.524 | 0.900 |
| Average (train) | 0.994 | 0.934 | 0.286 | 0.995 | 0.941 | 0.275 |
| Average (test) | 0.729 | 0.540 | 0.789 | 0.727 | 0.532 | 0.822 |
4 Conclusion
SARS-CoV-2 main protease (Mpro) is the most favorable target for COVID-19 drug discovery due to its conservative nature and low similarity with human genes. Structure and binding affinity of protein–drug complexes are of paramount importance for understanding the molecular mechanism in drug discovery. However, there are only two SARS-CoV-2 Mpro inhibitor structures available with binding affinities, highlighting current challenges in COVID-19 drug discovery.This work presents the reliable binding affinity prediction and ranking of 137 Mpro–inhibitor crystal structures that have no reported experimental binding affinity. We first curate a set of more than 600 Mpro inhibitors with binding affinities from public resources, such as PDBbind, ChEMBL and the scattered literature. Among these inhibitors, 141 are retained based on their high similarity with available Mpro–inhibitor complex structures and built with three dimensional (3D) poses using our MathPose.6 Together with 44 another SARS-CoV or SARS-CoV-2 Mpro–inhibitor complexes, we compose a training set of 185 reliable SARS-CoV-2 Mpro–inhibitor complexes. Our earlier MathDL models are reformulated with algebraic topology to accommodate 119 new complexes and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 complexes from the PDBbind v2019 general set in both single-task and multitask settings, which have never been available before. The resulting MathDL models are rigorously validated via PDBbind v2016 core set benchmark in which it outperforms state-of-the-art models in the literature. Most importantly, our MathDL achieves promising cross-validation accuracies on the SARS-CoV family inhibitors with the averaged Pearson's correlation coefficient as high as 0.73.
382 complexes from the PDBbind v2019 general set in both single-task and multitask settings, which have never been available before. The resulting MathDL models are rigorously validated via PDBbind v2016 core set benchmark in which it outperforms state-of-the-art models in the literature. Most importantly, our MathDL achieves promising cross-validation accuracies on the SARS-CoV family inhibitors with the averaged Pearson's correlation coefficient as high as 0.73.
Additionally, the present work unveils that Gly143 of Mpro is the most attractive region to form hydrogen bonds, followed by Glu166, Cys145, and His163. There are 71 inhibitors interacting with SARS-CoV-2 Mpro to form covalent complexes. Those covalent bonds are mostly composed between dicarbon monoxide groups in inhibitors and γ-sulfur on Cys145. There are only one non-covalent complex in our top 10 ranked, namely 5rg1. To provide a potential resource for lead molecule design, we employ the BRICS algorithm to decompose all the inhibitors of the prominent binding site on Mpro and obtain 185 unique fragments.
The predicted binding affinities and their ranking of 137 Mpro–inhibitor crystal structures, the bonding analysis, and the fragment decomposition have significantly extended current knowledge and understanding of SARS-CoV-2 Mpro and inhibitor interactions and, thus offered valuable information toward COVID-19 drug discovery.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by NIH grant GM126189, NSF Grants DMS-1721024, DMS-1761320, and IIS1900473, Michigan Economic Development Corporation, George Mason University award PD45722, Bristol-Myers Squibb, and Pfizer. The authors thank The IBM TJ Watson Research Center, The COVID-19 High Performance Computing Consortium, and NVIDIA for computational assistance.References
- Phase III Double-blind, Placebo-controlled Study of AZD1222 for the Prevention of COVID-19 in Adults, 2020, accessed September 15, 2020, https://clinicaltrials.gov/ct2/show/NCT04516746?term=NCT04516746%26draw=2%26rank=1 Search PubMed.
- Statement on AstraZeneca Oxford SARS-CoV-2 vaccine, AZD1222, COVID-19 vaccine trials temporary pause, 2020, accessed September 15, 2020, https://www.astrazeneca.com/media-centre/press-releases/2020/statement-on-astrazeneca-oxford-sars-cov-2-vaccine-azd1222-covid-19-vaccine-trials-temporary-pause.html Search PubMed.
- X. Xu, P. Chen, J. Wang, J. Feng, H. Zhou, X. Li, Wu Zhong and P. Hao, Evolution of the novel coronavirus from the ongoing wuhan outbreak and modeling of its spike protein for risk of human transmission, Sci. China: Life Sci., 2020, 63(3), 457–460 CrossRef CAS.
- M. Davies, M. Nowotka, G. Papadatos, N. Dedman, A. Gaulton, F. Atkinson, L. Bellis and J. P. Overington, Chembl web services: streamlining access to drug discovery data and utilities, Nucleic Acids Res., 2015, 43(W1), W612–W620 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, The protein data bank, Nucleic Acids Res., 2000, 28(1), 35–242 CrossRef.
- D. D. Nguyen, K. Gao, M. Wang and G.-W. Wei, MathDL: Mathematical deep learning for d3r grand challenge 4, J. Comput.-Aided Mol. Des., 2020, 34, 131–147 CrossRef CAS.
- D. A. Matthews, P. S. Dragovich, S. E. Webber, S. A. Fuhrman, A. K. Patick, L. S. Zalman, T. F. Hendrickson, R. A. Love, T. J. Prins and J. T. Marakovits, et al., Structure-assisted design of mechanism-based irreversible inhibitors of human rhinovirus 3c protease with potent antiviral activity against multiple rhinovirus serotypes, Proc. Natl. Acad. Sci. U. S. A., 1999, 96(20), 11000–11007 CrossRef CAS.
- H. Yang, W. Xie, X. Xue, K. Yang, J. Ma, W. Liang, Q. Zhao, Z. Zhou, D. Pei and J. Ziebuhr, et al., Design of wide-spectrum inhibitors targeting coronavirus main proteases, PLoS Biol., 2005, 3(10), e324 CrossRef.
- S. Yang, S.-J. Chen, M.-F. Hsu, J.-D. Wu, C.-T. K. Tseng, Y.-F. Liu, H.-C. Chen, C.-W. Kuo, C.-S. Wu and L.-W. Chang, et al., Synthesis, crystal structure, structure-activity relationships, and antiviral activity of a potent sars coronavirus 3cl protease inhibitor, J. Med. Chem., 2006, 49(16), 4971–4980 CrossRef CAS.
- F. Wang, C. Chen, W. Tan, K. Yang and H. Yang, Structure of main protease from human coronavirus nl63: insights for wide spectrum anti-coronavirus drug design, Sci. Rep., 2016, 6, 22677 CrossRef CAS.
- Z. Jin, X. Du, Y. Xu, Y. Deng, M. Liu, Y. Zhao, B. Zhang, X. Li, L. Zhang and C. Peng, et al., Structure of mpro from covid-19 virus and discovery of its inhibitors, bioRxiv, 2020 Search PubMed.
- A. D. Rathnayake, J. Zheng, Y. Kim, K. D. Perera, S. Mackin, D. K. Meyerholz, M. M. Kashipathy, K. P. Battaile, S. Lovell and S. Perlman, et al., 3c-like protease inhibitors block coronavirus replication in vitro and improve survival in mers-cov-infected mice, Sci. Transl. Med., 2020, 12(557), eabc5332 CrossRef CAS.
- G. Landrum et al. , Rdkit: Open-source cheminformatics, 2006 Search PubMed.
- K. Wu, Z. Zhao, R. Wang and G. W. Wei, TopP-S: Persistent Homology-Based Multi-Task Deep Neural Networks for Simultaneous Predictions of Partition Coefficient and Aqueous Solubility, J. Comput. Chem., 2018, 39, 1444–1454 CrossRef CAS.
- H.-P. Chang, C.-Y. Chou and G.-G. Chang, Reversible unfolding of the severe acute respiratory syndrome coronavirus main protease in guanidinium chloride, Biophys. J., 2007, 92(4), 1374–1383 CrossRef CAS.
- B. K. Park, A. Boobis, S. Clarke, C. E. P. Goldring, D. Jones, J. G. Kenna, C. Lambert, H. G. Laverty, D. J. Naisbitt and S. Nelson, et al., Managing the challenge of chemically reactive metabolites in drug development, Nat. Rev. Drug Discovery, 2011, 10(4), 292–306 CrossRef CAS.
- J. Degen, C. Wegscheid-Gerlach, A. Zaliani and M. Rarey, On the art of compiling and using’drug-like’chemical fragment spaces, ChemMedChem, 2008, 3(10), 1503–1507 CrossRef CAS.
- M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, Comparative assessment of scoring functions: The casf-2016 update, J. Chem. Inf. Model., 2018 Search PubMed.
- L. Zhang, D. Lin, X. Sun, U. Curth, C. Drosten, L. Sauerhering, S. Becker, K. Rox and R. Hilgenfeld, Crystal structure of sars-cov-2 main protease provides a basis for design of improved α-ketoamide inhibitors, Science, 2020, 368(6489), 409–412 CrossRef CAS.
- H. Su, S. Yao, W. Zhao, M. Li, L. Jia, W. Shang, H. Xie, C. Ke, M. Gao and K. Yu, et al., Discovery of baicalin and baicalein as novel, natural product inhibitors of sars-cov-2 3cl protease in vitro, bioRxiv, 2020 Search PubMed.
- H. Wang, S. He, W. Deng, Y. Zhang, G. Li, J. Sun, W. Zhao, Y. Guo, Y. Zheng and D. Li, et al., Comprehensive insights into the catalytic mechanism of middle east respiratory syndrome 3c-like protease and severe acute respiratory syndrome 3c-like protease, ACS Catal., 2020, 10(10), 5871–5890 CrossRef CAS.
- W. Dai, B. Zhang, X.-M. Jiang, H. Su, J. Li, Y. Zhao, X. Xie, Z. Jin, J. Peng and F. Liu, et al., Structure-based design of antiviral drug candidates targeting the sars-cov-2 main protease, Science, 2020, 368(6497), 1331–1335 CrossRef CAS.
- C. Ma, M. D. Sacco, B. Hurst, J. A. Townsend, Y. Hu, T. Szeto, X. Zhang, B. Tarbet, M. T. Marty and Y. Chen, et al., Boceprevir, gc-376, and calpain inhibitors ii, xii inhibit sars-cov-2 viral replication by targeting the viral main protease, bioRxiv, 2020 Search PubMed.
- A. Douangamath, D. Fearon, P. Gehrtz, T. Krojer, P. Lukacik, C. D. Owen, E. Resnick, C. Strain-Damerell, P. Ábrányi-Balogh and J. Brandaõ-Neto, et al., Crystallographic and electrophilic fragment screening of the sars-cov-2 main protease, Nat. Commun., 2020, 11, 5047 CrossRef CAS.
- U. Bacha, J. Barrila, S. B. Gabelli, Y. Kiso, L. M. Amzel and E. Freire, Development of broad-spectrum halomethyl ketone inhibitors against coronavirus main protease 3clpro, Chem. Biol. Drug Des., 2008, 72(1), 34–49 CrossRef CAS.
- A. K. Ghosh, M. Brindisi, D. Shahabi, M. E. Chapman and A. D. Mesecar, Drug development and medicinal chemistry efforts toward sars-coronavirus and covid-19 therapeutics, ChemMedChem, 2020, 15(11), 907–932 CrossRef CAS.
- P.-H. Liang, Characterization and inhibition of sars-coronavirus main protease, Curr. Top. Med. Chem., 2006, 6(4), 361–376 CrossRef CAS.
- H.-M. Wang and P.-H. Liang, Pharmacophores and biological activities of severe acute respiratory syndrome viral protease inhibitors, Expert Opin. Ther. Pat., 2007, 17(5), 533–546 CrossRef CAS.
- V. Kumar, Y.-S. Jung and P.-H. Liang, Anti-sars coronavirus agents: a patent review (2008–present), Expert Opin. Ther. Pat., 2013, 23(10), 1337–1348 CrossRef CAS.
- T. Pillaiyar, M. Manickam, V. Namasivayam, Y. Hayashi and S.-H. Jung, An overview of severe acute respiratory syndrome–coronavirus (sars-cov) 3cl protease inhibitors: peptidomimetics and small molecule chemotherapy, J. Med. Chem., 2016, 59(14), 6595–6628 CrossRef CAS.
- S. Ullrich and C. Nitsche, The sars-cov-2 main protease as drug target, Bioorg. Med. Chem. Lett., 2020, 127377 CrossRef CAS.
- Z. X. Cang, L. Mu and G. W. Wei, Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLoS Comput. Biol., 2018, 14(1), e1005929, DOI:10.1371/journal.pcbi.1005929.
- D. Nguyen and G.-W. Wei, AGL-Score: Algebraic graph learning score for protein–ligand binding scoring, ranking, docking, and screening, J. Chem. Inf. Model., 2019, 59(7), 3291–3304 CrossRef CAS.
- G. Carlsson, Topology and data, Bull. Am. Math. Soc., 2009, 46(2), 255–308 CrossRef.
- G. Jones, P. Willett, R. C. Glen, A. R. Leach and R. Taylor, Development and validation of a genetic algorithm for flexible docking, J. Mol. Biol., 1997, 267(3), 727–748 CrossRef CAS.
- O. Trott and A. J. Olson, AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading, J. Comput. Chem., 2010, 31(2), 455–461 CAS.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley and J. K. Perry, et al., Glide: a new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy, J. Med. Chem., 2004, 47(7), 1739–1749 CrossRef CAS.
- M. Wójcikowski, M. Kukiełka, M. Stepniewska-Dziubinska and P. Siedlecki, Development of a protein-ligand extended connectivity (plec) fingerprint and its application for binding affinity predictions, 2018 Search PubMed.
- D. D. Nguyen and G.-W. Wei, DG-GL: Differential geometry-based geometric learning of molecular datasets, Int. J. Numer. Method Biomed. Eng., 2019, 35(3), e3179 CrossRef.
- L. Zheng, J. Fan and Y. Mu, Onionnet: a multiple-layer intermolecular-contact-based convolutional neural network for protein–ligand binding affinity prediction, ACS Omega, 2019, 4(14), 15956–15965 CrossRef CAS.
- H. Li, K.-H. Sze, G. Lu and P. J. Ballester, Machine-learning scoring functions for structure-based drug lead optimization, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, e1465 Search PubMed.
- D. D. Nguyen, Z. Cang and G.-W. Wei, A review of mathematical representations of biomolecular data, Phys. Chem. Chem. Phys., 2020, 22(8), 4343–4367 RSC.
- J. Jiménez, M. Skalic, G. Martínez-Rosell and G. De Fabritiis, K DEEP: Protein–Ligand absolute binding affinity prediction via 3D-convolutional neural networks, J. Chem. Inf. Model., 2018, 58(2), 287–296 CrossRef.
- K. Wu and G. W. Wei, Quantitative Toxicity Prediction Using Topology Based Multitask Deep Neural Networks, J. Chem. Inf. Model., 2018, 58, 520–531 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: SupportingTables.xls: spreadsheets contain information for all supporting tables from S1 to S8; FileS1.zip: 3D structures generated by our MathPose for 141 ligands in SARS-CoV 2D set; FigS1.pdf: deep learning architecture of MathDL model. See DOI: 10.1039/d0sc04641h |
| This journal is © The Royal Society of Chemistry 2020 |