Open Access Article
Open Access ArticleFlat corannulene: when a transition state becomes a stable molecule†
Ephrath
Solel‡
 *a,
Doron
Pappo
*a,
Doron
Pappo
 b,
Ofer
Reany
b,
Ofer
Reany
 c,
Tom
Mejuch
a,
Renana
Gershoni-Poranne
c,
Tom
Mejuch
a,
Renana
Gershoni-Poranne
 a,
Mark
Botoshansky§
a,
Amnon
Stanger
a and
Ehud
Keinan
a,
Mark
Botoshansky§
a,
Amnon
Stanger
a and
Ehud
Keinan
 *a
*a
aThe Schulich Faculty of Chemistry, Technion – Israel Institute of Technology, Technion City, Haifa 3200001, Israel. E-mail: keinan@technion.ac.il; ephrath.solel@gmail.com
bDepartment of Chemistry, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel
cAvinoam Adam Department of Natural Sciences, The Open University of Israel, 1 University Road, P.O. Box 808, Ra'anana 4353701, Israel
First published on 22nd October 2020
Abstract
Flat corannulene has been considered so far only as a transition state of the bowl-to-bowl inversion process. This study was driven by the prediction that substituents with strong steric repulsion could destabilize the bowl-shaped conformation of this molecule to such an extent that the highly unstable planar geometry would become an isolable molecule. To examine the substituents' effect on the corannulene bowl depth, optimized structures for the highly-congested decakis(t-butylsulfido)corannulene were calculated. The computations, performed with both the M06-2X/def2-TZVP and the B3LYP/def2-TZVP methods (the latter with and without Grimme's D3 dispersion correction), predict that this molecule can achieve two minimum structures: a flat carbon framework and a bowl-shaped structure, which are very close in energy. This rather unusual compound was easily synthesized from decachlorocorannulene under mild reaction conditions, and X-ray crystallographic studies gave similar results to the theoretical predictions. This compound crystallized in two different polymorphs, one exhibiting a completely flat corannulene core and the other having a bowl-shaped conformation.
Introduction
Nature introduces curvature into two-dimensional graphene sheets by replacing one hexagonal unit with a ring of a different size. Thus, substitution by a 5-membered ring creates a positive Gaussian curvature1 whereas the introduction of either a 7- or 8-membered ring produces a negative Gaussian curvature.2–4 Combinations of multiple substitutions create more complex architectures,5 such as Scott's warped nanographenes.6–8 One of the simplest examples of a bowl-shaped structure created by the introduction of a pentagonal ring is the corannulene molecule9–13 (1) which represents a sub-structure of many three-dimensional graphene objects, such as the fullerenes and carbon nanotubes. Considering the great scientific and practical significance of the curved graphene structures and other materials with 5-fold symmetry, the ability to understand and control the extent of their curvature is of fundamental importance for any architectural design of such molecules.The corannulene bowl depth is defined as the shortest distance between the center of the pentagonal ring and the mean plane of the ten carbon atoms that form the molecular rim (see Fig. 1 for the bonds notations). Crystallographic studies have shown that the bowl depth of unsubstituted corannulene is 0.875 Å,14,15 and this value changes with the introduction of substituents on the molecular rim.16 Corannulene is known to undergo a bowl-to-bowl inversion, and the consensus is that the flat conformation represents the putative transition state of this equilibrium process.16 This is supported by quantum mechanical calculations, showing that the flat structure is a saddle-point on the potential energy surface. The energy barrier for this inversion has been shown by Siegel et al. to have a quartic dependence on the bowl depth: the shallower the bowl, the lower the inversion barrier.16 The inversion barrier for unsubstituted corannulene was estimated to be 10.2 kcal mol−1 or 11.5 kcal mol−1.16,17 Expectedly, increased bowl depths18,19 and higher inversion barriers20,21 were reported for derivatives in which two peri-positions were annulated to become part of an additional 5- or 6-membered ring.22–25 However, computations and experiments have shown that changing the aromatic system's electronic properties by either ring annelation26–30 or benzannulation30–33 on the rim reduces the bowl depth (Fig. 1).
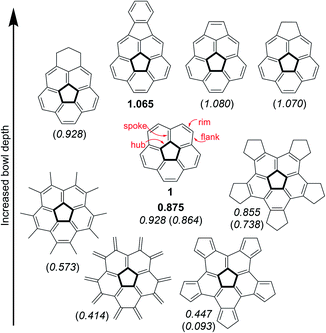 | ||
| Fig. 1 Experimental15,19 and calculated16,26,28 bowl depths (Å) of corannulene and its derivatives. Experimental values appear in bold, calculated at B97-D2/TZVP are in italics, and calculated at B3LYP/6-31G** or B3LYP/cc-pVDZ are in parenthesis. | ||
Specific modes of metal coordination, especially η2 complexes with interior carbons, were shown to increase the bowl depth.34 Other modes of metal complexation have resulted in significant reduction of bowl depths.35–41 For example, Angelici and Rabideau reported that η6 coordination of two metal atoms, one on each of the corannulene faces, completely flattened the carbon skeleton of the corannulene ligand.42 Other interactions can also affect the corannulene bowl depth, such as π–π interactions.43 Stacking of corannulene 1 with other, planar, aromatic systems shows bowl flattening and decrease of the inversion barrier, as was confirmed experimentally with ExBox4+ by Siegel,44 and also with other molecular cages serving as hosts,45–47 or as was calculated for graphene48 and planar aromatic hydrocarbons.49,50
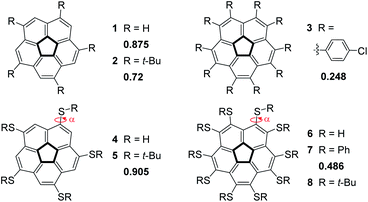
This study stems from the fundamental question: is it possible to achieve a completely flat, metal-free corannulene? We consider this question as a specific case of a more general problem: is it possible to stabilize what is thought to be a transition-state of a chemical process to such an extent that it would become a stable, isolable molecule?51–54 Though it is understood that the TS can never be directly experimentally verified, computational tools and indirect experimental observations can be employed to propose reasonable TS structures. Accordingly, such foundational physical-organic investigations have been undertaken with other types of reactions, e.g., cyclization reactions.55–57 We were encouraged by the reports that substituent electronic and steric effects could significantly influence the corannulene bowl depth (Fig. 2).58–60 For example, reduced depth of 0.72 Å was reported for sym-pentakis(t-butyl)corannulene (2).61 This effect was found to be even stronger with decakis(pentynyl)corannulene (0.60 Å),62 decapyrrylcorannulene63 (0.60–0.61 Å), deca(trifluoromethyl)-corannulene63 (computed bowl depth of 0.45 Å) and with decakis(phenylsulfido)corannulene (7, 0.486 Å).64 The record for the shallowest bowl observed experimentally was decakis(4-chlorophenyl)-corannulene (3, 0.248 Å).65 Nevertheless, a completely flat, metal-free corannulene has never been observed.
Here we report that a sufficiently strong substituent steric effect stabilizes the flat geometry to such an extent that this highly unstable geometry, which has been considered so far only in the context of a potential transition state, becomes a minimum on the potential energy surface for decakis(t-butylsulfido)-corannulene (8). Interestingly, this corannulene derivative is unique because it has two different possible stable structures – one with a flat core and one with a bowl structure. An interplay of different stereoelectronic effects stabilizes each of the two structures. This observation, which was first predicted by DFT calculations, was later confirmed by the synthesis of 8. X-ray crystallographic studies confirmed that 8 can exhibit both a perfectly flat and a bowl-shaped carbon framework, and different crystallization conditions prefer one structure over the other.
Results and discussion
Previous studies with unsubstituted corannulene estimated the energy difference between the ground state bowl-shaped conformation and the flat transition-state, to be 10.2 kcal mol−1 (209 K)17 or 11.5 kcal mol−1.16 Consequently, the total flattening of the carbon skeleton requires the introduction of stereo-electronic effects that would destabilize the bowl-shaped conformation and/or stabilize the flat structure by at least that much. In principle, substitution on the corannulene rim can affect the bowl depth through three possible mechanisms: (a) steric repulsion between the substituents is expected to decrease bowl depth; (b) electronic effects arising from groups with orbitals that could conjugate with the corannulene π system (an auxochrome effect)66 are also expected to decrease the bowl depth, and (c) attractive dispersion forces among substituents is expected to increase bowl depth.67 To examine these effects, we focused on decakis(sulfido)corannulene derivatives because the sulfur atoms have non-bonding electrons that could decrease the bowl depth via the auxochrome effect.64Theoretical predictions
To examine the validity of several chosen DFT methods and the effect of adding dispersion corrections, we used the M06-2X, B3LYP,68,69 B3LYP-D3 (with the Becke–Johnson damping),70 B97D3 and ωB97XD methods as implemented in the Gaussian16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 package with the def2-TZVP basis set72 to calculate the bowl depths of known compounds whose crystallographic parameters were available: corannulene 1, sym-pentakis(t-butyl)corannulene (2) and sym-pentakis(t-butylsulfido)-corannulene (5)73 (Table 1). As shown in Table 1, the best agreement between the calculated and the experimental bowl depths is achieved for M06-2X and ωB97XD. Both methods give a mean average error (MAE) of 0.021. B3LYP and B3LYP-D3 give MAEs of 0.030 and 0.031, respectively, while the dispersion-corrected functional gives consistently higher bowl depths. This can also be observed for B97D3, which shows the general worst fit between computations and theory. This functional gives computed bowl depths higher than the experimental ones for all these three examples. As a result, we chose to use M06-2X for our computations here.
71 package with the def2-TZVP basis set72 to calculate the bowl depths of known compounds whose crystallographic parameters were available: corannulene 1, sym-pentakis(t-butyl)corannulene (2) and sym-pentakis(t-butylsulfido)-corannulene (5)73 (Table 1). As shown in Table 1, the best agreement between the calculated and the experimental bowl depths is achieved for M06-2X and ωB97XD. Both methods give a mean average error (MAE) of 0.021. B3LYP and B3LYP-D3 give MAEs of 0.030 and 0.031, respectively, while the dispersion-corrected functional gives consistently higher bowl depths. This can also be observed for B97D3, which shows the general worst fit between computations and theory. This functional gives computed bowl depths higher than the experimental ones for all these three examples. As a result, we chose to use M06-2X for our computations here.
| Comp. | M06-2X | B3LYP | B3LYP-D3 | B97D3 | ωB97XD | Exp. |
|---|---|---|---|---|---|---|
| 1 | 0.888 | 0.880 | 0.916 | 0.941 | 0.881 | 0.87 |
| 2 | 0.712 | 0.681 | 0.762 | 0.791 | 0.720 | 0.72 |
| 5 | 0.864 | 0.858 | 0.895 | 0.916 | 0.848 | 0.90 |
To examine the effect of sulfur rim substitution on the bowl depth, corannulene 6 (R = H), which has the smallest possible group on the sulfur atoms, was analyzed at the M06-2X/def2-TZVP level of theory. The study showed that the most stable conformer of 6 has a bowl depth of 0.595 Å, shallower than unsubstituted corannulene. We suggest that this decrease of bowl depth operates through the auxochrome effect. It has already been proposed that extension of the π conjugation via orbital overlap between the corannulene π system and π orbitals of substituents would expand electron delocalization and enhance planarity.26,27 The overlap efficiency is expected to depend on geometrical parameters, mainly the Crim–Crim–S–R dihedral angle (α, Fig. 2), and on other geometrical features, such as the rim deformation. Repulsive steric interactions can deform the rim by pushing the carbon and sulfur atoms above and below the rim plane. The calculated structure shows that the Crim–Crim–S–R dihedral angles for compound 6 (R = H) are small, allowing for orbital overlap (an average −32.5° dihedral angle).
NBO analysis of 6 (see details in Table S1†) indeed confirmed this assumption. The second-order perturbation theory analysis of the Fock matrix in NBO basis shows that the most stabilizing interactions between the SH groups and the corannulene π system are the donor–acceptor interactions between the sulfur p orbital and the antibonding π* orbital of the rim carbons (amounting to 16–17 kcal mol−1 for each interaction). The energy of this interaction is expected to decrease as the dihedral angle increases from 0° to 90°. The second lone pair on sulfur (which is a hybrid of s and p orbitals) does not show any interactions with the corannulene π system, only interactions with the σ*(Crim–Crim) with values of ca. 6 kcal mol−1.The other contributions are relatively smaller: electron transfer from the σ(S–H) to the antibonding π*(Crim–Crim) orbital, and electron transfer between the bonding π(Crim–Crim) orbital to the antibonding σ*(S–H).
Thus, it is clear that the sulfur lone pair perpendicular to the Crim–S–R plane can form a better conjugation with the corannulene aromatic system than the other sulfur orbitals, either the spn lone pair or the σ(S–H) orbital (for a discussion of the conjugations effect on bowl depth in the less-sterically hindered 4 see ESI†).
Siegel observed that decakis(arylsulfido)-corannulene (7, Fig. 2) exhibits quite a shallow bowl (0.486 Å),64,74 even though the steric demands of a phenyl ring are not very high. Encouraged by this observation, we assumed that ten t-butylsulfido groups on the corannulene rim would exert sufficiently high steric demands to flatten the bowl. In our computations of the pentasubstituted 5 all the t-butyl groups are on the convex face of the corannulene core, and they are relatively far from one another, as can also be seen from the X-ray structure.73 However, once ten sulfido substituents are introduced, as in 7, they adopt an alternating arrangement, with five groups on either side of the corannulene molecule. In such molecules, a bowl structure is expected to drive the substituents on the concave face close to one another. In contrast, substituents on the convex face are expected to be further apart, such as in 5. Generally, the larger the repulsion between the substituents on the concave face, the shallower the bowl.
Consequently, the structure of 8 (R = t-Bu) was optimized at the M06-2X level of theory. Our computations resulted in two possible minimum structures. One exhibited a bowl depth of 0.620 Å, while the second showed a perfectly flat structure with a bowl depth of 0.008 Å. The latter shows sulfur atoms alternating slightly above and below the corannulene plane and the t-Bu groups connected to these sulfur atoms also residing above and below the plane. Both structures were also optimized at B3LYP/def2-TZVP, B3LYP-D3/def2-TZVP, and although individual geometric parameters slightly changed with the different methods, the corannulene core remained consistently planar for one of the geometries. Furthermore, taking into account dispersion forces through the D3 correction did not change the corannulene core's planarity.
M06-2X calculations predicted that the planar conformer of 8 would be more stable by 2.19 kcal mol−1 (ZPE-corrected energy) than the bowl-shaped conformer. To verify this prediction at higher levels of theory, we performed single point computations for the two conformers' energies using various DFT methods with the def2-QZVP basis set. The results (Table 2) at all DFT levels show that the energy difference does not exceed 10 kcal mol−1. Most methods indicate that the bowl is more stable than the planar structure. However, moving up from pure functionals to hybrids, double hybrids, and ab initio methods predicts lower energy difference. Few methods predict that the flat structure would be more stable. These methods represent the state-of-the-art computational methods available for this molecule. The use of higher basis sets with DLPNO-CCSD(T) is not feasible for such a large molecule. These results suggest that the two structures are very close in energy, differing by only a few kcal mol−1.
| Method | Basis set | ΔEflat-bowl |
|---|---|---|
| B97D3 | Def2-QZVP | −8.73 |
| MN15L | Def2-QZVP | −7.18 |
| PBE | Def2-QZVP | −5.32 |
| M06L | Def2-QZVP | −5.10 |
| TPSSh | Def2-QZVP | 0.03 |
| B3LYP-D3 | Def2-QZVP | −4.43 |
| B3LYP | Def2-QZVP | −0.87 |
| PBE0 | Def2-QZVP | 0.03 |
| M06 | Def2-QZVP | −8.85 |
| MN15 | Def2-QZVP | −0.06 |
| M06-2X | Def2-QZVP | 1.14 |
| ωB97XD | Def2-QZVP | −2.80 |
| DSDPBEP86 | Def2-QZVPP | −2.01 |
| DLPNO-CCSD(T)/normalPNO | cc-pVTZ | 0.14 |
| DLPNO-CCSD(T)/tightPNO | Def2-TZVP | −0.67 |
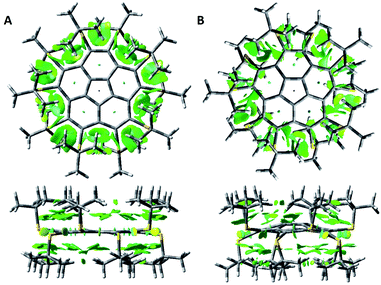
We computed NCIplots75 for the two conformers of 8 (Fig. 3), to better understand the effects of the t-Bu substituents on the structure.
The NCI plots suggest van der Waals (vdW) attractive interactions between neighboring sulfur atoms and between the t-Bu groups on the same side of the corannulene rim. However, the main interactions appear to be between the t-Bu groups and the aromatic corannulene core. In the flat conformer these dispersion interactions are of similar strength for the two sides of the aromatic plane. For the bowl conformer the interactions on the convex side of the corannulene are larger.
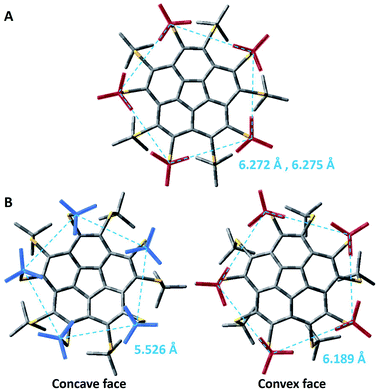
The comparative examination of the optimized geometries of the two conformers of 8 by M06-2X (Fig. 4, see ESI† for Cartesian coordinates) shows differences in the rotation angle of the t-Bu groups around the S–Ct-Bu bond. In the flat conformer, two methyl groups of every t-Bu group point towards the methyls of the nearest t-Bu groups, suggesting attractive dispersion forces (Fig. 4A). In the bowl-shaped conformer, the t-Bu groups on the convex face are oriented similarly (Fig. 4B, right). However, on the concave face, one methyl points towards the gap between two adjacent methyl groups of the nearest t-Bu group, resembling a set of intertwined cog-wheels (Fig. 4B, left). This arrangement is driven by the reduction of steric hindrance between the groups, allowing them to come closer together. The average distance between the quaternary carbons on the concave face is of 5.526 Å, as compared with 6.189 Å on the convex face (dashed lines in Fig. 4B). Both M06-2X and B3LYP-D3 predict qualitatively similar structures. Still, the B3LYP optimized structure, which does not include dispersion corrections, shows an intertwined cog-wheels orientation of the t-Bu groups also on the convex face.
The above findings reflect a delicate balance between repulsive interactions due to the steric hindrance, attractive interactions due to dispersion forces, and bond strain in the corannulene core. When the methyl groups of the t-Bu groups are close together, forming a bowl structure would require a reduction of the distances between them, causing a significant increase in the energy. This energy penalty compensates the strain energy of corannulene flattening, rendering the flat structure a minimum in energy. The flattening of the bowl increases the distance between the t-Bu groups to 6.272 Å and 6.275 Å between the quaternary carbons of nearest neighbours on the two faces. On the other hand, the intertwined cog-wheel orientation decreases the steric hindrance, allowing for the t-Bu groups to come closer together and stabilizing the bowl structure.
Our computations strongly suggest that 8 could adopt two competing conformers: a perfectly flat one (Fig. 3A) and a bowl-shaped one (Fig. 3B). A gentle interplay between repulsive steric interactions, attractive dispersion interactions, and the strain of flattening the corannulene core could stabilize either of these unique structures. As the difference in energy between the conformers is small, on the order of several kcal mol−1 (see Table 2), crystal packing forces could shift the preference for one over the other.
Synthesis
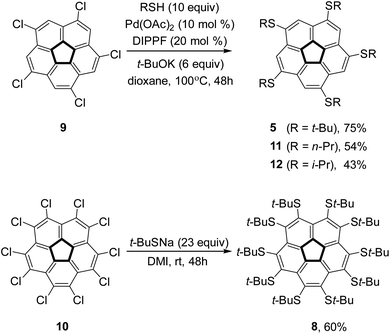
To verify the intriguing theoretical predictions, we aimed to synthesize 1,3,5,7,9-penta(t-butylsulfido)corannulene (5) and compound 8. The reaction of decachlorocorannulene,76,7710, with sodium t-butylsulfide in 1,3-dimethyl-2-imidazolidinone (DMI) at room temperature for 48 hours afforded compound 8 in 60% yield. However, under similar conditions compound 5 was obtained from 1,3,5,7,9-pentachlorocorannulene, 9, in only 22% yield (as reported by us before).73 Other pentakis(alkylsulfido)corannulenes,78–80 were reported previously, but also in rather low yields (typically between 20% and 55%). Therefore, to ensure the supply of these key compounds in sufficient amounts, we examined other synthetic approaches.Accordingly, metal-catalyzed coupling reactions were examined because compound 9 has been reacted successfully with various carbon61,81,82 or oxygen based coupling partners.83,84 Palladium or nickel-catalyzed coupling reactions have been used in the synthesis of aryl,18,85,86 alkyl,87–89 and alkynyl62,90 corannulene derivatives. We have demonstrated that copper-catalyzed Ullmann coupling reactions can be used efficiently in the synthesis of aryloxy83 and alkoxy84 analogs in good yields. Furthermore, it has been shown that either palladium91 or copper92,93 complexes can catalyze cross-coupling reactions between thiols and simple aryl halides. Although aryl chlorides are less reactive than the commonly used bromides and iodides, they have also been employed to synthesize thioethers via the Hartwig–Buchwald procedure.94–97 Considering that chlorocorannulenes are significantly more active than simple aryl chlorides,83 we decided to employ palladium catalysis to form corannulene poly-thioether.
For the synthesis of 5, the Pd-catalyzed reaction was found to be significantly advantageous over the uncatalyzed reaction. Thus, the reaction of 9 with t-butylthiol was carried out in the presence of palladium acetate (10 mol%), diisopropylphosphinoferrocene (DIPPF, 20 mol%), and sodium t-butoxide in dry dioxane at 100 °C to produce 5 in 75% yield as compared with 22% in the uncatalyzed substitution reaction (Scheme 1).73 We also checked the efficiency of this reaction with a primary and a secondary thiol. Thus, the reaction with n-propyl mercaptane produced pentakis(n-propylsulfido)corannulene, 11, in 54% yield in the Pd-catalyzed reaction, as compared with 38% reported for the uncatalyzed reaction.98 Interestingly, with i-propylthiol as the coupling partner the Pd-catalyzed reaction proceeded with lower yield (43%) than the uncatalyzed substitution (59%) to produce pentakis(i-propylsulfido)corannulene (12, more details in the ESI†).
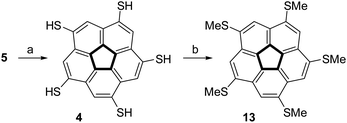
The steric crowding of the ten substituents in 8 was found to also affect the reactivity of the compound. Complete dealkylation of 5 to produce 1,3,5,7,9-pentamercapto-corannulene (4) could be easily achieved using strong acids (Scheme 2), such as either AlCl3 (59%) or an equimolar mixture of TFA and triflic acid (73%), as briefly described by us previously.99 In contrast, compound 8 was found to be stable in the presence of AlCl3, and harsher acidic conditions resulted only in unidentified decomposition products. The resistance to dealkylation conditions probably reflects the fact that the sulfur atoms are buried under the thick hydrophobic environment of the t-butyl groups, completely insulated from the solvent. Compound 4 could be used for either metal binding or the synthesis of various thioethers. We demonstrated the latter option by synthesizing pentakis(methylsulfido)corannulene (13) by reaction of 4 with methyl iodide under basic conditions.
X-ray crystallography
Recrystallization of 8 was attempted from various solvents and resulted in two different polymorphs, differing in shape. The first polymorph, polymorph 8α, was obtained from either toluene or mixtures of hexane and THF, whereas the second polymorph, 8β, was obtained from dichloromethane. 8α crystals were hexagonal-shaped crystals, built from very thin layers, while 8β crystals were needle-like. Our crystallization trials of 8 in both forms gave crystals, but in most of the cases the crystals were not suitable for diffraction measurements. Even those crystals gave very weak diffractions and required long acquisition times (R factors of 9.95 for 8α and of 9.68 for 8β). The best crystallographic data were achieved from measurements performed at relatively high temperatures (Table 3). While we are aware of the boundary values in the goodness of fit, all attempts to model a different assignment of space group to verify that we are not dealing with an average of two flip-disordered shallow bowls (e.g., in 8α), resulted in incomplete convergence of fit. Nevertheless, valuable information on the molecule's structure can be learned from these analyses. In addition, needle-like crystals suitable for X-ray analysis of compound 5 were obtained from dichloromethane. Table 3 provides the crystallographic data and refinement details of all three structures.| Compound | 8α | 8β | 5 |
|---|---|---|---|
| Empirical formula | C60H90S10·2.3H2O | C60H90S10 | C40H50S5 |
| Formula weight | 1173.62 | 1131.92 | 691.10 |
| Temperature, K | 240(1) | 293(2) | 293(2) |
| Wavelength, Å | 0.71073 | 0.71073 | 0.71073 |
| Crystal system | Trigonal | Monoclinic | Orthorhombic |
| Space group | P3 | Pn | Pna21 |
| a (Å) | 20.793(4) | 10.370(2) | 20.235(4) |
| b (Å) | 20.793(4) | 21.376(4) | 6.7800(10) |
| c (Å) | 16.882(3) | 14.870(3) | 27.996(6) |
| α (°) | 90 | 90 | 90 |
| β (°) | 90 | 90.74(2) | 90 |
| γ (°) | 120 | 90 | 90 |
| Volume (Å3) | 6321(2) | 3295.9(11) | 3842.6(13) |
| Z | 3 | 2 | 4 |
| Density (g × cm−3) | 0.925 | 1.141 | 1.195 |
| F(000) | 1899 | 1220 | 1480 |
| Crystal size (mm) | 0.30 × 0.27 × 0.02 | 0.24 × 0.06 × 0.04 | 0.50 × 0.18 × 0.09 |
| Θ range for data collection | 1.65 to 24.73 deg. | 1.67 to 25.10 deg. | 2.48 to 25.58 deg. |
| Limiting indices | 0 ≤ h ≥ 24 | 0 ≤ h ≥ 12 | 0 ≤ h ≥ 24 |
| −20 ≤ k ≥ 0 | 0 ≤ k ≥ 25 | 0 ≤ k ≥ 8 | |
| −19 ≤ l ≥ 19 | −17 ≤ l ≥ 17 | −33 ≤ l ≥ 0 | |
| Reflections collected/unique | 7198/3595 [R(int) = 0.0775] | 5555/1773 [R(int) = 0.1175] | 3621/2434 [R(int) = 0.0525] |
| Data/restraints/parameters | 7198/89/611 | 5555/56/565 | 3621/57/388 |
| Goodness-of-fit on F2 | 1.427 | 0.872 | 1.155 |
| R indices (all data) | R 1 = 0.1836 | R 1 = 0.2521 | R 1 = 0.1270 |
| wR = 0.2722 | wR = 0.3063 | wR = 0.2449 | |
| Final R indices (I > 2σ(I)) | R 1 = 0.0995 | R 1 = 0.0968 | R 1 = 0.0791 |
| wR = 0.2371 | wR = 0.2413 | wR = 0.2085 | |
| Residual electron density (max/min) | 0.758/−0.426 | 0.422/−0.259 | 1.027/−0.766 |
We examined critical structural parameters of the corannulene core: C–C bond lengths, C–C–C bond angles, and bowl depth, and compared them with those previously reported for penta(t-butyl)corannulene, 2,61 decakis(phenylsulfido)corannulene, 7,64 and decakis(4-chlorophenyl)corannulene, 3,65 (Fig. 5 and Table 4). We took advantage of the C5 symmetry of these molecules to average several geometrical parameters that relate to each other by this symmetry. This symmetrization operation removed distortions caused by crystal packing forces.15
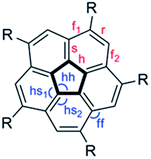 | ||
| Fig. 5 Notations of the various types of C–C bonds and C–C–C bond angles in penta- and deca-substituted corannulene: r = rim, h = hub, f = flank, s = spoke. | ||
| 2 (ref. 61) | 3 (ref. 65) | 5 | 7 (ref. 64) | 8α | 8α calc | 8β | 8β calc | |
|---|---|---|---|---|---|---|---|---|
| C–Cr | 1.404 | 1.415 | 1.440 | 1.381 | 1.530 | 1.420 | 1.472 | 1.410 |
| C–Cs | 1.384 | 1.372 | 1.484 | 1.376 | 1.423 | 1.362 | 1.436 | 1.370 |
| C–Ch | 1.434 | 1.400 | 1.328 | 1.416 | 1.371 | 1.402 | 1.338 | 1.409 |
| C–Cf1 | 1.464 | 1.471 | 1.356 | 1.443 | 1.429 | 1.477 | 1.444 | 1.460 |
| C–Cf2 | 1.474 | 1.414 | 1.334 | 1.477 | 1.467 | |||
| C–C–Chs1 | 123.3 | 125.3 | 130.0 | 124.8 | 135.4 | 126.0 | 124.2 | 124.7 |
| C–C–Chs2 | 115.6 | 116.6 | 126.0 | 123.8 | ||||
| C–C–Cf1−s | 113.3 | 111.3 | 110.4 | 110.8 | 107.7 | 111.5 | 113.5 | 113.2 |
| C–C–Cf2−s | 116.6 | 112.8 | 111.5 | 112.9 | ||||
| C–C–Cf1−r | 124.3 | 122.3 | 120.1 | 123.6 | 122.8 | 122.3 | 120.9 | 121.8 |
| C–C–Cf2−r | 119.3 | 125.4 | 122.3 | 121.0 | ||||
| C–C–Cf1−f2 | 132.3 | 136.7 | 131.0 | 138.2 | 138.2 | 137.0 | 132.2 | 133.6 |
| C–C–Chh | 107.5 | 108.0 | 108.0 | 108.0 | 108.0 | 108.0 | 107.3 | 108.0 |
| Bowl depth | 0.72 | 0.25 | 0.90 | 0.49 | 0.02 | 0.01 | 0.56 | 0.62 |
| Volume per “C” | 20.8 | 22.4 | 24.0 | 23.6 | 35.1 | 27.5 |
In the case of sym-pentakis(t-butylsulfido)corannulene 5, the observed hub–hub angles (hh, Fig. 5) ranged from 107° to 110° whereas the reported values for 2 varied more significantly – between 104° and 111°, indicating that 2 was highly distorted. Interestingly, the bowl depth in 5 (0.902 Å) is much larger than that of 2 (0.720 Å) and even larger than that of corannulene itself (0.875 Å). Although compound 5 differs from 2 only by a single sulfur atom inserted between the five t-Bu groups and the corannulene core, the relative orientation of the t-Bu groups and the aromatic core changes from coplanar in 2 to orthogonal in 5.
Consequently, while steric repulsion among the coplanar substituents in 2 causes reduction of the bowl depth, the orthogonal, one-sided orientation increases the bowl depth.
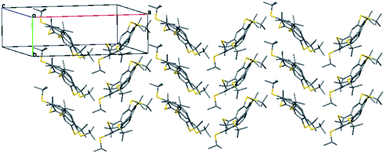
The crystal structure of 5 features herringbone stacking in an anti-parallel fashion along the b axis, with the molecules tilted relative to the column axis, as shown by a slice of the crystal structure at the ab plane (Fig. 6).
The intermolecular distance between the centroids of parallel molecules is 6.783 Å, ruling out any π–π stacking.43,100 Thus the intermolecular distances are determined mainly by the hydrophobic and dispersion forces among the t-Bu groups, with an average distance of 3.8 Å between the carbon atoms of the methyl groups from different columns, and 3.74–4.30 Å between t-Bu groups of one molecule and the π system of the molecule above it. These relatively short contacts suggest that attractive dispersion forces contribute to the overall well-ordered structure in the solid-state although the estimated volume per C atoms is higher than that of both 2 and corannulene (1) itself (24.0 vs. 20.8 and 15.3 Å3, respectively).
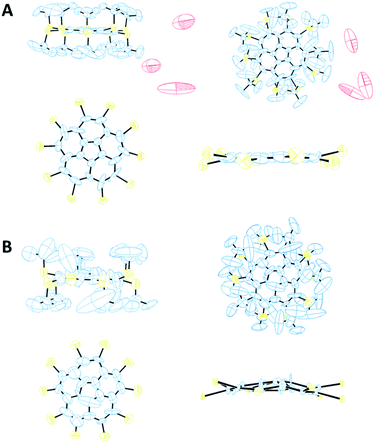
From visualization of the crystal structure of 8α by ORTEP101 diagrams (Fig. 7A), the relatively high R factor (9.95%) stems mainly from the displacement of the carbons in the t-Bu groups and of the water molecules. The ellipsoids of the corannulene core's carbon atoms are small and show displacement mainly in the molecule's plane and not above or below it. Thus, this X-ray structure supports our prediction that 8 exhibits a planar core. In contrast, polymorph 8β shows larger ellipsoids of its carbon core atoms, and thus the results of its bowl depth are less conclusive. However, there is a good agreement between the experimental (0.558 Å) and computed (0.620 Å) bowl depths. Also, the calculated residual electron density parameters (Table 3) for both polymorphs, divided by the atomic number of the heaviest atom, are within the range of ±0.075, indicating that the solution to the diffraction data does not leave any solvent molecules or a part of the structure unassigned.
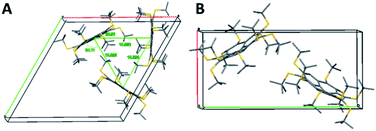
Polymorph 8α is substantially different from 5 and different from 8β in terms of geometric patterns and trends. The crystal packing of 8α is trigonal with three molecules in the unit cell, space group P3 and cell dimensions of a = b = 20.793; c = 16.882 Å, and γ = 120°. This structure shows an equilateral triangle comprising three molecules, each apex being a pentagon centroid (Fig. 8A).
The carbon core of the molecules is rotated 28.9° along the triangle edge. Interestingly, the distance between each apex is approximately 10.4 Å and the entire volume delineated by each of these triangles is filled with nine t-Bu groups, demonstrating the highly hydrophobic areas within the unit cell, aligning the molecules perpendicular to the ab plane with 3-fold symmetry axes (Fig. 8A). In this arrangement, the molecules form two-dimensional layers held together by hydrophobic interactions, with disordered water molecules between the layers. These water molecules are positioned too far away from one another to be hydrogen-bonded.
The crystal structure of 8β exhibits some similarities to that of 5. It is monoclinic with two molecules in the unit cell, space group Pn and cell dimension of a = 10.370; b = 21.376; c = 14.870 Å, and γ = 90.74°. The two molecules are oriented in a zig-zag mode, forming parallel columns (Fig. 8B).
The significant steric repulsion between neighboring substituents in 8α and 8β result in considerable zig-zag distortion of the corannulene rim. This distortion is much more pronounced in 8α than in 8β. In 8α the carbon rim atoms form two planes, each containing 5 rim carbons, 0.11 Å apart, one is 0.04 Å above, and the other is 0.07 Å below the pentagonal centroid. Thus, the distance between the center of the pentagonal ring and the mean plane of the rim carbons is 0.02 Å, and the corannulene carbon core here is essentially flat. In 8β this zig-zag distortion is smaller, and all ten carbon rim atoms are on one side of the central pentagonal ring, forming a bowl shape (Fig. 7B). Also, both polymorphs show large deviation of the sulfur atoms above and below the mean plane of the rim carbons in an alternating fashion (as can be seen in Fig. 7) with an average distance of 0.28 Å in 8α and of 0.37 Å in 8β.
We noticed small differences between the two polymorphs when looking at the distances between the quaternary carbon atoms of neighboring t-Bu groups residing on the same side of the corannulene core. In the flat structure, 8α, the average distances on the two faces are 6.20 and 6.29 Å whereas in the curved polymorph, 8β, the average distances are 6.19 Å on the convex face and 6.14 Å on the concave face. The difference in values could be explained by the differences in the forces exhibited from the neighboring molecules in the crystal. This larger compression operating on 8β is consistent with the smaller volume for “C” observed for 8β compared to 8α (Table 4). Very similar observations were reported for the distances between ipso carbons of neighboring phenyl groups on the same face (6.16 Å for both faces) of compound 7. Indeed, 8β and 7 show very similar bowl depths. These relatively short distances probably reflect severe repulsive steric interactions in decasubstituted corannulenes since in the pentasubstituted analog 5 the average distance between two neighboring t-Bu quaternary carbons is 7.01 Å (and from the calculated structure – 6.87 Å). Upon the theoretical addition of five more groups on the concave face of 5, going from penta to deca substitution, these concave groups clearly repulse one another, causing the groups on the convex face to come closer together, and reducing the bowl depth.
As mentioned above, we predicted that corannulene decasubstituted with t-butylsulfido groups could adopt two possible structures – one bowl-shaped and the other flat due to the increase of steric hindrance around the rim. Our experimental results fit these predictions, with a bowl depth of 0.558 Å in 8β, and flattening of the aromatic corannulene bowl achieved in 8α. Each of these structures is made more stable in its respective crystal, by the crystal packing forces.
Conclusions
In this report, we demonstrate that sufficiently strong substituent stereoelectronic effects can make the planar geometry of the corannulene molecule a thermodynamically stable conformation, similar in energy to the bowl-shaped conformer. Due to the small energetic difference between the flat and bowl-shaped conformers, they compete in the solid-state, leading to polymorphism. This phenomenon was predicted by DFT calculations with 8 at M06-2X/def2-TZVP and confirmed by X-ray crystallographic studies. It is noteworthy that this sterically-crowded molecule was easily synthesized in high yields in a single step under mild reaction conditions from decachlorocorannulene. Thus, the significance of this study arises from the demonstration that an essentially flat metal-free corannulene, which resembles the proposed transition state of the bowl-to-bowl inversion process, can be stabilized to such an extent that it is a synthetically accessible, highly stable molecule.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Sebastian Kozuch for insightful discussions and for granting access to computational resources for our study. E. K. is the incumbent of the Benno Gitter & Ilana Ben-Ami Chair of Biotechnology, Technion. E. K. and O. R. acknowledge the financial support by the Ministry of Science, Technology and Space (MOST, grant no. 3-10855), the Open University of Israel (OUI) and the Institute of Catalysis Science and Technology, Technion. A. S. thanks the Israeli Science Foundation (grant no. 1485/11) for financial support. E. S. acknowledges financial support from the Irwin and Joan Jacobs Fellowship and the Fine Scholarship for PhD Students. R. G. P. is grateful for a Schulich Graduate Fellowship.Notes and references
- K. Shoyama and F. Würthner, J. Am. Chem. Soc., 2019, 141, 13008–13012 CAS.
- R. Phillips, D. A. Drabold, T. Lenosky, G. B. Adams and O. F. Sankey, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1941–1943 CrossRef CAS.
- D. Vanderbilt and J. Tersoff, Phys. Rev. Lett., 1992, 68, 511–513 CrossRef CAS.
- Y. Sakamoto and T. Suzuki, J. Am. Chem. Soc., 2013, 135, 14074–14077 CrossRef CAS.
- H. Terrones and M. Terrones, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 9969–9974 CrossRef CAS.
- K. Kato, Y. Segawa, L. T. Scott and K. Itami, Chem.–Asian J., 2015, 10, 1635–1639 CrossRef CAS.
- K. Kawasumi, Q. Zhang, Y. Segawa, L. T. Scott and K. Itami, Nat. Chem., 2013, 5, 739–744 CrossRef CAS.
- J. I. Urgel, M. Di Giovannantonio, Y. Segawa, P. Ruffieux, L. T. Scott, C. A. Pignedoli, K. Itami and R. Fasel, J. Am. Chem. Soc., 2019, 141, 13158–13164 CrossRef CAS.
- Y.-T. Wu and J. S. Siegel, Chem. Rev., 2006, 106, 4843–4867 CrossRef CAS.
- X. Li, F. Kang and M. Inagaki, Small, 2016, 12, 3206–3223 CrossRef CAS.
- E. Nestoros and M. C. Stuparu, Chem. Commun., 2018, 54, 6503–6519 RSC.
- A. Haupt and D. Lentz, Chem.–Eur. J., 2019, 25, 3440–3454 CrossRef CAS.
- E. M. Muzammil, D. Halilovic and M. C. Stuparu, Commun. Chem., 2019, 2, 58 CrossRef.
- J. C. Hanson and C. E. Nordman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, B32, 1147–1153 CrossRef CAS.
- M. A. Petrukhina, K. W. Andreini, J. Mack and L. T. Scott, J. Org. Chem., 2005, 70, 5713–5716 CrossRef CAS.
- T. J. Seiders, K. K. Baldridge, G. H. Grube and J. S. Siegel, J. Am. Chem. Soc., 2001, 123, 517–525 CrossRef CAS.
- L. T. Scott, M. M. Hashemi and M. S. Bratcher, J. Am. Chem. Soc., 1992, 114, 1920–1921 CrossRef CAS.
- E. A. Jackson, B. D. Steinberg, M. Bancu, A. Wakamiya and L. T. Scott, J. Am. Chem. Soc., 2007, 129, 484–485 CrossRef CAS.
- B. D. Steinberg, E. A. Jackson, A. S. Filatov, A. Wakamiya, M. A. Petrukhina and L. T. Scott, J. Am. Chem. Soc., 2009, 131, 10537–10545 CrossRef CAS.
- A. Sygula, A. H. Abdourazak and P. W. Rabideau, J. Am. Chem. Soc., 1996, 118, 339–343 CrossRef CAS.
- A. H. Abdourazak, A. Sygula and P. W. Rabideau, J. Am. Chem. Soc., 1993, 115, 3010–3011 CrossRef CAS.
- L. M. Roch, L. Zoppi, J. S. Siegel and K. K. Baldridge, J. Phys. Chem. C, 2017, 121, 1220–1234 CrossRef CAS.
- K. Shoyama, D. Schmidt, M. Mahl and F. Würthner, Org. Lett., 2017, 19, 5328–5331 CrossRef CAS.
- X. Tian, L. M. Roch, N. Vanthuyne, J. Xu, K. K. Baldridge and J. S. Siegel, Org. Lett., 2019, 21, 3510–3513 CrossRef CAS.
- Y. Wang, O. Allemann, T. S. Balaban, N. Vanthuyne, A. Linden, K. K. Baldridge and J. S. Siegel, Angew. Chem., Int. Ed., 2018, 57, 6470–6474 CrossRef CAS.
- T. C. Dinadayalane, S. Deepa, A. S. Reddy and G. N. Sastry, J. Org. Chem., 2004, 69, 8111–8114 CrossRef CAS.
- T. C. Dinadayalane, S. Deepa and G. N. Sastry, Tetrahedron Lett., 2003, 44, 4527–4529 CrossRef CAS.
- D. Josa, L. Azevedo dos Santos, I. González-Veloso, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and T. de Castro Ramalho, RSC Adv., 2014, 4, 29826–29833 RSC.
- G. Narahari Sastry, J. Mol. Struct.: THEOCHEM, 2006, 771, 141–147 CrossRef CAS.
- S. Liu, L. M. Roch, O. Allemann, J. Xu, N. Vanthuyne, K. K. Baldridge and J. S. Siegel, J. Org. Chem., 2018, 83, 3979–3986 CrossRef CAS.
- T. C. Dinadayalane and G. N. Sastry, J. Org. Chem., 2002, 67, 4605–4607 CrossRef CAS.
- Z. Marcinow, A. Sygula, A. Ellern and P. W. Rabideau, Org. Lett., 2001, 3, 3527–3529 CrossRef CAS.
- Z. Zhou, S. N. Spisak, Q. Xu, A. Y. Rogachev, Z. Wei, M. Marcaccio and M. A. Petrukhina, Chem.–Eur. J., 2018, 24, 3455–3463 CrossRef CAS.
- A. S. Filatov, A. Y. Rogachev, E. A. Jackson, L. T. Scott and M. A. Petrukhina, Organometallics, 2010, 29, 1231–1237 CrossRef CAS.
- U. D. Priyakumar, M. Punnagai, G. P. Krishna Mohan and G. N. Sastry, Tetrahedron, 2004, 60, 3037–3043 CrossRef CAS.
- A. S. Filatov, A. K. Greene, E. A. Jackson, L. T. Scott and M. A. Petrukhina, J. Organomet. Chem., 2011, 696, 2877–2881 CrossRef CAS.
- M. A. Petrukhina, Y. Sevryugina, A. Y. Rogachev, E. A. Jackson and L. T. Scott, Organometallics, 2006, 25, 5492–5495 CrossRef CAS.
- A. S. Filatov and M. A. Petrukhina, Coord. Chem. Rev., 2010, 254, 2234–2246 CrossRef CAS.
- S. N. Spisak, A. V. Zabula, A. S. Filatov and M. A. Petrukhina, J. Organomet. Chem., 2015, 784, 69–74 CrossRef CAS.
- A. S. Filatov, A. V. Zabula, S. N. Spisak, A. Y. Rogachev and M. A. Petrukhina, Angew. Chem., Int. Ed., 2014, 53, 140–145 CrossRef CAS.
- S. N. Spisak, A. Y. Rogachev, A. V. Zabula, A. S. Filatov, R. Clérac and M. A. Petrukhina, Chem. Sci., 2017, 8, 3137–3145 RSC.
- P. A. Vecchi, C. M. Alvarez, A. Ellern, R. J. Angelici, A. Sygula, R. Sygula and P. W. Rabideau, Organometallics, 2005, 24, 4543–4552 CrossRef CAS.
- C. Dubceac, Y. Sevryugina, I. V. Kuvychko, O. V. Boltalina, S. H. Strauss and M. A. Petrukhina, Cryst. Growth Des., 2018, 18, 307–311 CrossRef CAS.
- M. Juríček, N. L. Strutt, J. C. Barnes, A. M. Butterfield, E. J. Dale, K. K. Baldridge, J. F. Stoddart and J. S. Siegel, Nat. Chem., 2014, 6, 222–228 CrossRef.
- P. A. Denis and F. Iribarne, Int. J. Quantum Chem., 2018, 118, e25539 CrossRef.
- B. M. Schmidt, T. Osuga, T. Sawada, M. Hoshino and M. Fujita, Angew. Chem., Int. Ed., 2016, 55, 1561–1564 CrossRef CAS.
- S. Ibáñez and E. Peris, Angew. Chem., Int. Ed., 2020, 59, 6860–6865 CrossRef.
- P. A. Denis, J. Phys. Chem. A, 2015, 119, 5770–5777 CrossRef CAS.
- A. Karton, Chem. Phys. Lett., 2014, 614, 156–161 CrossRef CAS.
- A. Karton, J. Phys. Chem. A, 2020, 124, 6977–6985 CrossRef CAS.
- Y. Chen, M. Hartmann, M. Diedenhofen and G. Frenking, Angew. Chem., Int. Ed., 2001, 40, 2051–2055 CrossRef.
- S. C. A. H. Pierrefixe, S. J. M. van Stralen, J. N. P. van Stralen, C. Fonseca Guerra and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2009, 48, 6469–6471 CrossRef CAS.
- H. S. Rzepa, Capturing penta-coordinate carbon! (Part 1), Henry Rzepa’s Blog, https://www.ch.imperial.ac.uk/rzepa/blog/?p=783, accessed 5 August 2020 Search PubMed.
- H. S. Rzepa, Frozen Semibullvalene, https://www.ch.imperial.ac.uk/rzepa/blog/?p=7678, accessed 5 August 2020 Search PubMed.
- A. Navarro-Vázquez, M. Prall and P. R. Schreiner, Org. Lett., 2004, 6, 2981–2984 CrossRef.
- K. Gilmore, M. Manoharan, J. I.-C. Wu, P. v. R. Schleyer and I. V. Alabugin, J. Am. Chem. Soc., 2012, 134, 10584–10594 CrossRef CAS.
- G. dos Passos Gomes and I. V. Alabugin, J. Am. Chem. Soc., 2017, 139, 3406–3416 CrossRef CAS.
- M. Yanney, F. R. Fronczek, W. P. Henry, D. J. Beard and A. Sygula, Eur. J. Org. Chem., 2011, 2011, 6636–6639 CrossRef CAS.
- D. Meng, G. Liu, C. Xiao, Y. Shi, L. Zhang, L. Jiang, K. K. Baldridge, Y. Li, J. S. Siegel and Z. Wang, J. Am. Chem. Soc., 2019, 141, 5402–5408 CAS.
- I. V. Kuvychko, T. Clikeman, C. Dubceac, Y.-S. Chen, M. A. Petrukhina, S. H. Strauss, A. A. Popov and O. V. Boltalina, Eur. J. Org. Chem., 2018, 2018, 4233–4245 CAS.
- Y. Sevryugina, A. Y. Rogachev, E. A. Jackson, L. T. Scott and M. A. Petrukhina, J. Org. Chem., 2006, 71, 6615–6618 CrossRef CAS.
- T. Hayama, Y.-T. Wu, A. Linden, K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 2007, 129, 12612–12613 CrossRef CAS.
- Y.-Y. Xu, H.-R. Tian, S.-H. Li, Z.-C. Chen, Y.-R. Yao, S.-S. Wang, X. Zhang, Z.-Z. Zhu, S.-L. Deng, Q. Zhang, S. Yang, S.-Y. Xie, R.-B. Huang and L.-S. Zheng, Nat. Commun., 2019, 10, 485 CrossRef CAS.
- K. K. Baldridge, K. I. Hardcastle, T. J. Seiders and J. S. Siegel, Org. Biomol. Chem., 2010, 8, 53–55 RSC.
- Q. Zhang, K. Kawasumi, Y. Segawa, K. Itami and L. T. Scott, J. Am. Chem. Soc., 2012, 134, 15664–15667 CrossRef CAS.
- M. S. H. Akash and K. Rehman, Essentials of Pharmaceutical Analysis, Springer Singapore, Singapore, 2020 Search PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision A.03), Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- P. Angelova, E. Solel, G. Parvari, A. Turchanin, M. Botoshansky, A. Gölzhäuser and E. Keinan, Langmuir, 2013, 29, 2217–2223 CrossRef CAS.
- Y. Deng, B. Xu, E. Castro, O. Fernandez-Delgado, L. Echegoyen, K. K. Baldridge and J. S. Siegel, Eur. J. Org. Chem., 2017, 2017, 4338–4342 CrossRef CAS.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef.
- P.-C. Cheng, PhD thesis, Boston College, 1996.
- L. T. Scott, Pure Appl. Chem., 1996, 68, 291–300 CAS.
- S. H. Mahadevegowda and M. C. Stuparu, ACS Omega, 2017, 2, 4964–4971 CrossRef CAS.
- S. H. Mahadevegowda and M. C. Stuparu, Eur. J. Org. Chem., 2017, 2017, 570–576 CrossRef CAS.
- P. E. Georghiou, A. H. Tran, S. Mizyed, M. Bancu and L. T. Scott, J. Org. Chem., 2005, 70, 6158–6163 CrossRef CAS.
- G. H. Grube, E. L. Elliott, R. J. Steffens, C. S. Jones, K. K. Baldridge and J. S. Siegel, Org. Lett., 2003, 5, 713–716 CrossRef CAS.
- Y. Xia, T. Guo, K. K. Baldridge and J. S. Siegel, Eur. J. Org. Chem., 2017, 2017, 875–879 CrossRef CAS.
- R. Gershoni-Poranne, D. Pappo, E. Solel and E. Keinan, Org. Lett., 2009, 11, 5146–5149 CrossRef CAS.
- A. Pogoreltsev, E. Solel, D. Pappo and E. Keinan, Chem. Commun., 2012, 48, 5425 RSC.
- T. Hayama, K. K. Baldridge, Y.-T. Wu, A. Linden and J. S. Siegel, J. Am. Chem. Soc., 2008, 130, 1583–1591 CrossRef CAS.
- D. Pappo, T. Mejuch, O. Reany, E. Solel, M. Gurram and E. Keinan, Org. Lett., 2009, 11, 1063–1066 CrossRef CAS.
- T. J. Seiders, E. L. Elliott, G. H. Grube and J. S. Siegel, J. Am. Chem. Soc., 1999, 121, 7804–7813 CrossRef CAS.
- T. J. Seiders, K. K. Baldridge, E. L. Elliott, G. H. Grube and J. S. Siegel, J. Am. Chem. Soc., 1999, 121, 7439–7440 CrossRef CAS.
- M. Mattarella and J. S. Siegel, Org. Biomol. Chem., 2012, 10, 5799 RSC.
- Y.-T. Wu, D. Bandera, R. Maag, A. Linden, K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 2008, 130, 10729–10739 CrossRef CAS.
- J. F. Hartwig, Nature, 2008, 455, 314–322 CrossRef CAS.
- C. G. Bates, R. K. Gujadhur and D. Venkataraman, Org. Lett., 2002, 4, 2803–2806 CrossRef CAS.
- F. Y. Kwong and S. L. Buchwald, Org. Lett., 2002, 4, 3517–3520 CrossRef CAS.
- M. A. Fernández-Rodríguez, Q. Shen and J. F. Hartwig, J. Am. Chem. Soc., 2006, 128, 2180–2181 CrossRef.
- J. F. Hartwig, Acc. Chem. Res., 2008, 41, 1534–1544 CrossRef CAS.
- M. A. Fernández-Rodríguez, Q. Shen and J. F. Hartwig, Chem.–Eur. J., 2006, 12, 7782–7796 CrossRef.
- M. Murata and S. L. Buchwald, Tetrahedron, 2004, 60, 7397–7403 CrossRef CAS.
- M. Bancu, A. K. Rai, P. Cheng, R. D. Gilardi and L. T. Scott, Synlett, 2004, 173–176 CAS.
- Y.-S. Chen, E. Solel, Y.-F. Huang, C.-L. Wang, T.-H. Tu, E. Keinan and Y.-T. Chan, Nat. Commun., 2019, 10, 3443 CrossRef.
- A. Sygula, H. E. Folsom, R. Sygula, A. H. Abdourazak, Z. Marcinow, F. R. Fronczek and P. W. Rabideau, J. Chem. Soc., Chem. Commun., 1994, 2571–2572 RSC.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures, compound characterizations, computational methods and geometries. CCDC 1040969–1040971. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04566g |
| ‡ Currently at Justus-Liebig University, Heinrich-Buff-Ring 17, Giessen 35392, Germany. |
| § Deceased. |
| This journal is © The Royal Society of Chemistry 2020 |