Open Access Article
Open Access ArticleA conductive metal–organic framework photoanode†
Brian
Pattengale
 *a,
Jessica G.
Freeze
*a,
Jessica G.
Freeze
 a,
Matthew J.
Guberman-Pfeffer
a,
Matthew J.
Guberman-Pfeffer
 b,
Ryotaro
Okabe‡
b,
Sarah
Ostresh
b,
Ryotaro
Okabe‡
b,
Sarah
Ostresh
 a,
Subhajyoti
Chaudhuri
a,
Subhajyoti
Chaudhuri
 a,
Victor S.
Batista
a,
Victor S.
Batista
 *a and
Charles A.
Schmuttenmaer§
*a and
Charles A.
Schmuttenmaer§
 a
a
aDepartment of Chemistry and Yale Energy Sciences Institute, Yale University, New Haven, Connecticut 06520-8107, USA. E-mail: brian.pattengale@yale.edu; victor.batista@yale.edu
bDepartment of Molecular Biophysics and Biochemistry, Yale Microbial Sciences Institute, Yale University, New Haven, Connecticut 06520-8107, USA
First published on 27th August 2020
Abstract
We report the development of photosensitizing arrays based on conductive metal–organic frameworks (MOFs) that enable light harvesting and efficient charge separation. Zn2TTFTB (TTFTB = tetrathiafulvalene tetrabenzoate) MOFs are deposited directly onto TiO2 photoanodes and structurally characterized by pXRD and EXAFS measurements. Photoinduced interfacial charge transfer dynamics are investigated by combining time-resolved THz spectroscopy and quantum dynamics simulations. Sub-600 fs electron injection into TiO2 is observed for Zn2TTFTB–TiO2 and is compared to the corresponding dynamics for TTFTB–TiO2 analogues that lack the extended MOF architecture. Rapid electron injection from the MOF into TiO2 is enhanced by facile migration of the hole away from the interfacial region. Holes migrate through strongly coupled HOMO orbitals localized on the tetrathiafulvalene cores of the columnar stacks of the MOF, whereas electrons are less easily transferred through the spiral staircase arrangement of phenyl substituents of the MOF. The reported findings suggest that conductive MOFs could be exploited as novel photosensitizing arrays in applications to slow, and thereby make difficult, photocatalytic reactions such as those required for water-splitting in artificial photosynthesis.
Introduction
Photocatalytic reactions, including those required for artificial photosynthesis, are initiated by photoinduced charge separation.1–8 Interfacial charge transfer at the electrode surface allows separation of the photogenerated electron–hole pair, transferring the electron (or, the hole) across the interface.9–16 The charge-separation process has been extensively studied in photoanodes of dye-sensitized photoelectrochemical cells17–20 where photoexcited molecular dyes inject electrons into the conduction band of a metal oxide, leaving electron–holes on the dyes anchored to the electrode surface. The holes are then transferred to an oxidation catalyst to perform, for example, water oxidation.21–25 A critical challenge with such systems, however, is electron–hole recombination (e.g., recombination of electrons from the conduction band of the metal oxide with holes localized on the surface chromophore, as in dye-sensitized solar cells (DSSCs)).26–30 Therefore, it is important to design architectures that extend the lifetime of charge-separated states and enable slow, multielectron photocatalytic reactions.Passivation of the metal-oxide surface with a blocking layer is a common technique applied to suppress recombination of electrons in the conduction band with redox species in the electrolyte.26,28–31 Another strategy is to focus on the localization of the hole within the photosensitizer component of the system. For example, recombination dynamics have been altered in molecular photosensitizers by modifying the anchoring group,32,33 the linker conjugation,34 or the linker length.35 However, such systems can be difficult to synthesize and tune, especially when an additional level of complexity is added by the requirement of interfacing the photosensitizer with a catalyst to perform useful redox reactions. Here, we focus on using a photosensitizer based on heterogeneous materials that can be highly tunable and easily functionalized to enable efficient separation of the hole from the metal-oxide surface, and transfer to an oxidation catalyst. Similar strategies has been used in various classes of heterogeneous materials.36–38 We focus on microporous materials that can be designed to have visible light absorption and suitable conductivity, namely conductive metal–organic frameworks.39–42
MOFs have an extensive track-record of utility in heterogeneous catalysis, either as intrinsically catalytic or by functionalization to incorporate catalysts.43–53 Conductive MOFs often have spatially overlapping ligands that form continuous electronic bands and mediate through-space charge transfer.39,40,42,54 In such systems, the overlapping ligands form a photosensitizing array that allows charge carrier migration along crystallographically-oriented chromophores. Such a design enables holes to migrate away from the metal oxide surface, or alternatively allow electrons to migrate to the surface for interfacial charge transfer. Therefore, conductive MOFs are attractive photosensitizing arrays for enabling charge separation as necessary to perform slow multielectron catalytic transformations. Such a design is reminiscent of light-harvesting and photocatalysis in natural photosynthesis, where the slow multielectron water oxidation reaction is enabled by photosensitizing chromophore units, such as P680 and pheophytin, that transfer electrons through quinone redox co-factors to separate electron–hole pairs over long distances, and inhibit charge recombination.55 Notably, related MOF systems relying on energy transfer mechanisms have been developed and applied to solar energy technologies,56–58 however their conductive counterparts relying on charge transfer have been much less investigated.59,60
In this work, we utilize a conductive MOF that functions as a visible-light photosensitizing array when deposited on TiO2. Optical-pump THz-probe spectroscopy (OPTP) shows that the Zn2TTFTB conductive MOF injects electrons into the conduction band of TiO2. Computational modelling provides understanding of the charge transport mechanism in Zn2TTFTB–TiO2. Nanosecond transient absorption spectroscopy (ns-TA) shows that the lifetime of the electron–hole pair is significantly increased in the MOF-sensitized system, when compared to TiO2 sensitized only with the ligand. Therefore, the conductive MOF array is essential for electron–hole pair separation, yielding photoanodes that might be particularly suitable to perform slow and, thereby, difficult photocatalytic oxidation reactions.
Results and discussion
Zn2TTFTB structural characterization
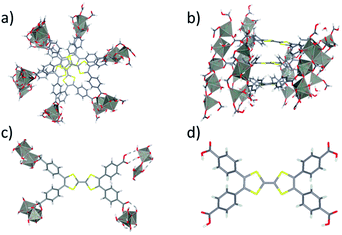
The Zn2TTFTB MOF was chosen for development of photosensitizing arrays due to its visible light absorption, stability under irradiation, and sub-picosecond photoconductivity dynamics.42,54,61 It was synthesized using tetrathiafulvalene tetrabenzoate (TTFTB) and Zn2+ and computationally characterized by using model systems of varying complexity, including a half-unit cell of the MOF structure consisting of a columnar stack of TTFTB ligands (denoted as the 3-layer model; Fig. 1a and b), a single TTFTB ligand coordinated to Zn2+ nodes (denoted as the 1-layer model; Fig. 1c), and the fully protonated H4TTFTB ligand (Fig. 1d).In the crystallized material, the TTFTB ligands overlap with a screw axis bisecting the ethylene bonds in TTFTB, giving a helical repeating pattern where the adjacent TTFTB ligands are rotated 60° with respect to one another.42 A previous study suggested that ground state conductivity in the MOF was provided by S–S overlap between the ligands – a through-space charge transport mechanism that does not rely on covalent interactions.42 We investigate the mechanisms of excited state inter-layer and interfacial charge transport for the MOF as described in the section: Charge transport in Zn2TTFTB.
The Zn2TTFTB MOF has been traditionally synthesized by dissolving the H4TTFTB ligand and Zn2+ ions in a heated DMF/ETOH/H2O solution.42 Here, it has been interfaced with the metal oxide to facilitate interfacial electron transfer. Solvothermal conditions were identified in which Zn2TTFTB could be grown directly on FTO (fluorine-doped tin oxide), TiO2, and ZrO2 by adjusting the DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH (dimethylformamide
EtOH (dimethylformamide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol) ratio, the concentrations of H4TTFTB and Zn2+, and by excluding excess H2O from the solvent. Further synthetic details are provided in the Experimental section of the ESI.† In these studies, FTO functions as a transparent conductive substrate and Zn2TTFTB–FTO is used for electrochemical and photoelectrochemical investigations of the MOF layer. Zn2TTFTB–TiO2 has a mesoporous layer of TiO2 on top of the conductive FTO substrate and acts as a photoanode. Zn2TTFTB–ZrO2 is prepared similarly to TiO2 and acts as a control in photophysical studies, utilizing ZrO2 as a non-injecting medium.
ethanol) ratio, the concentrations of H4TTFTB and Zn2+, and by excluding excess H2O from the solvent. Further synthetic details are provided in the Experimental section of the ESI.† In these studies, FTO functions as a transparent conductive substrate and Zn2TTFTB–FTO is used for electrochemical and photoelectrochemical investigations of the MOF layer. Zn2TTFTB–TiO2 has a mesoporous layer of TiO2 on top of the conductive FTO substrate and acts as a photoanode. Zn2TTFTB–ZrO2 is prepared similarly to TiO2 and acts as a control in photophysical studies, utilizing ZrO2 as a non-injecting medium.
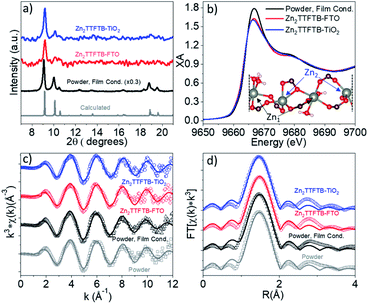
The formation of Zn2TTFTB on the substrates was confirmed using both pXRD and EXAFS at the Zn K-edge, providing both bulk and local structure information. The pXRD results are shown in Fig. 2a. The calculated pXRD pattern is based on the reported single crystal structure.42 On all three substrates, the main diffraction features of Zn2TTFTB (peaks at 9.3° and 10.2° 2θ) are observed and are well-isolated from the substrate pXRD diffraction patterns (Fig. S1†), suggesting that pure phase Zn2TTFTB is formed. While synthesis conditions can be adjusted to yield thicker films that more strongly diffract, the roughly 20 μm films investigated herein (vide infra) only diffract weakly, necessitating a more thorough structure investigation to confirm that the various synthetic conditions employed do not alter the structure.
X-ray absorption at the Zn K-edge was used to investigate the local structure of Zn2+ ions in four samples. The “Powder” sample is the sample prepared under the previously reported synthetic procedure without modification42 whereas “Powder, Film Cond.” is prepared under the conditions used when growing the MOFs on the films (without the addition of excess H2O to the reaction mixture and with a larger Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TTFTB ratio).
TTFTB ratio).
These two preparations give identical bulk structure via pXRD (Fig. S2a†). The Zn K-edge XANES and EXAFS spectra of these samples are compared in Fig. S2b–d† and are nearly identical implying similar local structure about Zn2+. The powder spectra are compared to ZnNO3·6H2O reference data in Fig. S3.† The powder XANES spectrum is compared to the spectra of Zn2TTFTB–FTO and Zn2TTFTB–TiO2 in Fig. 2b wherein similar edge position is observed along with similar oscillation features above the 1s-4p transition edge. The white line of the edge transition at 9.667 keV shows attenuation in the Zn2TTFTB–FTO and Zn2TTFTB–TiO2 likely due to self-absorption, as fluorescence detection was required for the film samples whereas transmission mode was used for powder samples.
The EXAFS data were quantitatively analyzed with FEFF fitting using the Demeter package to compare the first shell local structure of the samples.62 The k-space results and R-space results for each sample are compared in Fig. 2c and d, respectively. The input model for the FEFF calculation was prepared from the reported crystal structure coordinates.42 In the crystal structure, there are two nonequivalent Zn atoms. One of these Zn atoms, Zn1, has pseudo-octahedral coordination to six oxygen atoms, four of which are from carboxylate-bearing TTFTB ligands and two are water molecules. Zn2 has five oxygen neighbors in its distorted octahedral first shell (including all atoms with a Zn–O distance of less than roughly 2.3 Å). Zn2 has another O neighbor at about 2.7 Å that was considered to be in the second shell and therefore was not included in the fit model. A depiction of the Zn centers in a segment of the crystal structure is shown in the inset of Fig. 2b. Two separate FEFF calculations were performed and weighted at 50% in the analysis to incorporate the contributions of Zn1 and Zn2 to the data, which are each present at 50% in the crystal structure. It is worth noting that the self-absorption phenomenon observed in film samples attenuates the oscillations throughout the EXAFS spectrum and results in reduction in amplitude of the Fourier-transformed R-space spectra, typically contributing to the Debye–Waller parameter (σ2) that accounts for static and dynamic disorder, but does not affect the distances obtained from quantitative EXAFS analysis.
Results of EXAFS fitting are shown in Table 1. As noted, σ2 is in general larger for the film samples compared to the powder samples most likely due to self-absorption attenuation and not due to a physically relevant reason. The observed Zn–O distances are within uncertainty (±0.02 Å) between samples implying that the films have the same local structure as the powder samples. Interestingly, the distances observed from EXAFS analysis are shorter than those from the reported crystal structure. This is potentially because the reported bulk synthesis method (which produces particles on the order of 10 μm × 3 μm)54 differs from the reported synthesis to grow larger X-ray crystallography quality crystals.42
| Description/shared | Powder | Powder, film cond. | Zn2TTFTB–FTO | Zn2TTFTB–TiO2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vector | Ref. (Å) | N | S 0 2 | ΔE0 (eV) | σ 2 (Å2) | R (Å) | ΔE0 (eV) | σ 2 (Å2) | R (Å) | ΔE0 (eV) | σ 2 (Å2) | R (Å) | ΔE0 (eV) | σ 2 (Å2) | R (Å) |
| Zn1–O | 2.06 | 3 | 0.5 | 4.36 | 0.002 | 2.03 | 4.04 | 0.001 | 2.04 | 3.42 | 0.004 | 2.03 | 3.38 | 0.002 | 2.03 |
| 2.12 | 2 | 2.09 | 2.10 | 2.09 | 2.09 | ||||||||||
| 2.17 | 1 | 2.14 | 2.14 | 2.13 | 2.13 | ||||||||||
| Zn2–O | 1.95 | 1 | 0.5 | 8.52 | 0.001 | 1.91 | 7.64 | 0.001 | 1.91 | 10.00 | 0.002 | 1.93 | 9.35 | 0.001 | 1.91 |
| 1.98 | 2 | 1.94 | 1.94 | 1.96 | 1.94 | ||||||||||
| 2.04 | 1 | 2.00 | 1.99 | 2.02 | 2.00 | ||||||||||
| 2.33 | 1 | 2.29 | 2.29 | 2.31 | 2.29 | ||||||||||
With confirmation that the Zn2+ ions measured on films have local structure consistent with Zn2TTFTB formation, SEM was used to investigate the morphology of the samples. Synthesis of powder samples under the film-growth conditions produces a particle morphology that differs significantly from that when using the reported synthesis method (Fig. S4†), and the morphology of the MOF on films differs from either of the powder morphologies. Fig. 3 shows the SEM images for Zn2TTFTB–TiO2. The top-view images (Fig. 3a and b) show that there are MOF structures of larger (roughly 20 μm) and smaller sizes decorating the surface of the mesoporous TiO2 film. The larger particles form microflowers that are shown to be hemispherical from the side-view cross-section image (Fig. 3c) and evenly cover the surface of TiO2 from a tilted perspective (Fig. 3d). Zn2TTFTB–FTO was found to have the same morphology (Fig. S5†). EDS results show the expected localization of Zn, S, and C within the MOF structures (Fig. 3e). The morphology of Zn2TTFTB on films is therefore best described as a discontinuous monolayer of hemispherical microflower structures.
UV-visible Electronic Characterization
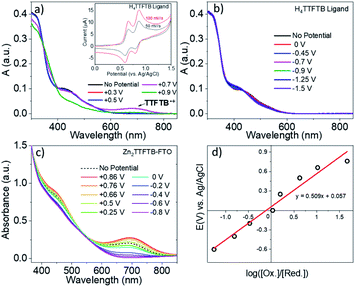
Tetrathiafulvalene is well known to display redox-state dependent UV-visible absorption features.63–65 Therefore, we compare the spectroelectrochemical properties of the H4TTFTB ligand and Zn2TTFTB MOF (i.e. Zn2TTFTB–FTO). The H4TTFTB sample was dissolved in 0.1 M TBAPF6 DMF electrolyte (TBAPF6 is tetrabutylammonium hexafluorophosphate, the supporting electrolyte) for cyclic voltammetry experiments. Two reversible oxidation features are observed (Fig. 4a, inset) for H4TTFTB, and no reversible features are observed on the reduction side (Fig. S6†). Therefore, spectroelectrochemistry was performed to target the reversible features for oxidation, and reduction was performed in steps between 0 V and −1.5 V. Fig. 4a shows the spectroelectrochemical oxidation of H4TTFTB. Upon the first oxidation at +0.7 V vs. Ag/AgCl, a broad absorption feature is observed in the region between 600–800 nm. This feature is in excellent agreement with the cation radical spectrum of closest reported structure, the ethyl ester derivative.66 The second oxidation at +0.9 V depletes this feature and causes further spectral changes. Reduction (Fig. 4b) results in more subtle changes in the <600 nm region of the spectrum but has no clear changes beyond 600 nm where oxidation displays a clear feature.Unlike H4TTFTB, Zn2TTFTB–FTO does not show clear signatures under cyclic voltammetry conditions; however, the high optical quality of the films allowed transmission mode spectroelectrochemical measurements to be made. The spectroelectrochemical results in 0.1 M TBAPF6 DMF show that prior to applying a bias, an absorption feature is present in the 600–800 nm region (Fig. 4c, “No Potential”). Upon the application of oxidizing potentials, growth of the feature is observed along with changes in the 400–500 nm region. When reducing potentials are applied, both of these features are depleted and the feature between 600–800 nm disappears completely. The ΔA spectra shown in Fig. S7† demonstrate that similar absorption changes are observed in H4TTFTB compared to Zn2TTFTB in the region above 500 nm. These results indicate that a well-resolved spectral signature of the MOF cation exists in the 600–800 nm region of the spectrum that is absent in both the neutral and reduced species.
A Nernst plot was generated utilizing this feature at 700 nm in the spectroelectrochemistry data (Fig. 4d) yielding an E0 value of 57 mV and an n-value of 0.15 from the slope corresponding to the number of electrons transferred. TTF polymer films have been previously studied via Nernst analysis where similar results were obtained, i.e. a redox potential for the first oxidation lower than that of the monomer and an n-value less than one.65,67 In other conductive polymer systems, an n-value lower than unity has also been observed and attributed to its being a per-monomer measure of the redox process.68,69 In such systems, there exists the possibility for oxidation events that are delocalized or, in the case of TTF, cation dimers have been observed implying that the cation may be localized on adjacent TTF units.65,67 These points are further investigated in the section: Charge transport in Zn2TTFTB.
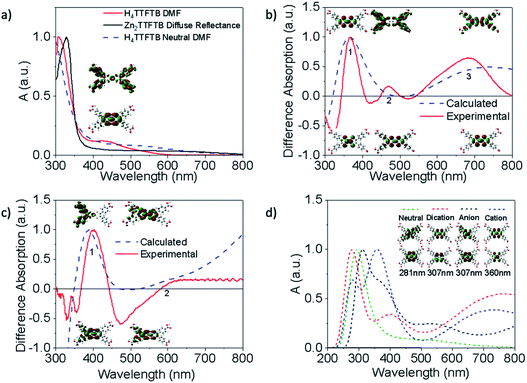
As noted above, Zn2TTFTB–FTO has a clear absorption feature in the region of the cation absorption prior to applying a potential. As-synthesized, Zn2TTFTB has a brown-red color that has been previously reported as early as 1970 in solid tetrathiafulvalene powders exposed to oxygen.63 It has also been demonstrated experimentally via EPR that Zn2TTFTB contains radicals.42 In agreement with the Zn2TTFTB–FTO spectrum, the diffuse reflectance UV-visible spectrum of Zn2TTFTB powder also shows the cation feature between 600–800 nm (Fig. 5a). The solid H4TTFTB powder also has this feature (Fig. S8†). However, when H4TTFTB is dissolved in DMF, the solution becomes a deep orange color and no longer shows the absorption feature between 600–800 nm (Fig. 5a). It appears that both the Zn2TTFTB MOF and H4TTFTB powders are oxidized in air to become partially cation doped. This is likely, in part, due to the formation of a stabilized radical dimer65 or other stabilized cation species.
To further investigate this hypothesis and to gain insight into the nature of the observed UV-visible features, we performed time-dependent density functional theory (TDDFT) calculations (Fig. 5) to examine the dependence of the absorption spectrum on the redox state of H4TTFTB. The neutral, cationic, anionic, and dicationic states of H4TTFTB were considered in a DMF environment using the polarizable continuum model (PCM).70 The experimental data from spectroelectrochemistry experiments is used for comparison to the computational results. The calculated UV-visible absorbance of the neutral H4TTFTB ligand is in reasonable agreement with the experimental spectra with each containing a prominent band and a shoulder that extends into the visible region of the spectrum. While the shape of the features in the experimental spectrum is reproduced, the entire spectrum appears to be blue-shifted with respect to the experimental spectrum. The Natural Transition Orbitals (NTO's) of the 426 nm peak (Fig. 5a) show a delocalization from the TTF core to the peripheral phenyl groups upon excitation.
Difference spectra between the cation and neutral species, and anion and neutral species are shown in Fig. 5b and c, respectively, for both the calculated and experimental spectra. The calculated cation difference spectrum shows good agreement with the experimental spectrum. Peak 2 in the calculated spectrum is found at 433 nm and underlies the broad band at 370 nm compared to the experimental location of 475 nm. Peaks 2 and 3 in the cationic difference spectra are attributed to delocalization transitions across the molecule while peak 1 remains localized. The broad peak 3 from approximately 500 nm to beyond 1000 nm is also consistent with the absorption feature in this region observed experimentally (Fig. 5b). The calculated anionic difference spectrum (Fig. 5c) also showed good agreement with the experimental spectrum. Peak 1 for this difference is attributed to movement of density away from the TTF core, while peak 2 shows greater localization onto the core. However, the experimental observation of only a slight increase in the anionic spectrum as compared to the neutral spectrum in the 600–800 nm region suggests the anion is not responsible for extended shoulder seen in the MOF diffuse reflectance spectrum (Fig. 5a)
Calculated spectra for the neutral, anion, cation, and dication species are overlaid in Fig. 5d and are seen to have a visible shift in dominant peaks, and the appearance of multiple peaks in the charged spectra. To ensure the same feature was being analyzed between each spectrum, the NTO's for vibrations found in the region of the dominant peak were analyzed. The NTO's with the greatest similarity to the neutral 281 nm transition, which was found to be isolated from other peaks in the spectrum and therefore clearly the sole originator of the intensity, were selected and are shown in Fig. 5d. These features all largely remain localized on the TTF core and do not contribute to the delocalized shoulder feature. Additional discussion about the ordering of the peaks can be found in the ESI.† Additional NTO's for each of the charged and neutral species are shown in Fig. S9 and S10.† To investigate whether ligand stacking produces a feature in the 600–800 nm region, a 2-layer model was utilized (Fig. S11†) rather than the half-unit cell 3-layer model due to computational constraints. Absorption spectra in Fig. S12† demonstrate that while simple stacking of the layers does show a broadening of the 300 nm peak, simple stacking does not lead to a new absorption band between 600–800 nm as is seen experimentally in the full MOF or the cationic systems. Therefore, it becomes clear that the 600–800 nm band is entirely a product of cation doping.
Zn2TTFTB as a photosensitizing array
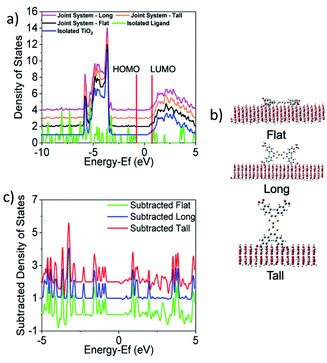
Given an understanding of both the optical properties and energetics of Zn2TTFTB, we investigated the conductive MOF film as a photosensitizer. In this scenario, visible light is absorbed by the photosensitizer followed by injection of an electron into the conduction band of TiO2. The UV-vis results demonstrated that the excitations are mainly ligand-centered, and this finding is unsurprising given that the metal oxide nodes of the MOF are composed of d10 Zn2+ ions. Therefore, the energetics of electron injection from Zn2TTFTB to TiO2 was modeled based on the TTFTB ligand as a computationally-feasible model system. TTFTB has four carboxylate groups, leading to various possibilities for attachment to the metal oxide surface. It is noted that one or more of these binding geometries could contribute to the model system and also to the Zn2TTFTB–TiO2 system, as the exact binding mode between Zn2TTFTB and TiO2 is uncertain.Taking these potential binding geometries into account, three models were created on a periodic TiO2 slab to investigate the density of states (DOS) with details on model formation and calculation in the ESI.† Their binding geometries are denoted flat, long, or tall (Fig. 6). The calculated DOS are presented in Fig. 6 showing the joint system DOS with the ligand in the three binding geometries as well as the isolated ligand and isolated TiO2 DOS. All density of states are shifted by the Fermi level of the joint flat system and were aligned to experimental values following the procedure outlined in the ESI.† The HOMO of the ligand is found to be within the bandgap of TiO2 whereas the LUMO is found to be slightly above the conduction band edge of isolated TiO2 (located at 0.21 eV), implying energetic favorability for electron injection. The strong interaction between the ligand and TiO2 can additionally be seen in the subtracted density of states shown in Fig. 6c where the DOS of the joint systems have each been subtracted from the summed DOS of the isolated ligand and surface. This figure shows that upon binding, the ligand and TiO2 interact to cause changes in the DOS up to as large as a third of the height of the maximum peak.
To investigate the electron injection process computationally, interfacial electron transfer (IET) calculations were performed for the tall, long, and flat orientations of the ligand on TiO2. Survival probabilities of an electron in the ligand, shown in Fig. S13,† support the experimental result to follow suggesting electron injection occurs in less than the instrument response function of 0.6 ps. Snapshots of the injection from each orientation are shown in Fig. 7 and movies can be viewed in the ESI.† At 0 fs, the LUMO density lies fully on the ligand. At later times, such as 27 fs, some density has moved from the ligand to the TiO2 slab for all orientations. The density spreads out horizontally into the periodic slab or is absorbed by an absorbing boundary condition at the bottom of the slab.
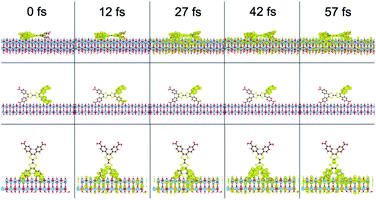 | ||
| Fig. 7 Interfacial electron transfer from H4TTFTB on TiO2 in a flat (top), long (middle), and tall (bottom) orientation. | ||
A well-established technique for experimentally investigating carrier injection and subsequent trapping/recombination dynamics in sensitized metal oxides is optical-pump THz-probe spectroscopy (OPTP). It has subpicosecond time resolution and is sensitive to mobile carriers, such as conduction band electrons, making it a non-contact probe for studying transient photoconductivity.71 As a result, OPTP has been widely applied to study dye-sensitized metal oxide systems.15,32,72–75 As indicated by our theoretical investigations, the carboxylate-bearing TTFTB ligand is energetically poised to photoinject electrons into TiO2. Therefore, TTFTB-sensitized samples were studied alongside Zn2TTFTB–TiO2 samples to compare how injection and/or recombination dynamics differ in the presence of an extended structure of overlapped chromophores, such as in Zn2TTFTB. The UV-visible spectra of these samples are shown in Fig. S14.†
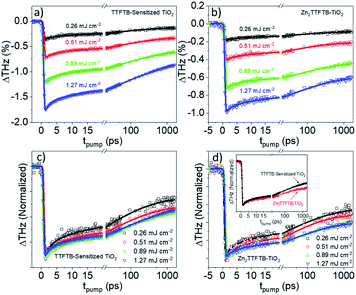
OPTP was performed on Zn2TTFTB–TiO2, TTFTB-sensitized TiO2, and, as a control to probe the intrinsic MOF photoconductivity on a non-injecting metal oxide, Zn2TTFTB–ZrO2. The samples were prepared on quartz substrates and photoexcited at 400 nm using various pump fluences as shown in Fig. 8. In our previous work, the optical penetration depth for Zn2TTFTB at 400 nm was determined to be about 7 μm, which is on the order of the largest radius of hemispherical MOF features observed (Fig. 3c).54 As the optical penetration depth is defined as the distance at which incident radiation intensity decays to 1/e (about 37%), the MOF features can be excited throughout their structure, even at their largest radii. TTFTB-sensitized TiO2 (Fig. 8a) shows an onset of THz attenuation that is limited by the instrument response function (IRF) of 600 fs due to electron injection into mobile conduction band states of TiO2. It is followed by a decay that is the result of trapping and recombination processes that depopulate the conductive states. The IRF-limited injection is supported by the computational IET results that show injection on a <100 fs timescale. Transients of a similar profile and degree of THz attenuation are seen with Zn2TTFTB–TiO2 (Fig. 8b), implying that Zn2TTFTB is also a suitable photosensitizer. A plot of the peak THz attenuation as a function of pump fluence shows that the THz attenuation scales linearly with pump fluence (Fig. S15†). When the control Zn2TTFTB–ZrO2 is measured under the highest fluence (1.27 mJ cm−2), a very small signal is observed that is over an order of magnitude weaker than that for Zn2TTFTB–TiO2. The signal from the Zn2TTFTB–ZrO2 film (Fig. S16†) is due to the intrinsic photoconductivity of Zn2TTFTB as we reported previously,54 and its negligible contribution to the injection signal is not considered in modeling.
The trapping and recombination processes observed in the timescale of OPTP experiments are inherently heterogeneous resulting in such processes occurring on a range of timescales. This has been previously accounted for with a stretched exponential model that results in modelling the exponential decay with a distribution of time constants described by the exponential term β.72 The fit model for OPTP data is given by eqn (1):
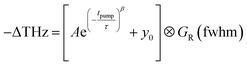 | (1) |
The amplitude of the stretched exponential is given by A. The post-decay offset, y0, accounts for remaining signal at the end of the measurable time range. The stretching factor β is fixed at 0.3 to allow straightforward comparisons of the fitted stretched time constants (τ). The stretched exponential with offset is convoluted with a Gaussian IRF with a fixed value of 0.6 ps.
The fit results are shown in Table 2. The time constants increase as a function of pump fluence, which we ascribe to band filling and trap state filling with increased electron density. The electron densities are not large enough to result in higher-order recombination processes, however, as these processes would result in a decrease in the observed time constants as a function of pump fluence and would also cause deviation from linearity in the THz attenuation as a function of pump fluence, which is not observed (Fig. S15†).
| Sample | Fluence | IRF (ps) | τ (ps) | A | β | Y 0 decay offset |
|---|---|---|---|---|---|---|
| TTFTB–TiO2 | 0.26 | 0.6 | 15.3 (0.4) | −0.34 | 0.3 | −0.13 |
| 0.51 | 21.3 (0.3) | −0.57 | −0.32 | |||
| 0.89 | 34.0 (0.3) | −0.85 | −0.58 | |||
| 1.27 | 35.0 (0.4) | −1.32 | −0.82 | |||
| Zn2TTFTB–TiO2 | 0.26 | 0.6 | 12.5 (0.3) | −0.17 | 0.3 | −0.09 |
| 0.51 | 18.2 (0.2) | −0.30 | −0.21 | |||
| 0.89 | 39.0 (0.3) | −0.42 | −0.42 | |||
| 1.27 | 37.2 (0.4) | −0.51 | −0.57 |
In comparing the normalized traces in the pump fluence regime where the dynamics were not fluence dependent for TTFTB-sensitized TiO2 and Zn2TTFTB–TiO2 (Fig. 8d, inset), it is observed that, especially on longer timescales, Zn2TTFTB–TiO2 deviates from TTFTB-sensitized and has a slower decay, which is corroborated by the fitted time constants. Additional comparisons were made (Fig. S17†) between data sets with similar ΔTHz magnitudes in both the regimes of fluence-dependent dynamics and fluence-independent dynamics yielding the same trend that the Zn2TTFTB signal is longer-lived. On longer timescales, it is expected that these dynamics are related to recombination of the electron in the TiO2 conduction band with the hole on the photosensitizer.
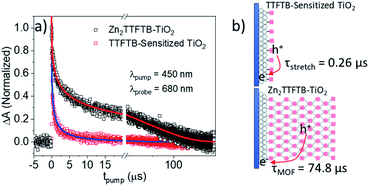
In order to compare the recombination dynamics between MOF-sensitized Zn2TTFTB–TiO2 and TTFTB-sensitized TiO2 on a longer timescale, we took advantage of the well-resolved TTFTB cation feature between 600–800 nm using nanosecond transient absorption (ns-TA) experiments. Upon electron injection into TiO2 using 450 nm excitation, a transient cation is formed on TTFTB or Zn2TTFTB which was probed at 680 nm. From the normalized TA data in Fig. 9a, it is clearly observed that Zn2TTFTB–TiO2 has a longer lifetime for the transient cation feature indicating delayed recombination with respect to TTFTB-sensitized TiO2 (Table 3).
| Sample | A stretch | τ stretch (μs) | β | A MOF | τ MOF (μs) |
|---|---|---|---|---|---|
| TTFTB–TiO2 | 1.09 | 0.26 | 0.35 | — | — |
| Zn2TTFTB–TiO2 | 0.94 | 1.43 | 0.35 | 0.22 | 74.8 |
The TTFTB-sensitized TiO2 transient was modeled with a stretched exponential (eqn (2)) to account for heterogeneity in the recombination process. The fit shown in Fig. 9a adequately describes the decay dynamics and a time constant of 0.26 μs is obtained. If the same model is used for the Zn2TTFTB-sensitized sample, then adequate agreement cannot be obtained (Fig. S18†). Therefore, a longer-lived single exponential contribution was added (eqn (3)) and used to fit the Zn2TTFTB–TiO2 data. Very good agreement is obtained, and the time constant for the long-lived component is 74.8 μs. The stretched time constant (τstretch) was also found to be larger for Zn2TTFTB–TiO2.
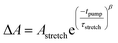 | (2) |
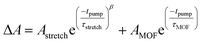 | (3) |
These ns-TA results are in agreement with OPTP results and show that recombination of the interfacially-separated electron–hole pair is significantly slower in the MOF-sensitized Zn2TTFTB–TiO2 system compared to the TTFTB-sensitized TiO2 system. Given the extended conductive MOF structure in Zn2TTFTB, a scheme is proposed in Fig. 9b to explain this result. In TTFTB-sensitized TiO2, the TTFTB-localized hole is constrained to the surface of TiO2 where it can recombine with the electron in TiO2. In the MOF system, however, this is not the case. Due to the MOF's conductivity, the hole is mobile and not restricted to the surface. In addition, the instrument-response limited electron injection observed may involve injection from more distant TTFTB chromophores of the MOF that are not directly linked to the surface. It takes much longer for the hole to diffuse to the interface and recombine with the electron compared to TTFTB-sensitized samples where it is constrained to be at the interface. Thus, the Zn2TTFTB MOF photosensitizer acts as a photosensitizing array that can separate the electron–hole pair to inhibit recombination.
Charge transport in Zn2TTFTB
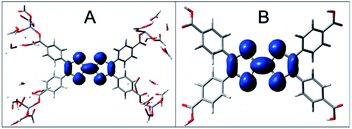
Computational and experimental results in the UV-visible electronic properties section implied that the UV-visible absorption of both the cation and the neutral oxidation states are ligand-centered in Zn2TTFTB. This point was further investigated by calculating the spin density of the radical cationic forms of H4TTFTB and the 1 layer model (Fig. 10). From the figure, it is clear that the hole is localized on the central S-containing rings of the TTFTB ligand. The molecular orbitals for the HOMO, LUMO, and LUMO+1 for both the 1 layer and 3 layer models were calculated and are shown in Fig. S19.† The HOMO appears to localize on the central S-rich region of TTFTB while the near-degenerate LUMO and LUMO+1 localize on the phenyls of the system. These results imply that upon photoexcitation, the photogenerated hole will localize on the S-rich central region of TTFTB while the electron will localize to the peripheral phenyl rings, thereby giving the hole and electron separate transport pathways within the MOF structure. The localization of the electron on the periphery is further supported by the calculated NTOs of H4TTFTB (Fig. S9†).To further explore the proposed charge transport mechanism, time-evolution of the inter-layer electron and hole dynamics upon photoexcitation were simulated at the extended Hückel level of theory (Fig. S20 and S21†). Wavepackets for the electron and hole were initialized in the LUMO and HOMO, respectively for each layer of a model composed of six TTFTB ligands oriented as in the crystallographic unit cell of the MOF. The wavepackets were propagated along the configurations sampled by four independent molecular dynamics trajectories at a DFT tight binding level of theory. The simulations revealed that the hole propagates through the tetrathiafulvalene cores at the center of the columnar stack with rates comparable to or greater than the photo-excited electron, which travels through the spiraling staircase of phenyl substituents on the periphery of the structure (Fig. 11). The photo-generated hole generally becomes more delocalized between ligand layers than the electron. These calculations are in agreement with the spectroelectrochemistry results in the “UV-visible electronic characterization” section and support a delocalized hole species as opposed to a strictly dimeric species.
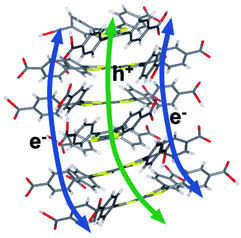 | ||
| Fig. 11 Proposed electron and hole transfer pathways. Calculations in this work suggest that electrons travel between phenyl stacks and holes through the S-rich TTF core. | ||
The wavepacket dynamics results (Fig. S20–S22†) suggest a difference in the inter-layer electronic coupling for the frontier orbitals. In fact, the HOMO–HOMO coupling for hole transport was computed to be 2.7–4.5 times larger on average than the LUMO–LUMO coupling for electron transport (Fig. S22†), a result that is consistent with the different extents of spatial overlap for these orbitals. Taken together, the wavepacket dynamics and electronic coupling calculations indicate that photo-generated electrons and holes are transported through spatially distinct pathways that afford holes much greater inter-layer mobility.
For both electrons and holes, the inter-layer transfer is predicted to take place within 200 fs upon photoexcitation, consistent with the instrument-response limited timescale measured experimentally for injection into TiO2. The intrinsic photoconductivity of the MOF suggests that the injected charge may originate from layers proximal or distal to the interface. In either case, the accelerated mobility of holes over electrons along the constrained channels in the MOF provides a mechanistic interpretation of the slower charge recombination observed experimentally for the MOF, as opposed to single ligand sensitized TiO2 surfaces. The results suggest a model wherein the ultrafast injection of the photo-generated electron is complemented by the rapid migration of the hole through the ligand rungs of the columnar stack away from the interfacial region. The ability to affect charge separation due to the different pathways for electron and hole conductance in the MOF (Fig. 11) can be exploited for artificial photosynthesis and photooxidation catalysis due to extended hole lifetime and the opportunity to rationally interface catalytic moieties directly within the hole transport pathway to strongly couple the catalyst to the photogenerated hole in the MOF photosensitizing array.
Conclusions
We have introduced a conductive MOF-sensitized TiO2 photoanode with photoconductivity properties particularly suitable for photocatalytic applications. We find that photoexcitation of Zn2TTFTB–TiO2 leads to efficient electron–hole pair separation, with holes migrating through the S-rich TTFTB cores while the electrons transfer through the peripheral phenyl groups. Time-resolved THz OPTP experiments indicate ultrafast electron injection into TiO2, leaving holes on the conductive Zn2TTFTB MOF photosensitizing array. The HOMOs of the TTFTB ligands are highly coupled, resulting in efficient transport of the photo-generated holes through the S-rich cores of the MOF. The ligand LUMOs are weakly coupled, and localized on the phenyl substituents. Nevertheless, both types of carriers (i.e., electrons and holes) are mobile and contribute to the efficient charge separation. In fact, our nanosecond transient absorption experiments have shown that the photogenerated hole feature has a much longer lifetime (at least two orders of magnitude longer) than in the ligand-sensitized TiO2 that lacks the extended MOF structure. Given these results, there is great promise in developing conductive MOF photoanode architectures for performing slow and thereby difficult oxidation reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under award DE-FG02-07ER15909, as well as from a generous donation from the TomKat Foundation. R. O. acknowledges funding from the Nakatani Foundation for performing research at Yale University in the Schmuttenmaer group. V. S. B. acknowledges high-performance computing time from NERSC.References
- A. J. Bard and M. A. Fox, Acc. Chem. Res., 1995, 28, 141 CrossRef CAS.
- T. J. Meyer, Acc. Chem. Res., 1989, 22, 163 CrossRef CAS.
- A. J. Esswein and D. G. Nocera, Chem. Rev., 2007, 107, 4022 CrossRef CAS PubMed.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503 CrossRef CAS PubMed.
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511 CrossRef CAS.
- I. McConnell, G. Li and G. W. Brudvig, Chem. Biol., 2010, 17, 434 CrossRef CAS PubMed.
- M. R. Wasielewski, Chem. Rev., 1992, 92, 435 CrossRef CAS.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 1993, 26, 198 CrossRef CAS.
- D. F. Watson and G. J. Meyer, Annu. Rev. Phys. Chem., 2005, 56, 119 CrossRef CAS PubMed.
- I. Robel, M. Kuno and P. V. Kamat, J. Am. Chem. Soc., 2007, 129, 4136 CrossRef CAS PubMed.
- M. Borgström, E. Blart, G. Boschloo, E. Mukhtar, A. Hagfeldt, L. Hammarström and F. Odobel, J. Phys. Chem. B, 2005, 109, 22928 CrossRef PubMed.
- J. Huang, O. Buyukcakir, M. W. Mara, A. Coskun, N. M. Dimitrijevic, G. Barin, O. Kokhan, A. B. Stickrath, R. Ruppert, D. M. Tiede, J. F. Stoddart, J.-P. Sauvage and L. X. Chen, Angew. Chem., Int. Ed., 2012, 51, 12711 CrossRef CAS PubMed.
- J. Kallioinen, G. Benkö, V. Sundström, J. E. I. Korppi-Tommola and A. P. Yartsev, J. Phys. Chem. B, 2002, 106, 4396 CrossRef CAS.
- S. K. Cushing, J. Li, J. Bright, B. T. Yost, P. Zheng, A. D. Bristow and N. Wu, J. Phys. Chem. C, 2015, 119, 16239 CrossRef CAS.
- G. M. Turner, M. C. Beard and C. A. Schmuttenmaer, J. Phys. Chem. B, 2002, 106, 11716 CrossRef CAS.
- S. G. Abuabara, C. W. Cady, J. B. Baxter, C. A. Schmuttenmaer, R. H. Crabtree, G. W. Brudvig and V. S. Batista, J. Phys. Chem. C, 2007, 111, 11982 CrossRef CAS.
- J. R. Swierk and T. E. Mallouk, Chem. Soc. Rev., 2013, 42, 2357 RSC.
- P. Xu, T. Huang, J. Huang, Y. Yan and T. E. Mallouk, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6946 CrossRef CAS PubMed.
- Y. Zhao, J. R. Swierk, J. D. Megiatto, B. Sherman, W. J. Youngblood, D. Qin, D. M. Lentz, A. L. Moore, T. A. Moore, D. Gust and T. E. Mallouk, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15612 CrossRef CAS PubMed.
- G. F. Moore, J. D. Blakemore, R. L. Milot, J. F. Hull, H.-e. Song, L. Cai, C. A. Schmuttenmaer, R. H. Crabtree and G. W. Brudvig, Energy Environ. Sci., 2011, 4, 2389 RSC.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37 CrossRef CAS PubMed.
- R. J. Kamire, K. L. Materna, W. L. Hoffeditz, B. T. Phelan, J. M. Thomsen, O. K. Farha, J. T. Hupp, G. W. Brudvig and M. R. Wasielewski, J. Phys. Chem. C, 2017, 121, 3752 CrossRef CAS.
- W. J. Youngblood, S.-H. A. Lee, Y. Kobayashi, E. A. Hernandez-Pagan, P. G. Hoertz, T. A. Moore, A. L. Moore, D. Gust and T. E. Mallouk, J. Am. Chem. Soc., 2009, 131, 926 CrossRef CAS PubMed.
- Y. Gao, L. Zhang, X. Ding and L. Sun, Phys. Chem. Chem. Phys., 2014, 16, 12008 RSC.
- L. Zhang, Y. Gao, X. Ding, Z. Yu and L. Sun, ChemSusChem, 2014, 7, 2801 CrossRef CAS PubMed.
- A. K. Chandiran, M. K. Nazeeruddin and M. Grätzel, Adv. Funct. Mater., 2014, 24, 1615 CrossRef CAS.
- J. Nissfolk, K. Fredin, A. Hagfeldt and G. Boschloo, J. Phys. Chem. B, 2006, 110, 17715 CrossRef CAS PubMed.
- N. Yao, J. Huang, K. Fu, X. Deng, M. Ding, S. Zhang, X. Xu and L. Li, Sci. Rep., 2016, 6, 31123 CrossRef CAS PubMed.
- L. Li, C. Xu, Y. Zhao, S. Chen and K. J. Ziegler, ACS Appl. Mater. Interfaces, 2015, 7, 12824 CrossRef CAS PubMed.
- E. Palomares, J. N. Clifford, S. A. Haque, T. Lutz and J. R. Durrant, Chem. Commun., 2002, 1464 RSC.
- E. Palomares, J. N. Clifford, S. A. Haque, T. Lutz and J. R. Durrant, J. Am. Chem. Soc., 2003, 125, 475 CrossRef CAS PubMed.
- J. Jiang, J. A. Spies, J. R. Swierk, A. J. Matula, K. P. Regan, N. Romano, B. J. Brennan, R. H. Crabtree, V. S. Batista, C. A. Schmuttenmaer and G. W. Brudvig, J. Phys. Chem. C, 2018, 122, 13529 CrossRef CAS.
- B. J. Brennan, M. J. Llansola Portolés, P. A. Liddell, T. A. Moore, A. L. Moore and D. Gust, Phys. Chem. Chem. Phys., 2013, 15, 16605 RSC.
- J. Jiang, J. R. Swierk, S. Hedström, A. J. Matula, R. H. Crabtree, V. S. Batista, C. A. Schmuttenmaer and G. W. Brudvig, Phys. Chem. Chem. Phys., 2016, 18, 18678 RSC.
- K. Hanson, M. K. Brennaman, A. Ito, H. Luo, W. Song, K. A. Parker, R. Ghosh, M. R. Norris, C. R. K. Glasson, J. J. Concepcion, R. Lopez and T. J. Meyer, J. Phys. Chem. C, 2012, 116, 14837 CrossRef CAS.
- M. Liu, S. Makuta, S. Tsuda, S. Russo, S. Seki, J. Terao and Y. Tachibana, J. Phys. Chem. C, 2017, 121, 25672 CrossRef CAS.
- S. Wang, X. Hai, X. Ding, S. Jin, Y. Xiang, P. Wang, B. Jiang, F. Ichihara, M. Oshikiri, X. Meng, Y. Li, W. Matsuda, J. Ma, S. Seki, X. Wang, H. Huang, Y. Wada, H. Chen and J. Ye, Nat. Commun., 2020, 11, 1149 CrossRef PubMed.
- S. Ghosh, A. Nakada, M. A. Springer, T. Kawaguchi, K. Suzuki, H. Kaji, I. Baburin, A. Kuc, T. Heine, H. Suzuki, R. Abe and S. Seki, J. Am. Chem. Soc., 2020, 142, 9752 CAS.
- L. Sun, M. G. Campbell and M. Dincă, Angew. Chem., Int. Ed., 2016, 55, 3566 CrossRef CAS PubMed.
- M. Ko, L. Mendecki and K. A. Mirica, Chem. Commun., 2018, 54, 7873 RSC.
- S. K. Bhardwaj, N. Bhardwaj, R. Kaur, J. Mehta, A. L. Sharma, K.-H. Kim and A. Deep, J. Mater. Chem. A, 2018, 6, 14992 RSC.
- T. C. Narayan, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2012, 134, 12932 CrossRef CAS PubMed.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450 RSC.
- M. Rimoldi, A. J. Howarth, M. R. DeStefano, L. Lin, S. Goswami, P. Li, J. T. Hupp and O. K. Farha, ACS Catal., 2017, 7, 997 CrossRef CAS.
- D. Yang and B. C. Gates, ACS Catal., 2019, 9, 1779 CrossRef CAS.
- K.-i. Otake, J. Ye, M. Mandal, T. Islamoglu, C. T. Buru, J. T. Hupp, M. Delferro, D. G. Truhlar, C. J. Cramer and O. K. Farha, ACS Catal., 2019, 9, 5383 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- J. Gascon, A. Corma, F. Kapteijn and F. X. Llabrés i Xamena, ACS Catal., 2014, 4, 361 CrossRef CAS.
- M. Liu, J. Wu and H. Hou, Chem.–Eur. J., 2019, 25, 2935 CAS.
- A. Dhakshinamoorthy, Z. Li and H. Garcia, Chem. Soc. Rev., 2018, 47, 8134 RSC.
- G. Lan, Y.-Y. Zhu, S. S. Veroneau, Z. Xu, D. Micheroni and W. Lin, J. Am. Chem. Soc., 2018, 140, 5326 CrossRef CAS PubMed.
- X. Zhao, B. Pattengale, D. Fan, Z. Zou, Y. Zhao, J. Du, J. Huang and C. Xu, ACS Energy Lett., 2018, 3, 2520 CrossRef CAS.
- S. Yang, B. Pattengale, S. Lee and J. Huang, ACS Energy Lett., 2018, 3, 532 CrossRef CAS.
- B. Pattengale, J. Neu, S. Ostresh, G. Hu, J. A. Spies, R. Okabe, G. W. Brudvig and C. A. Schmuttenmaer, J. Am. Chem. Soc., 2019, 141, 9793 CrossRef CAS PubMed.
- J. P. McEvoy and G. W. Brudvig, Chem. Rev., 2006, 106, 4455 CrossRef CAS PubMed.
- C. Y. Lee, O. K. Farha, B. J. Hong, A. A. Sarjeant, S. T. Nguyen and J. T. Hupp, J. Am. Chem. Soc., 2011, 133, 15858 CrossRef CAS PubMed.
- J. Zhu, W. A. Maza and A. J. Morris, J. Photochem. Photobiol., A, 2017, 344, 64 CrossRef CAS.
- W. A. Maza, A. J. Haring, S. R. Ahrenholtz, C. C. Epley, S. Y. Lin and A. J. Morris, Chem. Sci., 2016, 7, 719 RSC.
- S. R. Ahrenholtz, C. C. Epley and A. J. Morris, J. Am. Chem. Soc., 2014, 136, 2464 CrossRef CAS PubMed.
- M. Cai, Q. Loague and A. J. Morris, J. Phys. Chem. Lett., 2020, 11, 702 CrossRef CAS PubMed.
- S. S. Park, E. R. Hontz, L. Sun, C. H. Hendon, A. Walsh, T. Van Voorhis and M. Dincă, J. Am. Chem. Soc., 2015, 137, 1774 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537 CrossRef CAS PubMed.
- F. Wudl, G. M. Smith and E. J. Hufnagel, J. Chem. Soc. D, 1970, 1453 RSC.
- L. Huchet, S. Akoudad, E. Levillain, J. Roncali, A. Emge and P. Bäuerle, J. Phys. Chem. B, 1998, 102, 7776 CrossRef CAS.
- F. B. Kaufman, A. H. Schroeder, E. M. Engler, S. R. Kramer and J. Q. Chambers, J. Am. Chem. Soc., 1980, 102, 483 CrossRef CAS.
- Y. Mitamura, H. Yorimitsu, K. Oshima and A. Osuka, Chem. Sci., 2011, 2, 2017 RSC.
- G. Inzelt, J. Q. Chambers and F. B. Kaufman, J. Electroanal. Chem. Interfacial Electrochem., 1983, 159, 443 CrossRef CAS.
- T. Amemiya, J. Electrochem. Soc., 1991, 138, 2845 CrossRef CAS.
- K. Jackowska, A. Kudelski and J. Bukowska, Electrochim. Acta, 1994, 39, 1365 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef.
- M. C. Beard, G. M. Turner and C. A. Schmuttenmaer, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15764 CrossRef CAS.
- K. P. Regan, J. R. Swierk, J. Neu and C. A. Schmuttenmaer, J. Phys. Chem. C, 2017, 121, 15949 CrossRef CAS.
- J. B. Baxter and C. A. Schmuttenmaer, J. Phys. Chem. B, 2006, 110, 25229 CrossRef CAS PubMed.
- E. Hendry, M. Koeberg, B. O'Regan and M. Bonn, Nano Lett., 2006, 6, 755 CrossRef CAS PubMed.
- P. Tiwana, P. Parkinson, M. B. Johnston, H. J. Snaith and L. M. Herz, J. Phys. Chem. C, 2010, 114, 1365 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental methods and details, supplementary figures for characterization, spectroelectrochemistry, OPTP, and computational results including optimized coordinates for the utilized models. See DOI: 10.1039/d0sc04302h |
| ‡ Present address: School of Life Science and Technology, Tokyo Institute of Technology, Nagatsuta 4259, Midori-ku, Yokohama, Kanaga-wa 226-8503, Japan. |
| § Deceased July 26, 2020. |
| This journal is © The Royal Society of Chemistry 2020 |