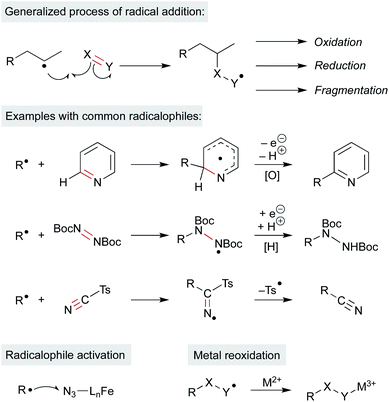
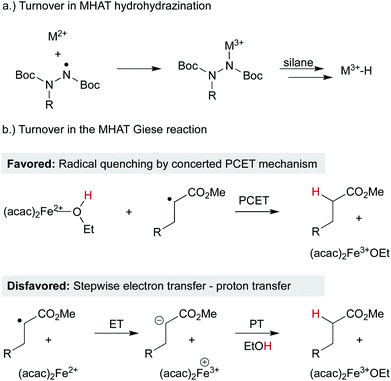
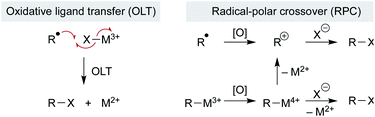
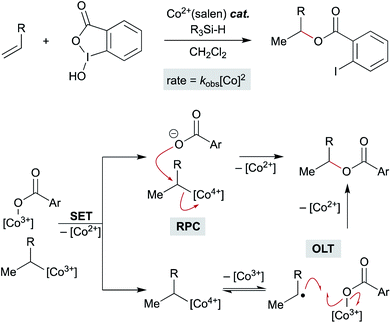
Open Access Article
Open Access ArticleCatalytic hydrogen atom transfer to alkenes: a roadmap for metal hydrides and radicals
Sophia L.
Shevick
 a,
Conner V.
Wilson
b,
Simona
Kotesova
a,
Dongyoung
Kim
b,
Patrick L.
Holland
a,
Conner V.
Wilson
b,
Simona
Kotesova
a,
Dongyoung
Kim
b,
Patrick L.
Holland
 *b and
Ryan A.
Shenvi
*b and
Ryan A.
Shenvi
 *a
*a
aDepartment of Chemistry, Scripps Research, 10550 North Torrey Pines Road, La Jolla, CA 92037, USA
bDepartment of Chemistry, Yale University, 225 Prospect St., New Haven, CT 06511, USA
First published on 29th September 2020
Abstract
Hydrogen atom transfer from a metal hydride (MHAT) has emerged as a powerful, if puzzling, technique in chemical synthesis. In catalytic MHAT reactions, earth-abundant metal complexes generate stabilized and unstabilized carbon-centered radicals from alkenes of various substitution patterns with robust chemoselectivity. This perspective combines organic and inorganic perspectives to outline challenges and opportunities, and to propose working models to assist further developments. We attempt to demystify the putative intermediates, the basic elementary steps, and the energetic implications, especially for cage pair formation, collapse and separation. Distinctions between catalysts with strong-field (SF) and weak-field (WF) ligand environments may explain some differences in reactivity and selectivity, and provide an organizing principle for kinetics that transcends the typical thermodynamic analysis. This blueprint should aid practitioners who hope to enter and expand this exciting area of chemistry.
1. Introduction
Many impactful advances in synthesis have come from organometallic chemistry, a field that leverages the synergy between organic and inorganic chemistry. The dominant concepts in organometallic chemistry simply extend the models of organic chemistry: for example, the SN1 reaction becomes dissociative substitution, and the octet rule expands to the 18-electron rule.1 These models serve the community well for complexes dominated by strong-field supporting ligands (e.g. cyclopentadienyl, carbonyl, phosphine, and pyridine), but a new generation of organometallic reactions has arisen in which the metal has no strong-field supporting ligands, and these systems require a different view.2 The availability of adjacent oxidation states facilitates homolysis to form radical intermediates; supporting ligands can be labile; multiple spin states may be present; the 18-electron rule is not obeyed routinely; and bonds are often weaker. Developing useful models for understanding these different organometallic compounds requires a renewed partnership between organic and inorganic chemists.3,4Here, we analyze metal hydride (M–H) hydrogen atom transfer (MHAT) methods for Markovnikov hydrofunctionalization of alkenes, where our groups have found common interests. The radical MHAT mechanism emanated from the work of Iguchi, Halpern, Jackman and others and explained the reactions of hydridocyano- and hydridocarbonylmetal complexes with activated alkenes as outer-sphere additions of hydrogen, as opposed to coordinative metal insertions, hydridic additions or protonations.5 MHAT is a powerful working model that also explains Drago-Mukaiyama hydrofunctionalizations, which now encompass diverse cross-coupling methods. This collaborative Perspective uses our organic and inorganic backgrounds to propose a mechanistic framework for MHAT reactions, highlighting areas of emerging consensus as well as areas where mechanistic studies are needed.
Prior to work by Mukaiyama and Norton, conversion of alkenes to carbon-centered radicals mainly involved the addition of tin-, carbon- or heteroatom-centered radicals to the alkene; formal addition of a hydrogen atom to an alkene to generate unstabilized radicals had little preparative precedent. Carreira's expansion of Mukaiyama-type chemistry to include an array of electrophilic partners, like diazodicarboxylates, signaled a key turning point.6 These methods established reagent combinations that could transform alkenes into Markovnikov addition products, but with reversed polarity and high chemoselectivity compared to conventional protic hydrofunctionalizations. In hindsight, these reactions likely proceed via MHAT.5
Scheme 1 shows representative examples of proton transfer and hydrogen atom transfer, which generate ion pairs and radical pairs, respectively. At first, the polar pathway may appear more reasonable, because it is a staple of introductory organic chemistry courses. Consider, however, that until the 1930s the invocation of an unstabilized carbocation had not reached the point of an organizing mechanistic principle.7 Whitmore recognized the generality of carbocations throughout organic chemistry,8 yet his depictions of ionic hydrocarbons (R3C+) were so controversial that they were excluded from J. Am. Chem. Soc.9 Our present comfort with carbocations as legitimate intermediates stems from their predictive and didactic power to explain many chemical reactions, from skeletal rearrangements10 to SN1 reactions.11 The complex solvation kinetics of carbocation/anion pairs explain the rate effects of salt additives,12 unusual stereochemical outcomes of tert-alkyl halide solvolyses,13,14 and isotope scrambling of alkyl arylsulfonates.15 Carbocation chemistry has now become an enabling technology that converts, for example, light olefins like isobutene, butene and propene to high-value gasoline-range blendstocks using strong Brønsted acids to protonate alkenes.16
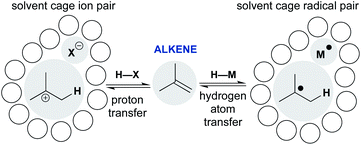 | ||
| Scheme 1 Comparing alkene addition through polar and radical pathways: proton transfer versus hydrogen atom transfer. | ||
The models developed for carbocation/anion pairs as reaction intermediates should guide our consideration of radical cage pairs. Whereas ion pairs are most influenced by electrostatics and ion–solvent interactions, neutral radical pairs are instead primarily affected by solvent viscosity, as well as spin state, radical mass and/or size (vide infra). Despite these differences, there are also similarities. Just as the contact-ion pair mechanistic paradigm provides a framework to understand the kinetics of cationic rearrangements and substitutions, the behavior of the radical pair—return to reactants, collapse to organometallics, or escape from the solvent cage—determines how the metal-catalyzed radical reaction unfolds.17,18 The proton transfer/contact ion pair model thus provides a conceptual scaffold on which to hang the less-familiar hydrogen transfer/radical cage pair model and incorporate it into our collective chemical psyche.
In this article, we classify transition-metal hydrides that can perform alkene MHAT into two rough categories: those bearing strong-field (SF) ligands and those bearing weak-field (WF) ligands. The SF systems, studied by Halpern, Bullock, Norton and others, utilize Mo, W, V, Cr, Mn, Fe and Co catalysts having strong-field supporting ligands, such as carbonyls, that lead to low-spin complexes.5,19 In catalytic reactions with SF complexes, the hydride complexes are often isolable, and the hydrogen atom source is often H2. The scope of MHAT reactions for SF systems is typically limited to isomerizations, cyclizations, and hydrogenations, and the rates of catalysis are generally slow. Below we attribute these slow rates to the higher bond dissociation enthalpy (BDE) of the M–H bond, which leads to an endothermic hydrogen atom transfer to many alkenes. The greater stability of these M–H bonds has allowed their extensive interrogation, in contrast to a more recent class of metal hydride. This second class, initially studied by Drago and Mukaiyama, uses an Fe, Mn or Co complex as catalyst.5,20,21 These catalysts have weak-field supporting ligands based on N or O donors, and thus we call them WF systems. With WF systems, the catalytic reactions are much more rapid, proceeding at room temperature, even when using electron-neutral alkenes. These reactions use a reductant such as PhSiH3 or NaBH4, which is assumed to generate a transition-metal hydride complex based on the MHAT reaction products, but the transient hydrides have not been isolated in these systems. Below, we attribute these phenomena to a lower M–H BDE in these systems, which hinders the identification of intermediates but leads to greater reactivity.
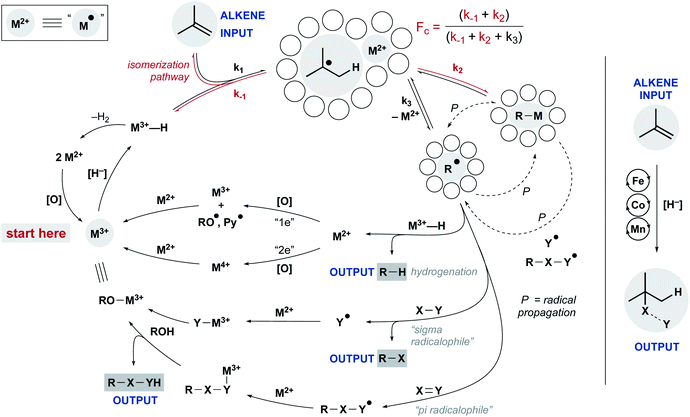
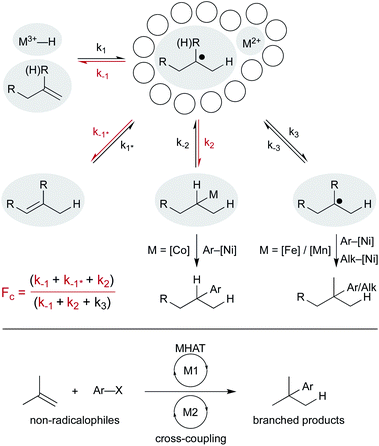
Despite these differences, a common mechanistic scaffold is now invoked for all the WF MHAT reactions. In Scheme 2, this is shown as a branching catalytic cycle. In this perspective, we consider the likely composition and behavior of transiently formed intermediates, especially the metal hydride and the caged radical pair. We emphasize that considering the thermodynamics and kinetics of radical pair generation provides an organizing principle similar to the powerful concept of contact ion pairing, and we describe some of the outstanding questions and opportunities. As with the carbocation, the model of MHAT provides explanatory, predictive and didactic power that is likely to accelerate the implementation and evolution of useful catalytic methods.
2. Metal hydrides in MHAT reactions
2.1 Formation of metal hydride
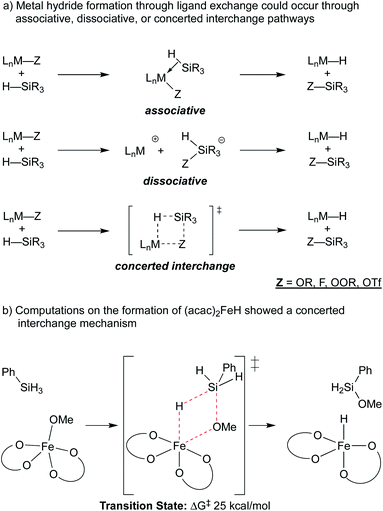
Metal hydride species have been a longstanding topic of study in organometallic chemistry, and bond dissociation enthalpies (BDE) are known for many M–H bonds in classic 18-electron organometallic hydride complexes.22 Measured BDE values are generally 52 kcal mol−1 or greater,22,23 which renders them thermodynamically stable with respect to H2 formation, and slow for MHAT.In the WF systems, M–H bonds are thought to be much weaker (vide infra). Formation of such weak M–H bonds must be compensated by a strong bond in another product. Thus, reductants in WF systems are typically silanes or borohydrides, which have Si–H or B–H bonds that can be broken to form much stronger Si–O, Si–F, B–O, or B–F bonds, providing a driving force. (For instance, the Si–H BDE of Me3Si–H is 95 kcal mol−1 and the Si–O BDE of Me3Si–OEt is 122 kcal mol−1.) Typical WF catalyst systems provide a source of alkoxide or fluoride, which is an important design feature (Scheme 3).5
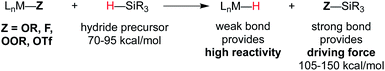 | ||
| Scheme 3 Top: use of O or F groups (indicated as Z) provides a strong Si–Z bond that drives uphill M–H formation. Bottom: potential mechanisms of metal-hydride formation. | ||
Seminal reports of alkene radical hydrofunctionalizations, prior to their recognition as WF MHAT reactions, noted the importance of alcoholic solvent or co-solvent.21 In a particularly clear example, when Mn(dpm)3 was treated with PhSiH3 in dichloromethane, no reaction was observed at room temperature until the addition of isopropyl alcohol.24 One important role of the alcohol may be to provide the alkoxide that supplies the aforementioned driving force for Si–O or B–O bond formation. Recently, in an MHAT Giese reaction (i.e. C-radical 1,4-addition to an acceptor alkene), we replaced Fe(acac)3 with an iron(III) ethoxide complex [(acac)2Fe(μ-OEt)]2, which eliminated an observed induction period and led to higher yields at a lower temperature.25 This information, combined with the observation of ethoxysilane byproducts, suggested that an acac-supported iron ethoxide species served as a reactive, on-cycle species to engage phenylsilane—compensating the weak M–H bond with a strong Si–O bond.
Alkoxysilanes have been observed as byproducts of metal hydride formation, but alkoxysilanes themselves may act as rapid hydride donors to metal pre-catalysts. For example, Mn(dpm)3 catalyzes the formation of isopropoxyphenylsilane from phenylsilane and isopropanol solvent, but this alkoxysilane is consumed by Mn(dpm)3 faster than it is formed.26 To generalize the impact of this discovery, we showed that PhSi(Oi-Pr)H2 is a more active hydride donor in several classes of MHAT reactions and in the absence of alcohol solvent.26 Interestingly, more than one alkoxide on the silane becomes detrimental; for example, PhSi(Oi-Pr)2H is less active than PhSiH3. Subsequent calculations suggested that the barrier heights for silane reactions with (acac)2Fe(OEt) increased in the order PhSi(OR)H2 < PhSiH3 ≪ PhSi(OR)2H, supporting the idea that there is a balance between steric and electronic factors in determining the hydride donor ability.27
The source of the OR− or F− also may derive from an added oxidant. In many WF catalyst systems, a cobalt(II) precatalyst must be oxidized in situ in order to form the necessary cobalt(III) hydride.28 Thus, catalytic conditions include an oxidant to both turn over the catalytic cycle as well as oxidize the precatalyst to the cobalt(III) oxidation state. The seminal Mukaiyama papers utilized cobalt β-diketonate catalysts and oxygen,21 and later Nojima reported a stoichiometric reaction in which an isolable cobalt alkylperoxide complex reacts with triethylsilane to form an alkyl silyl peroxide and a putative cobalt hydride, suggesting that this ligand exchange enabled regeneration of the cobalt hydride catalyst.29 This idea was further supported when the same cobalt alkylperoxide complex was shown to be catalytically competent in the triethylsilylperoxidation of an alkene in the presence of oxygen and triethylsilane. More recent MHAT papers use N-fluoro oxidants (e.g. Selectfluor, fluorocollidinium salts), which could both serve to oxidize the catalyst and drive formation of the metal hydride via ligand exchange and formation of a strong Si–F bond.30 However, the mechanistic pathways for metal hydride formation from M3+ alkoxide/fluoride precursors remain under-investigated.
A ligand exchange that gives the metal hydride could occur through associative, dissociative or concerted interchange pathways (Scheme 4a). In the case of β-diketonate-supported iron hydrides, DFT calculations were used to explore the exchange of hydride for alkoxide between (acac)2Fe–OMe and phenylsilane, suggesting that concerted ligand exchange would have a rate similar to that observed experimentally (Scheme 4b).27 This concerted interchange mechanism also appears feasible for Mn and Co bis-acetylacetonates but may not be possible for the popular cobalt salen complexes,17,30–32 which lack open cis-coordination sites. In these systems, initial insight comes from the oxidation of a (salen)Co2+ complex with N-fluorocollidinium triflate, which did not lead to the isolation of a Co3+–fluoride complex, but instead generated a cationic Co3+ complex with an outer sphere triflate counteranion. The related Co3+ tetrafluoroborate could be generated by oxidation of Co2+ with silver(I) tetrafluoroborate, which was shown to be catalytically competent.18,33 The mechanism of hydride formation in this instance is less obvious but one possibility is hydride delivery from a pentavalent silicate intermediate formed by the association of triflate, fluoride, or solvent.34 Both pathways would produce the previously mentioned Si–O or Si–F bond.
An alternative hypothesis comes from work on Co2+(dmg) systems, which had been proposed to generate a cobalt(III) hydride complex.35 The 1H NMR signal previously assigned to a cobalt(III) hydride was later shown to come from a paramagnetic cobalt(II) species. Another study suggested the formation of a monomeric cobalt(I) complex under related conditions. This cobalt(I) species could tautomerize to form a metal-centered cobalt(III)-hydride catalyst that could be the kinetically competent catalyst in MHAT with alkenes, as it has an effective bond dissociation free energy of only 50.5 kcal mol−1 (Scheme 5a). Alternatively, the cobalt(I) species could engage in proton-coupled electron transfer (PCET) to transfer the hydrogen atom directly from the O–H group. In the MHAT field, it is not often noted that complexes of reduced metals and acidic protons can perform PCET that renders them effective formal hydrogen atom donors,36–38 and therefore MHAT reactions could conceivably proceed via donation of a ligand-based and not metal-bound H atom. These possibilities can be distinguished using deuterium labeling experiments; for example, transfer from the carbon backbone of β-diketonate ligands was excluded in Drago-Mukaiyama reactions, as deuterated ligands did not give deuterium incorporation in the product (Scheme 5b).26 Similarly, hydrogen atom transfer from an O–H tautomer is excluded by use of exchangeable deuterated solvent, which would lead to deuteration of product. However, only protium incorporation from stoichiometric hydrides is observed in deuterated solvent. Similar labeling experiments exclude ligand hydrogen atom transfer (PCET) from analogous tautomers of salen analogs.30
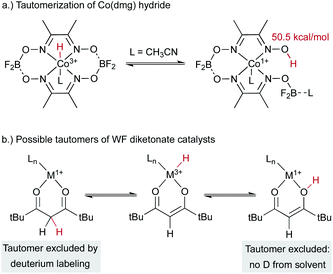 | ||
| Scheme 5 Hydrides can have isomers with weakly bound H on the ligand, and deuteration experiments can test for this possibility. | ||
2.2 Properties of metal hydrides in MHAT reactions
An interesting contrast emerges between the isolable SF metal hydride catalysts used for some MHAT reactions, such as HMn(CO)5, HCo(CO)4, and HCrCp(CO)3, and the expected (but so far non-isolable) WF metal hydride intermediates in other MHAT reactions (Fig. 1). First, the isolable metal hydrides in SF systems have lower oxidation states (1+ and 2+) than the oxidation states of the putative, in situ-generated metal hydrides (3+) in WF systems. WF reactions often require an oxidant, such as TBHP or O2, consistent with the requirement for higher oxidation states. Second, the SF hydrides are supported by strong-field CO and phosphine ligands, giving a low-spin electronic configuration, while the WF metal hydrides for catalytic HAT reactions instead have weak-field ligands, such as acetylacetonate and oxalate. Thus, the WF intermediates can have intermediate spin or high spin electronic configurations with unpaired electrons in antibonding orbitals, and the bonds are expected to be much weaker. Quantitative support of the M–H bond energy trend as a function of spin state is so far lacking, because the WF hydrides are not isolable, and so researchers have turned to computations.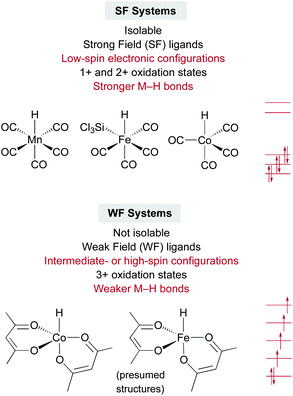 | ||
| Fig. 1 Contrasts between strong-field and weak-field catalyst systems for MHAT, with examples of catalysts and electronic configurations. | ||
Recently, two computational studies evaluated a putative WF iron(III) hydride intermediate (acac)2Fe–H using DFT and coupled-cluster methods, and both indicated that the Fe–H BDE is only 17–20 kcal mol−1.27,39 Interestingly, the Fe–H BDE of the reduced iron(II) [(acac)2Fe–H]− is calculated to be much stronger (66 kcal mol−1), because the formal iron(I) product from Fe–H bond homolysis is high in energy. A recent experimental study in a SF system showed the complementary trend, that the oxidation from vanadium(I) [CpV(CO)3H]− to vanadium(II) CpV(CO)3H decreases the V–H BDE from 55 to 36 kcal mol−1.23 These studies indicate that manipulating the oxidation states and redox potentials of MHAT catalysts (both SF and WF) is a promising area for continued study. It is likely that modification of the geometry will also be influential because this changes the relative energies of different spin states and oxidation states. The most systematic method to correlate structure and BDE may be computation, but correlating the computations with experiment can be complicated by interactions with ions and solvent, as well as exchange of labile ligands in WF systems. Therefore, a recursive approach of computational prediction and experimental testing is essential for reliable progress.
In general, hydrides of high-spin metal centers are uncommon, and the potential for weak M–H BDEs leading to useful MHAT reactivity motivates future study in this area. Moving from β-diketonates to higher-denticity supporting ligands would have multiple benefits. First, these ligands give more predictable geometries, leading to more reliable computations. Second, chelating ligands often give spectroscopic handles that could ease the characterization of fleeting hydride intermediates. Third, they may allow access to stable complexes in lower oxidation states, due to lower lability of the chelating ligand. Finally, they are more amenable to systematic modification of steric and electronic influences on the metal, giving flexibility to the catalyst design.
2.3 Effects of strong-field vs. weak-field hydrides on thermodynamics of HAT, rate-limiting step, kinetics, and chemoselectivity
Metal hydrides that have slightly weakened bonds (∼60 kcal mol−1, viz. tin-hydrides: 78 kcal mol−1) can transfer a hydrogen atom if the reaction partner is already an open shell species (e.g. TEMPO) or can significantly stabilize the resulting radical (e.g. α-methylstyrene). Therefore, expansion of this reactivity to unactivated alkenes raises a thermodynamic conundrum because MHAT forms two relatively unstable species: an unsaturated, reduced metal complex and an unstabilized organic radical. For example, metal hydride H-atom transfer to ethylene or propylene is thermodynamically favorable only if the M–H BDE is less than 36 kcal mol−1.40 Even assuming a barrierless reaction, then, the M–H BDE must be 50 kcal mol−1 or less for MHAT to be kinetically feasible near room temperature (taking into account an activation barrier of 24 kcal mol−1, which is a half-life of 11 hours at room temperature). This explains why the rates are low in MHAT systems with SF catalysts whose bonds are greater than 50 kcal mol−1 (Fig. 2, top).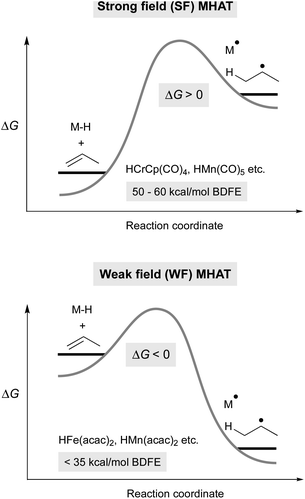 | ||
| Fig. 2 Thermodynamic model for differences between SF (top) and WF (bottom) MHAT reactions, which explains the higher reactivity of WF systems. | ||
Whereas SF CpCr(CO)3H forms rapidly from CpCr(CO)3 and H2 and undergoes slow MHAT, WF systems are thought to undergo fast MHAT, so that other steps in the catalytic cycle become turnover limiting. For example, replacement of phenylsilane with isopropoxyphenylsilane greatly increased reaction rates for many MHAT reactions catalyzed by Mn and Fe, which is consistent with the idea that M–H formation, not MHAT, can be turnover limiting.26 Combined with the different relative bond strengths described above, these results suggest a Hammond postulate model in which SF systems have a high barrier for MHAT because it is endothermic, while WF systems have a low barrier for MHAT because it is exothermic (Fig. 2).
Recently, mechanistic and computational evaluation of Fe3+–H formed in the HAT alkene coupling reaction suggested the formation of the reactive Fe3+–H as the turnover frequency determining step and the subsequent transfer of hydrogen atom to be a fast, irreversible and thermodynamically favorable step in the catalytic cycle.27 A kinetic model derived from the computational barriers in this study indicated that the HAT step is so rapid that the steady-state concentration of Fe3+–H in the catalytic reaction would be less than 10−16 M! In another example, (salen)Co3+–H was shown to consume alkyl-substituted, unactivated alkenes within 30 minutes even at substrate concentrations of 1 × 10−3 M and a pre-catalyst concentration of 1 × 10−4.33 More information could in principle be gleaned from determination of rate laws, but kinetic analysis has proven challenging. For example, the cobalt-catalyzed hydrohydrazination and hydroazidation, as well as the iron-catalyzed alkene–alkene coupling, exhibited partial-order rate dependencies on metal, alkene and silane,28 and apparent orders for alkene, radical acceptor, and silane that depended on the choice of alkene.25 In the future, greater insight could come from measuring the rates of elementary steps that are proposed in catalytic reactions.
The extraordinarily low BDFE proposed for WF M–H species may be one key to their widespread applications in synthetic chemistry. In contrast to SF systems, hydrogen atom transfer from WF systems to alkenes is exothermic, even to electronically-unbiased alkenes. This enables WF systems to also generate nucleophilic alkyl radicals, and the range of electrophilic radicalophiles for MHAT is expanded. As the concentration of the reactive metal hydride remains low, alkyl radicals generated react preferentially with stoichiometric radicalophile coupling partners instead of a second equivalent of metal hydride. SF MHAT systems, with higher BDFEs and endergonic HAT, exhibit more limited reaction rates and variety of reaction partners (giving hydrogenation and hydroformylation). However, the ability to observe and characterize these SF metal hydrides has provided a basis for our current mechanistic understanding of the MHAT mechanism and generality of MHAT within the literature.
Despite its increased utility, the weak M–H bond in WF systems also poses challenges. A recurring problem in high-energy WF systems is catalyst deactivation to a reduced species, such as the buildup of Fe2+(acac)2 in the iron(III)-catalyzed alkene coupling reaction,25 possibly due to bimolecular hydrogen evolution, as observed in SF systems.41 One role of the oxidants that are often added to the WF MHAT reactions may be to rescue these low-valent M2+ species and return them to the catalytic cycle as M3+. In the case of MHAT hydrogenation,42 M2+ species are necessary intermediates in the catalytic cycle and must be turned over by oxidant. Additionally, superstoichiometric amounts of reductants may be used to replace equivalents consumed by side reactions.
In WF systems, formation of the high-energy metal hydride may compete with other reactions, particularly those of the hydrosilane, so that appropriate silane choice is crucial. The dehydrogenative coupling of silanes and alcohols is one such process, and is known to be catalyzed by alkoxides43 as well as metal acetylacetonates.44 Formation of alkoxysilanes can prove beneficial (see Section 2.1), but these same alkoxysilanes decompose in protic solvents, so that aprotic solvents like benzene and ethyl acetate are preferred. Silanes may also yield byproducts via reduction of ketones, aldehydes, and nitriles.45 Replacement of phenylsilane with isopropoxyphenylsilane eliminated these side reactions in the Mn-catalyzed hydrogenation of alkenes, and significantly reduced the catalyst loading from 10 mol% to 0.05 mol%.26 This observation demonstrates the power of appropriate silane choice for speeding the desired hydride formation so that the desired catalytic MHAT cycle “outruns” side reactions.
Identification of metal hydride properties that are required for broad-scope MHAT might allow the design of ligand spheres with new functions (see also Section 7 for asymmetric reactions). For example, the Norton group has recently found that Gade's iso-PmBox nickel hydride can undergo MHAT with trifluoromethylstyrenes.46 Since WF MHAT (Mn–H and Fe–H) itself can be merged with canonical nickel cross-coupling via bimetallic dual catalysis,47 reactivity of the iso-PmBox nickel hydride hints at the possibility of a dual-functional, but mono-metallic catalytic cycle.
3. Trends in alkene selectivity for strong-field MHAT and weak-field MHAT
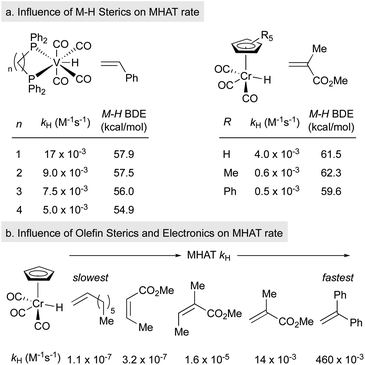
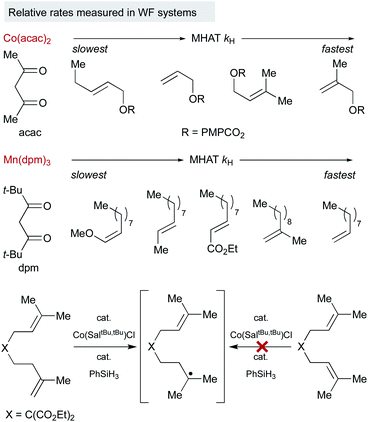
Much of the seminal work to understand MHAT kinetics relied on direct measurements of rate constants from isolable SF metal-hydrides and correlation with BDEs of the M–H bond. Although weaker bonds often lead to faster rates of MHAT, there have been many exceptions to this rule due to contributions from the steric environment around the metal–ligand complex and the substrate alkene. These observations directly excluded the competing hypothesis of direct homolysis to the free H˙ and clearly indicated that these reactions were bimolecular between metal-hydride and alkene. Several interesting relative rate studies are summarized below.Variation of the ligand environment of MHAT catalysts revealed the potential for departure from trends predicted by BDEs or pKa in both vanadium hydride and chromium hydride systems. For example, rates of MHAT from a [H–V(CO)4(diphosphine)] series decreased as the M–H bond weakened – a counterintuitive effect. This rate trend also opposed correlation with pKa values, which decreased as ligand bite angle increased. Instead, rates correlated well to the steric size of the chelating ligand: dppm (17 × 10−3 M−1 s−1) > dppe (9 × 10−3) > dppp (7 × 10−3) > dppb (5.7 × 10−3), implying that small increases in steric repulsion could oppose electronic acceleration (Fig. 3a, left).48 Similarly, hydrogen/deuterium exchange rates from a chromium hydride catalyst (η5-C5R5)Cr(CO)3H (R = Ph, Me, H) to methyl methacrylate-d5 indicated that as chromium hydride became more congested, the rate of the first MHAT event decreased (Fig. 3a, right).49,50 Taken together, a clean correlation of rate to M–H BDE or pKa was excluded and instead sterics were proposed to play a significant role in the relative rates of MHAT.
Similarly, steric and electronic properties of the alkene partner play a significant role in determining rate. The rates of MHAT from (η5-C5H5)Cr(CO)3H to phenyl-, alkyl- and carbomethoxy-substituted alkenes decreased with increasing steric bulk of substituents at the alkene terminus (Fig. 3b).51 MHAT rates increased according to electronic stabilization of the intermediate carbon-centered radical (measured by C–H BDE: R = alkyl, 97 kcal mol−1vs. carbomethoxy, 85 kcal mol−1vs. phenyl, 84 kcal mol−1): greater stabilization decreased the rate of hydrogen atom transfer back to the metal.51 Overall, relative rates showed that electronically biased (phenyl and carbomethoxy substituted) alkenes reacted more rapidly than electron neutral alkenes, but were slowed significantly by alkyl substitution at the reacting terminus.
Because of the low stability of WF systems, M–H BDEs have not been measured. Relative trends, however, have been deduced by probing the reaction partners in a way that is analogous to the SF systems (Fig. 4). For example, Herzon studied the relative rate of MHAT alkene hydrogenation and showed that rate trends were reversed compared to traditional reductions catalyzed by palladium. A survey of Co(acac)2-catalyzed hydrogenations showed more rapid consumption of 1,1-disubstituted alkenes over mono-substituted alkenes, consistent with rate acceleration by nascent radical stabilization and in contrast to relative rates governed by metal coordination.52 It is not clear whether the relative rates reflect the MHAT step itself or include collapse to an intermediate meta-stable organocobalt complex that then must homolyze.
Interpretation of electronic effects on MHAT rate can also be complicated by steric bulk about the WF ligands. For example, hydrogenation catalyzed by manganese bearing the larger dpm (dipivaloylmethane) ligand occurred more rapidly with mono-substituted alkenes than bulkier 1,1-disubstituted alkenes. In line with this observation, sterically-encumbered Co(salen) catalysts clearly distinguish between alkene substitution patterns, independent of any Co–C bond, reacting quickly with 1,1-disubstituted alkenes but sluggishly with trisubstituted alkenes, even though MHAT to both substrates would lead to an identical tertiary radical.17
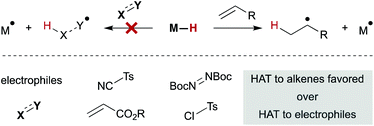
An interesting trend that appears in the WF systems is a preference for electron neutral and rich alkenes over electron withdrawn alkenes (see Fig. 4). Iron diketonates, for example, react preferentially with electron rich alkenes over electrophilic alkenes like enones and enoates.53 These relative rates differ from SF catalysts, which react more quickly with electron-deficient alkenes; for example, (η5-C5H5)Cr(CO)3H undergoes MHAT to acrylates roughly 5000 times faster than to unactivated 1,1-disubstituted alkenes.54 Anecdotal reports show WF Mn(dpm)3 pre-catalysts can cause preferential reaction of electron-deficient alkenes over electron-rich,55 but a systematic rate comparison showed the opposite preference and that trends are muted among alkenes of various substitution patterns. The preference for WF metal hydrides to react with electron-rich alkenes over electron-deficient alkenes is consistent with their general tolerance of electrophiles like diazodicarboxylates, chlorosulfonates and azides (Scheme 6), which instead react with the carbon radical generated by MHAT. This remarkable chemoselectivity has led to the widespread application of WF systems.42
By using the systematic kinetic characterization of SF systems as a guide, future interrogations of WF systems should establish general rate trends and allow correlation to steric environment, M–H BDE and pKa. This knowledge will illuminate MHAT preparative methods, many of which are still poorly understood.
4. MHAT catalysis proceeds through a solvent-caged radical pair
4.1 Radical pairs are surrounded by a solvent cage
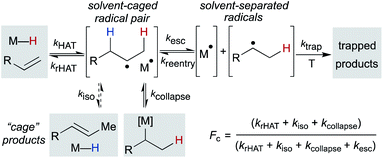
After formation of the metal hydride, the next step in the MHAT cycle (Scheme 2 above) involves collision between this metal hydride and an alkene, whereby a hydrogen atom is transferred to generate a carbon-centered radical and metal complex that is formally reduced by one electron. The resulting metal species is frequently described as a metal-centered radical or “metalloradical” which we use in accordance with the literature.19 It is also a convenient term that conceptually captures the ensuing reactivity from its solvent-caged pairing with the carbon radical, and their behavior together as a “radical pair.” In contrast with SF systems where the metalloradical typically has 17 valence electrons, in WF systems both the metal hydride and the metalloradical are likely to have unpaired electrons, and there is no requirement for this metalloradical to have an odd number of electrons.If these WF reactions indeed proceed via the same MHAT mechanism exhibited by SF complexes, then simultaneous formation of a metallo/organic radical pair will be surrounded by a “cage” of solvent molecules (see Scheme 1 above). The original conception of the “solvent-caged radical pair” mechanism was introduced by Franck and Rabinowitsch in 1934,56 and explains CIDNP effects, rate–viscosity correlations, isotope scrambling, stereochemistry of radical reactions and effects on quantum yields.57 In MHAT reactions, cage collapse – also called primary geminate recombination – includes β-hydrogen atom back transfer to reform starting materials or isomerization products, as well as collapse to an organometallic intermediate.58,59 Cage escape pathways include interception of a second metal-hydride equivalent to yield hydrogenation products or trapping with a suitable “radicalophile” yielding hydrofunctionalized products (see Scheme 2 above).
Described in purely kinetic terms, cage effects refer to the proportion of radical pairs that react from within this solvent cage to the sum of all radical pathways that result from diffusion into solvent (Scheme 7).60 Early models sought to understand the cage effect by modeling the Brownian motion of spherical particles surrounded by a solvent of uniform density.61–63 The solvent-caged radical pair was treated as a “hole” in the solvent; escape from this pocket was determined by the density of the surrounding molecules. Thus, an intuitive connection between bulk solvent viscosity was related to the magnitude of the cage effect for a given radical pair. Subsequent work on both organic radical pairs and SF metalloradical pairs showed a more complicated relationship in which non-uniform solvents, molecular rotation, and spin alignment led to deviations in cage effects that could not be explained by bulk solvent viscosity alone.62,64,65 Furthermore, it became increasingly clear that organic radical pairs and metallo/organic radical pairs required different considerations due to the method of radical pair formation, the large size of the metalloradicals formed, metal-solvent coordination and spin relaxation.
4.2 Early evidence for cage effects in MHAT reactions
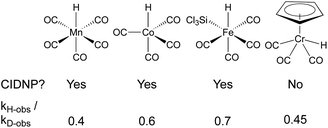
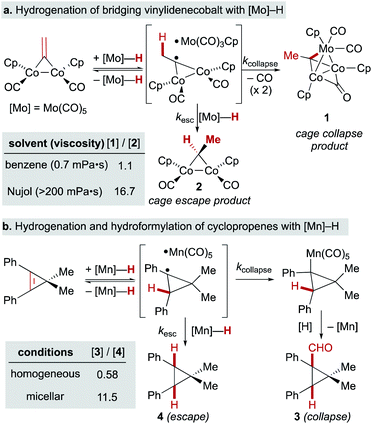
In a seminal report from Sweany and Halpern, observation of chemically induced dynamic nuclear polarization (CIDNP) in the hydrogenation of α-methylstyrene showed the reversible formation of a reactive radical-pair intermediate.66,67 They also observed an inverse kinetic isotope effect (kH/kD = 0.4), which could conceivably come from a single-step reaction with a very late transition state,68 but is easiest to rationalize through reversible formation of a cage pair. As the C–H(D) bond formed in the radical pair has a higher frequency than the M–H(D) bond of the starting metal hydride/deuteride, the equilibrium constant for this preequilibrium is higher for the metal deuteride, leading to a higher concentration of the deuterated radical pair and faster formation of deuterated products. Subsequent studies using SF hydridocarbonylmetal complexes of cobalt, iron and manganese in the hydrogenation of conjugated alkenes, similarly observed inverse KIE and CIDNP effects (Fig. 5).69–73 It is important to note that the lack of observed CIDNP or inverse KIE could occur with a radical-pair mechanism if it has an irreversible metal-hydride hydrogen atom transfer step. In contrast, WF systems like those catalyzed by β-diketonate iron and cobalt complexes typically display normal KIE values.27,28 However, Mn(dpm)3-catalyzed MHAT reactions have exhibited weak inverse KIE in overall reaction rates, as well as inverse KIE by competition between PhSiH3 and PhSiD3.26 Interpretation is frustrated by the influence of isotope effects in the preceding M–H formation step, and the difficulty of detecting unstable WF M–H species in situ.A few early examples of putative MHAT reactions sought to inform mechanistic considerations of a caged radical-pair by exploring the effect of solvent density. In work by Jacobsen and Bergman, the “cage effect” in the hydrogenation of a dicobalt bridging vinylidene complex with a molybdenum hydride could be measured by relative yields of cage collapse to organometallic clusters or cage escape to hydrogenated products. Even in nonpolar solvents such as benzene, the relative ratios of cage collapse and escape products were high relative to those implicated in the cage effects of typical organic radical pairs (vide infra). When a viscous solvent (Nujol) was used, the cage collapse product was formed almost exclusively (Scheme 8, top).74 Two other studies to evaluate cage effects in the manganese- and cobalt-hydride mediated hydrogenation of conjugated alkenes made similar observations. Cage collapse and escape products were measured via formation of hydroformylated and hydrogenated products, respectively. In both studies, significantly higher ratios of hydroformylated products to hydrogenated products were found in highly viscous solvents (Nujol and octane)75 or under micellar conditions with sodium undecanoate and sodium lauryl sulfate (Scheme 8, bottom).76 These studies used methods established for organic radical-pairs and applied them to the study of metallo/organic radical pairs.
4.3 Quantification of cage effects with fractional cage efficiency (Fc)
Pioneering work by Koenig, Finke and Tyler established that “cage effects” for metallo/organic radical pairs required distinctive mechanistic considerations from their organic radical counterparts.57,77,78 Similar to cage efficiencies described for organic radical pairs, fractional cage efficiency, Fc, was defined as the ratio of rate constants for cage collapse (kcollapse) to the sum of all pathways from the solvent cage (kcollapse and kdiffusion) (eqn (1)); a higher Fc indicated a “stronger” cage effect.59 In the presence of a suitable trapping reagent, even at modest concentrations (0.1 M), the observed rate of trapped product formation (kobs) would be decreased by Fc, as not all radical cage pairs formed (k1) would proceed toward product due to competition with cage collapse pathways (eqn (2)), noting that Fc for most metal–ligand homolytic bond dissociations had a value ranging from 0.1 < Fc < 0.9.78 Of particular note are the incredibly high Fc values measured for many organocobalt complexes; in the case of adocobinamide (coenzyme B12) in ethylene glycol, the Fc was measured to be greater than 0.94.58| Fc = kcollapse/(kcollapse + kdiffusion) | (1) |
| kobs = [1 − Fc] × k1 | (2) |
4.4 Comparing organic and metallo/organic radical cage pairs
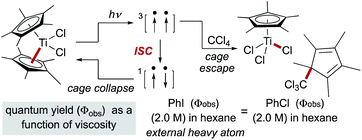
Early studies noted that radical pairs formed by MHAT exhibited a more pronounced “cage effect” than organic radical pairs.74 The latter are typically formed from perester, azo, hyponitrite or peroxo precursors, in which spin state (triplet versus singlet) and intervening gas molecules substantially increase the likelihood of diffusion into solvent versus primary geminate cage collapse.63 In contrast, radical pairs formed via MHAT arise from a ground-state bimolecular reaction of an alkene and a reactive metal hydride with no intervening gas molecules.In reactions in which organic radical pairs are formed, triplet or singlet states of the radical pair can significantly alter Fc, biasing subsequent cage escape versus cage collapse pathways. The presence of a heavy atom – either “internally” within the reactant molecule or “externally” as a solute – has been shown to have a pronounced effect on the intersystem crossover rate between radical singlet and triplet spin states, affecting the subsequent kinetic pathways (recombination or diffusion, respectively) of the radical pair independent of solvent viscosity.79 In metallo/organic radical pairs with strong field ligands, it has been demonstrated that the metalloradical serves as the heavy atom; no change in fractional cage efficiency was measured for the homolysis of  in a 2.0 M solution of iodobenzene (a heavy atom additive) versus a 2.0 M solution of chlorobenzene in solvent mixtures of identical viscosities (Scheme 9). This result was consistent with previous suggestions that metallo/organic radical pairs experience no significant spin barrier for radical recombination, even for comparatively “lighter” first-row transition metals.80
in a 2.0 M solution of iodobenzene (a heavy atom additive) versus a 2.0 M solution of chlorobenzene in solvent mixtures of identical viscosities (Scheme 9). This result was consistent with previous suggestions that metallo/organic radical pairs experience no significant spin barrier for radical recombination, even for comparatively “lighter” first-row transition metals.80
The issue of spin crossover (intersystem crossing) rates in organometallic chemistry has been studied in detail in a number of reactions that are unrelated to MHAT, but which have elucidated principles that apply as well to geminate cage recombination.81,82 In the language of transition state theory, crossing between potential-energy surfaces for two spin states occurs at minimum-energy crossing points (MECPs), which represent geometries at which the difference in energy between the spin states is minimized. At these geometries, the magnitude of the spin–orbit coupling determines the mixing between the two states, and the rate at which the molecule can jump from one potential energy surface to the other. The spin–orbit coupling in turn is dependent on the particular geometry and ligand-field parameters and is challenging to calculate. However, in general the crossing is easier in WF systems with low-lying excited states than in SF systems. Thus, the lifetime of the cage pair could have a dependence on the particular properties of the metalloradical, and computational studies in this area are imperative.
For a pair of organic radicals, the difference in enthalpy between a solvent-caged radical pair and the solvent-separated radicals is considered to be small and positive, so long as no radical–solvent complex is formed. However, for a metalloradical, differences in solvation energy are altered if Lewis basic additives or solvent molecules coordinate—and potentially stabilize—the metalloradical. For metalloradicals with strong field ligands, stabilizing interactions between the SOMO of the 17-electron metalloradical and the Lewis base lone pair have been suggested to form an energetically-stabilizing 2-center, 3-electron bond, sometimes referred to as a “19-electron” species.77,78,83 Although transiently formed “19-electron” reactive intermediates are speculative in MHAT catalyst systems, the identification of a “19-electron” dimethylglyoximato cobalt complex (Co(dmg)2(pyr)2) complex may be relevant, since the corresponding metal-hydride (or its ligand bound equivalent) undergoes MHAT to electronically-activated alkenes.84 Less is known about stabilizing interactions between WF MHAT “metalloradicals” and solvent, although calculations on Fe2+(acac)2 showed that binding of two molecules of ethanol had a net ΔG° = −0.6 kcal mol−1.85
4.5 Understanding factors that govern cage effects
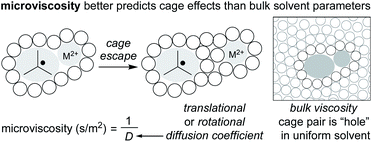
Given the potential for complexation between metalloradicals and solvent, an important question is raised about the entropic contribution to the “cage effect.” In general, it is assumed that radical cage escape results in an increase in entropy. This increase in entropy raises a contrast to contact ion pairs, for which solvent organization around charged ions results in an overall decrease in entropy. For this reason, the size of dissociated ions plays an important role in chemical solvation, as larger ions experience weaker interactions with the solvent, whereas small ions experience an energetic penalty (sodium ion versus tetrabutylammonium ion).86 If dissolution of the radical pair has positive entropy (as suggested), the “cage effect” would arise wholly from enthalpic factors.57Fortunately, the interest in understanding the cage effect on metal–ligand bond dissociation energies has created a better understanding of the thermodynamic forces creating the cage effect. In particular, earlier inconsistencies between correlating bulk solvent viscosity and cage effects have been remedied by considering “microviscosity” (Fig. 6). Whereas bulk viscosity is a measure of solvent fluidity, solvent microviscosity aims to quantify the local viscosity around the radical pair by examining rotational or translational diffusion coefficients, typically with NMR. In two studies by Tyler, the cage effect was found to be highly correlated to solvent microviscosities (measured by DOSY NMR of a probe molecule) and not bulk viscosities, in mixtures of both protic and aprotic solvents.87,88 Applying an understanding and quantification of microviscosities to MHAT cage effects may enable synthetic chemists to tune the “strength” of the solvent cage through careful selection of solvent and/or solvent mixtures.
Early examinations of MHAT using strong-field ligands provided a clear conceptual understanding of the radical cage pair because the in-cage reactions—reversion to the starting materials, collapse to the organometallic species—competed with diffusion out of the solvent cage, substantiated through observation of CIDNP and inverse KIE. As many contemporary methods utilize weak-field ligands, quantification of cage effects is more difficult because of the irreversibility of the first hydrogen atom transfer, inability to study proposed reaction intermediates outside of computation, and challenge in understanding reaction kinetics. However, building an understanding of cage effects for these weak-field ligands will be essential in order to bias reaction products and/or impart asymmetry in the products through “catalyst control.” In the following sections, we examine the pathways from the solvent-caged radical pair.
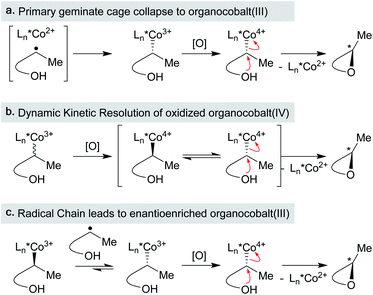
5. Possible roles of metal alkyls in MHAT with WF catalysts
One pathway from the MHAT-derived radical cage pair is collapse within the solvent cage to form an organometallic species (see Scheme 2 above). In the hydrogenation of conjugated alkenes the formation of hydroformylated side products was frequently proposed to proceed through the organometallic “cage collapse” product.75,76 A large body of literature (emanating from the study of vitamin B12) describes the thermodynamics and kinetics of Co3+–C bond homolysis, particularly with (salen)Co-alkyl complexes (Fig. 7A).89 Because of this supporting literature, alkyl–cobalt complexes have been hypothesized frequently as intermediates, beginning with seminal mechanistic work by Nishinaga on the Drago hydration.90 Only recently, however, was a MHAT-relevant sec-alkyl cobalt salen complex characterized by 1H NMR and implicated in a turnover-limiting transmetalation step to a nickel cocatalyst.18 The intermediacy of a sec-alkyl cobalt(III) salen species was required to explain catalyst control over MHAT epoxide formation versus pinacol rearrangement, and guided the proposal of an alkylcobalt(IV) species in reactions previously proposed to involve carbocations.91,92 However, not all organocobalt species formed through MHAT necessarily lie on the catalytic cycle; in certain cases, they may act as reservoirs of alkyl radicals. For example, one cobalt catalyst was sequestered as an alkylcobalt in an MHAT alkene isomerization and only re-entered the catalytic cycle through Co–C bond homolysis (via thermolysis).17 Despite weak bond strengths ranging from 19 kcal mol−1 to 40 kcal mol−1, the rate of decomposition through homolysis of a Co–C bond at room temperature can be slow (hours to days), depending on substitution patterns.89 Organocobalt intermediates may also release alkyl radicals through radical chain propagation whereby carbon-centered, heteroatom-centered radicals, solvent, or O2 promote Co–C homolysis.93 These intermediate radical chain processes may operate in concert with a catalytic cycle in many MHAT hydrofunctionalization variants (see Scheme 2 above) and were implicated via variable concentration radical clock experiments in a cobalt-catalyzed MHAT hydroarylation.18 In general, the kinetic stability of primary and secondary salen-supported alkylcobalt(III) complexes may differentiate cobalt MHAT catalysis from iron and manganese, insofar as organometallic intermediates may need to be considered.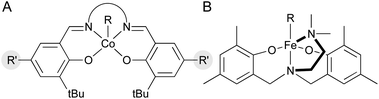 | ||
| Fig. 7 (A) General structure of (salen)Co alkyls. (B) Proposed structure of an iron(III) alkyl complex with an amine-bis(phenolate) supporting ligand. | ||
Other WF systems have yielded little direct evidence for metal–carbon bond formation. This may be because the metal–carbon bonds in WF systems are particularly weak and reactive. For example, despite the abundance of alkyl complexes in low-valent SF Mn organometallic chemistry, relatively few structurally characterized manganese(III) alkyl complexes have been reported.94 The difficulty in preparing WF Mn3+ alkyl complexes has been attributed to rapid disproportionation to more stable Mn2+ and Mn4+ species.94 Likewise, with WF iron systems, the simple iron(III) alkyl complex [Fe(CH3)4−] is thermally unstable.95 The stability may be even lower in catalytic WF iron systems; a recent computational study on Fe-catalyzed alkene MHAT reactions suggested that the homolytic bond energy of the iron(III) complex (acac)2Fe–tBu is only 1.5 kcal mol−1.27 In contrast, amine-bis(phenolate) iron complexes, which can catalyze MHAT hydroamination96,97 and hydrofluorination98 as well as radical polymerization that follows a related mechanism,99 have been studied by EPR, UV-Vis and Mössbauer spectroscopy during polymerization, and these suggested the formation of a transient iron(III) alkyl complex with a high-spin electronic configuration (Fig. 7B).100 In the future, more work is needed on trapping and in situ spectroscopic characterization of metal-alkyl intermediates in WF systems.
6. Reactions from the radical pair
6.1 Competing pathways: hydrogenation, isomerization, and cyclization
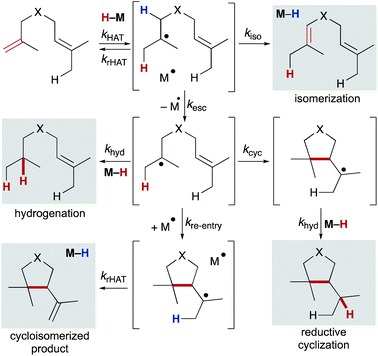
Using any method of radical generation, ensuring cross-selectivity in radical termination is important to establish useful transformations that extend beyond formation of symmetrical dimers. Radical dimerization products are rarely observed in MHAT reactions,101 consistent with early evidence that cage collapse and hydrogenation pathways can proceed at rates close to that of diffusion.102,103 In particular, cobalt salen catalyzed reactions may benefit from the “persistent radical effect.” As the (salen)Co2+ metalloradical does not homodimerize, self-termination of the alkyl radical results in an excess of metalloradical concentration relative to the alkyl radical concentration; any difference in concentration will drive rapid alkyl radical capture and favor the cross-reaction.104Once a substrate escapes the primary geminate solvent-caged pair, several pathways are possible: hydrogenation (via trapping of a second equivalent of M–H or H–bond donor), intramolecular cyclization, reaction with a suitable radicalophile (vide infra), or secondary geminate cage pair formation (which may lead to isomerization via β-hydrogen atom abstraction). Here, we will consider isomerization, hydrogenation, reductive cyclization and cycloisomerization pathways (Scheme 10). The relative distribution of these products is dependent on rates of the competing pathways – for bimolecular reactions such as hydrogenation and secondary geminate recombination, the concentration of the relevant metal species will affect its reaction rate. Cyclization, a unimolecular reaction, is possible if an appropriate internal bond or an abstractable hydrogen bond is available. As shown by radical clock studies of Beckwith and Ingold, cyclization follows Baldwin's rules, and is accelerated via Thorpe–Ingold effects, polar effects, and lowered sterics.54,105 Additionally, α-alkoxy substituents have been shown to increase the nucleophilicities of carbon-centered radicals. By virtue of the polar effect, the enhanced nucleophilicity accelerates the addition of radicals to electron-deficient alkenes and thus increases the rate of radical cyclization. When enol ethers are used to generate α-alkoxy radicals, cyclization onto a pendant styrene takes place.106
Once a substrate has cyclized, the nascent radical can undergo a second hydrogen atom transfer resulting in reductive cyclization. Alternatively, the substrate can re-engage the metalloradical (secondary geminate recombination), which can abstract a hydrogen atom leading to cycloisomerization and reformation of the metal-hydride (analogous to k−1, Scheme 2). Much like the competition between isomerization and hydrogenation, competition between reductive cyclization and cycloisomerization is influenced by the ratio of metalloradical to metal hydride.107 Therefore, the properties and concentration of the metal hydride are important in tuning selectivity of this trapping event.
The selectivity after cyclization can change depending on the choice of metal hydride. In studies of cyclization of α-substituted acrylate esters, use of CpCr(CO)3H maintained a high concentration of metal hydride in solution and resulted primarily in reductive cyclization. On the other hand, use of Co(dmgBF2)2L2, resulted in primarily cycloisomerization, as a large concentration of metalloradical was maintained in solution.107 Additionally, sterics of the acceptor alkenes played a role in controlling the rate of the second MHAT. In particular, substrates with tertiary C–H bonds underwent reductive cyclization, presumably because steric hindrance obstructed metalloradical approach.54
Kinetic studies of MHAT reactivity point to the importance of controlling the rate of the second MHAT in biasing product distribution.48,108 Factors such as M–H BDE, alkene BDEs, concentration and structure of the M–H and alkene can control whether back transfer, hydrogenation, or isomerization predominate. Similarly, factors that influence the rate of secondary MHAT – BDEs, M–H concentration, polar effects, and sterics – affect the competition between hydrogenation, reductive cyclization, cycloisomerization, or trapping with a radicalophile. By understanding the factors that control the distribution of these products, future studies may allow exertion of greater control over reactivity patterns and uncover novel reactivity.
Independently, we disclosed in 2014 a method similar to Norton's that utilized putative (salen)Co3+–H to effect the cycloisomerization of unbiased alkenes onto pendant alkenes or arene rings (Scheme 11).17 Substrates could undergo either single-bond isomerization or cycloisomerization, and the ratio of products was measured as a function of electronics on the salen ligand. Notably, increasing electron density on the salen ligand led to increased ratios of cycloisomerized to isomerized products. Several effects could account for the increase in persistence of the carbon radical: a more electron-rich catalyst could decrease the rate of β-hydrogen atom transfer to the catalyst, radical cage escape could be favored due to electrostatic repulsion, cage reentry could be disfavored due to polar effects or catalyst aggregation could reduce the concentration of Co2+ available for β-hydrogen atom transfer.
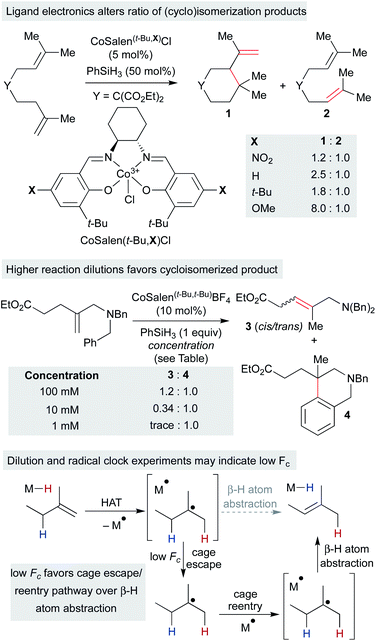 | ||
| Scheme 11 Radical isomerization of electron-neutral alkenes by MHAT: mechanistic information from radical clock competition experiments. | ||
Subsequent work called into question our initial consideration that the isomerization product arose only from the initial primary geminate radical pair. We observed that the ratio of isomerization to cycloisomerization depended on overall reaction concentration, rather than ligand electronics alone. Increasing dilution with no changes to the catalyst structure favored cycloisomerization.33 If isomerization took place exclusively from the primary geminate radical pair, then the ratio of isomerization to cycloisomerization would be expected to remain constant as both rates would depend only on the concentration of the primary geminate radical pair. To explain this result, isomerization and cycloisomerization products must be formed upon cage escape and re-entry. As the dilution increases, the radical has more time to cyclize before it is intercepted by a second cobalt(II) metalloradical. As isomerization observed in this experiment is predominantly due to secondary geminate recombination, it appears that Fc is low in this system when compared to the strong-field MHAT systems discussed earlier.106 This observation is in line with the decomposition of an analogous isopropyl organocobalt complex ([salophenCo(pyr)(iPr)]), in which cage escape/hydrogenation was the predominant pathway and isomerization was a minor product (relative khydrog/kiso ∼ 30), even though both products proceeded through the same solvent-caged radical pair upon Co–C homolysis.59
More recently, an exploration of cobalt-catalyzed polyene cyclization identified effects of the catalyst structure on the diastereomeric ratios of cyclization products with trans or cis ring junctions depending on the salen ligand backbone. This effect was attributed to the likely formation of secondary organocobalt(III) complexes,109 effectively increasing Fc by introducing a kinetically competitive cage collapse pathway. Substrate arene deuteration did not result in product alkane deuteration, which one would expect from M–D formation and engagement of another alkene. This result indicated that arene rearomatization did not occur via M˙ back-HAT to reform the M–H or M–D, and that termination of cycloisomerization onto arene rings likely proceeded via an oxidation/deprotonation pathway.
6.2 Alkyl radical trapping and turnover
MHAT chemistry generates a diverse set of alkene hydrofunctionalization products, which include the formation of C–C, –N, –O, –S, and –X (halogen) bonds. These product outputs arise from interception of the radical with traps. These are complex reaction networks; all inputs and additives must be compatible with intermediates within the MHAT catalytic system, including the reactive metal hydride (see Scheme 2). Remarkably, many radicalophiles from classical radical chemistry – persistent radicals (i.e. TEMPO), hydrogen or halogen transfer reagents, diazodicarboxylates, sulfonyl azides and cyanides, electron-deficient alkenes and electron-deficient heterocycles – have all been utilized productively in MHAT chemistry.5 The intermediate resulting from alkyl radical addition to the radicalophile trap is an open shell intermediate and must undergo either a redox or atom transfer step to form the closed-shell product (Scheme 12). An outstanding question in many MHAT methods is whether formation of the closed-shell product is also involved in (and necessary for) catalyst turnover.In contrast to classic radical chemistry, MHAT reactions undergo turnover through catalytic cycles and not radical chains (although radical chains may be present – for example, in radical transformations mediated by tin hydrides, open-shell addition products abstract a hydrogen atom from tin hydride, generating a tin radical which may subsequently generate alkyl radicals via atom abstraction).110 In radical chain reactions, the rates of propagation steps must be sufficiently fast to compete with radical dimerization and chain termination pathways. MHAT hydrofunctionalizations, in contrast, turn over the reduced M2+ by reaction with excess oxidant (oxygen, TBHP, fluorocollidinium, etc.) or by interception of open-shell addition intermediates. The M3+ must then intercept a hydride equivalent to reform the M–H active species.
As MHAT methods have expanded, understanding the turnover step – particularly under anaerobic conditions – has become more complicated. In the context of hydrohydrazination, Carreira insightfully proposed that Co2+ (and by analogy Mn2+) catalytic intermediates were oxidized in situ by the nitrogen-centered radical products resulting from alkyl radical addition, fulfilling the same role as molecular oxygen in the original Drago-Mukaiyama hydration (Scheme 13a).28 This radical reduction/M2+ oxidation mechanism likely permeates many variations of these catalytic cycles, given the number of radical traps that can engage alkyl radicals and become single-electron oxidants themselves. In contrast, in the MHAT Giese reaction, a different step was proposed. After MHAT and attack of the alkyl radical on the acceptor alkene, the α-ester radical could react with an iron(II)–alcohol complex through concerted proton-coupled electron transfer to give the observed product (Scheme 13b).27 The byproduct is an iron(III) alkoxide that could then continue the catalytic cycle as described above. The barrier height for concerted PCET was computed to be similar to a stepwise mechanism involving the protonation of an iron-bound enolate. The generality of this reoxidation step through PCET pathways is unknown and may depend on the presence or absence of alcohol and the specific metal complex.
Understanding catalyst turnover also enabled the hydrogenation of unbiased alkenes via MHAT, in which conditions did not include a radicalophile but required two equivalents of metal hydride for every equivalent of alkene. Overall, stoichiometric oxidant (TBHP) was necessary to turn over the catalytic cycle. Exact mechanistic details when using TBHP—a 2-electron oxidant—to effect a formal single electron oxidation have not been rigorously studied but may involve the formation of M3+–OH, M3+–OtBu, M3+–OOtBu or even M4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (which would undergo comproportionation with M2+).111,112
O (which would undergo comproportionation with M2+).111,112
6.3 Mechanisms with metal-mediated radical trapping
Addition of the nascent carbon radical to the radicalophile partner could use well-established radical addition pathways, but some reaction partners are resistant to radical capture directly and so additional mechanistic pathways may be considered. Below we consider examples in which a metal complex mediates more than just the MHAT step and, instead, may govern subsequent reactions of the alkyl radical. Three general pathways of bond formation are considered: (1) direct reaction of the alkyl radical with a trap (Scheme 12 above); (2) oxidative ligand transfer (OLT) whereby the alkyl radical abstracts a ligand from a metal-trap coordinated complex via radical addition and abstraction (Scheme 14 left); or (3) cage collapse to an organometallic complex which is oxidized prior to reaction with the nucleophile (Scheme 14 right). This last pathway (3) can be described as a radical-polar crossover (RPC), since the alkyl intermediate displays reactivity reminiscent of a carbocation. Both OLT and RPC can represent a polarity reversal since a nucleophilic alkyl radical exhibits electrophilic behavior, as described below. Each of these three pathways may predominate depending on minor changes to substrates, reagents, or catalyst.The consideration of metal coordination and an OLT or RPC pathway stems from examples where a reaction partner is unlikely to react with an alkyl radical directly. The most apparent examples include MHAT-catalyzed hydroazidations and hydrofluorinations, which may involve activation of the stoichiometric radical trap by the metal catalyst.113–115 Whereas classical radical azidations can occur by addition to sulfonyl azide followed by extrusion of sulfonyl radical (Scheme 12, above),116 anionic azide may require prior activation as it is unlikely to react directly with alkyl radicals.117 MHAT alkene hydroazidation using superstoichiometric iron oxalate and sodium azide may, therefore, involve formation of an iron(III)–azide complex which can directly intercept alkyl radicals, rather than radicals reacting with sodium azide itself.114 This mechanistic possibility mimics reactivity observed for iron azide complexes that transfer azide to carbon radicals (generated by means other than MHAT).118–120
The fluorine sources used in MHAT hydrofluorinations are well-studied in polar chemistry but less so in radical chemistry, confounding our understanding of radical MHAT hydrofluorination chemistry. N-Fluorobenzenesulfonimide (NFSI) and Selectfluor were shown to directly intercept alkyl radicals generated by perester thermolysis and photolysis, but N-fluoropyridinium salts could not.121 Instead, these fluorine sources are known to form metal fluoride species via oxidation or ligand exchange; metal fluorides formed in situ may act as radical fluorination reagents, and not the stoichiometric fluorine salts themselves. Literature precedent for OLT radical fluorination stems from a manganese tetramesitylporphyrin-catalyzed radical reaction, in which the manganese(IV) complex Mn(TMP)F2 is formed in situ from fluoride salts and can transfer a fluorine atom to alkyl radicals to form a C–F bond and a manganese(III) species.122,123 Similarly, silver-mediated alkyl radical fluorination with Selectfluor is proposed to occur via a silver fluoride radical trap.122 Within the MHAT literature, radical hydrofluorination using an iron hydride catalyst (from Fe2(ox)3 and NaBH4) with Selectfluor and NFSI as compatible fluorinating reagents has been reported.115 Interestingly, within this same catalytic system, switching to an in situ-generated cobalt hydride catalyst (from Co(acac)3 and phenylsilane) and Selectfluor did not lead to fluorinated product. These results suggest that the iron catalyst plays additional roles beyond alkyl radical generation and that formation of an iron–fluoride complex may participate in radical trapping. In additional, N-fluoropyridinium salts have also been used for radical MHAT fluorination in conjunction with cobalt salen catalysts.113 Given that N-fluoropyridinium salts may be resistant to direct radical capture (vide supra), OLT or RPC pathways are reasonable alternatives.
Recent studies on the (salen)Co-catalyzed hydrofunctionalization of alkenes with hypervalent iodine(III) carboxylates is consistent with an OLT or an RPC pathway that leads to product (Scheme 15).124 Selectivity for hydrofunctionalization over isomerization was found to be sensitive to both concentration and enantioenrichment of the catalyst, implying that hydrofunctionalization involves the interaction of multiple cobalt species. Further kinetic analysis showed that formation of isomerization byproducts had a first order dependence on [Co], whereas formation of hydrofunctionalized products had a second order dependence on [Co], suggesting that the turnover limiting step is a reaction between two distinct cobalt species – an organocobalt complex and a cobalt-bound nucleophile. Two pathways could be operative which proceed through an oxidized cobalt species: the cobalt-bound nucleophile complex may oxidize the organocobalt(III) species to a reactive organocobalt(IV) species, initiating alkyl ligand transfer by either OLT or RPC pathways. If OLT operates, homolysis of the organocobalt(IV) species would be followed by radical attack on a second cobalt-bound nucleophile. If RPC occurs, the organocobalt(IV) species can undergo displacement by the former carboxylate ligand of the hypervalent iodine atom to form the hydrofunctionalized product. These mechanisms of C–O bond formation via OLT and RPC from meta-stable organocobalt species differ from proposals in the literature that alkyl radicals formed via MHAT are directly oxidized to unstable carbocations. Such a mechanistic conundrum is not unprecedented. For example, C–O bond formation in manganese(III) acetate-mediated oxidative lactonization of alkenes had been proposed to involve carbocation formation, but the absence of rearranged products from a norbornene substrate, which is considered diagnostic of a carbocation intermediate, conflicted with this hypothesis.125 Instead, cyclization of the intermediate radical to forge the C–O bond in the γ-lactone was suggested to proceed through OLT without formation of a carbocation.
In the context of MHAT catalysis, the hypothesis of C-radical oxidation to a carbocation competes with the hypothesis of organometallic oxidation. Metastable organocobalt(III) species bearing porphyrin or salen ligands undergo reduction and oxidation to form unstable organocobalt(II) and organocobalt(IV) species, respectively, which can undergo carbon–cobalt bond cleavage more readily.126 In particular, organocobalt(IV) complexes may undergo homolysis or heterolysis, depending on the identity of the ligand and/or surrounding nucleophiles.127 Nucleophilic attack on the organocobalt(IV) species at the carbon center may form the new carbon–heteroatom bond and regenerate the cobalt(II) precatalyst.126 Several (salen)Co MHAT methods that form carbon–heteroatom bonds with nucleophilic coupling partners have revised the original carbon-centered radical oxidation model and now invoke these organocobalt(IV) species.18,31 An organocobalt(IV) species could heterolyze to form a transient carbocation, or homolyze the Co–C bond to release a carbon radical that undergoes OLT from another cobalt complex, for example fluorine from a Co–F complex. The overall transformation resembles an RPC, but the organocobalt species is oxidized instead of the carbon-centered radical. Considering organocobalt oxidation as opposed to direct oxidation of the carbon radical has interesting mechanistic implications, but also important preparative value. Organocobalt complexes have a much lower oxidation potential than alkyl radicals, therefore permitting the use of a wider set of chemical oxidants with a range of redox potentials.127 Furthermore, organocobalt(IV) species are considerably stabilized relative to electron-neutral alkyl carbocations and substitution or rearrangement pathways can be biased by changes to the ligand, relatively independent from substrate structure.91 In all, our knowledge of organocobalt reactivity can support the accelerating development of new methods, especially asymmetry, at the edge of mechanistic understanding (see Section 7).
Finally, combining MHAT catalysis in heterobimetallic catalytic cycles offers additional ways to engage non-radical coupling partners (Scheme 16). How the two catalytic cycles intersect may be determined by the fractional cage efficiency (Fc) of each MHAT reaction. In a cobalt-/nickel-dual catalytic terminal alkene-iodoarene coupling, we hypothesized that a metastable alkylcobalt(III) intermediate could undergo turnover limiting transmetalation to nickel via a cage-rebound type mechanism.18 The generality of this catalytic metalation/trans-metalation was shown in subsequent work that replaced the nickel complex with a chromium salt, effectively converting the weakly nucleophilic organocobalt complex to a strongly nucleophilic organochromium complex.128,129
Collapse to the meta-stable organocobalt reflected the instability of secondary radicals and the increased capacity to form a C–Co bond (k2) rather than escape the solvent cage (k3). Replacing the (salen)Co catalyst with an iron130 or a manganese47 hydride catalyst was part of a strategy to circumvent collapse/transmetalation and instead capture solvent-separated radicals with nickel co-catalysts. Cobalt catalysts did not readily form organometallics from tertiary radicals; instead isomerization (k−1*, differentiated from return to starting material, k−1) predominated. Iron and manganese catalysts were proposed to favor cage escape (k3) and capture intermediates in a nickel catalytic cycle. These heterobimetallic catalytic methods forged all-carbon quaternary carbon centers with aryl and alkyl electrophiles and expanded the range of MHAT catalysis outside classic radicalophiles to include traditional cross-coupling partners.
7. Asymmetric MHAT reactions
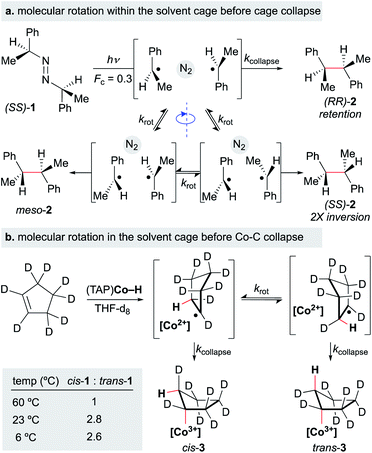
In Section 4, we discussed evidence for the MHAT radical-pair mechanism from reaction kinetics, isotope studies, CIDNP, and solvent-viscosity correlations. Another approach toward understanding radical-pair mechanisms evaluates the stereochemical retention from putative radical-pair intermediates. Organic rearrangements that proceed via radical pair formation, such as the 1,2-Wittig rearrangement, can still exhibit high levels of stereospecificity, reinforcing the notion that radical formation and recombination within the solvent cage can occur faster than racemization through solvent-cage escape and recapture.131Still, the retention of asymmetry as evidence for the cage effect may underestimate radical cage effects, since rotational motion within the solvent cage can lead to racemization before solvent cage escape (Scheme 17). For example, when the photolysis of azobis-α-phenylethane was carried out in the presence of scavengers (2-ethyl-2-nitrosopropane and thiophenol, 1.15 M), the “cage products” were comprised of three different dimers: non-meso RR and SS-dimers and meso dimers (Fc = 0.3) (Scheme 17a). Only the RR-dimer product can arise from immediate collapse of the radical-pair within the solvent cage, while the SS-dimer and meso product can only be observed after a 180° out-of-plane rotation of at least one of the partners of the radical pair. The ratios of products found within this study led to the conclusion that the relative rates of recombination, diffusion and rotation were 1.0, 2.4 and 15, respectively.132
A similar conclusion was made in the formation of an alkylcobalt(III) complex via MHAT (Scheme 17b). Several foundational studies on MHAT, particularly utilizing cobalt hydride complexes, have established that the formal addition of a hydrogen atom across an alkene proceeds stereospecifically to form the syn addition product (often observed as cage collapse to the organocobalt).133,134 When cyclopentene-d8 was treated with (tetraanisylporphyrinato)cobalt(III)hydride ((TAP)Co–H), two diastereomers – the cis and trans organocobalt addition products – were formed, in which formation of trans product implied that a secondary process after radical-pair formation was occurring. At higher temperatures (60 °C), the cis/trans ratio was equal to 1.0, while at lower temperatures (6–23 °C), the cis/trans ratio increased to a relatively constant value of 2.8. To test whether cis/trans isomerization was due to reformation of starting materials and addition after rotation or cage escape, the authors ran the experiment for different periods of time at 23 °C; extrapolation to zero time showed that the “baseline” ratio was only moderately selective for the cis-addition product (cis/trans = 3.5). Furthermore, no other products other than the cis and trans products were observed, which would be expected if isomerization were the main pathway for interconversion (via (TAP)Co–D deuterium scrambling). The authors attribute this moderate selectivity to molecular rotation of the alkyl radical within the solvent cage before cage collapse to form the organocobalt.135 Other studies have suggested that radical-pair collapse for organocobalt species is faster than molecular rotation; organocobalt formation could be highly dependent on the identity of the cobalt complex.133,134
In related experiments, the racemization of organometallic complexes through carbon–metal bond homolysis was evaluated in two systems. Measuring the optical rotation of enantioenriched (alkyl)bis(dimethylglyoximato)cobalt(III) at a constant temperature over time led to a first-order rate of racemization of the organocobalt.136 The identity of the axial pyridine base had a small effect on the racemization rate, while the presence of an electron-withdrawing group on the α-carbon led to slower racemization, likely by increasing the bond dissociation energy of the organocobalt complex. Another study monitored the racemization of an acyl-rhodium(III) alkyl complex over time, establishing a first order rate of racemization (krac = 6.4 × 10−6).137 Both examples describe positive enthalpies and entropies of racemization, as well as low barriers to recombination of the metallo/organic radical pairs formed upon homolysis (∼2 kcal mol−1). The aforementioned studies suggest that collapse of the primary geminate radical pair may result in limited enantioselectivies due to molecular rotation within the solvent cage. Below, we explore methods of MHAT asymmetric catalysis in which several mechanisms for asymmetric induction are considered.
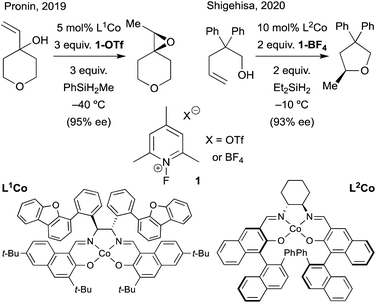
The emerging area of asymmetric MHAT transformations have so far utilized cobalt catalysts with salen-type ligands to explore enantioselective carbon–heteroatom bond formation via RPC pathways (Scheme 18). While chiral salen ligands are commonly employed in asymmetric alkene oxidation reactions, previous modes of enantioinduction are distinct in that facial selectivity is determined by a “side-on” approach of the alkene over the salen ligand.138 For (salen)Co-based MHAT methods, several different hypotheses have been put forward for the enantiodetermining step, but current evidence points to two possibilities: a dynamic kinetic resolution (DKR) of an oxidized organocobalt(IV) complex followed by nucleophile displacement (Scheme 18b), or enantioenrichment of a scalemic organocobalt(III) before oxidation to an organocobalt(IV) (Scheme 18c). In either scenario, an enantiospecific cage collapse pathway (Scheme 18a) was ruled out or considered unlikely.
The first example of asymmetric MHAT comes from the Pronin group, who developed a method to access enantioenriched epoxides (80–95% ee) from dialkyl(vinyl)carbinols using a modified cobalt salen catalyst (Scheme 19, left).91,139 This discovery was based on their prior observation of divergent reactivity in radical-polar crossover (RPC) MHAT transformations leading to semi-pinacol rearrangements and epoxide formation depending on the salen ligand backbone.91 The authors suggest a dynamic kinetic resolution of an organocobalt(IV) intermediate followed by enantiodetermining nucleophilic displacement (Scheme 18b). Support for this hypothesis came from an Eyring analysis of enantioselectivity, which showed that enantioselectivity was enthalpically controlled and that electron-rich and polarizable salen ligands of similar steric bulk exhibited higher levels of asymmetry. A proposed model of enantioinduction described a noncovalent interaction between the ligand-based radical cation on the aromatic rings of the salen stabilized by the aromatic rings of the backbone, leading to a relative stabilization of the intramolecular nucleophilic displacement of the (S)-organocobalt(IV) and formation of the (R)-epoxide product.
Expanding upon a preliminary disclosure of asymmetric tetrahydrofuran formation via RPC,92 the Shigehisa group explored the formation of enantioenriched tetrahydrofurans using alkenyl alcohols with substituted binaphthyl cobalt salen catalysts (Scheme 19, right).140 An interesting kinetic effect was observed with the silane; sterically-hindered silanes or slow addition of silane led to a switch in enantioselectivity, indicative of two enantiodetermining steps in the mechanism. The first step proposed was a radical chain mechanism leading to enantioenrichment of the (R)-organocobalt(III) species, which underwent oxidation to the organocobalt(IV) species and subsequent displacement by the pendant alcohol to form the (S)-enantiomer (63–94% ee) (Scheme 18c). When a bulky silane was used or silane was added slowly, the radical chain was less pronounced and a second enantiodetermining step dominated, leading to the switch in enantioselectivity. This second enantiodetermining step was like that suggested by Pronin, involving a DKR of an organocobalt(IV) complex, favoring displacement from the (S)-organocobalt(IV) intermediate, leading to the (R)-enantiomer in moderate enantioselectivities (33–72% ee). Eyring analysis was consistent with differential enthalpy as a main contributor to enantioselectivity for formation of both (R) and (S)-products. Computational analysis suggested that noncovalent interactions (CH–π) between the aromatic rings of the ligand and the arene groups of the substrate led to stabilization of the favored diasteromeric organocobalt intermediate (Scheme 18c) or the transition state for nucleophilic displacement (Scheme 18b).
The aforementioned examples exert catalyst control in asymmetric induction via formation of scalemic organometallic species and intramolecular displacement of a pendant nucleophile. It should be noted that an intermolecular asymmetric Markovnikov hydroamination of alkenes from electronically unbiased alkenes and donor–acceptor diazo reagents (77–84% ee) could potentially proceed via a MHAT mechanism as well.141 In this case, a newly developed N-imidazolinylphenyl 8-aminoquinoline ligand was used. A detailed exploration of the enantiodetermining step is not included in this report, although the presence of radicals was implicated by cyclopropyl ring opening. Other radical clocks to differentiate polar ring opening from radical ring opening were not included. For transformations involving Mn- or Fe-catalyzed MHAT, the inherent instability of these organometallic complexes may make differentiation between diastereomeric organometallic species untenable for asymmetric transformations (see Section 5). Other approaches towards asymmetric MHAT methods may bias facial selectivity in the initial hydrogen atom transfer step or trap solvent-separated radicals generated in MHAT in dual catalytic cycles or with stereogenic radical traps. Understanding the energetics of the solvent-caged radical pair in MHAT will significantly affect the development of these asymmetric methods.
8. Conclusions
The mechanistic framework provided by well-characterized SF systems has illuminated the murkier mechanisms of high-energy MHAT reactions of WF systems, and has identified gaps in our knowledge. The M–H bond strengths are lower in WF systems, and their unique reactivity derives in part from the thermodynamics of forming and cleaving these bonds, and the attendant effects on the kinetics. However, M–H BDE values are not sufficient to explain differences in selectivity between SF and WF systems: in general, SF systems react preferentially with conjugated, electron-deficient alkenes and WF systems react first with unconjugated, electron-rich alkenes, even when conjugated alkenes are present. The differences in selectivity are reminiscent of normal- versus inverse-demand Diels–Alder cycloadditions. Here, HOMO–LUMO interactions serve as useful tools to conceptualize reactivity, and are reversed when considering partners of opposite electron densities and orbital energy levels. The more complicated interactions of the alkene orbitals with SOMOs in the WF metal-hydride species, however, are not as amenable to easy interpretation. Further insight will require a better understanding of the electronic and geometric structures of WF hydride complexes.We have also highlighted the ubiquity of solvent cage effects, which can have a marked influence on selectivities and rates, yet have rarely been considered in the new WF catalytic systems. Careful characterization of radical lifetimes using different radical clocks with varying reactant concentrations and a range of solvents could help identify idiosyncratic cage effects and radical cage pair lifetimes.
The payoff for improved understanding is substantial in terms of applications. A prior review posited that intersection of MHAT with canonical cross-coupling cycles could expand coupling partners beyond classical radical traps.5 This proposal has now come to fruition: haloarenes, haloalkanes and aldehydes now serve as viable reactants, and more can be imagined based on this established platform. An evaluation of non-canonical radical traps points to dual roles for many MHAT catalysts in both alkyl radical generation and in situ generation of metal-complexed radicalophiles. The expansion of MHAT to include additional reaction partners may rest on the incorporation of these dual roles and our understanding of the various reactive metal complexes that are present in situ.
As described above, MHAT from scalemic catalysts can enable enantioselective transformations outside the reach of coordinating transition metals and traditional chiral Lewis acids. The two breakthrough examples in the literature are intramolecular reactions that establish important principles for absolute stereocontrol, but intermolecular variants may find greater utility. These examples accomplish asymmetric hydrofunctionalizations which cannot be achieved with classical, polar modes of reactivity. One pitfall of current methods is that the ligands used for asymmetry are extremely large and synthetically cumbersome. In the future, it would be beneficial to use smaller or higher turnover number (TON) catalysts to achieve a reduction of Process Mass Intensity (PMI), the ratio of total mass input to product mass output.
Yet another potential application of MHAT is in polymerization methods,142,143 as classical mediators of atom transfer radical polymerization (ATRP) and organometallic-mediated radical polymerization (OMRP) do not typically utilize electron-neutral alkenes. Incorporation of a wider range of alkenes would allow materials scientists to source different feedstocks whose corresponding radicals exhibit unique reactivity preferences.
A limiting factor within current MHAT methodology is the need for compatibility between stoichiometric reductants and oxidants to turn over catalytic cycles. In the future, generation of catalytic WF metal(III) hydrides through stoichiometric or electrocatalytic reduction to a metal(I) species in the presence of proton sources could provide a sustainable method to generate catalytic metal hydrides. Since electrocatalytic H2 production from water uses similar metals as WF MHAT catalysts,144 this large body of research could provide a starting point from which to design new MHAT catalytic systems.
The catalytic formation of alkyl radicals from alkenes via MHAT has established synthetic utility, evident through its widespread adoption in chemical synthesis. It has also raised many mechanistic questions. Given the complex web of reaction pathways that rely on various, coexisting metal species in solution, it is remarkable that these reactions can be orchestrated with high selectivity for desired product formation. Further explorations are needed, beginning with characterization of the catalytic intermediates and study of the rates of the elementary steps. In addition, the various, competing fates of the radical intermediates must be determined to better adapt them to our needs in synthesis. In our view, MHAT represents a revolutionary method to generate high-energy carbon-centered radicals, and its transformational potential in synthesis is just emerging.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. L. H. is supported by the National Institutes of Health (GM129081). R. A. S. is supported by the National Institutes of Health (GM122606) and the National Science Foundation (CHE 1955922). Sophia Shevick is funded by a CTSA NIH TL1 fellowship (TL1 TR002551). Simona Kotesova is a Kellogg Fellow of the Skaggs Graduate Program.Notes and references
- J. F. Hartwig, Organotransition Metal Chemistry, University Science Books, Sausalito, CA, 2010 Search PubMed.
- P. L. Holland, Acc. Chem. Res., 2015, 48, 1696–1702 CrossRef CAS.
- J. D. Sears, P. G. N. Neate and M. L. Neidig, J. Am. Chem. Soc., 2018, 140, 11872–11883 CrossRef CAS.
- R. Arevalo and P. J. Chirik, J. Am. Chem. Soc., 2019, 141, 9106–9123 CrossRef.
- S. W. M. Crossley, C. Obradors, R. M. Martinez and R. A. Shenvi, Chem. Rev., 2016, 116, 8912–9000 CrossRef CAS.
- J. Waser and E. M. Carreira, J. Am. Chem. Soc., 2004, 126, 5676–5677 CrossRef CAS.
- R. Kohler, PhD thesis, Harvard University, 1965.
- F. C. Whitmore, Chem. Eng. News, 1948, 26, 668–674 CrossRef CAS.
- G. A. Olah, Angew. Chem., Int. Ed., 1995, 34, 1393–1405 CrossRef CAS.
- S. V. Pronin and R. A. Shenvi, Nat. Chem., 2012, 4, 915–920 CrossRef CAS.
- S. V. Pronin, C. A. Reiher and R. A. Shenvi, Nature, 2013, 501, 195–199 CrossRef CAS.
- S. Winstein, E. Clippinger, A. H. Fainberg and G. C. Robinson, J. Am. Chem. Soc., 1954, 76, 2597–2598 CrossRef CAS.
- E. D. Hughes, C. K. Ingold, R. J. L. Martin and D. F. Meigh, Nature, 1950, 166, 679–680 CrossRef CAS.
- C. A. Bunton, E. D. Hughes, C. K. Ingold and D. F. Meigh, Nature, 1950, 166, 680 CrossRef CAS.
- A. F. Diaz, I. Lazdins and S. Winstein, J. Am. Chem. Soc., 1968, 90, 1904–1905 CrossRef CAS.
- G. A. Olah and A. Molnar, Hydrocarbon Chemistry, Wiley, Hoboken, NJ, 2003 Search PubMed.
- S. W. M. Crossley, F. Barabé and R. A. Shenvi, J. Am. Chem. Soc., 2014, 136, 16788–16791 CrossRef CAS.
- S. L. Shevick, C. Obradors and R. A. Shenvi, J. Am. Chem. Soc., 2018, 140, 12056–12068 CrossRef CAS.
- D. C. Eisenberg and J. R. Norton, Isr. J. Chem., 1991, 31, 55–66 CrossRef CAS.
- C. L. Bailey and R. S. Drago, Coord. Chem. Rev., 1987, 79, 321–332 CrossRef CAS.
- T. Mukaiyama and T. Yamada, Bull. Chem. Soc. Jpn., 1995, 68, 17–35 CrossRef CAS.
- M. Tilset and V. D. Parker, J. Am. Chem. Soc., 1989, 111, 6711–6717 CrossRef CAS.
- J. L. Kuo, T. Gunasekara, A. Hansen, H. B. Vibbert, F. Bohle, J. R. Norton, S. Grimme and P. J. Quinlivan, Organometallics, 2019, 38, 4319–4328 CrossRef CAS.
- P. Magnus, A. H. Payne, M. J. Waring, D. A. Scott and V. Lynch, Tetrahedron Lett., 2000, 41, 9725–9730 CrossRef CAS.
- J. C. Lo, D. Kim, C.-M. Pan, J. T. Edwards, Y. Yabe, J. Gui, T. Qin, S. Gutiérrez, J. Giacoboni, M. W. Smith, P. L. Holland and P. S. Baran, J. Am. Chem. Soc., 2017, 139, 2484–2503 CrossRef CAS.
- C. Obradors, R. M. Martinez and R. A. Shenvi, J. Am. Chem. Soc., 2016, 138, 4962–4971 CrossRef CAS.
- D. Kim, S. M. W. Rahaman, B. Q. Mercado, R. Poli and P. L. Holland, J. Am. Chem. Soc., 2019, 141, 7473–7485 CrossRef CAS.
- J. Waser, B. Gaspar, H. Nambu and E. M. Carreira, J. Am. Chem. Soc., 2006, 128, 11693–11712 CrossRef CAS.
- T. Tokuyasu, S. Kunikawa, A. Masuyama and M. Nojima, Org. Lett., 2002, 4, 3595–3598 CrossRef CAS.
- H. Shigehisa, T. Aoki, S. Yamaguchi, N. Shimizu and K. Hiroya, J. Am. Chem. Soc., 2013, 135, 10306–10309 CrossRef CAS.
- E. E. Touney, N. J. Foy and S. V. Pronin, J. Am. Chem. Soc., 2018, 140, 16982–16987 CrossRef CAS.
- B. Gaspar and E. M. Carreira, Angew. Chem., Int. Ed., 2007, 46, 4519–4522 CrossRef CAS.
- J. L. M. Matos, S. A. Green, Y. Chun, V. Q. Dang, R. Dushin, P. Richardson, J. Chen, D. Piotrowski, B. Paegel and R. A. Shenvi, Angew. Chem., Int. Ed., 2020, 59, 2–8 CrossRef.
- C. Chult, R. J. P. Corriu, C. Reye and J. C. Young, Chem. Rev., 1993, 93, 1371–1448 CrossRef.
- D. C. Lacy, G. M. Roberts and J. C. Peters, J. Am. Chem. Soc., 2015, 137, 4860–4864 CrossRef CAS.
- T. V. Chciuk, W. R. Anderson and R. A. Flowers, J. Am. Chem. Soc., 2016, 138, 8738–8741 CrossRef CAS.
- M. Paradas, A. G. Campaña, T. Jiménez, R. Robles, J. E. Oltra, E. Buñuel, J. Justicia, D. J. Cárdenas and J. M. Cuerva, J. Am. Chem. Soc., 2010, 132, 12748–12756 CrossRef CAS.
- S. S. Kolmar and J. M. Mayer, J. Am. Chem. Soc., 2017, 139, 10687–10692 CrossRef CAS.
- H. Jiang, W. Lai and H. Chen, ACS Catal., 2019, 9, 6080–6086 CrossRef CAS.
- Y. R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, 1st edn, 2007 Search PubMed.
- G. Li, A. Han, M. E. Pulling, D. P. Estes and J. R. Norton, J. Am. Chem. Soc., 2012, 134, 14662–14665 CrossRef CAS.
- K. Iwasaki, K. K. Wan, A. Oppedisano, S. W. M. Crossley and R. A. Shenvi, J. Am. Chem. Soc., 2014, 136, 1300–1303 CrossRef CAS.
- A. Weickgenannt and M. Oestreich, Chem.–Asian J., 2009, 4, 406–410 CrossRef CAS.
- Y. Gunji, Y. Yamashita, T. Ikeno and T. Yamada, Chem. Lett., 2006, 35, 714–715 CrossRef CAS.
- C. Chuit, R. J. P. Corriu, R. Perz and C. Reye, Synthesis, 1982, 11, 981–984 Search PubMed.
- C. Yao, S. Wang, J. R. Norton and M. Hammond, J. Am. Chem. Soc., 2020, 142, 4793–4799 CrossRef CAS.
- S. A. Green, T. R. Huffman, R. O. McCourt, V. van der Puyl and R. A. Shenvi, J. Am. Chem. Soc., 2019, 141, 7709–7714 CrossRef CAS.
- J. Choi, M. E. Pulling, D. M. Smith and J. R. Norton, J. Am. Chem. Soc., 2008, 130, 4250–4252 CrossRef CAS.
- L. H. Tang, E. T. Papish, G. P. Abramo, J. R. Norton, M. H. Baik, R. A. Friesner and A. Rappe, J. Am. Chem. Soc., 2003, 125, 10093–10102 CrossRef CAS.
- L. H. Tang, E. T. Papish, G. P. Abramo, J. R. Norton, M. H. Baik, R. A. Friesner and A. Rappe, J. Am. Chem. Soc., 2006, 128, 11314 CrossRef CAS.
- J. Choi, L. Tang and J. R. Norton, J. Am. Chem. Soc., 2007, 129, 234–240 CrossRef CAS.
- X. Ma and S. B. Herzon, Chem. Sci., 2015, 6, 6250–6255 RSC.
- J. C. Lo, Y. Yabe and P. S. Baran, J. Am. Chem. Soc., 2014, 136, 1304–1307 CrossRef CAS.
- D. M. Smith, M. E. Pulling and J. R. Norton, J. Am. Chem. Soc., 2007, 129, 770–771 CrossRef CAS.
- P. Magnus, A. H. Payne, M. J. Waring, D. A. Scott and V. Lynch, Tetrahedron Lett., 2000, 41, 9725–9730 CrossRef CAS.
- J. Franck and E. Rabinowitch, Trans. Faraday Soc., 1934, 30, 120–130 RSC.
- T. W. Koenig, B. P. Hay and R. G. Finke, Polyhedron, 1988, 7, 1499–1516 CrossRef CAS.
- C. D. Garr and R. G. Finke, J. Am. Chem. Soc., 1992, 114, 10440–10445 CrossRef CAS.
- T. T. Tsou, M. Loots and J. Halpern, J. Am. Chem. Soc., 1982, 104, 623–624 CrossRef CAS.
- R. G. Lawler, Acc. Chem. Res., 1972, 5, 25–33 CrossRef CAS.
- E. Rabinowitch and W. C. Wood, Trans. Faraday Soc., 1936, 32, 1381–1387 RSC.
- O. Dobis, J. Chem. Phys., 1976, 65, 4264–4271 CrossRef CAS.
- T. Koenig and H. Fischer, in Free Radicals, ed. J. K. Kochi, John Wiley & Sons, Inc., 1973, vol. I, Ch. “Cage” Effects, pp. 157–189 Search PubMed.
- O. Dobis, J. M. Pearson and M. Szwarc, J. Am. Chem. Soc., 1968, 90, 278–282 CrossRef CAS.
- K. Chakravorty, J. M. Pearson and M. Szwarc, J. Am. Chem. Soc., 1968, 90, 283–285 CrossRef CAS.
- R. Sweany and J. Halpern, J. Am. Chem. Soc., 1977, 99, 8335–8337 CrossRef CAS.
- H. R. Ward and R. G. Lawler, J. Am. Chem. Soc., 1967, 89, 5518–5519 CrossRef CAS.
- A. J. Leusink, H. A. Budding and W. Drenth, J. Organomet. Chem., 1967, 9, 295–306 CrossRef CAS.
- T. E. Nalesnik and M. Orchin, Organometallics, 1982, 1, 222–223 CrossRef CAS.
- J. A. Roth and M. Orchin, J. Organomet. Chem., 1979, 182, 299–311 CrossRef CAS.
- T. M. Bockman, J. F. Garst, R. B. King, L. Markó and F. Ungváry, J. Organomet. Chem., 1985, 279, 165–169 CrossRef CAS.
- J. W. Connolly, Organometallics, 1984, 3, 1333–1337 CrossRef CAS.
- J. F. Garst, T. M. Bookman and R. Batlaw, J. Am. Chem. Soc., 1986, 108, 1689–1691 CrossRef CAS.
- E. N. Jacobsen and R. G. Bergman, J. Am. Chem. Soc., 1985, 107, 2023–2032 CrossRef CAS.
- F. Ungváry and L. Markó, J. Organomet. Chem., 1983, 249, 411–414 CrossRef.
- Y. Matsui and M. Orchin, J. Organomet. Chem., 1983, 244, 369–373 CrossRef CAS.
- T. Koenig and R. G. Finke, J. Am. Chem. Soc., 1988, 110, 2657–2658 CrossRef CAS.
- K. J. Covert, E. F. Askew, J. Grunkemeier, T. Koenig and D. R. Tyler, J. Am. Chem. Soc., 1992, 114, 10446–10448 CrossRef CAS.
- R. Hoffman, P. Wells and H. Morrison, J. Org. Chem., 1971, 36, 102–108 CrossRef CAS.
- J. D. Harris, A. B. Oelkers and D. R. Tyler, J. Am. Chem. Soc., 2007, 129, 6255–6262 CrossRef CAS.
- R. Poli, Chem. Rev., 1996, 96, 2135–2204 CrossRef CAS.
- J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2003, 238–239, 347–361 CrossRef CAS.
- D. R. Tyler and F. E. Mao, Coord. Chem. Rev., 1990, 97, 119–140 CrossRef CAS.
- G. D. Fallon and B. M. Gatehouse, Cryst. Struct. Commun., 1978, 7, 263–267 CAS.
- D. Kim, S. M. W. Rahaman, B. Q. Mercado, R. Poli and P. L. Holland, J. Am. Chem. Soc., 2019, 141, 7473–7485 CrossRef CAS.
- M. Szwarc, Acc. Chem. Res., 1969, 2, 87–96 CrossRef CAS.
- J. T. Barry, D. J. Berg and D. R. Tyler, J. Am. Chem. Soc., 2016, 138, 9389–9392 CrossRef CAS.
- J. T. Barry, D. J. Berg and D. R. Tyler, J. Am. Chem. Soc., 2017, 139, 14399–14405 CrossRef CAS.
- J. Demarteau, A. Debuigne and C. Detrembleur, Chem. Rev., 2019, 119, 6906–6955 CrossRef CAS.
- A. Nishinaga, T. Yamada, H. Fujisawa, K. Ishizaki, H. Ihara and T. Matsuura, J. Mol. Catal., 1988, 48, 2–3 CrossRef.
- E. E. Touney, N. J. Foy and S. V. Pronin, J. Am. Chem. Soc., 2018, 140, 16982–16987 CrossRef CAS.
- H. Shigehisa, M. Hayashi, H. Ohkawa, T. Suzuki, H. Okayasu, M. Mukai, A. Yamazaki, R. Kawai, H. Kikuchi, Y. Satoh, A. Fukuyama and K. Hiroya, J. Am. Chem. Soc., 2016, 138, 10597–10604 CrossRef CAS.
- E. G. Samsel and J. K. Kochi, J. Am. Chem. Soc., 1986, 108, 4790–4804 CrossRef CAS.
- R. J. Morris and G. S. Girolami, Organometallics, 1991, 10, 792–799 CrossRef CAS.
- M. H. Al-Afyouni, K. L. Fillman, W. W. Brennessel and M. L. Neidig, J. Am. Chem. Soc., 2014, 136, 15457–15460 CrossRef CAS.
- K. Zhu, M. P. Shaver and S. P. Thomas, Chem.–Asian J., 2016, 11, 977–980 CrossRef CAS.
- K. Zhu, M. P. Shaver and S. P. Thomas, Chem. Sci., 2016, 7, 3031–3035 RSC.
- Y. Xie, P.-W. Sun, Y. Li, S. Wang, M. Ye and Z. Li, Angew. Chem., Int. Ed., 2019, 58, 7097–7101 CrossRef CAS.
- L. E. N. Allan, M. R. Perry and M. P. Shaver, Prog. Polym. Sci., 2012, 37, 127–156 CrossRef CAS.
- H. Schroeder, B. R. M. Lake, S. Demeshko, M. P. Shaver and M. Buback, Macromolecules, 2015, 48, 4329–4338 CrossRef CAS.
- J. Shey, C. M. McGinley, K. M. McCauley, A. S. Dearth, B. T. Young and W. A. Van der Donk, J. Org. Chem., 2002, 67, 837–846 CrossRef CAS.
- J. Halpern, Pure Appl. Chem., 1979, 51, 2171–2182 CAS.
- R. M. Bullock and E. G. Samsel, J. Am. Chem. Soc., 1987, 109, 6542–6544 CrossRef CAS.
- H. Fischer, J. Am. Chem. Soc., 1986, 108, 3925–3927 CrossRef CAS.
- A. L. J. Beckwith, Tetrahedron, 1981, 37, 3073–3100 CrossRef CAS.
- J. L. Kuo, J. Hartung, A. Han and J. R. Norton, J. Am. Chem. Soc., 2015, 137, 1036–1039 CrossRef CAS.
- G. Li, J. L. Kuo, A. Han, J. M. Abuyuan, L. C. Young, J. R. Norton and J. H. Palmer, J. Am. Chem. Soc., 2016, 138, 7698–7704 CrossRef CAS.
- J. Choi, L. Tang and J. R. Norton, J. Am. Chem. Soc., 2007, 129, 234–240 CrossRef CAS.
- D. Vrubliauskas and C. D. Vanderwal, Angew. Chem., Int. Ed., 2020, 59, 6115–6121 CrossRef CAS.
- B. Giese, Angew. Chem., Int. Ed., 1983, 22, 753–764 CrossRef.
- A. Nishinaga, H. Tomita and H. Ohara, Chem. Lett., 1983, 12, 1751–1754 CrossRef.
- E. P. Talsi, V. D. Chinakov, V. P. Babenko, V. N. Sidelnikov and K. I. Zamaraev, J. Mol. Catal., 1993, 81, 215–233 CrossRef CAS.
- H. Shigehisa, E. Nishi, H. Fujisawa and K. Hiroya, Org. Lett., 2013, 15, 5158–5161 CrossRef CAS.
- E. K. Leggans, T. J. Barker, K. K. Duncan and D. L. Boger, Org. Lett., 2012, 14, 1428–1431 CrossRef CAS.
- T. J. Barker and D. L. Boger, J. Am. Chem. Soc., 2012, 134, 13588–13591 CrossRef CAS.
- F. Bertrand, F. Le Guyader, L. Liguori and G. Ouvry, C. R. Acad. Sci., Ser. IIc: Chim., 2001, 4, 547–555 CrossRef CAS.
- D. S. Masterson and J. P. Shackleford, Synlett, 2007, 2007, 1302–1304 CrossRef.
- X. Huang and J. T. Groves, ACS Catal., 2016, 6, 751–759 CrossRef CAS.
- C.-L. Zhu, C. Wang, Q.-X. Qin, S. Yruegas, C. D. Martin and H. Xu, ACS Catal., 2018, 8, 5032–5037 CrossRef CAS.
- A. Sharma and J. F. Hartwig, Nature, 2015, 517, 600–604 CrossRef CAS.
- M. Rueda-Becerril, C. Chatalova Sazepin, J. C. T. Leung, T. Okbinoglu, P. Kennepohl, J.-F. Paquin and G. M. Sammis, J. Am. Chem. Soc., 2012, 134, 4026–4029 CrossRef CAS.
- M. P. Sibi and Y. Landais, Angew. Chem., Int. Ed., 2013, 52, 3570–3572 CrossRef CAS.
- W. Liu, X. Huang, M.-J. Cheng, R. J. Nielsen, W. A. Goddard and J. T. Groves, Science, 2012, 337, 1322 CrossRef CAS.
- X. L. Zhou, F. Yang, H. L. Sun, Y. N. Yin, W. T. Ye and R. Zhu, J. Am. Chem. Soc., 2019, 141, 7250–7255 CrossRef CAS.
- W. E. Fristad and J. R. Peterson, J. Org. Chem., 1983, 50, 10–18 CrossRef.
- M. E. Vol'pin, I. Y. Levitin, A. L. Sigan, J. Halpern and G. M. Tom, Inorg. Chim. Acta, 1980, 41, 271–277 CrossRef.
- M. E. Vol'pin, I. Y. Levitin, A. L. Sigan and A. T. Nikitaev, J. Organomet. Chem., 1985, 279, 263–280 CrossRef.
- J. L. M. Matos, S. Vásquez-Céspedes, J. Gu, T. Oguma and R. A. Shenvi, J. Am. Chem. Soc., 2018, 140, 16976–16981 CrossRef CAS.
- S. A. Green, S. W. M. Crossley, J. L. M. Matos, S. Vásquez-Céspedes, S. L. Shevick and R. A. Shenvi, Acc. Chem. Res., 2018, 51, 2628–2640 CrossRef CAS.
- S. A. Green, S. Vásquez-Céspedes and R. A. Shenvi, J. Am. Chem. Soc., 2018, 140, 11317–11324 CrossRef CAS.
- K. Tomooka, H. Yamamoto and T. Nakai, J. Am. Chem. Soc., 1996, 118, 3317–3318 CrossRef CAS.
- F. D. Greene, M. A. Berwick and J. C. Stowell, J. Am. Chem. Soc., 1970, 92, 867–874 CrossRef CAS.
- J. Kwiatek and J. K. Seyler, J. Organomet. Chem., 1965, 3, 421–432 CrossRef CAS.
- L. M. Jackman, J. A. Hamilton and J. M. Lawlor, J. Am. Chem. Soc., 1968, 90, 1914–1916 CrossRef CAS.
- A. A. Gridnev, S. D. Ittel, B. B. Wayland and M. Fryd, Organometallics, 1996, 15, 5116–5126 CrossRef CAS.
- Y. Ohgo, K. Orisaku, E. Hasegawa and S. Takeuchi, Chem. Lett., 1986, 27–30 CrossRef CAS.
- J. W. Suggs and C. H. Jun, J. Am. Chem. Soc., 1986, 108, 4679–4681 CrossRef CAS.
- T. Linker, Angew. Chem., Int. Ed., 1997, 36, 2060–2062 CrossRef CAS.
- C. A. Discolo, E. E. Touney and S. V. Pronin, J. Am. Chem. Soc., 2019, 141, 17527–17532 CrossRef CAS.
- K. Ebisawa, K. Izumi, Y. Ooka, H. Kato, S. Kanazawa, S. Komatsu, E. Nishi and H. Shigehisa, J. Am. Chem. Soc., 2020, 142, 13481–13490 CrossRef CAS.
- X. Shen, X. Chen, J. Chen, Y. Sun, Z. Cheng and Z. Lu, Nat. Commun., 2020, 11, 1–8 Search PubMed.
- R. Poli, Angew. Chem., Int. Ed., 2006, 45, 5058–5070 CrossRef CAS.
- R. Poli, Chem. – Eur. J., 2015, 21, 6988–7001 CrossRef CAS.
- V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |