 Open Access Article
Open Access ArticleAssessing the performance of rotational spectroscopy in chiral analysis
Sérgio R.
Domingos†
 a,
Cristóbal
Pérez
a,
Cristóbal
Pérez
 a,
Mark D.
Marshall
a,
Mark D.
Marshall
 b,
Helen O.
Leung
b,
Helen O.
Leung
 b and
Melanie
Schnell
b and
Melanie
Schnell
 *ac
*ac
aDeutsches Elektronen-Synchrotron DESY, Notkestraße 85, 22607 Hamburg, Germany. E-mail: melanie.schnell@desy.de
bDepartment of Chemistry, Amherst College, P.O. Box 5000, Amherst, Massachusetts 01002-5000, USA
cInstitut für Physikalische Chemie, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Str.1, 24118 Kiel, Germany
First published on 28th September 2020
Abstract
The capabilities of rotational spectroscopy-based methods as tools to deliver accurate and precise chirality-sensitive information are still breaking ground, but their applicability in the challenging field of analytical chemistry is already clear. In this mini review, we explore the current abilities and challenges of two emergent techniques for chiral analysis based on rotational spectroscopy. For that, we will showcase the two methods (microwave 3-wave mixing and chiral tag rotational spectroscopy) while testing their performance to solve the absolute configuration and the enantiomeric excess of a blind sample containing a mixture of enantiomers of styrene oxide.
1 Introduction
Molecular chirality is widely recognised for its relevance to the building blocks of life and its vital role in medicine and health: most biomolecules are chiral, and consequently, their handedness steers stereoselectivity in biochemical interactions.1 Furthermore, it is known that conformational flexibility can influence biological activity, i.e., it can affect the ability of molecules to adopt certain conformations to allow for optimal docking to a (chiral) receptor. Therefore, being able to differentiate between enantiomers and determining the conformation and handedness of chiral molecules is crucial in establishing how molecular structure and biological activity are related.One widespread approach for chiral characterisation and discrimination is the use of chirality-selective columns coupled with various detection techniques.2 However, the development of separation protocols for a particular sample often encompasses a costly and time-consuming process. Chiroptical methods are valuable tools with increasing demand in chemical and pharmaceutical sciences and can retrieve chiral information from a molecular system, either in the gas phase or in the condensed phase. For this purpose, there are currently a number of established chiral-sensitive techniques, such as optical rotary dispersion,3 circular dichroism (CD),4 and also vibrational optical activity5 methods, namely vibrational circular dichroism6 and Raman optical activity.7 In these methods, the mirror symmetry of enantiomers is broken using circularly polarised electromagnetic radiation, and the absolute configuration and enantiomeric excess (ee) of chiral samples can be confidently determined. However, manoeuvring through complex conformational landscapes, where many conformations may contribute to the observed spectra, can become a cumbersome task that requires more advanced computational approaches.8 These challenges are particularly relevant for complex chiral mixtures, and they are often strongly solvent dependent.9
Recent instrumental developments led to a number of groundbreaking new experiments in the gas phase, which developed into alternative routes for distinguishing enantiomers and measuring the ee. Among these are microwave three-wave mixing10–13 (M3WM), photoelectron circular dichroism (PECD) using intense circularly polarised laser light14–16 or synchrotron sources;17 and Coulomb explosion with coincidence imaging.18–20 Chirality research is now even extending to the atto-second regime, which will allow the study of the electron dynamics of chiral systems.21 The great precision and control that can be achieved using gas-phase samples, due to an outstanding species- and quantum-state specificity, opens the door towards new advances for studying, controlling, and manipulating chiral molecules.
Recently, M3WM was extended to achieve enantiomer-selective population transfer in gas-phase samples.22–25 Using tailored microwave pulse sequences, the population of one enantiomer can be enriched in one particular rotational state, while it is reduced for the other enantiomer. This “separation in energy” is an important step towards spatial separation of enantiomers. Such an “on the fly” enantiomer separation can enable more advanced precision spectroscopy experiments aiming at detecting the parity-violating character of the weak interaction in mirror-image molecules.26 For these experiments, systematic errors could be largely reduced if the respective enantiomer can be chosen by just changing the appropriate phases of the tailored microwave pulses. Such an approach can also be applied to chiral molecules whose enantiomers cannot be separated using common techniques, for example due to short racemization times.27
Not too long ago, another method based on rotational spectroscopy, the chiral-tagging approach, arose.28,29 Chiral tagging takes advantage of the well-known concept of non-covalently bound diastereomer formation, which is also the basis of chirality recognition. Enantiomers of chiral molecules of interest can be complexed with a well-characterised chiral molecule of known handedness, the chiral tag. This results in the formation of two diastereomeric complexes, which can be directly differentiated using rotational spectroscopy. This allows for the determination of the handedness of a given enantiomer of the chiral molecule of interest, since the handedness of the chiral tag is known. Via the variations in the transition intensities, the ee of the molecule of interest can also be determined. It thus relies on similar principles as chiral shift reagent in NMR30 and chiral column separation, i.e., the different interaction of the two enantiomers of a chiral molecule with another well-characterised, chiral binding partner.
Both methods, M3WM and chiral tagging, rely on the high resolving power of modern rotational spectroscopy. Even small changes to the structural arrangement result in clear and resolvable differences in the rotational spectrum, because of the changes in the respective moments of inertia. In this mini-review, we will showcase M3WM and chiral tagging and their prospects as analytical tools, in particular their usefulness with respect to ee determination. First, we will introduce the two different approaches and review some of the recent developments. New experiments on the chiral analysis of styrene oxide (SO) are then presented in a comparative approach between M3WM and chiral tagging. A focus will be on the determination of the absolute configuration of SO using a well-characterised chiral tag molecule with known handedness, namely (R)-(+)-3,3,3-trifluoro-1,2-epoxypropane (TFO), as well as on the determination of the ee of an unknown SO mixture. The latter is performed in independent measurements using both chiral tagging and M3WM to allow also for a useful comparison between the two techniques.
2 The techniques: M3WM and chiral tag rotational spectroscopy
Chiral tagging and M3WM are based on the high structural sensitivity and resolving properties of rotational spectroscopy in the gas phase. In the simplest case of a rigid-rotor molecule, the rotational spectrum of a molecule is characterised by the rotational constants, A, B, and C. These rotational constants are inversely proportional to the moments of inertia of the molecules so that a rotational spectrum strongly depends on the structure of the molecule. Different orientations of a particular side group with respect to the rest of the molecule, as in the case of β-estradiol,31 for example, or the exchange of a 12C by a 13C isotope, result in different moments of inertia and thus in different rotational constants and spectra. The latter is routinely employed to obtain accurate experimental structures of molecules and molecular complexes via isotopic substitution.In rotational spectroscopy, the cold and collision-free conditions of a supersonic jet or the low temperatures of a buffer-gas environment are often exploited. The low temperatures greatly simplify the obtained spectra, because the molecules typically only populate the vibronic ground state, and only a reduced number of rotational states are populated at low rotational temperatures of around 1–2 K, which are routinely achieved. Another great advantage of cold jets is the stabilisation of non-covalently bound molecular clusters. This allows for the detailed study of intermolecular interactions, such as the interplay between hydrogen bonding and dispersion, as well as their role in chirality recognition,32 which is relevant for the chiral tagging technique as outlined below.
The internally cold, isolated molecules or molecular complexes are probed with a broadband microwave chirp, covering a certain frequency range of several GHz widths in a few microseconds. This approach is called chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy, or Molecular Rotational Resonance (MRR) spectroscopy. If rotational transitions of the molecules are resonant to one or more frequencies in the chirp, the respective molecules will orient and form a macroscopic dipole moment. This polarisation has an analogy to the magnetisation in NMR spectroscopy.33 In the experiments, we record the decay of the electromagnetic field generated by the polarisation in the time domain, the free-induction decay (FID). Also the phase of this FID is recorded, which is important for the M3WM experiment described below. Once the excitation pulse is over, fast Fourier transformation of the FID from the time to the frequency domain provides us with the rotational spectrum. The experiments are set up such that a large number of acquisitions can be recorded and averaged to gain sufficient signal-to-noise ratios, which requires high phase reproducibility. The high dynamic range of CP-FTMW spectrometers allows for the simultaneous detection of rare isotopologues. The individual sets of rotational constants obtained for the rare isotopologues can then be used to determine the structures of the molecules, for example using the Kraitchman equations34 or other structure fitting approaches.35
It is important to realise that isolated enantiomers cannot be directly differentiated from their rotational spectrum yet, because their rotational constants are identical apart from some very small differences arising from parity violation, which cannot be resolved with the current resolution of typical rotational spectrometers.
2.1 Chiral tag rotational spectroscopy
The formation of non-covalently bound complexes is central to the chiral tagging technique.29 A sample of the chiral molecule of interest will be mixed with a sample of a different, well-characterised chiral molecule of known handedness, the chiral tag. The two enantiomers of the chiral molecule of interest will form complexes with the chiral tag, resulting in two so-called diastereomers. Diastereomers have distinct 3D structures and thus differ in their moments of inertia, which are reciprocal to the rotational constants, so that they can be directly differentiated using high-resolution rotational spectroscopy. In the non-covalently bound complexes of racemic SO with R-TFO, for example, the homochiral R-SO–R-TFO diastereomer has the rotational constants (A, B, C) = (801, 305, 260) MHz, while the heterochiral S-SO–R-TFO species has (A, B, C) = (755, 343, 277) MHz (see Table 1). Given the precision of typical microwave spectrometers, such rotational constants are in fact measured to one part in 106 or better, and two molecules with constants differing by the amounts seen here are trivially distinguished by their spectra. Thus, the absolute configuration of a sample of SO is directly determined by analysis of the microwave spectrum. The transition intensities of the two diastereomers provide information on its ee. By comparing the line strength ratio obtained for a pair of lines, one each for the homochiral and heterochiral diastereomers, when using a racemic sample of the chiral tag to the ratio obtained when using a single enantiomer of the tag, instrumental effects as well as those arising from molecular transition moments and potentially differing populations of the diastereomers (such as might result from chiral recognition) can be normalised and the ee obtained.29 In practice, the procedure is repeated for many pairs of lines in the spectrum to achieve better statistics for the determination. More details are given in Section 3 for the specific example of SO/TFO.| (R)-TFO–(R)-SO | (R)-TFO–(S)-SO | |||
|---|---|---|---|---|
| Expt. | Theory | Expt. | Theory | |
| A/MHz | 800.86970(37) | 800 | 754.996470(92) | 755 |
| B/MHz | 305.408414(87) | 305 | 343.389363(62) | 344 |
| C/MHz | 259.854729(86) | 259 | 276.525928(63) | 278 |
Effective chiral tags are small molecules, so that the non-covalently bound complexes they form with the analyte do not have inconveniently small rotational constants. Conversely, they should be large enough so that rotational constants of the two diastereomers are sufficiently different from each other. Clearly, the tag must be chiral and readily available in enantiopure form. It should be easy to introduce into the molecular jet expansion and be functionalized so to favor non-covalent interactions. The tag should have a simple, well-characterised microwave spectrum with no complications from fine or hyperfine interactions and minimal isotopic dilution.36
Chiral tagging benefits greatly from broadband chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy developed more than a decade ago by Pate and coworkers.37 The ability to record large fractions of a rotational spectrum of sufficient strength in a significantly shorter time than what is possible with cavity-based rotational spectroscopy was an important milestone towards modern applications of rotational spectroscopy.38 The detailed analysis of rotational spectra of complex chiral molecules and diastereomeric complexes are facilitated by obtaining broadband spectra, which allows the evaluation of differences in analyte concentrations within competitive timescales.
2.2 Microwave three-wave mixing
M3WM is a non-linear, resonant, and coherent approach and exploits the narrow line widths, high phase reproducibility, and sensitivity of rotational spectroscopy. The π radian phase difference observed in the time-domain, which allows for enantiomer differentiation and identification, emerges from the difference in sign of the triple product of the dipole-moment components of the respective molecule, μa·(μb × μc), for the two different enantiomers, which arise from their mirror-image character. The excitation scheme for M3WM consists of a closed loop of rotational transitions. It involves two resonant excitation pulses, the drive and the twist, which are linearly polarised in perpendicular directions in the laboratory frame. The molecular response signal is recorded in the third, mutually orthogonal direction at the listen frequency. The characteristic π radian phase difference of the enantiomers is obtained in the FID at the frequency of this third transition closing the loop. It can thus be understood as a polarisation-sensitive double-resonance experiment. It only results in a measurable chiral signal if there is an ee; for racemic samples, no FID signal will be recorded at the listen frequency because of mutual signal cancelation. As such, M3WM is well suited for accurate measurements of even small ee.To retrieve the absolute configuration of a specific chiral molecule from a M3WM experiment, one is required to compare the FID phase information with that of a sample of the same molecule with known handedness. The phase thus directly assigns the correct enantiomer. In principle, a more general approach should also be possible, where the absolute phase of the FID signal at the listen frequency can be extracted and the absolute configuration derived without need for a reference sample. This approach is not completely solved from the experimental side yet and further work is required on that front. For a more comprehensive discussion on this topic, the reader is referred to ref. 25, 39 and 40.
3 An unbiased comparison of two methods
To independently test the performance of both methods to determine the absolute configuration and enantiomeric excess of a sample, a mixture of known but unrevealed composition of R- and S-SO (26.4% R-SO and 73.6% S-SO) was prepared from enantiopure (ee > 99%) samples of the two enantiomers. The mixture was made by two members of our group who did not communicate the values to us until after our measurements were made. The ee of the mixture as prepared is 47.2 ± 0.4% (S), with a ratio of S-SO to R-SO = 2.79. The uncertainty in the ee comes from the accuracy of the balance used.3.1 Microwave three-wave mixing
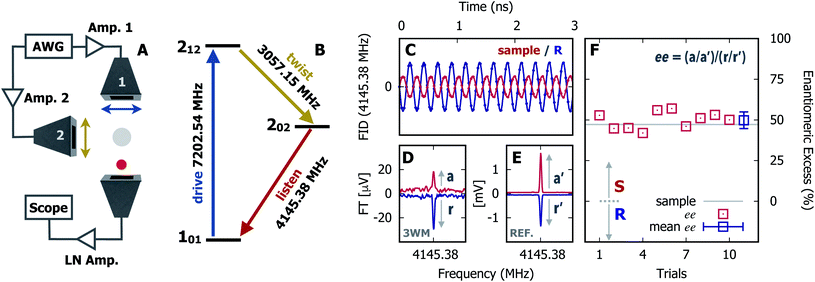
In Fig. 1 we show the steps required to determine the ee of the sample using M3WM. For a deep-dive into the core theory and experimental aspects of the technique, the reader is referred to previous work in the literature12,41 and references therein. A schematic representation of the experimental setup is given in panel A. In panel B, the triad of rotational states and transition frequencies used to probe the chiral signal of SO are shown. The relevant polarisations of the microwave pulses are color coded with respect to panel A for clarity. The drive pulse generates a coherence for the 101 ← 212 resonance (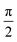 conditions), and is followed by the twist pulse, which transfers that coherence to the 101 ← 202 resonance (π conditions), which is then detected as a free-induction decay (FID) in the time domain. The signal detected at the listen frequency is shown in panel C for both the target sample and for enantiopure R-SO (our reference sample). The π-shifted phase signature of the FID of the sample, with respect to the R enantiomer, reveals readily that the excess enantiomer in the sample is of S-handedness. In panel D we show the Fourier-transformed signals given in panel C. The resulting relative intensities of the listen transitions for the sample (a, in red) and R-SO (r, in blue) will deliver the ee of our sample. However, because the reference signal using R-SO is obtained in a separate measurement, a normalisation procedure is required. For that, the transition intensities followed by direct excitation of the 101 ← 202 resonance are measured (a′ and r′ in panel E) and used as normalisation factors for ee determination. In panel F we show the results of ten consecutive experiments, where the ee values are obtained via the relation
conditions), and is followed by the twist pulse, which transfers that coherence to the 101 ← 202 resonance (π conditions), which is then detected as a free-induction decay (FID) in the time domain. The signal detected at the listen frequency is shown in panel C for both the target sample and for enantiopure R-SO (our reference sample). The π-shifted phase signature of the FID of the sample, with respect to the R enantiomer, reveals readily that the excess enantiomer in the sample is of S-handedness. In panel D we show the Fourier-transformed signals given in panel C. The resulting relative intensities of the listen transitions for the sample (a, in red) and R-SO (r, in blue) will deliver the ee of our sample. However, because the reference signal using R-SO is obtained in a separate measurement, a normalisation procedure is required. For that, the transition intensities followed by direct excitation of the 101 ← 202 resonance are measured (a′ and r′ in panel E) and used as normalisation factors for ee determination. In panel F we show the results of ten consecutive experiments, where the ee values are obtained via the relation 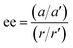 . To account for any fluctuations in the molecular jet, which can lead to overall signal increase/decrease over the course of the 10 measurements, we have acquired new normalisation values (direct excitation) every other data point. The average ee value obtained from the ten experiments indicates an ee of S over R of 49.8 ± 5.1%. These results are in very good agreement with the ee of 47.2 ± 0.4% (S over R) of the sample, as prepared.
. To account for any fluctuations in the molecular jet, which can lead to overall signal increase/decrease over the course of the 10 measurements, we have acquired new normalisation values (direct excitation) every other data point. The average ee value obtained from the ten experiments indicates an ee of S over R of 49.8 ± 5.1%. These results are in very good agreement with the ee of 47.2 ± 0.4% (S over R) of the sample, as prepared.
3.2 Chiral tag rotational spectroscopy
Chiral tagging exploits the conversion of different enantiomers of an analyte into spectroscopically distinguishable diastereomers through the formation of non-covalently bound dimers with an enantiopure chiral tag. Identification of an analyte's absolute stereochemistry is done via comparison of observed rotational constants with those predicted from even modest quantum chemistry calculations (Table 1).42 In a sample containing both enantiomers of the analyte, the ee of the sample can be determined from a comparison of the intensities of transitions assigned to the heterochiral and to the homochiral diastereomers, although it is necessary to normalize the line strength ratio.The method assumes that the line strength of the specific diastereomer is a linear function of the concentrations of the analyte and of the tag.29 That is,
| AHetero = CHetero([R-tag][S-analyte] + [S-tag][R-analyte]) | (1) |
| AHomo = CHomo([R-tag][R-analyte] + [S-tag][S-analyte]) | (2) |
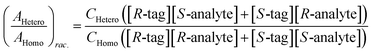 | (3) |
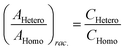 | (4) |
Then, the same two lines are compared in a spectrum using another portion of the same sample of the analyte, but with, say, enantiopure R-tag. Here, [S-tag] = 0, and
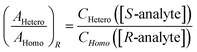 | (5) |
The ratio of ratios gives the relative concentrations of the enantiomeric forms of the analyte in the sample. The enantiomeric excess is found via
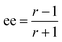 | (6) |
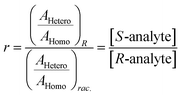 | (7) |
This process can be repeated for as many pairs of lines in the spectra of the two diastereomers as desired. It is necessary to choose unblended lines with line strengths that can be reliably determined. In practice, this will mean avoiding weak lines for which the relative uncertainty for the line strength can be quite large.
Spectra were taken of the blind mixture (Fig. 2, panels B–E), one each with racemic TFO (black trace, [rac]-tag) and R-TFO (grey trace, R-tag). For the TFO–SO heterochiral complex (RS), the line strengths of 45 unblended rotational transitions were measured and the same was done for 39 lines of the homochiral complex (RR). Transitions with SNR < 40 were discarded. The enantiomeric excess was calculated using all possible pairs of the lines, a total of 1755 pairs, and a histogram of the results is presented in panel F of Fig. 2. The individual results appear to be nearly normally distributed about a mean of 46.7% with a 95% confidence interval of ±0.2%. We note that this value assumes an optical purity of the tag of 100%. Considering the actual optical purity of the tag (99%) the ee mean value becomes 47.2%, which is numerically identical to the sample as prepared.
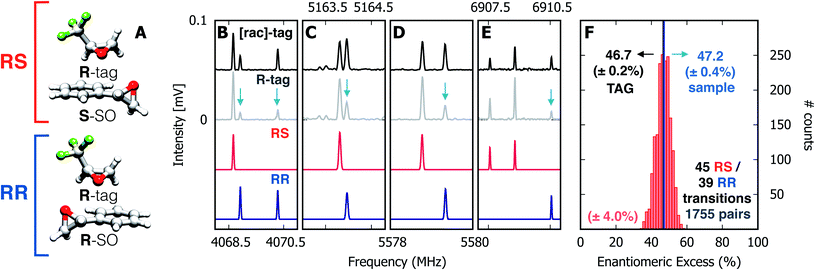 | ||
| Fig. 2 Enantiomeric excess determination using chiral tag rotational spectroscopy. (A) Diastereomeric complexes comprising R-TFO (R-tag) non-covalently bound to the S- and R-enantiomers of styrene oxide, forming RS and RR species, respectively. (B–E) Four sections of the microwave spectrum, highlighting the relative intensities of rotational transitions for the RS (in red) and RR (in blue) complexes in the presence of the enantiopure R-tag (grey trace) and the racemic tag (black trace). The red and blue traces are simulations based on the fitted spectroscopic parameters given in Table 1. The change in relative intensities ([rac]-tag vs. R-tag) for rotational transitions of RS and RR are highlighted with blue arrows as a guide to the eye. The ratio of intensities for RS and RR transitions indicates an over-population of RS complexes in the R-tag spectrum, readily indicating an excess of the S-enantiomer of SO in the sample mixture. (F) Histogram containing ee values retrieved from 1755 pairs of lines using eqn (6) and (7) with a standard deviation of ±4%. The normal distribution reveals a mean value of 46.7%with a 95% confidence interval of ±0.2%. | ||
4 Conclusions
In conclusion, we have assessed the performance of rotational spectroscopy to perform quantitative chiral analysis. This emerging field comprises two qualitatively different, often complementary techniques, namely M3WM and chiral-tag rotational spectroscopy. We have presented both techniques by analysing the ee of a blind sample of enantiomers of SO (47.2 ± 0.4% (S)). Both techniques provided satisfactory results when determining the chirality of the enantiomer in excess and delivered ee values of 49.8 ± 5.1% and 46.7 ± 0.2% for M3WM and the chiral tag approach, respectively. Although for many target systems either technique may be equally well applied, they each present some advantages and drawbacks that should be borne in mind when applying them to a particular system. Unquestionably, the absolute configuration of the enantiomer in excess can be confidently determined with both techniques. In chiral tagging, this determination is based on comparisons between calculated and experimental rotational constants and electric dipole moment features for both homo- and heterochiral diastereomer complexes. While in most cases these differences might be large enough to make a compelling assignment, the availability of full structural information through isotopic substitution is desirable to back such a determination. This can be particularly challenging for complex chiral mixtures with several chiral centers where the different diastereomers will likely have similar rotational constants and isotopic information is not available due to signal strength dilution. On the other hand, typical chiral molecules of biological interest bear nitrogen nuclei that will show configuration-dependent hyperfine rotational structure due to nuclear quadrupole coupling. This case unfolds the complexity of the assignment, but will assist in reaching a definite assignment for complex chiral mixtures. In this case, M3WM may be advantageous when enantiopure reference materials of known absolute configuration of the analyte are available as it can be applied regardless of the spectral complexity. Then, a simple comparison of the phase of the FIDs for both, reference and target samples at the listen frequency provides the absolute configuration of the sample (Fig. 1C). At the same time, this poses the main limitation of this technique when such reference samples are not available. There remains the need for an experimental procedure to directly extract the absolute configuration of the sample from the absolute phase of the emitted signal.When implementing either method for ee determination, it is in general interesting to consider two extreme cases where some difficulties might be encountered. First, if a mixture with low ee is considered, chiral tag rotational spectroscopy exhibits some features that will enable it to perform well in this situation. This is due to the fact that both homo- and heterochiral diastereomer complexes will form in large enough amounts to be detected experimentally with measurable signal strength. As the observed signal strength dictates the observations of isotopologues, this can be particularly advantageous to achieve the required isotopic sensitivity for absolute configuration determination without large amounts of sample. Additionally, this scenario usually provides a sufficient number of lines for both complexes, which translates into a large sample of pairs for ee determination. This makes the statistics robust and unsusceptible to undesired signal variations, which are more noticeable for weaker signals. As an example of this, with the current dataset, we have found a remarkable decrease in the spread of experimentally determined ee values when lines with a SNR < 55 are rejected. What is more, the choice of such lines makes the ee determination less dependent on the particular pairs chosen. On the other hand, in M3WM the enantiomer-sensitive signal strength is proportional to the ee, which gives rise to no signal for a racemic mixture. This provides a way to detect small ee in a background-free experiment.11 However, in practice, this can be troublesome when the line strength of the rotational spectrum is not high enough, which can be a common situation for ever larger systems. We have observed that due to the directional features of the chiral signal among other factors, the strength of the listen signal may be downsized to 15–20% of the direct excitation of the same transition, which in turn might prevent a detection of low ee.
The second scenario to consider is a sample with large ee. In this case, the particular features of M3WM can be exploited more efficiently. For the reasons mentioned above, while M3WM will be able to detect small signal variations from ee changes when the ee is large (large signal strength), chiral-tag spectroscopy might find trouble detecting weak signal from a molecular complex of an already low-abundance monomer. This leads to the observation of no to few lines for the minority enantiomer, which hinders the statistical ee determination.
Overall, the introduction of both techniques has opened uncharted avenues to apply molecular rotational spectroscopy to chiral analysis.44–46 Although there remains work to fully exploit the capabilities of rotational spectroscopy for quantitative chiral analysis, this mini-review illustrates the accomplishments so far and demonstrates clearly the promises of the two methods presented.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - Projektnummer 328961117 - SFB 1319 ELCH. The authors acknowledge the use of the GWDG and Maxwell computer clusters. This material is based on work supported by the National Science Foundation under Grant No. CHE-1856637. H. O. L. and M. D. M. gratefully acknowledge the H. Axel Schupf '57 Fund for Intellectual Life for support of the Faculty Research Awards Program at Amherst College and of sabbatical leaves.References
- A. Berthod, Anal. Chem., 2006, 78, 2093–2099 CrossRef.
- G. Gübitz and M. G. Schmid, Biopharm. Drug Dispos., 2001, 22, 291–336 CrossRef.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge Univ. Press, Cambridge, UK, 2004 Search PubMed.
- N. Berova and K. Nakanishi, Circular Dichroism: Principles and Applications, John Wiley & Sons, 2000 Search PubMed.
- L. A. Nafie, Vibrational Optical Activity: Principles and Applications, John Wiley & Sons, Ltd, Chichester, UK, 2011 Search PubMed.
- L. A. Nafie, T. A. Keiderling and P. J. Stephens, J. Am. Chem. Soc., 1976, 98, 2715–2723 CrossRef CAS.
- L. D. Barron, F. Zhu, L. Hecht, G. E. Tranter and N. W. Isaacs, J. Mol. Struct., 2007, 834, 7–16 CrossRef.
- M. A. J. Koenis, Y. Xia, S. R. Domingos, L. Visscher, W. J. Buma and V. P. Nicu, Chem. Sci., 2019, 10, 7680–7689 RSC.
- V. P. Nicu, E. J. Baerends and P. L. Polavarapu, J. Phys. Chem. A, 2012, 116, 8366–8373 CrossRef CAS.
- D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475 CrossRef CAS.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 023008 CrossRef.
- S. R. Domingos, C. Pérez and M. Schnell, Annu. Rev. Phys. Chem., 2018, 69, 499–519 CrossRef CAS.
- V. A. Shubert, D. Schmitz, C. Pérez, C. Medcraft, A. Krin, S. R. Domingos, D. Patterson and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 341–350 CrossRef CAS.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Kohler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 20, 5001–5005 CrossRef.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- A. Kastner, T. Ring, H. Braun, A. Senftleben and T. Baumert, ChemPhysChem, 2019, 20, 1416–1419 CAS.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Nat. Commun., 2013, 4, 2132 CrossRef.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Science, 2013, 341, 1096–1100 CrossRef CAS.
- P. Herwig, K. Zawatzky, M. Grieser, O. Heber, B. Jordon-Thaden, C. Krantz, O. Novotny, R. Repnow, V. Schurig, D. Schwalm, Z. Vager, A. Wolf, O. Trapp and H. Kreckel, Science, 2013, 342, 1084–1086 CrossRef CAS.
- K. Fehre, S. Eckart, M. Kunitski, M. Pitzer, S. Zeller, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Berger, R. Dörner and M. S. Schöffler, Sci. Adv., 2019, 5, eaau7923 CrossRef CAS.
- D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866–871 CrossRef CAS.
- S. Eibenberger, J. M. Doyle and D. Patterson, Phys. Rev. Lett., 2017, 118, 123002 CrossRef.
- C. Pérez, A. L. Steber, S. R. Domingos, A. Krin, D. Schmitz and M. Schnell, Angew. Chem., Int. Ed., 2017, 56, 12512–12517 CrossRef.
- D. W. Pratt and B. H. Pate, Angew. Chem., Int. Ed., 2017, 56, 16122–16124 CrossRef CAS.
- J.-U. Grabow, 70th International Symposium on Molecular Spectroscopy, 2015, p. MA02 Search PubMed.
- M. Quack, J. Stohner and M. Willeke, Annu. Rev. Phys. Chem., 2008, 59, 741–769 CrossRef CAS.
- C. Pérez, A. L. Steber, A. Krin and M. Schnell, J. Phys. Chem. Lett., 2018, 9, 4539–4543 CrossRef.
- L. Evangelisti, W. Caminati, D. Patterson, J. Thomas, Y. Xu, C. West and B. Pate, The 72nd International Symposium on Molecular Spectroscopy, Talk RG03, Urbana-Champaign, IL, 2017, DOI:10.15278/isms.2017.RG0328.
- B. H. Pate, L. Evangelisti, W. Caminati, Y. Xu, J. Thomas, D. Patterson, C. Pérez and M. Schnell, Chiral Analysis, Elsevier, 2nd edn, 2018, pp. 679–729 Search PubMed.
- D. Parker, Chem. Rev., 1991, 91, 1441–1457 CrossRef CAS.
- S. Zinn and M. Schnell, ChemPhysChem, 2018, 19, 2915–2920 CrossRef CAS.
- A. Zehnacker and M. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992 CrossRef CAS.
- D. L. Bryce and R. E. Wasylishen, Acc. Chem. Res., 2003, 36, 327–334 CrossRef CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- M. D. Marshall, H. O. Leung, K. Wang and M. D. Acha, J. Phys. Chem. A, 2018, 122, 4670–4680 CrossRef CAS.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef.
- G. Barratt Park and R. Field, J. Chem. Phys., 2016, 144, 200901 CrossRef.
- V. A. Shubert, D. Schmitz, C. Medcraft, A. Krin, D. Patterson, J. M. Doyle and M. Schnell, J. Chem. Phys., 2015, 142, 214201 CrossRef.
- K. K. Lehmann, J. Chem. Phys., 2018, 149, 094201 CrossRef.
- J.-U. Grabow, Angew. Chem., Int. Ed., 2013, 52, 11698–11700 CrossRef CAS.
- M. D. Marshall, H. O. Leung, M. Schnell, S. R. Domingos and A. Krin, The 74th International Symposium on Molecular Spectroscopy, Talk RH-02, Urbana-Champaign, IL, 2019 Search PubMed.
- A comprehensive analysis of the rotational spectrum, spectroscopic paramenters and structural details of the TFO–SO complexes will be reported in a separate manuscript.
- D. W. Armstrong, M. Talebi, N. Thakur, M. F. Wahab, A. V. Mikhonin, M. T. Muckle and J. L. Neill, Angew. Chem., Int. Ed., 2020, 59, 192–196 CrossRef CAS.
- L. A. Joyce, D. Schultz, E. C. Sherer, J. L. Neill, R. E. Sonstrom and B. H. Pate, Chem. Sci., 2020, 11, 6332–6338 RSC.
- J. L. Neill, A. V. Mikhonin, T. Chen, R. E. Sonstrom and B. H. Pate, J. Pharm. Biomed. Anal., 2020, 189, 113474 CrossRef CAS.
Footnote |
| † Present address: CFisUC, Department of Physics, University of Coimbra, 3004-516 Coimbra, Portugal. |
| This journal is © The Royal Society of Chemistry 2020 |





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 FIDs for both M3WM (D) and direct excitation (E) measurements. The mean value derived for the ee is 49.8 ± 5.1% (
000 FIDs for both M3WM (D) and direct excitation (E) measurements. The mean value derived for the ee is 49.8 ± 5.1% (