Exploring the self-assembly of dumbbell-shaped polyoxometalate hybrids, from molecular building units to nanostructured soft materials

Abstract

The formation of hierarchical nanostructures using preformed dumbbell-like species made of covalent organic–inorganic polyoxometalate (POM)-based hybrids is herein described. In this system, the presence of charged subunits (POM, metal linkers, and counter ions) in the complex molecular architecture can drive their aggregation, which results from a competition between the solvation energy of the discrete species and intermolecular electrostatic interactions. We show that the nature of the POM and the charge of the metal linker are key parameters for the hierarchical nanoorganization. The experimental findings were corroborated with a computational investigation combining DFT and molecular dynamics simulation methods, which outlines the importance of solvation of the counter ion and POM/counter ion association in the aggregation process. The dumbbell-like species can also form gels, in the presence of a poorer solvent, displaying similar nanoorganization of the aggregates. We show that starting from the designed molecular building units whose internal charges can be controlled by redox trigger we can achieve their implementation into soft nanostructured materials through the control of their supramolecular organization.

---

Introduction

The development of nanostructured soft materials through hierarchical self-assembly is drawing growing attention of scientists inspired by the structural complexity of natural systems.^1–3 These compounds involve a variety of interaction combinations that can lead to the emergence of innovative structures or even functionalities.⁴ Classical synthetic strategies of such artificial assemblies with multiple levels of organization rely on the use of molecular building units displaying orthogonal and switchable interactions (e.g. metal coordination, electrostatic and hydrophobic effects…).^5–7 In this context we recently described the hierarchical self-assembly of organic/inorganic polyoxometalate (POM)-based hybrids in which the POM is covalently bonded to remote binding sites.^8–10 POMs are nanosized polyanionic molecular metal-oxo clusters that constitute original building units for the elaboration of multi-functional materials^11–17 owing to their multiple properties (such as electron reservoirs)¹⁸ and sensitiveness to different interactions.^19–22 As they are polyanionic species they establish strong electrostatic interactions with cationic species. Furthermore, owing to their large size and their delocalized charges they display chaotropic behavior^23,24 and may give rise to self-assemblies with large association constants, albeit resulting from very weak interactions.²⁵ In our reported system, the coordination-driven self-assembly of a ditopic hybrid (displaying two remote terpyridine binding sites) in the presence of a cationic metal linker (Fe²⁺, Co²⁺ or Co³⁺) provided different supramolecular organizations (discrete metallomacrocycles, dense nanoparticles, and 1D worm-like nanoobjects), according to the solvent composition or the redox state of the metal ion. We concluded that the aggregation of the discrete metallomacrocycles combining negatively charged POMs and cationic metal linkers, resulted from a competition between the solvation energy of the discrete species with the electrostatic interactions between the charged units. In order to understand the thermodynamics of the formation of the discrete metallomacrocycles, we also compared the metal coordination behavior of two analogue ditopic building units differing by the nature (and hence the charge) of the POM (i.e. Keggin-versus Dawson-types).²⁶ This study outlined the decisive effect of the charge of the POM disfavouring the formation of large assemblies probably due to an important entropic contribution. This was confirmed by an isothermal titration calorimetry (ITC) experiment that confirmed the stronger association in the case of the Keggin hybrids. However, the analysis of the previous system was particularly intricate since mixtures of molecular triangles and squares were observed, which limited the interpretation. In order to simplify the system, we decided to investigate the self-assembly behavior of monotopic hybrids either in the Keggin or the Dawson series. We herein describe the formation of molecular dimers with dumbbell structures from these hybrids. We also show that these supramolecular systems are prone to aggregation according to the solvent composition and demonstrate that the difference in the nature of the POM, the charge of the metal linker or the solvent composition considerably affects the supramolecular organization, which in some cases lead to the formation of molecular gels retaining the initial nanostructuration. Since in previous studies some of us and other authors have shown that molecular dynamics (MD) simulations provided unique insight into the origin of POMs/counter-cation interactions,^27–32 we show here that the solvent plays a key role by modulating ion-pairing and thus self-assembly.

Results and discussion

Synthesis of the POM-based molecular units

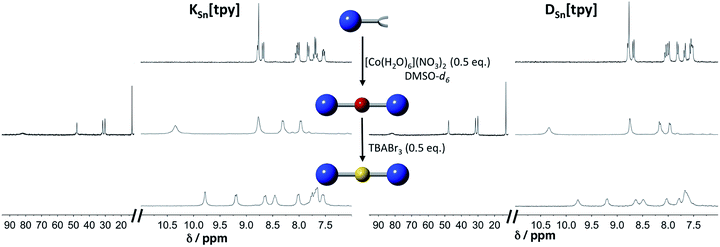
The POM-based building units [PW₁₁O₃₉{SnC₂₉H₁₈N₃}]^4- and [P₂W₁₇O₆₁{SnC₂₉H₁₈N₃}]^7- respectively denoted as K_Sn[tpy] and D_Sn[tpy]‡ contain one terpyridine (tpy) unit connected to the mono-lacunary site of a Keggin-([PW₁₁O₃₉]⁷⁻) and Dawson-(α₂-[P₂W₁₇O₆₁]¹⁰⁻) type polyoxotungstate. Their synthesis is performed in one step from the iodo-aryl terminated POM-based platforms K_Sn[I] and D_Sn[I] by adapting our reported procedure involving a Sonogashira cross-coupling reaction (Scheme 1).³³ The hybrid POMs are isolated as tetrabutyl ammonium (TBA) salts and characterized by ¹H and ³¹P NMR spectroscopy, mass spectrometry, elemental analyses and FTIR spectroscopy (Fig. S1–S4†).

Scheme 1 Synthetic route to K_Sn[tpy] and D_Sn[tpy] (in the polyhedral representation, the WO₆ octahedra are depicted with oxygen atoms at the vertices and metal cations buried inside). Color code: WO₆ octahedra, blue; PO₄ tetrahedra, green.

Formation and characterization of discrete molecular dumbbells

Terpyridine ligands produce a linear arrangement when coordinated to a metal center such as Co(II). The addition of [Co(H₂O)₆](NO₃)₂ to a solution of K_Sn[tpy] or D_Sn[tpy] (2 mM) in DMSO-d₆ instantly leads to the appearance of a single set of signals in the ¹H low-field region (above 10 ppm) attributed to the formation of paramagnetic Co(II) terpyridine complexes (Fig. 1). The reaction is complete after the addition of 0.5 equiv. of Co per POM hybrid, in agreement with the formation of a supramolecular species displaying a 2 : 1 stoichiometry between the POM and the metal linker. The ¹H signals of the supramolecular species (especially those of protons located at the vicinity of the metal centre) are considerably broadened compared to those of the parent hybrid K_Sn[tpy] or D_Sn[tpy] as a result of the paramagnetism of the Co(II) center. However, their linewidths are similar to those of a reference Co(II) bis-terpyridine complex (Fig. S5†), suggesting that the POM-based supramolecular compounds are discrete species in DMSO-d₆. The addition of tetrabutyl ammonium tribromide (0.5 equiv., 20 mM in DMSO-d₆) into a DMSO-d₆ solution containing K_Sn[tpy] or D_Sn[tpy] in the presence of 0.5 equiv. of [Co(H₂O)₆](NO₃)₂ leads to a rapid fading of the solution colour from bright orange to the characteristic yellow colour of the low-spin Co(III) bis(terpyridine) complex, the process being complete in a few minutes.

Fig. 1 ¹H NMR (300 MHz) in DMSO-d₆ solution containing K_Sn[tpy] (2 mM, top left) and D_Sn[tpy] (top right) in the presence of 0.5 equiv. of [Co(H₂O)₆](NO₃)₂ (middle); after oxidation of the Co(II) with 0.5 equiv. TBABr₃ (down).

The ¹H NMR spectra of the resulting species display well-resolved ¹H NMR signals, yet broader than those of the parent hybrid since transverse relaxation T₂ is faster for large molecules. No signal is observed above 10 ppm, indicating the absence of paramagnetic species. These studies suggest that in DMSO-d₆, all POM.Co^N complexes (in the following, POM.M^N stands for the supramolecular species displaying a 2 : 1 stoichiometry between the POM hybrid and the metal linker at the oxidation state N) behave as discrete species. Computational studies confirm the stability of the 2 : 1 supramolecular structures. The optimized DFT structures of K_Sn[tpy].Co^II, D_Sn[tpy].Co^II, K_Sn[tpy].Co^III and D_Sn[tpy].Co^III show an octahedral coordination of central cobalt (Fig. 2 and S6†). The most stable electronic and spin configuration for both Co(II) complexes is a paramagnetic doublet state with one unpaired electron in a orbital of sigma character, in which the d metal orbital and equatorial nitrogen atom lone pairs are involved. For Co(III) systems, the ground-state is a singlet low-spin. This difference in electronic configuration gives significant differences in Co–N distances, which are enlarged from 1.96 to 2.19 when going from K_Sn[tpy].Co^III to K_Sn[tpy].Co^II. While the energy-minimized structures of the dumbbell-like species K_Sn[tpy].Co^II and K_Sn[tpy].Co^III are almost identical (d_P–P = 4.29 nm for both structures), we observe a slight discrepancy in the structures of D_Sn[tpy].Co^II and D_Sn[tpy].Co^III. Keggin systems show more linear structures, than the corresponding Dawson complexes. Indeed, as D_Sn[tpy] lacks the additional pseudo symmetry plane found in K_Sn[tpy],²⁶ various conformers differing by the relative orientation between the Dawson units exist with D_Sn[tpy].Co^N. The conformational difference between the energy minimized structures of D_Sn[tpy].Co^II and D_Sn[tpy].Co^III (d_P1–P1 = 4.19 and 4.16 nm, d_P2–P2 = 4.94 and 4.65 nm for D_Sn[tpy].Co^II and D_Sn[tpy].Co^III respectively) does not correspond to a specific structural modification upon the change of the Co centre charge but mostly reflects the structural diversity of the Dawson-based dumbbell-like species D_Sn[tpy].Co^N.

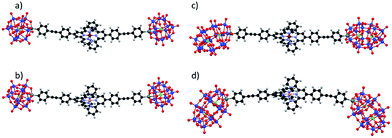Fig. 2 Energy-minimized structures of the dumbbell-like species K_Sn[tpy].Co^II (a), K_Sn[tpy].Co^III (b), D_Sn[tpy].Co^II (c) and D_Sn[tpy].Co^III (d).

We performed small-angle X-ray scattering (SAXS) to complete the characterization of the dumbbell-like species in DMSO-d₆.

SAXS is a powerful technique to characterize the structures of large synthetic molecules, molecular assemblies, nanoparticles³⁴ and aggregates with sizes ranging from 1 to 100 nm.^35,36 With regard to POM chemistry, we and others have shown that this technique is particularly well-suited to characterize nanosized metal-oxo cluster assemblies.^8,9,37–41 A significant SAXS signal is visible for both molecular building units, consistent with well-dispersed nanometric objects (Fig. 3). Electrostatic interactions between the POMs result in a small decrease in intensity at small wave vectors, which prevents the observation of the Guinier regime as previously observed.^8–10,41 The SAXS diagrams of all dumbbell-like Co(II) and Co(III) complexes display oscillations as we have observed in other supramolecular systems.^8,9 These oscillations reveal characteristic distances larger than the POM dimension and have, in the low q region, a higher intensity than the starting building units, as a consequence of larger structures. Interestingly, for both hybrids, the SAXS pattern of the Co(II) and Co(III) complexes is almost identical, even in the low q region, which indicates that neither the structure nor the dispersion of the supramolecular systems is altered by the change in the redox state of the metal linker. To confirm the structure of the dumbbell-shaped species, theoretical SAXS patterns of the energy-minimized structures of the POM-based building units and molecular dimers have been computed using the program CRYSOL⁴² without any adjustment of free parameters (Fig. 3 and S7†). For both dumbbells, the theoretical intensity is very similar to the experimental that in the SAXS patterns. In particular, the two oscillations and the intensity at small q values (neglecting the decrease in intensity below 0.04 Å⁻¹ caused by the electrostatic interactions) are nicely reproduced, which further supports the structure and the discrete character of the dumbbell-like species in DMSO-d₆. It should be noted that despite the slight discrepancy between the energy-minimized structures of D_Sn[tpy].Co^II and D_Sn[tpy].Co^III, their computed SAXS patterns are very similar (Fig. S7†).

Fig. 3 SAXS pattern of a 1 mmol solution of the molecular building-units K_Sn[tpy] (left, black curve) and D_Sn[tpy] (right, black curve) in DMSO-d₆, and their resulting dumbbell-shaped Co(II) (red curves) and Co(III) (blue curves) complexes and the computed SAXS pattern (CRYSOL) of the optimized structures of K_Sn[tpy].Co^III and D_Sn[tpy].Co^III (dotted black). The solvent and the capillary were subtracted to obtain these patterns.

Comparison of the complexation energy between the Keggin-type and Dawson-type POM-based hybrids

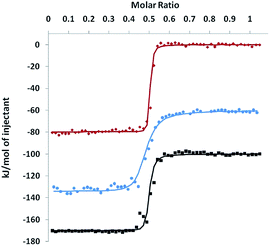
In order to probe the thermodynamics of the formation of these complexes, an isothermal titration calorimetry (ITC) experiment was performed. A solution of [Co(H₂O)₆](NO₃)₂ in DMSO (2.2 mM) was incrementally injected into a solution of K_Sn[tpy], D_Sn[tpy] or 4′-(4-ethynylphenyl)-2,2′:6′,2′′-terpyridine (a terpyridine reference) in DMSO. The resulting isotherms are displayed in Fig. 4. For all compounds, the exothermal heat effects show an inflection point at a molar ratio of 0.5, which implies that the stoichiometry of the assembly is 2 : 1. Therefore, calorimetric data were fitted according to a model considering the formation of the 2 : 1 assembly directly from the free species. To perform such analysis, the sequential binding site model was used with the number of sites equal to 2, but with a formation constant of the 1 : 1 assembly fixed to 1. The values of fitted parameters are summarized in Table 1. For the terpyridine reference compound, the strong affinity results from a strong enthalpy stabilization (70.1 kJ.mol⁻¹) that is compensated by a weak entropic destabilization (−10.7 J.K⁻¹.mol⁻¹). Indeed, the overall reaction leads to the removal of the molecules previously coordinated to the Co(II) centre, which lowers the entropic cost. The complexation of K_Sn[tpy] and D_Sn[tpy] follows a similar trend but with different association constants. The enthalpic stabilization is more important with the POM-based hybrids and especially with K_Sn[tpy]. This is attributed to the coulombic interactions related to the intramolecular POM–Co and POM–POM interactions. If we neglect the overall contributions of the TBA cations in the electrostatic interactions, the coulombic work term associated with the complexation of the Co(II) centre is a balance between the attractive POM–Co and repulsive POM–POM interactions.
According to the energy minimized structures R_POM–Co = 2.2 nm and 2.3 nm and R_POM–POM = 4.3 nm and 4.6 nm, (the centre of the POM is estimated to be the P atom for K_Sn[tpy] and the midway point between the two P atoms for D_Sn[tpy]) for K_Sn[tpy].Co^II and D_Sn[tpy].Co^II respectively.

Fig. 4 ITC isotherm obtained by injecting a [Co(H₂O)₆](NO₃)₂ solution in DMSO (2.2 mM) into a K_Sn[tpy] (red), D_Sn[tpy] (blue, with a vertical shift of −60 kJ.mol⁻¹) or 4′-(4-ethynylphenyl)-2,2′:6′,2′′-terpyridine (black, with a vertical shift of −100 kJ.mol⁻¹) solution in DMSO (0.385, 0.150 and 0.385 mM, respectively) at 25 °C. The lines correspond to fits according to a model considering a direct formation of the 2 : 1 assembly.

Table 1 Thermodynamic parameters for the binding of the POM-based hybrids and the terpyridine reference compound to [Co(H₂O)₆](NO₃)₂

Ligand	K/M^−2	ΔH/kJ mol^−1	ΔS/J K^−1 mol^−1
KSn[tpy]	3.48 × 10^12	−79.7	−27.4
DSn[tpy]	1.10 × 10^11	−74.1	−37.0
4′-(4-Ethynylphenyl)-2,2′:6′,2′′-terpyridine	5.28 × 10^11	−70.1	−10.7

---

The calculated electrostatic stabilization energies are 10.6 kJ mol⁻¹ (K_Sn[tpy]) and 4.5 kJ mol⁻¹ (D_Sn[tpy]) in excellent agreement with the enthalpic differences observed between the POM-based hybrids and the terpyridine reference. Simple calculations thus show that an optimum electrostatic interaction occurs when q_POM = 2q_Coi.e. for K_Sn[tpy]. The comparison of the entropy of the complexation of all systems shows that it is significantly higher for the POM-based hybrids than for the terpyridine reference. Furthermore, D_Sn[tpy] has a higher entropic destabilization, than K_Sn[tpy] as previously suggested for the complexation of ditopic POM-based hybrids.²⁶

Aggregation of the molecular dumbbells

The coordination of K_Sn[tpy] and D_Sn[tpy] by [Co(H₂O)₆](NO₃)₂ in CD₃CN, leads to the appearance of broad and ill-defined signals in the ¹H low-field region (Fig. S8 and S9†) characteristic of colloidal systems while the solutions remain homogeneous and instantly displays the characteristic reddish orange coloration of Co(II) bis-terpyridine complexes. Similarly, the addition of CD₃CN or D₂O to a solution of the discrete dumbbell-shaped species in DMSO-d₆, leads to the drastic broadening of the ¹H signals. The aggregation of the dumbbell-shaped species was investigated by SAXS. We evaluated with this modular system the effect of the nature of the POM (K_Sn[tpy]versusD_Sn[tpy]) and the charge of the metal linker (Co²⁺versus Co³⁺) on the size and nano-organization of the aggregates. As expected, the SAXS patterns of the aggregates display an increase of the intensity in the low q region compared to the starting POM-based hybrid in solution at a similar concentration. Considering that the intensity in the low q region is proportional to the molar mass of the molecular system, the evaluation of the intensity allows us to estimate the number of POMs and hence of dumbbell-shaped species per aggregate. We observe that some POM-based assemblies display a decrease in intensity at small wave vectors.

This effect, attributed to the electrostatic interactions between the POM assemblies, is more pronounced with the Co²⁺ linker and with Dawson-type POMs. As all solutions contain the same initial concentration of hybrid POMs, large aggregates have lower concentrations. The amplitude of the decrease at low q is in agreement with the concentration (and hence the size) of the aggregate (Table 2). Finally, for all SAXS patterns, the oscillations corresponding to the discrete species, displayed in Fig. 3, are not observed anymore. However, each SAXS pattern exhibits two new peaks at intermediate q values (0.3 Å⁻¹ < q < 0.5 Å⁻¹) denoted as q₁ and q₂, which were not present for the discrete dumbbell-like species in DMSO-d₆. These peaks, which were also observed in previous POM-based aggregates,^9,10 arise from the nanostructured features of the aggregates and correspond to POM–POM correlations within the aggregates (Fig. 5 and S10–S13†). The data extracted from the SAXS analysis are listed in Table 2. Typically, the aggregates made of K_Sn[tpy] contain much more POM building units than those of D_Sn[tpy]. Furthermore, the q₁ and q₂ peaks are more intense for the Keggin system than for the Dawson one, probably as a consequence of the lower nuclearity of the Dawson aggregates (and hence the less important numbers of POM–POM interactions within these aggregates). Finally, one can observe that increasing the charge of the metal linker leads to the formation of bigger aggregates with shorter POM–POM distances (e.g. higher q₁ and q₂ values) owing to increased electrostatic interactions between the POMs and the Co complexes. These results indicate that the aggregation is favoured (bigger aggregates with shorter POM–POM distances) when the charge of the metal linker approaches that of the POM.

Table 2 Data extracted from the SAXS curves of K_Sn[tpy].Co^II, K_Sn[tpy].Co^III, D_Sn[tpy].Co^II, and D_Sn[tpy].Co^III in CD₃CN solution, d = 2π/q. The value noted in bold corresponds to the main peak

Compound	Nber dimers	q 1/Å^−1	d 1/Å	q 2/Å^−1	d 2/Å
KSn[tpy].Co^II	10–12	0.344	18.3	0.464	13.5
KSn[tpy].Co^III	50–60	0.350	18.0	0.481	13.1
DSn[tpy].Co^II	2–3	0.311	20.2	0.426	14.8
DSn[tpy].Co^III	3–4	0.323	19.5	0.426	14.8

---

Fig. 5 SAXS pattern of a 1 mmol solution of the molecular building-unit K_Sn[tpy] (left, black curve) and D_Sn[tpy] (right, black curve) and the resulting aggregates POM.Co^II (red curves) and POM.Co^III (blue curves) assemblies in CD₃CN (respectively obtained upon the addition of 0.5 equiv. [Co(H₂O)₆](NO₃)₂ and further oxidation of the Co(II) with 0.5 equiv. TBABr₃). The solvent and the capillary were subtracted to obtain these patterns.

Transmission electron microscopy (TEM) of the aggregates K_Sn[tpy].Co^II and K_Sn[tpy].Co^III in MeCN was performed after the deposition of few drops of solutions containing the supramolecular assemblies dispersed in MeCN on a Cu grid covered with an amorphous carbon film. The resulting micrographs of K_Sn[tpy].Co^II and K_Sn[tpy].Co^III only show ill-defined aggregates of few nanometers (5 to 20 nm) probably due to the removal of the solvent (imposed by the high vacuum conditions), while the solvent certainly plays a key role in maintaining the structuration of the aggregates. Nevertheless we observe that the aggregates of K_Sn[tpy].Co^III are slightly bigger than those of K_Sn[tpy].Co^II, in agreement with SAXS (Fig. S14†).

Molecular dynamics simulation

The electrostatic potential maps in Fig. 6 illustrate the charge distribution of K_Sn[tpy].Co^III that identifies two regions of opposite charge within the molecular system: the POM region, which shows a high negative charge, and the Co(III) region that shows a relatively high positive charge. This opens the possibility of intermolecular aggregation by means of complementary coulombic electrostatic interactions. Due to the high negative charge of POMs, aggregation is expected to strongly depend also on the competitive interactions with the counter-cations and the solvent. Thus, explicit treatment of solvent and cations (TBA) is needed to describe the behaviour of dumbbell-type hybrid POMs in solution (DMSO and water). It should be noted that SAXS studies conducted in DMSO/water mixtures also indicated the formation of aggregates (Fig. S15†). Through MD simulations we investigated the aggregation phenomena and the factors on which they depend. Our analysis connects the intermolecular hybrid POM aggregate formation with the solvent dependence of the POM/TBA interactions. We analysed each phenomenon separately. First, we present the results of the structural features of K_Sn[tpy].Co^III anion-pairs formed spontaneously during MD simulations, and secondly the key role of TBA cations and the solvent in the aggregation process. Simulations starting from a model constructed by randomly distributed K_Sn[tpy].Co^III units in the simulation box led to the spontaneous formation of aggregates, pairs and even a trimer, in water but not in DMSO.

Fig. 6 Computed electrostatic potential map of K_Sn[tpy].Co^III.

The distance distribution function (g(r)) between a POM (P atom) of one K_Sn[tpy].Co^III unit and the Co atom of the other unit, computed from the whole trajectories, permits analyzing the dynamical structure of the solution. We performed this analysis for the two solvents as shown in Fig. 7 and S16.† In water, g(r) reveals high and well defined peaks at short distances (∼9 Å) indicating close contacts between different units. In contrast, no peaks exist at short distances for DMSO. Visual inspection of the trajectory showed formation of K_Sn[tpy].Co^III pairs by means of the expected electrostatic interactions between the two distinctly charged regions of the hybrid POM, that led to a dimer structure depicted in Fig. 7. It should be noted that when we started the simulation from a pre-organized PACKED setup, the peaks in Fig. 7 (right side) totally match those of the UNPACKED setup (see the description of the MD simulation setup in the ESI† file), in position but not in intensity due to the presence of the pre-organized tetramer. Therefore, this confirms that the coulombic aggregation patterns are maintained in assemblies of different building units in water. Interestingly, by computing g(r) between the two POMs (P atom) of different forms of K_Sn[tpy].Co^III units, we can observe at a close distance (below 2 nm) a peak at 14.7 Å and a broader set of peaks between 17.0 and 18.5 Å (Fig. 7 and S17†2). These values are in very good agreement with SAXS that indicates two preferential POM–POM short distances within the aggregates. We simulated the scattering data of six snapshots of tetramer aggregates (Fig. S18†). Each simulated SAXS pattern displays two broad peaks at ca. 0.35 Å⁻¹ and 0.45 Å⁻¹ in perfect agreement with the experimental SAXS data. Going from DMSO to water we observed an increase in the number of K_Sn[tpy].Co^III pairs, and realized that the number of TBA cations around the anions also seemed to increase. Aimed at analysing whether TBA played some role in the aggregation process, we computed g(r) between the negative region of POM (P atom) and TBA cations. Indeed, the results in Fig. 7 show intense peaks in water and not in DMSO. Hence, though TBA molecules are strongly associated with dumbbells in water solution, they are much more labile in DMSO. Actually, the distance distribution function between TBA cations also reveals strong differences in the behaviour of TBA in the different solvents (Fig. S19†). TBA cations partly aggregate in water, but they are very well solvated in DMSO. Thus, there is a strong correlation between aggregation and TBA association, the higher the POM/TBA association, the higher the aggregation.

Fig. 7 Top left: distance distribution functions (g(r)) between a POM (P atom) of one K_Sn[tpy].Co^III unit and the Co atom of the other unit for the UNPACKED setup in water (blue) and in DMSO (pink). Middle: g(r) between POM (P atom) of one K_Sn[tpy].Co^III unit and the Co atom of the other unit for initial setups UNPACKED (blue) and PACKED (green) in water. Right: g(r) between two POMs (P atom) of different K_Sn[tpy].Co^III units for initial setups UNPACKED (blue) and PACKED (green) in water. Bottom left: distance distribution functions g(r) between POM and TBA for the UNPACKED setup in water (orange) and DMSO (purple). Snapshots: spontaneously formed dimer in the UNPACKED setup (blue), and tetramer in the PACKED setup (green). TBA ions colored pinkish; POM oxygens colored red; organic chains colored blue.

We observed the different steps that led to the formation of a K_Sn[tpy].Co^III dimeric pair for the UNPACKED setup in water (Fig. 8). The most important feature that can be extracted is that TBA counter cations assist the formation of the dimers. The first step is a POM–POM anchorage mediated by TBA cations. Two TBA cations, which are associated with each POM, interact excluding water between them, by forming a supramolecular POM–TBA–TBA–POM assembly. Then, in the second step organic chain–TBA interactions come into play. TBA maintains the contact with the organic chain, and triggered by POM–Co(III) coulombic driving force, a kind of K_Sn[tpy].Co^III walking along the chain was recorded. In this movement TBA cations help to avoid POM–POM repulsion. Subsequently, in the last step of this walking, the first Co(III)–POM contact is rather stable. Afterwards, in step four, like in a Ferris wheel, both dumbbells units rotate around the POM–Co axis until reaching the second POM–Co(III) interaction, which leads to the formation of the anion–anion dimeric pair, the pattern of aggregation of assemblies of different subunits. Also in this case TBA helps to avoid POM–POM repulsion. This marvellous sequence of movements assisted by TBA leads to the formation of aggregates in water. In contrast, as no TBA cations are associated with POM in DMSO, dimeric pair formation is not favoured.

Fig. 8 Time-evolution snapshots of dumbbell–dumbbell dimer assisted by TBA counter cations.

Formation of nanostructured gels

With the aim of isolating the different dumbbell species, we observed that the solutions of K_Sn[tpy].Co^III and D_Sn[tpy].Co^III in DMSO-d₆, quickly precipitate in the presence of an excess of ethanol or ethanol/diethyl ether (2/1) for K_Sn[tpy].Co^III and D_Sn[tpy].Co^III, respectively. After washing with pure ethanol, the resulting precipitates appear as a gel containing ca. 7% of the hybrids (Fig. 9a), according to thermogravimetric analysis (TGA). When the resulting organogels are dipped into aqueous solution they initially float, owing to the lower density of ethanol compared to water. After a few minutes they start to sink into the aqueous solution suggesting the exchange of ethanol molecules by water. The formation of a hydrogel was confirmed by TGA, which shows that the resulting systems contain ca. 5% of the hybrid POMs and lose the solvent molecules at higher temperature, in agreement with the difference of volatility between ethanol and water (Fig. 9b and S20†). The organogels of K_Sn[tpy].Co^II and D_Sn[tpy].Co^II can also form upon the addition of an excess of ethanol/diethyl ether (2/1) to solutions of the dumbbell species in DMSO-d₆ solution, followed by washing with ethanol. SAXS analysis of all organogels was performed to complete their characterization (Fig. 10a). All SAXS curves display a rather intense peak at q values between 0.2 and 0.7 Å⁻¹ (similar to previously observed values in CD₃CN) suggesting that some nano-organization is maintained in the organogels. Similarly, the trends previously described for q₁ and q₂ for the aggregates in CD₃CN are also observed for the organogels (Table 3 and Fig. S21–S24†).

Fig. 9 (a) Ethanol organogel of K_Sn[tpy].Co^III. (b) Thermogravimetric analysis of K_Sn[tpy] (black) and K_Sn[tpy].Co^III as an ethanol organogel (red) and hydrogel (blue).

Fig. 10 (Left) SAXS pattern the POM.Coⁿ organogels: K_Sn[tpy].Co^III (plain blue), K_Sn[tpy].Co^II (plain red), D_Sn[tpy].Co^III (dotted blue) and D_Sn[tpy].Co^III (dotted red). (Right) Evolution of the SAXS pattern of K_Sn[tpy].Co^III under successive acquisitions; the bold blue and red lines correspond to the first and last scans respectively. The solvent and the capillary were subtracted to obtain these patterns.

Table 3 Data extracted from the SAXS curves of K_Sn[tpy].Co^II, K_Sn[tpy].Co^III, D_Sn[tpy].Co^II, and D_Sn[tpy].Co^III as organogels, d = 2 π/q. The value noted in bold correspond to the main absorption peak

Compound	Scan	q 1/Å^−1	d 1/Å	q 2/Å^−1	d 2/Å
KSn[tpy].Co^II	1^st	0.369	17.0	0.477	13.2
KSn[tpy].Co^III	1^st	0.354	17.7	0.492	12.8
	5^th	0.364	17.2	0.486	12.9
DSn[tpy].Co^II	1^st	0.332	18.9	0.417	15.1
DSn[tpy].Co^III	1^st	0.344	18.3	0.437	14.4
	5^th	0.343	18.3	0.433	14.5

---

For instance, q₁ and q₂ values are higher in the Keggin systems than in the Dawson ones and the gels with the Co(III) metal linker display higher q₁ and q₂ values than the POM.Co^II gels. For all compounds, the SAXS intensity keeps increasing for q → 0 with a slope of ca. q⁻², which suggests that the gels have a lamellar organization (Fig. S25†). Interestingly the POM.Co^III systems evolve under the X-ray beam during successive SAXS acquisition at the synchrotron (Fig. 10b and S26†), which was evidenced by a local colour change (from orange to red) after beam exposure. We performed 5 successive acquisitions separately and noticed that the peaks at ca. 0.4–0.5 Å⁻¹ continuously shift towards smaller q values in agreement with the partial formation of POM.Co^II (Table 3), the effect being more pronounced for the Keggin than the Dawson-based system. It seems likely that the gel formation arises from the nano-organization of the POM-based dumbbells that is imposed by the electrostatic interactions between the charged moieties. These interactions maintain the POMs at a controlled distance in the aggregates. This leaves some void, which is filled with the solvent molecules. When the solvent molecules evaporate the gel irreversibly collapses in order to fill the voids. The intermolecular interactions between the dumbbells species are thus, in this system, at the basis of the formation of the gels. Smart materials with controllable properties can be obtained when the interplay between the intermolecular interactions within the molecular material is properly understood.⁴³ The properties and performance of these materials notably depend on the spatial organization and the distances between the components.⁴⁴ In the present system, the redox state of the metal linker of the gels can be photoswitched resulting in the modification of the POM–POM distances. These soft nanostructured materials thus have potential applications as redox-responsive smart materials.

Conclusions

We reported the formation of a series of discrete dumbbell-like POM-based hybrids displaying positive and negative charges. These complex molecular architectures, that differ by the nature of the POM (Keggin versus Dawson) and the charge of the cobalt linker (2+ and 3+) are able to further self-assemble into different hierarchical species (aggregates of different size, nanostructured gels) owing to a competition between the solvation energy of the discrete species and intermolecular electrostatic interactions. In DMSO, a strongly dissociating solvent, the systems behave as discrete species and were thoroughly characterized by combination of ¹H NMR spectroscopy, SAXS and DFT calculations. The formation of the dumbbell-like species in DMSO was also studied by ITC. These measurements showed that the metal coordination to the POM-based building unit was reinforced by coulombic interactions between the POMs and the metal linker and counter balanced by an entropic cost associated with the POM (the Dawson entropic contribution being more important than that of the Keggin). When lowering the dissociating character of the solvent or in the presence of a protic solvent the aggregation of the species occurred. In MeCN, we observed by SAXS the formation of nanostructured aggregates of different sizes according to the nature of the POM and the charge of the cobalt linker. We concluded that aggregation is favoured (bigger size and shorter POM–POM distances) when the charge of the metal linker approaches that of the POM. Molecular dynamics simulations, in combination with DFT calculations, corroborated that the dumbbell-like species are discrete in DMSO and that they aggregate in H₂O. Interestingly, the computational results outlined the non-innocent role of the TBA counter ions in the aggregation process. Typically, the aggregation occurs when some TBA cations are strongly associated with the POMs and assist the interaction between the molecular dumbbells. Finally, we observed the formation of gels in the presence of ethanol. In this case the solvation energy of the aggregate becomes too low and promotes precipitation. SAXS analysis of the gel indicated that the gel retained some nanostructural features of the aggregates. We thus showed that starting from the designed molecular building units of controlled size and topologies we can achieve their implementation into soft nanostructured materials through the control of their supramolecular organization.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Carlos Afonso and Hélène Lavanant for assistance in mass spectrometry measurments. We also thank Javiez Perez and Thomas Bizien for assistance in using beamline SWING. SOLEIL Synchrotron is acknowledged for providing beamtime and synchrotron radiation facilities. This work was supported by the French National Research Agency (EXPAND Project Grant ANR 14-CE08-0002). The authors thank the ICIQ Foundation, CERCA Program and AGAUR (grant 2017SGR00290) of the Generalitat de Catalunya, and the Spanish Ministerio de Ciencia, Innovacion y Universidades through project CTQ2017-88777-R for financial support.

Notes and references

1. G. M. Whitesides, J. K. Kriebel and B. T. Mayers, Self-Assembly and Nanostructured Materials, Springer, Berlin, 2005.
2. A. Babloyantz, Molecules, Dynamics, and Life: An Introduction to Self-Organization of Matter, John Wiley & Sons, New York, 1986.
3. Y. Sun, C. Y. Chen and P. J. Stang, Acc. Chem. Res., 2019, 52, 802.
4. P. Luisi, Found. Chem., 2002, 4, 183.
5. S. Datta, M. L. Saha and P. J. Stang, Acc. Chem. Res., 2018, 51, 2047.
6. C. Rest, R. Kandanelli and G. Fernandez, Chem. Soc. Rev., 2015, 44, 2543.
7. Y. Yan and J. B. Huang, Coord. Chem. Rev., 2010, 254, 1072.
8. G. Izzet, B. Abécassis, D. Brouri, M. Piot, B. Matt, S. A. Serapian, C. Bo and A. Proust, J. Am. Chem. Soc., 2016, 138, 5093.
9. M. Piot, B. Abécassis, D. Brouri, C. Troufflard, A. Proust and G. Izzet, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8895.
10. R. Salles, B. Abécassis, E. Derat, D. Brouri, A. Bernard, Q. C. Zhang, A. Proust, C. Desmarets and G. Izzet, Inorg. Chem., 2020, 59, 2458.
11. Y. F. Song and R. Tsunashima, Chem. Soc. Rev., 2012, 41, 7384.
12. A. Proust, B. Matt, R. Villanneau, G. Guillemot, P. Gouzerh and G. Izzet, Chem. Soc. Rev., 2012, 41, 7605.
13. M. P. Santoni, G. S. Hanan and B. Hasenknopf, Coord. Chem. Rev., 2014, 281, 64.
14. G. Izzet, F. Volatron and A. Proust, Chem. Rec., 2017, 17, 250.
15. M. Stuckart and K. Y. Monakhov, Chem. Sci., 2019, 10, 4364.
16. A. V. Anyushin, A. Kondinski and T. N. Parac-Vogt, Chem. Soc. Rev., 2020, 49, 382.
17. L. J. Ren, H. K. Liu, H. Wu, M. B. Hu and W. Wang, Adv. Mater., 2020, 32.
18. M. Sadakane and E. Steckhan, Chem. Rev., 1998, 98, 219.
19. B. Li, W. Li, H. L. Li and L. X. Wu, Acc. Chem. Res., 2017, 50, 1391.
20. A. Misra, K. Kozma, C. Streb and M. Nyman, Angew. Chem., Int. Ed., 2020, 59, 596.
21. H. N. Miras, J. Yan, D. L. Long and L. Cronin, Chem. Soc. Rev., 2012, 41, 7403.
22. P. C. Yin, D. Li and T. B. Liu, Chem. Soc. Rev., 2012, 41, 7368.
23. K. I. Assaf and W. M. Nau, Angew. Chem., Int. Ed., 2018, 57, 13968.
24. T. Buchecker, P. Schmid, S. Renaudineau, O. Diat, A. Proust, A. Pfitzner and P. Bauduin, Chem. Commun., 2018, 54, 1833.
25. M. A. Moussawi, N. Leclerc-Laronze, S. Floquet, P. A. Abramov, M. N. Sokolov, S. Cordier, A. Ponchel, E. Monflier, H. Bricout, D. Landy, M. Haouas, J. Marrot and E. Cadot, J. Am. Chem. Soc., 2017, 139, 12793.
26. M. Piot, S. Hupin, H. Lavanan, C. Afonso, L. Bouteiller, A. Proust and G. Izzet, Inorg. Chem., 2017, 56, 8490.
27. M. K. Bera, B. F. Qiao, S. Seifert, B. P. Burton-Pye, M. O. de la Cruz and M. R. Antonio, J. Phys. Chem. C, 2016, 120, 1317.
28. Y. Mei, W. Huang, Z. Yang, J. Wang and X. N. Yang, Fluid Phase Equilib., 2016, 425, 31.
29. S. A. Serapian and C. Bo, J. Phys. Chem. B, 2016, 120, 12959.
30. D. Sures, M. Segado, C. Bo and M. Nyman, J. Am. Chem. Soc., 2018, 140, 10803.
31. M. Segado, M. Nyman and C. Bo, J. Phys. Chem. B, 2019, 123, 10505.
32. A. Sole-Daura, A. Notario-Estevez, J. J. Carbo, J. M. Poblet, C. de Graaf, K. Y. Monakhov and X. Lopez, Inorg. Chem., 2019, 58, 3881.
33. V. Duffort, R. Thouvenot, C. Afonso, G. Izzet and A. Proust, Chem. Commun., 2009, 6062.
34. J. Maes, N. Castro, K. De Nolf, W. Walravens, B. Abecassis and Z. Hens, Chem. Mater., 2018, 30, 3952.
35. A. Guinier and G. Fournet, Small Angle Scaterring of X-Rays., Wiley, New York, 1955.
36. J. Als-Nielsen and D. McMorrow, Elements of Modern X-ray Physics, Wiley, New York, 2001.
37. M. Li, W. Y. Wang and P. C. Yin, Chem.–Eur. J., 2018, 24, 6639.
38. M. Nyman, Coord. Chem. Rev., 2017, 352, 461.
39. Y. L. Wu, R. F. Shi, Y. L. Wu, J. M. Holcroft, Z. C. Liu, M. Frasconi, M. R. Wasielewski, H. Li and J. F. Stoddart, J. Am. Chem. Soc., 2015, 137, 4111.
40. V. Jallet, G. Guillemot, J. Lai, P. Bauduin, V. Nardello-Rataj and A. Proust, Chem. Commun., 2014, 50, 6610.
41. G. Izzet, A. Macdonell, C. Rinfray, M. Piot, S. Renaudineau, E. Derat, B. Abécassis, C. Afonso and A. Proust, Chem.–Eur. J., 2015, 21, 19010.
42. D. Svergun, C. Barberato and M. H. J. Koch, J. Appl. Crystallogr., 1995, 28, 768.
43. A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686.
44. A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002.

---

Footnotes

† Electronic supplementary information (ESI) available: general methods, synthetic protocols, NMR spectra, ESI MS spectra, SAXS fits, TEM micrographs and MD simulation setups. See DOI: 10.1039/d0sc03243c

‡ Acronyms used for the hybrid POMs: K and D refer to the Keggin- and Dawson-type anions respectively, Sn as a subscript relates to the primary functionalization and the term in brackets corresponds to the remote organic moieties.

---