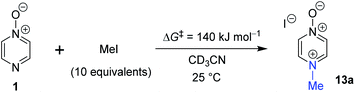Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Competition between N and O: use of diazine N-oxides as a test case for the Marcus theory rationale for ambident reactivity†
Kevin J.
Sheehy
 a,
Lorraine M.
Bateman
a,
Lorraine M.
Bateman
 abd,
Niko T.
Flosbach
c,
Martin
Breugst
abd,
Niko T.
Flosbach
c,
Martin
Breugst
 *c and
Peter A.
Byrne
*c and
Peter A.
Byrne
 *ad
*ad
aSchool of Chemistry, Analytical and Biological Chemistry Research Facility, University College Cork, College Road, Cork, Ireland. E-mail: peter.byrne@ucc.ie
bSchool of Pharmacy, University College Cork, College Road, Ireland
cDepartment für Chemie, Universität zu Köln, Greinstraße 4, 50939 Köln, Germany. E-mail: mbreugst@uni-koeln.de
dSSPC (Synthesis and Solid State Pharmaceutical Centre), Cork, Ireland
First published on 23rd July 2020
Abstract
The preferred site of alkylation of diazine N-oxides by representative hard and soft alkylating agents was established conclusively using the 1H–15N HMBC NMR technique in combination with other NMR spectroscopic methods. Alkylation of pyrazine N-oxides (1 and 2) occurs preferentially on nitrogen regardless of the alkylating agent employed, while O-methylation of pyrimidine N-oxide (3) is favoured in its reaction with MeOTf. As these outcomes cannot be explained in the context of the hard/soft acid/base (HSAB) principle, we have instead turned to Marcus theory to rationalise these results. Marcus intrinsic barriers (ΔG‡0) and ΔrG° values were calculated at the DLPNO-CCSD(T)/def2-TZVPPD/SMD//M06-2X-D3/6-311+G(d,p)/SMD level of theory for methylation reactions of 1 and 3 by MeI and MeOTf, and used to derive Gibbs energies of activation (ΔG‡) for the processes of N- and O-methylation, respectively. These values, as well as those derived directly from the DFT calculations, closely reproduce the observed experimental N- vs. O-alkylation selectivities for methylation reactions of 1 and 3, indicating that Marcus theory can be used in a semi-quantitative manner to understand how the activation barriers for these reactions are constructed. It was found that N-alkylation of 1 is favoured due to the dominant contribution of ΔrG° to the activation barrier in this case, while O-alkylation of 3 is favoured due to the dominant contribution of the intrinsic barrier (ΔG‡0) for this process. These results are of profound significance in understanding the outcomes of reactions of ambident reactants in general.
Introduction
Selectivity in reactions of ambident nucleophiles
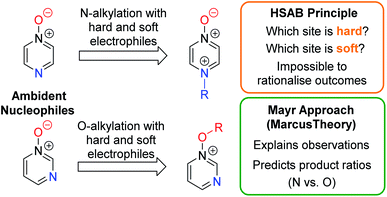
A fundamental goal in organic chemistry is to be able to understand and rationalise why chemical processes occur as they do. Naturally, therefore, an understanding of the factors that govern regioselectivity in chemical reactions is of paramount importance – i.e. if a compound contains more than one reactive site, which one is preferred, and why? Reliably accounting for the regioselectivity observed in reactions of ambident nucleophiles and electrophiles is a challenge laden with difficulties and potential pitfalls. By far the most popular rationale for this purpose1 makes use of the principle of hard and soft acids and bases (the HSAB principle),2 and the related concept of charge vs. orbital control.3 The difficulty inherent in accounting for the selectivities observed in reactions of ambident nucleophiles is exemplified by the fact that the HSAB principle predicts the incorrect product in a very large number of cases, as has been reviewed in detail by Mayr and co-workers.4 The data in this review call starkly into question whether the principle adequately explains the observed selectivity in reactions of ambident nucleophiles in which the expected outcome (based on HSAB theory) does match the experimental outcome.5Mayr and co-workers have suggested employing Marcus theory (described below) as an alternative method of accounting qualitatively for the selectivities of reactions of ambident reactants.4
Recently, Wang, Barnes and co-workers conducted computational investigations to establish a theoretical basis for applying the HSAB principle in rationalising ambident reactivity, and used this, along with Marcus theory, to explain the results of their calculations on gas phase reactions of amide anions.6 However, so far, the Marcus theory-based approach has not been adopted by the wider research community, and in fact the HSAB rationale continues to be cited in cases in which the experimental results do align, perhaps arbitrarily, with expectations based on this principle.5 Furthermore, the elements of the intuitively alluring HSAB rationale pervade all discussions of ambident reactivity in undergraduate chemistry courses, and in the most comprehensive organic chemistry textbooks.1 Given the clear deficiencies of the HSAB rationale in the context of ambident reactivity, it now behoves organic chemists to test Mayr's approach and other alternatives on their capacity to account for the outcomes of reactions of ambident reactants.
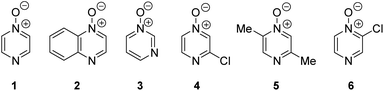
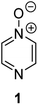
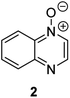
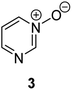
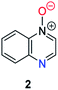
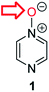
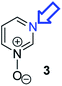
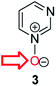
Herein, we focus on the notoriously difficult problem of competition between N and O nucleophilic sites (Scheme 1).4,5c,6,7–14 We chose diazine N-oxides 1, 2 and 3 (Fig. 1) as test substrates in reactions with various representative hard and soft electrophiles because, although these reactions show very high site-selectivity (i.e. for N- or O-alkylation),7 their outcomes are intractable to rationalisation using the HSAB principle (Scheme 1), as will be discussed in the next section. An additional contributing factor that confounds any attempt to analyse the reactions of these species using the HSAB rationale is that it is not possible to unambiguously identify which nucleophilic site of a diazine N-oxide is the hard site, and which is the soft site (see later).15
 | ||
| Scheme 1 Approaches for rationalising selectivity in reactions of diazine N-oxides as representative ambident nucleophiles. | ||
In this work, we will show that the approach of Mayr and co-workers enables accurate prediction of the preferred site of alkylation of ambident nucleophiles 1–3. Furthermore, we will also show that it is even possible to calculate the ratio of the selectivities for the different nucleophilic sites in these compounds (N vs. O) with an impressive degree of accuracy (Scheme 1).16 Our results bolster the applicability of the Marcus theory-based approach and establish, for the first time, its capacity to semi-quantitatively account for the ratios of site-selectivities in reactions of ambident nucleophiles.
It should be noted that the limitations of the HSAB principle were highlighted by its developer (Pearson),2d,f and that in its original formulation,2a,b it was not derived with the intention of rationalising the selectivities of reactions of ambident reactants. However, thereafter, it has been2c and continues to be applied in this manner.1,5 In recent years, a theoretical grounding demonstrating the applicability of the “global” HSAB principle (which does not apply to ambident reactants) has been developed.17,18 Despite the authors' inclusion in the articles on this topic of precise statements such as “The local HSAB principle, which makes predictions about ambident acids and bases, is on much shakier theoretical ground, so experimental evidence against it is not surprising”,15a,17b these papers are nonetheless cited in other articles in support of application of the HSAB principle to the analysis of reactions of ambident nucleophiles.5c This is illustrative of the continued application of the HSAB principle to rationalisation of ambident reactivity in the wider chemistry community despite the large body of evidence demonstrating that it does not apply in such instances.
Competition between N and O nucleophilic sites
Numerous examples of reactions of ambident nucleophiles containing competing O and N nucleophilic sites exist in the literature.6,10–14,19–32 Compounds 1–3 are particularly suitable for the present investigation for the following reasons: (i) unlike the reactions of many other ambident nucleophiles containing N and O nucleophilic sites,6,14,20–31 reactions of 1–3 are not influenced by the presence of a counter-cation,33 and (ii) their alkylation products do not undergo secondary reactions (cf. amide alkylations).19d,eThere exist several literature precedents of relevance to the ambident nucleophilicity of diazine N-oxides. Exclusive O-alkylation has been reported to occur in reactions of pyrazine N-oxide (1), quinoxaline N-oxide (2) and pyrimidine N-oxide (3) with hard alkylating agent dimethylsulfate,7 and predominant O-ethylation has been reported to occur in the reaction of compound 4 with hard electrophile [Et3O]BF4 (Scheme 2a).10 Reactions of 1, of 2 and of 5 with soft electrophile methyl iodide have been reported to yield N-alkylated adducts (Scheme 2b),11,12 as has the reaction of 5 with benzyl chloride.12c In contrast, compound 6 undergoes exclusive N-ethylation on reaction with hard electrophile [Et3O]BF4 (Scheme 2c).10 Notwithstanding the ambiguity inherent in assigning hard and soft sites in these diazine N-oxides, it is clear that these results cannot all simultaneously be consistent with the HSAB principle.
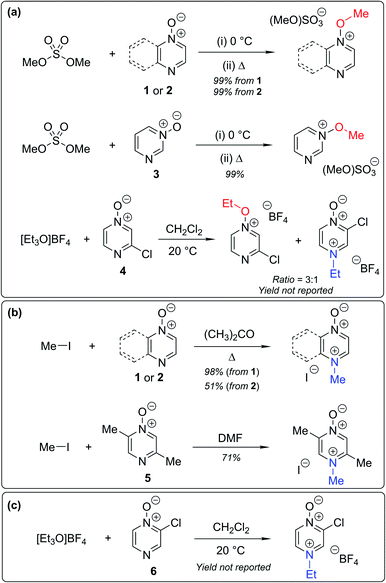 | ||
| Scheme 2 Alkylation of diazine N-oxides 1–6 using various hard and soft electrophiles. (a) O-alkylation using hard electrophiles,7,10 (b) N-alkylation using soft electrophiles,11,12 (c) N-alkylation using a hard electrophile.10 | ||
An additional fundamental difficulty exists in the context of reactions of diazine N-oxides: the act of establishing the structure of the product is itself fraught with ambiguity. The spectral features of the products of O-alkylation and N-alkylation of a particular diazine N-oxide are not necessarily readily distinguishable. Most instances in the literature in which product structures have been assigned have been based on the results of chemical derivatisations,12 prior to the development of modern spectroscopic methods. In only one instance (involving two compounds) have modern two-dimensional NMR spectroscopic techniques been used to establish the precise structures of alkylation products of diazine N-oxides.10,34 Hence, even in instances in which structural assignments have been made, it is not certain that the correct product structures have been identified.
To unambiguously establish the ratios of N vs. O selectivity for the alkylation reactions of 1–3, we took advantage of the technique of indirect detection natural abundance 1H–15N HMBC NMR spectroscopy.34–38 This is an extremely useful diagnostic tool but, is very notably under-exploited – to our knowledge, there are only a handful of examples of its use to establish the site of attachment of an alkyl electrophile to an ambident reactant.10,31,34,37 We have also conducted high level quantum chemical calculations to help us in understanding the outcomes of these experiments.
Background data and reference δN values
In order to be able to employ 1H–15N HMBC NMR spectral data in a diagnostic manner to establish the site of alkylation of ambident nucleophiles 1–3, we have made use of a set of results described in our recent publication.39 In this preliminary study, we carried out various alkylations of representative diazines and azine N-oxides (see examples shown in Scheme 3, involving N-methylation of 7 and O-methylation of 8), and monitored the change in the 15N NMR chemical shifts (referred to as Δ(δN) values) of each nitrogen atom in the N-alkylated product relative to its δN value in the starting material using 1H–15N HMBC NMR spectroscopy. We consistently observed that upon N-alkylation of diazines, a large upfield shift of the δN value of the alkylated nitrogen atom occurs (i.e. Δ(δN) ≪ 0 ppm).40 In fact, across a total of 22 examples from the chemical literature and our own work, involving N-methylation or ethylation of pyridines, diazines, diazine N-oxides, quinolines, and isoquinolines, the average upfield Δ(δN) value of the alkylated nitrogen atom is −115 ppm.10,41 Similarly, the average upfield Δ(δN) value associated with N-benzhydrylation was −91 ppm (3 examples). In contrast, the shift upfield in the N-oxide nitrogen δN value upon O-alkylation is significantly smaller – across 7 examples involving N-methylation or ethylation, the average upfield Δ(δN) value was determined to be only −40 ppm, while for O-benzhydrylation the average Δ(δN) value was −45 ppm. That the upfield signal in each case belongs to the alkylated nitrogen atom is shown by the existence of a correlation in the 1H–15N HMBC NMR spectrum of the product between the upfield 15N signal and the proton(s) of the N- or O-alkyl group.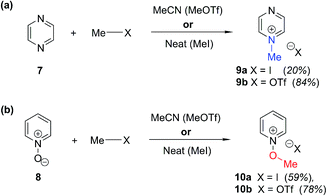 | ||
| Scheme 3 Examples of use of hard and soft methylating agents to effect (a) N-methylation of 7; (b) O-methylation of 8. X = I or OTf throughout. Isolated yields are shown in parentheses. | ||
From the above, we can conclude that there is a characteristic Δ(δN) value associated with N-alkylation of an aromatic N-heterocycle, distinct from (and significantly larger than) the Δ(δN) value associated with O-alkylation of an aromatic N-oxide. Analogous observations have been made in an 15N NMR spectroscopic studies of protonation of pyridine and 4-methylpyridine N-oxide, which induces Δ(δN) values of −113.3 ppm41a and −50.1 ppm,41b respectively. Furthermore, complexation of aromatic N-heterocycles to metals has been shown to result in upfield Δ(δN) values of ca. −100 ppm.42
Our previous investigation also allowed us to determine that in the 1H–13C HMBC NMR spectra of N-alkylated products, three-bond correlations exist between the N-alkyl group carbons and hydrogens and the ortho carbons and hydrogens of the aromatic moiety.39 No correlations were observed in the 1H–13C HMBC NMR spectra of O-alkylated products between the O-alkyl group carbons and hydrogens and the ortho carbons and hydrogens. Furthermore, these unambiguous NMR spectroscopic correlation methods also allowed us to establish definitive diagnostic trends in the 13C NMR chemical shifts of the alkyl group carbons immediately bound to aromatic nitrogen or aromatic N-oxide oxygen. For example, the N-methyl carbon of the adduct of N-methylation of an aromatic nitrogen nucleophile was shown to typically have a δC value in the range 36–53 ppm, while the O-methyl carbon of the adduct of aromatic N-oxide methylation typically exhibits a δC value in the range 62–75 ppm.39 Consequently, it should be possible to employ a combination of Δ(δN) values (obtained from 1H–15N HMBC NMR spectra) together with 1H–13C HMBC and 13C{1H} NMR spectroscopic data to distinguish between N- and O-alkylated diazine N-oxides.
Results
Site of alkylation of diazine N-oxides
The data discussed above show that natural abundance 1H–15N HMBC is a highly useful diagnostic tool to determine whether or not the site of attachment of an alkyl electrophile is at a nitrogen atom. We will now describe how we have employed the 1H–15N HMBC NMR technique, in tandem with information from 13C{1H} and 1H–13C HSQC and HMBC NMR spectra, to establish the site of alkylation of ambident nucleophiles 1–3 in reactions with representative hard and soft alkylating agents.Reactions of ambident nucleophiles 1 and 2 with electrophiles MeI, MeOTf, and benzhydrylium triflates 11 and 12 were carried out using the conditions shown in Scheme 4 and Table 1.44–46 The reaction of 1 with MeI in CD3CN or CH3CN resulted in formation of a single product, albeit with low conversion and yield – i.e. the process of alkylation was completely selective for one site (N or O) – see Table 1 entry (i). We did not observe any product formation in our 1H NMR spectra of the reaction of 2 + MeI in CD3CN. Product formation was only observed when the reagents were mixed together in the absence of solvent (neat); the data in Table 1 entry (v) refer to the reaction run under these conditions. As in the case of 1 + MeI, only a single product was observed by 1H NMR spectroscopy. Attempted reactions of 3 with MeI in CD3CN or MeCN did not yield any products, i.e. neither 21a nor 23a were observed (Scheme 4c).
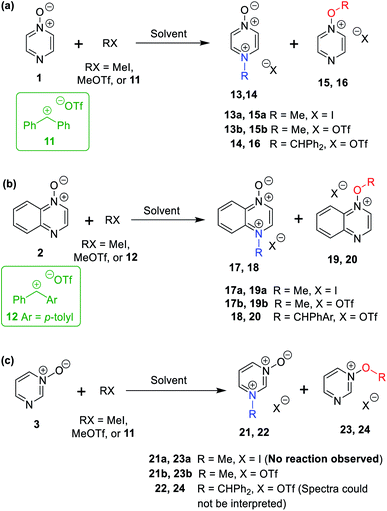 | ||
| Scheme 4 N- and O-alkylation reactions of ambident nucleophiles 1–3. Methylation reactions (using MeI or MeOTf) were conducted in (CD3)2SO, CD3CN, or CH3CN. Upon completion of reactions in CD3CN or CH3CN, the solvent was removed, and (CD3)2SO was added. Benzhydrylation reactions were conducted in CD2Cl2.43 See Table 1 for details of conversions and yields. | ||
| Diazine N-oxide | # | Reaction solventa | R | X | Products | Conversion (isolated% yield)b | N/O product ratioc | |
|---|---|---|---|---|---|---|---|---|
| N-methyl | O-methyl | |||||||
| a See ESI for experimental conditions employed and details of conversion calculations and yields.44 b Conversions represent the combined amount of N- and O-alkylated product formed relative to the amount added of the alkylating agent (always the limiting reagent). These were determined using integrations of appropriate signals in the 1H NMR spectra. For entry (viii), the deviation from quantitative conversion was due to hydrolysis of the alkylating agent. Percentage yields (where applicable) of isolated products were determined from separate reactions run on larger scale using MeCN solvent, or with no solvent (neat reagents) for entries (i) and (v). Products 14, 18, 20, 21b and 23b (entries (iv), (viii) and (x), respectively) decompose upon attempted isolation, and hence no isolated yields could be obtained in these cases. c The identities of the products cannot be determined directly from the 1H NMR spectra. Information from other spectra is needed to establish which product is N-alkylated and which is O-alkylated, and hence to establish the N/O ratio. See main text for full details. d 2 + MeI were reacted together without solvent. The product was purified prior to NMR spectral characterisation, so the conversion was not determined for this reaction. However, the low isolated yield shown above is indicative of low conversion in this reaction. e Ar = para-tolyl. | ||||||||
|
(i) | CD3CN or no solvent | Me | I | 13a | 15a | Reaction in CD3CN: 24% (solvent-free reaction 26%) | >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| (ii) | CD3CN | Me | OTf | 13b | 15b | Quantitative (68% yield of 13b)a | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
|
| (iii) | (CD3)2SO | Me | OTf | 13b | 15b | 87% | >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|
| (iv)a | CD3CN or CH2Cl2a | CH2Ph | OTf | 14 | 16 | Quantitativea | >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|
|
(v) | No solvent | Me | I | 17a | 19a | (Yield = 16%)d | >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| (vi) | CD3CN | Me | OTf | 17b | 19b | Quantitative (57% yield of 17b)a | 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 11 |
|
| (vii) | (CD3)2SO | Me | OTf | 17b | 19b | 78% | >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|
| (viii) | CD2Cl2 | CHPhAre | OTf | 18 | 20 | 93% | 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
|
|
(ix) | CD3CN | Me | I | 21a | 23a | No products formed | — |
| (x) | CD3CN | Me | OTf | 21b | 23b | Quantitativea | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93 93 |
|
| (xi) | (CD3)2SO | Me | OTf | 21b | 23b | 76% | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93 93 |
|
| (xii) | CD2Cl2 | CHPhAre | OTf | 22 | 24 | Spectra could not be interpreted | — | |
The reaction of 1 with benzhydrylium triflate 11 in CH2Cl2 or CD3CN also resulted in formation of single products (Table 1 entry (iv)).43 The 1H NMR spectrum of the reaction of 2 + 13 in CD2Cl2 (Scheme 4b) shows formation of two products in a 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio (combined conversion = 93%; the remaining 7% was accounted for by hydrolysis product; see (Table 1 entry (viii)). Reaction of 3 with 11 gave 1H NMR and 1H–15N HMBC NMR spectra that we could not interpret,47 containing broad and unusually shaped signals – i.e. we could not detect formation of 22 or 24 (Scheme 4). We ascribe this to the very low Lewis basicity of 3, i.e. the reaction of 3 + 11 is reversible, and thermodynamically disfavoured.
9 ratio (combined conversion = 93%; the remaining 7% was accounted for by hydrolysis product; see (Table 1 entry (viii)). Reaction of 3 with 11 gave 1H NMR and 1H–15N HMBC NMR spectra that we could not interpret,47 containing broad and unusually shaped signals – i.e. we could not detect formation of 22 or 24 (Scheme 4). We ascribe this to the very low Lewis basicity of 3, i.e. the reaction of 3 + 11 is reversible, and thermodynamically disfavoured.
The reactions of 1–3 with MeOTf in CD3CN yielded mixtures of O- and N-methylation products (Table 1 entries (ii), (vi), and (x)). Addition of MeOTf to (CD3)2SO solutions of 1 and 2 resulted in formation of a single product in each case (Table 1 entries (iii) and (vii)), while the corresponding reaction of 3 gave two products (Table 1 entry (xi)). The rates of these reactions differed greatly depending on the solvent used. Product formation was rapid for reactions in CD3CN (i.e. complete within minutes), but was exceptionally slow in (CD3)2SO, requiring weeks for high conversions to be obtained. It is highly likely that the active methylating agent in (CD3)2SO was the methoxysulfonium salt [(CD3)2S(OMe)]OTf,48–50 and that this electrophile is much less reactive than MeOTf in MeCN.
Many of the initial products of the reactions of Scheme 4 and Table 1 do not survive attempts at isolation. Hence, all reactions were conducted on small scale, and the entirety of each reaction mixture was transferred (under inert atmosphere) to a NMR tube for analysis by NMR spectroscopy. In instances in which stable, isolable products were formed, the final (stable) products were isolated from separate reactions, conducted on larger scale. The adducts of benzhydrylation of 1 and 2 are hydrolytically unstable and could not be isolated. The adduct of 2 + MeI was formed in very low conversion,51 and the adduct of 3 + MeOTf became contaminated with multiple decomposition products;52 hence neither adduct could be isolated in pure form. In addition, for the reactions of 1–3 with MeOTf in MeCN or CD3CN solvent, decomposition of the minor product (detected in 1H NMR spectra in CD3CN) occurred upon removal of the MeCN/CD3CN solvent under vacuum, resulting in the observation of the signals of the major product only in the 1H NMR spectrum of the mixture upon dissolution in (CD3)2SO.53
In all cases shown in Table 1, it was impossible to distinguish the site of attachment of the alkyl group unambiguously using standard 1H- or 13C-based one or two-dimensional NMR techniques. That is, the identity of the product(s) in each case could not be reliably assigned as O-alkylated or N-alkylated. In the instances in which mixtures of O- and N-methylation products were obtained, product ratios could be determined using the integrations of signals in 1H NMR spectra, but which product was favoured was not clear. The product ratios determined in this way are shown in Table 1.
In order to determine which site (N or O) of each of the ambident nucleophiles 1–3 is favoured in the alkylation reactions shown in Scheme 4 and Table 1, we made use of the indirect detection natural abundance 1H–15N HMBC NMR spectroscopic technique described above. The 15N NMR chemical shifts of starting compounds 1–3 and of the observed alkylation adducts are shown in Table 2. The Δ(δN) values associated with these reactions (also shown in Table 2) show the extent to which the chemical shifts of the 15N nuclei of the alkylation product(s) differ from the chemical shifts of the corresponding 15N nuclei in the starting materials 1–3. As above, a negative value of Δ(δN) indicates an upfield shift of the δN value of an 15N environment upon alkylation, while a positive value indicates a downfield shift. In several instances (all described above), only one product was formed in the alkylation reactions of 1–3, while in others, the minor product did not survive the process of removal of the MeCN or CD3CN reaction solvent and replacement with (CD3)2SO.53 Hence, in almost all cases, only one product could be characterized using the 1H–15N HMBC NMR technique. In the 1H–15N HMBC spectrum of the reaction of 2 + 12, no correlations were observed to the small signals of the minor product that was shown to be present by the 1H NMR spectrum. The only instance in which it was possible to determine the δN values of both the major and minor alkylation products involved methylation of 3 in (CD3)2SO using MeOTf (Scheme 4c; through methoxysulfonium triflate).
| Diazine N-oxide | # | Products | R | X | Reaction solvent/NMR solventa | δ N of starting compound (ppm) | N-alkylation | O-alkylation | ||
|---|---|---|---|---|---|---|---|---|---|---|
| δ N of product (ppm) | Δ(δN) (ppm) | δ N of product (ppm) | Δ(δN) (ppm) | |||||||
| a See ESI for experimental conditions employed.45 b Literature δN values: 309.33, 303.85 ((CD3)2SO, referenced to nitromethane at 380 ppm; equivalent to ammonia at 0 ppm).54 c These values were reported in ref. 55 as δN −76.8 and −80.7 ppm (referenced to nitromethane at 0 ppm). d The reported δN values for these signals was from a spectrum referenced to nitromethane at 0.0 ppm. Since our 1H–15N HMBC spectra were referenced to ammonia at 0 ppm, the literature δN value has been re-calculated here relative to ammonia at 0 ppm. e Ar = para-tolyl. | ||||||||||

|
(i) | 13a, 15a | Me | I | MeCN/(CD3)2SO | 309.3 | 322.3 | +13.0 | Product (15a) not formed | |
| 303.9b | 187.1 | −116.8 | ||||||||
| (ii) | 13b, 15b | Me | OTf | MeCN/(CD3)2SO | 309.3 | 322.9 | +13.6 | Product (15b) decomposed during solvent exchange | ||
| 303.9b | 187.8 | −116.1 | ||||||||
| (iii) | 13b, 15b | Me | OTf | (CD3)2SO | 309.3 | 322.9 | +13.6 | Product (15b) not formed | ||
| 303.9b | 187.7 | −116.2 | ||||||||
| (iv) | 14, 16 | CH2Ph | OTf | CD2Cl2 | 311.0 | 325.0 | +14.0 | Product (16) not formed | ||
| 303.5 | 201.6 | −101.9 | ||||||||
|
(v) | 17a, 19a | Me | I | MeCN/(CD3)2SO | 303.2 | 314.4 | +11.2 | Product (19a) not formed | |
| 299.3c,d | 178.0 | −121.3 | ||||||||
| (vi) | 17b, 19b | Me | OTf | MeCN/(CD3)2SO | 303.2 | 314.4 | +11.2 | Product (19b) decomposed during solvent exchange | ||
| 299.3c,d | 177.6 | −121.7 | ||||||||
| (vii) | 17b, 19b | Me | OTf | (CD3)2SO | 303.2 | 314.4 | +11.2 | Product (19b) not formed | ||
| 299.3c,d | 177.9 | −121.4 | ||||||||
| (viii) | 18, 20 | CHPhAre | OTf | CD2Cl2 | 302.0 | 317.6 | +14.4 | Signal of 20 not detected in 1H–15N HMBC | ||
| 300.3 | 190.5 | −108.8 | ||||||||

|
(ix) | 21b, 23b | Me | OTf | CD3CN/(CD3)2SO | 301.3 | Product (21b) decomposed during solvent exchange | 303.4 | +2.1 | |
| 291.7 | 249.4 | −42.3 | ||||||||
| (x) | 21b, 23b | Me | OTf | (CD3)2SO | 301.3 | 293.6 | −7.7 | 303.1 | +1.8 | |
| 291.7 | 205.2 | −86.5 | 249.0 | −42.7 | ||||||
The 1H–15N HMBC NMR spectra of the major or exclusive products formed in the reactions of 1 or 2 with electrophiles MeI, MeOTf, and benzhydrylium 11 and 12 (Scheme 4a and b) all show that the δN values of the upfield nitrogen nuclei are shifted upfield by over 100 ppm relative to the δN values of the corresponding nitrogen NMR environments in the starting materials, i.e. Δ(δN) > −100 ppm in each case (see Table 2 entries (i), (ii), (iii), (v), (vi) and (vii) for methylations and entries (iv) and (viii) for benzhydrylation reactions).56 That the upfield signal in the 15N dimension belongs to the alkylated nitrogen is confirmed by the existence of a correlation in the 1H–15N HMBC NMR spectrum of this signal with the 1H signal of the N-alkyl proton(s) (see example spectrum from the reaction of 1 + MeOTf in Fig. 2a).
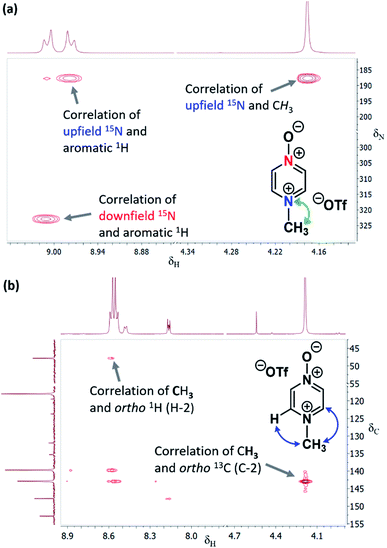 | ||
| Fig. 2 (a) Section of the 1H–15N HMBC NMR spectrum of 13b in (CD3)2SO (from reaction of Table 2 entry (ii)) showing correlation of N-methyl 1H signal with upfield 15N signal, (b) section of the 1H–13C HMBC NMR spectrum of 13b in CD3CN (from reaction of Table 2 entry (ii)) showing correlations between (i) N-methyl 1H signal and ortho-13C signals, and (ii) ortho-1H signals and N-methyl group 13C signal. | ||
In the 1H–13C HMBC NMR spectra of each of the major products of the reactions of 1 and 2, a correlation is shown to exist between the alkyl group (aliphatic) proton(s) and the carbons ortho to the upfield nitrogen for all alkylation adducts (see example in Fig. 2b). A correlation between the alkyl group aliphatic carbon and the protons ortho to the upfield nitrogen is also evident in these spectra. The large upfield Δ(δN) values and correlation data associated with the alkylation reactions of 1 and 2 are consistent with the preferential (and in some cases exclusive) occurrence of N-alkylation in these reactions.
In support of this conclusion, the 13C{1H} NMR chemical shifts of the methyl group carbon in the major products of the methylation reactions of 1 and 2 are, respectively, 44.1 and 46.6 ppm.57 These values lie in the middle of the range of δC values identified in our previous work as being characteristic of N-methylation of aromatic N-heterocycles (vide supra).39 The δC values of the minor products of these methylation reactions were, respectively, 68.9 and 70.2 ppm. These values appear in the middle of the δC range that is indicative of adducts of O-methylated aromatic N-oxides.39,57 The δC values of the benzhydryl group aliphatic carbons (Ar2CH) in the products of the benzhydrylation reactions of 1 and 2 were, respectively, 77.2 and 73.2 ppm.57 These values are characteristic of N-benzhydrylated products, based on our previous work.39 The above data are all consistent with the conclusion that the major products formed are N-alkylation adducts 13, 14, 17 and 18 (Scheme 4a and b). These are formed in preference to O-alkylation adducts 15, 16, 19 and 20.
The 1H–15N HMBC NMR spectrum of the reaction mixture produced by adding MeOTf to a (CD3)2SO solution of 3 (Scheme 4c) showed signals for the major product at δN 303.1 and 249.0 ppm (Table 2, entry (x)).58 The upfield 15N NMR signal showed a correlation with the methyl group CH3 protons, indicating that this belongs to the alkylated nitrogen. However, no correlation existed in the 1H–13C HMBC NMR spectrum for the signal of the methyl protons with the signal of the carbons ortho to the upfield nitrogen, nor for the signal of the methyl carbon with the signal of the protons ortho to upfield nitrogen. Based on the δN value of the upfield nitrogen signal, the δC value of the methyl group carbon of 70.2 ppm (characteristic of a N+–O–CH313C NMR signal of a N-methoxypyridinium ion),39 and the features of the 1H–13C HMBC NMR spectrum, the spectral characteristics of the major product are very similar to those of compound 10 (the O-methylated adduct of pyridine N-oxide (8); Scheme 3b), and other aromatic N-oxide O-methylation adducts.39
We therefore conclude that the major product of this reaction is O-methylation adduct 23b (Scheme 4c). The upfield signal (δN = 249.1 ppm) is assigned to the N–OMe nitrogen atom, and hence has a Δ(δN) value of −42.7 ppm relative to the signal of the N-oxide nitrogen atom of 3 (at δN = 291.7 ppm; see Table 2 entry (x)), while the downfield signal has Δ(δN) = +1.8 ppm relative to the corresponding signal of 3 (δN = 301.3 ppm). The upfield Δ(δN) value of −42.7 ppm for this reaction is very similar to the Δ(δN) values observed in formation of methoxypyridinium salts during O-methylation reactions of N-oxides (e.g. Δ(δN) = −43.6 ppm for formation of 10 from 8 + MeOTf; Scheme 3b).39
The Δ(δN) value associated with formation of the minor product of the reaction of pyrimidine N-oxide (3) + [(CD3)2S(OMe)]OTf in (CD3)2SO is considerably larger than the Δ(δN) value for O-alkylation (Table 2 entry (x); Δ(δN) = −86.5 vs. −42.7 ppm). In addition, the 1H–13C HMBC NMR spectrum exhibits multiple bond correlations between the N-methyl group and ortho aromatic 1H and 13C signals.59 The δC value of the methyl group carbon of the minor product was 46.6 ppm,57 which is characteristic of an aromatic N+–CH3 carbon (vide supra).39 These data are consistent with the minor product being N-methylation adduct 21b (Scheme 4c). Our spectral data on the reaction of 3 + MeOTf in CD3CN (or MeCN) also show that 23b is the major product formed in this solvent.54 Although 21b is formed in the reaction (as shown by 1H NMR spectral analysis), it does not survive the process of solvent removal and dissolution in (CD3)2SO (vide supra).
Based on the above data, we can conclude that the N- vs. O-methylation ratios in the reactions of 3 with MeOTf (in CD3CN) and [(CD3)2S(OMe)]OTf in (CD3)2SO are both 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93 (in favour of O-methylation; see Table 1 entries (x) and (xi)).
93 (in favour of O-methylation; see Table 1 entries (x) and (xi)).
Crossover experiments
The N- vs. O-alkylation ratios observed in the reactions of 1–3 did not change over time in the absence of perturbation. In order to establish whether or not these reactions occurred under kinetic control, we carried out several crossover experiments involving reactions of MeOTf with 1–3 (and of MeI with 1) in CD3CN followed by addition of a second nucleophile.60 An internal standard (1,3,5-trimethoxybenzene) was added to the reaction mixture to allow the amounts of the products present to be quantified (using integrations of 1H NMR spectral signals of the products) before and after addition of the second nucleophile, and to enable quantification of the amount of crossover product formed. Nucleophiles 7 and 25 were selected as second nucleophiles because they have been shown in separate studies to be considerably stronger Lewis bases than compounds 1–3,61 and hence are expected to out-compete 1–3 for any free alkylating agent present due to (i) their stronger nucleophilicity and (ii) the fact that they are present in considerable excess over 1–3 under the conditions of the crossover experiment.We observed that the amount of major product formed in the methylation reactions of each of 1 and 2 remained constant with respect to the internal standard during the crossover experiments, i.e. the formation of the major product in each case is irreversible (i.e.13a, 13b, and 17b respectively). For example, the amount of 13b formed in the reaction of 1 + MeOTf in CD3CN at 16 °C is invariant at 96% of methylation product throughout the experiment (Scheme 5). In the reactions of 1 and 2 with MeOTf (using 25 or 7 as the second nucleophile), crossover product formed at the expense of the minor product (O-methylation adducts 15b and 19b) with commensurate production of starting diazine N-oxide (1 or 2). Although crossover product (9b or 26) is formed from the minor products in these experiments, we conclude in each case that this is a consequence of the occurrence of an SN2 reaction between the second nucleophile (7 or 25) and the minor product. If this were not the case, then repeated observations of the N/O-methylation ratios over time in alkylation reactions of 1 and 2 should show this ratio changing (to favour the major product), since formation of the major product is irreversible in each case. Consequently, we conclude that O-methylation of 1 and 2 are also irreversible processes in CD3CN solvent at ambient temperatures. Thus, N-methylation of each of 1 and 2 is observed this is the kinetically favoured process in each instance.
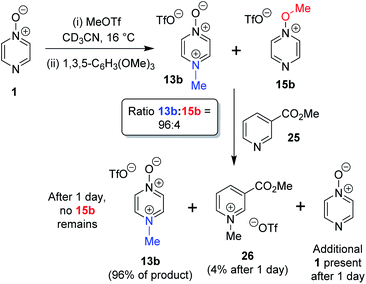 | ||
| Scheme 5 Crossover experiment investigating reversibility of reaction of 1 + MeOTf using 1,3,5-trimethoxybenzene as internal standard, and “crossover nucleophile” 25. The crossover product is compound 26.62 | ||
A similar crossover experiment involving the reaction of pyrimidine N-oxide (3) + MeOTf in CD3CN (with an internal standard added) and pyrazine (7) as 2nd nucleophile also showed formation of crossover product 9b. In 1H NMR spectra of this reaction mixture recorded early in the reaction, the crossover product (9b) was observed to form primarily at the expense of N-methylation product 21b (minor product of this reaction), but some O-methylation product (23b) was also consumed.62 An amount of 3 formed that was commensurate with the amount of 9b produced. After several days, further crossover product was observed to form at the expense of major product 23b.62 It is not clear from these experiments whether formation of 21b and 23b from 3 + MeOTf is reversible, i.e. whether 7 reacts with MeOTf formed by reversal of 21b and/or 23b to 3 + MeOTf, or whether crossover product 9b is formed by direct SN2 reactions of 7 with 21b and/or 23b.
Computational investigations
Our experimental investigations indicate that ambident nucleophiles pyrazine N-oxide (1) and quinoxaline N-oxide (2) (with competing N and O nucleophilic sites) undergo preferential alkylation on nitrogen regardless of the nature of the alkylating agent used, i.e. independent of whether the electrophile is hard or soft. Ambident nucleophile pyrimidine N-oxide (3), by contrast, has been shown to undergo preferential O-methylation by MeOTf. In order to be able to understand and rationalise the outcomes of the reactions described above, high level quantum chemical calculations at the DLPNO-CCSD(T)/def2-TZVPPD/SMD(CH3CN)//M06-2X-D3/6-311+G(d,p)/SMD(CH3CN) level of theory were carried out to determine the relative Gibbs energies of the reactants, transition states and products of the reactions of each of compounds 1, 3, 7 (pyrazine), and 8 (pyridine N-oxide) (structures shown in Fig. 1 and Scheme 3) with MeI and MeOTf.63 The reactions of pyrimidine (27) and pyridine (28) with MeI and MeOTf were also investigated in the same manner. The computational results can be used to estimate the Gibbs energy of activation (ΔG‡) and standard enthalpy and Gibbs energy of reaction (ΔrH° and ΔrG°, respectively) for each process. The accuracy and predictive capability of this computational method have been verified by the close agreement of the ΔG‡ values determined experimentally and computationally for the reaction of pyrazine N-oxide (1) with MeI (vide infra). The results of the computational investigations of the methylation reactions of 7, 8, 27 and 28 are presented in Table 3 (left side). Compounds 7, 27 and 28 undergo N-methylation, and compound 8 undergoes O-methylation. These results allow us to see representative values of ΔG‡, ΔrH° and ΔrG° for N- and O-methylation reactions in which there is no ambiguity over the site of methylation.| Nucleophiles with single alkylation sitec | Ambident nucleophiles | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Nu | X | Product & number | ΔG‡ | ΔrG° | ΔrH°b | # | Nu | X | Product & number | ΔG‡ | ΔrG° | ΔrH°b | ||
| a Enthalpies and Gibbs energy values (in kJ mol−1) were calculated at the DLPNO-CCSD(T)/def2-TZVPPD/SMD(CH3CN)//M06-2X-D3/6-311+G(d,p)/SMD(CH3CN) level of theory. b ΔrS° values calculated for these reactions were similar across all reactions of MeI (ΔrS° = −55 ± 2 J K−1 mol−1), and across all reactions of MeOTf (ΔrS° = −2 ± 2 J K−1 mol−1). These data are included in Tables S1–S3 in the ESI, along with calculated ΔH‡ and ΔS‡ values for these reactions.68 c Pyrazine (7) and pyrimidine (27) clearly have two possible alkylation sites, but the sites are identical by symmetry. | |||||||||||||||
| (i) | 7 | I |
|
9a | +131 | −21 | −37 | (ix) | 1 | I |
|
13a | +133 | −20 | −37 |
| (ii) | 7 | OTf | 9b | +107 | −90 | −90 | (x) | 1 | OTf | 13b | +108 | −88 | −90 | ||
| (iii) | 8 | I |
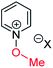
|
10a | +123 | −7 | −24 | (xi) | 1 | I |
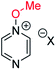
|
15a | +140 | +31 | +14 |
| (iv) | 8 | OTf | 10b | +97 | −75 | −76 | (xii) | 1 | OTf | 15b | +115 | −38 | −38 | ||
| (v) | 27 | I |
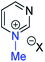
|
29a | +130 | −23 | −39 | (xiii) | 3 | I |
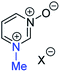
|
21a | +138 | +4 | −13 |
| (vi) | 27 | OTf | 29b | +106 | −91 | −91 | (xiv) | 3 | OTf | 21b | +113 | −64 | −66 | ||
| (vii) | 28 | I |

|
30a | +120 | −48 | −64 | (xv) | 3 | I |
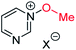
|
23a | +127 | +21 | +3 |
| (viii) | 28 | OTf | 30b | +96 | −117 | −117 | (xvi) | 3 | OTf | 23b | +103 | −48 | −49 | ||
Unsurprisingly, the reactions involving MeOTf have systematically smaller calculated ΔG‡ values and are more exergonic than the reactions involving MeI. The values of ΔG‡ and ΔrG° for methylation of 7 by MeI are very similar to the corresponding values for 27 (Table 3 entries (i) and (v)). The ΔG‡ and ΔrG° values for the reactions of 7 and 27 with MeOTf are also very similar (Table 3 entries (ii) and (vi)). This suggests that the nucleophilicities and Lewis basicities of 7 and 27 are very similar. The reactions involving pyridine (28; Table 3 entries (vii) and (viii)) were found computationally to be both more kinetically and thermodynamically favourable than the corresponding reactions of 7 and 27 with the two methylating agents.64 Our calculations indicate that the O-methylation reactions of 8 are more kinetically favourable than the corresponding reactions of 7 and 27, despite being less thermodynamically favourable than those reactions (compare Table 3 entry (iii) with entries (i) and (v), and entry (iv) with entries (ii) and (vi)).
The reaction of pyrazine N-oxide (1) with MeOTf was found computationally to result in kinetically and thermodynamically preferred N-methylation (compare Table 3 entries (x) and (xii)). This calculation indicates that methylation of 1 by MeOTf is an irreversible process at room temperature (regardless of the site of methylation), in agreement with the results of our crossover experiments (see above). The relative magnitudes of ΔG‡(N) and ΔG‡(O) calculated for this reaction suggest that a small amount of O-methylated product (ca. 5–7%) should be produced, as is observed experimentally (N/O methylation ratio = 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for reaction at 20 °C; see Table 2 entry (ii)).65
5 for reaction at 20 °C; see Table 2 entry (ii)).65
The reaction of 1 with MeI was also found to result in kinetically and thermodynamically preferred N-methylation (compare Table 3 entries (ix) and (xi)), which is consistent with the results of our crossover experiments. This reaction has been observed experimentally to be very slow. Only a small amount of conversion had occurred after several days, consistent with the high activation barrier found computationally (shown in Table 3) and determined through a kinetic investigation (described below). In contrast to the reaction of 1 with MeOTf (above), O-methylation of 1 by MeI was found computationally to be thermodynamically disfavoured and therefore reversible (Table 3 entry (xi)). No O-methyl adduct (17a) was observed experimentally for this reaction, which is consistent with kinetically disfavoured and reversible O-methylation.
The ΔG‡(N) and ΔrG°(N) values for N-methylation of 1 (by MeOTf or MeI) are similar to the corresponding values for diazines 7 and 27 (compare Table 3 entry (x) with entries (ii) and (vi), and entry (ix) with entries (i) and (v)). In contrast, the ΔG‡(O) and ΔrG°(O) values for O-methylation of 1 (by MeOTf or MeI) are significantly less favourable than the corresponding reactions of N-oxide 8 (compare Table 3 entry (xii) with entry (iv), and entry (xi) with entry (iii)). The implication of this is that the oxygen site of 1 is deactivated relative to the oxygen site of 8, both as a nucleophile and as a Lewis base.66
Our calculations on the reaction of pyrimidine N-oxide (3) with MeOTf indicate that, despite the fact that N-methylation (formation of 21b) is thermodynamically favoured over O-methylation (formation of 23b), the kinetically preferred process in this reaction is O-methylation (compare Table 3 entries (xiv) and (xvi)). The difference between the calculated values of ΔG‡(N) and ΔG‡(O) suggests that a small amount of N-methylation (ca. 1–3%) should occur. These results are in quite close agreement with the experimental observations – O-methylation is indeed favoured, and approximately 7% of the product formed is N-methylation adduct 21b (in CD3CN or (CD3)2SO; see Table 2 entries (ix) and (x)).67 These calculations indicate that both reactions are essentially irreversible (however, see the results of our crossover experiment involving 3 + MeOTf above).63 Our calculations on the reaction of 3 with MeI indicate that both O- and N-methylation (formation of 23a and 21a, respectively) are reversible. O-Methylation was found to be kinetically preferred, again despite the fact that this process is less thermodynamically favourable than N-methylation (compare Table 3 entries (xiii) and (xv)). As no product formation was observed experimentally when this reaction was attempted in CD3CN or MeCN, it is not possible to verify the applicability of these particular computational results.
The calculated Gibbs energies of activation for N- and O-methylation of pyrimidine N-oxide (3) by MeI or MeOTf, while higher than the ΔG‡ values for comparable reactions of similar compounds (e.g. pyrazine N-oxide (1), pyrazine (7), pyridine N-oxide (8) and pyridine (27)), are not especially different to those ΔG‡ values (compare Table 3 entry (xiv) with entries (ii) and (vi), entry (xiii) with entries (i) and (v), entry (xvi) with entry (iv), and entry (xv) with entry (iii)). However, comparison of the ΔrG° values for the same reactions indicates that both O- and N-methylation reactions of pyrimidine N-oxide (3) are far less thermodynamically favourable than the corresponding reactions of 1, 7, 8 and 27. This computational observation has been verified experimentally through a thermodynamic competition experiment in which product 32 (derived from pyrazine N-oxide (1) in a reversible reaction) is formed to the complete exclusion of 33 (derived from pyrimidine N-oxide (3)) when 1, 3 and benzhydrylium ion 31 are mixed in CD3CN (Scheme 6). It seems that the O and N nucleophilic/Lewis basic sites of 3 are deactivated in a similar manner to the O site of 1.66
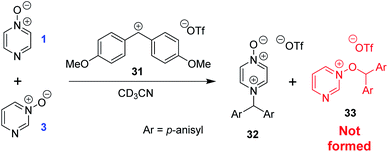 | ||
| Scheme 6 Competition experiment between reversible reactions of 1 and 3 with benzhydrylium ion 31.44 | ||
According to our computational data, N-methylation of both 1 and 3 results in a minor shortening of the N-oxide N–O bond. The calculated N–O bond lengths of diazine N-oxides 1 and 3 and N-methyldiazinium cations 13 and 21 are, respectively, 1.27 Å, 1.29 Å, 1.25 Å and 1.27 Å.63O-Methylation of 1 and 3 results in a lengthening of the N–O bond (to 1.36 Å for each of 15 and 23, the O-methylated cationic derivatives of 1 and 3).63O-methylation of 1 or 3 removes the favourable electrostatic interaction between N and O, and also diminishes the partial resonance of the N-oxide with the aromatic system, thereby removing resonance stabilisation effects that may help to stabilise the positive charge in the product. This may contribute to making N-methylation of 1 and 3 more thermodynamically favourable than O-methylation.
Finally, for completeness, we will comment on the values of the other thermodynamic functions associated with the above reactions. Computationally determined values of ΔrS° do not differ greatly from each other across all reactions of MeI with 1, 3, 7, 8, 27 and 28, or across all reactions of MeOTf with the same nucleophiles, regardless of whether N- or O-methylation is occurring.68 Across all reactions of MeI in Table 3, ΔrS° remains constant around −55 ± 2 J K−1 mol−1, while a value of −2 ± 2 J K−1 mol−1 was observed across the reactions of MeOTf (using 99% confidence intervals).68 Therefore, the computational data suggest that enthalpy changes are primarily responsible for dictating the differences between the ΔrG° values in the various reactions in Table 3. It is not possible to unambiguously ascribe the differences in ΔrH° to specific effects, and hence we refrain from doing so.
Activation barrier calculations using Marcus theory
Noting the deficiencies of the HSAB principle, Mayr and co-workers have advanced Marcus theory for rationalising the outcomes of reactions of ambident nucleophiles.4 The Marcus equation (eqn (1)) allows ΔG‡ to be separated out into its contributions from ΔrG° (the standard Gibbs energy of reaction) and ΔG‡0, the Marcus intrinsic barrier.69–71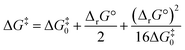 | (1) |
In reactions of ambident nucleophiles with competing sites of differing nucleophilicity, the different nucleophilic sites have different values of each of ΔG‡0 and ΔrG°. Mayr and co-workers have suggested that the selectivities in such reactions can be rationalised through an appraisal of the factors that influence the values of the two parameters in the Marcus equation (ΔG‡0 and ΔrG°).4 They have employed this approach to qualitatively rationalise the outcomes of reactions of a variety of ambident nucleophiles.4,72 In order to build up a more comprehensive understanding of the factors that influence selectivity in reactions of 1–3, we have calculated values of ΔG‡0 and ΔrG° for these reactions, and used them to construct values of the activation barriers (ΔG‡) using the Marcus equation.
Using the procedure described in detail in the ESI,†73 values of the intrinsic barrier (ΔG‡0) were calculated for each of the reactions of compounds 1 and 3 with MeI and MeOTf. The ΔG‡0 values for reactions of 1 and 3 are shown in Table 4.74 It is noteworthy that, for both ambident nucleophiles 1 and 3, the intrinsic barrier for methyl transfer to oxygen (ΔG‡0(O)) is lower than that for methylation of nitrogen (ΔG‡0(N)) – e.g. compare Table 4 entries (iii) and (i), and entries (vii) and (v). Hoz and co-workers previously established through computational investigations that the ΔG‡0 values associated with reactions of nucleophiles centred on 2nd row elements depend on the identity of the element at the nucleophilic site, with ΔG‡0 decreasing in the order C > N > O > F, i.e. from left to right across the periodic table.75 The lower intrinsic barriers (intrinsic preference) for O-alkylation over N-alkylation we observe for 1 and 3 are in line with this general trend.
| Nucleophile | # | X | ΔG‡0 | ΔrG° | DFT ΔG‡ | Marcus ΔG‡ |
|---|---|---|---|---|---|---|
| a The site of methylation of each nucleophile is indicated by an arrow. The Gibbs energy values have units of kJ mol−1. b ΔrG° and ΔG‡ (DFT ΔG‡) values here are reproduced from Table 3. | ||||||
|
(i) | OTf | +149.5 | −88 | +108.0 | +108.7 |
| (ii) | I | +144.0 | −20 | +133.0 | +134.2 | |
|
(iii) | OTf | +132.5 | −38 | +115.0 | +114.3 |
| (iv) | I | +127.0 | +31 | +140.0 | +143.0 | |
|
(v) | OTf | +145.0 | −64 | +113.0 | +114.8 |
| (vi) | I | +139.5 | +4 | +138.0 | +141.5 | |
|
(vii) | OTf | +124.0 | −48 | +103.0 | +101.2 |
| (viii) | I | +118.5 | +21 | +127.0 | +129.2 | |
Substitution of the calculated ΔG‡0 values into eqn (1) (the Marcus equation) along with the values of ΔrG° calculated as described above (Table 3 and associated discussion; these ΔrG° values are reproduced in Table 4 to aid the understanding of the reader) allows values of ΔG‡ to be calculated using the Marcus equation. Comparison of the ΔG‡ values obtained using the Marcus equation (shown in Marcus ΔG‡ column in Table 4) with the ΔG‡ values directly calculated as described above (values from Table 3, labelled DFT ΔG‡, are reproduced in Table 4) shows a close correspondence between the two methods. Importantly, the experimentally observed N vs. O selectivities for the reactions of the ambident nucleophiles 1 and 3 are reproduced quite closely by both methods of calculation.18 Analysing how the factors that contribute to the Gibbs energy of activation for a reaction influence its magnitude (i.e. how the interplay between ΔG‡0 and ΔrG° influences ΔG‡) provides a very useful means of understanding the origins of the differences between the rates of different reactions. Nowhere is this more apposite than in understanding which nucleophilic site of an ambident nucleophile is kinetically preferred. A full analysis of this kind for the reactions of 1 and 3 will be described in detail below.
The applicability of Marcus theory has been challenged in recent years,76 and alternatives have been suggested.77,78 However, such alternatives also incorporate in some manner an intrinsic barrier or a proxy thereof. In addition to using the Marcus equation, we have also used an adaptation of the Zhu equation (see the ESI†)79 to calculate ΔG‡ values for the methylation reactions of nucleophiles 1 and 3. The ΔG‡ values calculated using the adapted Zhu equation are very similar to the values calculated using eqn (1) (see Table S5 in the ESI†).73
The experimentally observed ratio of N- to O-methylation for the reaction of 1 + MeOTf was 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (Table 2). Direct calculation of the ΔG‡ values at the DLPNO-CCSD(T)/def2-TZVPPD/SMD(CH3CN)//M06-2X-D3/6-311+G(d,p)/SMD(CH3CN) level of theory indicated a N/O ratio of 94
5 (Table 2). Direct calculation of the ΔG‡ values at the DLPNO-CCSD(T)/def2-TZVPPD/SMD(CH3CN)//M06-2X-D3/6-311+G(d,p)/SMD(CH3CN) level of theory indicated a N/O ratio of 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 for this reaction, while calculation of the N/O ratio using the Marcus equation gave a ratio of 90
6 for this reaction, while calculation of the N/O ratio using the Marcus equation gave a ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (compare Table 4 entries (i) and (iii)). Use of the Zhu equation gave a N/O ratio of 96
10 (compare Table 4 entries (i) and (iii)). Use of the Zhu equation gave a N/O ratio of 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.73 The experimentally observed ratio of N- to O-methylation for the reaction of 3 + MeOTf was 7
4.73 The experimentally observed ratio of N- to O-methylation for the reaction of 3 + MeOTf was 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93. Our calculations indicated a ratio of 2
93. Our calculations indicated a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98 for this reaction, while calculation of the N/O ratio using the Marcus equation gave a ratio of 0.4
98 for this reaction, while calculation of the N/O ratio using the Marcus equation gave a ratio of 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99.6, (compare Table 4 entries (v) and (vii)) and calculation using the Zhu equation gave a ratio of 0.5
99.6, (compare Table 4 entries (v) and (vii)) and calculation using the Zhu equation gave a ratio of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99.5.73 That the experimental selectivities (in N- vs. O-methylations of 1 and 3 by MeOTf) are reproduced quite closely using the Marcus and Zhu equations73 and direct computation indicates that these methods are highly useful in understanding the factors that control Gibbs energies of activation in nucleophilic substitution reactions.
99.5.73 That the experimental selectivities (in N- vs. O-methylations of 1 and 3 by MeOTf) are reproduced quite closely using the Marcus and Zhu equations73 and direct computation indicates that these methods are highly useful in understanding the factors that control Gibbs energies of activation in nucleophilic substitution reactions.
Experimental verification of accuracy of calculated ΔG‡
In order to verify the applicability of the computational methods discussed above to determine the magnitudes of activation barriers, we conducted a kinetic investigation on the reaction of pyrazine N-oxide (1) with MeI in CD3CN at 25 °C using 1H NMR spectroscopy to determine the concentrations of the reactants and product (13a). The experiment was conducted under pseudo-first order conditions, with MeI present in ten-fold excess over 1. Using the method described in detail in the ESI,†80 we determined an approximate ΔG‡ value for this reaction of 1.4 × 102 kJ mol−1. This value is within 5% of the ΔG‡ values predicted for this reaction using the Marcus equation (134.2 kJ mol−1), and using direct application of the DLPNO-CCSD(T)/def2-TZVPPD/SMD(CH3CN)//M06-2X-D3/6-311+G(d,p)/SMD(CH3CN) method (133 kJ mol−1). This striking agreement between computational theory and experiment demonstrates that these computational methods are capable of modelling kinetic phenomena of this type rather accurately (Scheme 7).Discussion
Rationalisation of experimental N vs. O selectivities
The kinetic preference of compound pyrazine N-oxide (1) for N-methylation by soft electrophile MeI (forming compound 13a) and by hard electrophile MeOTf (forming compound 13b) has been demonstrated experimentally and computationally. The alkylation reactions of quinoxaline N-oxide (2) by MeI, MeOTf and benzhydrylium triflates (11 or 12) and of 1 by 11 or 12 are all also almost certainly irreversible, and all yield N-alkylated products preferentially or exclusively. The reaction of pyrimidine N-oxide (3) + MeOTf gives O-methylated product (23b) predominantly, and our computational investigations indicate that this is due to the kinetic favourability of formation of 23b. Although no product formation is observed in the reaction of 3 + soft electrophile MeI (due to the formation of products 21a and 23a being thermodynamically disfavoured and hence reversible), our computational results indicate that O-methylation (formation of 23a) is the kinetically favoured process in this reaction (see Table 4 entries (vi) and (viii)).It is evident from these results that each nucleophile exhibits a preferred site of alkylation which is independent of the nature of the electrophile used (N for 1 and 2, and O for 3), i.e. these outcomes cannot be dictated by hard/soft acid/base interactions. A fundamentally different set of factors must dictate the observed selectivities in these reactions. We discuss an alternative rationale to account for these observations later in this article.
Although the above evidence clearly shows that the HSAB principle does not apply in this set of reactions, and thereby renders unnecessary the identification of which nucleophilic site of each of 1–3 is “harder” and which is “softer”, it is nonetheless appropriate at this point to discuss the difficulty and ambiguity inherent in attempts at such identifications. The features that are employed to determine whether a reactant is hard or soft are charge (charge density), size, polarizability and electronegativity.2a,b,g,18b,c For hard bases, the donor atom is typically negatively charged and/or has a local excess of electron density, and is of small size, low polarizability and high electronegativity. For soft bases, the donor atom typically does not bear a formal negative charge and exhibits low negative charge density, and is of large size, high polarizability and low electronegativity. Derivation of functions that reliably indicate the “local hardness” and “local softness” of sites in a molecule (such as an ambident nucleophile) has proved a difficult endeavour.15 At present, such approaches cannot be applied without ambiguity.
On the basis that oxygen is more electronegative than nitrogen, one could perhaps anticipate that the oxygen site of a diazine N-oxide such as 1–3 should be harder than the nitrogen site. However, although there is a formal negative charge on the N-oxide oxygen atoms in these compounds, it is not clear which nucleophilic site in each ambident nucleophile should have the highest negative charge density, thereby potentially complicating the issue. To probe this question, we calculated the charge distribution for the ambident N-oxides with a variety of methods (ChelpG, Merz–Singh–Kollman, natural bond order (NBO), and atoms in molecules (AIM)),81 but found that there was no uniform agreement between methods on which site bears the highest negative charge density in compounds 1 and 3. Full details of this are given in the ESI.†81
We now present an alternative rationale, based on Marcus theory, to explain these results (see eqn (1) above). In the following discussion, the intrinsic barriers for alkylation at oxygen and nitrogen are referred to, respectively, as ΔG‡0(O) and ΔG‡0(N). The standard Gibbs energies of reaction for O- and N-alkylation are referred to, respectively, as ΔrG°(O) and ΔrG°(N).
Although O-methylation is intrinsically preferred over N-methylation (for diazine N-oxides, and in general; vide supra),75 in reactions of 1 and 2, the intrinsic preference for O-alkylation is modest. ΔG‡0(O) is calculated to be only 17 kJ mol−1 lower than ΔG‡0(N) for the reactions of 1 with MeI or MeOTf (Table 4 entry (i) vs. (iii), and entry (ii) vs. (iv)). The ΔrG°(N) values for these reactions are substantially more favourable than the corresponding ΔrG°(O) values. Consequently, the very favourable contribution of ΔrG°(N) to ΔG‡(N) supersedes the favourable contribution of ΔG‡0(O) to ΔG‡(O), such that ΔG‡(N) is much lower than ΔG‡(O) for alkylations of 1 and 2. That is, the intrinsic favourability of O-alkylation is outweighed by the thermodynamic favourability of N-alkylation, so in these irreversible reactions, N-alkylation is kinetically preferred.82
In the reaction of pyrimidine N-oxide (3) with MeOTf, the value of ΔrG°(N) is much less favourable with respect to ΔrG°(O) than is the case for the corresponding reaction of pyrazine N-oxide (1). ΔG‡0(O) is calculated to be 21 kJ mol−1 lower than ΔG‡0(N) for both MeOTf and MeI (compare Table 4 entry (vii) with entry (v), and entry (viii) with entry (vi)), so O-methylation of 3 is intrinsically preferred. Since the thermodynamic favourability of N-methylation of 3 is diminished (relative to the corresponding reactions of 1), and O-methylation is intrinsically favoured, ΔG‡(O) is lower than ΔG‡(N), and hence O-methylation of 3 is the kinetically dominant reaction. Instances in which N-alkylation is likely to have been “deactivated” due to steric interactions, resulting in preferential O-alkylation, have been reported previously.4,22b,c,d,e,31 In this case, it seems likely that the free nitrogen Lewis basic site of 3 is deactivated due to an electronic effect. This Lewis basic site is connected through a network of π-bonds to an N-oxide group in a meta position relative to it, which may act as an electron withdrawing group, thereby diminishing the Lewis basicity (electron donor capacity) of the free nitrogen atom.
The reaction of 3 with MeI was calculated to be thermodynamically unfavourable (ΔrG° > 0 for both O- and N-methylation by MeI), and therefore reversible. This is consistent with our experimental observation that no product was formed in this reaction. However, our calculations do indicate that O-methylation (formation of 23a) is kinetically favoured over N-methylation. A similar rationale to that presented above for the reaction of 3 + MeOTf applies in this case – i.e. O-methylation is intrinsically preferred (ΔG‡0(O) < ΔG‡0(N)) and the thermodynamic advantage of N-methylation over O-methylation is small, and consequently O-methylation is the kinetically favoured process (see Table 4 entries (vi) and (viii)).
As discussed above, the ΔrG° values calculated for N- and O-methylations of 3 by both MeI and MeOTf are much less favourable than the ΔrG° values of methylation reactions of other, similar compounds (e.g.1, 7, 8 and 27; vide supra). In the context of our analysis based on the Marcus equation, we can make use of this information to rationalise the relatively high ΔG‡(O) and ΔG‡(N) values calculated for the methylation reactions of 3. The less favourable ΔrG° values for O- and N-methylations of 3 influence the magnitudes of the ΔG‡ values for these reactions, causing them to be higher than the ΔG‡ values of reactions of similar nucleophiles.
As is described in detail in the ESI,†73 operationally, the value of the intrinsic barrier (ΔG‡0) for a reaction is accessed as the average of two identity reactions. Since there is no leaving group formed in the addition of a nucleophile to carbenium ions such as 11 and 12 (structures in Scheme 4 above), only one identity reaction of the required two can be identified to model such processes using Marcus theory. Hence, the straightforward method described in the ESI†73 for accessing values of intrinsic barriers cannot be employed for reactions involving carbenium ions. Alternative methods for estimating the magnitudes of the intrinsic barriers for such reactions or analogues thereof have been reported,83 but these do not allow quantitative determinations of the type performed above for reactions involving electrophiles from which leaving groups become cleaved. Hence only a qualitative appraisal of the outcomes of the reactions of 1 and 2 with benzhydrylium ions is possible, which we give below.
We consider that the observation of strongly preferred or exclusive N-benzhydrylation of nucleophiles pyrazine N-oxide (1) and quinoxaline N-oxide (2) in their reactions with benzhydrylium ions (11 or 12) arises as a consequence of the same factors that dictate the outcomes of the reactions of these nucleophiles with MeI or MeOTf. That is, in each case, O-benzhydrylation is intrinsically favoured (ΔG‡0(O) is smaller than ΔG‡0(N)) but the influence of ΔrG°(N) on ΔG‡(N) outweighs the influence of ΔG‡0(O) on ΔG‡(O), and consequently N-benzhydrylation is the kinetically preferred process. As discussed above, it was not possible to determine what occurred in the reaction of 3 + benzhydrylium ion 11, so further comment on this is not warranted.
Literature examples of N vs. O alkylation
We have noted in passing above that, due to the ambiguity that has up until now been inherent in determining which product is formed predominantly in reactions of ambident nucleophiles containing N and O nucleophilic sites, there exist notable cases in the literature in which the products of such reactions may have been misidentified.8,9,84Comparison of the 1H NMR spectrum of N-methylated product 13b (from reactions of MeOTf with 1; Scheme 4a) with the 1H NMR spectra assigned to O-methylation adduct 15c (Scheme 8) in ref. 7 shows that the spectra are essentially identical. A similar observation can also be made on comparison of the 1H NMR spectrum of N-methylated product 17b (from 2 + MeOTf; Scheme 4b) and that assigned to O-methylated adduct 19c in ref. 7. We have identified a distinct set of signals belonging to the O-methylated adducts 15b and 19b that appear at different chemical shifts to the N-methylated adducts 13b and 17b (vide supra). Furthermore, the 13C NMR chemical shifts reported for the methyl group carbons (either N–CH3 or O–CH3) of the products are 47.2 and 44.5 ppm, respectively.7 These δC values are indicative of formation of N-methylation products 13c and 17c (vide supra). Hence, our data indicate that it is highly unlikely that 1 and 2 undergo preferential O-methylation in reactions with dimethylsulfate, a close analogue of MeOTf. The methodology reported in ref. 7 was predicated on the use of N-methoxypyridinium salts. That this otherwise highly successful methodology did not work for these compounds can be explained by the fact that N-methylated compounds 13c and 17c were almost certainly employed rather than the intended O-methylated compounds 15c and 19c. Problems of this type are illustrative of the need for a much more rigorous understanding of the factors that dictate the outcomes in reactions of ambident nucleophiles such as diazine N-oxides.
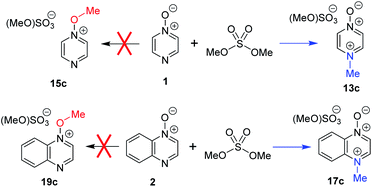 | ||
| Scheme 8 Reactions of compounds 1 and 2 with dimethylsulfate have been reported to give O-methylated products 15c and 19c.7 Our data indicate that N-methylated adducts 13c and 17c are likely to be the major products. | ||
Conclusions
If one must verify on a case-by-case basis whether the predictive capabilities of a theory apply or not, then those predictive capabilities must be seriously called into question. For this reason, the continued use of the HSAB principle in rationalising the selectivities of ambident reactants in research articles and undergraduate courses and textbooks should be ceased. It appears to us that the approach of Mayr and co-workers, based around Marcus theory, is able to account for the behaviour of ambident reactants in a manner in which the HSAB principle cannot. We hope through this study to have contributed to a more general understanding of ambident reactivity, to have developed upon the approach of Mayr and co-workers to show that it can be applied to semi-quantitatively rationalise product ratios in reactions of ambident nucleophiles, and to have demonstrated the utility of 1H–15N HMBC NMR spectroscopy in establishing the site of attachment in reactions of nitrogen-containing compounds.In the cases we have investigated here, calculation of ΔG‡ values using the equations of Marcus or Zhu yields values that reproduce closely the experimental N/O methylation ratios for reactions of ambident nucleophiles pyrazine N-oxide (1) and pyrimidine N-oxide (3). Based on this, it is reasonable to expect that calculations based on Marcus theory will allow semi-quantitative predictions of the nucleophilic site-selectivities in reactions of other ambident nucleophiles – not just those involving competition between N and O nucleophilic sites. The close agreement between the reaction selectivities determined experimentally and those calculated using the Marcus and Zhu equations (see Table 4 and associated discussion) is demonstrative of the utility of the concept of the intrinsic barrier.
The intrinsic barrier (ΔG‡0) associated with an alkylation reaction of a nucleophile can be considered a property of the compounds involved in the reaction. The interplay between this quantity and the thermodynamic favourability of the reaction (quantified through ΔrG°) dictates the magnitude of the activation barrier for the reaction (ΔG‡). Having established herein a computational method that stands up to the stern test posed by modelling of the disparate behaviour of diazine N-oxides 1 and 3, we intend in future publications to determine the magnitudes of intrinsic barriers for reactions of a wide variety of other nucleophiles, and hence establish systematic trends in intrinsic barriers (developing upon the work of Hoz).75 This will allow the factors that control intrinsic barriers to be understood, and hence deepen our understanding of activation barriers in general.
Details on computational methodology
The conformational space for each structure was explored with the OPLS-2005 force field85 and a modified Monte Carlo search algorithm implemented in Macromodel.86 An energy cut-off of 84 kJ mol−1 was employed for the conformational analysis, and structures with heavy-atom root-mean-square deviations (RMSD) up to 0.5 Å after the force field optimizations where considered to be the same conformer. All remaining structures were subsequently optimized with the dispersion-corrected M06-2X functional87 with Grimme's dispersion correction D3 (zero-damping),88 the triple-ζ basis set 6-311+G(d,p), and SMD solvation model89 for acetonitrile. An ultrafine grid was used throughout this study for the numerical integration of the density. Vibrational analysis verified that each structure was a minimum or a transition state and for the latter, following the intrinsic reaction coordinates (IRC) confirmed that all transition states connected the corresponding reactants and products on the potential energy surface. Thermal corrections were obtained from unscaled harmonic vibrational frequencies at the same level of theory for a standard state of 1 mol L−1 and 298.15 K. Entropic contributions to free energies were obtained from partition functions evaluated with Grimme's quasi-harmonic approximation.90 This method employs the free-rotor approximation for all frequencies below 100 cm−1, the rigid-rotor-harmonic-oscillator (RRHO) approximation for all frequencies above 100 cm−1, and a damping function to interpolate between the two expressions. Similar results were obtained from partition functions evaluated with Cramer's and Truhlar's quasiharmonic approximation.91 This method uses the same approximations as the usual harmonic oscillator approximation, except that all vibrational frequencies lower than 100 cm−1 are set equal to 100 cm−1. Electronic energies were subsequently obtained from single point calculations of the M06-2X-D3 geometries employing Neese's domain-based local pair-natural orbital (DLPNO) approach to the CCSD(T) method [DLPNO-CCSD(T)] with the default normalPNO settings,92–94 the triple-ζ def2-TZVPPD95,96 in combination with the corresponding auxiliary basis set97 and the SMD continuum model for acetonitrile.89 All density functional theory calculations were performed with Gaussian 16,98 while the DLPNO-CCSD(T) calculations were performed with ORCA 4.99Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was undertaken using equipment provided by Science Foundation Ireland though a research infrastructure award for process flow spectroscopy (ProSpect) (grant: SFI 15/RI/3221) and as part of the Synthesis and Solid State Pharmaceutical Centre (SSPC) supported by Science Foundation Ireland (grant: SFI SSPC2 12/RC/2275). We would also like to acknowledge funding from the SSPC through grant 12/RC/2275_P2. K. J. S. would like to thank the Irish Research Council for provision of a GOIPG Scholarship to fund his research (IRC GOIPG/2018/1517). Support from the Fonds der Chemischen Industrie (Liebig scholarship to M. B.) and the University of Cologne within the excellence initiative is gratefully acknowledged. We gratefully acknowledge the Regional Computing Center of the University of Cologne for providing computing time in the DFG-funded High-Performance Computing (HPC) System CHEOPS as well as for their support, the excellent analytical services provided in the School of Chemistry and ABCRF in UCC, Prof. Justin Holmes and research group for access to an inert atmosphere glove box, Dr Denis Lynch for assistance with NMR spectroscopy, Mick O'Shea for HRMS data, and Prof. Eoghan McGarrigle, Prof. Declan Gilheany (University College Dublin) and Dr Tim O'Sullivan and Dr Ger McGlacken (University College Cork) for helpful discussions.Notes and references
- (a) J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, New York, 2nd edn, 2012, pp. 355–357, 453–454, 506–509, 590, 658 Search PubMed; (b) E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, 2006, pp. 288–292, 567–568 Search PubMed; (c) M. B. Smith, March's Advanced Organic Chemistry, Wiley, Hoboken, 7th edn, 2013, pp. 446–450 Search PubMed.
- (a) R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533 CrossRef CAS; (b) R. G. Pearson, Science, 1966, 151, 172 CrossRef CAS PubMed; (c) R. G. Pearson and J. Songstad, J. Am. Chem. Soc., 1967, 89, 1827 CrossRef CAS; (d) R. G. Pearson, J. Chem. Educ., 1968, 45, 581 CrossRef CAS; (e) R. G. Pearson, J. Chem. Educ., 1968, 45, 643 CrossRef CAS; (f) R. G. Pearson, Inorg. Chim. Acta, 1995, 240, 93 CrossRef CAS; (g) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef CAS.
- (a) G. Klopman, J. Am. Chem. Soc., 1968, 90, 223 CrossRef CAS; (b) L. Salem, J. Am. Chem. Soc., 1968, 90, 543 CrossRef CAS; (c) T.-L. Ho, Chem. Rev., 1975, 75, 1 CrossRef CAS.
- H. Mayr, M. Breugst and A. R. Ofial, Angew. Chem., Int. Ed., 2011, 50, 6470 CrossRef CAS PubMed.
- For selected recent examples, see: (a) S. Maiti and P. Mal, J. Org. Chem., 2018, 83, 1340 CrossRef CAS PubMed; (b) S. Maiti, T. Alam and P. Mal, Asian J. Org. Chem., 2018, 7, 715 CrossRef CAS; (c) Y.-G. Wang and E. C. Barnes, ACS Omega, 2018, 3, 4557 CrossRef CAS PubMed; (d) A. Burmudžija, S. Marković, J. Muškinja, A. Pejović and J. Tošović, React. Kinet., Mech. Catal., 2018, 123, 201 CrossRef; (e) S. Yaragorla, A. Pareek and R. Dada, Tetrahedron Lett., 2017, 58, 4642 CrossRef CAS; (f) C. Slawik, C. Rickmeyer, M. Brehm, A. Böhme and G. Schürmann, Environ. Sci. Technol., 2017, 51, 4018 CrossRef CAS PubMed.
- Y.-G. Wang, E. C. Barnes, S. Kaya and V. Sharma, J. Comput. Chem., 2019, 40, 2761 CrossRef CAS PubMed.
- X. Ma, H. Dang, J. A. Rose, P. Rablen and S. B. Herzon, J. Am. Chem. Soc., 2017, 139, 5998 CrossRef CAS PubMed.
- D. Demberelnyamba, B. K. Shin and H. Lee, Chem. Commun., 2002, 1538 RSC . In this paper on amide-derived ionic liquids, N-alkylation of an amide upon refluxing in acetonitrile is reported.
- J. Yang, Q. Zhang, L. Zhu, S. Zhang, J. Li and X. Zhang, Chem. Mater., 2007, 19, 2544 CrossRef CAS . In this paper on amide-derived ionic liquids, N-alkylation of ε-caprolactam by alkyl tosylates and mesylates in acetonitrile at 80 °C is reported.
- P. Cmoch, Magn. Reson. Chem., 2003, 41, 693 CrossRef CAS.
- M. V. Jovanovic, Heterocycles, 1985, 23, 2299 CrossRef CAS.
- Assignment of N-methylated pyrazine product structures made on the basis of the results of chemical derivatisations: (a) J. K. Landquist, J. Chem. Soc., 1953, 2816 RSC; (b) A. Ohta, M. Matsunaga, N. Iwata and T. Watanabe, Heterocycles, 1977, 8, 351 CrossRef CAS; (c) C. F. Koelsch and W. H. Gumprecht, J. Org. Chem., 1958, 23, 1603 CrossRef CAS.
- R. Głaszczka and J. Jaźwiński, J. Mol. Struct., 2014, 1061, 150 CrossRef.
- (a) M. Breugst, T. Tokuyasu and H. Mayr, J. Org. Chem., 2010, 75, 5250 CrossRef CAS PubMed; (b) M. Breugst and H. Mayr, J. Am. Chem. Soc., 2010, 132, 15380 CrossRef CAS PubMed.
- (a) F. H. Zadeh, P. Fuentealba, C. Cárdenas and P. W. Ayers, Phys. Chem. Chem. Phys., 2014, 16, 6019 RSCSee also references therein; (b) M. Torrent-Sucarrat, F. De Proft, P. Geerlings and P. W. Ayers, Chem.–Eur. J., 2008, 14, 8652 CrossRef CAS PubMed , and references therein.
- J. M. Gonzales, W. D. Allen and H. F. Schaefer III, J. Phys. Chem. A, 2005, 109, 10613 CrossRef CAS PubMed.
- (a) P. W. Ayers, Faraday Discuss., 2007, 135, 161 RSC; (b) P. W. Ayers and C. Cárdenas, J. Chem. Phys., 2013, 138, 181106 CrossRef PubMed.
- (a) P. W. Ayers, J. Chem. Phys., 2005, 122, 141102 CrossRef PubMed; (b) C. Cárdenas and P. W. Ayers, Phys. Chem. Chem. Phys., 2013, 15, 13959 RSC; (c) P. W. Ayers, R. G. Parr and R. G. Pearson, J. Chem. Phys., 2006, 124, 194107 CrossRef PubMed; (d) P. K. Chattaraj, P. W. Ayers and J. Melin, Phys. Chem. Chem. Phys., 2007, 9, 3853 RSC.
- Amides: (a) Z.-J. Chen, H.-W. Xi, K. H. Lim and J.-M. Lee, Angew. Chem., Int. Ed., 2013, 52, 13392 CrossRef CAS PubMed; (b) T. Nanjo, E. C. de Lucca Jr and M. C. White, J. Am. Chem. Soc., 2017, 139, 14586 CrossRef CAS PubMed; (c) H.-G. Cheng, M. Pu, G. Kundu and F. Schoenebeck, Org. Lett., 2020, 22, 331 CrossRef CAS PubMed; (d) H. Bredereck, R. Gompper, H. Rempfer, K. Klemm and H. Keck, Chem. Ber., 1959, 92, 329 CrossRef CAS; (e) B. C. Challis and J. Challis, in The Chemistry of Amides, ed. J. Zabicky, Interscience, London, UK, 1970, p. 731–858 Search PubMed; (f) H. Bredereck, F. Effenberger and G. Simchen, Chem. Ber., 1963, 96, 1350 CrossRef CAS.
- 2-Pyridone and 4-pyridone: B. Feng, Y. Li, H. Li, X. Zhang, H. Xie, H. Cao, L. Yu and Q. Xu, J. Org. Chem., 2018, 83, 6769 CrossRef CAS PubMed.
- Amide anions: (a) See ref. 14a; (b) See ref. 19b.
- Pyridone or quinolone anions: (a) See ref. 14b; ; (b) G. C. Hopkins, J. P. Jonak, H. J. Minnemeyer and H. Tieckelmann, J. Org. Chem., 1967, 32, 4040 CrossRef CAS; (c) K. Pissinate, A. D. Villela, V. Rodrigues, B. C. Giacobbo, E. S. Grams, B. L. Abbadi, R. V. Trindade, L. R. Nery, C. D. Bonan, D. F. Back, M. M. Campos, L. A. Basso, D. S. Santos and P. Machado, ACS Med. Chem. Lett., 2016, 7, 235 CrossRef CAS PubMed; (d) N. M. Chung and H. Tieckelmann, J. Org. Chem., 1970, 35, 2517 CrossRef CAS; (e) N. Nishiwaki, M. Hisaki, M. Ono and M. Ariga, Tetrahedron, 2009, 65, 7403 CrossRef CAS.
- Imide anions: (a) L. Z. Avila, S. H. Loo and J. W. Frost, J. Am. Chem. Soc., 1987, 109, 6758 CrossRef CAS; (b) A. Arévalo, S. Ovando-Segovia, M. Flores-Alamo and J. J. García, Organometallics, 2013, 32, 2939 CrossRef.
- (a) T. H. Koch, R. J. Sluski and R. H. Moseley, J. Am. Chem. Soc., 1973, 95, 3957 CrossRef CAS; (b) D. R. Anderson, J. S. Keute, T. H. Koch and R. H. Moseley, J. Am. Chem. Soc., 1977, 99, 6332 CrossRef CAS . O-Alkylation is observed for silver salts of imide anions; this is ascribed to blocking of the nitrogen site due to coordination to silver in ref. 4 and 14a.
- Uracil anions: (a) See ref. 5c ; (b) Y.-G. Wang and E. C. Barnes, J. Phys. Chem. A, 2017, 121, 8866 CrossRef CAS PubMed.
- Aryl diazoacetate anions: N. Kornblum, R. A. Smiley, R. K. Blackwood and D. C. Iffland, J. Am. Chem. Soc., 1955, 77, 6269 CrossRef CAS.
- Nitrite ion: (a) A. A. Tishkov, U. Schmidhammer, S. Roth, E. Riedle and H. Mayr, Angew. Chem., Int. Ed., 2005, 44, 4623 CrossRef CAS PubMed; (b) See ref. 26.
- Cyanate ion: see ref. 4 and references therein.
- O-Alkylation of anions of 2-methylquinolin-4-ols: E. Pitta, M. K. Rogacki, O. Balabon, S. Huss, F. Cunningham, E. M. Lopez-Roman, J. Joossens, K. Augustyns, L. Ballell, R. H. Bates and P. Van der Veken, J. Med. Chem., 2016, 59, 6709 CrossRef CAS PubMed.
- Oximate anions: S. G. Smith and M. P. Hanson, J. Org. Chem., 1971, 36, 1931 CrossRef CAS.
- Anions of quinolin-4-ols, quinazolin-4-ols and 1,5-naphthyrid-4-ols: E. Pitta, O. Balabon, M. K. Rogacki, J. Gómez, F. Cunningham, J. Joosens, K. Augustyns, P. van der Veken and R. Bates, Eur. J. Med. Chem., 2017, 125, 890 CrossRef CAS PubMed.
- Numerous additional literature references containing examples of competition between N- and O-alkylation of ambident nucleophiles are given in the ESI, pg. S117.†.
- The site selectivity observed in reactions of anionic ambident nucleophiles may be a consequence of one of the nucleophilic sites being blocked through coordination to a counter-cation. See ref. 5c, 14a, 24 and 30, and also. L. M. Jackman and T. S. Dunne, J. Am. Chem. Soc., 1985, 107, 2805 CrossRef CAS.
- However, see also: T. Storz, M. D. Bartberger, S. Sukits, C. Wilde and T. Soukup, Synthesis, 2008, 2, 201 CrossRef.
- (a) G. E. Martin and A. J. Williams, Annu. Rev. NMR Spectrosc., 2015, 84, 1–76 CrossRef CAS; (b) R. Marek, A. Lyčka, E. Kolehmainen, E. Sievänen and J. Toušek, Curr. Org. Chem., 2007, 11, 1154 CrossRef CAS; (c) G. E. Martin and A. J. Williams, Annu. Rev. NMR Spectrosc., 2005, 55, 1–119 CrossRef CAS; (d) R. Marek and A. Lyčka, Curr. Org. Chem., 2002, 6, 35 CrossRef CAS; (e) J. Saurí, A. J. Williams and G. E. Martin, in Modern NMR Approaches to the Structure Elucidation of Natural Products, ed. A. J. Williams, G. E. Martin and D. Rovnyak, RSC, Cambridge, 2016, vol. 2, pp. 71–116 Search PubMed; (f) B. D. Hilton and G. E. Martin, J. Heterocycl. Chem., 2012, 49, 526 CrossRef CAS; (g) S. L. Black, P. D. O'Connor, M. Boyd, A. Blaser and J. D. Kendall, Tetrahedron, 2018, 74, 2797 CrossRef CAS; (h) R. T. Williamson, A. V. Buevich and G. E. Martin, Tetrahedron Lett., 2014, 55, 3365 CrossRef CAS.
- Applications of natural abundance 17O NMR spectroscopy: (a) D. E. Frantz and D. A. Singleton, J. Am. Chem. Soc., 2000, 122, 3288 CrossRef CAS; (b) M. P. Meyer, A. J. DelMonte and D. A. Singleton, J. Am. Chem. Soc., 1999, 121, 10865 CrossRef CAS.
- The natural abundance 1H–15N HMBC NMR experiments were obtained using an NMR spectrometer equipped with a broadband cryoprobe, which greatly enhances the capabilities of this technique. The 15N resonance was acquired in little time without the need for any costly isotopic enrichment, thus overcoming the traditional barriers against direct observation 15N NMR spectroscopic studies.
- A. Salgado, C. Varela, A. M. García Collazo and P. Pevarello, Magn. Reson. Chem., 2010, 48, 614 CAS.
- K. J. Sheehy, L. M. Bateman, N. Flosbach, M. Breugst and P. A. Byrne, Eur. J. Org. Chem., 2020, 3270 CrossRef CAS.
- The δN values of non-alkylated nitrogens of diazines undergo small downfield shifts during these reactions (i.e. Δ(δN) ≥ 0 ppm).
- (a) E. Lukevics, E. Leipiņš, I. Segal and M. Fleisher, J. Organomet. Chem., 1991, 406, 283 CrossRef CAS; (b) Z. Dega-Szafran, M. Szafran, J. Sitkowski and L. Stefaniak, J. Phys. Org. Chem., 1996, 9, 746 CrossRef CAS; (c) B. Costisella, J. Schulz, H. Teichmann, C. Donaths and M. Meisels, Phosphorus, Sulfur Silicon Relat. Elem., 1990, 53, 367 CrossRef CAS; (d) M. Szafran, Z. Dega-Szafran, A. Katrusiak, G. Buczak, T. Głowiak, J. Sitkowski and L. Stefaniak, J. Org. Chem., 1998, 63, 2898 CrossRef CAS.
- (a) L. Pazderski, Annu. Rep. NMR Spectrosc., 2013, 80, 33 CrossRef CAS; (b) L. Pazderski, Magn. Reson. Chem., 2008, 46, S3 CrossRef PubMed; (c) R. M. Shanahan, A. Hickey, L. M. Bateman, M. E. Light and G. P. McGlacken, J. Org. Chem., 2020, 85, 2585 CrossRef CAS PubMed.
- Benzhydrylium triflates were generated in the presence of nucleophiles 1, 2 or 3 by treating the parent benzhydryl chloride with AgOTf in CD2Cl2. The entirety of the reaction mixture filtered into an NMR tube (to remove AgCl) under inert atmosphere. For full experimental details, see the ESI.†.
- Experimental data are given in Section 4 of the ESI, beginning on page S8.†.
- A detailed description of how inert NMR spectral analysis was carried out is given on page S8 of the ESI (Procedure B).†.
- Note that MeCN or CD3CN could not be used for 1H–15N HMBC spectroscopic characterization due to the presence of nitrogen in the solvent. Hence, for the purposes of obtaining 1H–15N HMBC spectra, the solvent was removed and the residue re-dissolved in (CD3)2SO. CD2Cl2 was not a suitable solvent for methylation reactions of diazine N-oxides 1–3 due to the negligible solubility of the adducts in this solvent.
- The reaction of 3 with Ph2CH+ produced a spectrum with broad signals that could not be interpreted. See pages S36 and S37 of the ESI† for details.
- Methylation of DMSO by dimethylsulfate: J. Forrester, R. V. H. Jones, P. N. Preston and E. S. C. Simpson, J. Chem. Soc., Perkin Trans. 1, 1995, 2289 RSC.
- Reversibility of methoxysulfonium salt formation: G. F. Koser, P. B. Kokil and M. Shah, Tetrahedron Lett., 1987, 28, 5431 CrossRef CAS.
- See spectra from methylation reactions of 1, 2 and 3 in (CD3)2SO on pages S14, S15, S24, S25 and S33–S35 of the ESI.†.
- See details on pages S18 and S19 of the ESI.†.
- Decomposition was evident in the all of the spectra obtained of this material, regardless of the method employed to synthesize it. The major product remained intact for several days if kept under inert atmosphere (invariably contaminated with decomposition products), but did not survive attempts at isolation. 1H NMR spectra containing signals of the decomposition products are shown in Fig. S15 and S18 of the ESI (pages S29 and S33).†.
- See ESI pages S11–13, S21–23 and S31–33.†.
- C. Sakuma, M. Maeda, K. Tabei, A. Ohta, A. Kerim and T. Kurihara, Magn. Reson. Chem., 1996, 34, 567 CrossRef CAS.
- W. Städeli and W. von Philipsborn, Helv. Chim. Acta, 1980, 63, 504 CrossRef.
- See 1H–15N HMBC NMR spectra in ESI on pages S55, S59, S60, S62, S64, S67, S68 and S70.†.
- See pages S12, S14, S16, S20, S21, S26, and S31 of the ESI for details on 13C{1H} NMR spectra of the N- and O-alkylation products.†.
- See 1H–15N HMBC NMR spectrum on page S71 of the ESI.†.
- See 1H–13C HMBC NMR spectrum on page S73 in the ESI.†.
- All crossover experiments described in this section can be found in the ESI in Section 5, beginning on page S38.†.
- E.g. 7 is a stronger Lewis base than 2 by a factor of ca.16, while 25 is a stronger Lewis base than 1 by a factor of ca.20: (a) P. A. Byrne, K. J. Sheehy, S. Buckley and H. Mayr, unpublished results; (b) H. Mayr, J. Ammer, M. Baidya, B. Maji, T. A. Nigst, A. R. Ofial and T. Singer, J. Am. Chem. Soc., 2015, 137, 2580 CrossRef CAS PubMed.
- The experimental data pertaining to this experiment can be found on pages S46–S50 in the ESI.†.
- Full details on our computational investigations are given in the ESI, pg. S83–S110.†.
- This is consistent with a report by Mayr, Ofial and co-workers indicating greater Lewis basicity of 28 compared to 27 in reactions with reference benzhydrylium ions: see ref. 61b above.
- See page S11 and 12 in the ESI.†.
- Precedent exists for remote deactivation of a Lewis basic nitrogen site: P. A. Byrne, S. Kobayasi, M. Breugst, H. Laub and H. Mayr, J. Phys. Org. Chem., 2016, 29, 759 CrossRef CAS.
- See calculation on pages S31 and S35 in the ESI.†.
- As cations and anions were assumed to be solvent separated, this trend can be expected for these bimolecular reactions. See Tables S1–S3 on pages S83–S85 of the ESI.†.
- For details on Marcus theory, see: (a) R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155 CrossRef CAS; (b) R. A. Marcus, J. Phys. Chem., 1968, 72, 891 CrossRef CAS; (c) R. A. Marcus, J. Am. Chem. Soc., 1969, 91, 7224 CrossRef CAS; (d) W. J. Albery and M. M. Kreevoy, Adv. Phys. Org. Chem., 1978, 16, 87 CrossRef CAS; (e) W. J. Albery, Annu. Rev. Phys. Chem., 1980, 31, 227 CrossRef CAS; (f) R. A. Marcus, Pure Appl. Chem., 1997, 69, 13 CAS; (g) R. A. Marcus, Angew. Chem., Int. Ed., 1993, 32, 1111 CrossRef.
- As pointed out in ref. 4, the omission of the work terms from eqn (1) is justified when considering intramolecular selectivity such as selectivity between nucleophilic sites of an ambident nucleophile.
- Introductions to Marcus theory are available in chemistry textbooks: (a) E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, California, 2006, pp. 403–406 Search PubMed; (b) P. W. Atkins and J. De Paula, Physical Chemistry, Oxford University Press, Oxford, 9th edn, 2010, p. 820, 857–861 Search PubMed; (c) M. B. Smith, March's Advanced Organic Chemistry, Wiley-VCH, Hoboken, New Jersey, 7th edn, 2013, pp. 273–274 Search PubMed.
- (a) Phenoxides: R. Mayer, M. Breugst, N. Hampel, A. R. Ofial and H. Mayr, J. Org. Chem., 2019, 84, 8837 CrossRef CAS PubMed; (b) Carbonyl-stabilised phosphonium ylides: P. A. Byrne, K. Karaghiosoff and H. Mayr, J. Am. Chem. Soc., 2016, 138, 11272 CrossRef CAS PubMed; (c) Azolium enolates: B. Maji and H. Mayr, Angew. Chem., Int. Ed., 2013, 52, 11163 CrossRef CAS PubMed; (d) Formaldehyde N,N-dialkylhydrazones: B. Maji, K. Troshin and H. Mayr, Angew. Chem., Int. Ed., 2013, 52, 11900 CrossRef CAS PubMed; (e) Methylhydrazines: T. A. Nigst, J. Ammer and H. Mayr, Angew. Chem., Int. Ed., 2012, 51, 1353 CrossRef CAS PubMed.
- See intrinsic barrier ΔG‡0 calculations in Section 9 of the ESI, beginning on page S86.†.
- See Table S5 on page S90 in the ESI for calculated values of ΔG‡0 and ΔG‡.†.
- S. Hoz, H. Basch, J. L. Wolk, T. Hoz and E. Rozental, J. Am. Chem. Soc., 1999, 121, 7724 CrossRef CAS . Note that similar trends were also observed across the 3rd to 5th rows of the periodic table (p-block elements; noble gases not included).
- X.-Q. Zhu and J.-D. Yang, J. Phys. Org. Chem., 2013, 26, 271 CrossRef CAS.
- S. S. Shaik, H. B. Schlegel and P. Wolfe, Theoretical Aspects of Physical Organic Chemistry: The SN2 Mechanism; Wiley, New York, 1992 Search PubMed.
- (a) X.-Q. Zhu, F.-H. Deng, J.-D. Yang, X.-T. Li, Q. Chen, N.-P. Lei, F.-K. Meng, X.-P. Zhao, S.-H. Han, E.-J. Hao and Y.-Y. Mu, Org. Biomol. Chem., 2013, 11, 6071 RSC; (b) Y.-H. Fu, G.-B. Shen, Y. Li, L. Yuan, J.-L. Li, L. Li, A.-K. Fu, J.-T. Chen, B.-L. Chen, L. Zhu and X.-Q. Zhu, ChemistrySelect, 2017, 2, 904 CrossRef CAS; (c) G.-B. Shen, K. Xia, X.-T. Li, J.-L. Li, Y.-H. Fu, L. Yuan and X.-Q. Zhu, J. Phys. Chem. A, 2016, 120, 1779 CrossRef CAS PubMed; (d) Y. Li and X.-Q. Zhu, ACS Omega, 2018, 3, 872 CrossRef CAS PubMed.
- The introduction and usage of the Zhu equation is discussed in the ESI, beginning on page S89.†.
- See pg S111–S116 of ESI† for details of the experimental determination of an approximate ΔG‡ value for the reaction of 1 + MeI to give 13a.
- See Table S8 on pg S92 of the ESI.†.
- Numerous precedents for kinetically controlled N-alkylation of other ambident nucleophiles with competing O and N nucleophilic sites (e.g. amide anions) exist in the literature. See ref. 19b, e and 22b, d and also additional ref. S-1c, h, i, and S-3b given on page S117 of the ESI.†.
- (a) P. A. Byrne, S. Kobayashi, E.-U. Würthwein, J. Ammer and H. Mayr, J. Am. Chem. Soc., 2017, 139, 1499 CrossRef CAS PubMed; (b) J. P. Richard, M. M. Toteva and J. Crugeiras, J. Am. Chem. Soc., 2000, 122, 1664 CrossRef CAS.
- Amide O-alkylation appears to be kinetically favoured over N-alkylation. Although O-methylation of DMF has been shown to be reversible at temperatures > 100 °C,19a,d,f reports of N-alkylation of amides in refluxing acetonitrile (boiling point 82 °C at atmospheric pressure) are likely to involve misidentification of the products. Certainly, the spectral data supplied are insufficient for definitive assignment of N-alkylated products.8,9.
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed.
- Schrödinger Release 2018-3; Macromodel, Schrödinger, LLC, New York, NY, 2018 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappopor and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Wallingford, CT, 2016 Search PubMed.
- (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, characterisation data for products and reaction mixtures, details of crossover experiments, copies of NMR spectra, and details on computational investigations. See DOI: 10.1039/d0sc02834g |
| This journal is © The Royal Society of Chemistry 2020 |