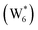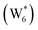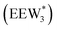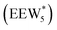Open Access Article
Open Access ArticleStructure and solvation of confined water and water–ethanol clusters within microporous Brønsted acids and their effects on ethanol dehydration catalysis†
Jason S.
Bates‡
 ,
Brandon C.
Bukowski‡
,
Brandon C.
Bukowski‡
 ,
Jeffrey
Greeley
,
Jeffrey
Greeley
 * and
Rajamani
Gounder
* and
Rajamani
Gounder
 *
*
Charles D. Davidson School of Chemical Engineering, Purdue University, 480 Stadium Mall Drive, West Lafayette, IN 47907, USA. E-mail: jgreeley@purdue.edu; rgounder@purdue.edu
First published on 18th June 2020
Abstract
Aqueous-phase reactions within microporous Brønsted acids occur at active centers comprised of water-reactant-clustered hydronium ions, solvated within extended hydrogen-bonded water networks that tend to stabilize reactive intermediates and transition states differently. The effects of these diverse clustered and networked structures were disentangled here by measuring turnover rates of gas-phase ethanol dehydration to diethyl ether (DEE) on H-form zeolites as water pressure was increased to the point of intrapore condensation, causing protons to become solvated in larger clusters that subsequently become solvated by extended hydrogen-bonded water networks, according to in situ IR spectra. Measured first-order rate constants in ethanol quantify the stability of SN2 transition states that eliminate DEE relative to (C2H5OH)(H+)(H2O)n clusters of increasing molecularity, whose structures were respectively determined using metadynamics and ab initio molecular dynamics simulations. At low water pressures (2–10 kPa H2O), rate inhibition by water (−1 reaction order) reflects the need to displace one water by ethanol in the cluster en route to the DEE-formation transition state, which resides at the periphery of water–ethanol clusters. At higher water pressures (10–75 kPa H2O), water–ethanol clusters reach their maximum stable size ((C2H5OH)(H+)(H2O)4–5), and water begins to form extended hydrogen-bonded networks; concomitantly, rate inhibition by water (up to −3 reaction order) becomes stronger than expected from the molecularity of the reaction, reflecting the more extensive disruption of hydrogen bonds at DEE-formation transition states that contain an additional solvated non-polar ethyl group compared to the relevant reactant cluster, as described by non-ideal thermodynamic formalisms of reaction rates. Microporous voids of different hydrophilic binding site density (Beta; varying H+ and Si–OH density) and different size and shape (Beta, MFI, TON, CHA, AEI, FAU), influence the relative extents to which intermediates and transition states disrupt their confined water networks, which manifest as different kinetic orders of inhibition at high water pressures. The confinement of water within sub-nanometer spaces influences the structures and dynamics of the complexes and extended networks formed, and in turn their ability to accommodate the evolution in polarity and hydrogen-bonding capacity as reactive intermediates become transition states in Brønsted acid-catalyzed reactions.
1. Introduction
In heterogeneous catalysis, the interface between liquid or liquid-like solvating environments and active sites at solid surfaces can significantly alter reaction rates and selectivities,1 and its ubiquitous effects have been documented in electrocatalysis,2–6 aqueous-phase reactions on metal nanoparticles,7–12 and gas-phase reactions at high pressures sufficient to cause condensation within porous solids (e.g., Fischer–Tropsch synthesis13–16 and alkene oligomerization17–19). In addition, confinement within sub-nanometer spaces imposes constraints on the structures that solvents can adopt, and in turn their influence on reactive intermediates and transition states stabilized at active sites, as demonstrated by the breadth of water structures and dynamics within carbon nanotubes of different dimensions,20–23 and the diverse function of enzymes with different hydrophobicity.24 Inorganic, crystalline, microporous frameworks offer independent synthetic control of the density, chemical identity, and coordination of catalytic active sites, and the structure and polarity of the environments that confine them, which make zeolites and zeotype-molecular sieves a versatile platform to study fundamental principles underlying the structure and catalytic behavior of confined solvents. Lewis acid zeolites containing framework Ti4+ or Sn4+ centers have been reported recently to show significant differences in reactivity for aqueous-phase olefin epoxidation25–29 and sugar isomerization30–34 in response to changes in active site structure and the stabilization or exclusion of extended water networks within microporous environments. The interplay between the solvated structures and reactivity of Brønsted acidic H+ sites associated with framework Al3+ in siliceous zeolites (Si–O(H+)–Al), however, are less well-understood because of the greater diversity of H+, reactant, and transition state complexes engendered by solvating water within confining voids.Zeolite frameworks are comprised primarily of siloxane bonds that are non-polar and hydrophobic,35 but they also contain hydrophilic binding sites in the form of H+ sites and defect Si–OH groups that preferentially bind H2O.35–38 At low coverages (<1 H2O per H+), H2O forms hydrogen-bonded complexes with H+ sites;39,40 as additional H2O molecules adsorb (>1 H2O per H+), hydronium ions (H3O+) form.41,42 Vjunov et al.43 reported IR spectra, DFT calculations, and Al K-edge XANES spectra of H-Al-MFI zeolites that indicate formation of H+(H2O)n clusters analogous to those present in gaseous phases, which causes delocalization of the positive charge away from the charge-compensating framework [AlO4/2]−. The molecularity of these H+(H2O)n clusters, determined from vapor-phase H2O adsorption isotherms (298 K) on H-Al-MFI samples of varying H+ content (Si/Al = 15–110), was reported to be 7–8 H2O per H+; this stoichiometry is consistent with aqueous-phase cyclohexanol adsorption saturation uptakes (298 K) that decrease with increasing H+ content as H+(H2O)7–8 clusters occupy higher fractions of available void space.44 The stoichiometry of 7–8 H2O per cluster was also corroborated by 1H and 1H–29Si CP MAS NMR spectra of H-Al-MFI (Si/Al = 15, 40) samples as a function of H2O coverage (at ambient temperature) and by ab initio molecular dynamics (AIMD) simulations (at 300 K).45 These results highlight not only the distinct clustered structures of H2O stabilized at H+ sites located within the confined sub-nanometer spaces of zeolites, unlike the classical solution-phase Zundel (H5O2+)46 and Eigen (H9O4+)47 structures or the H13O6+ cluster reported by Stoyanov et al.,48 but also the more compressed structures and different proton-hopping dynamics than gas-phase clusters according to AIMD simulations.45 Despite these detailed structural characterizations of H+(H2O)n in confined spaces, changes to their structure upon interacting with reactants under conditions relevant to catalysis, and the kinetic consequences of such solvated reactant and transition state complexes, are not as well-understood.
Solvent effects in reactions catalyzed by Brønsted acid zeolites have been studied at the extremes of low solvent pressures that form gas-like species, and of high solvent pressures that form liquid-like species, but seldom integrate insights from these disparate surface coverage regimes into a cohesive kinetic and mechanistic description of the catalytic chemistry. Haw and coworkers reported that co-solvating nitromethane enhanced the extent of gas-phase proton-transfer from H-Al-MFI to 13C-labeled acetone detected by 13C NMR, which enabled acetone dimerization only when nitromethane was co-fed in a flow reactor (513 K).49 These concepts can be extended to co-adsorbed H2O, which enhances gas-phase rates of alkane C–H bond activation,50 H–D exchange,51 and steam dealumination52 in H-zeolites, and enables distinct H3O+-mediated pathways in aqueous-phase hydrogenation of furanics53 and aldol condensation of ketones.54 In gas-phase alcohol dehydration reactions, H2O inhibits the rates of forming both alkenes and ethers in unimolecular and bimolecular pathways, respectively.55 H2O inhibition quantified by negative reaction orders is often described by reaction mechanisms that include inhibitory alcohol–water dimer species, as observed in alcohol dehydration catalyzed by Brønsted acidic Keggin-type polyoxometalate clusters56 and Lewis acidic γ-Al2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57,58 and Sn-Beta zeolites.59,60 Others have suggested that co-adsorbed H2O inhibits alcohol dehydration by stabilizing adsorbed alcohols preferentially over transition states, in the case of 1-propanol dehydration on H-Al-MFI zeolites.61 In the liquid phase, confinement of H3O+ within H-Al-Beta zeolite pores (∼0.7 nm in diameter) leads to higher rates of cyclohexanol dehydration than in bulk solution, because of enhanced association between H3O+ and reactants and the entropic destabilization of this precursor relative to the transition state,62 and solvation of H+ by non-polar solvents rather than water leads to higher rates of phenol alkylation.63 Kinetic and adsorption measurements showed that increasing densities of H3O+ resulted in lower reactant coverages at H3O+ active sites in aqueous-phase alkylation of phenol in H-Al-MFI zeolites (523 K),64 and NMR measurements performed in operando showed that tuning organic/aqueous solvent compositions could change reactant coverages during glucose isomerization catalysis (403 K) within Na-FAU zeolites.65 Turnover rates of homogeneously catalyzed unimolecular dehydration reactions, measured under conditions that reflect the stability of elimination transition states relative to the solvated proton, indicate that the composition of the H2O–organic solvent mixture predominantly influences the free energy of the solvated proton, which is stabilized when solvated by water66,67 and which influences selectivity when reactants are able to undergo parallel unimolecular pathways.68 Equilibrium constants to protonate pyridine (293 K) within zeolites differ when their pores are filled by solvents of different polarity, also highlighting the important role of proton-solvent complex stability.69 Other studies of co-solvents within zeolites, based on IR spectra and gas-phase isopropanol dehydration probe reactions, suggest that the protic nature of solvents (e.g., acetic acid) and co-existing cations (e.g., Na+) can change the type, number, and strength of Brønsted acid sites in zeolites.70–72 Bridging the gap in mechanistic understanding from that of molecular species and complexes prevalent during gas-phase studies at H2O pressures well below saturation, to those of extended solvent networks and condensed phases around active sites that prevail during liquid-phase studies, requires considering how the clustered nature of alcohol–water intermediates at active sites evolves with the structure of solvating water networks confined within the same pores.73,74 In contrast to gas-phase studies, however, the scope of mechanistic investigations in heterogeneous catalysis is limited in liquid phases because aqueous solvent structures at the liquid–solid interface cannot be varied independently of reactant or co-solvent concentrations.
57,58 and Sn-Beta zeolites.59,60 Others have suggested that co-adsorbed H2O inhibits alcohol dehydration by stabilizing adsorbed alcohols preferentially over transition states, in the case of 1-propanol dehydration on H-Al-MFI zeolites.61 In the liquid phase, confinement of H3O+ within H-Al-Beta zeolite pores (∼0.7 nm in diameter) leads to higher rates of cyclohexanol dehydration than in bulk solution, because of enhanced association between H3O+ and reactants and the entropic destabilization of this precursor relative to the transition state,62 and solvation of H+ by non-polar solvents rather than water leads to higher rates of phenol alkylation.63 Kinetic and adsorption measurements showed that increasing densities of H3O+ resulted in lower reactant coverages at H3O+ active sites in aqueous-phase alkylation of phenol in H-Al-MFI zeolites (523 K),64 and NMR measurements performed in operando showed that tuning organic/aqueous solvent compositions could change reactant coverages during glucose isomerization catalysis (403 K) within Na-FAU zeolites.65 Turnover rates of homogeneously catalyzed unimolecular dehydration reactions, measured under conditions that reflect the stability of elimination transition states relative to the solvated proton, indicate that the composition of the H2O–organic solvent mixture predominantly influences the free energy of the solvated proton, which is stabilized when solvated by water66,67 and which influences selectivity when reactants are able to undergo parallel unimolecular pathways.68 Equilibrium constants to protonate pyridine (293 K) within zeolites differ when their pores are filled by solvents of different polarity, also highlighting the important role of proton-solvent complex stability.69 Other studies of co-solvents within zeolites, based on IR spectra and gas-phase isopropanol dehydration probe reactions, suggest that the protic nature of solvents (e.g., acetic acid) and co-existing cations (e.g., Na+) can change the type, number, and strength of Brønsted acid sites in zeolites.70–72 Bridging the gap in mechanistic understanding from that of molecular species and complexes prevalent during gas-phase studies at H2O pressures well below saturation, to those of extended solvent networks and condensed phases around active sites that prevail during liquid-phase studies, requires considering how the clustered nature of alcohol–water intermediates at active sites evolves with the structure of solvating water networks confined within the same pores.73,74 In contrast to gas-phase studies, however, the scope of mechanistic investigations in heterogeneous catalysis is limited in liquid phases because aqueous solvent structures at the liquid–solid interface cannot be varied independently of reactant or co-solvent concentrations.
Here, we combine theoretical simulations with experimental kinetic measurements and in situ IR spectroscopy to obtain molecular-level insights into the structures of water and water–ethanol clusters and extended networks confined within micropores of different sizes and shapes, and their resulting effects on Brønsted acid catalysis. A suite of H-Al-Beta zeolites were synthesized with a wide range of H+ densities (0.11–2.0 per unit cell) and Si–OH defects (∼0.3–5 per unit cell) to obtain inorganic microporous materials with well defined densities of hydrophilic binding sites that can be used to interrogate the structures of adsorbed H2O. Different H2O structures are stabilized at H+ and Si–OH groups within Beta zeolites, as probed by volumetric adsorption isotherms and their isosteric heats of adsorption, and by in situ IR spectra under conditions relevant to ethanol dehydration catalysis. Turnover rates of ethanol dehydration to diethyl ether (373 K, per H+) are measured across a wide range of H2O pressures (0.02–75 kPa) that encompass intrapore coverage regimes including alcohol–water dimers, alcohol–water–hydronium ion clusters, and extended hydrogen-bonded water networks that solvate them. Experimental turnover rates are interpreted mechanistically, aided by identifying the structures of most abundant reactive intermediates (MARI) by AIMD simulations and of kinetically relevant transition states by DFT calculations and metadynamics simulations. Interactions of transition states and precursors with extended hydrogen-bonded water networks manifest as inhibitory effects of H2O on ethanol dehydration rates, which are much stronger than predicted by the molecularity of the reaction and require non-ideal thermodynamic formalisms to describe. This approach is also extended to microporous Brønsted acids with varying pore architectures, highlighting how the shapes of confining environments influence the structure and reorganization of solvents around reactive intermediates and transition states in Brønsted acid catalysis.
2. Results and discussion
2.1. Kinetics of Brønsted acid-catalyzed ethanol dehydration and water inhibition in zeolites
Different densities of Brønsted acid H+ or Si–OH groups within zeolites stabilize water networks of distinct clustered and extended hydrogen-bonded structures,43–45,75 which have been reported to influence reactivity in numerous ways, including different competitive adsorption of solvent(s) and reactants,64,65 entropic gains when water networks are disrupted by transition states,28,76 and entropic losses when transition states are disrupted by water networks.34 Thus, interrogation of H-zeolite samples with varying H+ and Si–OH density is required to disentangle their separate effects on intrapore solvent structure, prior to relating systematically varying solvent structures to the rate and equilibrium constants of a probe reaction catalyzed by H+ sites, such as bimolecular ethanol dehydration to diethyl ether (DEE). Here, a suite of Brønsted acidic H-Al-Beta zeolites was synthesized in fluoride medium according to Camblor et al.77 (denoted H-Al-Beta-F(X), where X is the number of H+ per unit cell (u.c.−1) determined by NH3 TPD, Table 1). The use of fluoride as the mineralizing agent enabled preparing zeolites containing a wide range of proton densities (0.1–2 H+ u.c.−1) while minimizing the number of silanol defects (∼0.3–0.6 Si–OH u.c.−1, quantified by CD3CN IR on Ti-Beta-F zeolites34) that otherwise form when hydroxide is used as the mineralizing agent (∼3–5 Si–OH u.c.−1, quantified by CD3CN IR on Ti-Beta-OH zeolites34), because anionic siloxy (Si–O−) defects form to balance the cationic charge of occluded tetraethylammonium cations in as-synthesized solids.78 The H-Al-Beta-F samples in Table 1 therefore provide control of the density of H+ sites within otherwise hydrophobic siliceous zeolite channels, whereas an H-Al-Beta-OH sample was synthesized in hydroxide medium to contain a higher density of Si–OH defects within micropores.| Sample | Si/Ala | V micro /cm3 g−1 | H+/Al (NH4+)c | H+/Al (DTBP)d | H+c/u.c. | V micro (de-Al)e |
|---|---|---|---|---|---|---|
a Determined by AAS.
b Determined by minimum in ∂Vads/∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(P/P0) in N2 adsorption isotherms.
c Determined by TPD of NH3 after aqueous-phase ion exchange with 1 M NH4NO3, 24 h, 353 K.
d Determined by in situ 2,6-di-tert-butylpyridine titration during ethanol dehydration catalysis (378 K, 5 kPa C2H5OH, 1 kPa H2O).
e “de-Al” reflects deAl-Beta samples generated by treatment of H-Al-Beta in 69% HNO3 (353 K, 16 h). log(P/P0) in N2 adsorption isotherms.
c Determined by TPD of NH3 after aqueous-phase ion exchange with 1 M NH4NO3, 24 h, 353 K.
d Determined by in situ 2,6-di-tert-butylpyridine titration during ethanol dehydration catalysis (378 K, 5 kPa C2H5OH, 1 kPa H2O).
e “de-Al” reflects deAl-Beta samples generated by treatment of H-Al-Beta in 69% HNO3 (353 K, 16 h).
|
||||||
| Si-Beta-F | — | 0.21 | — | — | 0 | — |
| H-Al-Beta-F(2.0) | 23 | 0.22 | 0.75 | 0.54 | 2.0 | 0.22 |
| H-Al-Beta-F(1.4) | 34 | 0.18 | 0.78 | — | 1.4 | 0.21 |
| H-Al-Beta-F(1.2) | 45 | 0.20 | 0.84 | 0.79 | 1.2 | 0.21 |
| H-Al-Beta-F(0.78) | 65 | 0.21 | 0.79 | — | 0.78 | 0.20 |
| H-Al-Beta-F(0.57) | 93 | 0.23 | 0.84 | — | 0.57 | 0.22 |
| H-Al-Beta-F(0.16) | 220 | 0.20 | 0.54 | 1.1 | 0.16 | — |
| H-Al-Beta-F(0.11) | 500 | 0.20 | 0.84 | — | 0.11 | — |
| H-Al-Beta-OH(1.7) | 40 | 0.23 | 1.1 | 0.38 | 1.7 | — |
Turnover rates (373 K, per H+) of ethanol dehydration to DEE were measured in differential reactors (details in Section S.2.1, ESI†) across a wide range of ethanol and water pressures (2 × 10−3 to 10 kPa C2H5OH, 0–75 kPa H2O, Fig. 1) in order to quantify the effects of co-fed H2O pressure in terms of rate constants that reflect the stabilities of intermediates and transition states in accepted reaction mechanisms. Such rate data were measured on H-Al-Beta zeolites with varying H+ density (0.16–2.0 u.c.−1), quantified during ethanol dehydration catalysis by in situ poisoning with 2,6-di-tert-butylpyridine (DTBP) to enable accurate normalization of turnover rates79,80 (Fig. S4–S10, ESI†). Kinetic data in the absence of co-fed water serve to benchmark81 experimental measurements to prior literature reports and set the stage for detailed investigations of the effects of water under conditions that approach capillary condensation and catalysis within liquid-like phases confined within microporous environments. In the absence of co-fed water, turnover rates increase linearly with ethanol pressure (<0.01 kPa) and approach constant values at higher ethanol pressures (∼0.05 kPa, Fig. 1a). This functional dependence is consistent with an associative mechanism for bimolecular ethanol dehydration to DEE82–85 (Fig. S11,† with further discussion in Sections S.2.4–S.2.5, ESI†), in which H+ sites are occupied by MARI consisting of hydrogen-bonded ethanol monomers and protonated ethanol–ethanol dimers that are in quasi-equilibrium with gaseous ethanol; protonated dimers subsequently rearrange to form co-adsorbed DEE and water in the kinetically relevant step followed by product desorption in kinetically irrelevant steps to complete the catalytic cycle. These mechanistic assumptions lead to a rate expression for the bimolecular dehydration turnover rate that captures the measured dependence on ethanol pressure:
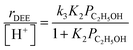 | (1) |
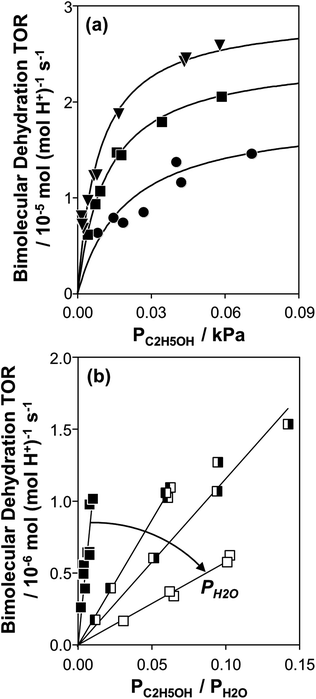 | ||
Fig. 1 (a) Bimolecular ethanol dehydration turnover rate (per H+, 373 K) as a function of C2H5OH pressure, without co-fed H2O, on H-Al-Beta-F(1.2) (●), H-Al-Beta-F(2.0) (■), and H-Al-Beta-OH(1.7) (▼). Solid lines represent regression to eqn (1). (b) Bimolecular ethanol dehydration turnover rate (per H+, 373 K) on H-Al-Beta-F(2.0) as a function of the C2H5OH/H2O pressure ratio, in the range 2–10 kPa H2O (■), and at 40 kPa H2O (![[square filled left]](https://www.rsc.org/images/entities/char_25e7.gif) ), 50 kPa H2O ( ), 50 kPa H2O (![[square filled right]](https://www.rsc.org/images/entities/char_25e8.gif) ), and 75 kPa H2O (□). ), and 75 kPa H2O (□). | ||
Bimolecular dehydration turnover rates (373 K, per H+) measured on H-Al-Beta-F(2.0) in the presence of co-fed water (2–75 kPa H2O) are presented in Fig. 1b as a function of the ethanol/water pressure ratio. The inhibitory effects of water are consistent with the formation of an ethanol–water dimer species invoked previously to account for inhibition of monomolecular 2-butanol dehydration rates by water on Brønsted acidic polyoxometalate clusters56 (343 K, <0.5 kPa H2O). Including the ethanol–water dimer as a candidate MARI alongside ethanol monomer and ethanol–ethanol dimer species leads to a modified rate expression:
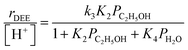 | (2) |
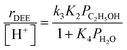 | (3) |
In the limiting case of excess water pressures, ethanol–water dimers are the sole MARI and rates depend linearly on the ethanol-to-water pressure ratio:
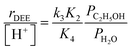 | (4) |
At moderate water pressures (2–10 kPa, filled data points in Fig. 1b), eqn (4) accurately predicts the inhibitory effects of water, which reflects the requirement to displace water with ethanol in precursor complexes en route to the bimolecular dehydration transition state. The bimolecular dehydration turnover rate (373 K, per H+) is a single-valued function of ethanol/water pressure ratio in the range of 2–10 kPa of water (PC2H5OH/PH2O = 0.002–0.01, solid data points in Fig. 1b), consistent with full coverage of H+ sites by ethanol–water dimers. DFT calculations of water-assisted associative pathways (Fig. S64, ESI†) indicate that water co-adsorbs with an ethanol monomer to form an ethanol–water dimer (+5 kJ mol−1; Fig. S64, ESI†), and a gas-phase ethanol subsequently adsorbs to form an ethanol–ethanol–water trimer (+24 kJ mol−1, Fig. S64, ESI†), which can form DEE via an SN2 transition state analogous to that formed when water is absent. The additional water molecule in the ethanol–ethanol–water trimer, however, acts as a proton shuttle between the framework and the H2O leaving group, allowing the transition state to reside more distant from the framework [AlO4/2]− and gain additional stabilization through dispersive interactions with the surrounding framework (Fig. S64, ESI†). Thus, apparent activation free energies for water-free and water-assisted associative pathways are comparable (Fig. S64, ESI†), indicating that as H+ become covered by (C2H5OH)(H+)(H2O)n MARI species, their corresponding transition states containing co-adsorbed H2O become kinetically relevant (Section S.2.4, ESI†). These findings also indicate that mechanistic interpretation of the inhibitory effects of H2O with varying water coverage requires more precise descriptions of the (C2H5OH)(H+)(H2O)n intermediates of different molecularity that can form DEE without complete desorption of H2O, as we discuss below (Section 2.5).
At water pressures above 10 kPa (partially filled and unfilled data points in Fig. 1b), measured rates deviate from the single-valued function observed between 2–10 kPa and described by eqn (4), but remain first-order in ethanol pressure, according to the empirical relation:
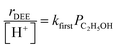 | (5) |
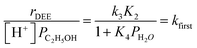 | (6) |
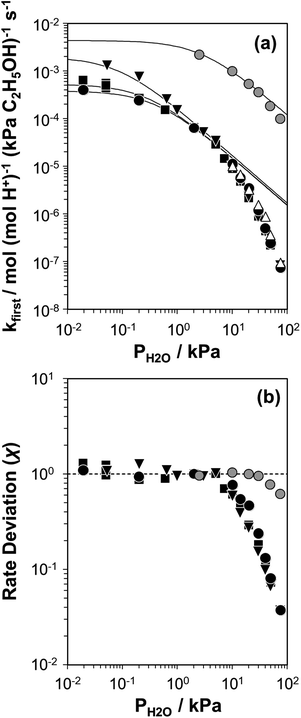 | ||
Fig. 2 (a) Apparent first-order bimolecular ethanol dehydration rate constant (per H+, 373 K) and (b) rate deviation (χ) from the functional dependence of eqn (6), as a function of H2O pressure on H-Al-Beta-F(0.16) (△), H-Al-Beta-F(1.2) (●,  at 423 K), H-Al-Beta-F(2.0) (■), and H-Al-Beta-OH(1.7) (▼). Solid lines reflect regression to eqn (6). at 423 K), H-Al-Beta-F(2.0) (■), and H-Al-Beta-OH(1.7) (▼). Solid lines reflect regression to eqn (6). | ||
The solid lines in Fig. 2a represent regression of kfirst values (∼0.02–10 kPa H2O) to eqn (6), and give values for the lumped rate and equilibrium constant groups k3K2 and k3K2K4−1 in the low and high water pressure limits, respectively (Table S2, ESI†). The value of k3K2 reflects the free energy of the confined bimolecular dehydration transition state relative to the free energy of the confined ethanol monomer and gas-phase ethanol, and k3K2K4−1 reflects that of the confined transition state and gas-phase water relative to the confined ethanol–water dimer and gas-phase ethanol (additional discussion and derivations in Section S.2.6, ESI†). Values of k3K2K4−1 are essentially identical among the three H-Al-Beta samples (1.5–1.7 × 10−4 mol (mol H+)−1 s−1, Table S2, ESI†), indicating that once H+ are saturated with ethanol–water dimer intermediates, the free energy difference required to replace adsorbed water with adsorbed ethanol at the transition state is insensitive to differences in Si–OH density or other sample heterogeneities.
The deviation of kfirst values from those predicted by eqn (6) at water pressures above ∼10 kPa (Fig. 2a) was quantified as a function of water pressure up to 75 kPa. This deviation can be expressed as a function of water pressure by combining eqn (5) and (6):
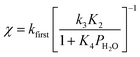 | (7) |
Values of kfirst at 423 K on H-Al-Beta-F(2.0) (Fig. 2) are accurately described by eqn (6) between 2.5–30 kPa H2O and are −1 order in water above 20 kPa H2O (eqn (4)), in contrast to values of kfirst at 373 K that are −1 order in water above 2 kPa H2O. The delayed onset of the inverse water order kinetic regime to higher H2O pressures at 423 K is consistent with lower coverages of inhibitory ethanol–water dimer intermediates at higher temperature, and is reflected by a lower K4 value at 423 K (0.35, Table S3, ESI†) than at 373 K (2.5, Table S3, ESI†). In addition, χ values quantified at 423 K deviate from unity only above 30 kPa of H2O, whereas χ values deviate from unity above 10 kPa H2O at 373 K. The onset of sub-unity deviations in χ values becomes shifted to higher H2O pressures at higher temperatures, similar to the later saturation of the surface by ethanol–water dimers when the kinetic regime is −1 order in water. By analogy, it is hypothesized that the dependence of χ on H2O pressure is related to increasing coverages of water within micropores. Thus, we next probe the structures of adsorbed water and reaction intermediates in regimes approaching capillary condensation within micropores.
2.2. Characterization of intracrystalline water structures
The coverages and structures of H2O prevalent during ethanol dehydration catalysis at 373 K were assessed using a combination of volumetric adsorption isotherms and in situ IR spectroscopy. The individual contributions of polar hydroxyl groups associated with both Brønsted acid sites (H+) and Si–OH nests were systematically varied using the suite of H-Al-Beta-F samples that contain varying densities of H+ u.c.−1 (0.11–2.0, Table 1) and minimal densities of intracrystalline Si–OH defects (0.3–0.6 Si–OH u.c.−1, quantified by CD3CN IR on Ti-Beta-F zeolites34) because they were prepared in fluoride media.77 Complete dealumination yielded deAl-Beta-F samples that contained Si–OH nest densities approximately equal to the number of H+ u.c.−1 before dealumination (Fig. S38†). Measured volumetric water adsorption isotherms (293 K, Fig. S31–S32a, ESI†) indicate that the adsorbed amount of water systematically increases with the density of hydrophilic groups on H-Al-Beta-F (H+) or deAl-Beta-F (Si–OH), consistent with prior reports.44,88 The isotherm measured on Si-Beta-F was subtracted from those of H-Al-Beta-F and deAl-Beta-F to obtain isotherms that predominantly reflect H2O adsorption at their intracrystalline hydrophilic binding sites (H+, Si–OH nest),44 and these isotherms were then normalized by the densities of H+ or Si–OH nests to interrogate whether adsorption at individual functional groups is influenced by their density within crystallites.H+-normalized H2O adsorption isotherms (Fig. 3) are invariant across the full range of H+ densities (0.11–2.0 u.c.−1) in H-Al-Beta-F zeolites at low relative pressures (P/P0 < ∼0.2, 293 K), indicating that adsorption occurs preferentially at H+ sites and generates (H3O+)(H2O)n clusters of increasing size with increasing H2O pressure. H+-normalized isotherms deviate among samples at higher relative pressures (P/P0 > 0.2), implying that (H3O+)(H2O)n clusters have reached their maximum size and any additional H2O that adsorbs instead is located within void spaces that are not occupied by (H3O+)(H2O)n clusters, and at intracrystalline and extracrystalline Si–OH groups45 that may be present in different amounts among samples. The saturation of (H3O+)(H2O)n clusters at P/P0 ∼ 0.2 is also consistent with H2O adsorption isotherms that are identical above P/P0 = 0.2 on H-Al-Beta-F(0.57) and Na-Al-Beta-F(0.57), but offset by the difference in size of clusters stabilized by the different cations (Fig. S33, ESI†). At a P/P0 value of 0.2, the average value of H2O/H+ is 7 ± 1 on H-Al-Beta-F samples with H+ u.c.−1 varying from 0.11–2.0 (Table S4, ESI†), similar to that reported previously.44 The preferential adsorption of H2O at H+ and Si–OH nest defects was corroborated by volumetric adsorption isotherms and by determining isosteric heats of adsorption as a function of coverage from adsorption isotherms measured at different temperatures (details in Section S.2.7, ESI†). Measured isotherms provide a quantitative relationship between H2O coverage and partial pressure that can be further related to the spectroscopic signatures of adsorbed H2O structures present at different H2O coverages.
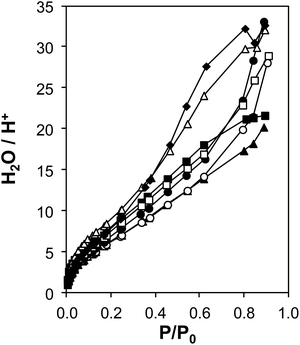 | ||
| Fig. 3 Volumetric H2O adsorption isotherms (293 K) on H-Al-Beta-F samples, with H+ u.c.−1 = 0.11 (♦), 0.16 (△), 0.57 (▲), 0.78 (○), 1.2 (●), 1.4 (□), 2.0 (■), after subtraction of the Si-Beta-F isotherm and normalizing by H+ (raw isotherms are in Fig. S31, ESI†). | ||
Transmission IR spectra were collected on the suite of H-Al-Beta-F and deAl-Beta-F zeolites at 293 K exposed to H2O pressures between 0.2–1.7 kPa (P/P0 = 0.1–0.75). The spectrum of the zeolite before H2O adsorption and that of gas-phase H2O within the IR cell at the given P/P0 value were subtracted from measured spectra (as illustrated in Fig. S39, ESI†) to provide difference spectra that reflect the vibrational signatures of adsorbed H2O and of zeolite functional groups that are perturbed after adsorption. Representative spectra on Si-Beta-F, H–Al-Beta-F(2.0), and deAl-Beta-F(2.0) are shown in Fig. 4a and b (spectra on all samples in Fig. S40–S54, ESI†). Fig. 4b shows the peak centered between 1620–1630 cm−1 that corresponds to the δ(HOH) scissoring mode of adsorbed H2O.89 The position of the center of the δ(HOH) peak does not change significantly when H2O adsorbs at different functional groups (H+, Si–OH) or at different coverages, and its integrated area is proportional to the amount of water adsorbed at the same P/P0 value quantified by volumetric adsorption isotherms (Fig. 3). The linear relationship between quantity adsorbed and δ(HOH) peak area is shown in Fig. 4c and quantitatively predicts the amount adsorbed with a mean absolute error (MAE) of 0.3 mmol g−1 averaged among fifteen samples with H+/Si–OH nests u.c.−1 between 0–2.0, which enables measuring the amount of adsorbed H2O on zeolite wafers directly from IR spectra instead of resorting to repeatedly estimating it from data collected at an equivalent external water chemical potential (T, P/P0) in equilibrium with zeolite powders in separate volumetric adsorption isotherm measurements.
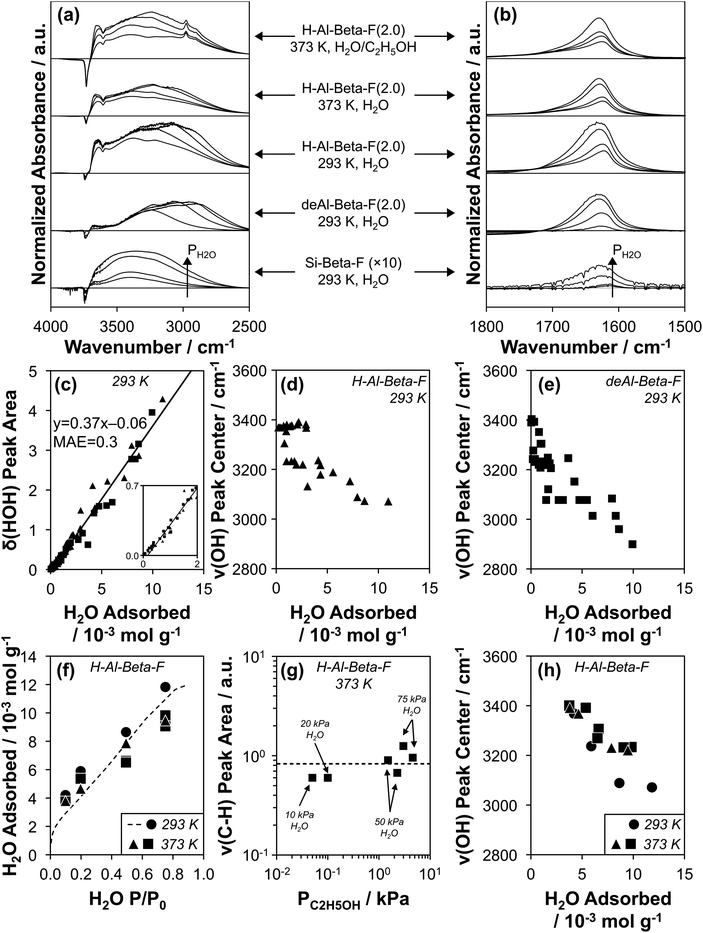 | ||
| Fig. 4 (a and b) Baseline-corrected, normalized difference IR spectra of H2O adsorbed on Si-Beta-F (×10 for clarity), deAl-Beta-F(2.0), and H-Al-Beta-F(2.0) at 293 K, of H2O adsorbed on H-Al-Beta-F(2.0) at 373 K at H2O P/P0 values of 0.1, 0.2, 0.5, and 0.75, and of H2O adsorbed on H-Al-Beta-F(2.0) with co-fed C2H5OH (C2H5OH/H2O = 0.005 (10, 20 kPa H2O) and 0.03 (50, 75 kPa H2O)), in (a) the ν(OH) stretching region and (b) the δ(HOH) scissoring region. (c) Correlation of δ(HOH) area quantified from subtracted spectra at 293 K on all H-Al-Beta-F (▲) and siliceous Beta samples (deAl-Beta-F, Si-Beta-F, ■) listed in Table 1 with the amount of H2O adsorbed at the same P/P0 in volumetric adsorption isotherms (Fig. 3 and S32, ESI†). Solid line reflects line-of-best-fit. (d and e) Correlation of the ν(OH) peak center with the amount of H2O adsorbed on (d) H-Al-Beta-F (▲) and (e) siliceous Beta samples (deAl-Beta-F, Si-Beta-F, ■). (f) Amount of H2O adsorbed on H-Al-Beta-F(2.0) determined from δ(HOH) scissoring areas and the correlation in (c) at 293 K (●), 373 K (▲), and 373 K with co-fed C2H5OH (■). Dashed function corresponds to the volumetric adsorption isotherm of H2O at 293 K (Fig. 3). (g) Variation in ν(CH) peak area with C2H5OH pressure on H-Al-Beta-F(2.0) at 373 K with co-fed H2O at 10, 20, 50, and 75 kPa. Dashed line represents the average value. (h) Correlation of the ν(OH) peak center with the amount of H2O adsorbed on H-Al-Beta-F(2.0) at 293 K (●), 373 K (▲), and 373 K with co-fed C2H5OH (0.05–4.6 kPa) (■). | ||
The O–H stretching region in Fig. 4a (2800–4000 cm−1) includes negative peaks at 3735 cm−1 and 3745 cm−1 associated with the perturbation of isolated Si–OH groups within pores and at external crystallite surfaces, respectively,90,91 a negative peak at 3600 cm−1 associated with the perturbation or disappearance of Brønsted acidic H+ coordinated to the zeolite framework (ν(OH) of Al–OH)90,92 in the case of H-Al-Beta-F(2.0), and a broad positive peak between ∼2800–3700 cm−1 that reflects a convolution of perturbed H+/Si–OH groups and adsorbed H2O molecules. The strong A, B, C triplet (∼2900, ∼2400, and ∼1700 cm−1) generated by Fermi resonance between the ν(OH), δ(HOH) and γ(OH) fundamentals of the Al–OH group in hydrogen-bonded 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2O/H+ complexes93–96 is absent because all spectra are collected at higher coverages (P/P0 ≥ 0.1) after H+ have been liberated from the framework as (H3O+)(H2O)n clusters,43 consistent with complete disappearance of the 3600 cm−1 peak at P/P0 = 0.1 (Fig. S48b, ESI†).
1 H2O/H+ complexes93–96 is absent because all spectra are collected at higher coverages (P/P0 ≥ 0.1) after H+ have been liberated from the framework as (H3O+)(H2O)n clusters,43 consistent with complete disappearance of the 3600 cm−1 peak at P/P0 = 0.1 (Fig. S48b, ESI†).
The positive ν(OH) peak (Fig. 4a) is comprised of multiple components proposed to reflect O–H oscillators with increasing extents of hydrogen bonding as the wavenumber of the peak center decreases.23,75,97 The peak between 3600–3700 cm−1 is reminiscent of a peak assigned to H2O bound in one-dimensional chains within 0.8 nm diameter carbon nanotubes and to H2O with non-hydrogen-bonded O–H groups pointing toward carbon nanotube walls in pores ≥1.4 nm in diameter (ν(OH) = 3640 cm−1).23 A similar peak has been assigned recently to the ν(OH) of H2O (liquid) with one O–H group (3660 cm−1) pointing toward a siloxane bridge on fused SiO2 surfaces with 3.5–4.5 Si–OH nm−2 by vibrational sum frequency generation spectroscopy (vSFG).98 These literature assignments are consistent with interpretation of this peak in Si-Beta-F and deAl-Beta-F (3600–3700 cm−1) to reflect weakly correlated H2O molecules that explore the full hydrophobic channel system, as we have identified previously in AIMD simulations of defect-free Si-Beta (1–3 H2O u.c.−1).75 The ν(OH) peak at 3600–3700 cm−1 is present at higher intensity for H-Al-Beta-F(2.0) than for deAl-Beta-F(2.0) or Si-Beta-F, indicating that it is predominantly associated with non-hydrogen-bonded (“free”) O–H groups of H2O molecules that are part of (H3O+)(H2O)6 clusters, consistent with assignments made for free O–H groups (3700 cm−1) at the interface between water and air by vSFG,99 and in gas-phase Cs+(H2O)20 clusters by cryogenic photofragmentation mass spectrometry.100 These assignments and spectral interpretations enable inferences into how the structure of water complexes and extended networks evolve within confined spaces with increasing water pressure and coverage.
At low relative pressure (P/P0 = 0.1), the dominant positive ν(OH) peak (Fig. 4a) is centered at 3390 cm−1 on Si-Beta-F, 3360–3380 cm−1 on H-Al-Beta-F zeolites (0.11–2.0 H+ u.c.−1), and 3220–3320 cm−1 on deAl-Beta-F zeolites (0.11–2.0 Si–OH nest u.c.−1), and progressively shifts to lower wavenumbers as a function of coverage on both H-Al-Beta-F (Fig. 4d) and deAl-Beta-F (Fig. 4e). The ν(OH) peak on Si-Beta-F does not change its shape nor the position of its center significantly (within ∼40 cm−1) with increasing coverage, and contains contributions from hydrogen-bonded Si–OH groups (∼3400 cm−1)101 and from the O–H oscillators of the H2O molecules bound at them. Bound H2O molecules lead to additional contributions that broaden the ν(OH) peak both above and below its center at ∼3400 cm−1, and have been assigned to the hydrogen-bonded O–H group of water molecules in gas-phase Cs+(H2O)20 clusters whose second O–H group is either hydrogen-bonded (∼3410–3570 cm−1) or free (∼3080–3370 cm−1), respectively.100 Overtones of 2δ(HOH) ∼ 3200 cm−1 also contribute in this region.100,102 The ν(OH) peak centered within a narrow range (3360–3380 cm−1) at P/P0 = 0.1 on H-Al-Beta-F samples (0.11–2.0 H+ u.c.−1) reflects predominantly (H3O+)(H2O)n clusters of similar structure regardless of H+ density (n = 4, Table S5, ESI†), and is broader than the ν(OH) peak on Si-Beta-F because of higher intensity in both the 3600–3700 cm−1 region (free O–H) and the ∼3080–3370 cm−1 region (hydrogen-bonded O–H in H2O with free O–H), likely because the clustered structure of (H3O+)(H2O)4 leads to more free O–H groups than in the H2O molecules hydrogen-bound at Si–OH groups in Si-Beta-F. The ν(OH) peak for H2O adsorbed at Si–OH nests in deAl-Beta-F zeolites at P/P0 = 0.1 (H2O/Si–OH nest = 5 ± 2, Table S6, ESI†) contains contributions from the aforementioned OH groups belonging to H2O and perturbed Si–OH groups, but is centered at lower wavenumbers (3220–3320 cm−1). The lower wavenumber and broader range of the peak center reflects contributions from clustered hydrogen-bonded H2O molecules with free O–H groups at Si–OH nest defects, but not from perturbation among OH groups within Si–OH nests that were already hydrogen-bonded (to one another) prior to H2O adsorption, in contrast to H+ that are isolated and then become solvated as (H3O+)(H2O)n after H2O adsorption. Hydrogen-bonded clusters of H2O molecules at Si–OH nests at lower coverages are consistent with AIMD simulations that show H2O binding at the Si–OH nest at coverages between 1–5 H2O per nest.75
As the coverage of H2O increases at higher partial pressures (P/P0 = 0.2–0.75), the ν(OH) peak centers on both H-Al-Beta-F and deAl-Beta-F zeolites decrease in wavenumbers (Fig. 4d and e) because additional H2O primarily leads to increased peak area in the 2800–3200 cm−1 region (see peak centers of differential-subtracted spectra between P/P0 = 0.2–0.75, Fig. S40b–S52b, ESI†). These peaks are not associated with ice-like water structures103 despite their similar wavenumbers to that of ice (3200 cm−1),104 but instead have been shown to result from Fermi resonance between 2δ(HOH) modes and ν(OH) modes when H2O molecules are coupled in extended hydrogen-bonded networks.102,105,106 As the extent of hydrogen-bonding increases, the ν(OH) mode shifts to lower wavenumber and the splitting caused by Fermi resonance results in an apparent decrease in intensity above 2δ(HOH) and an increase below it.102,105,106 This O–H oscillator signal is made further diffuse by its coupling to the modes of the local extended hydrogen-bonded network.107 Isotopic D2O/HOD/H2O mixtures that are dilute in H2O were used previously to identify this phenomenon because the ν(OH) mode is not split by the 2δ(HOD) = 2900 cm−1 mode,102 and has been verified here using a 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 D2O
1 D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HOD
HOD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixture106 on Si-Beta-F and deAl-Beta-F(2.0), where the ν(OH) peak center does not shift to lower wavenumbers under the same coverage regimes (Fig. S55–S56, ESI†). Although increased ν(OH) intensity between 2800–3200 cm−1 does not quantitatively correspond to a particular species or structure, it does reflect the formation of extended hydrogen-bonded networks, as we have identified in AIMD simulations of Beta zeolites containing one Si–OH nest per unit cell.75 These networks form in both H-Al-Beta-F and deAl-Beta-F zeolites at relative pressures of H2O above ∼0.2, consistent with shifts in the ν(OH) peak center to lower wavenumbers with increasing coverage (Fig. 4d and e), and with adsorption isotherms on H-Al-Beta-F zeolites that are proportional to H+ density up to P/P0 ∼ 0.2 to generate (H3O+)(H2O)6 clusters before extended hydrogen-bonded networks form and surround these clusters. These (H3O+)(H2O)6 clusters remain intact as H2O networks surround them, in contrast to H2O clusters at Si–OH nests that restructure to integrate within these extended hydrogen-bonded networks as observed in our prior AIMD simulations (>5 H2O u.c.−1),75 which is consistent with ν(OH) peak centers in IR spectra that represent the majority of H2O molecules participating in extended networks and thus reach lower values in deAl-Beta-F zeolites (Fig. 4e) than in H-Al-Beta-F zeolites (Fig. 4d). Extended hydrogen-bonded H2O networks within H-Al-Beta-F zeolites form in similar relative pressure regimes (P/P0 = 0.2–0.75) to those where kinetically measured χ values deviate from unity, indicating that such networks are responsible for more severe H2O inhibition; however, a mechanistic basis that validates the identity of the assumed reaction intermediates (cf. Fig. S11†) is required.
H2O mixture106 on Si-Beta-F and deAl-Beta-F(2.0), where the ν(OH) peak center does not shift to lower wavenumbers under the same coverage regimes (Fig. S55–S56, ESI†). Although increased ν(OH) intensity between 2800–3200 cm−1 does not quantitatively correspond to a particular species or structure, it does reflect the formation of extended hydrogen-bonded networks, as we have identified in AIMD simulations of Beta zeolites containing one Si–OH nest per unit cell.75 These networks form in both H-Al-Beta-F and deAl-Beta-F zeolites at relative pressures of H2O above ∼0.2, consistent with shifts in the ν(OH) peak center to lower wavenumbers with increasing coverage (Fig. 4d and e), and with adsorption isotherms on H-Al-Beta-F zeolites that are proportional to H+ density up to P/P0 ∼ 0.2 to generate (H3O+)(H2O)6 clusters before extended hydrogen-bonded networks form and surround these clusters. These (H3O+)(H2O)6 clusters remain intact as H2O networks surround them, in contrast to H2O clusters at Si–OH nests that restructure to integrate within these extended hydrogen-bonded networks as observed in our prior AIMD simulations (>5 H2O u.c.−1),75 which is consistent with ν(OH) peak centers in IR spectra that represent the majority of H2O molecules participating in extended networks and thus reach lower values in deAl-Beta-F zeolites (Fig. 4e) than in H-Al-Beta-F zeolites (Fig. 4d). Extended hydrogen-bonded H2O networks within H-Al-Beta-F zeolites form in similar relative pressure regimes (P/P0 = 0.2–0.75) to those where kinetically measured χ values deviate from unity, indicating that such networks are responsible for more severe H2O inhibition; however, a mechanistic basis that validates the identity of the assumed reaction intermediates (cf. Fig. S11†) is required.
In situ IR spectra were collected at 373 K on H-Al-Beta-F(2.0) under conditions analogous to those of turnover rate measurements to verify the formation of extended hydrogen-bonded networks in the presence of C2H5OH at reaction temperature. H2O was fed at pressures of 10–75 kPa (P/P0 = 0.1–0.75) corresponding to the regime where χ values deviate from unity (Fig. 2b), and C2H5OH was additionally included at C2H5OH/H2O ratios between 0.005–0.06 where kfirst values were quantified on H-Al-Beta-F(2.0) (Fig. 1b). The shape and position of δ(HOH) peaks at 373 K and 293 K are similar (Fig. 4b), and their areas indicate that the coverage of H2O (at 373 K) within micropores as quantified by the correlation in Fig. 4c is similar to that quantified by volumetric adsorption isotherms (at 293 K) in the same relative pressure regime (P/P0 = 0.1–0.75, Fig. 4f). We note, in passing, that using the correlation in Fig. 4c assumes that the integrated molar extinction coefficient for δ(HOH) is invariant between 293–373 K. Values of H2O coverage were similar (within 20%) with and without co-fed C2H5OH (Table S8, ESI†), indicating that under these conditions (C2H5OH/H2O = 0.005–0.06), C2H5OH does not significantly displace H2O in the bulk adsorbed H2O phase. Adsorbed C2H5OH can be identified in IR spectra by ν(C–H) peaks at 2905 and 2980 cm−1 (Fig. 4a). Similar ν(C–H) peak areas (within 2×, Fig. 4g) quantified over a wide range of C2H5OH pressures (0.05–4.6 kPa) are consistent with saturation of sites with (C2H5OH)(H+)(H2O)n MARI that give rise to apparent first-order kinetics in PC2H5OH (Fig. 1b). The ν(OH) region (Fig. 4a) shows similar increases in peak area (2800–3200 cm−1, see also differential subtracted spectra in Fig. S57–S58, ESI†) corresponding to the formation of extended hydrogen-bonded H2O networks between 10–75 kPa H2O at 373 K both with and without co-fed C2H5OH, which is reflected in shifts in the ν(OH) peak center (Fig. 4h) from 3400 cm−1 (10 kPa H2O) to 3220–3230 cm−1 (75 kPa H2O).
In summary, volumetric adsorption isotherms and heats of adsorption of H2O indicate that water adsorbs preferentially at low coverages at hydrophilic binding sites (H+, Si–OH) within hydrophobic zeolite pores, then forms (H3O+)(H2O)6 clusters44,45 (P/P0 < 0.2) and extended hydrogen-bonded networks (P/P0 > 0.2). In situ IR spectra measured at 373 K under conditions corresponding to those where χ values deviate from unity (>10 kPa H2O) reveal concomitant formation of extended hydrogen-bonded H2O structures that solvate clustered (C2H5OH)(H+)(H2O)n MARI at active sites within H-Al-Beta-F zeolites. The free energies of these intermediates and putative transition states are next interrogated by AIMD and metadynamics, respectively. AIMD simulations were performed to sample the many possible configurations that these water–ethanol clusters can adopt under reaction conditions. While one additional water may act as a proton shuttle at the transition state (Section 2.1), the participation of larger (H2O)n clusters in ethanol dehydration transition states may introduce qualitatively different behavior that can be explored using metadynamics simulations.
2.3. Ab initio molecular dynamics of water–ethanol mixtures
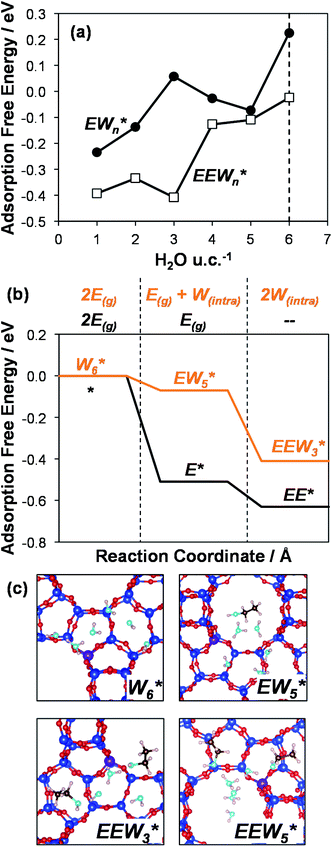
AIMD simulations were performed at 373 K with H2O in H-Al-Beta (1 H+ u.c.−1) to determine the structure of the confined, protonated water network and compare with experimentally measured water coverages. Higher water coverages require AIMD simulations because the many potential adsorbate configurations are intractable to model using static DFT calculations. Our previous work on the structure and stability of water networks in Sn-Beta and deAl-Beta zeolites showed that locally stable water clusters form at coverages between 5–8 H2O u.c.−1 and that such clusters coexist with extended water networks at higher coverages.75 Here, we used this coverage range (5–8 H2O u.c.−1) as a starting point to reduce the number of computationally demanding AIMD simulations required to find locally stable water cluster sizes, and we expect this will serve as an example of how the techniques developed in Bukowski et al.75 can be practically applied. Shuttling of the H+ among H2O molecules in the cluster is facile, which requires special considerations for adsorbate entropy (detailed discussion in Section S.2.8, ESI†). A local free energy minimum was found at 6 H2O u.c.−1 (Fig. S69, ESI†), which corresponds to a (H3O+)(H2O)5 cluster (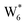 , Fig. 5c). This stable cluster size is within error of that measured by experimental volumetric H2O adsorption isotherms (7 ± 1 H2O u.c.−1) and is consistent with the cluster sizes identified in prior investigations of H-Al-MFI zeolites.43–45
, Fig. 5c). This stable cluster size is within error of that measured by experimental volumetric H2O adsorption isotherms (7 ± 1 H2O u.c.−1) and is consistent with the cluster sizes identified in prior investigations of H-Al-MFI zeolites.43–45
In AIMD simulations, the H+ is solvated within the H2O cluster, consistent with the disappearance of ν(OH) stretches for Al–O(H)–Si groups in experimentally measured IR spectra (Fig. 4a). The fraction of time that H+ is solvated as H3O+ rather than coordinated to the framework was evaluated by quantifying the distance of the closest H atom to a framework oxygen bound to Al in each frame of each trajectory. For the smallest water cluster size simulated 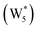 , H+ is solvated in the cluster for 66% of the 20 ps simulation (Fig. S68, ESI†), indicating that H+ primarily, but not exclusively, resides within the solvated H3O+ cluster at 373 K. These AIMD simulations at 373 K reveal an equilibrium between solvated and framework H+ states that depends on water coverage, in contrast to DFT calculations at 0 K indicating that a solvated H+ is more stable than a framework H+ for all water coverages greater than 1 H2O/H+. Thus, caution should be used in interpreting the location of H+ from DFT calculations at 0 K, as AIMD simulations provide more rigorous assessment of the solvation environment of H+ at reaction conditions. These simulations in the absence of reactant molecules (C2H5OH) successfully predict the structures of clustered (H3O+)(H2O)n that have been previously studied,43–45 and suggest that analogous AIMD simulations incorporating C2H5OH molecules can provide accurate insights into the structure sand dynamics of reactant-solvent complexes relevant for catalysis.
, H+ is solvated in the cluster for 66% of the 20 ps simulation (Fig. S68, ESI†), indicating that H+ primarily, but not exclusively, resides within the solvated H3O+ cluster at 373 K. These AIMD simulations at 373 K reveal an equilibrium between solvated and framework H+ states that depends on water coverage, in contrast to DFT calculations at 0 K indicating that a solvated H+ is more stable than a framework H+ for all water coverages greater than 1 H2O/H+. Thus, caution should be used in interpreting the location of H+ from DFT calculations at 0 K, as AIMD simulations provide more rigorous assessment of the solvation environment of H+ at reaction conditions. These simulations in the absence of reactant molecules (C2H5OH) successfully predict the structures of clustered (H3O+)(H2O)n that have been previously studied,43–45 and suggest that analogous AIMD simulations incorporating C2H5OH molecules can provide accurate insights into the structure sand dynamics of reactant-solvent complexes relevant for catalysis.
We next used AIMD to simulate (C2H5OH)m(H+)(H2O)n clusters adsorbed in H-Al-Beta zeolites at 373 K, where n was varied between 1–6 and m = 1, 2, corresponding to ethanol monomer and ethanol–ethanol dimer species with different degrees of solvation by H2O. The free energy of adsorption of these ethanol molecules was calculated from AIMD relative to gas-phase ethanol and the same number of H2O molecules adsorbed within the zeolite:
| ΔGEm,ads = GEm,solv − mGE(g) − GWn,solv | (8) |
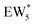 , Fig. 5c), consistent with displacement of one H2O molecule in the (H+)(H2O)6 cluster by C2H5OH, which is found to be located near the H3O+ ion during the simulations. This (C2H5OH)(H+)(H2O)5 species is likely the MARI in experimentally measured kinetics and IR spectra (373 K), and it becomes increasingly solvated by extended hydrogen-bonded water networks that surround it in the water pressure regimes (10–75 kPa H2O) where χ values deviate from unity, as detected by in situ IR spectra (Fig. 4). The local free energy minimum for (C2H5OH)2(H+)(H2O)n species occurs at n = 3, indicating that adsorption of an additional ethanol prior to reaction further disrupts the hydrogen-bonding network of the H2O cluster; thus, at n = 5 (
, Fig. 5c), consistent with displacement of one H2O molecule in the (H+)(H2O)6 cluster by C2H5OH, which is found to be located near the H3O+ ion during the simulations. This (C2H5OH)(H+)(H2O)5 species is likely the MARI in experimentally measured kinetics and IR spectra (373 K), and it becomes increasingly solvated by extended hydrogen-bonded water networks that surround it in the water pressure regimes (10–75 kPa H2O) where χ values deviate from unity, as detected by in situ IR spectra (Fig. 4). The local free energy minimum for (C2H5OH)2(H+)(H2O)n species occurs at n = 3, indicating that adsorption of an additional ethanol prior to reaction further disrupts the hydrogen-bonding network of the H2O cluster; thus, at n = 5 (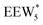 , Fig. 5), both adsorbed ethanol molecules participate in hydrogen bonding with three clustered waters, but not the remaining water molecules in the cluster. Analogous disruption of extended water networks is therefore expected when they solvate bimolecular transition states at high water coverages.
, Fig. 5), both adsorbed ethanol molecules participate in hydrogen bonding with three clustered waters, but not the remaining water molecules in the cluster. Analogous disruption of extended water networks is therefore expected when they solvate bimolecular transition states at high water coverages.
The free energy of ethanol adsorption at water-solvated hydronium ions is compared to adsorption at protons without any solvent in Fig. 5b. Free energies of ethanol adsorption are referenced to the stable water cluster 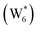 , where ethanol displaces one water from this cluster to form
, where ethanol displaces one water from this cluster to form 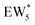 and a displaced intraporous water molecule in equilibrium with the most stable water cluster (W(intra)). The free energy of ethanol adsorption is weaker by 0.44 eV in the presence of solvent because the water network must reorganize to form a stable ethanol–water cluster, and interactions with the proton are redistributed among the water molecules. Adsorption of a second ethanol further reduces the number of clustered water molecules
and a displaced intraporous water molecule in equilibrium with the most stable water cluster (W(intra)). The free energy of ethanol adsorption is weaker by 0.44 eV in the presence of solvent because the water network must reorganize to form a stable ethanol–water cluster, and interactions with the proton are redistributed among the water molecules. Adsorption of a second ethanol further reduces the number of clustered water molecules 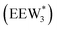 , which releases two additional intraporous water molecules (3W(intra) total) and leads to a differential free energy of adsorption (−0.34 eV) that is more than twice that of the gas phase (−0.12 eV). This difference is primarily enthalpic in origin, as entropies of adsorption in the solvated and gas phases differ by only 10 J mol−1 K−1, reflecting how the presence of confined water and its reorganization influence heats of adsorption of reactive intermediates.
, which releases two additional intraporous water molecules (3W(intra) total) and leads to a differential free energy of adsorption (−0.34 eV) that is more than twice that of the gas phase (−0.12 eV). This difference is primarily enthalpic in origin, as entropies of adsorption in the solvated and gas phases differ by only 10 J mol−1 K−1, reflecting how the presence of confined water and its reorganization influence heats of adsorption of reactive intermediates.
The solvation of H+ within (C2H5OH)m(H+)(H2O)n was also compared with that in (H+)(H2O)n clusters, using the same criterion that any H+ within 1.1 Å of a framework oxygen is considered to be coordinated to the zeolite framework (Fig. S68, ESI†). Whereas the protonated dimer was the most energetically stable configuration in 0 K DFT calculations, AIMD simulations show that at 373 K the proton remains bound to a framework site for 89% of the simulation time for the ethanol–water dimer (m = 1, n = 1). Both the framework-protonated state and solvated hydronium ion state of EW* are close in energy (∼0.2 eV) in the 0 K DFT calculations, such that the free energy differences at 373 K likely reflect entropic effects on H+ solvation. In the locally stable ethanol monomer cluster 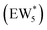 , the proton remains solvated for >98% of the simulation time, indicating that larger water clusters more effectively solvate protons away from the zeolite framework. Two ethanol molecules are sufficient to solvate the H+ away from the zeolite framework without water,108 and thus the H+ remains solvated nearly 100% of the simulation time across the entire range of water coverages (n = 1–6 H2O, m = 2). The H+ remains solvated as H3O+ in (C2H5OH)2(H+)(H2O)n species rather than being shared between the two C2H5OH in a protonated dimer, which we surmise leads to additional free energy penalties to reorganize positive charges and localize them at the ethyl group in SN2 transition states that form diethyl ether and water, as investigated next.
, the proton remains solvated for >98% of the simulation time, indicating that larger water clusters more effectively solvate protons away from the zeolite framework. Two ethanol molecules are sufficient to solvate the H+ away from the zeolite framework without water,108 and thus the H+ remains solvated nearly 100% of the simulation time across the entire range of water coverages (n = 1–6 H2O, m = 2). The H+ remains solvated as H3O+ in (C2H5OH)2(H+)(H2O)n species rather than being shared between the two C2H5OH in a protonated dimer, which we surmise leads to additional free energy penalties to reorganize positive charges and localize them at the ethyl group in SN2 transition states that form diethyl ether and water, as investigated next.
2.4. Ab initio simulation of dehydration transition state solvation using metadynamics
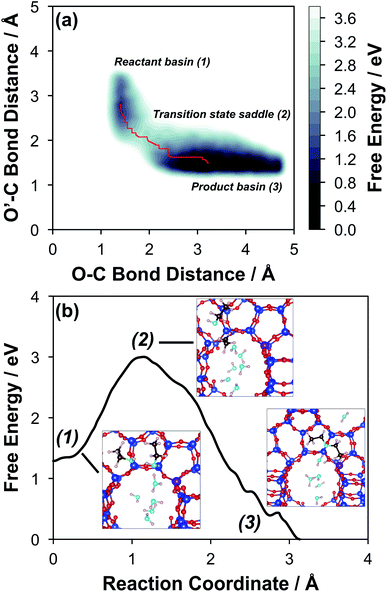
The configurations of the bimolecular dehydration transition state in the presence of five H2O molecules were explored further in metadynamics simulations. While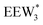 was identified as the most stable solvated ethanol dimer, a different number of solvent molecules may preferentially stabilize the dehydration transition state given different opportunities for available hydrogen-bonding configurations in H2O that surround the transition state. A water phase diagram could be constructed for the transition state; however, this would require biased AIMD for every water cluster size. It is necessary to choose a reasonable number of waters to simulate a realistic solvating environment. If the chosen cluster size is larger than that present at equilibrium, water will phase separate to form the most stable cluster and gas-like water given sufficient simulation time, based on previous data for Lewis acids.75 This indicates that an overestimate of the simulated cluster size is more rigorous than an underestimated cluster size, which would be unstable and prevented from phase separating to form a stable solvation shell. The (C2H5OH)2(H+)(H2O)5 intermediate was thus chosen as a reasonable upper bound for the solvated transition state, and the collective variables were chosen as the distances between the Cα atom of the ethanol bound to H3O+ and its O atom, which becomes the H2O leaving group at the transition state, and the distance between this same Cα atom in the first ethanol and the O′ atom of the second ethanol molecule, which is the nucleophilic O atom at the transition state. As such, at the initial state ((1), Fig. 6), the O–Cα bond distance is ∼1 Å, while the O′–Cα distance explores a larger configurational space limited to ∼2–3 Å by the hydrogen-bonding interaction between the two ethanol molecules. The opposite is true at the final state ((3), Fig. 6) once the O′–Cα bond has been fully formed in diethyl ether at a distance of ∼1 Å, while the leaving group H2O that determines the O–Cα distance may diffuse 2–5 Å away from the product DEE.
was identified as the most stable solvated ethanol dimer, a different number of solvent molecules may preferentially stabilize the dehydration transition state given different opportunities for available hydrogen-bonding configurations in H2O that surround the transition state. A water phase diagram could be constructed for the transition state; however, this would require biased AIMD for every water cluster size. It is necessary to choose a reasonable number of waters to simulate a realistic solvating environment. If the chosen cluster size is larger than that present at equilibrium, water will phase separate to form the most stable cluster and gas-like water given sufficient simulation time, based on previous data for Lewis acids.75 This indicates that an overestimate of the simulated cluster size is more rigorous than an underestimated cluster size, which would be unstable and prevented from phase separating to form a stable solvation shell. The (C2H5OH)2(H+)(H2O)5 intermediate was thus chosen as a reasonable upper bound for the solvated transition state, and the collective variables were chosen as the distances between the Cα atom of the ethanol bound to H3O+ and its O atom, which becomes the H2O leaving group at the transition state, and the distance between this same Cα atom in the first ethanol and the O′ atom of the second ethanol molecule, which is the nucleophilic O atom at the transition state. As such, at the initial state ((1), Fig. 6), the O–Cα bond distance is ∼1 Å, while the O′–Cα distance explores a larger configurational space limited to ∼2–3 Å by the hydrogen-bonding interaction between the two ethanol molecules. The opposite is true at the final state ((3), Fig. 6) once the O′–Cα bond has been fully formed in diethyl ether at a distance of ∼1 Å, while the leaving group H2O that determines the O–Cα distance may diffuse 2–5 Å away from the product DEE.
The metadynamics simulation was carried out for a total time of 175 ps and included 27 barrier re-crossings in the span of 5 ps. The 1-D projection of the minimum free energy path (Fig. 6b) between the reactant and product basins gives a forward barrier of 1.7 eV and a reverse barrier of 3.0 eV. These are larger than those values calculated by gas-phase DFT with one water molecule (0.8 eV and 1.2 eV, respectively), in part reflecting the biased metadynamics sampling of initial and product states with high configurational entropy due to the number of solvent molecules. The number of transition states sampled in the simulation (27 barrier re-crossings) may not reflect the full relative number of microstates available to the system at the transition state versus the reactant and product basins. This is not uncommon for MD sampling techniques, and once the saddle point is identified, umbrella sampling can be used to refine the reaction barriers with biasing potentials along the reaction coordinate.109 Umbrella sampling is, however, unfeasible in an AIMD simulation this large in scale. An additional 18 ps AIMD simulation with O–Cα–O bonds constrained to the metadynamics saddle point was therefore used to improve sampling of the solvated transition state. The apparent activation energy referenced to the 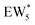 MASI was 1.3 eV, which is reasonable in comparison to the gas-phase energetics.
MASI was 1.3 eV, which is reasonable in comparison to the gas-phase energetics.
Metadynamics saddle points also provide physical insight into how solvent molecules structure at the transition state. A representative transition state from metadynamics ((2), Fig. 6) resembles the SN2 configurations of DEE-formation transition states calculated with zero or one co-adsorbed H2O molecule, respectively (Fig. S64, ESI†). The O–C and O′-C distances are approximately equivalent, where the C2H5+ group lies equidistant between the nucleophilic C2H5OH and the leaving group H2O. Here, charge has transferred from H3O+ to the C2H5+ group, and thus five H2O molecules solvate the transition state, rather than the four that solvate the (C2H5OH)2H3O+ precursor complex. The requirement to dissociate this bound H2O molecule from the H+ active site en route to the bimolecular dehydration transition state results in the limiting case of a −1 reaction order in H2O. In contrast to transition states with zero or one co-adsorbed H2O (Fig. S64, ESI†), transition state (2) in Fig. 6 is stabilized distant from the framework Al atom because of the delocalization of the H+ charge as H3O+ in its precursor state. This enables the transition state to effectively maximize its van der Waals contacts with the surrounding pore environment compared to when it is electrostatically constrained near the framework Al. The transition state and adsorbed precursors reside on the periphery of the H2O cluster rather than within it, indicating that under this coverage regime (up to 5 H2O per H+), the primary function of H2O is to solvate the H+ active site as (H3O+)(H2O)n. The location of the transition state on the periphery of the H2O cluster is consistent with kinetically relevant formation of DEE catalyzed by H3O+ through transition states that do not require a reduction in the size of H2O clusters.
In summary, these combined theoretical simulations indicate that the structure of (C2H5OH)(H+)(H2O)n MARI are analogous to those of (H+)(H2O)n, where one C2H5OH molecule displaces one H2O molecule, and that these MARI may access kinetically relevant DEE formation transition states after adsorption of a second ethanol and displacement of one H2O molecule from the H+ active site. At coverages up to 5 H2O/H+, prior to the formation of extended hydrogen-bonded H2O networks, C2H5OH molecules interact minimally with clustered H2O and prefer to react at the periphery of such clusters within zeolite voids.
2.5. Mechanistic implications of solvation by condensed water structures
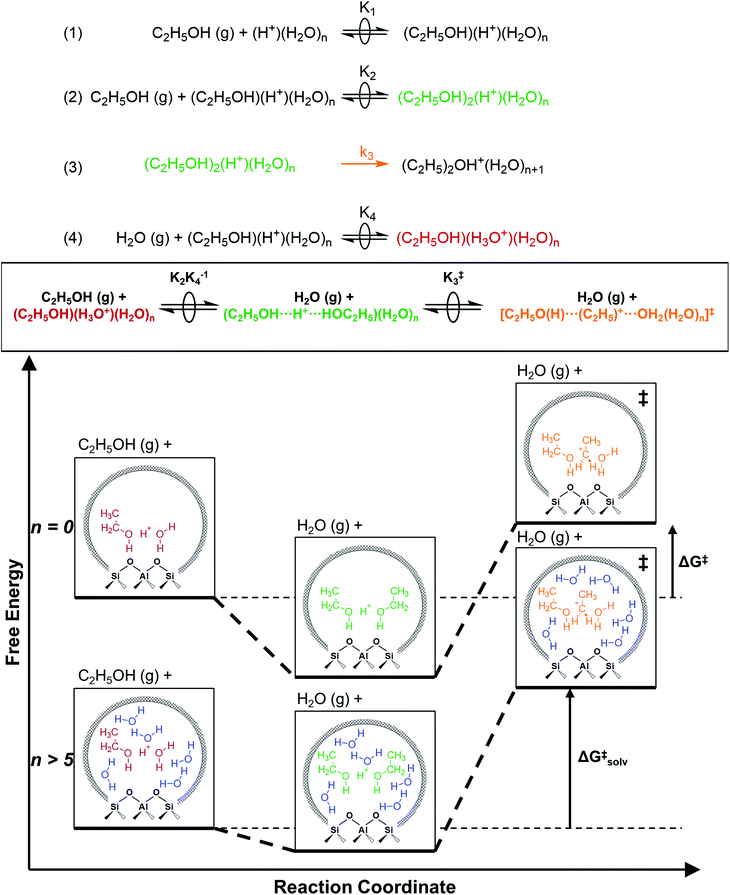
The similarity of diethyl ether transition state free energies, regardless of the number of H2O molecules in (C2H5OH)(H+)(H2O)n MARI, is consistent with the elementary steps to form DEE in Fig. S11,† but with the additional complexity that increasing solvation of H+ by H2O leads to new configurations of (C2H5OH)(H3O+)(H2O)1–5 as MARI rather than only (C2H5OH)(H+)(H2O) species, as shown in Scheme 1. When n = 0, the elementary steps in Scheme 1 are identical to those in Fig. S11,† so that addition of H2O to form (H3O+)(H2O)n does not impact the functional form of the rate expressions. Clustered (C2H5OH)(H3O+)(H2O)1–5 MARI must desorb one H2O molecule en route to transition states that localize positive charge at the ethyl group, recovering the −1 reaction order in H2O as the limiting case when surfaces are saturated by (C2H5OH)(H3O+)(H2O)4–5 MARI (5 predicted by experiments, 4 by theory). Beyond the maximum cluster size, as shown by in situ IR spectra (293 and 373 K), additional adsorbed water begins to form extended hydrogen-bonded networks that solvate the MARI, which corresponds to kinetic regimes where χ values deviate from unity. Rate expressions derived from steps 1–4 in Scheme 1 that take this solvation into account, given that eqn (3) does not, are therefore required to provide a mechanistic basis for the stronger inhibition by H2O when extended water networks are formed. Within the formalism of transition state theory,110 (C2H5OH)(H3O+)(H2O)n MARI and gas-phase C2H5OH (i.e., the apparent initial state) are considered to be in equilibrium with [C2H5O(H)⋯(C2H5)+⋯OH2(H2O)n]‡ and gas-phase H2O (i.e., the apparent final state):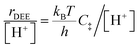 | (9) |
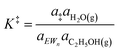 | (10) |
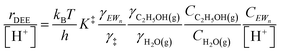 | (11) |
Eqn (11) can be simplified further by restricting its use to the conditions where experimental kinetics were collected with (C2H5OH)(H3O+)(H2O)n as the sole MARI (373 K, 2 × 10−3 to 10 kPa C2H5OH, 0–75 kPa H2O), under which CEWn/[H+] = 1 because of the MARI assumption, and γC2H5OH(g)/γH2O(g) = 1 because the gas-phase activity coefficients of both C2H5OH and H2O are nearly unity under these conditions, which are far from their critical temperatures and pressures (H2O Pc = 22 MPa, Tc = 647 K; C2H5OH Pc = 6.4 MPa, Tc = 516 K).112 Assumption of an ideal gas phase also allows converting the ratio of concentrations to one of pressures to arrive at an expression for the bimolecular ethanol dehydration turnover rate that is similar to eqn (4):
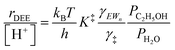 | (12) |
Upon relating the transition state equilibrium constant to those of elementary steps in Scheme 1 (full derivation in Section S.2.9, ESI†):
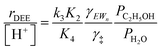 | (13) |
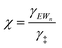 | (14) |
As extended hydrogen-bonded H2O networks form and solvate (C2H5OH)(H3O+)(H2O)4–5 MARI and transition states, the activity coefficient of the transition state increases more rapidly than that of the MARI. This ratio effectively cancels in rate equations before the formation of extended H2O networks because both MARI and transition states reside on the periphery of (H3O+)(H2O)n clusters, and only become solvated after these clusters have reached their maximum size, as indicated by AIMD and metadynamics simulations. Inhibition by H2O in the ideal regime (up to −1 order, <10 kPa H2O) is therefore accounted for by solvation of H+ within clusters of increasing molecularity as H3O+, as shown previously in H2O–organic solvent mixtures;66,67 however, extended hydrogen-bonded networks that solvate the MARI and transition state clusters after they are formed lead to more severe inhibition than that caused by stabilization of H+ alone.
The less effective solvation of the transition state that leads to more rapidly increasing values of γ‡ relative to γEWn is likely a consequence of the inability of the non-polar ethyl groups of ethanol molecules to participate in hydrogen bonding networks. The transition state engages the hydroxyl groups of both C2H5OH molecules as nucleophile and leaving groups, and thus both ethyl groups present at the transition state may disrupt hydrogen bonds in surrounding H2O networks. In contrast, the (C2H5OH)(H3O+)(H2O)4–5 MARI contains only one non-polar ethyl group, which disrupts surrounding H2O networks to a lesser extent than the two ethyl groups of the transition state. This analysis is conceptually similar to that of the activation volume114–117 in liquid-phase reactions or the activation area on two-dimensional surfaces,118 where increasing pressures and concomitant increasing densification of the solvent phase destabilizes transition states with positive activation volume, according to the empirical equation:115
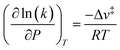 | (15) |
Here, we have demonstrated that gas-phase kinetic measurements and spectroscopic characterizations with co-fed solvent molecules under conditions that lead to intrapore condensation of extended liquid-like networks enable quantifying the thermodynamic nonidealities introduced by the solvation of kinetically relevant intermediates and transition states within confining environments, which are inaccessible to measurements performed in the liquid phase. These thermodynamic activity coefficients contain molecular information about the disruption and reorganization of hydrogen-bonded water networks by transition states that are larger and less polar than their relevant precursors. This approach can be used to investigate the effects of the shape and size of confining pore environments on stabilizing water structures, which in turn influence the solvation of reactive intermediates and transition states, independent of other phenomena that also change concomitantly with pore architecture, such as reactant coverage regimes or co-solvent interactions that often complicate precise mechanistic interpretation of measured rate data.
2.6. Influence of pore topology on solvation effects
The generality of non-ideal solvation effects in confined liquid-like H2O networks, and the effect of the topology of the pores that confine them, was explored at 373 K in different zeolite frameworks (CHA, AEI, FAU, TON, MFI) and in a less-confined solid acid (H3PW12O40/Si-MCM-41), whose pore topologies and acid site densities are described in Table 2. The values of kfirst were quantified at H2O pressures between 0.1–75 kPa and reported in Fig. 7a. Regardless of confining environment, bimolecular ethanol dehydration turnover rates (373 K, per H+) on Brønsted acids were inhibited by H2O, and this inhibition could be described by eqn (6) only at lower H2O pressures, which enabled quantifying k3K2K4−1 values in regimes where kfirst values were −1 order in H2O. These lumped rate and equilibrium constants reflect the free energy of the confined bimolecular dehydration transition state ([C2H5O(H)⋯(C2H5)+⋯OH2(H2O)n]‡) and gas-phase water with respect to the confined (C2H5OH)(H3O+)(H2O)n MARI and gas-phase ethanol (Scheme 1). Gaseous species are insensitive to confinement within zeolite pores and their stabilities are unaffected by changes in topology, while the MARI and transition state are expected to be stabilized to different extents by van der Waals contacts within confining micropores of different dimensions.120 The microporous voids where the MARI and transition state reside can be reasonably approximated by the diameter of the largest contained sphere within the zeolite, dLC.119| Sample | Si/Ala | V micro /cm3 g−1 | H+/Al (NH4+)c | H+/Al (DTBP)d | d PL /nm | d LC /nm | Undulation parameterg |
|---|---|---|---|---|---|---|---|
a Determined by AAS.
b Determined by N2 adsorption minimum in ∂Vads/∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(P/P0).
c Determined by TPD of NH3 after aqueous-phase ion exchange with 1 M NH4NO3, 24 h, 353 K.
d Determined by in situ 2,6-di-tert-butylpyridine titration during ethanol dehydration catalysis (378 K, 5 kPa C2H5OH, 1 kPa H2O).
e Pore-limiting diameter.119
f Diameter of largest included sphere.119
g Undulation parameter = dPL/dLC.
h Determined by Ar adsorption minimum in ∂Vads/∂ log(P/P0).
c Determined by TPD of NH3 after aqueous-phase ion exchange with 1 M NH4NO3, 24 h, 353 K.
d Determined by in situ 2,6-di-tert-butylpyridine titration during ethanol dehydration catalysis (378 K, 5 kPa C2H5OH, 1 kPa H2O).
e Pore-limiting diameter.119
f Diameter of largest included sphere.119
g Undulation parameter = dPL/dLC.
h Determined by Ar adsorption minimum in ∂Vads/∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(P/P0).
i W/P ratio quantified by ICP.
j H+/POM.
k Average of pore-size distribution determined by N2 adsorption isotherm and NLDFT (Fig. S30, ESI). log(P/P0).
i W/P ratio quantified by ICP.
j H+/POM.
k Average of pore-size distribution determined by N2 adsorption isotherm and NLDFT (Fig. S30, ESI).
|
|||||||
| H-Al-CHA | 15 | 0.21h | 0.98 | — | 0.372 | 0.737 | 0.505 |
| H-Al-AEI | 9.5 | 0.20h | 0.85 | — | 0.384 | 0.733 | 0.524 |
| H-Al-FAU | 56 | 0.30 | 0.35 | 0.88 | 0.735 | 1.124 | 0.654 |
| H-Al-MFI | 43 | 0.13 | 0.85 | — | 0.470 | 0.636 | 0.739 |
| H-Al-TON | 43 | 0.05 | 0.77 | — | 0.511 | 0.571 | 0.895 |
| H-Al-Beta-F(2.0) | 23 | 0.22 | 0.75 | 0.54 | 0.595 | 0.668 | 0.891 |
| HPW/Si-MCM-41 | 11i | — | — | 1.6j | 3.8k | 3.8k | 1.0 |
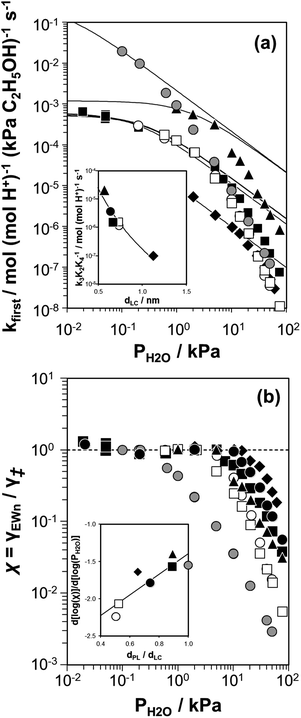 | ||
Fig. 7 (a) Apparent first-order bimolecular ethanol dehydration rate constant (per H+, 373 K) and (b) activity coefficient ratio (χ = γEWn/γ‡) from eqn (7), as a function of H2O pressure on H-Al-Beta-F(2.0) (■), H-Al-TON (▲), H-Al-FAU (♦), H-Al-MFI (●), H-Al-AEI (□), H-Al-CHA (○), and HPW/Si-MCM-41 ( ). Solid lines in (a) reflect regression of measured rate constants to eqn (7). Inset (a): dependence of k3K2K4−1 values on the largest included sphere diameter of zeolite pores (dLC). Inset (b): slopes of the data sets in (b) in the high water pressure limit, as a function of the channel undulation parameter (dPL/dLC). Solid lines in both insets are to guide the eye. ). Solid lines in (a) reflect regression of measured rate constants to eqn (7). Inset (a): dependence of k3K2K4−1 values on the largest included sphere diameter of zeolite pores (dLC). Inset (b): slopes of the data sets in (b) in the high water pressure limit, as a function of the channel undulation parameter (dPL/dLC). Solid lines in both insets are to guide the eye. | ||
Values of k3K2K4−1 systematically decrease with increasing dLC (Fig. 7a inset), consistent with the expectation that bimolecular dehydration transition states are preferentially stabilized within confining pore environments relative to (C2H5OH)(H3O+)(H2O)n MARI, which are smaller in size and therefore benefit less than transition states do from van der Waals contacts (Scheme 1). The HPW/Si-MCM-41 sample is not included in this correlation because POMs are stronger acids than zeolites (deprotonation energy (DPE) = 1087 kJ mol−1 for HPW121 < 1201 ± 11 kJ mol−1 for H-Al-zeolites122), whose acid strength is independent of topology.122 Notably, values of k3K2K4−1 are similar in CHA, AEI, and Beta, suggesting that reacting species are confined within the larger cages of CHA and AEI (dLC = 0.73–0.74 nm) that are similar in size to the channels of Beta (dLC = 0.67 nm), rather than their constrained 8-MR windows (pore-limiting diameter, dPL = 0.37–0.38 nm, Table 2). While the kinetic behavior of zeolites in regimes where χ = 1 is consistent with well-known principles of stabilization by attractive dispersion forces in confining environments, it is unclear whether the condensation of liquid-like water within micropores may attenuate or enhance the effects of confinement.
Measured χ values are shown as a function of H2O pressure (373 K) in Fig. 7b. Brønsted acid zeolites begin to deviate from χ values of unity in the range ∼5–20 kPa H2O, while HPW/Si-MCM-41 shows deviations in χ starting at ∼1 kPa of H2O. The earlier onset pressure of deviations observed on HPW/Si-MCM-41 may be related to its higher acid strength, which we surmise would stabilize H3O+ liberated from the conjugate anion at lower gas-phase H2O chemical potentials; a systematic study using POMs of different acid strength would provide clarification, but is beyond the scope of this investigation. The earlier onset of deviations in HPW/Si-MCM-41 has striking consequences for measured kfirst values, which are more than one order of magnitude higher than on H-Al-Beta zeolites in the χ = 1 regime, but decrease to similar values between 10–75 kPa H2O (Fig. 7a), indicating that solvation by extended hydrogen-bonded water networks attenuates any benefits of acid strength conferred by forming a more stable solid conjugate anion.85 The presence of these extended hydrogen-bonded water networks was observed as increasing ν(OH) IR peak areas below 3200 cm−1 on H-Al-zeolites and HPW/Si-MCM-41 at 373 K between 10–75 kPa H2O (Fig. S57–S63, ESI†), as observed on H-Al-Beta-F (Fig. 4). Similar liquid-phase reactivity of solid acids of different strength was previously observed for dehydration of xylose to furfural (418 K, 0.15 M in H2O or γ-valerolactone solvent) with H-Al-Beta zeolites and H4SiW12O40 clusters in solution.66
In addition to the onset pressure of deviations in χ, its dependence on H2O pressure was compared among samples and quantified as the slope of the data in Fig. 7b in the high pressure limit, d[log(χ)]/d[log(PH2O)]. The value of d[log(χ)]/d[log(PH2O)] is numerically equivalent to the reaction order of kfirst in H2O plus one, because χ reflects the deviation from an apparent −1 kinetic order in water. The value of d[log(χ)]/d[log(PH2O)] was ca. −1.5 for Beta, TON, and FAU zeolites, and HPW/MCM-41, while it was −1.8 for MFI zeolites, and less than −2 for CHA and AEI zeolites (Fig. 7b inset). The values of d[log(χ)]/d[log(PH2O)] do not correlate with confinement (dLC, Fig. S28, ESI†) and are similar regardless of acid strength (cf. HPW/MCM-41, Beta, TON, FAU). In contrast, both CHA and AEI zeolites show χ values that decrease more sharply with H2O pressure, and possess small-pore window-cage motifs different from the other structures characterized by channels (Beta, TON, MCM-41) or large-pore supercages (FAU). The MFI topology lies between these two cases because it possesses channels (dPL = 0.470 nm) that meet at less-confined intersections (dLC = 0.636 nm). These topological differences have been described previously as the undulation parameter,123,124 expressed as dPL/dLC (Table 2), which correlates with the values of d[log(χ)]/d[log(PH2O)] (Fig. 7b inset). The undulation parameter has been invoked to account for the preferential retention of certain reaction products that can undergo additional reactions before egress from the crystallite because of the difficulty of egress through more confining windows.123,124 We hypothesize that χ values deviate more severely from unity within small-pore cage-window topologies (CHA, AEI) than in channel-based topologies (Beta, TON, MCM-41) because extended H2O networks encounter additional barriers to reorganization when their structures are constrained into adjacent cages through confining windows. The different dependence of water inhibition on zeolite framework topology in regimes that approach liquid-phase catalysis (373 K, 10–75 kPa) and the deviation of kfirst values from those expected based on measurements in low water-coverage regimes indicate that the structures of adsorbed solvents within micropores of different size and shape play a significant role in determining their reactivity.
3. Conclusions
Ethanol dehydration turnover rates to form diethyl ether (373 K, per H+) are quantified on H-Al-Beta-F zeolites with 0.11–2.0 H+ per unit cell under conditions that lead to acid sites with MARI consisting of one C2H5OH molecule and increasing amounts of H2O (2 × 10−3 to 10 kPa C2H5OH, 0–75 kPa H2O), reflected in turnover rates that are first-order in C2H5OH and systematically decrease with H2O pressure. First-order rate constants (373 K, per H+) show −1 order dependences on H2O pressure at less than 10 kPa H2O because one water in water–ethanol–hydronium clusters must be displaced by ethanol to form the SN2 transition state that eliminates diethyl ether, but they are inhibited more severely at higher H2O pressures (10–75 kPa).Under conditions of severe H2O inhibition (373 K, 10–75 kPa H2O, 0.05–4.6 kPa C2H5OH), in situ IR spectra and AIMD simulations reveal stabilization of (C2H5OH)(H3O+)(H2O)4–5 clusters and, at even higher water pressures, hydrogen-bonded H2O networks that solvate such clusters. AIMD demonstrates that H+ are solvated as H3O+ within the MARI, and that C2H5OH adsorption becomes less favorable at higher water pressures as it disrupts more extensive hydrogen bonds within clusters of higher molecularity. Metadynamics simulations indicate that the corresponding transition states reside on the periphery of H2O clusters and thus are formed without desorbing H2O from clusters beyond the one H2O required to be displaced by C2H5OH at the transition state. Non-ideal thermodynamic formalisms describe the different solvation of MARI and transition states by extended H2O networks, which are disrupted to a greater extent by the transition state because it contains one additional non-polar ethyl moiety that is less effective at H-bonding, leading to severe inhibition of turnover rates; such effects are reminiscent of liquid-phase reactions with positive activation volume.
The different solvation of MARI and transition states by water networks prevails among Brønsted acid zeolites of different topology (FAU, TON, MFI, CHA, AEI), whose micropore shapes influence the severity of H2O inhibition by influencing the ease of solvent reorganization within channel or window-cage motifs. Similar extended H-bonded H2O structures have also been identified within the pores of hydrophilic metal–organic frameworks125,126 whose diverse topologies may stabilize an even broader range of solvent structures. The theoretical techniques developed here enable more direct comparison with experimental kinetics using solvent models based on locally stable phases at catalyst active sites. Greater insights into the structure of solvents confined within porous voids are provided by kinetics, spectroscopy, and theoretical calculations of solvated reaction coordinates under conditions that approach intrapore condensation, because this approach allows systematic variation of confined solvent structures. This study highlights the kinetic relevance of water- and water-reactant clusters at H+ active sites in aqueous-phase Brønsted acid catalysis, and the extended H-bonded networks that surround them, which are disrupted to different extents by reacting moieties of different size and chemical functionality, and which reorganize differently within pores of varied geometry.
4. Methods and materials
4.1. Zeolite synthesis and post-synthetic treatments
H-Al-Beta-F zeolites were hydrothermally synthesized in fluoride medium with a wide range of Al contents by adapting a procedure reported by Camblor et al.77 An Al-Beta-OH zeolite sample was hydrothermally synthesized in hydroxide medium as reported by Chang et al.127 These samples are denoted H-Al-Beta-X(Y), where X is the mineralizing agent in the gel (F, OH), and Y is the number of H+ per unit cell quantified by temperature-programmed desorption of NH3 (Section S.1.5, ESI†). H-Al-Beta-F zeolites were dealuminated in concentrated nitric acid, denoted deAl-Beta-F. The other H-zeolite samples were sourced commercially (TON, MFI, FAU), or reported in prior publications (CHA,128 AEI129). Phosphotungstic acid polyoxometalate clusters were supported on Si-MCM-41 using incipient wetness impregnation. Full synthetic details are provided in Section S.1.1 of the ESI.†4.2. Characterization of zeolites
Routine characterizations, including powder X-ray diffraction, N2 and H2O adsorption, atomic absorption spectroscopy, inductively coupled plasma optical emission spectrometry (ICP-OES), and temperature-programmed desorption of NH3, are described in Section S.1.2–S.1.5 of the ESI.†Infrared spectra of H2O adsorbed within zeolites were collected as a function of relative pressure (P/P0 = 0.1–0.75) using procedures described previously.34,75 Spectra were collected at 293 K using a quartz cell and heated block assembly130 described in our prior work,34,75 and spectra were collected in separate experiments at 373 K using a low-dead-volume cell developed by Ribeiro and coworkers.131 Additional details are provided in Section S.1.6 of the ESI.†
4.3. Ethanol dehydration kinetics
The kinetics of bimolecular ethanol dehydration to diethyl ether were measured in a differential packed-bed reactor system described previously.60,132 The pressures of C2H5OH (2 × 10−3 to 10 kPa) and H2O (0–75 kPa) were varied non-systematically over the course of the experiment. No deactivation was detected over the course of kinetic measurements (∼7–21 days), verified by periodically returning to a reference condition (5 kPa C2H5OH, 50 kPa H2O). At the end of kinetic measurements on H-Al-Beta, H-Al-FAU, and HPW/Si-MCM-41 catalysts, H+ were titrated in situ with 2,6-di-tert-butylpyridine (DTBP) at 378 K. After suppression of measured rates, the irreversibility of titration was confirmed by observing no recovery of measured rates or desorption of DTBP after returning the DTBP-free stream to the reactor. Additional details are provided in Section S.1.7 of the ESI.†4.4. Gas-phase DFT
Static DFT calculations were performed using VASP133–135 and are similar to those we have reported previously.59 The BEEF-vdW functional was used along with a 520 eV cutoff energy, and a force convergence criteria of 0.02 eV Å−1 where lattice atoms were all unconstrained. The projector augmented wave (PAW) pseudopotentials were included. Transition states were obtained using the climbing-image nudged elastic band (CI-NEB) method developed by Henkelman.136–138 As a result of the large diffusion contribution in gas-phase adsorbates, the entropies of reactive intermediates were calculated using the Campbell–Sellers equation,139,140 where adsorbates were treated as a 2-D gas. The reported energies of each intermediate and transition state reflect the lowest-energy configuration among multiple considered configurations. Additional details are provided in Section S.1.8 of the ESI.†4.5 Ab initio molecular dynamics
AIMD simulations were performed with VASP, with an NVT Nosé–Hoover thermostat.141,142 Water structures were heated, and then equilibrated at 373 K for at least 10 ps at a timestep of 1 ps. Production runs were performed for 20 ps. All framework atoms were unconstrained. It was assumed that the proton entropy is constant, and so at each timestep the acidic proton was removed in post-production. The root-mean-squared (RMS) diffusion of each water molecule was calculated according to the technique of Alexopoulos et al.108 to yield the 3-D translational entropy of water. The same technique was used to calculate the translational entropy of ethanol molecules introduced into the system. See Section S.2.8 of the ESI† for additional discussion of the entropy calculations and contributions from rotational and vibrational degrees of freedom, which were not included. Additional methodological details are provided in Section S.1.9 of the ESI.†4.6 Metadynamics
Metadynamics simulations were performed in VASP using the same pseudopotentials, energy cutoff, and K-point grid as the AIMD simulations. The thermostat and masses were the same as the AIMD calculations. The positions and trajectories from the AIMD thermodynamic calculations were used to ensure a well-equilibrated simulation. The collective variables (CVs) were defined to be a carbon–oxygen bond distance of a carbon belonging to one ethanol and a carbon–oxygen bond distance of the same carbon and the oxygen atom of the second ethanol. Gaussian hills were added every 70 fs with a height of 50 meV and width of 75 meV for the first 140 ps. For the last 35 ps the hill height was increased to 100 meV with a width of 150 meV. Hills were added with the same frequency. The total metadynamics simulation was 175 ps with 2500 Gaussian hills inserted in the free energy surface. From the transition state configurations obtained from metadynamics, a constrained molecular dynamics simulation was performed with the C–O bond distances constrained to the saddle point. The duration of this simulation was 18 ps. Additional details are provided in Section S.1.10 of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. S. B. and R. G. acknowledge financial support from the Ralph W. and Grace M. Showalter Research Trust, the Purdue Process Safety and Assurance Center (P2SAC), and a 3M Non-Tenured Faculty Award. B. C. B. and J. G. acknowledge support from the Department of Energy Office of Science, Office of Basic Energy Sciences, Chemical, Biological, and Geosciences Division under DE-SC0010379. Use of the Center for Nanoscale Materials, a U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences User Facility under Contract No. DE-AC02-06CH11357, and of computational resources from the National Energy Research Scientific Computing Center, are gratefully acknowledged. We thank John Di Iorio and Claire Nimlos for providing H-CHA and H-AEI zeolites, Juan Carlos Vega-Vila for updating and maintaining in situ IR equipment, Claire Nimlos for assistance with ICP-OES measurements, and Jamie Harris, John Di Iorio, Trevor Lardinois, and Siddarth Krishna for helpful technical discussions and feedback.References
- G. Li, B. Wang and D. E. Resasco, ACS Catal., 2020, 10, 1294–1309 CrossRef CAS.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 11277–11287 CrossRef CAS PubMed.
- Z. K. Goldsmith, Y. C. Lam, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2019, 141, 1084–1090 CrossRef CAS PubMed.
- M. N. Jackson, O. Jung, H. C. Lamotte and Y. Surendranath, ACS Catal., 2019, 9, 3737–3743 CrossRef CAS.
- X. Yang, J. Nash, N. Oliveira, Y. Yan and B. Xu, Angew. Chem., Int. Ed., 2019, 58, 17718–17723 CrossRef CAS PubMed.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777 CrossRef CAS PubMed.
- B. N. Zope, D. D. Hibbitts, M. Neurock and R. J. Davis, Science, 2010, 330, 74–78 CrossRef CAS PubMed.
- N. M. Wilson and D. W. Flaherty, J. Am. Chem. Soc., 2016, 138, 574–586 CrossRef CAS PubMed.
- J. Saavedra, C. J. Pursell and B. D. Chandler, J. Am. Chem. Soc., 2018, 140, 3712–3723 CrossRef CAS PubMed.
- D. Muñoz-Santiburcio, M. F. Camellone and D. Marx, Angew. Chem., Int. Ed., 2018, 57, 3327–3331 CrossRef PubMed.
- G. Yang, S. A. Akhade, X. Chen, Y. Liu, M.-S. Lee, V.-A. Glezakou, R. Rousseau and J. A. Lercher, Angew. Chem., Int. Ed., 2019, 58, 3527–3532 CrossRef CAS PubMed.
- K. B. Sravan Kumar, T. N. Whittaker, C. Peterson, L. C. Grabow and B. D. Chandler, J. Am. Chem. Soc., 2020, 142, 5760–5772 CrossRef CAS PubMed.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS.
- A. K. Dalai, T. K. Das, K. V. Chaudhari, G. Jacobs and B. H. Davis, Appl. Catal., A, 2005, 289, 135–142 CrossRef CAS.
- D. D. Hibbitts, B. T. Loveless, M. Neurock and E. Iglesia, Angew. Chem., Int. Ed., 2013, 52, 12273–12278 CrossRef CAS PubMed.
- F. Anaya and D. E. Resasco, ACS Catal., 2020, 10, 4433–4443 CrossRef CAS.
- Y. T. Kim, J. P. Chada, Z. Xu, Y. J. Pagan-Torres, D. C. Rosenfeld, W. L. Winniford, E. Schmidt and G. W. Huber, J. Catal., 2015, 323, 33–44 CrossRef CAS.
- I. Agirrezabal-Telleria and E. Iglesia, J. Catal., 2017, 352, 505–514 CrossRef CAS.
- I. Agirrezabal-Telleria, I. Luz, M. A. Ortuño, M. Oregui-Bengoechea, I. Gandarias, N. López, M. A. Lail and M. Soukri, Nat. Commun., 2019, 10, 2076 CrossRef PubMed.
- S. Ghosh, K. V. Ramanathan and A. K. Sood, Europhys. Lett., 2004, 65, 678 CrossRef CAS.
- Q. Chen, J. L. Herberg, G. Mogilevsky, H.-J. Wang, M. Stadermann, J. K. Holt and Y. Wu, Nano Lett., 2008, 8, 1902–1905 CrossRef CAS PubMed.
- T. Ohba, Angew. Chem., Int. Ed., 2014, 53, 8032–8036 CrossRef CAS PubMed.
- S. Dalla Bernardina, E. Paineau, J.-B. Brubach, P. Judeinstein, S. Rouzière, P. Launois and P. Roy, J. Am. Chem. Soc., 2016, 138, 10437–10443 CrossRef CAS PubMed.
- P. W. Snyder, M. R. Lockett, D. T. Moustakas and G. M. Whitesides, Eur. Phys. J.: Spec. Top., 2014, 223, 853–891 Search PubMed.
- G. Langhendries, D. E. De Vos, G. V. Baron and P. A. Jacobs, J. Catal., 1999, 187, 453–463 CrossRef CAS.
- M. G. Clerici, Top. Catal., 2001, 15, 257–263 CrossRef CAS.
- N. A. Grosso-Giordano, C. Schroeder, A. Okrut, A. Solovyov, C. Schöttle, W. Chassé, N. Marinković, H. Koller, S. I. Zones and A. Katz, J. Am. Chem. Soc., 2018, 140, 4956–4960 CrossRef CAS PubMed.
- D. T. Bregante, A. M. Johnson, A. Y. Patel, E. Z. Ayla, M. J. Cordon, B. C. Bukowski, J. Greeley, R. Gounder and D. W. Flaherty, J. Am. Chem. Soc., 2019, 141, 7302–7319 CrossRef CAS PubMed.
- N. A. Grosso-Giordano, A. S. Hoffman, A. Boubnov, D. W. Small, S. R. Bare, S. I. Zones and A. Katz, J. Am. Chem. Soc., 2019, 141, 7090–7106 CrossRef CAS PubMed.
- R. Gounder and M. E. Davis, J. Catal., 2013, 308, 176–188 CrossRef CAS.
- R. Gounder and M. E. Davis, ACS Catal., 2013, 3, 1469–1476 CrossRef CAS.
- J. W. Harris, M. J. Cordon, J. R. Di Iorio, J. C. Vega-Vila, F. H. Ribeiro and R. Gounder, J. Catal., 2016, 335, 141–154 CrossRef CAS.
- J. C. Vega-Vila, J. W. Harris and R. Gounder, J. Catal., 2016, 344, 108–120 CrossRef CAS.
- M. J. Cordon, J. W. Harris, J. C. Vega-Vila, J. S. Bates, S. Kaur, M. Gupta, M. E. Witzke, E. C. Wegener, J. T. Miller, D. W. Flaherty, D. D. Hibbitts and R. Gounder, J. Am. Chem. Soc., 2018, 140, 14244–14266 CrossRef CAS PubMed.
- N. Y. Chen, J. Phys. Chem., 1976, 80, 60–64 CrossRef CAS.
- M. Hunger, J. Kärger, H. Pfeifer, J. Caro, B. Zibrowius, M. Bülow and R. Mostowicz, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 3459–3468 RSC.
- J. Stelzer, M. Paulus, M. Hunger and J. Weitkamp, Microporous Mesoporous Mater., 1998, 22, 1–8 CrossRef CAS.
- D. H. Olson, W. O. Haag and W. S. Borghard, Microporous Mesoporous Mater., 2000, 35–36, 435–446 CrossRef CAS.
- A. Zecchina, F. Geobaldo, G. Spoto, S. Bordiga, G. Ricchiardi, R. Buzzoni and G. Petrini, J. Phys. Chem., 1996, 100, 16584–16599 CrossRef CAS.
- M. Krossner and J. Sauer, J. Phys. Chem., 1996, 100, 6199–6211 CrossRef CAS.
- L. Smith, A. K. Cheetham, R. E. Morris, L. Marchese, J. M. Thomas, P. A. Wright and J. Chen, Science, 1996, 271, 799–802 CrossRef CAS.
- M. Jiménez-Ruiz, D. S. Gahle, T. Lemishko, S. Valencia, G. Sastre and F. Rey, J. Phys. Chem. C, 2020, 124, 5436–5443 CrossRef.
- A. Vjunov, M. Wang, N. Govind, T. Huthwelker, H. Shi, D. Mei, J. L. Fulton and J. A. Lercher, Chem. Mater., 2017, 29, 9030–9042 CrossRef CAS.
- S. Eckstein, P. H. Hintermeier, R. Zhao, E. Baráth, H. Shi, Y. Liu and J. A. Lercher, Angew. Chem., Int. Ed., 2019, 58, 3450–3455 CrossRef CAS PubMed.
- M. Wang, N. R. Jaegers, M.-S. Lee, C. Wan, J. Z. Hu, H. Shi, D. Mei, S. D. Burton, D. M. Camaioni, O. Y. Gutiérrez, V.-A. Glezakou, R. Rousseau, Y. Wang and J. A. Lercher, J. Am. Chem. Soc., 2019, 141, 3444–3455 CrossRef CAS PubMed.
- G. Zundel, Angew. Chem., Int. Ed. Engl., 1969, 8, 499–509 CrossRef CAS.
- M. Eigen, Angew. Chem., Int. Ed. Engl., 1964, 3, 1–19 CrossRef.
- E. S. Stoyanov, I. V. Stoyanova and C. A. Reed, J. Am. Chem. Soc., 2010, 132, 1484–1485 CrossRef CAS.
- J. F. Haw, T. Xu, J. B. Nicholas and P. W. Goguen, Nature, 1997, 389, 832–835 CrossRef CAS.
- K. Chen, J. Damron, C. Pearson, D. Resasco, L. Zhang and J. L. White, ACS Catal., 2014, 4, 3039–3044 CrossRef CAS.
- K. Chen, A. Gumidyala, M. Abdolrhamani, C. Villines, S. Crossley and J. L. White, J. Catal., 2017, 351, 130–135 CrossRef CAS.
- M. Nielsen, A. Hafreager, R. Y. Brogaard, K. D. Wispelaere, H. Falsig, P. Beato, V. V. Speybroeck and S. Svelle, Catal. Sci. Technol., 2019, 9, 3721–3725 RSC.
- Z. Zhao, R. Bababrik, W. Xue, Y. Li, N. M. Briggs, D.-T. Nguyen, U. Nguyen, S. P. Crossley, S. Wang, B. Wang and D. E. Resasco, Nat. Catal., 2019, 2, 431–436 CrossRef CAS.
- G. Li, B. Wang, B. Chen and D. E. Resasco, J. Catal., 2019, 377, 245–254 CrossRef CAS.
- H. Knözinger, Angew. Chem., Int. Ed. Engl., 1968, 7, 791–805 CrossRef.
- J. Macht, M. J. Janik, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2008, 130, 10369–10379 CrossRef CAS PubMed.
- J. F. DeWilde, H. Chiang, D. A. Hickman, C. R. Ho and A. Bhan, ACS Catal., 2013, 3, 798–807 CrossRef CAS.
- M. Kang and A. Bhan, Catal. Sci. Technol., 2016, 6, 6667–6678 RSC.
- B. C. Bukowski, J. S. Bates, R. Gounder and J. Greeley, J. Catal., 2018, 365, 261–276 CrossRef CAS.
- J. S. Bates and R. Gounder, J. Catal., 2018, 365, 213–226 CrossRef CAS.
- Y. Zhi, H. Shi, L. Mu, Y. Liu, D. Mei, D. M. Camaioni and J. A. Lercher, J. Am. Chem. Soc., 2015, 137, 15781–15794 CrossRef CAS PubMed.
- Y. Liu, A. Vjunov, H. Shi, S. Eckstein, D. M. Camaioni, D. Mei, E. Baráth and J. A. Lercher, Nat. Commun., 2017, 8, 14113 CrossRef PubMed.
- Y. Liu, E. Baráth, H. Shi, J. Hu, D. M. Camaioni and J. A. Lercher, Nat. Catal., 2018, 1, 141–147 CrossRef CAS.
- S. Eckstein, P. H. Hintermeier, M. V. Olarte, Y. Liu, E. Baráth and J. A. Lercher, J. Catal., 2017, 352, 329–336 CrossRef CAS.
- L. Qi, R. Alamillo, W. A. Elliott, A. Andersen, D. W. Hoyt, E. D. Walter, K. S. Han, N. M. Washton, R. M. Rioux, J. A. Dumesic and S. L. Scott, ACS Catal., 2017, 7, 3489–3500 CrossRef CAS.
- M. A. Mellmer, C. Sener, J. M. R. Gallo, J. S. Luterbacher, D. M. Alonso and J. A. Dumesic, Angew. Chem., Int. Ed., 2014, 53, 11872–11875 CrossRef CAS PubMed.
- M. A. Mellmer, C. Sanpitakseree, B. Demir, P. Bai, K. Ma, M. Neurock and J. A. Dumesic, Nat. Catal., 2018, 1, 199–207 CrossRef CAS.
- A. K. Chew, T. W. Walker, Z. Shen, B. Demir, L. Witteman, J. Euclide, G. W. Huber, J. A. Dumesic and R. C. Van Lehn, ACS Catal., 2020, 10, 1679–1691 CrossRef CAS.
- N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Nat. Commun., 2020, 11, 1–13 Search PubMed.
- N. S. Gould and B. Xu, J. Catal., 2016, 342, 193–202 CrossRef CAS.
- N. S. Gould and B. Xu, J. Catal., 2018, 358, 80–88 CrossRef CAS.
- B. M. Murphy, J. Wu, H. J. Cho, J. Soreo, C. Wang, L. Ma and B. Xu, ACS Catal., 2019, 9, 1931–1942 CrossRef CAS.
- D. Mei and J. A. Lercher, AIChE J., 2017, 63, 172–184 CrossRef CAS.
- D. Mei and J. A. Lercher, J. Phys. Chem. C, 2019, 123, 25255–25266 CrossRef CAS.
- B. C. Bukowski, J. S. Bates, R. Gounder and J. Greeley, Angew. Chem., Int. Ed., 2019, 58, 16422–16426 CrossRef CAS PubMed.
- D. T. Bregante and D. W. Flaherty, ACS Catal., 2019, 9, 10951–10962 CrossRef CAS.
- M. A. Camblor, A. Corma and S. Valencia, J. Mater. Chem., 1998, 8, 2137–2145 RSC.
- H. Koller, R. F. Lobo, S. L. Burkett and M. E. Davis, J. Phys. Chem., 1995, 99, 12588–12596 CrossRef CAS.
- C. D. Baertsch, K. T. Komala, Y.-H. Chua and E. Iglesia, J. Catal., 2002, 205, 44–57 CrossRef CAS.
- R. T. Carr, M. Neurock and E. Iglesia, J. Catal., 2011, 278, 78–93 CrossRef CAS.
- T. Bligaard, R. M. Bullock, C. T. Campbell, J. G. Chen, B. C. Gates, R. J. Gorte, C. W. Jones, W. D. Jones, J. R. Kitchin and S. L. Scott, ACS Catal., 2016, 6, 2590–2602 CrossRef CAS.
- S. R. Blaszkowski and R. A. van Santen, J. Am. Chem. Soc., 1996, 118, 5152–5153 CrossRef CAS.
- C. B. Phillips and R. Datta, Ind. Eng. Chem. Res., 1997, 36, 4466–4475 CrossRef CAS.
- H. Chiang and A. Bhan, J. Catal., 2010, 271, 251–261 CrossRef CAS.
- W. Knaeble and E. Iglesia, J. Phys. Chem. C, 2016, 120, 3371–3389 CrossRef CAS.
- R. J. Madon and M. Boudart, Ind. Eng. Chem. Fundam., 1982, 21, 438–447 CrossRef CAS.
- D. Mears, Ind. Eng. Chem. Process Des. Dev., 1971, 10, 541–547 CrossRef CAS.
- R. Gounder and M. E. Davis, AIChE J., 2013, 59, 3349–3358 CrossRef CAS.
- P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385 CrossRef CAS.
- I. Kiricsi, C. Flego, G. Pazzuconi, W. O. Parker Jr, R. Millini, C. Perego and G. Bellussi, J. Phys. Chem., 1994, 98, 4627–4634 CrossRef CAS.
- J. A. Lercher and A. Jentys, in Studies in Surface Science and Catalysis, ed. H. van B. Jiří Čejka Avelino Corma and F. Schüth, Elsevier, 2007, vol. 168, pp. 435–476 Search PubMed.
- A. Corma, V. Fornés, F. Melo and J. Pérez-Pariente, in Fluid Catalytic Cracking, American Chemical Society, 1988, vol. 375, pp. 49–63 Search PubMed.
- A. Zecchina, S. Bordiga, G. Spoto, D. Scarano, G. Spanò and F. Geobaldo, J. Chem. Soc., Faraday Trans., 1996, 92, 4863–4875 RSC.
- M. F. Claydon and N. Sheppard, J. Chem. Soc. D, 1969, 1431–1433 RSC.
- A. G. Pelmenschikov, R. A. van Santen, J. H. M. C. van Wolput and J. Jänchen, in Studies in Surface Science and Catalysis, ed. J. Weitkamp, H. G. Karge, H. Pfeifer and W. Hölderich, Elsevier, 1994, vol. 84, pp. 2179–2186 Search PubMed.
- A. G. Pelmenschikov, J. H. M. C. van Wolput, J. Jaenchen and R. A. van Santen, J. Phys. Chem., 1995, 99, 3612–3617 CrossRef CAS.
- C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2002, 118, 264–272 CrossRef.
- J. D. Cyran, M. A. Donovan, D. Vollmer, F. S. Brigiano, S. Pezzotti, D. R. Galimberti, M.-P. Gaigeot, M. Bonn and E. H. G. Backus, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1520–1525 CrossRef CAS PubMed.
- J. Schaefer, E. H. G. Backus, Y. Nagata and M. Bonn, J. Phys. Chem. Lett., 2016, 7, 4591–4595 CrossRef CAS PubMed.
- N. Yang, C. H. Duong, P. J. Kelleher, A. B. McCoy and M. A. Johnson, Science, 2019, 364, 275–278 CAS.
- A. G. Pelmenschikov, R. A. van Santen, J. Janchen and E. Meijer, J. Phys. Chem., 1993, 97, 11071–11074 CrossRef CAS.
- M. Sovago, R. K. Campen, G. W. H. Wurpel, M. Müller, H. J. Bakker and M. Bonn, Phys. Rev. Lett., 2008, 100, 173901 CrossRef PubMed.
- E. A. Raymond, T. L. Tarbuck and G. L. Richmond, J. Phys. Chem. B, 2002, 106, 2817–2820 CrossRef CAS.
- P. B. Miranda and Y. R. Shen, J. Phys. Chem. B, 1999, 103, 3292–3307 CrossRef CAS.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Am. Chem. Soc., 2010, 132, 6867–6869 CrossRef CAS PubMed.
- A. Myalitsin, S. Urashima, S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2016, 120, 9357–9363 CrossRef CAS.
- N. Yang, C. H. Duong, P. J. Kelleher and M. A. Johnson, Nat. Chem., 2020, 12, 159–164 CrossRef CAS PubMed.
- K. Alexopoulos, M.-S. Lee, Y. Liu, Y. Zhi, Y. Liu, M.-F. Reyniers, G. B. Marin, V.-A. Glezakou, R. Rousseau and J. A. Lercher, J. Phys. Chem. C, 2016, 120, 7172–7182 CrossRef CAS.
- J. Kästner, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 1, 932–942 CrossRef.
- B. L. Foley and A. Bhan, J. Catal., 2020, 384, 231–251 CrossRef CAS.
- C. Eckert and M. Boudart, Chem. Eng. Sci., 1963, 18, 144–147 CAS.
- S. I. Sandler, Chemical, biochemical, and engineering thermodynamics, John Wiley, Hoboken, N.J, 4th edn, 2006 Search PubMed.
- R. J. Madon and E. Iglesia, J. Mol. Catal. A: Chem., 2000, 163, 189–204 CrossRef CAS.
- K. J. Laidler and D. Chen, Trans. Faraday Soc., 1958, 54, 1026 RSC.
- R. A. Grieger and C. A. Eckert, Trans. Faraday Soc., 1970, 66, 2579–2584 RSC.
- K. F. Wong and C. A. Eckert, Trans. Faraday Soc., 1970, 66, 2313–2319 RSC.
- G. A. Lawrance and D. R. Stranks, Acc. Chem. Res., 1979, 12, 403–409 CrossRef CAS.
- J. Liu, D. Hibbitts and E. Iglesia, J. Am. Chem. Soc., 2017, 139, 11789–11802 CrossRef CAS PubMed.
- Ch. Baerlocher and L. B. McCusker, Database of Zeolite Structures, http://www.iza-structure.org/databases/, accessed October 14, 2019 Search PubMed.
- R. Gounder and E. Iglesia, Chem. Commun., 2013, 49, 3491–3509 RSC.
- J. Macht, M. J. Janik, M. Neurock and E. Iglesia, Angew. Chem., Int. Ed., 2007, 46, 7864–7868 CrossRef CAS PubMed.
- A. J. Jones and E. Iglesia, ACS Catal., 2015, 5, 5741–5755 Search PubMed.
- M. L. Sarazen, E. Doskocil and E. Iglesia, ACS Catal., 2016, 6, 7059–7070 Search PubMed.
- G. Noh, S. I. Zones and E. Iglesia, J. Catal., 2019, 377, 255–270 CrossRef CAS.
- A. J. Rieth, A. M. Wright, G. Skorupskii, J. L. Mancuso, C. H. Hendon and M. Dincă, J. Am. Chem. Soc., 2019, 141, 13858–13866 CrossRef CAS PubMed.
- A. J. Rieth, K. M. Hunter, M. Dincă and F. Paesani, Nat. Commun., 2019, 10, 4771 CrossRef PubMed.
- C.-C. Chang, Z. Wang, P. Dornath, H. J. Cho and W. Fan, RSC Adv., 2012, 2, 10475–10477 RSC.
- J. R. Di Iorio and R. Gounder, Chem. Mater., 2016, 28, 2236–2247 CrossRef CAS.
- J. D. Albarracin-Caballero, I. Khurana, J. R. D. Iorio, A. J. Shih, J. E. Schmidt, M. Dusselier, M. E. Davis, A. Yezerets, J. T. Miller, F. H. Ribeiro and R. Gounder, React. Chem. Eng., 2017, 2, 168–179 RSC.
- V. J. Cybulskis, J. W. Harris, Y. Zvinevich, F. H. Ribeiro and R. Gounder, Rev. Sci. Instrum., 2016, 87, 103101 CrossRef PubMed.
- J. Wang, V. F. Kispersky, W. N. Delgass and F. H. Ribeiro, J. Catal., 2012, 289, 171–178 CrossRef CAS.
- J. S. Bates, B. C. Bukowski, J. W. Harris, J. Greeley and R. Gounder, ACS Catal., 2019, 9, 6146–6168 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- C. T. Campbell and J. R. V. Sellers, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- C. T. Campbell and J. R. V. Sellers, Chem. Rev., 2013, 113, 4106–4135 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02589e |
| ‡ J. S. B. and B. C. B. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |