Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Orbital-free photophysical descriptors to predict directional excitations in metal-based photosensitizers†
Pedro A.
Sánchez-Murcia
 *a,
Juan J.
Nogueira
*a,
Juan J.
Nogueira
 b,
Felix
Plasser
b,
Felix
Plasser
 c and
Leticia
González
c and
Leticia
González
 *ad
*ad
aInstitute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Str. 17, 1090 Vienna, Austria. E-mail: pedro.murcia@univie.ac.at; leticia.gonzalez@univie.ac.at
bDepartment of Chemistry and Institute for Advanced Research in Chemistry, Universidad Autónoma de Madrid, Madrid, 28049, Spain
cDepartment of Chemistry, Loughborough University, Loughborough, LE11 3TU, UK
dVienna Research Platform for Accelerating Photoreaction Discovery, University of Vienna, Währinger Str. 17, 1090 Vienna, Austria
First published on 15th May 2020
Abstract
The development of dye-sensitized solar cells, metalloenzyme photocatalysis or biological labeling heavily relies on the design of metal-based photosensitizes with directional excitations. Directionality is most often predicted by characterizing the excitations manually via canonical frontier orbitals. Although widespread, this traditional approach is, at the very least, cumbersome and subject to personal bias, as well as limited in many cases. Here, we demonstrate how two orbital-free photophysical descriptors allow an easy and straightforward quantification of the degree of directionality in electron excitations using chemical fragments. As proof of concept we scrutinize the effect of 22 chemical modifications on the archetype [Ru(bpy)3]2+ with a new descriptor coined “substituent-induced exciton localization” (SIEL), together with the concept of “excited-electron delocalization length” (EEDLn). Applied to quantum ensembles of initially excited singlet and the relaxed triplet metal-to-ligand charge-transfer states, the SIEL descriptor allows quantifying how much and whereto the exciton is promoted, as well as anticipating the effect of single modifications, e.g. on C-4 atoms of bpy units of [Ru(bpy)3]2+. The general applicability of SIEL and EEDLn is further established by rationalizing experimental trends through quantification of the directionality of the photoexcitation. We thus demonstrate that SIEL and EEDL descriptors can be synergistically employed to design improved photosensitizers with highly directional and localized electron-transfer transitions.
Introduction
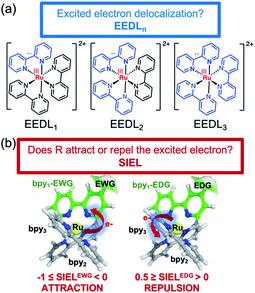
Transformation of light into chemical energy is one of the central challenges of this century. Inspired by nature, scientists are constantly searching for rules to design molecular devices made of chemical structures able to absorb light in a particular wavelength range. After light absorption, the excited electron may be transferred to an acceptor located in the surroundings from where it can reduce a third species,1,2 it can be stored as energy as in Grätzel cells,3,4 or it might evolve through other paths.5 These electron-transfer and charge-separation processes can be highly directional and are controlled by the chemical nature of the donor and acceptor species,6–8 their relative spatial orientation within the optical device, and the environmental conditions.A prototypical chromophore employed in charge-separation experiments is [Ru(bpy)3]2+. It presents a long-lived (ca. 1 μs in solution)9 triplet metal-to-ligand charge transfer (3MLCT) state from which electron transfer can further evolve, as sketched in Fig. 1. The exciton picture (hole + excited electron) of [Ru(bpy)3]2+ is highly dynamical, i.e. it changes upon light absorption, so that e.g. whereas in the initial and short-lived 1MLCT state the exciton is delocalized, after evolution to the 3MLCT the excited electron is localized on only one unit.10 The effect of chemical modifications on the electron excitations within chromophores like [Ru(bpy)3]2+ has been traditionally analyzed by inspecting the canonical frontier orbitals HOMO and LUMO.11–15 General trends have been formulated in coordination complexes, such that electron-withdrawing groups (EWG) located on the ligands tend to have a stronger stabilizing effect on the ligand-centered orbitals (usually LUMO) than on the metal-centered orbitals (HOMO). In contrast, electron donating groups (EDG) behave opposite and destabilize more the HOMO with respect to the LUMO.11,16 Although widespread, this traditional approach is an oversimplification that neglects that, more often than not, electronic excitations involve more than one orbital, complicating the interpretation. This scenario is even more intricate when the number of calculations increases, e.g., if an ensemble of structures is considered to account for nuclear vibrational energy or if a large sampling of geometries is required to describe the chromophore within an explicit environment, or if the analysis is to be done within a time-resolved simulation. In such cases, a characterization by visual inspection of orbitals is a very time-consuming process or simply unaffordable, let alone be quantitative.
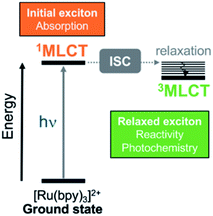 | ||
| Fig. 1 Simplified Jablonski diagram that shows the initially excited singlet metal-to-ligand charge-transfer (1MLCT) and relaxed triplet metal-to-ligand charge transfer (3MLCT) states in [Ru(bpy)3]2+. The relaxed 3MLCT state is populated after ultrafast intersystem crossing (ISC)17–19 from 1MLCT20 and then, subsequent vibrational relaxation can take place. | ||
In order to circumvent these limitations, universal orbital-free molecular descriptors are highly commendable and a large body of groups have worked on the development of density-based descriptors in the last decade.21–33 Particular effort has been spent on quantifying the overall amount of charge transfer including its effect on excitation energies.34,35 However, a more fine-grained picture is advantageous for multichromophoric systems, such as transition metal complexes, where a fragment-based analysis approach36,37 was shown to be particularly powerful.38 In this work, we extend the reach of this toolbox by introducing a new photophysical descriptor based on the analysis of the one-electron transition-density matrix:23,38,39 the substituent-induced exciton localization (SIEL), and showing its power in real-life situations. We show that, allied with the excited-electron delocalization length (EEDLn)36,40 definition, it is straightforward to quantify and predict the effect that chemical functionalization has on exciton populations using the familiar chemical concept of building blocks and thereby eliminating molecular orbitals.
While the EEDLn measures over how many fragments or ligands (for instance a bipyridyl ligand) the excited electron is delocalized, SIEL predicts quantitatively how the presence of a functional group affects the electron population in a ligand of the coordination sphere. The power of this approach is showcased on the archetypical [Ru(bpy)3]2+ modified with 22 functional groups R as a systematic platform of study. The descriptors are used to quantify the effect that a particular functional group has on the localization of both initially excited singlet and relaxed triplet states within a quantum distribution of geometries that accounts for nuclear vibrational motion. Finally, we illustrate the general predictiveness of SIEL with in four different experimental playgrounds where the directional excitation process determines the properties of the photosensitizer.41–46
Systems under study
The selected chemical modifications on [Ru(bpy)3]2+ (1a) are shown in Scheme 1. Most of them correspond to synthetically accessible modifications with EWGs and EDGs in the 4-position of one bpy unit of [Ru(bpy)3]2+ (Table S1†) and many of them are chemically interconvertible by standard chemical transformations. We have explored a halogen series (1b–1d), an amine series where the amine group (1e) is methylated (1f), permethylated (1h), acetylated (1g) and oxidized to NO2 (1i), a hydroxyl/carbonyl series with a hydroxyl group (1j) and its methylated form (1k) as well as the oxidized aldehyde (1l), ketone (1m), carboxylic acid (1n), methyl ester (1o), amide (1q) and methyl amide (1r). In addition, in this series a nitrile 1s (precursor after hydrolysis of an amide) and the α,β-unsaturated carbonyl 1p are included. Finally, the phenyl ring (1t), the methyl group (1u) and the methyl sulfone (1v) are also evaluated.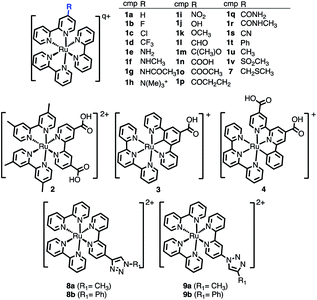 | ||
| Scheme 1 Chemical derivatives 1b–1v of [Ru(bpy)3]2+ (1a), 2–4, and 7–9 considered in this work. In the table, total charge q = 2 for all compounds except for 1h (q = 3). | ||
Additionally, the [Ru(dmb)2(dcb)]2+ (2), the carbometallated Ru-complexes [Ru((COOH)-N∧C∧N)(tpy)]+ (3) and [Ru((COOH)2-C∧N∧N)(tpy)]+ (4),42 the Ru–diimine complex [Ru(bpy)2(bpy-CH2SCH3)]2+ (7)43 and two click-chemistry products,45,468a–8b and 9a–9b, were considered for study, see Scheme 1.
Theory
Computational details
For each compound we have computed the exciton properties of the initially excited 1MLCT state as well as of the relaxed 3MLCT state obtained after intersystem crossing (ISC) (recall Fig. 1). Whereas the initial exciton is responsible for the absorption properties of the complex, the latter exciton is key for emission and the subsequent photochemistry of the triplet CT state. Each complex was optimized in the ground state and in the first triplet state by means of density functional theory (DFT) and its time-dependent version TD-DFT. Then, a quantum ensemble of 100 geometries at 300 K was considered for each of the spin cases (1MLCT and 3MLCT) to account for an appropriate conformational sampling due to nuclear vibrational energy.38,40,47,48 The computation of the 1MLCT absorption band involved the lowest 25 singlet states for each geometry (i.e. 25 × 100 geometries = 2500 excited states per derivative) and the computation of the 3MLCT emission band involved 1 state for each geometry (i.e. 1 × 100 geometries = 100 excited states per derivative). Since the 3MLCT is a manifold of states close in energy, a total of three excited triplet states per complex was first explored for statistical significance (see the Boltzmann weighting, Table S4†) before computing the emission spectrum.All the electronically excited-state energies and properties in the different ensembles were computed by TD-DFT within the Tamm–Dancoff approximation (see Section S1† for further computational details).
Definition of descriptors
The excited electron delocalization length on n-fragments (EEDLn), introduced elsewhere,40 is defined as the percentage of the total excited electron population that is localized on n, where n = 1, 2, 3 or 4 fragments, regardless of which one it is. It is computed based on the final partition ratio (PRf) defined as: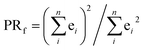 | (1) |
| EEDLn = N(PRfn)/N × 100, % | (2) |
The new descriptor SIEL reports how a particular substituent R attracts or repels the excited electron into the ligand where this functional group R is located. SIEL is computed as a weighted sum of the population of the excited electron (eR) on the ligand where the substituent is located, bpy1-R, and the population of the excited electron over all other ligand fragments (ei):
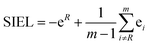 | (3) |
The automatized electronic-structure analysis to compute EEDL and SIEL was implemented within the program package TheoDORE.37 The computational protocol to compute EEDLn and SIEL numbers is described in Section S2 of the ESI.† For each of the [Ru(bpy)3]2+ compounds 1b–1v, the system was divided into four fragments: the metal center and the three bpy ligands. The same fragment definition was applied to those compounds based on the same scaffold. For 3 and 4, three fragments were defined.
Results and discussion
Excited-electron delocalization length (EEDLn) on [Ru(bpy)3]2+ derivatives
We start the discussion with the EEDLn values of the 22 derivatives of [Ru(bpy)3]2+1a–1v (recall Scheme 1), collected in Fig. 3 as percentage bars (see also Tables S2 and S3†). All 2500 excited states of the prototype 1a (R = H) indicate that the singlet excited electron is mainly delocalized over two (EEDL2 = 44%, blue bar, Fig. 3a) and three bipyridine units (EEDL3 = 43%, yellow bar). Only 15% of the states are localized on one ligand (EEDL1, red bar) and a very small fraction of states are delocalized over the three ligands and the metal center (EEDL4 = 4%, green bar). These numbers agree well with experimental results that confirm initial excited electron delocalization in the excited singlet state.10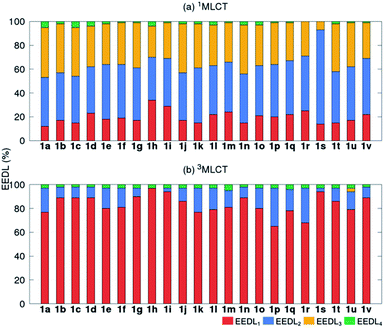 | ||
| Fig. 3 Mean EEDLn values (%) for 1a–1v [Ru(bpy)3]2+ derivatives in the (a) 1MLCT (averaged over 2500 states) and (b) relaxed lowest 3MLCT (averaged over 100 states) bands. | ||
The introduction of EWG or EDG affects to a small extent the net localization of the initial excited electron compared to 1a (compounds 1b–1v, Fig. 3a). In all cases, the excited electron is mainly delocalized over 2 bpy ligands (blue bars) with significant (but smaller) contributions from EEDL1 (red bar) and EEDL3 (yellow bar). Only the presence of strong EWG groups like N(CH3)3+ (1h) and NO2 (1i) increases the population of the singlet excited electron on only one bpy unit with values for EEDL1 of ca. 30%.
In the relaxed 3MLCT state of [Ru(bpy3)]2+, which is formed after ISC and vibrational relaxation, the exciton has been proven experimentally to be localized.17,18,49 This is confirmed in our analysis that predicts EEDL1 larger than 65% (red bar, Fig. 3b) and a delocalization over two ligands of less than 25%. This analysis clearly evidences how the electronic distribution strongly changes between the initial singlet and relaxed triplet excited states. It is worth to stress that such changes would barely be predictable and quantified within a simplified inspection of HOMO–LUMO orbitals.
Substituent-induced exciton localization (SIEL) on [Ru(bpy)3]2+ derivatives
Fundamental further insight is provided by the SIEL descriptor, which reveals where the excited electron is directed. The SIEL values of 1a–1v are plotted in Fig. 4a for both the singlet and triplet states (see also Table S5†). The parent compound 1a shows SIEL values in both singlet and triplet manifolds close to 0 because all three ligands are the same (R = H). In contrast, SIEL in 1b–1v beautifully illustrates how the chemical nature of the substituent determines the directionality of the excitation, in both singlet and triplet states. It could be argued that the general trends could have been expected from chemical intuition: the EWGs (e.g. all the halogens (1b–1d), N(CH3)3+ (1h), NO2 (1i) or CN (1s)) attract (SIEL < 0) and EDGs (e.g. all the amines (1e–1g), OH (1j) or OCH3 (1k)) repel (SIEL > 0) the excited electron. However, the use of SIEL is much more powerful than simple chemical sense, as e.g. it allows to identify subtle and not so obvious differences within a chemical family. For instance, all the neutral amine derivatives (1e–1g) have positive SIEL values, but whereas the alkylation of the amine (1e → 1f) almost does not affect the SIEL value in the 1MLCT state, the acetylation in 1g reduces the SIEL value compared to 1e (green bars, Fig. 4). Remarkably, full methylation in 1h changes the sign of SIEL. Within the carbonyl series (1l–1r), the increase of the oxidation state on the carbonyl carbon reduces the SIEL absolute value. Whereas the aldehyde 1l and the methyl ester 1o show a large negative SIEL value, the amide 1p show smaller negative SIEL values. Interestingly, in the 3MLCT state, the methylation of the amide (1q) increases the attraction of the excited electron in the same extend as a in the methyl ester 1o. The NO2 (1i) and N(CH3)3+ (1h) derivatives show the largest negative SIEL values of all the compounds.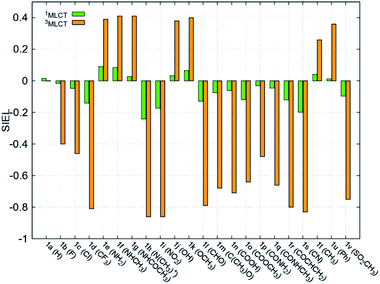 | ||
| Fig. 4 Mean SIEL values for the initial singlet excited band (1MLCT, green bars, averaged over 2500 states) and the relaxed triplet excited band (3MLCT, orange bars, averaged over 100 states). | ||
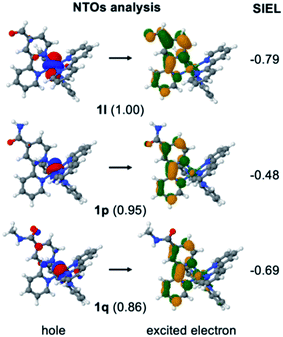
In order to stress the virtues of the SIEL descriptor against traditional orbital inspection, we plot the corresponding natural transition orbitals (NTOs) of the former 1l, 1p and 1q compounds in Fig. 5. The aim is to try to explain the effect of the substituent on the electronic excitation of the 3MLCT state. However, we can see that in all three cases the excited electron is localized on bpy1 – the ligand that bears the functional group. Also, in the three cases the hole comes from the metal center, and so all three compounds evince identical MLCT character. How then to differentiate amid the three cases? Which is the stronger electron acceptor involved in the excitation? Clearly, the weights for the NTOs do not help either, as all of them are similar, representing over 85% of the excitation. In contrast, the shrewd SIEL descriptors can be introduced and applied to revelatory effect (Fig. 5): the population of the excited electron in the 3MLCT state evinces a clear increase in bpy1-R in the order 1p < 1q < 1l.
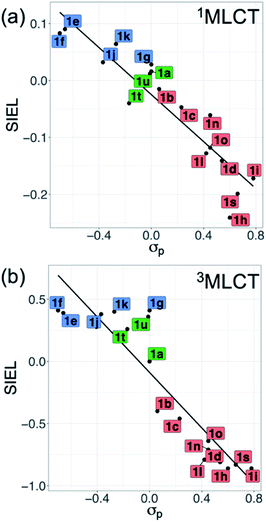
Also revealing are the differences between the SIEL values for the singlet and triplet states (Fig. 4). Although the sign of SIEL for each functional group is the same in both 1MLCT and 3MLCT states, the values are different: the absolute values are larger in the triplet state, as expected from the EEDLn values. This confirms that caution should be exercised when considering computed properties at the Franck–Condon region to explain the behavior of the electronic states beyond this region (e.g. at the relaxed triplet state). As an example, we compare the SIEL descriptor with the empirical substitution constants of Hammet (σp)50 and the electrophilic substituent constants of Brown and Okamoto (σp+)51 (Table S5†) – descriptors that have been previously used to describe the substituent effect on the photophysics of polypyridine Ru-based complexes.52–54 The best correlation was found with σp, plotted in Fig. 6a and b, for both SIEL values of the initial 1MLCT band (R2 = 0.841) and of the relaxed 3MLCT states (R2 = 0.829), respectively. However, since these σp parameters have been established for the electronic ground state, they cannot discriminate between the electronic behavior in the initial and the final relaxed exciton. SIEL does. For example, it shows larger absolute values for states localized on one ligand and smaller values for states largely delocalized. Even more, compared to the empirical parameters, SIEL can reflect for a particular functional group not only its electronic nature – as proven above – but also the effect of the environment (e.g. aqueous solution or within a protein)40 and the dynamics of the photoactive compound.
Substituent-induced exciton localization (SIEL) on other Ru systems
In order to illustrate the predictive power of the SIEL descriptor, we apply this concept to several systems previously characterized experimentally. The first is [Ru(dmb)2(dcb)]2+ (2), which has been extensively used as molecular dye to photosensitize TiO2 surfaces.412 is decorated with two methyl groups on the dimethylbipyridine dmb units (four in total) and with two carboxylic acid groups in the dicarboxylicbipyridine dcb unit (Fig. 7a). The latter are used to bind to the metallic surface and to injects electrons, after excitation and subsequent population of the lowest excited 3MLCT state. By quickly adding up the tabulated SIEL values for the introduction of a methyl group (0.26) and a carboxylic acid group (−0.71) in the 3MLCT state (Table S5†), the estimated net SIEL value on each of the two dcb ligands is −1.42 (attraction of the excited electron) and 0.52 in dmb (repulsion). It can therefore be concluded that the excitation will clearly happen to dcb, and thus in the direction of the TiO2 surface. An explicit calculation of the SIEL values more accurately in 2 using ab initio computations leads to the same conclusion (Tables S6 and S7†). Importantly, this tell us that the computed values displayed in Fig. 4 can be used to quickly anticipate the effect of single modifications on C-4 atoms of bpy units of [Ru(bpy)3]2+.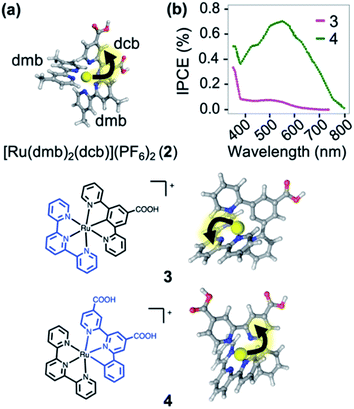 | ||
| Fig. 7 (a) [Ru(dmb)2(dcb)]2+ (2), where dmb = 4,4′-dimethyl-2,2′-bipyridine and dcb = 4,4′-dicarboxylic-2,2′-bipyridine. (b) Plot of the prediction of “incident photon to current efficiency” (IPCE) into TiO2, adapted from ref. 42. Below are shown the carbometallated Ru-complexes423 and 4 decorated with a 2,2′:6′,2′′-terpyridine (tpy) ligands (left) and the directionality of the excited electron highlighted with an arrow (right). | ||
The applicability of SIEL to other chemical configurations is illustrated next by rationalizing the origin of the discrepancies in the photocurrent action spectra/sensitizing properties between the two cyclometalated complexes [Ru((COOH)-N∧C∧N)(tpy)]+ (3) and [Ru((COOH)2-C∧N∧N)(tpy)]+ (4)42 (Fig. 7b). Both pigments for dye-sensitized solar cells have been also anchored on a TiO2 surface through their carboxylic acid groups55,56 to generate currents upon light absorption by injection of the excited electron into the metal support. However, complexes 3 and 4 differ in their scaffolds. Van Koten and colleagues42 found that the nature of the excited state highly depends on the complex, affecting their proficiency as photosensitizer. Fig. 7b shows that the experimental photocurrent action spectra42 of 3 (magenta line) is less intense than that of 4 (green line). We computed the SIEL values on their lowest excited triplet states using three fragments (Table S9†). Based on our analysis, in the lowest 3MLCT excited state of the less active compound 3, the excited electron is transferred to the distal 2,2′:6′,2′′-terpyridine (tpy) unit (SIEL = −0.415) with respect to the TiO2 surface. On the contrary, in the more active compound 4, the excited electron localizes on the ligand that carries the carboxylic acids ((COOH)2-C∧N∧N, SIEL = −0.376) and, therefore, electron transfer from that ligand to the surface is highly favored. Both cases feature a 3MLCT excited triplet, but they possess a non-negligible ligand-to-ligand charge transfer (LLCT) contribution, which is almost double in 3 than in 4 (Table S8†).
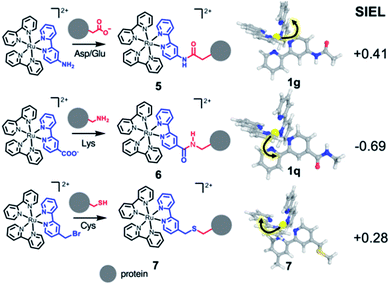
As third example, we analyzed three Ru–diimine complexes covalently bound to proteins – one of the most explored avenues to couple light and enzyme activities by mediation of electron transfer processes.43,57 As main strategy, a synthetic Ru-based polypyridine species is reacted with the side chain of an amino acid that is positioned in proximity to the active site or to the place where the electron transfer process happens (Scheme 2). Frequently targeted residues are Asp, Glu or Lys, via an amide bond (compounds 5 and 6, respectively), or Cys,43 connected through a thioether group (compound 7). The different nature of the residue is expected to affect the localization of the excited electron. Since the kinetics of the electron transfer process depends, among others, on the distance between donor and acceptor,58 the electron transfer processes could be modulated by the quantification of the SIEL values on the photosensitizer and the proper orientation of the coordination complex with respect to the acceptor species.
According to the SIEL values for relaxed 3MLCT states tabulated in Fig. 4, NHCOCH3 (1g) would repel the excited electron and would trigger the excitation into the ligand in cis (5, SIEL = 0.41). In contrast, the use of CONHCH3 (1q) would attract the excited electron to the ligand where the functional group is located (6, SIEL = −0.69). Coupling with a Cys residue through a thioether group (7) will play the same role, repelling the excited electron from the ligand that binds to the protein (SIEL = 0.28) although to the trans bpy unit (Tables S10 and S11†). We see thus that the selection of a particular chemical linker changes the directionality of the excited electron and the use of SIEL can predict it, to the advantage of the experimental setup.44
The final example consists of two click-chemistry products, 8 and 9, synthesized from the precursors [Ru(bpy)2(bpy-CCH)]2+ and [Ru(bpy)2(bpy-N3)]2+, respectively (Scheme 3), and described by Aukauloo et al.45,46 Since the number of proteinogenic residues is limited, different approaches emerged in the last years to expand the chemical reactivity space of the amino acids. One of them is the well-known click chemistry methodology,59,60 that allows a modular approach within Chemical Biology. In particular, the CuAAC (Cu(I) catalyzed azide–alkyne cycloaddition) click chemistry only requires the presence of two reactants, an alkyne and an azide species, together with Cu(I) as catalyst. The chemical stability of these species allows that the click reaction can be carried out in vivo in a mild manner. This triazole group can be a useful linker for electron-transfer processes. Some examples have been developed using [Ru(bpy)3]2+ as scaffold.45,46,61,62 In particular, we have studied the effect of a methyl group (R1 = Me, 8a and 9a) and a phenyl group (R1 = Ph, 8b and 9b) on the triazole moiety (Scheme 3, Tables S12 and S13†). In contrast to the experimental observation that the 1,2,3-triazoles in 8 and 9 are electrochemically silent and do not alter the intrinsic photophysical properties of the Ru-based chromophore in solution,45,46 the nature of the triazole group is expected to affect the exciton directionality.
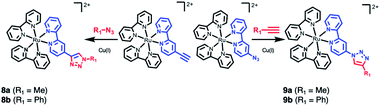 | ||
| Scheme 3 CuAAC (Cu(I) catalyzed azide–alkyne cycloaddition) click chemistry adducts 8 and 9.45,46 | ||
The SIEL numbers for bpy1-R of 8 and 9 are shown in Table 1. We see that whereas in the two derivatives of 9 the 1,2,3-triazole attracts the excited electron to bpy1 (SIEL = −0.656 (Me) and −0.497 (Ph)), the former heterocycle repels the excitations in 8a/b to bpy2/bpy3 (SIEL = 0.345 (Me) and 0.039 (Ph)). Thus, the nature of triazole change the directionality of the excitation (8avs.9a, 8bvs.9b) but the change Me → Ph in 8 and/or in 9 affects in less extend the directionality of the excitation (8avs.8b, 9avs.9b).
| Cmp. | R1 | SIEL | Excited electron populationa (%) | |||
|---|---|---|---|---|---|---|
| 1,2,3-triazole-R1 | bpy1a | bpy2 (trans) | bpy3 (cis) | |||
| a For the calculation of the excited electron populations, the complexes have been divided into 5 fragments (Ru, bpy1, triazole, bpy2 and bpy3). trans and cis refer to the relative position of the bpy unit to the substituted one. The excited electron population on Ru is 0% in all cases. | ||||||
| 8a | Me | 0.345 | 4 | 4 | 79 | 13 |
| 9a | Me | −0.656 | 3 | 75 | 11 | 11 |
| 8b | Ph | 0.039 | 13 | 17 | 16 | 54 |
| 9b | Ph | −0.497 | 15 | 54 | 14 | 17 |
In addition to the calculations done with 4 fragments, we also split the system into 5 fragments to compute separately the excited electron population in the bare bpy1 and in the substituted triazole with the functional group R1 (Table 1). As an example, we can see that, whereas in 8a (R = Me) 8% of the population of the excited electron is located on bpy1 + R1, the introduction of a phenyl ring in 8b (R = Ph) increases this population only up to a 30%. In the change 9a → 9b the effect on the Ph ring has a smaller impact on the population on bpy1 + R1 of the N-connected triazole (78% vs. 69%).
Conclusions
We demonstrate that the substituent-induced exciton localization (SIEL) descriptor, combined with the excited-electron delocalization length (EEDLn) is a powerful tool to quantify exciton directionality and localization, paving the way for easy rational design of photosensitizers. SIEL, as well as EEDLn, are implemented to be universally used on any chemical system in a black-box fashion, rendering a straightforward quantification of the effect of chemical modifications on electronic excitations. No visual inspection of molecular orbitals is necessary, eliminating sources of bias and subjectivity. The achieved quantification proves particularly advantageous when large ensembles of molecules are considered, for instance to take into account environment, or in data mining studies, where increasingly larger sets of generated data can reveal important features if appropriate quantitative measures are available.As proof of concept, we quantified the effect of 22 chemical modifications on the archetype [Ru(bpy)3]2+ and rationalized the directionality of the excitation in four experimental cases with technological and biological relevance: photosensitizers for solar cells, metalloproteins for enzymatic photocatalysis and click chemistry for biological labeling – processes where the directional electron transfer is key for the overall photoinduced mechanism. We proved that our descriptors can, (i) help in the design of directional electron transfer within chromophores attending to their chemical functionalization, and (ii) explain experimental trends. We thus expect these descriptors to become a valuable tool to design new photosensitizers with improved electronic properties.
Data availability
The research data supporting this publication can be accessed via the institutional open repository of the University of Vienna https://doi.org/11353/10.1032866. The code for the 1TDM analysis can be found at theodore-qc.sourceforge.net.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. A. S.-M. thanks the Austrian Science Fund (FWF, Project M 2260) for funding. Further support from the Comunidad de Madrid through the Programa de Atracción de Talento 2018, project 2018-T1/BMD-10261 (J. J. N.) and the University of Vienna (L. G.) is acknowledged. The Vienna Scientific Cluster is acknowledged for generous computational time.Notes and references
- J. Xuan and W. J. Xiao, Angew. Chem., Int. Ed., 2012, 51, 6828–6838 CrossRef CAS PubMed.
- J. M. R. Narayanam and C. R. J. Stephenson, Chem. Soc. Rev., 2011, 40, 102–113 RSC.
- A. Hagfeldt and M. Grätzel, Acc. Chem. Res., 2000, 33, 269–277 CrossRef CAS PubMed.
- J. Liu, G. Cao, Z. Yang, D. Wang, D. Dubois, X. Zhou, G. L. Graff, L. R. Pederson and J. G. Zhang, ChemSusChem, 2008, 1, 676–697 CrossRef CAS PubMed.
- S. Rau, D. Walther and J. G. Vos, J. Chem. Soc., Dalton Trans., 2007, 915–919 RSC.
- N. H. Damrauer, T. R. Boussie, M. Devenney and J. K. McCusker, J. Am. Chem. Soc., 1997, 119, 8253–8268 CrossRef CAS.
- T. J. Whittemore, T. A. White and C. Turro, J. Am. Chem. Soc., 2018, 140, 229–234 CrossRef CAS PubMed.
- K. Teegardin, J. I. Day, J. Chan and J. Weaver, Org. Process Res. Dev., 2016, 20, 1156–1163 CrossRef CAS PubMed.
- A. N. Tarnovsky, W. Gawelda, M. Johnson, C. Bressler and M. Chergui, J. Phys. Chem. B, 2006, 110, 26497–26505 CrossRef CAS PubMed.
- P. Dongare, B. D. B. Myron, L. Wang, D. W. Thompson and T. J. Meyer, Coord. Chem. Rev., 2017, 345, 86–107 CrossRef CAS.
- M. Maestri, N. Armaroli, V. Balzani, E. C. Constable and A. M. W. C. Thompson, Inorg. Chem., 1995, 34, 2759–2767 CrossRef CAS.
- E. A. Medlycott and G. S. Hanan, Chem. Soc. Rev., 2005, 34, 133–142 RSC.
- G. R. Freeman and G. W. Williams, in Organometallics and Related Molecules for Energy Conversion, ed. W.-Y. Wong, Berlin Heidelberg, 2015, pp. 29–59 Search PubMed.
- M. Jäger, L. Freitag and L. González, Coord. Chem. Rev., 2015, 304–305, 146–165 CrossRef.
- J. Karges, F. Heinemann, M. Jakubaszek, F. Maschietto, C. Subecz, M. Dotou, R. Vinck, O. Blacque, M. Tharaud, B. Goud, E. Viñuelas Zahĺnos, B. Spingler, I. Ciofini and G. Gasser, J. Am. Chem. Soc., 2020, 142, 6578–6587 CrossRef CAS PubMed.
- M. J. Cook, A. P. Lewis, G. S. G. Mcauliffe, V. Skarda, A. J. Thompson, J. L. Glasper and D. J. Robbins, J. Chem. Soc., Perkin Trans. 2, 1984, 1293–1301 RSC.
- N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Science, 1997, 275, 54–57 CrossRef CAS PubMed.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- A. J. Atkins and L. González, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
- A. Cannizzo, F. Van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174–3176 CrossRef CAS PubMed.
- T. Le Bahers, E. Brémond, I. Ciofini and C. Adamo, Phys. Chem. Chem. Phys., 2014, 16, 14435–14444 RSC.
- C. Adamo, T. Le Bahers, M. Savarese, L. Wilbraham, G. García, R. Fukuda, M. Ehara, N. Rega and I. Ciofini, Coord. Chem. Rev., 2015, 304–305, 166–178 CrossRef CAS.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- S. A. Bäppler, F. Plasser, M. Wormit and A. Dreuw, Phys. Rev. A, 2014, 90, 052521 CrossRef.
- T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3896–3905 CrossRef CAS PubMed.
- M. Savarese, P. A. Netti, C. Adamo, N. Rega and I. Ciofini, J. Phys. Chem. B, 2013, 117, 16165–16173 CrossRef CAS PubMed.
- M. Ehara, R. Fukuda, C. Adamo and I. Ciofini, J. Comput. Chem., 2013, 34, 2498–2501 CrossRef CAS PubMed.
- M. Savarese, C. A. Guido, E. Brémond, I. Ciofini and C. Adamo, J. Phys. Chem. A, 2017, 121, 7543–7549 CrossRef CAS PubMed.
- J. J. Nogueira, F. Plasser and L. González, Chem. Sci., 2017, 8, 5682–5691 RSC.
- T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3906–3914 CrossRef CAS PubMed.
- E. Ronca, M. Pastore, L. Belpassi, F. De Angelis, C. Angeli, R. Cimiraglia and F. Tarantelli, J. Chem. Phys., 2014, 140, 054110 CrossRef PubMed.
- J. W. Furness, U. Ekström, T. Helgaker and A. M. Teale, Mol. Phys., 2016, 114, 1415–1422 CrossRef CAS.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- M. Campetella, F. Maschietto, M. J. Frisch, G. Scalmani, I. Ciofini and C. Adamo, J. Comput. Chem., 2017, 38, 2151–2156 CrossRef CAS PubMed.
- P. Kimber and F. Plasser, Phys. Chem. Chem. Phys., 2020, 22, 6058–6080 RSC.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- S. Mai, F. Plasser, J. Dorn, M. Fumanal, C. Daniel and L. González, Coord. Chem. Rev., 2018, 361, 74–97 CrossRef CAS.
- Y. Li and C. A. Ullrich, Chem. Phys., 2011, 391, 157–163 CrossRef CAS.
- P. A. Sánchez-Murcia, J. J. Nogueira and L. González, J. Phys. Chem. Lett., 2018, 9, 683–688 CrossRef PubMed.
- H. Y. Chen and S. Ardo, Nat. Chem., 2018, 10, 17–23 CrossRef CAS PubMed.
- S. H. Wadman, J. M. Kroon, K. Bakker, R. W. A. Havenith, G. P. M. Van Klink and G. Van Koten, Organometallics, 2010, 29, 1569–1579 CrossRef CAS.
- L. M. Geren, J. R. Beasley, B. R. Fine, A. J. Saunders, S. Hibdon, G. J. Pielak, B. Durham and F. Millett, J. Biol. Chem., 1965, 270, 2466–2472 CrossRef PubMed.
- M. J. Bjerrum, D. R. Casimiro, I. Chang, A. J. Di Bilio, H. B. Gray, M. G. Hill, R. Langen, G. A. Mines, L. K. Skov, J. R. Winkler and S. Wuttke, J. Bioenerg. Biomembr., 1995, 27, 295–302 CrossRef CAS PubMed.
- A. Baron, C. Herrero, A. Quaranta, M. F. Charlot, W. Leibl, B. Vauzeilles and A. Aukauloo, Chem. Commun., 2011, 47, 11011–11013 RSC.
- A. Baron, C. Herrero, A. Quaranta, M. F. Charlot, W. Leibl, B. Vauzeilles and A. Aukauloo, Inorg. Chem., 2012, 51, 5985–5987 CrossRef CAS PubMed.
- J. J. Nogueira and L. González, Annu. Rev. Phys. Chem., 2018, 69, 473–497 CrossRef CAS PubMed.
- J. P. Zobel, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915 RSC.
- A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- H. C. Brown and Y. Okamoto, J. Am. Chem. Soc., 1958, 80, 4979–4987 CrossRef CAS.
- M. K. Nazeeruddin, S. M. Zakeeruddin and K. Kalyanasundaram, J. Phys. Chem., 1993, 97, 9607–9612 CrossRef CAS.
- F. Kawai, T. Kawabata and M. Oda, Appl. Microbiol. Biotechnol., 2019, 103, 4253–4268 CrossRef CAS PubMed.
- H. Shalan, A. Colbert, T. T. Nguyen, M. Kato and L. Cheruzel, Inorg. Chem., 2017, 56, 6558–6564 CrossRef CAS PubMed.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- F. Millett, J. Havens, S. Rajagukguk and B. Durham, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1309–1319 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021 CrossRef CAS.
- Z. P. Demko and K. B. Sharpless, Angew. Chem., 2002, 41, 2110–2113 CrossRef CAS.
- J. B. Gerken, M. L. Rigsby, R. E. Ruther, R. J. Pérez-Rodríguez, I. A. Guzei, R. J. Hamers and S. S. Stahl, Inorg. Chem., 2013, 52, 2796–2798 CrossRef CAS PubMed.
- N. Zabarska, A. Stumper and S. Rau, Dalton Trans., 2016, 45, 2338–2351 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Further computational details and additional tables. See DOI: 10.1039/d0sc01684e |
| This journal is © The Royal Society of Chemistry 2020 |