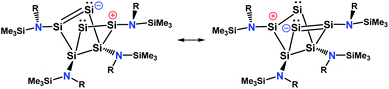Open Access Article
Open Access ArticleA highly unsaturated six-vertex amido-substituted silicon cluster†
Jan
Keuter
a,
Christian
Schwermann
 b,
Alexander
Hepp
a,
Klaus
Bergander
c,
Jörn
Droste
b,
Alexander
Hepp
a,
Klaus
Bergander
c,
Jörn
Droste
 d,
Michael Ryan
Hansen
d,
Michael Ryan
Hansen
 d,
Nikos L.
Doltsinis
d,
Nikos L.
Doltsinis
 *b,
Christian
Mück-Lichtenfeld
*b,
Christian
Mück-Lichtenfeld
 *c and
Felicitas
Lips
*c and
Felicitas
Lips
 *a
*a
aWestfälische Wilhelms-Universität Münster, Institut für Anorganische und Analytische Chemie, Corrensstraße 28-30, 48149 Münster, Germany
bWestfälische Wilhelms-Universität Münster, Institut für Festkörpertheorie, Center for Multiscale Theory and Computation, Wilhelm-Klemm-Straße 10, 48149 Münster, Germany
cWestfälische Wilhelms-Universität Münster, Organisch-Chemisches Institut, Center for Multiscale Theory and Computation, Corrensstraße 40, 48149 Münster, Germany
dWestfälische Wilhelms-Universität Münster, Institut für Physikalische Chemie, Corrensstraße 30, 48149 Münster, Germany
First published on 11th May 2020
Abstract
Thermal treatment of the bicyclo[1.1.0]tetrasilatetraamide [Si4{N(SiMe3)Dipp}4] 1 resulted in the formation of a highly unsaturated six-vertex silicon cluster [Si6{N(SiMe3)Dipp}4] 2 with only four amine-substituents and two ligand-free silicon atoms. In solution, a major and a minor conformer of this cluster are in equilibrium according to multinuclear NMR spectroscopy, lineshape analysis, DFT calculations and molecular dynamics simulations. The bonding situation in the highly unsaturated cluster features lone pair type character at the ligand-free silicon atoms and partial single and double bond character in the upper butterfly-shaped ring of 2. This allows to consider 2 as the silicon analogue of a butalene isomer.
Introduction
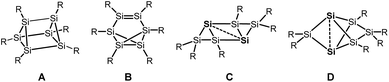
Silicon analogues to benzene were successfully isolated with sterically demanding substituents. Isomers with a prismatic silicon scaffold A,1 a benzvalene-type isomer B,2 a tricyclic species C3 and a propellane-type compound D4 turned out from these investigations.Computational investigation into Si6H6 isomers5 revealed the spherical propellane-type compound D, recently termed benzpolarene,6 to be the global minimum structure and to be much lower in energy than benzene-, benzvalene-, prismatic- or Dewar-benzene-type isomers.
In the isolated silicon analogues of benzene as well as in the computationally investigated Si6H6 isomers, silicon atoms with no substituent occur that are only connected to other silicon atoms. These so-called unsubstituted or “naked” silicon atoms display inverted tetrahedral7 or hemispheroidal configurations.8 Therefore, the topology of these clusters resembles surface structures of bulk silicon or silicon nanoparticles.9 This type of clusters is named siliconoids1b,8 in analogy to metalloid clusters10 and can further be considered as model compounds for intermediates of the chemical vapour deposition process of molecular silane precursors.11
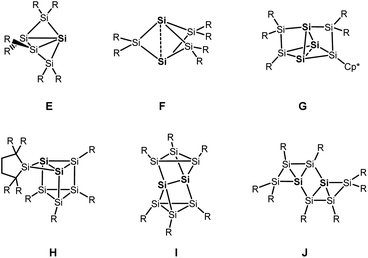
Besides the six-vertex clusters depicted in Scheme 1, five-vertex silicon clusters with one E12 or two ligand-free atoms F,13 seven-vertex G14 and H15 and eight-vertex siliconoid clusters I16 and J17 are reported in the literature (Scheme 2).
Recent progress in this field includes a systematic stepwise synthesis from a six- to an eight-vertex siliconoid cluster,14 and thermolysis of a siliconoid cluster into novel seven and eight-vertex silicon clusters.15 Furthermore, functionalization of the benzpolarene-type cluster D at different positions6,18 and the introduction of boron- and phosphorous-based groups, which corresponds to n- and p-type doping of elemental silicon, was achieved.19
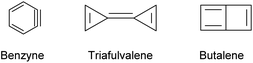
Unsaturated isomers of benzene with the formula C6H4 were considered computationally and feature structural motifs shown in Scheme 3.20
Considering the lower tendency of silicon to form π-bonds and the above mentioned observation for the preference of silicon clusters for spherical scaffolds with a high number of σ-bonds, we expect a silicon analogue to C6H4 to adopt a Si6 structural motif that differs from the carbon-based isomers shown in Scheme 3. Previous computational investigations using Car–Parrinello molecular dynamics simulations21 and DFT calculations22 suggested a structure with spherical scaffold for Si6H4. However, no such compound has been isolated yet.
Results and discussion
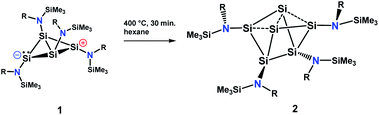
The silicon clusters mentioned in the introduction have the common feature that they are surrounded either by aryl, alkyl or silyl substituents. However, reports on unsaturated main group clusters with higher nuclearity stabilized by amine substituents are rare.23 One such compound is the metalloid cluster Sn15{N(SiMe3)Dipp}6 featuring eight ligand-free tin atoms, that was synthesized in a reductive dehalogenation of the dimeric [{N(SiMe3)Dipp}SnCl]2 using KC8 as the reducing agent.24 Recently, we reported on the bicyclo[1.1.0]tetrasilatetraamide Si4{N(SiMe3)Dipp}41 displaying two three-coordinate silicon atoms with different degree of pyramidalization.25 By thermal treatment of 1 at ca. 400 °C under argon, removal of all volatile components in vacuo at 400 °C, and subsequent extraction of the yellow residue in hexane at room temperature, we were able to synthesize the first amido-substituted highly unsaturated silicon cluster Si6{N(SiMe3)Dipp}42 in form of yellow crystals in ca. 23% yield (see Scheme 4).Compound 2 was also obtained in much lower yield in a co-reduction of {N(SiMe3)Dipp}SiBr3 and SiBr4 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
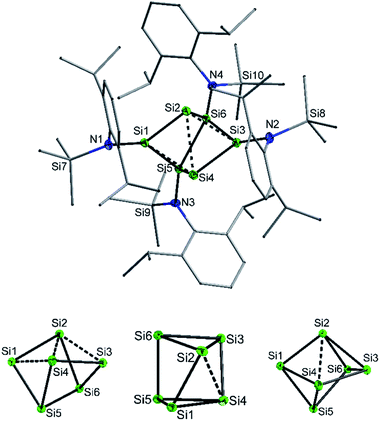
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with potassium graphite (KC8). In this case, however, 2 co-crystallized with 1. The formation mechanism of 2 is unclear due to the difficulty to assign side products at 400 °C. Two possible formation pathways that proceed under release of bis(amido)-substituted silylene are suggested in the ESI (page S48).† The formation of siliconoid clusters H and J was also found to proceed with silylene elimination.15 Single crystal X-ray diffraction revealed that in 2, a Si6 cluster core with two unsubstituted silicon atoms is surrounded by four {N(SiMe3)Dipp}-substituents. All silicon atoms in 2 are fourfold-coordinated. The Si6 cluster core in 2 resembles to the six-vertex propellane- or benzpolarene-type cluster D, but can also be considered as a heavily distorted octahedron missing two edges or as a twisted trigonal prism (see Fig. 1, bottom). The distance between the two unsubstituted silicon atoms (Si2, Si4) amounts to 2.636(6) Å which is very similar to the distance between atoms of this type in the propellane-type clusters D (2.708 Å) and F (2.636 Å). These two unsubstituted silicon atoms are part of a butterfly-shaped moiety of the cluster constituted by Si1–Si4. Within this unit the two bond lengths Si1–Si2 and Si3–Si4 (2.281(5) Å and 2.292(6)) are very short for Si–Si single bonds and approach the value reported for Si
1 ratio with potassium graphite (KC8). In this case, however, 2 co-crystallized with 1. The formation mechanism of 2 is unclear due to the difficulty to assign side products at 400 °C. Two possible formation pathways that proceed under release of bis(amido)-substituted silylene are suggested in the ESI (page S48).† The formation of siliconoid clusters H and J was also found to proceed with silylene elimination.15 Single crystal X-ray diffraction revealed that in 2, a Si6 cluster core with two unsubstituted silicon atoms is surrounded by four {N(SiMe3)Dipp}-substituents. All silicon atoms in 2 are fourfold-coordinated. The Si6 cluster core in 2 resembles to the six-vertex propellane- or benzpolarene-type cluster D, but can also be considered as a heavily distorted octahedron missing two edges or as a twisted trigonal prism (see Fig. 1, bottom). The distance between the two unsubstituted silicon atoms (Si2, Si4) amounts to 2.636(6) Å which is very similar to the distance between atoms of this type in the propellane-type clusters D (2.708 Å) and F (2.636 Å). These two unsubstituted silicon atoms are part of a butterfly-shaped moiety of the cluster constituted by Si1–Si4. Within this unit the two bond lengths Si1–Si2 and Si3–Si4 (2.281(5) Å and 2.292(6)) are very short for Si–Si single bonds and approach the value reported for Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si double bonds (2.138–2.289 Å).26 In contrast, the bond lengths Si2–Si3 and Si1–Si4 (2.502(6) and 2.532(6) Å) are longer than typical single bonds (2.34 Å). The butterfly-shaped moiety is capped by a dumbbell consisting of Si5 and Si6 (2.357(1) Å). The bond lengths Si2–Si6 and Si4–Si5 (2.403(6) and 2.389(6) Å) connecting the butterfly-type ring and the Si5–Si6-dumbbell are somewhat elongated compared to the standard Si–Si single bond length. All other bond lengths are in the range of usual single bonds. The Si–N bond lengths (1.730(1)–1.740(1) Å) are only somewhat shorter than single bonds (ca. 1.76 Å).27
Si double bonds (2.138–2.289 Å).26 In contrast, the bond lengths Si2–Si3 and Si1–Si4 (2.502(6) and 2.532(6) Å) are longer than typical single bonds (2.34 Å). The butterfly-shaped moiety is capped by a dumbbell consisting of Si5 and Si6 (2.357(1) Å). The bond lengths Si2–Si6 and Si4–Si5 (2.403(6) and 2.389(6) Å) connecting the butterfly-type ring and the Si5–Si6-dumbbell are somewhat elongated compared to the standard Si–Si single bond length. All other bond lengths are in the range of usual single bonds. The Si–N bond lengths (1.730(1)–1.740(1) Å) are only somewhat shorter than single bonds (ca. 1.76 Å).27
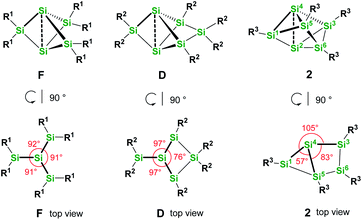
We were interested to compare the configuration of the unsubstituted silicon atoms in 2 with those in the propellane-type clusters F and D in the solid state (see Fig. 2). In the propellane-type clusters the bond angles around the ligand-free silicon atoms are all ca. 90° in F and 97°, 97°, and 76° in D.
Thus, the configuration at the unsubstituted silicon atoms is inverted tetrahedral or hemispheroidal in F and D. This is a common feature of “naked” Si atoms as it was analyzed by Ishida and Iwamoto7 and by Scheschkewitz.8
Measuring these angles in 2 results in significantly different angles of 57°, 83°, and 103°, which allows to describe the configuration of the unsubstituted Si atoms (Si2, Si4) in 2 as hemispheroidal with a hemispheroidality parameter φ = 1.45 Å. This represent the highest hemispheroidality parameter so far observed for silicon clusters.8 More specifically, the environment at Si2/Si4 can be considered as the apical position of a distorted square-based pyramid. A persila-pyramidane was not reported yet, but was investigated computationally using DFT methods for the compounds Si5H4, Si5(SiH3)4 and Si5(SiMe3)4.28
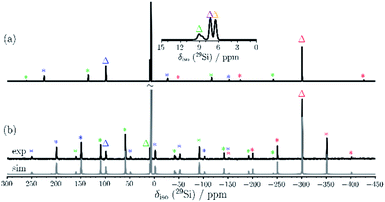
The C2-symmetric 2 was investigated by multinuclear NMR spectroscopy in PhMe-d8 and THF-d8. The absence of hydride substituents at Si2, Si4 was evidenced by a 2D correlated 29Si/1H experiment (Fig. S26†) and by a quantitative 1H NMR spectrum that revealed no hydride signal between 4 and 6 ppm. In the 1H NMR spectrum at 300 K signal broadening is observed indicating dynamic behavior of 2 in solution. In the 29Si NMR spectrum at 300 K signals at 94.2 ppm for Si1 and Si3, at 7.7 ppm for Si5 and Si6 and at −309.4 ppm for Si2 and Si4 appear in THF-d8 besides signals at 7.0 and 7.4 ppm for the two chemically and magnetically different SiMe3 groups. These measured signals are in good accordance with DFT calculated values (see Table S4†). The signal at very high field for the unsubstituted Si atoms at −309.4 ppm is in line with that observed for this type of atoms in F and D (−273.2 and −274.2 ppm, respectively). The dynamic behavior of 2 was analyzed by variable temperature (VT) 1H NMR spectroscopy, 2D NMR experiments and lineshape analysis. This analysis revealed that two species in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio are in equilibrium with each other (see Fig. 3, S19 and page S42†). The minor component has three signals in the 29Si NMR spectrum at 51.3, −5.1 and −294.0 ppm.
1 ratio are in equilibrium with each other (see Fig. 3, S19 and page S42†). The minor component has three signals in the 29Si NMR spectrum at 51.3, −5.1 and −294.0 ppm.
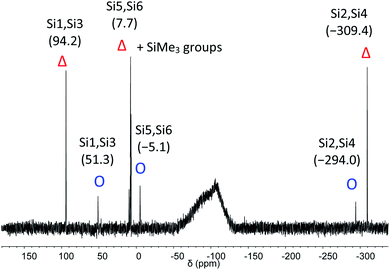 | ||
| Fig. 3 29Si NMR spectrum of 2 in THF-d8 at 210 K. Δ represents the major component and O the minor component. | ||
Examination of 2via solid state 29Si{1H} CP/MAS NMR spectroscopy was performed, confirming that only the major component is present in the solid state signals at δ = 98.7, 8.9 and −301.2 ppm, besides two 29Si signals at δ = 7.4 and 6.6 ppm for the SiMe3 groups (see Fig. 4). The solid-state 29Si chemical shifts differ slightly from the solution state shifts, most likely due to ring current effects of the aromatic ligands in the solid, which are averaged out by motion in solution. In the solid-state, the 29Si chemical shift anisotropy (CSA)29 supported by DFT calculations can be used for signal assignment. The 29Si CSAs were determined from analysis of the spinning sidebands at low spinning speed (4.0 kHz MAS, see Fig. 4b). The 29Si signals of the SiMe3 groups at δ = 6.6 and 7.4 ppm show the smallest CSA (δaniso = 20 ± 10 ppm) as expected and in good agreement with DFT calculations (see Table S9†). The two unsubstituted silicon atoms (Si2/4) correspond to the 29Si resonance at δ = −301 ppm. The low 29Si CSA of δaniso = 95 ± 10 ppm with ησ = 0.25 for these two atoms suggests only a weak coordination between these silicon atoms, since the distance (2.636(6) Å) is significantly longer than a Si–Si single bond (2.34 Å). The 29Si signals of Si1/3 at δ = 99 ppm and Si5/6 at δ = 9 ppm show similar 29Si CSA values (δaniso = −230 ± 20 ppm and −226 ± 20 ppm, respectively) in accordance with DFT calculations (δaniso = −284 ppm and −297 ppm). Here, Si1/3 have ησ = 0.1 whereas Si5/Si6 show an axial symmetric tensor with ησ = 0. These differences in 29Si CSA parameters can be understood by comparing the different bonding situations at Si5/6 in contrast to Si1/Si3.
The bond lengths involving Si5/Si6 are all very similar whereas those of Si1/Si3 include the two short bonds (2.292(6) and 2.281(5) Å) to the adjacent Si2/Si4 atoms and the longer bonds to Si4/Si2 (2.532(6) and 2.502(6) Å), respectively. This results in a non-axial 29Si CSA tensor for Si1/Si3. The slight discrepancy between experiment and calculations of 29Si δaniso values for Si1–Si6 may indicate that some residual local mobility is present even in the solid state.
The experimental UV Vis spectrum of 2 at room temperature shows a shoulder at 361 nm and at 314 nm. These absorptions can be assigned to a HOMO−1 → LUMO transition and a HOMO → LUMO+1 transition, respectively, according to TDDFT calculation with ORCA on the optimized structure (2-A) of Si6{N(SiMe3)Dipp}4, using the CAM-B3LYP functional, a double zeta basis set (def2-SVP) and the CPCM implicit solvent model for toluene (page S28).† The HOMO–LUMO transition at 392 nm is very weak and cannot be identified in the experimental spectrum.
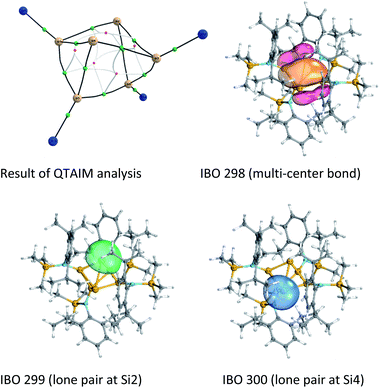
Quantum theory of atoms in molecules (QTAIM)30 analysis was performed to elucidate more precisely the bonding situation of 2. According to this analysis bond critical points, represented as green circles in Fig. 5 (and Fig. S3†), exist between all bonds except for that connecting the two ligand-free silicon atoms (Si2 and Si4). This was also observed for the benzpolarene-type cluster D and the tricyclic hexasilabenzene isomer C.31
Additionally, Mayer bond orders32 (Table S3†) were determined that indicate highest bond orders for the Si1–Si5, Si3–Si6 bonds (0.90) from the butterfly-shaped ring to the Si5–Si6-dumbbell and for the two short bonds Si1–Si2 and Si3–Si4 in the upper butterfly-shaped ring (0.86). The bond order of the transannular distance Si2⋯Si4 (0.46) is only half as much and does not differ greatly from that of the long bonds Si2–Si3 and Si1–Si4 (0.52) in the four-membered butterfly ring composed of Si1–Si2–Si3–Si4.
The Si–N bonds have bond orders of (1.11 and 1.02). This demonstrates that the amine substituents are very weak π-donors and strong σ-acceptors. Additionally, the molecular orbitals do not include Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N π-bonds (see Fig. S4†). Together with the trigonal planar configuration at the N atoms, stabilized by the large substituents, this suggests, that to some degree negative hyperconjugation between the p-type lone pair at each N atom and the antibonding σ*-orbitals of the Si–Si bonds occurs.
N π-bonds (see Fig. S4†). Together with the trigonal planar configuration at the N atoms, stabilized by the large substituents, this suggests, that to some degree negative hyperconjugation between the p-type lone pair at each N atom and the antibonding σ*-orbitals of the Si–Si bonds occurs.
An intrinsic bond orbital (IBO)33 analysis of 2 was conducted with a double zeta basis set (def2-SVP) and gave IBOs in the Si6 core as shown in Fig. 5 and S5.† This analysis reveals 10 IBOs relevant for the Si6 cluster core. This corresponds to 20 cluster electrons, which is in line with the four amido-substituted silicon atoms contributing each three electrons to the cluster, and the two ligand-free silicon atoms that each provide four electrons. In particular, we note seven single σ-bonds (IBO 291–297), that include all Si–Si bonds except the Si1–Si4 and Si2–Si3 bonds and the transannular distance between Si2 and Si4. Furthermore, lone pairs on Si2 and Si4 (IBO 299 and 300) and a multi-center bond at the butterfly-shaped ring (IBO 298) turned out from this analysis. The multi-center bond explains the observed partial double bond character of the Si1–Si2/Si3–Si4 bonds and the partial σ-bonds between Si1–Si4, Si2–Si3 and Si2⋯Si4 (dashed lines in Fig. 1). According to these findings, the molecular structure 2 carries a certain contribution of the resonance structures represented in Fig. 6. These resonance structures indicate somewhat the analogy of 2 to the butalene-type isomer C6H4 which was recently reinvestigated.34
The three signals in the 29Si NMR spectrum in THF-d8 of the minor component 2-C at 51.3, −5.1 and −294.0 ppm indicate that this component is also C2 symmetric. Two of the signals (at −5.1 and at −294.0 ppm) are very close to the major component. This provides strong evidence, that the minor component is very similar to the major component. The occurrence of a major and a minor isomer with different chemical shifts in solution was recently also observed for anionic mixed silicon germanium benzpolarene-type clusters.35 Lineshape analysis revealed a non-mutual exchange between the two components and a Gibbs free energy of activation of 57.2 kJ mol−1 (13.7 kcal mol−1) at 300 K for the equilibrium between the major and the minor isomer (see page S42 and S43†).
With this information we generated conformational isomers of 2 by rotating the ligands successively around the SiCluster–N single bonds in steps of 60° and optimizing the structures with DFT calculations. From the generated set of conformers, only the four most stable are reported here (Scheme 5).
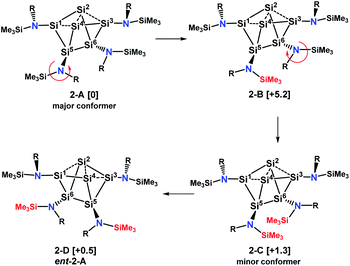 | ||
| Scheme 5 Major and minor conformer and enantiomer of 2 in solution. Values in brackets are solvent corrected relative free energies ΔG(298)solv. | ||
Conformer 2-B results from counterclockwise rotation around the Si5–N bond. Conformer 2-C is obtained when the Si6–N bond from 2-B is rotated clockwise. The enantiomer of 2-A, which is conformer 2-D, can be generated by a twist within the four-membered ring Si2–Si4–Si5–Si6 of the Si6 scaffold in conformer 2-C (Scheme S1†). This is accompanied by a slight movement of the amine substituents attached to the butterfly-shaped ring. We note that both enantiomers 2-A and 2-D are present in the crystal structure obtained from single crystals grown from hexane. Conformers in which the substituents of Si1 and Si3 were rotated around the Sicluster–N bond were found to have significantly higher (>7 kcal mol−1) relative free energies and are not discussed. The relative free energies, obtained with PW6B95-D3 and DLPNO-CCSD(T) are given in Table S1.† Calculations of chemical shifts for these isomers revealed that those of the C2-symmetric isomer 2-C (57.5, −15.9, −273.4 ppm, Table S4†) display very good agreement with those measured for the minor component in THF-d8 at 210 K (51.3, −5.1 and −294.0 ppm).
In order to get an estimate for the (electronic) potential barriers of each step and to find out whether these transformations proceed stepwise or concertedly, three optimizations of the minimum energy path between conformers 2-A, 2-B, 2-C and 2-D (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ent-2-A) were conducted. The growing string method (GSM)36 was applied to construct these paths from 2-A to 2-D. The three minimum energy paths were connected to a complete path as shown in Fig. 7.
ent-2-A) were conducted. The growing string method (GSM)36 was applied to construct these paths from 2-A to 2-D. The three minimum energy paths were connected to a complete path as shown in Fig. 7.
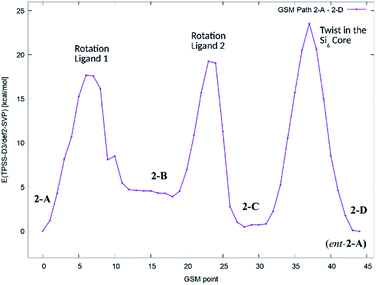 | ||
| Fig. 7 Potential energy diagram (TPSS-D3/def2-SVP) of the minimum energy path for the stepwise transformation of 2-A to the minority conformer 2-C and the formation of the enantiomer of 2-A (2-D). | ||
We found, that the barriers for ligand rotation both lie well below 20 kcal mol−1, which is in accord with the result obtained from lineshape analysis. The subsequent twist in the Si2–Si4–Si5–Si6 ring has to overcome an (electronic) energy barrier of approximately 24 kcal mol−1. Attempts to optimize reaction paths of the synchronous (symmetric) rotation of two ligands (2-A → 2-C) and eventually including the twist in the Si2–Si4–Si5–Si6 ring (2-A → 2-D) results in paths with significantly higher potential energy barriers.
Additionally, molecular dynamics (MD) simulations with the ReaxFF force field37 were performed for the four DFT-optimized structures 2-A, 2-B, 2-C and 2-D. In order to qualitatively assess the formation mechanism of the enantiomer 2-D starting from structure 2-A, a targeted MD simulation38 was performed slowly pulling the system from 2-A to 2-D over a duration of 2 ns. A video visualizing this process is available via the ESI link.†
In this simulation, the necessary structural changes, i.e. rotation of a first ligand, rotation of a second ligand, and distortion within the Si6 cluster core, occur sequentially one after another. This suggests that the transformation 2-A → 2-D takes place by a stepwise process via structures 2-B and 2-C, supported by the clearly visible minima in the free energy profile (Fig. S7†). The barrier heights for the individual processes (Table S5 and Fig. S8†) are well below ΔF‡ = 12 kcal mol−1. They are thus easily accessible at T = 300 K. In particular, if both enantiomers, 2-A and 2-D, are present, two competing pathways, 2-A → 2-C and 2-D → 2-C, are possible.
The reactivity of 2 with ethylene, CO2, CCl4, H2O, MeOH, I2 and NHCMe4 (2,3,4,5-tetramethyl-imidazolium-2-ylidene) was investigated in NMR scale reactions. But, these reagents either show no reactivity with 2 (ethylene, CO2, MeOH) or react very unselectively (CCl4, H2O, I2, NHCMe4) which hinders characterization of the products based only on NMR spectroscopy and the growths of single crystals in solution.
Conclusions
In summary, we synthesized a highly unsaturated Si6 cluster with only four amine substituents and two ligand-free silicon atoms that exhibits an unusual equilibrium in solution between a major and a minor conformer. Variable temperature and 2D-correlated NMR experiments, DFT calculations and molecular dynamics simulations were performed to collect information on this process. These calculations suggest, that the equilibration of the two conformers detected in solution by NMR spectroscopy of 2 (2-A and 2-C) may occur at room temperature by two subsequent ligand rotations or by a twist in the Si6 core. Analysis of the bonding situation in the Si6 cluster using the QTAIM method revealed no bond critical point between the ligand-free silicon atoms. Generating intrinsic bond orbitals (IBOs) for the Si6 cluster core demonstrates lone pair type character at the ligand free silicon atoms and a multi-center bond involving all silicon atoms in the butterfly-shaped ring. In future experiments, the potential of amine substituents for the stabilization of other highly unsaturated silicon clusters will be investigated.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work received financial support from the Fonds of the Chemical Industry (Liebig-Fellowship to F. L.) and the DFG (SFB 858). We thank Prof. W. Uhl for his generous support.Notes and references
- (a) A. Sekiguchi, T. Yatabe, C. Kabuto and H. Sakurai, J. Am. Chem. Soc., 1993, 115, 5853 CrossRef CAS; (b) K. Abersfelder, A. Russell, H. S. Rzepa, A. J. P. White, P. R. Haycock and D. Scheschkewitz, J. Am. Chem. Soc., 2012, 134, 16008 CrossRef CAS PubMed.
- (a) A. Tsurusaki, C. Iizuka, K. Otsuka and S. Kyushin, J. Am. Chem. Soc., 2013, 135, 16340 CrossRef CAS PubMed; (b) S. Ishida, K. Otsuka, Y. Toma and S. Kyushin, Angew. Chem., Int. Ed., 2013, 52, 2507 CrossRef CAS PubMed.
- K. Abersfelder, A. J. P. White, H. S. Rzepa and D. Scheschkewitz, Science, 2011, 327, 564 CrossRef PubMed.
- K. Abersfelder, A. J. P. White, R. J. F. Berger, H. S. Rzepa and D. Scheschkewitz, Angew. Chem., Int. Ed., 2011, 50, 7936 CrossRef CAS PubMed.
- M. Moteki, S. Maeda and K. Ohno, Organometallics, 2009, 28, 2218 CrossRef CAS.
- Y. Heider, N. E. Poitiers, P. Willmes, K. I. Leszczyńska, V. Huch and D. Scheschkewitz, Chem. Sci., 2019, 10, 4523 RSC.
- T. Iwamoto and S. Ishida, Chem. Lett., 2014, 43, 164 CrossRef CAS.
- Y. Heider and D. Scheschkewitz, Dalton Trans., 2018, 47, 7104 RSC.
- (a) J. M. Buriak, Chem. Rev., 2002, 102, 1271 CrossRef CAS PubMed; (b) N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610 CrossRef CAS PubMed; (c) P. Munnik, P. E de Jongh and K. P. de Jong, Chem. Rev., 2015, 115, 6687 CrossRef CAS PubMed.
- (a) A. Schnepf, Chem. Soc. Rev., 2007, 36, 745 RSC; (b) A. Schnepf, Angew. Chem., Int. Ed., 2004, 43, 664 CrossRef CAS PubMed; (c) A. Schnepf, New J. Chem., 2010, 34, 2079 RSC.
- (a) C. Hollenstein, Plasma Phys. Contr. Fusion, 2000, 42, R93–R104 CrossRef CAS; (b) F. Zhang, K. Sautter, A. M. Larsen, D. A. Findley, R. C. Davis, H. Samha and M. R. Linford, Langmuir, 2010, 26, 14648 CrossRef CAS PubMed.
- D. Scheschkewitz, Angew. Chem., Int. Ed., 2005, 44, 2954 CrossRef CAS PubMed.
- D. Nied, R. Köppe, W. Klopper, H. Schnöckel and F. Breher, J. Am. Chem. Soc., 2010, 132, 10264 CrossRef CAS PubMed.
- K. Leszczyńska, V. Huch, C. Präsang, J. Schwabedissen, R. J. F. Berger and D. Scheschkewitz, Angew. Chem., Int. Ed., 2019, 58, 5124 CrossRef PubMed.
- N. Akasaka, S. Ishida and T. Iwamoto, Inorganics, 2018, 6, 107 CrossRef CAS.
- (a) N. Wiberg, C. M. M. Finger and K. Polborn, Angew. Chem., Int. Ed., 1993, 32, 1054 CrossRef; (b) N. Wiberg, C. M. M. Finger, H. Auer and K. Polborn, J. Organomet. Chem., 1996, 521, 377 CrossRef CAS.
- T. Iwamoto, N. Akasaka and S. Ishida, Nat. Commun., 2014, 5, 5353 CrossRef CAS PubMed.
- P. Willmes, K. Leszczyńska, Y. Heider, K. Abersfelder, M. Zimmer, V. Huch and D. Scheschkewitz, Angew. Chem., Int. Ed., 2016, 55, 2907 CrossRef CAS PubMed.
- Y. Heider, P. Willmes, V. Huch, M. Zimmer and D. Scheschkewitz, J. Am. Chem. Soc., 2019, 141, 19498 CrossRef CAS PubMed.
- P. M. Warner and G. B. Jones, J. Am. Chem. Soc., 2001, 123, 10322 CrossRef CAS PubMed.
- M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302 CrossRef PubMed.
- (a) A. J. Adamczyk and L. J. Broadbelt, J. Phys. Chem. A, 2011, 115, 8969 CrossRef CAS PubMed; (b) T. Miyazaki, T. Uda, I. Stich and K. Terakura, Chem. Phys. Lett., 1996, 261, 346 CrossRef CAS.
- M. Lappert, A. Protchenko, P. Power, and A. Seeber, Metal Amide Chemistry, Wiley-VCH, 2008 Search PubMed.
- M. Brynda, R. Herber, P. B. Hitchcock, M. F. Lappert, I. Nowik, P. P. Power, A. V. Protchenko, A. Růžička and J. Steiner, Angew. Chem., Int. Ed., 2006, 45, 4333 CrossRef CAS PubMed.
- J. Keuter, K. Schwedtmann, A. Hepp, K. Bergander, O. Janka, C. Doerenkamp, H. Eckert, C. Mück-Lichtenfeld and F. Lips, Angew. Chem., Int. Ed., 2017, 56, 13866 CrossRef CAS PubMed.
- (a) P. P. Power, Chem. Rev., 1999, 99, 3463 CrossRef CAS PubMed; (b) A. Sekiguchi and V. Y. Lee, Chem. Rev., 2003, 103, 1429 CrossRef CAS PubMed.
- M. Kaftory, M. Kapon, and M. Botoshansky, The Chemistry of Organic Silicon Compounds, ed. Z. Rappoport and Y. Apeloig, Wiley, Chichester, 1998, vol. 2 Search PubMed.
- V. Y. Lee, Y. Ito, O. A. Gapurenko, A. Sekiguchi, V. I. Minkin, R. M. Minyaev and H. Gornitzka, Angew. Chem., Int. Ed., 2015, 54, 5654 CrossRef CAS PubMed.
- The CSA parameters are defined as
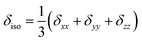 , δσ = δiso − δzz, ησ = (δxx + δyy)/δσ, with |δzz − δiso| ≥ |δxx − δiso| ≥ |δyy − δiso|. The asymmetry parameter ησ describes the symmetry of the CSA tensor. The CSA tensor is axial symmetric if ησ = 0 and deviates from axial symmetry for 0 < η < 1..
, δσ = δiso − δzz, ησ = (δxx + δyy)/δσ, with |δzz − δiso| ≥ |δxx − δiso| ≥ |δyy − δiso|. The asymmetry parameter ησ describes the symmetry of the CSA tensor. The CSA tensor is axial symmetric if ησ = 0 and deviates from axial symmetry for 0 < η < 1.. - R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- D. Kratzert, D. Leusser, J. J. Holstein, B. Dittrich, K. Abersfelder, D. Scheschkewitz and D. Stalke, Angew. Chem., Int. Ed., 2013, 52, 4478 CrossRef CAS PubMed.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270 CrossRef CAS.
- (a) G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834 CrossRef CAS PubMed; (b) G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518 CrossRef CAS PubMed.
- D. L. Cooper, P. B. Karadakov and B. J. Duke, J. Phys. Chem. A, 2015, 119, 2169 CrossRef CAS PubMed.
- L. Klemmer, V. Huch, A. Jana and D. Scheschkewitz, Chem. Commun., 2019, 55, 10100 RSC.
- P. M. Zimmerman, J. Chem. Phys., 2013, 138, 184102 CrossRef PubMed.
- (a) K. Chenoweth, A. C. T. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040 CrossRef CAS PubMed; (b) H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel Comput., 2012, 38, 245 CrossRef; (c) A. D. Kulkarni, D. G. Truhlar, S. Goverapet Srinivasan, A. C. T. van Duin, P. Norman and T. E. Schwartzentruber, J. Phys. Chem. C, 2013, 117, 258 CrossRef CAS; (d) G. Barcaro, S. Monti, L. Sementa and V. Carravetta, J. Chem. Theory Comput., 2017, 13, 3854 CrossRef CAS PubMed.
- (a) J. Schlitter, W. Swegat and T. Mülders, J. Mol. Model., 2001, 7, 171 CrossRef CAS; (b) J. Schlitter and M. Klähn, Mol. Phys., 2003, 101, 3439 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Further experimental and computational details and the video are available. CCDC 1989146 contains the crystallographic information for 2. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01427c |
| This journal is © The Royal Society of Chemistry 2020 |