Open Access Article
Open Access ArticleComparison of tetravalent cerium and terbium ions in a conserved, homoleptic imidophosphorane ligand field†
Natalie T.
Rice‡
a,
Ivan A.
Popov‡
b,
Dominic R.
Russo
a,
Thaige P.
Gompa
a,
Arun
Ramanathan
a,
John
Bacsa
a,
Enrique R.
Batista
 *b,
Ping
Yang
*b,
Ping
Yang
 *b and
Henry S.
La Pierre
*b and
Henry S.
La Pierre
 *ac
*ac
aSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: hsl@gatech.edu
bTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: pyang@lanl.gov; erb@lanl.gov
cNuclear and Radiological Engineering and Medical Physics Program, School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
First published on 18th May 2020
Abstract
A redox pair of Ce4+ and Ce3+ complexes has been prepared that is stabilized by the [(NP(1,2-bis-tBu-diamidoethane)(NEt2))]1− ligand. Since these complexes are isostructural to the recently reported isovalent terbium analogs, a detailed structural and spectroscopic comparative analysis was pursued via Voronoi–Dirichlet polyhedra analysis, UV-vis-NIR, L3-edge X-ray absorption near edge spectroscopy (XANES), cyclic voltammetry, and natural transitions orbital (NTO) analysis and natural bond orbital (NBO) analysis. The electrochemical studies confirm previous theoretical studies of the redox properties of the related complex [K][Ce3+(NP(pip)3)4] (pip = piperidinyl), 1-Ce(PN). Complex 1-Ce(PN*) presents the most negative Epc of −2.88 V vs. Fc/Fc+ in THF of any cerium complex studied electrochemically. Likewise 1-Tb(PN*) has the most negative Epc for electrochemically interrogated terbium complexes at −1.79 V vs. Fc/Fc+ in THF. Complexes 1-Ce(PN*) and 2-Ce(PN*) were also studied by L3-edge X-ray absorption near edges spectroscopy (XANES) and a comparison to previously reported spectra for 1-Tb(PN*), 2-Tb(PN*), 1-Ce(PN), and, [Ce4+(NP(pip)3)4], 2-Ce(PN), demonstrates similar nf values for all the tetravalent lanthanide complexes. According to the natural bond orbital analysis, a greater covalent character of the M–L bonds is found in 2-Ce(PN*) than in 1-Ce(PN*), in agreement with the shorter Ce–N bonds in the tetravalent counterpart. The greater contribution of Ce orbitals in the Ce–N bonding and, specifically, the higher participation of 4f electrons accounts for the stronger covalent interactions in 2-Ce(PN*) as compared to 2-Tb(PN*).
Introduction
In recent years the molecular redox chemistry of the lanthanides has expanded rapidly – in particular the isolation of divalent lanthanides.1–4 Typically, lanthanide ions in solution exist in the trivalent oxidation state with a few exceptions (the traditional divalent ions, Sm, Eu, Yb, and one well-established tetravalent ion, Ce).5–7 Historically, this limited number of accessible oxidation states in the lanthanides has been attributed to limited influence of the ligand field on the valence electronic structure and the significant thermodynamic driving force necessary to reduce or oxidize trivalent lanthanide complexes.Lappert and Evans have demonstrated that non-traditional divalent lanthanides can be stabilized in tris-Cp ligand frameworks as anions with 4fn5d1 valence electron configurations.1–3 A significant finding in the analysis of these complexes and their trivalent precursors is that there is little to no change in the metal–Cp centroid distances (∼0.03 Å) on reduction from the neutral precursor to the divalent anion. This feature has been attributed to the population of the 5dz2 orbital on reduction.2,8 In contrast, the traditional divalent ions with a 4fn+1 electronic configuration in the reduced state experience a more significant change in this metric (up to ∼0.2 Å).2,9,10 This large change is also reflected in the difference in the ionic radii of the Sm2+/3+, Eu2+/3+, and Yb2+/3+ redox pairs.11 This expansion on reduction suggests that for systems in which the redox event results in a change in the f orbital population significant structural rearrangement can be anticipated.12 These changes are much larger than those encountered in the d-block, for example the difference in the ionic radii for the Fe2+/3+ redox pair (low-spin) is 0.06 Å.11 For the isolation of tetravalent lanthanides, these changes in ionic radii are particularly stark (Ce3+/4+, 0.16 Å; Tb3+/4+, 0.14 Å).11
In conjunction with structural changes encountered during redox events, the energy and radial extent of the f and d orbitals varies across the lanthanide series. In particular for oxidation of trivalent lanthanides to tetravalent lanthanides, this variation of the f and d orbital energy and radial extent is crucial since it governs a significant onset of covalent bonding.13,14 These two ligand design parameters – accommodating large structural rearrangements and capitalizing on covalency in tetravalent ions – are critical for expanding the library of known molecular tetravalent lanthanide complexes. We, and Mazzanti and co-workers, have recently reported the first tetravalent terbium complexes employing complementary design processes.15–17 Mazzanti and co-workers have recently extended this chemistry to tetravalent praseodymium.18 Our terbium system is prepared by the oxidation of a trivalent precursor, [K][Tb3+(NP(1,2-bis-tBu-diamidoethane)(NEt2))4], 1-Tb(PN*), to give a four coordinate complex, [Tb4+(NP(1,2-bis-tBu-diamidoethane)(NEt2))4], 2-Tb(PN*).
Determining the chemical and physical basis for the stability of molecular lanthanide complexes with unusual oxidation states is critical for enabling the development of technical applications such as topological insulators, magnetocaloric refrigerants, and single molecular magnets or qubits for quantum information science (QIS).19–27 These QIS applications stem from the lanthanides' inherent anisotropy and magnetic properties through the contribution of f, d, and s character. These magnetic contributions are influenced through both modulation of the ligand field about the lanthanide ion as well as the identity and oxidation state of the lanthanide ion itself. Recently, non-traditional divalent lanthanides, such as Tb, Dy, and La, have been shown to exhibit promising magnetic behaviour for QIS technology.21,22 Thus, expanding accessible oxidation states is important for developing new design principles for emerging magnetic and quantum technologies. Recent gas-phase work suggests that the range of accessible oxidation states in the condensed phases may extend beyond tetravalent ions to pentavalent lanthanide ions as well.28–30
Herein, we report the synthesis and characterization of the isotypic tetravalent cerium equivalent of 2-Tb(PN*), [Ce4+(NP(1,2-bis-tBu-diamidoethane)(NEt2))4], 2-Ce(PN*), and its trivalent precursor, [K][Ce3+(NP(1,2-bis-tBu-diamidoethane)(NEt2))4], 1-Ce(PN*), (Scheme 1), and provide a systematic structural, spectroscopic, and electrochemical comparison of these complexes to understand ligand field's effects across the series on the stability and electronic structure of tetravalent lanthanide ions. The nearly monotonic contraction of ionic size across the lanthanide series for a given oxidation state leads to few examples where a given structural type is held across the series. However, this system, with tetravalent cerium and terbium, is one of only two ligand types that have the same ligand sphere and coordination environment for two tetravalent lanthanide ions. The only variable in the system is the metal identity, thus is a key comparison to disentangle competing phenomena that drive the chemical and physical properties of tetravalent lanthanides.
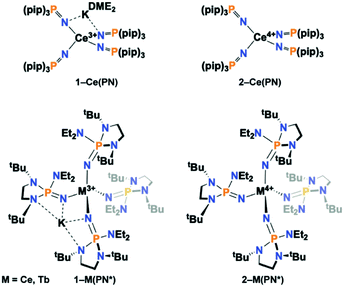 | ||
| Scheme 1 Depiction of (top) 1-Ce(PN) and 2-Ce(PN) and (bottom) 1-Ce(PN*), 2-Ce(PN*), 1-Tb(PN*), 2-Tb(PN*). | ||
Results and discussion
Synthesis and structural characterization
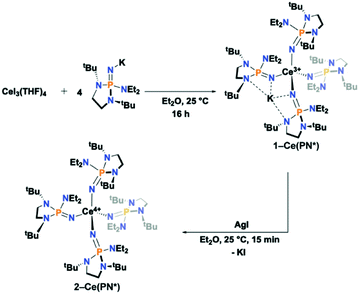
The anionic Ce3+ tetrahomoleptic complex featuring an inner sphere potassium cation, 1-Ce(PN*), was prepared directly through a salt metathesis reaction of four equivalents of K[(NP(1,2-bis-tBu-diamidoethane)(NEt2))] with CeI3(THF)4 in diethyl ether in 62% yield (Scheme 2). Yellow crystals of 1-Ce(PN*) were grown from cold hexanes for single-crystal X-ray diffraction analysis (SC-XRD) but may also be isolated from diethyl ether. The complex 1-Ce(PN*) was oxidized in diethyl ether with AgI to afford the neutral tetrahomoleptic Ce4+ complex, 2-Ce(PN*) as red-orange crystals in 77% yield. The solution and solid-state structural features of these compounds were established by 1H, 31P and 13C NMR and SC-XRD.The molecular structures of the reported compounds as determined by SC-XRD are shown in Fig. S8 and S9.† Complexes 1-Ce(PN*) and 2-Ce(PN*) are isostructural to 1-Tb(PN*) and 2-Tb(PN*), reported previously.15 Complex 1-Ce(PN*) crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and is four-coordinate featuring an inner sphere potassium cation. The potassium ion is four-coordinate, bound by two of the ligands. The compound is pseudotetrahedral with N–Ce–N bond angles varying from 92.00(9) to 114.52(9)° and averaging 109.3(1)°. The potassium capped Ce–N bond lengths are 2.377(2) Å on average while the terminal ligands have Ce–N bond lengths of 2.313(3) Å.
space group and is four-coordinate featuring an inner sphere potassium cation. The potassium ion is four-coordinate, bound by two of the ligands. The compound is pseudotetrahedral with N–Ce–N bond angles varying from 92.00(9) to 114.52(9)° and averaging 109.3(1)°. The potassium capped Ce–N bond lengths are 2.377(2) Å on average while the terminal ligands have Ce–N bond lengths of 2.313(3) Å.
For the previously reported Ce3+ homoleptic imidophosphorane compound, [K][Ce3+(NP(pip)3)4] (1-Ce(PN)), the bond lengths were 2.37(1) Å and 2.31(1) Å for the potassium capped and terminal ligands, respectively.31 The Ce–N–P bond angles in 1-Ce(PN*) are 168.2(2)° on average for both the potassium capped ligands and the terminal ligands. There is no difference on average in deflection of the angle for the terminal or potassium bound ligands in 1-Ce(PN*). This structural feature is in contrast to that observed in 1-Ce(PN) that had a Ce–N–P bond angle of 141.4(4)° for the potassium capped ligands while terminal ligand angle was 174.1(4)°. The P–Nimide bond lengths of 1-Ce(PN*) are 1.531(2) Å on average for both the capped and terminal ligands, essentially equivalent to that of 1-Ce(PN) within error of the measurement (1.529(6) and 1.528(7) Å for the capped and terminal ligands, respectively).
Complex 2-Ce(PN*) crystallizes in the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) space group. The Ce–N bond lengths shorten on oxidation by about 0.14 Å and 0.08 Å for the capped and terminal ligands, respectively, to 2.237(2) Å in comparison to 1-Ce(PN*), consistent with a decrease in the ionic radius from Ce3+ to Ce4+ (0.14 Å).11 As in the analysis of the terbium analogs, this contraction of the M–N distance on oxidation is indicative of a metal-centred oxidation. The Ce–N bond lengths are similar to those of the previously reported [Ce4+(NP(pip)3)4] (2-Ce(PN)), whose Ce–N bond lengths averaged 2.20(3) Å.31
space group. The Ce–N bond lengths shorten on oxidation by about 0.14 Å and 0.08 Å for the capped and terminal ligands, respectively, to 2.237(2) Å in comparison to 1-Ce(PN*), consistent with a decrease in the ionic radius from Ce3+ to Ce4+ (0.14 Å).11 As in the analysis of the terbium analogs, this contraction of the M–N distance on oxidation is indicative of a metal-centred oxidation. The Ce–N bond lengths are similar to those of the previously reported [Ce4+(NP(pip)3)4] (2-Ce(PN)), whose Ce–N bond lengths averaged 2.20(3) Å.31
The degree of structural rearrangement during oxidation is reflected in changes in the M–N–P angles for the trivalent and tetravalent complexes. The Ce–N–P bond angles in 2-Ce(PN*) are 163.02(11)°, about 5° smaller than in 1-Ce(PN*). The equivalent changes in 2-Ce(PN) are ∼18.9° increase and 13.8° decrease from the capped and terminal ligands, respectively in 1-Ce(PN). In the terbium complexes a 3.5° decrease in the Tb–N–P angle from 1-Tb(PN*) to 2-Tb(PN*) is observed on average.15 This indicates that for the larger cerium ions there is more structural flexibility during the oxidation. The relevant bond lengths and angles for 1-Ce(PN*), 2-Ce(PN*), 1-Tb(PN*), 2-Tb(PN*), 1-Ce(PN), and 2-Ce(PN) are summarized in Table 1.
| Metric | Compound | |||||
|---|---|---|---|---|---|---|
| 1-Ce(PN*) | 2-Ce(PN*) | 1-Ce(PN) | 2-Ce(PN) | 1-Tb(PN*) | 2-Tb(PN*) | |
| Avg. M–N | K+ capped: 2.377(2), terminal: 2.313(3) | 2.237(1) | K+ capped: 2.37(1) terminal: 2.31(1) | 2.20(3) | K+ capped: 2.264(1) terminal: 2.2307(11) | 2.106(3) |
| Avg. Nimido–P | K+ capped: 1.531(2), terminal: 1.531(2) | 1.557(2) | K+ capped: 1.529(6) terminal: 1.528(7) | 1.47(3) | K+ capped: 1.532(1) terminal: 1.528(1) | 1.555(3) |
| Avg. M–N–P | K+ capped: 168.2(2), terminal: 168.2(2) | 163.0(1) | K+ capped: 141.4(4) terminal: 174.1(4) | 160.28(15) | K+ capped: 167.67(8) terminal: 168.78(8) | 164.7(4) |
| Avg. N–M–N | 109.3(1) | 109.5 | 109.4(3) | 109.4(6) | 109.4(6) | 109.5(9) |
Solution spectroscopic characterization of 1-Ce(PN*) and 2-Ce(PN*) agrees with the structures determined in the solid-state. The high symmetry of the complexes in solution is clearly seen in the 31P{1H} NMR spectra. For 2-Ce(PN*), a single 31P{1H} NMR shift at −24.89 ppm is observed as expected for the tetrahomoleptic compound. For 1-Ce(PN*), a single 31P{1H} NMR shift is observed at 108.03 ppm instead of the expected two shifts for the potassium bound and terminal ligands. However, this solution behaviour has been shown to occur previously for 1-Ce(PN) and may be attributable to a low barrier to intramolecular potassium exchange within the complex.31
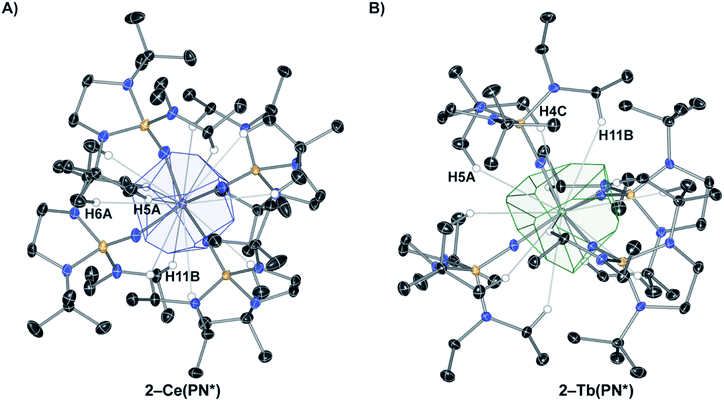
Comparative Voronoi–Dirichlet polyhedral analysis of 2-Ce(PN*) and 2-Tb(PN*)
In order to understand the differences in steric protection provided by the ligand upon changing metal size from an ionic radius of 0.87 Å in Ce4+ to 0.76 Å in Tb4+,11 a Voronoi–Dirichlet Polyhedra (VDP) analysis of 2-Ce(PN*) and 2-Tb(PN*) was undertaken.32,33 Historically, two approaches have been commonly employed to quantify the steric profile of coordinated ligands. The ligand cone angle is principally defined for symmetric ligands in order to make comparisons at a fixed metal and oxidation state.34 While alternative methods have been devised for the comparison of asymmetric ligands, these do not directly quantify changes in steric protection when a ligand is held constant and a metal identity is varied. Buried volume analysis has a different approach, describing the steric profile of ligand by the percent protected volume of a sphere with the ligand at a fixed distance (either 2.00 Å or 2.28 Å) from the metal.35Voronoi–Dirichlet analysis provides a method for understanding the difference in the ligand shielding of the metal ion as a function of metal identity. In this method, the volume of the metal atom is defined by constructing a Voronoi–Dirichlet polyhedron from its direct neighbours. For each of these neighbours, the percentage contributions to the VD polyhedron (for every M–X neighbour) are a percent value for the covering of that polyhedron by individual constituent atoms in the ligand. This analysis of metal complexes allows for the determination of the coordination number (CN) of the metal using the number of faces to the VDP. Unlike the conventionally defined coordination number, this CN includes atoms further away than the four N atoms directly bonded to the metal center. This method is particularly advantageous as it provides a more precise characterization of metal ion-atom interactions in the crystal since the faces of the VD polyhedron can be related to the amount of valence density shared between interacting atoms. 32
The computational results for the Ce4+ and Tb4+ polyhedra and geometrical characteristics were computed using Dirichlet included in the structure topology program package TOPOS.36 The output of this analysis includes three CNs: these are the number of direct neighbours (the line passing through the contacting atoms crosses the corresponding VDP face), half-direct neighbours (the line crosses a VDP edge), and indirect neighbours (the line does not cross the face). The value of the solid angle corresponding to the face of a VDP is numerically equal to the segment of asphere with 4πr2 (r = Rsd). TOPOS computes the solid angles in percentage of the total solid angle of this sphere. In this approach, it is assumed that the contribution to the observed valence by the donor atoms is distributed among the N (N = coordination number of the VDP) M–L interactions, and is proportional to the values of solid angles, SAngs, corresponding to the faces. Therefore, the solid angle of the VDP can be interpreted as an analog of valence-electron density in space among interacting atoms.37
The coordination and VD polyhedra around 2-Ce(PN*) and 2-Tb(PN*) are depicted in Fig. 1. The four-coordinate complexes show nearly perfect Td symmetry in both the 2-Ce(PN*) and 2-Tb(PN*) structures (in consideration only of the 4 nitrogen donor atoms), with 2-Tb(PN*) being less distorted. Replacing the Ce4+ ion with the smaller Tb4+ ion results in a size decrease of the M–N bond lengths. This change is reflected in a decrease of about of 17% of the polyhedral volume. For 2-Ce(PN*), the number of VDP vertices is twelve and the volume of the Voronoi polyhedron is 15.743 Å3, while the VDP surface area, S, is 36.674 Å2 (Table S6†). The computational results for the 2-Tb(PN*) polyhedron and its geometric characteristics are given in Table S7.† The number of VDP vertices is also twelve reflecting the isotypic structures. The volume of the Voronoi polyhedron is smaller than the Ce complex at 13.769 Å3, with a VDP surface area of 36.618 Å2.
The computational results for the 2-Ce(PN*) show that the N atoms contribute 78% of the surface area of the VDP and the H atoms contribute 22%. VDP analysis assumes that the area of the faces is proportional to the number of electrons that the donor atom contributes to the Ce–L interaction. Since the oxidation state of the Ce atom is +4, the nitrogen atom contributes 3.125 electrons and the hydrogen atoms contribute 0.875 electrons to the Ce–L interaction. There are three different types of H atom contacts that contribute to the VDP in 2-Ce(PN*), shown in Fig. 1. H11B resides on the methylene group of the diethyl amide while H5A and H6A are from one t-butyl group of each ligand. These percentages represent the contribution of each donor–acceptor pair to the overall valence-density of the complex. This analysis highlights the importance of contacts outside of the four primary nitrogens to the overall stability of the structure. When compared to 2-Ce(PN*), The N atoms in 2-Tb(PN*) contribute to a larger degree, 84%, while the H atoms contribute to a lesser degree, only 16%. The nitrogen atom contributes 3.36 electrons and the hydrogen atoms 0.64 electrons to the Tb–L interaction. The same three H atoms of the ligand contribute to the VDP of 2-Tb(PN*), H11B, H5A, and H4C (Tb) = H6A (Ce). In the cerium complex, there is a greater contribution of the hydrogen atoms to the surface area of the VDP despite the longer M–N distance in comparison to the terbium complex. This inverse correlation between hydrogen contribution to the VDP and M–N distance reflects subtle changes in the ligand coordination to fit around the smaller tetravalent terbium ion. As a result, VDP analysis reveals how M–L interactions vary as ion size is changed and that these interactions are not directly correlated to the ion size and M–N distance.
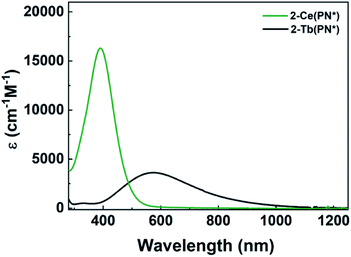
Electronic absorption spectra
The electronic absorption spectra of 1-Ce(PN*) and 2-Ce(PN*) are consistent with the expected oxidation states of Ce3+ and Ce4+, respectively, and are similar to those of 1-Ce(PN) and 2-Ce(PN).31 The UV-vis absorption spectrum of the yellow 1-Ce(PN*) in THF shows an absorption feature at 369 nm with an extinction coefficient of 883 cm−1 M−1, consistent with an f–d transition expected for the 4f1 ion (Fig. 2). The f–d transition for 1-Ce(PN) was very close in energy at 366 nm but with a lower molar absorptivity of 600 cm−1 M−1.31 In contrast, 1-Tb(PN*), a 4f8 ion, has no f–d or f–f transitions in the observable UV-vis-NIR window (∼1400–300 nm).The UV-vis absorption spectrum of the red-orange 2-Ce(PN*) is characterized by a broad absorption feature, red-shifted from that of 1-Ce(PN*), at 391 nm with an extinction coefficient of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1 in THF. This feature is consistent with a ligand to metal charge transfer (LMCT), as expected for the formally closed shell 4f0 system, and has a full-width at half maximum peak of 10.7 eV (116 nm) at 93 μM (Fig. 2). In contrast to 2-Tb(PN*), the absorption feature of 2-Ce(PN*) is much less broad (by 174 nm) and with a much larger extinction coefficient (four times larger). The extinction coefficient of 2-Ce(PN*) is on the same order of magnitude of that observed for 2-Ce(PN) at 11
000 cm−1 M−1 in THF. This feature is consistent with a ligand to metal charge transfer (LMCT), as expected for the formally closed shell 4f0 system, and has a full-width at half maximum peak of 10.7 eV (116 nm) at 93 μM (Fig. 2). In contrast to 2-Tb(PN*), the absorption feature of 2-Ce(PN*) is much less broad (by 174 nm) and with a much larger extinction coefficient (four times larger). The extinction coefficient of 2-Ce(PN*) is on the same order of magnitude of that observed for 2-Ce(PN) at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1 but at lower energy, 335 nm. In comparison to tetravalent terbium, 2-Tb(PN*), the higher energy LMCT for 2-Ce(PN*) is expected due to the higher energy f manifold in cerium.15 The decrease in the width of the absorption is due to the narrower energy region where the allowed transitions occur as reflected in the TD-DFT spectra (Fig. 5 and S21†).
000 cm−1 M−1 but at lower energy, 335 nm. In comparison to tetravalent terbium, 2-Tb(PN*), the higher energy LMCT for 2-Ce(PN*) is expected due to the higher energy f manifold in cerium.15 The decrease in the width of the absorption is due to the narrower energy region where the allowed transitions occur as reflected in the TD-DFT spectra (Fig. 5 and S21†).
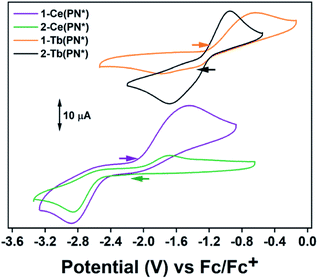
Electrochemistry
Electrochemical measurements were performed to understand the degree of stabilization of the tetravalent oxidation state in the Ce and Tb systems. The complex 2-Ce(PN*) has a reduction event at Epc = −2.86 V vs. Fc/Fc+ [−2.06 V vs. NHE] at 200 mV s−1 (Fig. 3 and S14†) (−2.88 V vs. Fc/Fc+ for 1-Ce(PN*); 2.5 mM analyte, 0.1 M [(nBu)4N][PF6] in THF for both experiments). This value is close (within 120 mV) to the calculated reduction potential for 2-Ce(PN) (−2.99 V vs./Fc/Fc+).31 This experiment not only lends confirmation to the previous theoretical and reactivity studies that demonstrate that a homoleptic imidophosphorane ligand sphere can push the Ce3+/4+ redox couple to negative values, these studies also confirm the most negative shift in redox potential from that of the free Ce ion observed electrochemically in any cerium coordination complex.38–40 The quasi-reversible oxidation event occurs at −1.44 V for 1-Ce(PN*) and at −1.63 V for 2-Ce(PN*)vs. Fc/Fc+ at 200 mV s−1. This difference could be the result of a cation binding effect due to presence of a potassium ion in 1-Ce(PN*) but not in 2-Ce(PN*). Future studies will seek to elucidate the cation dependence of the oxidation potential.The complex 2-Tb(PN*) has a reduction event at Epc = −1.68 V vs. Fc/Fc+ [−0.88 V vs. NHE] (3 mM analyte, 0.1 M[(nBu)4N] [PF6] in THF), Fig. 3 and S16.† Though not directly comparable, this reduction potential is drastically shifted from the Tb4+/3+ reduction potential in acidic solution, +3.1 V vs. NHE (1.0 M HClO4).7 The oxidation event for 2-Tb(PN*), Epa, occurs at −0.95 V vs. Fc/Fc+. For 1-Tb(PN*), however, at slow scan rates, between 25 and 75 mV s−1, a single reduction event is seen at −1.32 V vs. Fc/Fc+. Higher scan rates of 200–800 mV s−1 produce an additional reduction event at a more negative potential (−1.79 V at 200 mV s−1) (Fig. S15†) while a single oxidation event occurs across all scan rates and is at Epa = −0.64 V at 200 mV s−1, more positive than the Epa of 2-Tb(PN*), consistent with the CV analysis of 1-Ce(PN*) and 2-Ce(PN*). This difference in reduction potential at slow versus fast scan rates is likely due to the presence of the K+ ion in solution that produces a cation effect in the 1-Tb(PN*) system. In other words, in the presence of an inner sphere potassium cation, a competing chemical event (diffusion of K+ from the inner coordination sphere) is observed. In this model, slower scan rates provide enough time for diffusion of K+ from the ligand sphere producing the less negative reduction. Under faster scan rates, the diffusion of K+ from the complex is incomplete resulting in the observation of a more negative reduction potential due to association of the cation to the Tb4+ complex in solution. These observed reduction potentials are in line with the thermodynamic calculations on the related redox pair 1-Ce(PN) and 2-Ce(PN) that demonstrate a more negative reduction potential for the potassium adduct.31 The observed dependence of reduction potential on scan rate is divergent from 1-Ce(PN*) and may be related to the difference in the size of the trivalent lanthanide ion.
The only two other Tb4+ complexes were reported by Mazzanti and co-workers. The complex, [Tb4+(OSi(OtBu)3)3(κ2-OSi(OtBu))3], has an Epc = −0.70 V and Epa = 0.85 V vs. Fc/Fc+ in THF at 250 mV s−1 in 0.1 M [(nBu4)N][B(C6F5)4] (Table 2).16 The complex, [Tb4+(OSiPh3)4(MeCN)2],17 has an Epc = −0.99 V and Epa = 0.49 V vs. Fc/Fc+ in THF at 250 mV s−1 in 0.1 M [(nBu)4N][B(C6F5)4]. The imidophosphorane complex, 2-Tb(PN*), has a 980 mV more negative reduction potential than the tris-tert-butoxysiloxide complex, and a 690 mV more negative reduction potential than the tri-phenylsiloxide complex, and therefore a stronger thermodynamic preference for Tb4+. This dramatic shift in the Tb4+/3+ reduction potential in 2-Tb(PN*) and for the Ce4+/3+ reduction potential in 2-Ce(PN*) noticeably demonstrates that such significant modulation of other lanthanide redox couples should be accessible from a thermodynamic perspective.18
Ln L3-edge X-ray absorption near edge spectroscopy (XANES)
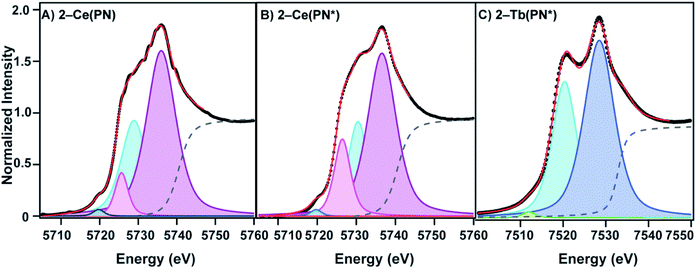
The L3-edge XANES spectra of 1-Ce(PN*) and 2-Ce(PN*) were acquired at SSRL beamline 11-2 in order to examine oxidation state of the cerium complexes and to compare the spectral features of the tetravalent complex to its isostructural tetravalent terbium analog, 2-Tb(PN*), and the tetravalent cerium analog, 2-Ce(PN). The comparative analyses are undertaken to understand ligand effects on the electric dipole allowed transitions from Ln 2p orbitals to unoccupied states with Ln 5d character (i.e. 2p64fn5d0 → 2p54fn5d1, where n corresponds to the number of f electrons in the ground state). Complex 1-Ce(PN*) exhibits a single white line feature in its L3-edge XANES spectrum, consistent with a trivalent lanthanide, with an inflection point of 5722.7 eV, the same energy as observed for 1-Ce(PN).31 The spectrum of 1-Ce(PN*) can be fit with a single pseudo-Voigt function at 5725.8(0) eV (again similar to that for 1-Ce(PN) at 5725.2(1) eV).The spectrum of 2-Ce(PN*) exhibits a structured white-line feature, characteristic of tetravalent lanthanide compounds13,41–47 with an inflection point of the rising edge at 5724.7 eV, 2 eV higher in energy than the inflection point of 1-Ce(PN*), indicating an increase in effective charge at the metal and consistent with an increase in oxidation state. This structured white-line feature, often a resolved doublet, has been thought to be a consequence of a multiconfigurational ground state that consists of partial 4fn5d0L and 4fn+15d0![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) (where
(where ![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) is a ligand hole) character that transition to excited states 4fn5d1L and 4fn+15d1
is a ligand hole) character that transition to excited states 4fn5d1L and 4fn+15d1![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) , respectively.13,41,48,49 The spectrum of 2-Ce(PN), reported previously,31 is unique in that the intensity of the lower energy feature of the white line doublet, attributed to the 4fn+15d1
, respectively.13,41,48,49 The spectrum of 2-Ce(PN), reported previously,31 is unique in that the intensity of the lower energy feature of the white line doublet, attributed to the 4fn+15d1![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) final state – i.e. partial trivalent character – was significantly decreased in comparison to other Ce4+ compounds, such as ceria (CeO2). The spectrum of 2-Ce(PN*) is consistent with that of 2-Ce(PN), shown in Fig. 4 (shown with the spectrum of CeO2 in S18†).
final state – i.e. partial trivalent character – was significantly decreased in comparison to other Ce4+ compounds, such as ceria (CeO2). The spectrum of 2-Ce(PN*) is consistent with that of 2-Ce(PN), shown in Fig. 4 (shown with the spectrum of CeO2 in S18†).
Where this compound differs slightly from our previously reported Ce4+ compound, 2-Ce(PN), is in the absolute energy of the feature (the inflection point for 2-Ce(PN*) is slightly higher in energy than in 2-Ce(PN) at 5723.6 eV) and in the shape of the lower energy feature. A two-peak model of the white line feature that is typically employed for tetravalent lanthanide L3-edge spectra, including our previously reported, 2-Ce(PN) and 2-Tb(PN*), does not satisfactorily describe the shape of 2-Ce(PN*). In addition to the traditional two-peak model that consists of lower energy p2 at 5730.44(9) eV (4fn+15d1![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) ) and higher energy p3 at 5736.57(6) eV (4fn5d1L), an additional p4 at 5726.45(8) eV, must be included in the lower energy region to obtain a satisfactory fit. The need to include additional peaks in order to describe white line shapes of tetravalent lanthanides is well documented.13,50–52 However, a cohesive physical model for these spectroscopic features does not yet exist. In light of the consensus interpretation, we present a directly analogous model in the fit of 2-Ce(PN) with an additional pseudo-Voigt, p4, at 5725.7(1) eV. Additionally, both the step function (moved to higher energy like in 2-Tb(PN*)) and p1 at 5719.73(0) eV (generally assigned as the quadrupole allowed 2p64fn5d0 → 2p54fn+15d0 transition)13 were held constant for 2-Ce(PN*) and 2-Ce(PN) to provide a consistent fitting model.
) and higher energy p3 at 5736.57(6) eV (4fn5d1L), an additional p4 at 5726.45(8) eV, must be included in the lower energy region to obtain a satisfactory fit. The need to include additional peaks in order to describe white line shapes of tetravalent lanthanides is well documented.13,50–52 However, a cohesive physical model for these spectroscopic features does not yet exist. In light of the consensus interpretation, we present a directly analogous model in the fit of 2-Ce(PN) with an additional pseudo-Voigt, p4, at 5725.7(1) eV. Additionally, both the step function (moved to higher energy like in 2-Tb(PN*)) and p1 at 5719.73(0) eV (generally assigned as the quadrupole allowed 2p64fn5d0 → 2p54fn+15d0 transition)13 were held constant for 2-Ce(PN*) and 2-Ce(PN) to provide a consistent fitting model.
In the conventional two-peak model, a useful comparison between Ce4+ compounds is the nf value, a metric that describes the partial trivalent character in the multiconfigurational ground state where nf = Ap2/(Ap2 + Ap3). With the additional pseudo-Voigt function included in the fits of 2-Ce(PN*) and 2-Ce(PN) the nf value becomes nf = (Ap2 + Ap4)/(Ap2 + Ap4 + Ap3). Peak p4 was included in the lower energy feature in order to give an upper bound of trivalent character under this model. Using this description of nf, the value for 2-Ce(PN*) is 0.40(4). This value is still considerably lower than most formally Ce4+ compounds, in line with the lowest nf value reported for 2-Ce(PN) previously, such as [CeCl6]2− (0.51(5)),13 CeO2 (0.58(3)),41 and [Ce(C8H8)2] (0.82(3) and 0.89) (Table 3).41,53 With the re-evaluated fitting model for 2-Ce(PN), the nf value is 0.38(2) where previously, the 2-Ce(PN)nf value was 0.21(1) with the conventional two-peak model. To our knowledge, this is still the lowest nf value reported to date and agrees well with the observed nf value for 2-Ce(PN*). The previously reported nf value obtained for 2-Tb(PN*) of 0.39(4) is similar to that of terbia, TbO2 (0.42(4)).42 It should be noted that the terbium complex, 2-Tb(PN*), is satisfactorily fit with two peaks.
| Compound | n f | 4fn+1 (eV) | 4fn (eV) |
|---|---|---|---|
| a n.d. peak energies not defined by the authors. | |||
| 2-Ce(PN*) | 0.40(4) | 5730.4(1), 5726.5(1) | 5736.6(1) |
| 2-Ce(PN) | 0.38(2) | 5728.9(1), 5725.7(1) | 5736.0(1) |
CeO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
0.56(4) | 5728.0(1) | 5736.2(2) |
| [CeCl6]2–13 | 0.51(5) | 5720–5734 (3 peaks, n.d.)a | 5734–5742 (2 peaks, n.d.)a |
| [Ce(C8H8)2]41,53 | 0.82(3) | 5725.0(3) | 5736.5(3) |
| 2-Tb(PN*) | 0.39(4) | 7520.3(1) | 7528.5(1) |
TbO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
0.42(4) | 7518.9(1) | 7526.1(1) |
Molecular orbital (MO) diagrams
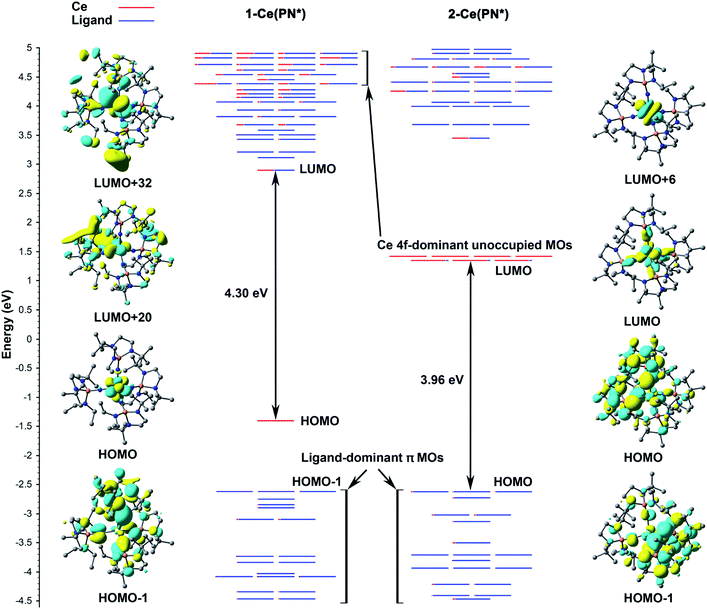
According to the α-MO diagram of the 1-Ce(PN*) and 2-Ce(PN*) complexes (see Theoretical details section in the ESI†), upon oxidation, all MO levels shift down appreciably (Fig. 5). Specifically, the highest ligand-dominant π MO (HOMO−1) of 1-Ce(PN*) becomes the HOMO of 2-Ce(PN*) lowering its energy by 2.57 eV (Fig. 5), in resemblance with the case of 1-Tb(PN*) oxidizing into 2-Tb(PN*) with similar shift by 2.37 eV.15 As in the Tb counterparts, the oxidation of 1-Ce(PN*) is purely metal-centred as evidenced by the composition of its HOMO (98% Ce 4f) that loses an electron upon oxidation. The similarity between the Tb and Ce complexes also extends to the composition of the top twenty highest doubly occupied MOs that are also found to be ligand-based π MOs composed of primarily N 2p AOs. However, in contrast to the 1-Tb(PN*) complex, wherein the oxidation occurs due to the removal of the β electron from the deeper MO, i.e. HOMO−8, oxidation of 1-Ce(PN*) is due to the removal of the α electron from its highest singly occupied orbital that is a localized 4f-orbital (HOMO in the left panel of Fig. 5). Indeed, the presence of the Ce 4f electron at the HOMO level allows for the f–d transitions originating from HOMO to the unoccupied MOs with d-character (e.g. LUMO+20, LUMO+32 in Fig. 5) as opposed to 4f81-Tb(PN*), wherein no such transitions were observed.15 Another difference is seen in the HOMO–LUMO gaps. In 1-Ce(PN*), it is smaller by ∼1.2 eV than in 1-Tb(PN*), in agreement with the appearance of the electronic excitations in the lower energy region, i.e. ∼370 nm in 1-Ce(PN*)vs. ∼300 nm in 1-Tb(PN*). However, the HOMO–LUMO gap is significantly smaller in 2-Tb(PN*) than in 2-Ce(PN*). This difference explains the appearance of the absorption bands in the appreciably higher energy region in 2-Ce(PN*), i.e. absorption maxima of the most intense bands are at 391 nm in 2-Ce(PN*)vs. 575 nm in 2-Tb(PN*).Computed UV-vis spectra
Computed UV-vis spectra of 1-Ce(PN*) and 2-Ce(PN*) (see Theoretical details section in the ESI†) are in good agreement with the experimental data, confirming the apparent differences in their absorption spectra in both the absorption peaks and relative intensities (Fig. 6). Specifically, while there is no absorption in the low energy region of 1-Ce(PN*) (up to ∼370 nm), the theoretical spectrum of 2-Ce(PN*) exhibits more intense electronic excitations in the ∼330–480 nm range. According to the natural transition orbital (NTO) analysis of 1-Ce(PN*) (see Fig. S19† for the NTO pairs), there are three f–d transitions at 350 nm, 346 nm, and 320 nm exhibiting very low oscillator strength values (Fig. 6). In comparison to 2-Ce(PN*), the intensity ratio is about 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, respectively, in agreement with the low extinction coefficient of 883 cm−1 M−1 of the experimental absorption feature at 369 nm.
50, respectively, in agreement with the low extinction coefficient of 883 cm−1 M−1 of the experimental absorption feature at 369 nm.
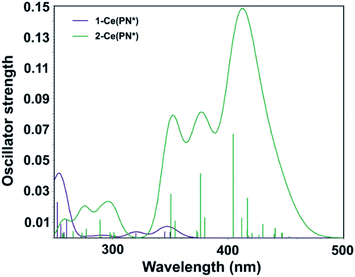 | ||
| Fig. 6 Computed TD-DFT spectra of 1-Ce(PN*) (purple) and 2-Ce(PN*) (green). Vertical bars depict theoretical oscillator strength of single-electron excitations. | ||
In contrast to 1-Ce(PN*), there are more electronic excitations in the ∼330–480 nm region of 2-Ce(PN*) with notably higher oscillator strength values, in agreement with the significantly higher extinction coefficient of the broad absorption feature (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1 at the 391 nm maximum). As expected for the closed shell 4f0 system, these are assigned as the LMCT transitions arising from the top eight occupied ligand-dominant π MOs (primarily N 2p orbitals, i.e. HOMO through HOMO−7) to the seven unoccupied Ce 4f orbitals appearing at LUMO to LUMO+6 levels (see Fig. S20† for the NTO pairs). The ratio of the highest oscillator strength of the f–d excitations in 1-Ce(PN*) to the highest oscillator strength of the LMCT excitations in 2-Ce(PN*), i.e., 1
000 cm−1 M−1 at the 391 nm maximum). As expected for the closed shell 4f0 system, these are assigned as the LMCT transitions arising from the top eight occupied ligand-dominant π MOs (primarily N 2p orbitals, i.e. HOMO through HOMO−7) to the seven unoccupied Ce 4f orbitals appearing at LUMO to LUMO+6 levels (see Fig. S20† for the NTO pairs). The ratio of the highest oscillator strength of the f–d excitations in 1-Ce(PN*) to the highest oscillator strength of the LMCT excitations in 2-Ce(PN*), i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, is in excellent agreement with the ratio of the experimental extinction coefficients of the corresponding absorption maxima, i.e. 1
17, is in excellent agreement with the ratio of the experimental extinction coefficients of the corresponding absorption maxima, i.e. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18. The higher energy band of 2-Ce(PN*) appearing at ∼320 nm is also attributed to the same type of the LMCT transitions, though from the lower ligand-dominant MOs (HOMO−8 through HOMO−19) to the Ce 4f unoccupied MOs.
18. The higher energy band of 2-Ce(PN*) appearing at ∼320 nm is also attributed to the same type of the LMCT transitions, though from the lower ligand-dominant MOs (HOMO−8 through HOMO−19) to the Ce 4f unoccupied MOs.
Natural bond orbital analysis
To understand the difference in electronic structure between 1-Ce(PN*) and 2-Ce(PN*), a chemical bonding analysis was performed. Since the canonical MOs are intrinsically hard to interpret in terms of chemical bonds due to delocalization, a natural bond orbital analysis (NBO) was employed to assess the degree of the M–L covalency. In both complexes, a similar set of bonding elements was identified (see NBOs of 2-Ce(PN*) in Fig. S22†), with an additional one-center one-electron (1c–1e) NBO in 1-Ce(PN*) (Fig. S23†) with the occupation number (ON) equal to 1.00|e|. This 1c–1e NBO is 99.6% 4f-character, representing an unpaired Ce 4f electron originating from the HOMO of 1-Ce(PN*), in accordance with the 4f1 configuration. In both complexes, the bonding interaction between the Ce ion and the ligands occurs due to the formation of four, two-center, two-electron (2c–2e) Ce–N σ bonds (Fig. S22A†) and eight, three–center, two–electron (3c–2e) Ce–N–P π bonds (Fig. S22C†), though with slightly different ON values (see Table S11† for comparison).Similar to 2-Tb(PN*), the 2c–2e Ce–N σ bonds (ON = 1.98|e|) in 2-Ce(PN*) are highly polarized towards N atoms (Table S12†), accounting for 89.6% of the electron density associated with this bond. Specifically, the Ce contribution (10.4%) in these bonds in 2-Ce(PN*) is approximately 2% higher than the Tb contribution in the Tb–N σ bonds in 2-Tb(PN*).15 While the d-character is dominant in the Ce hybrids (64.4%) forming the Ce–N σ bonds, the f-character is also substantial (34.8%) (Table S13†). In fact, the f-character is appreciably higher than that in the Tb counterpart (6.1%). Overall, the greater contribution of Ce orbitals in the Ce–N σ bonding and, specifically, the higher participation of 4f electrons accounts for the stronger σ covalent interactions in 2-Ce(PN*) as compared to 2-Tb(PN*).
In 1-Ce(PN*), the 2c–2e Ce–N σ bonds (ON = 1.97|e|) are more polarized towards N atoms than in 2-Ce(PN*), resulting in the less covalent Ce–N σ interactions, i.e. Ce contribution is only 5.8% (Table S12†). The observed changes in covalency is consistent with the longer Ce–N bonds in 1-Ce(PN*) than in 2-Ce(PN*). Noteworthy, the Ce contribution is comparable to the Tb contribution in the Tb–N σ bonds of 1-Tb(PN*), i.e. 5.2%. These findings are also in concordance with the previous studies on the 1-Ce(PN) and 2-Ce(PN) complexes,31 showing a greater covalent character of the M–L bonds in a tetravalent state rather than in the trivalent one. The d-character of the NBO hybrid of Ce in Ce–N σ bonds of 1-Ce(PN*) is dominant and slightly higher than in 2-Ce(PN*), i.e. 69.7% vs. 64.4%, while the f-character is a bit smaller (28.4% vs. 34.8%, see Table S13†).
In addition to the σ bonding, NBO recovers eight 3c–2e Ce–N–P π bonds (two per ligand, Fig. S22C†) that originate from the top eight ligand-dominant π MOs (Fig. 5). They are also highly polarized towards N atoms, with the slightly bigger contribution of N in 1-Ce(PN*) (96.5%) than in 2-Ce(PN*) (94.0%). In 2-Ce(PN*), the N 2p π donation to the Ce center is found to be appreciably higher (4.4%) than in 1-Ce(PN*) (1.3%), consistent with the lengthening of the P–Nimide bond length upon metal oxidation. In both cases, the f-character in the Ce NBO hybrids of the Ce–N–P π bonds is significantly higher than the d-character, i.e. ∼65% vs. ∼27%. This is opposed to the Tb counterparts of the Tb–N–P π bonds, where the d-character prevailed over the f-character. Overall, this emphasizes the enhanced participation of the 4f orbitals in the M–L bonds in complexes of Ce as compared to the corresponding Tb complexes.
Conclusions
The [(NP(1,2-bis-tBu-diamidoethane)(NEt2))]1− imidophosphorane ligand system enables the preferential stabilization of the tetravalent oxidation state over the trivalent state for Ce and Tb and produces isotypic tetravalent compounds. This structural homology for two molecular complexes of tetravalent lanthanides creates the opportunity for a detailed comparative structural and spectroscopic analysis. Traditional analysis of the coordination sphere indicates that structural rearrangement of the ligand sphere as a consequence of oxidation is limited to the contraction of the M–N bond lengths. However, the use of VDP analysis reveals that, within the isotypic structures, there are subtle rearrangements of the ligand that reduce the degree of hydrogen contribution to the VD polyhedra, despite the contracted Tb–N bond in comparison to the Ce–N bond. This reduction of the hydrogen contribution to the VDP suggests that ligand gearing and packing are also effected by the reduced metal ion size.For both trivalent Ce and Tb, NBO analyses confirm the metal-centred oxidation of the Ln3+ complexes, shortening the M–N bonds and increasing their covalent character in Ln4+. The Ce contribution in Ce–N bonds in both 1-Ce(PN*) and 2-Ce(PN*) complexes is found to be higher than the Tb contribution in the Tb–N bonds of the Tb counterparts. Specifically, an enhanced participation of the 4f electrons in the M–N bonding is found in complexes of Ce as compared to the corresponding Tb complexes. In 2-Ce(PN*), the lower energy excitations are assigned to the LMCT transitions arising from ligand-dominant π MOs to the unoccupied Ce 4f orbitals.
Cyclic voltammetry studies of the cerium and terbium redox pairs demonstrate experimentally the significant stabilization of the tetravalent oxidation state in both complexes. The observed Epc of −2.86 V vs. Fc/Fc+ for 2-Ce(PN*) is the most negative known by 490 mV. Similarly, the Epc of 2-Tb(PN*) (−1.68 V vs. Fc/Fc+) is 980 mV and 690 mV more negative than that observed for the only two other tetravalent terbium complexes currently in existence. Collectively, these data indicate that a homoleptic imidophosphorane ligand field significantly stabilizes tetravalent lanthanide ions. Additionally, the 980 mV difference between the Epc of 2-Tb(PN*) and that of [Tb4+(OSi(OtBu)3)3(κ2-OSi(OtBu)3)] suggests that a wide range of ligand systems should be capable of stabilizing tetravalent terbium.
The similar L3-edge XANES features for 1-Ce(PN*) and 2-Ce(PN*) with respect to 1-Ce(PN) and 2-Ce(PN) and 1-Tb(PN*) and 2-Tb(PN*) further confirm the oxidation state assignments within the imidophosphorane ligand field. This new class of imidophosphorane complexes with distinct redox properties and unusual L3-edge spectra for tetravalent cerium complexes, 2-Ce(PN) and 2-Ce(PN*), suggest that the dominant two-peak model may not provide a complete physical description of the spectra of tetravalent lanthanides in all cases. The physical origin of p4 in the fit of the tetravalent cerium complexes is not inherently clear. Further studies using high energy resolution fluorescence detection XANES (HERFD-XANES), Ln M-edge XAS studies, magnetic susceptibility, and CASSCF modeling of the tetravalent imidophosphorane compounds will be pursued in order to answer these questions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by Georgia Institute of Technology and the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry Program under Award Number DE-SC0019385. Single-crystal diffraction experiments were performed at the GT SC-XRD facility directed by J. B. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). I. A. P. is supported by a J. Robert Oppenheimer Distinguished Postdoctoral Fellowship at Los Alamos National Laboratory. E. R. B. and P. Y. are supported by the Heavy Element Chemistry Program sponsored by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy, at Los Alamos National Laboratory (LANL). LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001).Notes and references
- Y. K. Gun'ko, P. B. Hitchcock and M. F. Lappert, J. Organomet. Chem., 1995, 499, 213–219 CrossRef.
- M. R. MacDonald, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2013, 135, 9857–9868 CrossRef CAS PubMed.
- M. R. MacDonald, J. E. Bates, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2012, 134, 8420–8423 CrossRef CAS PubMed.
- R. P. Kelly, L. Maron, R. Scopelliti and M. Mazzanti, Angew. Chem., Int. Ed., 2017, 56, 15663–15666 CrossRef CAS PubMed.
- F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, in Advanced Inorganic ChemistryWiley-Interscience, New York, 6th edn, 1999, pp. 1108–1129 Search PubMed.
- L. J. Nugent, R. D. Baybarz and J. L. Burnett, J. Phys. Chem., 1969, 73, 1177–1178 CrossRef CAS.
- L. J. Nugent, R. D. Baybarz, J. L. Burnett and J. L. Ryan, J. Inorg. Nucl. Chem., 1971, 33, 2503–2530 CrossRef CAS.
- K. R. Meihaus, M. E. Fieser, J. F. Corbey, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2015, 137, 9855–9860 CrossRef CAS PubMed.
- W. J. Evans and S. E. Foster, J. Organomet. Chem., 1992, 433, 79–94 CrossRef CAS.
- M. N. Bochkarev, Coord. Chem. Rev., 2004, 248, 835–851 CrossRef CAS.
- R. Shannon, Acta Crystallogr. A., 1976, 32, 751–767 CrossRef.
- M. E. Fieser, M. G. Ferrier, J. Su, E. Batista, S. K. Cary, J. W. Engle, W. J. Evans, J. S. Lezama Pacheco, S. A. Kozimor, A. C. Olson, A. J. Ryan, B. W. Stein, G. L. Wagner, D. H. Woen, T. Vitova and P. Yang, Chem. Sci., 2017, 8, 6076–6091 RSC.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef PubMed.
- J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2018, 140, 17977–17984 CrossRef CAS PubMed.
- N. T. Rice, I. A. Popov, D. R. Russo, J. Bacsa, E. R. Batista, P. Yang, J. Telser and H. S. La Pierre, J. Am. Chem. Soc., 2019, 141, 13222–13233 CrossRef CAS PubMed.
- C. T. Palumbo, I. Zivkovic, R. Scopelliti and M. Mazzanti, J. Am. Chem. Soc., 2019, 141, 9827–9831 CrossRef CAS PubMed.
- M. Mazzanti, C. Palumbo, A. Willauer, R. Scopelliti, I. Douair, I. Zivkovic and L. Maron, Angew. Chem., Int. Ed., 2019, 59, 3549–3553 Search PubMed.
- A. R. Willauer, C. T. Palumbo, I. Zivkovic, F. Fadaei Tirani, I. Douair, L. Maron and M. Mazzanti, J. Am. Chem. Soc., 2020, 141, 9827–9831 Search PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973 CrossRef CAS PubMed.
- A.-M. Ariciu, D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Nat. Commun., 2019, 10, 3330 CrossRef PubMed.
- A. M. Tishin, J. Alloys Compd., 1997, 250, 635–641 CrossRef CAS.
- J. W. Sharples and D. Collison, in Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VCH Verlad & Co. KGaA, Boschstr, Weinheim, Germany, 2015, ch. 9 Search PubMed.
- Y. Li, Q. Ma, S. X. Huang and C. L. Chien, Sci. Adv., 2018, 4, eaap8294 CrossRef PubMed.
- M. Sundermann, H. Yavaş, K. Chen, D. J. Kim, Z. Fisk, D. Kasinathan, M. W. Haverkort, P. Thalmeier, A. Severing and L. H. Tjeng, Phys. Rev. Lett., 2018, 120, 016402 CrossRef CAS PubMed.
- R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 43–45 CrossRef CAS PubMed.
- B. Monteiro, N. A. G. Bandeira, C. Lourenço, A. F. Lucena, J. M. Carretas, J. K. Gibson and J. Marçalo, Chem. Commun., 2019, 55, 14139–14142 RSC.
- A. Kovács, P. D. Dau, J. Marçalo and J. K. Gibson, Inorg. Chem., 2018, 57, 9453–9467 CrossRef PubMed.
- S.-X. Hu, J. Jian, J. Su, X. Wu, J. Li and M. Zhou, Chem. Sci., 2017, 8, 4035–4043 RSC.
- N. T. Rice, J. Su, T. P. Gompa, D. R. Russo, J. Telser, L. Palatinus, J. Bacsa, P. Yang, E. R. Batista and H. S. La Pierre, Inorg. Chem., 2019, 58, 5289–5304 CrossRef CAS PubMed.
- V. A. Blatov, A. P. Shevchenko and V. N. Serenzhkin, Acta Crystallogr. A., 1995, 51, 909–916 CrossRef.
- V. A. Blatov, Crystallogr. Rev., 2004, 10, 249–318 CrossRef CAS.
- C. A. Tolman, Chem. Rev., 1977, 77, 313–348 CrossRef CAS.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
- V. A. Blatov, A. P. Shevchenko and V. N. Serezhkin, J. Struct. Chem., 1994, 34, 820–822 CrossRef.
- A. A. Ivanenko, V. A. Blatov and V. N. Serezhkin, Kristallografiya, 1992, 37, 1365–1371 CAS.
- N. A. Piro, J. R. Robinson, P. J. Walsh and E. J. Schelter, Coord. Chem. Rev., 2014, 260, 21–36 CrossRef CAS.
- E. M. Broderick, P. S. Thuy-Boun, N. Guo, C. S. Vogel, J. Sutter, J. T. Miller, K. Meyer and P. L. Diaconescu, Inorg. Chem., 2011, 50, 2870–2877 CrossRef CAS PubMed.
- M. K. Assefa, D.-C. Sergentu, L. A. Seaman, G. Wu, J. Autschbach and T. W. Hayton, Inorg. Chem., 2019, 58, 12654–12661 CrossRef CAS PubMed.
- R. L. Halbach, G. Nocton, C. H. Booth, L. Maron and R. A. Andersen, Inorg. Chem., 2018, 57, 7290–7298 CrossRef CAS PubMed.
- S. G. Minasian, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, W. W. Lukens, R. L. Martin, D. K. Shuh, S. C. E. Stieber, T. Tylisczcak and X.-d. Wen, J. Am. Chem. Soc., 2017, 139, 18052–18064 CrossRef CAS PubMed.
- J. A. Bogart, A. J. Lewis, S. A. Medling, N. A. Piro, P. J. Carroll, C. H. Booth and E. J. Schelter, Inorg. Chem., 2013, 52, 11600–11607 CrossRef CAS PubMed.
- A. Bianconi, A. Marcelli, M. Tomellini and I. Davoli, J. Magn. Magn. Mater., 1985, 47–48, 209–211 CrossRef CAS.
- H. Dexpert, R. C. Karnatak, J. M. Esteva, J. P. Connerade, M. Gasgnier, P. E. Caro and L. Albert, Phys. Rev. B, 1987, 36, 1750–1753 CrossRef CAS PubMed.
- G. Kaindl, G. K. Wertheim, G. Schmiester and E. V. Sampathkumaran, Phys. Rev. Lett., 1987, 58, 606–609 CrossRef CAS PubMed.
- A. M. Shahin, F. Grandjean, G. J. Long and T. P. Schuman, Chem. Mater., 2005, 17, 315–321 CrossRef CAS.
- C. H. Booth, M. D. Walter, M. Daniel, W. W. Lukens and R. A. Andersen, Phys. Rev. Lett., 2005, 95, 267202 CrossRef CAS PubMed.
- D. E. Smiles, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, R. L. Martin, S. G. Minasian, D. K. Shuh, S. C. E. Stieber and T. Tyliszczak, Chem. Sci., 2020, 11, 2796–2809 RSC.
- G. Kaindl, G. Schmiester, E. V. Sampathkumaran and P. Wachter, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 10174–10177 CrossRef CAS PubMed.
- Z. Hu, E. J. Cho, G. Kaindl and B. G. Müller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 7514–7520 CrossRef CAS PubMed.
- G. Kalkowski, G. Kaindl, G. Wortmann, D. Lentz and S. Krause, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 1376–1382 CrossRef CAS PubMed.
- M. D. Walter, C. H. Booth, W. W. Lukens and R. A. Andersen, Organometallics, 2009, 28, 698–707 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic, computational, spectroscopic, and crystallographic details. CCDC 1988238 and 1895852. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01414a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |