Open Access Article
Open Access ArticleExploiting clock transitions for the chemical design of resilient molecular spin qubits†
Silvia
Giménez-Santamarina
 ,
Salvador
Cardona-Serra
,
Salvador
Cardona-Serra
 ,
Juan M.
Clemente-Juan
,
Juan M.
Clemente-Juan
 *,
Alejandro
Gaita-Ariño
*,
Alejandro
Gaita-Ariño
 * and
Eugenio
Coronado
* and
Eugenio
Coronado
 *
*
ICMol, Universitat de València, C/Catedrático José Beltrán no 2, 46980 Paterna, Valencia, Spain. E-mail: juan.m.clemente@uv.es; alejandro.gaita@uv.es; eugenio.coronado@uv.es
First published on 26th May 2020
Abstract
Molecular spin qubits are chemical nanoobjects with promising applications that are so far hampered by the rapid loss of quantum information, a process known as decoherence. A strategy to improve this situation involves employing so-called Clock Transitions (CTs), which arise at anticrossings between spin energy levels. At CTs, the spin states are protected from magnetic noise and present an enhanced quantum coherence. Unfortunately, these optimal points are intrinsically hard to control since their transition energy cannot be tuned by an external magnetic field; moreover, their resilience towards geometric distortions has not yet been analyzed. Here we employ a python-based computational tool for the systematic theoretical analysis and chemical optimization of CTs. We compare three relevant case studies with increasingly complex ground states. First, we start with vanadium(IV)-based spin qubits, where the avoided crossings are controlled by hyperfine interaction and find that these S = 1/2 systems are very promising, in particular in the case of vanadyl complexes in an L-band pulsed EPR setup. Second, we proceed with a study of the effect of symmetry distortions in a holmium polyoxotungstate of formula [Ho(W5O18)2]9− where CTs had already been experimentally demonstrated. Here we determine the relative importance of the different structural distortions that causes the anticrossings. Third, we study the most complicated case, a polyoxopalladate cube [HoPd12(AsPh)8O32]5− which presents an unusually rich ground spin multiplet. This system allows us to find uniquely favorable CTs that could nevertheless be accessible with standard pulsed EPR equipment (X-band or Q-band) after a suitable chemical distortion to break the perfect cubic symmetry. Since anticrossings and CTs constitute a rich source of physical phenomena in very different kinds of quantum systems, the generalization of this study is expected to have impact not only in molecular spin science but also in other related fields such as molecular photophysics and photochemistry.
Introduction
Quantum two-level systems based on spin states, or simply “spin qubits”, are promising candidates as building blocks for quantum technologies.1–3 The potential of a magnetic system for its application as a qubit relies on the capacity to generate, control and read out different quantum superpositions of two spin states (|0> and |1>). These requirements can be achieved within essentially any two-level quantum system, such as the simplest case of a spin S = 1/2. However, quantum information is fragile and is quickly lost for most quantum systems. The physical processes that lead to this information loss are collectively known as decoherence and can be grouped into two major sources: magnetic noise and vibrations. Different degrees of resilience against the two decoherence sources can be found in the many possible different spins systems.Molecular magnetism offers an attractive approach to design spin qubits.4,5 In molecular spin qubits, the spin typically resides on a magnetic metal ion, and chemical design of the coordination complex offers possibilities for a rational optimization of the physical properties, making them a promising pathway to achieve coherent qubits. The local coordination of the ion strongly influences the qubit properties by determining the wave functions of its |0> and |1> states. In comparison with solid-state approaches, coordination chemistry offers a tremendous range of possible environments and, therefore, of designing qubits with suitable characteristics, conferring a competitive advantage to magnetic molecules over other promising candidates such as NV centers in diamond6–8 or phosphorus impurities in silicon.2,9 At the same time, molecular spin qubits allow comparable survival time of quantum spin coherence T2, the characteristic time of the exponential decay of spin echoes, typically associated to spin–spin relaxation processes.3 The optimal conditions to obtain the maximum values of T2 for all solid state approaches include extreme dilution of the spin in a diamagnetic matrix. The reason for this requirement is the linear dependence of the transition energy between two states of a spin qubit as a function of the local field, due to the Zeeman effect, which means that qubits are strongly affected by the magnetic noise generated by neighboring spins.
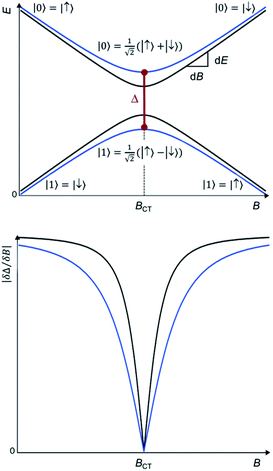
Chemistry provides a promising method, complementary to dilution, to effectively “engineer” the molecular spin states to reduce this noise and thereby obtain longer quantum coherence times T2. The origin of this quantum stability is the special wavefunction mixing happening when the spin states |↑> and |↓> experience an avoided level crossing, giving rise to a tunneling splitting ΔCT.10 At these avoided crossings the two spin states present zero Zeeman slope, making the transition frequency Δ between these two states insensitive to small changes in the magnetic field. This results in optimal operating points, known as Clock Transitions (CTs) and are characterized by the magnitude of their tunneling splitting ΔCT (see Fig. 1 up). Since this protection is only absolute at a particular field BCT, one can compare the protection offered by CTs in different systems by quantifying the curvature at the anticrossing, or, equivalently, by the sensitivity to the magnetic field ∂Δ/∂B in the vicinity of the anticrossing (see Fig. 1, down).
However, working with CTs possesses particular challenges. In most EPR experiments, the resonance condition between the magnetic energy level splitting and the microwave frequency can always be met just by sweeping the magnetic field, achieving a continuous increase of the splitting due to the Zeeman effect. In contrast, each CT happens at a defined magnetic field BCT and has a unique value of energy ΔCT given by the spin Hamiltonian and which cannot be controlled by the Zeeman term. Since the microwave frequencies are typically difficult to control, this possesses an intrinsic limitation in experimentally characterizing and exploiting CTs. As a consequence, in order to exploit CTs one requires a certain control over the energy level structure; this can be achieved by designing either the crystal-field around the magnetic ion and/or the electro-nuclear hyperfine interactions.9,11 The former merely requires to choose the appropriate combination of metal ion and coordination environment, but the hyperfine interaction may also be tuned in molecules, for example, through s–d orbital mixing.12 Rational chemical design in principle offers a path forward, and indeed some of us demonstrated this in the [Ho(W5O18)2]9− polyoxometalate (in short, HoW10 POM) that presents CTs because of a combination of the local symmetry and the nature of the ground doublet.13 These POMs can then be packed in the solid state at unusually high concentrations while retaining desirably long coherence times. Since this initial contribution, a few further works have employed the same kind of strategy to obtain coherence in molecular spin qubits at unusually high concentrations.12,14,15 However, this has so far mostly been a matter of trial-and-error.
Generally speaking, CTs appear for every avoided crossing, which is to say in any and every magnetic molecule presenting extradiagonal elements in their spin Hamiltonians, independently of whether these arise from the crystal field or from the hyperfine coupling. From the theoretical point of view, if the form of the spin Hamiltonian is known, it is in principle possible to obtain either exact or approximate analytical solutions that describe at which magnetic field and excitation energy the CTs will appear, as well as their curvature. However, there is no systematic procedure for the exploration of chemical structures that allows the optimization of CTs. Furthermore, there are also perturbations in the molecular geometry or in the parameters of the spin Hamiltonian due for example to crystalline defects or to thermal molecular vibrations. Depending on the nature of the spin Hamiltonian, CTs can be more or less sensitive to this source of noise. Still, there is currently no developed methodology to deal with this problem.
In this work we characterize the behavior of anticrossings in molecular spin qubits. The robustness against magnetic noise is quantified via the curvature of the levels participating in the CT, while the robustness versus molecular distortions is quantified as the relative change in the transition frequency at reasonable degrees of distortions. We perform this kind of analysis for different representative kinds of spin Hamiltonians: from a simple S = 1/2 transition metal, well isolated from its excited states, to a lanthanide in cubic symmetry presenting a highly degenerate ground multiplet. Our final purpose here is to find some insights into the chemical design of “shallow” CTs where a spin qubit can be most resilient. For these goals, in this work we develop and employ a computational tool that assists in the automated exploration the influence of different molecular parameters.
Methods: algorithmic detection of avoided crossings
Herein we present the numerical method and the software implementation which we developed in this work and which is capable of getting an autonomous numerical characterization of the coordinates and curvature of any anticrossing in discrete {x, y1, y2, …, yn}-type datasets. In the case of magnetic molecules this means that, starting from files containing Zeeman diagrams for a set of energy levels {B, E1, E2, …, En}, the program automatically obtains, for every possible CT, its magnetic field intensity (BCT), its tunneling splitting (ΔCT) and more crucially also the curvature at the CT, which allows to quantify the robustness of each CT vs. magnetic field noise.The program starts by translating the set of discrete energy points into continuous functions, a task which involves automatically distinguishing between crossings and anticrossings (see Fig. 2 for illustration and ESI Section S1 for details†). It processes energy differences only up to a specified frequency threshold, which is defined by the user, e.g. 15 GHz (0.5 cm−1). Within the chosen frequency window, the program then obtains for each anticrossing the second derivative ∂2Δ/∂B2-which is a very good approximation for the curvature (k) – (see ESI Section S1 for details†). A systematic application of the code to a data set obtained by diagonalization of a spin Hamiltonian with a controlled parameter variation allows a fast and systematic study of the influence of each parameter on the frequency and curvature of the anticrossings.
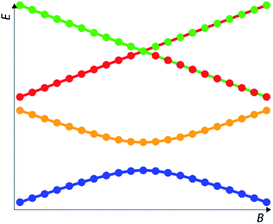 | ||
| Fig. 2 Ordering of the energy levels between pre-processing (numerical data, symbols) and post-processing (analytical fit, lines) is the same in anticrossings but altered in crossings. | ||
We have applied this methodology to study representative cases in order to deepen our understanding of the nature of the parameters governing the behavior. In some cases, we rely on the computational package SIMPRE to obtain the spin Hamiltonian parameters from a controlled variation in the coordination environment.11,16 SIMPRE is based on the following Hamiltonian:17,18
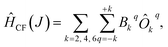 | (1) |
| Bkq = ak(1 − σk)Akq〈rk〉, | (2) |
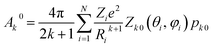 | (3) |
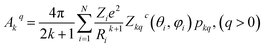 | (4) |
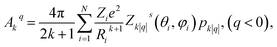 | (5) |
Application to three case studies
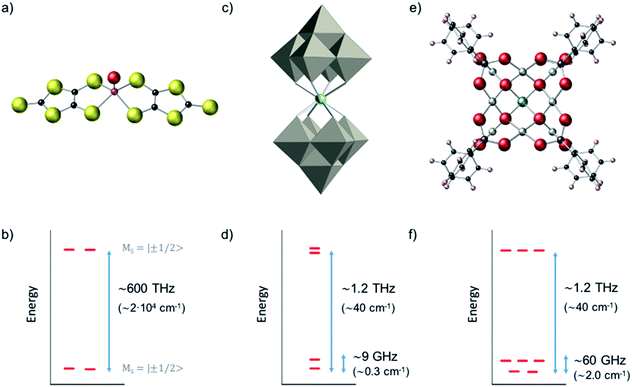
We compared the robustness of CT, in terms of curvature and stability of the transition energy, for three metal-based complexes with three different representative kinds of spin Hamiltonians. We start with a vanadyl complex (a well isolated S = 1/2 ground doublet) where we study the influence of parallel and perpendicular hyperfine couplings (A∥, A⊥); a well-known example of this kind is provided by the [VO(C3S5)2] complex (Fig. 3a and b).20 We subsequently applied our methodology to study the HoW10 POM where one can find a large tunneling splitting in the electronic ground state, ΔCT = 9 GHz (0.3 cm−1), due to the effect of the antiprismatic crystal field around the Ho3+, with the rest of the electronic spin states being higher in energy (Fig. 3c and d). For this second system we determine the variation of the CTs with regard to different molecular distortions. As a final case study, we focus on the polyoxopalladate [HoPd12(AsPh)8O32]5− (in short HoPd12). This POM has an exceptionally complicated ground state as a result of the cubic coordination symmetry around the Ho3+, which leads to a spin doublet and a spin triplet in near degeneracy (Fig. 3e and f). The study of the variation of this complicated energy level scheme with respect to molecular distortions of the cube allows to gain some novel perspective on the relative robustness towards both magnetic noise and thermal noise in this system.Vanadyl dithiolate complexes
Behavior of the CTs
Vanadium(IV) complexes have been proven to be exceptionally promising as spin qubits, given their records in phase memory times, T2 (ref. 21 and 22) and the existing proposals for quantum gates and spin filters based on them.23–25 Beyond that, vanadium(IV) complexes can offer the advantage of studying a well isolated S = 1/2 system (see for example Fig. 3, left). This is ideal from the point of view of the theory as it serves as a perfect test bed for our computational tool since an analytical solution is available. We employed the following Hamiltonian:| Ĥ = μBB × g × Ŝ + Ŝ × A × Î | (6) |
Note that vanadyl complexes and their vanadium analogues, as for example [VO(CxSy)2]2−vs. [V(CxSx)3]2−, tend to present very different A∥/A⊥ ratios:3,20A∥ is much higher in vanadyl complexes, while A⊥ presents higher values in vanadium complexes. Moreover, the dispersion of the hyperfine parameters between different complexes tends to be lower for the vanadyl complexes, because of the major role played by the closely bonded oxygen in the spatial distribution of the vanadium d-electron density. Therefore, as case study we will focus vanadyl complexes.
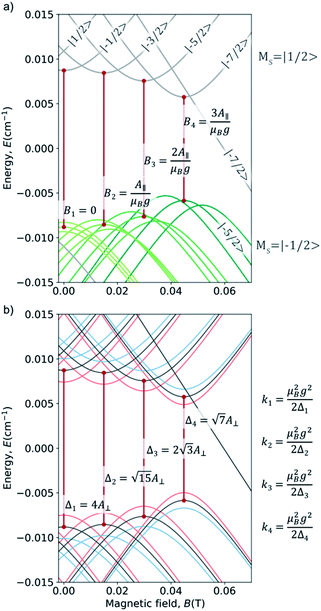
For our study, we employed the averaged values of the four vanadyl dithiolates complexes referenced in ref. 20 and 21: 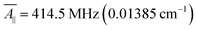 ;
; 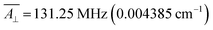 . We varied them by ±15%, a reasonable range given their typically narrow parametric dispersion.26 We limit the study to the variation of each one of the two parameters, keeping the other in its typical value. In simple anticrossings such as this, the curvature can be analytically estimated as k = γz2/2Δ, with γz = g × ΔMS × μB, where g = 2 for vanadyl, and ΔMS = 1. The numerical processing of the 658 calculated curves, of which we represent a selection in Fig. 4, coincides exactly with the analytical solutions (see ESI Section S2a†). In particular, one can see that the fields at which CTs appear are exclusively a linear function of A∥ (Fig. 4a), while Δ and k are exclusively a linear function of A⊥ (Fig. 4b). A deeper wavefunction analysis demonstrates that these CTs are only allowed in EPR parallel operating mode (see details in ESI Section S6†).
. We varied them by ±15%, a reasonable range given their typically narrow parametric dispersion.26 We limit the study to the variation of each one of the two parameters, keeping the other in its typical value. In simple anticrossings such as this, the curvature can be analytically estimated as k = γz2/2Δ, with γz = g × ΔMS × μB, where g = 2 for vanadyl, and ΔMS = 1. The numerical processing of the 658 calculated curves, of which we represent a selection in Fig. 4, coincides exactly with the analytical solutions (see ESI Section S2a†). In particular, one can see that the fields at which CTs appear are exclusively a linear function of A∥ (Fig. 4a), while Δ and k are exclusively a linear function of A⊥ (Fig. 4b). A deeper wavefunction analysis demonstrates that these CTs are only allowed in EPR parallel operating mode (see details in ESI Section S6†).
 | ||
| Fig. 4 (a) Zeeman diagrams (Bz) showing the effects of a ±15% variation in A∥; the full graphs (see Fig. S7†) presents vertical and horizontal symmetry planes, but for clarity here the effects of the A∥ are only shown for the bottom right part of the graph. Analytically-derived magnetic field positions (BCT) of CTs 1–4 as a function of A∥ are included as annotations. Curves in the same color correspond to the same spin levels along the variation. (b) Zeeman diagrams (Bz) showing the effects of −15% (red) and +15% (blue) variation in A⊥, together with the analytically-derived transition energies ΔCT of the different CTs. The analytically-derived curvatures (k) of the different CTs as a function of ΔCT. | ||
In our case example, CTs present the frequencies Δ1 = 0.53 GHz (0.01768 cm−1), Δ2 = 0.51 GHz (0.01701 cm−1), Δ3 = 0.45 GHz (0.01501 cm−1), Δ4 = 0.35 GHz (0.01167 cm−1), with curvatures in the range 25–35 cm−1 T−2. Table S1† summarizes the characteristic relevant parameters of this compound; more details can be found in the ESI Section S2.†
Although the tunneling splittings, Δi, in this kind of complexes are relatively small, their curvatures ki, are remarkably low due to the low value of S. A further advantage of CTs derived from hyperfine coupling is the fact that for a given vanadyl complex there are CTs at four different transition frequencies, with the widest tunneling splitting being 50% larger than the narrowest. Since the values of the hyperfine coupling can vary from complex to complex, more opportunities for obtaining a resonance at the appropriate microwave source (L-band, 0.8–1.4 GHz, ∼0.03–0.045 cm−1) are possible,22,27,28 as well as novel possibilities to operate a multi-qubit system by applying local magnetic fields.29
Influence of hyperfine coupling on the CTs
Although estimating the variation of A with distortions is computationally expensive for heavy atoms,30 the effect of a parameter strain on these CTs can be estimated from Fig. 4. A relatively large deviation of 15% in the value of either A⊥ or A∥ has an effect on the transition frequency that is equivalent to a magnetic noise of about 10 mT, meaning the resilience towards magnetic noise is expected to be in tandem with a resilience towards vibrational noise. Therefore, high resilience is expected to be obtained using this hyperfine-driven approach. The price to pay for this is the equipment needed to access the very low energies that characterize these CTs, which will make them more challenging to detect and use. The generalization of this case study would be relevant to other hyperfine-based spin qubits such as the flip-flop qubit scheme based on 31P impurities in a 28Si Matrix.31Antiprismatic holmium POM complex
Behavior of the CTs
The complex HoW10 behaves as a molecular spin qubit where, as mentioned above, certain quantum resonances were demonstrated to be exceptionally robust against a highly concentrated electronic spin bath (coherence times T2 = 8 μs at 1% concentration in an isostructural YW10 matrix).13 This behavior is due to the large tunneling splitting in the ground multiplet anticrossings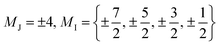 (Fig. 5a), which ultimately can be related with the molecular structure (Fig. 3c) and its distortions (Fig. 5b). This tunneling splitting has been experimentally determined to be ΔCT = 9 GHz (0.3 cm−1).32 A recent effort has been made to rationalize the limit of the T2 divergence at the CTs in terms of the nuclear spin bath,33 but a study in terms of molecular structure is still lacking.
(Fig. 5a), which ultimately can be related with the molecular structure (Fig. 3c) and its distortions (Fig. 5b). This tunneling splitting has been experimentally determined to be ΔCT = 9 GHz (0.3 cm−1).32 A recent effort has been made to rationalize the limit of the T2 divergence at the CTs in terms of the nuclear spin bath,33 but a study in terms of molecular structure is still lacking.
 | ||
| Fig. 5 (a) Zeeman diagrams (Bz) for the ground multiplet of HoW10 with the CF parameters reported in the ESI Section S3† (black lines) and with B44 parameters that are 2σ larger (blue lines) or 2σ smaller (red lines), see text for details. Energy origin has been chosen at the center of the anticrossing for convenience. (b) Coordination sphere of HoW10, emphasizing the deviation from the ideal D4d symmetry: a skew angle ϕ ≠ 45° and the off-center position of Ho h ≠ h′. (c) Evolution of the calculated tunneling splitting ΔCT for rising values of angular distortion α. The average crystallographic value is marked with a vertical line. (d) Evolution of ΔCT for rising values of the vertical displacement d. The averaged crystallographic value is marked with a vertical line and the splitting determined by EPR is marked with a horizontal line. | ||
To describe this system, one needs to extend the Hamiltonian in eqn (6) by including Crystal Field parameters:
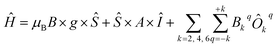 | (7) |
In terms of the analysis of the CF parameters, we focused on the B44 parameter, since the MJ = ±4 ground doublet together with the C4 coordination symmetry in HoW10 mean that Ô44 (or, equivalently, Ô64) is the extradiagonal operator that governs the anticrossings in this system (see ESI Section S3†). We used the reported average value of B44 = 3.14 × 10−3 cm−1; as a variation range, ΔB44 = B44 ± 2σ, we chose twice the empirical width for the Gaussian distribution 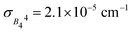 responsible for the observed inhomogeneous broadening.13
responsible for the observed inhomogeneous broadening.13
We solved the system for increasing values of B44 in 43 steps and processed each case automatically with our script to extract magnetic fields, BCT, transition energies, Δi, and curvatures, ki, of each of the 43 × 8 = 344 anticrossings in the desired energy window (in this case, E < 15 GHz ≈ 0.5 cm−1). Our numerical determination of Δi and ki at the anticrossings here serves as a confirmation of an approximate but excellent analytical solution of a problem that was already discussed in ref. 13 and that was also employed in the V(IV) above: the curvature is analytically estimated as k = γz2/2Δ, with γz = g × ΔMJ × μB, where g is 1.25 for Ho3+ and ΔMJ is equal to 8. These parameters are summarized in Table 1.
Control of CTs by crystal field
Both the transition energies and the curvatures of the anticrossings vary with the extradiagonal parameter B44. From the point of view of the chemical structure, the presence of any extradiagonal parameters in this structure is related with the distortion of the coordination sphere with respect of a perfect D4d. This has commonly been attributed, in absence of calculations, to the C4-preserving skewing distortion characterized by an angle ϕ (see Fig. 5b). This skew angle has been structurally characterized in at least four POM families with LnO8 similar coordination environments: LnW10, [Ln(β2-SiW11O39)2]13− (ref. 35) [Ln(β-Mo8O26)2]5− and [Ln{Mo5O13(OCH3)4NNC6H4-p-NO2}2]3−.36 Depending on the Ln ion, skew angles in the range 39° < ϕ < 44.5° have been found but no rationalization has been done in terms of the molecular structure.In general, the dependence of the extradiagonal parameters with the distortions are neither linear nor simple. To test the most commonly invoked hypothesis, we studied an idealized version of HoW10 where the coordination sphere is a perfect square antiprism except for the skew angle ϕ ≠ 45°. The Δ vs. ϕ dependence shows that the experimental average skew angle ϕ = 44.2° in HoW10 only accounts for a small fraction of the experimental tunneling splitting (Fig. 5c). Undoubtedly, other molecular distortions play a significant role in the appearance of the large Δ in this case. Among these are surely the off-center position of Ho3+, which is 2d = h − h′ = 0.05 Å closer to one of the [W5O18]6− moieties, and the non-coplanarity of the planes containing the two O4 squares, which in this case form an angle β = 1.11°.
We explored the influence of the off-center vertical displacement in the position of Ho3+, expressed as d (see Fig. 5b). We found a much stronger effect of this experimental distortion in the crystal structure compared with the torsion angle. The experimental splitting, is completely recovered by the combination of the experimental (averaged) skew angle ϕ = 44.2 and d = 0.0225 Å, remarkably close to the experimental (averaged) value d = 0.025 Å (see Fig. 5d), with the latter having the responsibility for most of the tunneling splitting and the former playing a comparatively minor role. This is expected to change from case to case along the different series of near-D4d POMs, given the different distortions that they present (accounted by ϕ and d values).
Of course, to understand the behavior beyond this static picture that employ averaged crystallographic positions at high temperature, one would need to consider the thermal displacements due to vibrations at any finite temperatures. The degree of structural variation that one might expect from vibrations in the solid state, and in particular the magnitude of the real-time distortions of Ln-ligand distances in comparatively soft lanthanide complexes were estimated recently by some of us from the study of sub-picosecond dynamics of spin energy levels in magnetic biomolecules.37 This allows an upper bound to the instantaneous distortions expected at low temperature to be extracted: instantaneous distortions of up to 0.01–0.02 Å in the coordination bond length are calculated in the femtosecond time scale, with averaged distortions decreasing with the averaging time following a square root law (see ESI Section S5 for details†).
While a complete analysis of the static and dynamic distortions in the Ho3+ coordination sphere HoO8 in the different series of POMs is outside the scope of the present work, the theoretical framework presented herein, combined with a recently developed theoretical methodology,38 would allow the systematic analysis and rationalization of the resilience of CTs of the different POMs against thermal noise.
Let us rationalize the comparison between anticrossings in HoW10 and in vanadyl complexes. The differences in ΔCT, g and in MJ result in curvatures for HoW10 of approximately 35 cm−1 T−2, meaning the protection against magnetic noise is comparable or worse than in the vanadyl case. In terms of resilience towards vibrational noise, one can consider that HoW10 molecules which in the timescale of the pulsed EPR experiment present an extradiagonal parameter that deviates  from the average value of B44 present a larger (or smaller) transition frequency; this effect is comparable to a local magnetic field of over 25 mT, again similar or worse than in the vanadyl case. In terms of molecular approaches to CTs, HoW10 serves here as an example of CT based on the crystal field in lanthanide ions. In comparison with the strategy of employing S = 1/2 systems with CTs based on hyperfine coupling such as vanadyl systems, employing lanthanide ions offer the possibility of the chemical design of molecules with a certain control over crystal field, as a way of tuning ΔCT. In the case of HoW10, ΔCT = 9 GHz, allowing to access the CTs with commercial X-band equipment.
from the average value of B44 present a larger (or smaller) transition frequency; this effect is comparable to a local magnetic field of over 25 mT, again similar or worse than in the vanadyl case. In terms of molecular approaches to CTs, HoW10 serves here as an example of CT based on the crystal field in lanthanide ions. In comparison with the strategy of employing S = 1/2 systems with CTs based on hyperfine coupling such as vanadyl systems, employing lanthanide ions offer the possibility of the chemical design of molecules with a certain control over crystal field, as a way of tuning ΔCT. In the case of HoW10, ΔCT = 9 GHz, allowing to access the CTs with commercial X-band equipment.
Cubic holmium POM complex
Behavior of the CTs
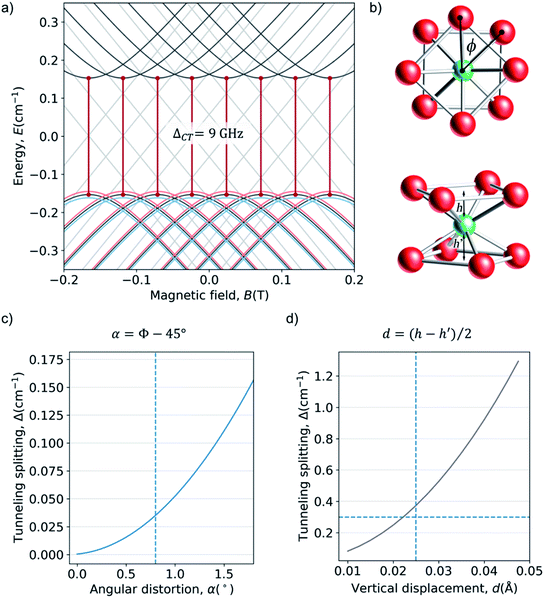
As a last case study case we chose a Ho3+ ion in a cubic or near-cubic environment, where the high symmetry can produce a highly degenerate low-energy spectrum with 40 electronuclear spin levels within a ∼2 cm−1 window. This is the case of a cubic, in short, HoPd12 POM (Fig. 3e and f).39,40 On a preliminary study on this system, we employed a minimalistic theoretical treatment that neglected the nuclear spin to suggest that the avoided crossings could result in exceptionally high coherence times.41 Herein, we extend that simplified Hamiltonian to include the hyperfine interaction (eqn (7)).What in the original study appeared as a ground spin doublet and a closely lying triplet (Fig. 3f) is after consideration of hyperfine coupling, which we assumed equal to the value for A = 0.83 GHz (0.0277 cm−1), transformed into a much more complicated structure. We have now five manifolds displaying an intricated set of anticrossings (see ESI for a detailed analysis†). There are of course an enormous number of possible CTs in this system, of which we have selected just two for illustration. In absence of distortion, there is a promising region between the third and the fourth manifolds, where transitions can be found near the X-band energy window and with rather small curvature, which result from the competition between the effective energy level repulsion exerted by the upper and lower manifolds.
Control of CTs by crystal field
Starting from this energy level scheme, the application of a moderate structural axial compression was studied in order to estimate the variation on the relative energies upon distortion of the exact cubic symmetry (Fig. 6c). Note that any possible distortion will create a comparable effect, and in this respect note the recent experimental results on quantum coherent spin-electric control in molecular nanomagnets, where a quantum coherent manipulation of spin states was achieved relying on minute distortions created by an external electric field.59 Compression rate is defined as c = ((h0 − hc)/h0) × 100. Calculations up to c = 1% show that the main effect of increasing the axial compression is to rise the energy of the “light blue” manifold (see Fig. 6d–f for three snapshots of the energy level scheme at different compressions).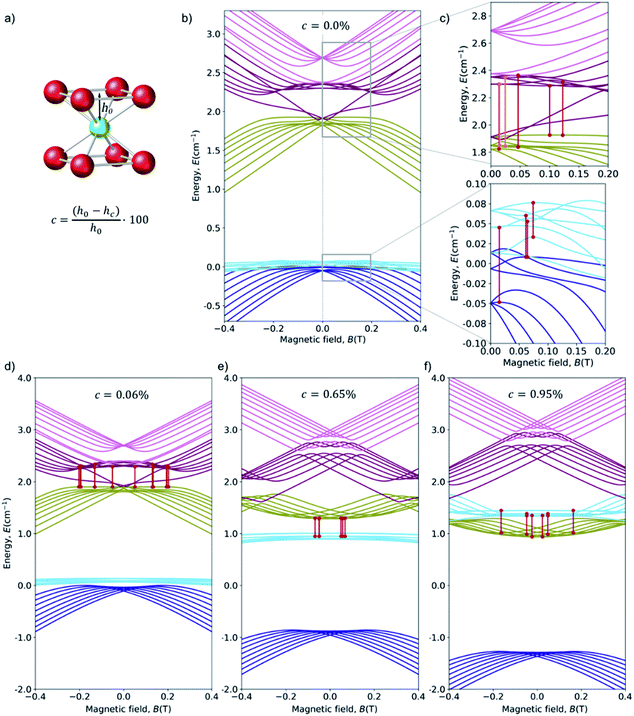 | ||
| Fig. 6 (a) Coordination sphere of HoPd12, emphasizing the deviation we create from the ideal Oh cubic symmetry via an axial compression c. The distance hc between the Ho3+ ion and the upper (or lower) O4 planes is progressively decreased from its ideal value hc = h0 (c = 0%) down to hc = 0.99 × h0 (c = 1%). (b) Zeeman diagrams (Bz) for the low energy region with the average crystal field parameters. Each color corresponds to an octuplet with consistent Zeeman behavior at high fields. For convenience, the energy origin has been chosen at the center of the fundamental multiplets in the non-distorted cube. (c) Zoom of the upper and lower region and the avoided crossings with Δ in the range: (up) 9–30 GHz (0.3–1 cm−1) and (down) 0.8–15 GHz (0.03–0.5 cm−1). Minimum and maximum value of the curvature of the highlighted CTs, in cm−1 T−2: (up) 0.0–70 and (down) 2.5–26. (d) 0.06% of compression (e) 0.65% of compression (f) 0.95% of compression. More details in ESI Section S4b.† | ||
While this cubic system is in many aspects analogous to HoW10, the novel ingredient in this case is the high degeneracy in the spin states, which gives rise to a competition of anticrossings. Our calculations points towards a very high probability of finding suitable CTs in this compound, both in the ideal cubic geometry and also if the experimental reality of the crystallization and/or cooling processes create minor distortions.
Among the large number and variety of CTs that can be found on this system, we can highlight the transition between levels 5 and 14 at a field 0.0247 T, with a transition energy Δ = 15 GHz (0.50 cm−1). See Fig. 6c up. Not only are the two levels are very flat, with curvatures k5 = 0.82386 and k14 = 0.39665: the curvature of both are in the same direction, meaning the second derivative of the transition energy is the difference – instead of the addition – of their curvatures.
Moreover, comparing HoPd12 with previous systems, we conclude that HoPd12 offers a unique protection from magnetic noise but an extreme sensitivity to molecular distortions. The reason for this is that the magnitude of ΔCT in some of the CTs is not solely determined by a tunneling splitting, but rather by the energy difference between two different manifolds. In other words, the change in the diagonal CF terms directly affect the transition energy. Even in absence of dynamical calculations, this is likely to mean a high thermal effect, since any distortion will dramatically affect the transition energies, precisely at the CTs. Comparison with previous studies on the time-averaged effects of vibrations on spin energy levels48 allows us to expect important spectral diffusion effects, which should be addressed experimentally by hole-burning. A way of looking at the difference between HoPd12 and HoW10 in the control requirements for the electrical manipulation of CTs is by comparing the effect of a vertical compression, c, for HoPd12 to the effect of a d in HoW10. Linear interpolating from Fig. 5d, shows that a vertical displacement of the Ho atom of the order of 10−6 Å results in a variation of Δ of about 1 MHz, so in the range of what is achieved in the experiments on HoW10via an electrical field.59 A comparable compression onto HoPd12 results, for transition 21–30 (Δ = 13.5 GHz = 0.45 cm−1, k = 5.2 cm−1 T−2) (see ESI Section S4a†), in a change of about 200 MHz (see ESI Section S4a†): an effect that is stronger by two orders of magnitude. This means that the extraordinary sensitivity of HoPd12 against molecular distortions creates a unique situation also in terms of electrical control of spin states at the CT. Note that to validate these predictions we are still missing an experimental EPR spectrum of HoPd12, which is predicted to present an extremely complex structure. Most importantly, all relevant transitions are occurring from excited levels, which will be depopulated at low temperature. As an alternative, if the temperature is high enough, T2 will be limited in practice by a relatively fast T1, thus limiting the actual applicability of this system.
Conclusions
Anticrossings between quantum states are the source of different kinds of attractive physical phenomena, including clock transitions. At the same time, these optimal working points cannot be externally tuned by an external magnetic field and need to be tuned by chemical means. In this work we have addressed this problem theoretically by developing a python-based computational tool for the systematic analysis and chemical optimization of CTs. We employed the code to study three representative systems from lower to higher complexity on its electronic structure and Hamiltonian.To analyze the influence of transverse hyperfine coupling in simple S = 1/2 systems, we started by studying CTs in V(IV) complexes. More precisely, in vanadyl complexes the hyperfine coupling is relatively robust against distortions from the coordination environment, a good protection against magnetic noise can be obtained in these systems. Nevertheless, these CTs present very low energies that make them difficult to access experimentally.
Next, by studying HoW10, a paradigmatic system where CTs arise from the ligand field, we numerically rationalized the variation of both the transition frequency and the curvature of CTs with different kinds of molecular distortions from the ideal D4d symmetry and give insights about the influence of the distortions that originates the anticrossings. Compared with the vanadyl case, we found a large sensitivity towards molecular distortions, since the energy levels are controlled by the crystal field, and a similar protection against magnetic noise. In addition to CTs with quantum tunneling splitting proportional to a most common frequency EPR band, such as X-band. Our final case study was a near-cubic HoPd12 polyoxopalladate, which served to illustrate the cubic high-symmetry limit in which the ground state determined by the CF contains a large admixture of energy levels. In this regime we found new kinds of CTs resulting from different combinations of anticrossing levels, that result in a unique sensitivity to molecular distortions, offering a large range of tunneling splitting frequencies; and an equally unique protection from magnetic noise.
Note that CTs do not only appear in the context of molecular spin qubits. Rather, they are a general kind of quantum transitions that are uniquely robust against environmental noise. CTs are known since their use in the first cesium atomic standards of frequency and time interval,42 which gave rise to similar effects in atomic traps or atomic lattices,43–46 and to the so-called ZEFOZs (for ‘zero first order Zeeman shift’).47,48 Unique physical effects have been reported in very different systems and fields and employing a variety of terms, including “avoided level crossings”,17,49 “avoided resonance crossings”50 and “Landau-Zener crossings”.51–55 The method developed and employed in this work is general and therefore can be used to study the evolution of the energy levels and crossings of a quantum system when an external physical stimulus is applied (magnetic field, electric field, pressure, etc.). It can equally be used to automatically explore physical or chemical modifications of any kind of systems presenting anticrossings, independently of the nature of the noise. The model employed herein can be applied to facilitate the detection of anticrossings in a number of fields, from the theoretical molecular design of strong coupling between plasmons and single-molecule excitons56,57 to the prediction of the electronic and optical properties of twisted bilayer graphene.58
As a final remark, the present work serves as a first numerical estimate of the sensitivity to structural or vibrational distortions of different kinds of CTs. Note it is possible to adjust molecular geometries by either physical pressure59 or chemically.60,61 Furthermore, recent experimental progress in the coherent control of spin states employing electrical fields,62 where the control is mediated via minimal molecular distortions, are another possible avenue for the applicability of the present methodology. On the other hand, if coupled with recently developed theoretical methodology,38 this could serve to rationalize the influence of molecular vibrations in the effectiveness of CTs, and, eventually, to the chemical engineering of molecular spin qubits where the electron spin is not just shielded from magnetic noise but at the same time also protected from molecular vibrations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work has been funded by the EU (ERC-CoG 647301 DECRESIM, ERC-AdG-788222-Mol2D, COST 15128 Molecular Spintronics Project and the EU-QUANTERA project SUMO) the Spanish MINECO program (grants MAT2017-89993 and CTQ2017-89528 cofinanced by FEDER (EQC2018-004888-P), and Excellence Unit María de Maeztu MDM-2015-0538), and the Generalitat Valenciana (PROMETEU/2017/066, PROMETEU/2019/066) and PO FEDER (IDIFEDER/2018/061). S. C. S. thanks the Spanish MINECO for a Juan de la Cierva Incorporación postdoctoral Fellowship. S. G. S acknowledges the Ministry of Education of Spain (grant PRE2018-083350).References
- R. Hanson, V. V. Dobrovitski, A. E. Feiguin, O. Gywat and D. D. Awschalom, Science, 2008, 320, 352 CrossRef CAS PubMed.
- M. Steger, K. Saeedi, M. L. W. Thewalt, J. J. L. Morton, H. Riemann, N. V. Abrosimov, P. Becker and H.-J. Pohl, Science, 2012, 336, 1280 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301 CrossRef PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87 CrossRef.
- R. Hanson, V. V. Dobrovitski, A. E. Feiguin, O. Gywat and D. D. Awschalom, Science, 2008, 320, 352 CrossRef CAS PubMed.
- D. Scarabelli, M. Trusheim, O. Gaathon, D. Englund and S. J. Wind, Nano Lett., 2016, 16, 4982 CrossRef CAS PubMed.
- M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. Hollenberg, Phys. Rep., 2013, 528, 1 CrossRef CAS.
- J. T. Muhonen, J. P. Dehollain, A. Laucht, F. E. Hudson, R. Kalra, T. Sekiguchi and A. Morello, Nat. Nanotechnol., 2014, 9, 986 CrossRef CAS PubMed.
- C. Zener, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1932, 137, 696 Search PubMed.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51, 12565 CrossRef PubMed.
- J. M. Zadrozny, A. T. Gallagher, T. D. Harris and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 7089 CrossRef CAS PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348 CrossRef CAS PubMed.
- C. A. Collett, K. I. Ellers, N. Russo, K. R. Kittilstved, G. A. Timco, R. E. Winpenny and J. R. Friedman, Magnetochemistry, 2019, 5, 4 CrossRef CAS.
- R. T. Harding, S. Zhou, J. Zhou, T. Lindvall, W. K. Myers, A. Ardavan, G. A. D. Briggs, K. Porfyrakis and E. A. Laird, Phys. Rev. Lett., 2017, 119, 140801 CrossRef CAS PubMed.
- J. J. Baldoví, J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Dalton Trans., 2012, 41, 13705 RSC.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961 CrossRef PubMed.
- J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2014, 35, 1930 CrossRef PubMed.
- I. D. Ryabov, J. Magn. Reson., 1999, 140, 141 CrossRef CAS PubMed.
- C. J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183 RSC.
- S. Cardona-Serra, A. Gaita-Ariño, E. Navarro-Moratalla and S. Sanvito, J. Phys. Chem. C, 2018, 122, 6417 CrossRef CAS.
- S. Cardona-Serra, A. Gaita-Ariño, M. Stamenova and S. Sanvito, J. Phys. Chem. Lett., 2017, 8, 3056 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154 CrossRef CAS PubMed.
- C. V. Grant, W. Cope, J. A. Ball, G. G. Maresch, B. J. Gaffney, W. Fink and R. D. Britt, J. Phys. Chem. B, 1999, 103, 10627 CrossRef CAS PubMed.
- P. Pietrzyk and Z. Sojka, Appl. Magn. Reson., 2011, 40, 471 CrossRef CAS PubMed.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682 RSC.
- F. Neese, Spin-Hamiltonian parameters from first principle calculations: theory and application, in High Resolution EPR, Springer, New York, 2009, pp. 175–229 Search PubMed.
- G. Tosi, F. A. Mohiyaddin, V. Schmitt, S. Tenberg, R. Rahman, G. Klimeck and A. Morello, Nat. Commun., 2017, 8, 1 CrossRef CAS PubMed.
- S. Ghosh, S. Datta, L. Friend, S. Cardona-Serra, A. Gaita-Ariño, E. Coronado and S. Hill, Dalton Trans., 2012, 41, 13697 RSC.
- L. Escalera-Moreno, A. Gaita-Ariño and E. Coronado, Phys. Rev. B, 2019, 100, 064405 CrossRef CAS.
- S. Cardona-Serra and A. Gaita-Ariño, Dalton Trans., 2018, 47, 5533 RSC.
- J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Ariño and C. Giménez-Saiz, Inorg. Chem., 2014, 53, 9976 CrossRef PubMed.
- J. J. Baldoví, Y. Duan, C. Bustos, S. Cardona-Serra, P. Gouzerh, R. Villanneau, G. Gontard, J. M. Clemente-Juan, A. Gaita-Ariño, C. Giménez-Saiz and A. Proust, Dalton Trans., 2016, 45, 16653 RSC.
- L. E. Rosaleny, K. Zinovjev, I. Tuñón and A. Gaita-Ariño, Phys. Chem. Chem. Phys., 2019, 21, 10908 RSC.
- A. Ullah, J. Cerdá, J. J. Baldoví, S. Varganov, J. Aragó and A. Gaita-Ariño, J. Phys. Chem. Lett., 2019, 10(24), 7678–7683 CrossRef CAS PubMed.
- E. V. Chubarova, M. H. Dickman, B. Keita, L. Nadjo, F. Miserque, M. Mifsud, I. W. C. E. Arends and U. Kortz, Angew. Chem., Int. Ed., 2008, 47, 9542 CrossRef CAS PubMed.
- N. V. Izarova, M. T. Pope and U. Kortz, Angew. Chem., Int. Ed., 2012, 51, 9492 CrossRef CAS PubMed.
- J. J. Baldoví, L. E. Rosaleny, V. Ramachandran, J. Christian, N. S. Dalal, J. M. Clemente-Juan, P. Yang, U. Kortz, A. Gaita-Ariño and E. Coronado, Inorg. Chem. Front., 2015, 2, 893 RSC.
- L. Essen and J. V. Parry, Nature, 1955, 176, 280 CrossRef.
- M. Takamoto, F. L. Hong, R. Higashi and H. Katori, Nature, 2005, 435, 321 CrossRef CAS PubMed.
- T. Rosenband, P. O. Schmidt, D. B. Hume, W. M. Itano, T. M. Fortier, J. E. Stalnaker, K. Kim, S. A. Diddams, J. C. J. Koelemeij, J. C. Bergquist and D. J. Wineland, Phys. Rev. Lett., 2007, 98, 220801 CrossRef CAS PubMed.
- A. D. Ludlow, M. M. Boyd, T. Zelevinsky, S. M. Foreman, S. Blatt, M. Notcutt, T. Ido and J. Ye, Phys. Rev. Lett., 2006, 96, 033003 CrossRef PubMed.
- A. D. Ludlow, T. Zelevinsky, G. K. Campbell, S. Blatt, M. M. Boyd, M. H. de Miranda, M. J. Martin, J. W. Thomsen, S. M. Foreman, J. Ye, T. M. Fortier, J. E. Stalnaker, S. A. Diddams, Y. Le Coq, Z. W. Barber, N. Poli, N. D. Lemke, K. M. Beck and C. W. Oates, Science, 2008, 319, 1805 CrossRef CAS PubMed.
- G. Heinze, C. Hubrich and T. Halfmann, Phys. Rev. Lett., 2013, 111, 033601 CrossRef PubMed.
- M. Zhong, M. P. Hedges, R. L. Ahlefeldt, J. G. Bartholomew, S. E. Beavan, S. M. Wittig, J. J. Longdell and M. J. Sellars, Nature, 2015, 517, 177 CrossRef CAS PubMed.
- J. P. Pekola, D. S. Golubev and D. V. Averin, Phys. Rev. B, 2016, 93, 024501 CrossRef.
- J. Wiersig, Phys. Rev. Lett., 2006, 97, 253901 CrossRef PubMed.
- S. N. Shevchenko, S. Ashhab and F. Nori, Phys. Rep., 2010, 492, 1 CrossRef CAS.
- M. Urdampilleta, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195412 CrossRef.
- G. Sun, X. Wen, M. Gong, D. W. Zhang, Y. Yu, S. L. Zhu, J. Chen, P. Wu and S. Han, Sci. Rep., 2015, 5, 8463 CrossRef CAS PubMed.
- A. Russomanno, A. Silva and G. E. Santoro, Phys. Rev. Lett., 2012, 109, 257201 CrossRef PubMed.
- A. Palii, B. Tsukerblat, J. M. Clemente-Juan, A. Gaita-Ariño and E. Coronado, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184426 CrossRef.
- R. Chikkaraddy, B. De Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, H. Ortwin and J. J. Baumberg, Nature, 2016, 535, 127 CrossRef CAS PubMed.
- T. Itoh, Y. S. Yamamoto and T. Okamoto, Phys. Rev. B, 2019, 99, 235409 CrossRef CAS.
- H. Patel, L. Huang, C. J. Kim, J. Park and M. W. Graham, Nature, 2019, 10, 1 Search PubMed.
- J. Hao, F. Hu, J. T. Wang, F. R. Shen, Z. Yu, H. Zhou, H. Wu, Q. Huang, K. Qiao, J. Wang, J. He, L. He, J. R. Sun and B. Shen, Chem. Mater., 2020, 32, 1807 CrossRef CAS.
- Y. Mizuguchi, E. Paris, T. Sugimoto, A. Iadecola, J. Kajitani, O. Miura, T. Mizokawa and N. L. Saini, Phys. Chem. Chem. Phys., 2015, 17, 22090 RSC.
- H. Kamebuchi, A. Nakamoto, T. Yokoyama and N. Kojima, Bull. Chem. Soc. Jpn., 2015, 88, 419 CrossRef CAS.
- J. Liu, J. Mrozek, Y. Duan, A. Ullah, J. J. Baldoví, E. Coronado, A. Gaita-Ariño and A. Ardavan, 2020, arXiv:2005.01029 [cond-mat.mes-hall].
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01187h |
| This journal is © The Royal Society of Chemistry 2020 |