Strain visualization for strained macrocycles

Abstract

Strain has a unique and sometimes unpredictable impact on the properties and reactivity of molecules. To thoroughly describe strain in molecules, a computational tool that relates strain energy to reactivity by localizing and quantifying strain was developed. Strain energy is calculated local to every coordinate in the molecule and areas of higher strain are shown experimentally to be more reactive. Not only does this tool directly compare strain energy in parts of the same molecule, but it also computes total strain to give a full picture of molecular strain energy. It is freely available to the public on GitHub under the name StrainViz and much of the workflow is automated to simplify use for non-experts. Unique insight into the reactivity of curved aromatic molecules and strained alkyne bioorthogonal reagents is described within.

---

Introduction

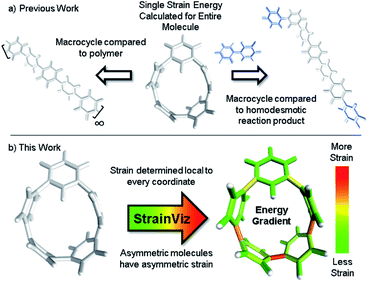
Strain has a unique impact on molecular properties and reactivity. Macrocyclic strain is leveraged in chemical biology for bioorthogonal reactivity^1,2 and in polymer chemistry for ring opening metathesis.^3,4 Additionally, graphitic macrocycles, such as carbon nanohoops,⁵ have enhanced solubility,⁶ remarkable photophysical properties,^7,8 and reactivity^9–12 that all arise from strain. These attributes, and improvements in methods for their synthesis,^13–16 have caused a renewed interest in strained macrocyclic molecules. While methods for probing solubility and photophysical properties are well established, macrocyclic strain is a challenging characteristic to analyze and quantify. The best known methods for calculating macrocyclic strain energy (the potential energy released upon breaking the macrocycle) compare heat of formation for strained and unstrained molecules in a theoretical strain releasing reaction.^17–19 While combustion calorimetry can be used,^20,21 computationally determined energies are now standard due to the quality of current computational methods and the challenge of obtaining accurate experimental results. It has become routine to report the calculated strain energy of new strained macrocycles with their synthesis due to the fundamental effects of this tension.

Total strain energies are commonly reported and the strain in specific parts of the molecule cannot be discerned. While the total strain energy does provide some information, it does not correlate perfectly to reactivity. For example, when the same amount of strain energy is spread over more atoms, the molecule is more stable than when it is concentrated in fewer atoms. If this is corrected for by dividing by the total atoms, non-participating atoms artificially lower the strain energy per atom determined. Local strain can sometimes be inferred in highly symmetric molecules, such as strain per phenylene in a cycloparaphenylene (CPP). However, unsymmetric molecules have unevenly distributed strain energy leading to locations of higher reactivity that may be unintuitive. Some alternative metrics have been devised to measure local strain. For example, the deplanarization of an aromatic ring, torsional angle in a biphenyl segment, and bond lengths can be compared to an unstrained comparative molecule.^15,22 For non-planar π-systems, a measure of pyramidalization was developed that estimates relative strain in non-planar aromatics such as corannulene and fullerene.^23,24 However, these measurements are not quantitative and, therefore, cannot be compared across molecules which limits their utility. Even when combining total strain calculation with these other metrics, it results in an incomplete depiction of molecular strain energy.

A method that determines strain both quantitatively and locally is quite useful. Therefore, a computational method was developed that identifies the quantity of strain energy local to every coordinate (bond, angle, and torsional angle) in a molecule. This strain visualization software is called StrainViz and has been made freely available. A similar method was previously reported for mechanochemistry where unstrained molecules are stretched and the tension that appears upon stretching is analyzed.²⁵ Attempts were made to apply this method to macrocycles by comparing stretched and unstretched macrocycles as well as conformational changes that induce stretching,^26,27 however, the inherent strain was not addressed. StrainViz can find this elusive strain energy. Our new method was evaluated to establish its accuracy using prior calculated strain energies and experimental reaction results from the literature. It is freely available on GitHub.²⁸ The resulting computational method provides an interactive and insightful strain map. Knowledge of specific strain location facilitates and enhances synthetic efforts towards strained macrocycles by providing the exact and specific impact on strain of structural changes in a molecule. As is demonstrated herein with StrainViz, it is now possible to make inferences about the local properties and reactivity in strained molecules.

Computational method

This new computational method is fundamentally an advancement on the use of a homodesmotic reaction to estimate strain energy (Fig. 1, previous work going right).²⁹ Here, the macrocyclic strain energy may be defined as the energy associated with deforming a linear molecular segment when included in a macrocycle. For example, the deformation of a phenylene when included in a CPP. To use a homodesmotic reaction to determine this quantity, the molecular geometry is optimized and the single point energy of the lowest energy conformation is determined (E_macrocycle). In this state, the molecule retains strain energy that cannot be realized until the molecule is broken so that tension is released. Breaking the molecule creates radicals at each side of the break that must be capped with a capping molecule that is similarly broken and placed at each end aiming to retain the local environment of the ends. Then, the lowest energy conformation of this strain released theoretical molecule (E_linear) is calculated and compared to the original molecule while accounting for the atoms added to cap the broken ends (E_cap) by determining the single point energy of the capping molecule shown in blue in Fig. 1. The difference in total energy between the starting materials and products of this theoretical homodesmotic reaction is the total strain energy (E_strain) in the macrocycle shown in eqn (1).

E_strain = (E_macrocycle + E_cap) − E_linear (1)

Fig. 1 (a) Strain energy is calculated by comparing the strained molecule to an unstrained polymer or homodesmotic reaction product resulting in a single strain energy for the entire molecule. (b) StrainViz determines strain energy local to every coordinate.

This is an example of how a homodesmotic reaction may be used for estimating strain energy. The homodesmotic reaction has been rigorously defined elsewhere.³⁰

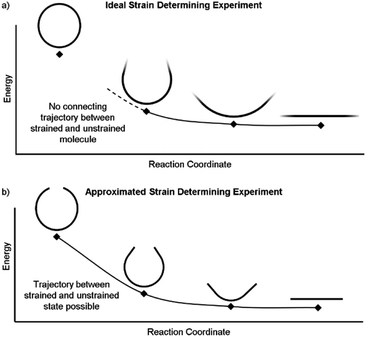
It is also possible to disassemble the molecule into an infinite polymer and compare the repeating unit energies in both the macrocycle and the unstrained polymer.^31,32 If it were possible to connect these geometries by creating a trajectory between the strained and unstrained states, one could comment on how the energy of each atom changes to release strain energy as the trajectory proceeds. Ideally, the trajectory would begin in the optimized geometry of the strained molecule and descend to an unstrained infinite polymer (Fig. 2a). The macrocycle cannot be broken without changing the atomic environment and introducing additional strain into the analysis. A theoretical trajectory between the strained macrocycle and unstrained infinite polymer that isolates macrocyclic strain energy is therefore impossible.

Fig. 2 (a) This ideal experiment begins with the strained macrocycle and ends with an infinite polymer where the strain has been released. (b) By removing part of the molecule, the beginning and end geometries can now be connected by a strain releasing trajectory. This allows the local trajectory of each atom to be determined.

It is, however, possible to fragment the molecule so that it may descend into an unstrained state without introducing new strain. By deleting certain atoms, the trajectory shown in Fig. 2b becomes possible and allows the initial geometry to share the location of its atoms (highlighted in the inset of Fig. 3) with the strained molecule while still relaxing to an unstrained state upon geometry optimization. The trajectory of each atom accurately represents the trajectory of atoms in the strained molecule to atoms in an unstrained state. This approximates an ideal strain energy determining experiment by averaging these trajectories for multiple fragments.

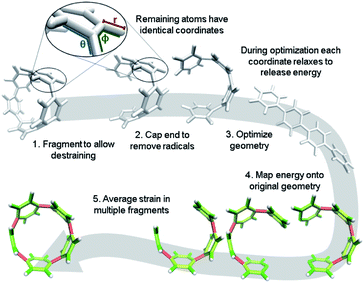Fig. 3 Workflow for strain analysis. The coordinates in each molecule fragment relax to release strain energy that is quantified per coordinate (r: bond length, θ: angle, ϕ: torsional angle).

In practice, a segment of the molecule is removed, such as a phenylene or ethylene, to create a fragment as shown in steps 1 and 2 of Fig. 3. The choice of fragments does not appear to significantly impact overall strain energy determination, however, it can impact strain distribution. Therefore, obtaining accurate results requires as many symmetrically created fragments as possible. For example, when analyzing CPPs, there should be as many fragments as there are phenylenes to be removed. Once a fragment is removed the ends are capped with hydrogen atoms. This requires the segment removed to be at least two atoms (e.g. ethylene) to accommodate replacement with hydrogens. These capping hydrogen atoms are optimized by freezing all atoms in the fragment that match the initial geometry. This ensures they do not add additional strain to the fragment when the fragment is optimized. All fragments created for the analyses in this paper are in the ESI† to remove any ambiguity.

The trajectory of each individual atom during this process follows the optimization algorithm given by the program used. In these studies, Gaussian09 (ref. 33) was used with the quasi-Newton rational function optimization (RFO) method that is the default for Gaussian03 due to it converging more smoothly than the newer direct inversion in the iterative subspace (DIIS) method.³⁴ StrainViz can also be used with Orca, delivering similar results and being free for academic users.^35,36 The energy of each atom is given by its relationship to other atoms via internal coordinates. The internal coordinates describe the distances and angles between atoms shown in a zoomed in image in Fig. 3. There are three coordinates that together describe the position of every atom relative to each other: the distance between two atoms, the angle between three atoms, and the torsional angle between four atoms. The optimization algorithm minimizes the energy of the geometry by interrogating these internal coordinates and adjusting them to release energy. The algorithm estimates a force for each coordinate (F) and, depending on step size, assigns a displacement (Δx). It is also possible to define “strain” as the force and “strain energy” as the total energy associated with that force. Multiplying the force by the displacement, as shown in eqn (2), identifies the change in energy (ΔE_{coord est}) each coordinate experiences in each step.

FΔx = ΔE_{coord est} (2)

The energy determined from this specific calculation is only an estimate. The algorithm overestimates the total energy released for each displacement due to the necessary use of redundant internal coordinates.³⁷ Therefore, each step is scaled relative to the actual change in the single point energy calculated (ΔE_{step actual} in eqn (3)) at each step.

ΔE_{coord actual} ≈ ΔE_{coord est}(ΔE_{step actual}/ΔE_{step est}) (3)

where ΔE_{step est} is the sum of all ΔE_{coord est} present. As the optimization proceeds, these energies become smaller until the relaxed geometry is found and ΔE approaches zero for all coordinates. For a given coordinate, summing the energy determined for each optimization step gives the total amount of energy stored in that internal coordinate.

After symmetrically fragmenting the molecule, optimizing the fragments, and analyzing the trajectory of the internal coordinates, this data must be displayed in a way that effectively communicates the information gathered. The effective color mapping scheme used for analyzing mechanical force was adopted.²⁵ The bond strain energy associated is simple to display because there is a single value per bond and the bonds are colored accordingly. For the energy associated with the angle between three atoms, the energy is divided in half among the two contributing bonds. Finally, for the torsional angle between four atoms, the energy is split evenly among the three bonds connecting the four contributing atoms. These maps are produced for bond, angle, and torsional strain energy in each fragment. Then the energies per bond are averaged among every fragment containing that bond and a single map for each type of strain energy. Finally, the three types are summed and a total strain map is produced.

It is important to note that almost none of the above mentioned processes are done manually. A package of freely available scripts on GitHub automate Gaussian input file creation, job submission, and VMD script generation.²⁸ Each analysis only requires the manual generation of an optimized geometry and appropriate fragments, StrainViz does the rest.

Results & discussion

With a framework in place for analyzing strained molecules, it is important to check the assumptions made when creating this method. There are three main assumptions that underpin the validity of this computational method: (1) the fragments chosen accurately represent the base molecule. (2) The sum of all energies for all internal coordinates total to an energy that is corroborated by previous methods. (3) The local strain energy determined relates to reactivity. If these three assumptions are proven valid, then StrainViz is useful for determining strain energy.

Fragments accurately represent the molecule

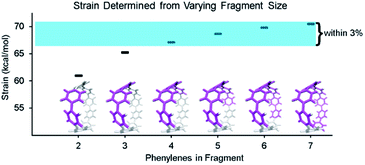
By using fragments to calculate strain energy in the molecule we lose the information provided by the portion omitted. Although it is not possible to compare the fragment directly with the base molecule, it is possible to identify differences when varying the fragment size. [8]CPP was analyzed using fragments of increasing size (Fig. 4). From this analysis we will see how much information is lost dependent on the size of the omitted portion.

Fig. 4 Fragments of [8]CPP having 2–7 phenylenes (highlighted in pink) were used in the strain analysis. Fragments retaining 50% or more of the molecule all determined strain energies within 3% of each other. All calculations were performed at the B3LYP/6-31G(d) level of theory unless otherwise noted.

When molecule fragments are being analyzed, the fragment size must be judiciously chosen to reduce the impact of edge effects where the molecule is cut. It has been previously seen, in the strain-induced retro-Huisgen cycloaddition of triazoles,³⁸ that when the edge atoms are connected to the triazole by coordinates (torsional angle across an ethyl or propyl group), results do not match expectations. Therefore, the program does not include any coordinates that contain the end capping atoms or the atoms attached to them. This trims away forces at the ends of the geometry that are most susceptible to these edge effects. By doing so, the results become more relevant regardless of fragment size, but limits how small the fragments may be made. Despite this consideration, the chosen fragment size does still have an impact on the accuracy. Within each fragment, the variability of strain energy measurement for each bond from the analysis also increases with decreasing fragment size. The four largest[8]CPP fragment sizes, shown in Fig. 4, all determine strain energies within 3% of their mean. These fragments also are internally consistent. Each individual strain energy determined for each bond is also within 3% of the mean. This consistency shows that when the fragments used are at least half the original molecule edge effects are minimal.

Energies are expectedly similar to previous results

A relevant computational technique must deliver results that are relatively consistent with previously described techniques while providing new insight. Unfortunately, there is no computational benchmark or easily obtainable experimental data for strain and the amount determined can vary depending on the technique used. For example, [12]CPP has a range of strain energies depending on the computational technique (summarized in Table 1). Given this relatively wide range in the literature, there is significant room for error in any new computational method. However, when using a similar computational technique, (entries 1–4) the range narrows significantly even when using different levels of theory. Therefore, StrainViz will be compared directly to known examples using the homodesmotic reaction at the same level of theory. Values similar to previous reports should be expected.

Table 1 Reported strain energies of [12]CPP

Strain energy	Theory	Reference
50 kcal mol^−1	B3LYP/6-31G(d)	39
48.1 kcal mol^−1	B3LYP/6-31G(d)	17
49.0 kcal mol^−1	B3LYP/6-31G(d)	40
50.2 kcal mol^−1	M06-2X/6-31G(d)	40
42 kcal mol^−1	Gaussian Pseudopotentials	31
48.3 kcal mol^−1	B3LYP/6-31G(d)	This work

---

A variety of molecules with macrocyclic strain energy were used in this analysis (Fig. 5). Given that CPPs are well studied in this respect, CPPs having six to ten phenylenes were analyzed and compared to an analysis using homodesmotic reactions (Fig. 5a).¹⁷ Comparing these two analyses, we can see that the results are most similar at larger CPP sizes. This is consistent with the aforementioned accuracy of the StrainViz analysis where larger CPP fragments result in more accurate strain energy determinations. Analyzing Itami's carbon nanobelt resulted in even better matching with previous efforts (Fig. 5b).⁴¹ The high accuracy may be owed to the fragment optimization trajectory quality. See ESI† for further comments. A recently synthesized highly strained small cyclophane from the Bodwell group⁴² and [2.2]paracyclophane⁴³ were also analyzed and confirm that StrainViz is consistent with prior computational efforts (Fig. 5c).

Fig. 5 Literature examples of strain energy determinations compared to StrainViz analysis. (a) CPP strain determined by homodesmotic reactions.¹⁷ (b) Carbon nanobelt strain energy extrapolated from increasing size belts.⁴¹ (c) [2.2]paracyclophane strain and Bodwell's more strained analogue determined by isodesmotic reaction B3LYP/6-31G(d,p)⁴³ and M06-2X/Def2TZVP⁴² respectively. Please see the ESI† for links to the 3D models.

The literature report of [2.2]paracyclophane does attempt to quantify the strain energy present in the phenylene and ethylene segments.⁴³ This was done in a similar manner to our method. The molecule was broken up and the strain energy in each fragment was determined by comparing single point energies of the strained and unstrained states. Their analysis, however, found different amounts of strain than their homodesmotic reaction; 10.2 kcal mol⁻¹ per phenylene and 5.6 kcal mol⁻¹ per ethylene summing to 31.6 kcal mol⁻¹, but 30.8 kcal mol⁻¹ from a homodesmotic reaction using the ωB97X-D functional. This begs the question which analysis is more accurate. With our method, the local strain adds up to the total strain by definition.

By corroborating results found in the literature, we establish that StrainViz determines total strain energies that are reasonable. This shows that generating a map of local strain does not compromise the total strain analysis quality. More importantly, we see exactly where in the structure the strain is distributed. We hope to confirm that local strain is more instructive than total strain for reactivity.

Local strain energy relates to reactivity

In a previous paper, we described the synthesis of CPPs having one phenylene switched from being para to meta connected.⁴⁴ We described the strain using homodesmotic reactions and concluded that the meta-CPPs are less strained than CPPs with an equal amount of phenylenes (Fig. 6). A structural strain parameter from the crystal structure, the torsional angle between adjacent phenylenes, had values above and below comparable CPPs which hinted that strain may not be evenly distributed. Lacking a tool to directly locate and quantify strain at specific locations on the molecule, we could not at that time make any further claims about strain in these molecules. Now, StrainViz locates the strain and predicts the reactivity of meta-CPPs.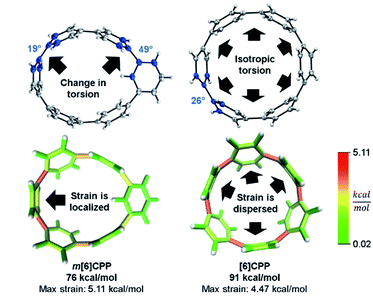

Fig. 6 Torsional angles and total strain of [6]CPP and m[6]CPP. Changing connectivity from para to meta decreases total strain, but increases local strain energy. Please see the ESI† for links to the 3D models.

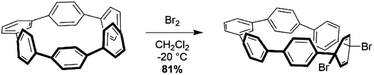
Analysis using StrainViz in Fig. 6 shows that strain is concentrated across from the meta phenylene. Changing a phenylene in a CPP from being para to meta connected relieves strain at that end of the molecule, but adds strain at the opposite end. If this program provides a meaningful molecular strain analysis, then this high strain area should react faster in a strain relieving reaction. For example, bromination of a meta-CPP should occur exactly across from the meta phenylene where the majority of the strain is located. Indeed, upon bromination of a m[6]CPP, bromination occurs exactly where predicted by our calculations (Scheme 1).

Scheme 1 Bromination of m[6]CPP.

Even more striking from the analysis is that despite meta-CPPs being less strained in total, they should be more reactive due to a higher amount of local strain relative to a CPP where strain is spread equally over the molecule. This phenomenon is seen clearly in the aforementioned publications by Yamago. In the case of either bromination¹⁰ or C–C bond activation by platinum,¹¹ a reaction at one phenylene is followed by a faster second reaction. This is not consistent with the total quantity of strain present in each reacting molecule. A homodesmotic reaction of the starting CPP and singly brominated CPP shows that the second has much less strain energy. However, when analyzed using StrainViz as shown in Fig. 7, it is clear that the singly brominated intermediate has more strain across from the first site of bromination and that the molecule has been activated to brominate the second time at a faster rate.

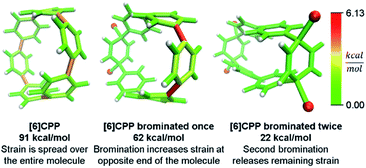Fig. 7 Strain release during bromination of [6]CPP. First bromination activates molecule to be more reactive in the second step. Please see the ESI† for links to the 3D models.

Despite these specific examples of reactivity correlating extremely well to the strain energy present at certain locations in the molecule, it is important to note that the specific reaction taking place is being aided by relief of strain to effect the transformation. This is why it is not the bond with the highest determined strain energy that is broken during the reaction, but that the chemical reactivity occurring is preferred when in proximity to higher strain energy.

Unique strain analysis of macrocycles from the literature

In addition to validating the method, we thought it instructive to provide use cases for StrainViz. Additional molecules from the literature were analyzed using this method to determine strain energies and the location of it as a heat map. The Tanaka group recently reported two strained nanobelt structures where one has a turn in it so that it forms a Möbius loop shown in Fig. 8a.⁴⁵ This geometry is intriguing in that the turn introduces additional strain energy to the molecule. The non-Möbius geometry is strained similarly to the corresponding CPP, however, the Möbius geometry is quite different. Despite having five repeating units instead of four, it is more strained overall. The additional strain is introduced at the entry points to the turn. This is similar to a polymer knot where strain is mostly located at a choke point at the knot entry.^46,47 Within the turn there is higher strain and outside of the turn there is significantly less. The symmetry of this Möbius molecule prevents direct comparison to a non-Möbius molecule, however, it is possible to instead study molecules with higher symmetry (Fig. 8b). A Vögtle belt⁴⁸ has high enough symmetry to directly compare molecularly degenerate molecules with and without a Möbius turn. The Vögtle belt has evenly distributed strain resulting in relatively little at any single point. Adding a Möbius twist places extreme strain (four times as much) on two symmetrically separated bonds at the entrance and exit of the twist. In total, strain increases from 105 kcal mol⁻¹ to 238 kcal mol⁻¹. This speaks to the challenge of synthesizing rigid Möbius molecules that are of fundamental interest.⁴⁹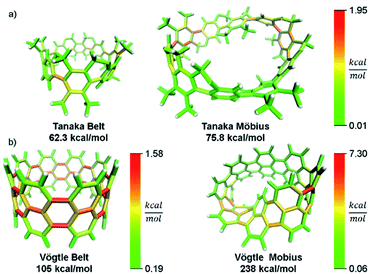

Fig. 8 Möbius molecules have more strain due to an internal twist when compared to a non-Möbius belt. (a) The Möbius molecule synthesized in the Tanaka group is more strained than the non-Möbius despite being a larger size. (b) In a symmetric Möbius molecule, strain is centered at the twist entry point. Please see the ESI† for links to the 3D models.

In addition to macrocyclic molecules, multimacrocyclic molecules can be analyzed as long as each fragment fully releases all strain present. The Yamago group has reported a highly symmetric nanoball with multiple macrocyclic connections (Fig. 9).⁵⁰ Analyzing a single panel shows that strain is spread relatively evenly around the periphery aside from some anisotropy induced by the C₂ symmetry of this lowest energy conformation. In the ball, however, it appears that there is more strain at the corners as opposed to the edges. This indicates that the three additional macrocycles in the ball add strain where they attach at the corners of a panel. As they do not apply force directly in the direction of any edges, the force is split between the edges and concentrates at the corners. This unique multimacrocyclic strain contribution is easily apparent using this analysis.

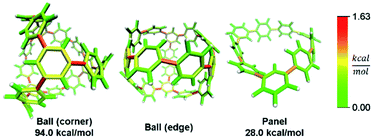Fig. 9 Strain energy present in Yamago's nanoball. More strain at the ball corners relative to the edge. Please see the ESI† for links to the 3D models.

While this analysis was designed for analyzing curved aromatic molecules, it applies widely in the analysis of strained molecules. For example, strained hydrocarbons play a very important role as bioorthogonal reagents. Specifically, cyclooctynes and trans-cyclooctenes are used as reactive reagents for copper-free click reactivity in biological media. A previous Houk group analysis⁵¹ noted that a strain energy based analysis fails to accurately predict molecular reactivity and instead used a distortion/interaction model⁵² to accurately predict reactivity. However, our novel analysis can correctly order the reactivity of these strained reagents using a local strain analysis. The analysis of cyclooctyne in Fig. 10 reveals 13.7 kcal mol⁻¹ of strain whereas trans-cyclooctene has 17.4 kcal mol⁻¹ both have nearly the same proportion (42% and 41%) located at the reactive site. This is in agreement with the relative rate of reaction with a tetrazine of 30 and 13 000 M⁻¹ s⁻¹ respectively. Furthermore, when comparing the more reactive trans-bicyclo[6.1.0]nonene to trans-cyclooctene in Fig. 10, the total strain energy increases only slightly to 18.9 kcal mol⁻¹, however, the reaction rate increases 160 fold.⁵³ By increasing the macrocycle rigidity, the strain is shifted to the reactive alkene. The trans-cyclooctene has 7.2 kcal mol⁻¹ of strain energy located in the alkene, whereas trans-bicyclo[6.1.0]nonene has 9.3 kcal mol⁻¹. This increases the reactivity more than would be predicted by total strain energy. Again, the StrainViz analysis provides the missing information that previous strain analyses lack. While this analysis does not provide accurate prediction of rates as the distortion/interaction model of the Houk group does,⁵² it may be put to good use in informing the design of new strained bioorthogonal reagents by evaluating strain local to the reactive site.

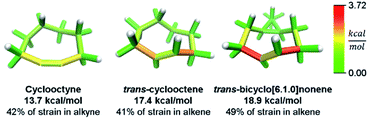Fig. 10 Strain energy in copper-free click reagents. Trans-cyclooctene is more strained than cyclooctyne, but has similar strain distribution. Increasing rigidity by addition of a cyclopropyl fusion increases strain energy and shifts it to the reactive site. Please see the ESI† for links to the 3D models.

Conclusions

A new computational method is reported for the determination of strain energy in macrocycles. This method improves on the current standard of using homodesmotic reactions to determine strain energy by locating contributions to the total strain. The robustness of the method was tested to show that fragment sizes of at least more than half of the molecule give accurate results. The method is accurate in that it delivers reasonable total strain energy relative to previous computational results. It is effective in strain promoted reaction prediction by successfully locating the site of bromination in unsymmetric molecules. Finally, a sampling of literature examples were analyzed with new insight gathered including design considerations for new strained bioorthogonal reagents. This new computational strain determination method is, therefore, broadly useful for the research of strained macrocycles.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. C., T. P. and R. J. would like to thank the National Science Foundation (NSF) for funding under grant number CHE-1800586. T. S. gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (Grant No. STA 1526/1-1 and STA 1526/2-1). This work benefited from access to the University of Oregon high performance computer, Talapas.

Notes and references

1. N. J. Agard, J. A. Prescher and C. R. Bertozzi, J. Am. Chem. Soc., 2004, 126, 15046–15047.
2. J. M. Baskin, J. A. Prescher, S. T. Laughlin, N. J. Agard, P. V. Chang, I. A. Miller, A. Lo, J. A. Codelli and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16793–16797.
3. C. W. Bielawski and R. H. Grubbs, Prog. Polym. Sci., 2007, 32, 1–29.
4. R. Walker, R. M. Conrad and R. H. Grubbs, Macromolecules, 2009, 42, 599–605.
5. E. J. Leonhardt and R. Jasti, Nat. Rev. Chem., 2019, 3, 672–686.
6. Molecules within would not have solubilities observed if not for strain. (a) E. Kayahara, Y. Cheng and S. Yamago, Chem. Lett., 2018, 47, 1108–1111; (b) M. R. Golder, C. E. Colwell, B. M. Wong, L. N. Zakharov, J. Zhen and R. Jasti, J. Am. Chem. Soc., 2016, 138, 6577–6582.
7. T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361.
8. E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410.
9. T. A. Schaub, J. T. Margraf, L. Zakharov, K. Reuter and R. Jasti, Angew. Chem., Int. Ed., 2018, 57, 16348–16353.
10. E. Kayahara, R. Qu and S. Yamago, Angew. Chem., Int. Ed., 2017, 56, 10428–10432.
11. E. Kayahara, T. Hayashi, K. Takeuchi, F. Ozawa, K. Ashida, S. Ogoshi and S. Yamago, Angew. Chem., Int. Ed., 2018, 57, 11418–11421.
12. K. Miki and K. Ohe, Chem.–Eur. J., 2020, 26, 2529–2575.
13. V. K. Patel, E. Kayahara and S. Yamago, Chem.–Eur. J., 2015, 21, 5742–5749.
14. N. Hayase, Y. Miyauchi, Y. Aida, H. Sugiyama, H. Uekusa, Y. Shibata and K. Tanaka, Org. Lett., 2017, 19, 2993–2996.
15. E. R. Darzi, B. M. White, L. K. Loventhal, L. N. Zakharov and R. Jasti, J. Am. Chem. Soc., 2017, 139, 3106–3114.
16. E. R. Darzi, T. J. Sisto and R. Jasti, J. Org. Chem., 2012, 77, 6624–6628.
17. Y. Segawa, H. Omachi and K. Itami, Org. Lett., 2010, 12, 2262–2265.
18. S. M. Bachrach, Computational Organic Chemistry, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2nd edn, 2007.
19. K. J. Daoust, S. M. Hernandez, K. M. Konrad, I. D. Mackie, J. Winstanley and R. P. Johnson, J. Org. Chem., 2006, 71, 5708–5714.
20. M. V. Roux, J. Z. Dávalos, P. Jiménez, R. Notario, O. Castaño, J. S. Chickos, W. Hanshaw, H. Zhao, N. Rath, J. F. Liebman, B. S. Farivar and A. Bashir-Hashemi, J. Org. Chem., 2005, 70, 5461–5470.
21. A. De Meijere, S. I. Kozhushkov, K. Rauch, H. Schill, S. P. Verevkin, M. Kümmerlin, H. D. Beckhaus, C. Rüchardt and D. S. Yufit, J. Am. Chem. Soc., 2003, 125, 15110–15113.
22. P. J. Evans, E. R. Darzi and R. Jasti, Nat. Chem., 2014, 6, 404–408.
23. R. C. Haddon and L. T. Scott, Pure Appl. Chem., 1986, 58, 137–142.
24. R. C. Haddon, Science, 1993, 261, 1545–1550.
25. T. Stauch and A. Dreuw, Acc. Chem. Res., 2017, 50, 1041–1048.
26. T. Stauch, B. Günther and A. Dreuw, J. Phys. Chem. A, 2016, 120, 7198–7204.
27. C. Slavov, C. Yang, A. H. Heindl, T. Stauch, H. A. Wegner, A. Dreuw and J. Wachtveitl, J. Phys. Chem. Lett., 2018, 9, 4776–4781.
28. C. E. Colwell, StrainViz, https://github.com/CurtisColwell/StrainViz.git.
29. S. M. Bachrach, J. Chem. Educ., 1990, 67, 907–908.
30. S. E. Wheeler, K. N. Houk, P. v. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560.
31. J. Rio, D. Erbahar, M. Rayson, P. Briddon, C. P. Ewels, S. Sato, H. Kono, S. Fukuzumi, H. Isobe, V. G. Baonza, J. Casado and B. Humbert, Phys. Chem. Chem. Phys., 2016, 18, 23257–23263.
32. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa and M. Ishida, 2013.
34. X. Li and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 835–839.
35. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
36. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
37. S. M. Avdoshenko, S. S. M. Konda and D. E. Makarov, J. Chem. Phys., 2014, 141, 134115.
38. T. Stauch and A. Dreuw, Chem. Sci., 2017, 8, 5567–5575.
39. S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759.
40. S. M. Bachrach and D. Stück, J. Org. Chem., 2010, 75, 6595–6604.
41. G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi and K. Itami, Science, 2017, 356, 172–175.
42. S. Biswas, C. S. Qiu, L. N. Dawe, Y. Zhao and G. J. Bodwell, Angew. Chem., Int. Ed., 2019, 58, 9166–9170.
43. S. M. Bachrach, J. Phys. Chem. A, 2011, 115, 2396–2401.
44. T. C. Lovell, C. E. Colwell, L. N. Zakharov and R. Jasti, Chem. Sci., 2019, 10, 3786–3790.
45. S. Nishigaki, Y. Shibata, A. Nakajima, H. Okajima, Y. Masumoto, T. Osawa, A. Muranaka, H. Sugiyama, A. Horikawa, H. Uekusa, H. Koshino, M. Uchiyama, A. Sakamoto and K. Tanaka, J. Am. Chem. Soc., 2019, 141, 14955–14960.
46. A. M. Saitta, P. D. Soper, E. Wasserman and M. L. Klein, Nature, 1999, 399, 46–48.
47. T. Stauch and A. Dreuw, Angew. Chem., Int. Ed., 2016, 55, 811–814.
48. F. Vögtle, A. Schröder and D. Karbach, Angew. Chem., Int. Ed., 1991, 30, 575–577.
49. R. Herges, Chem. Rev., 2006, 106, 4820–4842.
50. E. Kayahara, T. Iwamoto, H. Takaya, T. Suzuki, M. Fujitsuka, T. Majima, N. Yasuda, N. Matsuyama, S. Seki and S. Yamago, Nat. Commun., 2013, 4, 2694.
51. Houk's paper: (a) F. Liu, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 11483–11493. Using data from: (b) R. D. Bach, J. Am. Chem. Soc., 2009, 131, 5233–5243.
52. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
53. M. T. Taylor, M. L. Blackman, O. Dmitrenko and J. M. Fox, J. Am. Chem. Soc., 2011, 133, 9646–9649.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details on computations and synthesis (PDF). Raw data for all calculations (ZIP). See DOI: 10.1039/d0sc00629g

---