Open Access Article
Open Access ArticleProximal charge effects on guest binding to a non-polar pocket†‡§
Paolo
Suating
 a,
Thong T.
Nguyen¶
a,
Thong T.
Nguyen¶
 a,
Nicholas E.
Ernst
a,
Nicholas E.
Ernst
 a,
Yang
Wang
a,
Yang
Wang
 b,
Jacobs H.
Jordan||
b,
Jacobs H.
Jordan||
 a,
Corinne L. D.
Gibb
a,
Henry S.
Ashbaugh
a,
Corinne L. D.
Gibb
a,
Henry S.
Ashbaugh
 b and
Bruce C.
Gibb
b and
Bruce C.
Gibb
 *a
*a
aDepartment of Chemistry, Tulane University, New Orleans, LA 70118, USA. E-mail: bgibb@tulane.edu
bDepartment of Chemical and Biomolecular Engineering, Tulane University, New Orleans, LA 70118, USA
First published on 17th March 2020
Abstract
Science still does not have the ability to accurately predict the affinity that ligands have for proteins. In an attempt to address this, the Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) series of blind predictive challenges is a community-wide exercise aimed at advancing computational techniques as standard predictive tools in rational drug design. In each cycle, a range of biologically relevant systems of different levels of complexity are selected to test the latest modeling methods. As part of this on-going exercise, and as a step towards understanding the important factors in context dependent guest binding, we challenged the computational community to determine the affinity of a series of negatively and positively charged guests to two constitutionally isomeric cavitand hosts: octa-acid 1, and exo-octa acid 2. Our affinity determinations, combined with molecular dynamics simulations, reveal asymmetries in affinities between host–guest pairs that cannot alone be explained by simple coulombic interactions, but also point to the importance of host–water interactions. Our work reveals the key facets of molecular recognition in water, emphasizes where improvements need to be made in modelling, and shed light on the complex problem of ligand-protein binding in the aqueous realm.
Introduction
That nature abhors a vacuum is a well-established trope in the chemical sciences, but a more considered analysis of the wettability of surfaces challenges this idea. Thus although the smallest of solvents – water – is predicted to pull away from and dewet purely-repulsive large non-polar solutes,1–3 and to evacuate tubes or other concavities smaller than a context dependent “drying” lengthscale,4–6 ubiquitous attractive van der Waals interactions between solute and water temper this somewhat.7,8 This is a knife-edge balance, and hence whether a concavity on the surface of a protein for example is wetted or not is dependent not only on its precise shape and nature,9,10 but also its context, for example the nature11 and presence of proximal charge groups. As a result, experimental and theoretical studies of the non-polar cavities of proteins such as T4 lysozyme,5,12 bovine β-lactoglobulin,6 or interleukin-1 often provide conflicting information about the extent of wetting.13–15In collaboration with the Ben-Amotz and Ashbaugh groups, we recently identified the first direct evidence of the dewetting of a synthetic host in aqueous solution.16 Wetting of the pocket was found to be dependent on the precise aperture to the cavity. Thus, pockets with the wider aperture were found to be mostly wetted, whereas the ostensibly identical pocket but with a slightly narrower aperture was found to be primarily dry. More precisely, this wetting/dewetting was found to be dependent on the precise orientation of four methyl groups around the rim of the pocket of the host. We also determined that the dryer pocketed host bound guests more strongly and with greater exothermicity; suggesting that un-solvated pockets lie behind the “non-classical hydrophobic effect” in which complexation events are enthalpically dominated.17–20 Our results also emphasized the dependence of the hydrophobic effect on subtle shape differences of surfaces,9 and suggested a new perspective regarding the role of water molecules in non-polar host cavities.19 Namely, whether a pocket is in a dry or wet state depends on the balance between the energetic requirements of establishing an air/water interface at the threshold of the former, and the attractive (host–water) van der Waals interactions and limited (water–water) hydrogen-bonding within the host of the latter; and when the balance is shifted to the wet state, guest complexation is relatively (and enthalpically) attenuated because of competition from the water. In short, wet pockets beget weak binding.
Here, as part of the 7th Statistical Assessment of Modeling of Proteins and Ligands (SAMPL7),21 and as a step towards understanding the important factors in context dependent guest binding, we examine the properties of two constitutional isomeric hosts to probe the effects of introducing charges proximal to a non-polar pocket. The SAMPL series of blind predictive challenges is a National Institutes of Health supported community-wide exercise aimed at advancing computational techniques as standard predictive tools in rational drug design. In each cycle, a range of biologically relevant systems of different levels of complexity – including proteins and drug-like small molecules or host–guest complexes – are selected to test the latest modeling methods and force fields.22 In this latest cycle, we examine the binding thermodynamics of a range of positive and negative guests to the octa-carboxylates of octa-acid 1 and exo-octa-acid 2 (Fig. 1), and use molecular dynamics (MD) simulations to probe how each host is solvated. Our studies reveal complex thermodynamic trends indicative of multiple interacting non-covalent forces, including (but not limited to) host–guest coulombic and host–water ion–dipole interactions. Our data therefore suggests new design criteria for synthetic non-polar pockets, and sheds light on the more complex situation of ligand–protein binding.
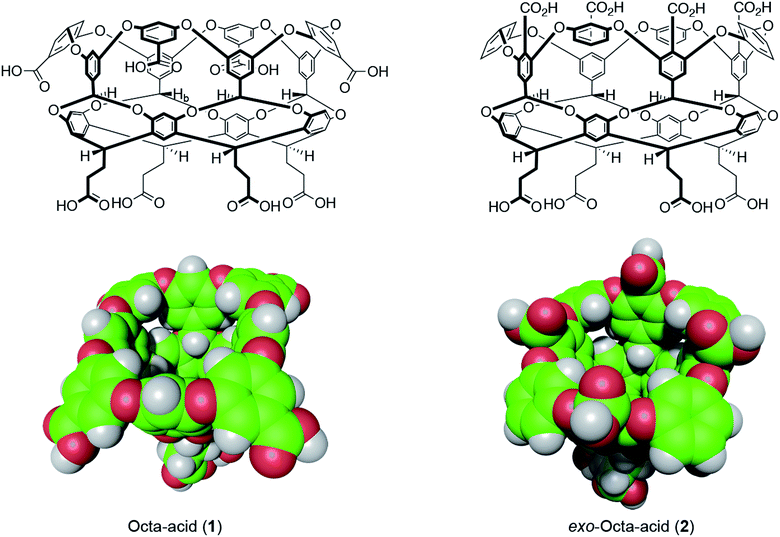 | ||
| Fig. 1 Structures and space-filling models of the two hosts in this study: octa-acid (1) and exo-octa-acid (2).23 | ||
Hosts 1 and 2 differ only in the position of the set of four benzoic acid groups around the upper rim of the host (Fig. 1). In the case of octa-acid 1, the peri-benzoic acid groups are quite remote from the pocket: ∼6 Å from the rim of the pocket and ∼9 Å from the principal C4 axis of the host. In contrast, for exo-octa-acid 2 the exo-benzoic acid groups are located on the rim and only ∼5 Å from the principal C4 axis. Under the basic conditions used to solubilize 1 and 2, the carboxylic acids of each are deprotonated. Hence, guests bound to the pocket of 2 can be expected to experience a more intense electrostatic potential field because of the proximity of the charge groups. We anticipated that such direct coulombic interactions would have a significant effect on guest binding thermodynamics. However, we also considered the possibility that water-mediated effects on guest binding, such as changes in the solvation of the pocket via modulation of host–water ion–dipole interactions, might also be evident in guest binding.
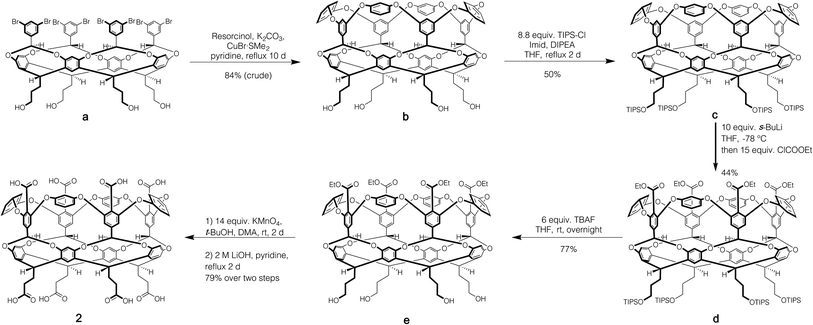
Host 1 has been previously described.24 The formation of novel exo-octa acid 2 is described in the ESI.†Scheme 1 summarizes its overall synthesis starting from known octa-halide a.25 First, a was treated with excess resorcinol in an eight-fold Ullmann ether process to give tetrol b. Protection of this tetrol with triisopropylsilyl chloride led smoothly to c. Subsequently, ortho-metalation26 of c with sec-butyl lithium and quenching with ethyl chloroformate led to cavitand d. Deprotection led to tetrol e, and oxidation and finally ester hydrolysis led to 2.
Fig. 2 shows the guests for hosts 1 and 2. We selected four negatively charged guests: hexanoate (G1), 4-chlorobenzoate (G2), perillate (G3), and citronellate (G4); and four positively charged alkyltrimethyl ammonium possessing: phenethyl (G5), hexyl (G6), trans-4-methyl-cyclohexyl (G7), and adamantyl (G8) alkyl groups. Guests G1 to G4 were commercially available, whilst guests G5 to G8, were synthesized by reaction of the corresponding amine with methyl iodide and ion-exchange with chloride anion (ESI†). Note that for the purposes of guest diversity in the SAMPL exercise we did not select positively and negatively charged guests with identical non-polar tails. However, for comparative purposes (vide infra) we did ensure that the sum of the non-hydrogen atoms in the hydrophobic tails of all the positive guests, was approximately the same as the corresponding set of these atoms in all of the negative guests; namely 31 and 30 atoms respectively.
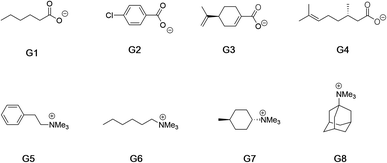 | ||
| Fig. 2 Guests used in this study. Guests G1–G4 were used as the sodium salts, and guests G5–G8 were used as their chloride salts. | ||
Results and discussion
We determine the affinity of guests G1–G8 to the poly-anions of 1 and 2 using host solutions of concentrations between 0.1 and 1 mM in 10 mM sodium phosphate buffer (pH 11.5). It has been previously shown that under such conditions small charged guests form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest complexes with these types of cavitands.27,28 Interestingly however, rather than exchanging slowly on the NMR timescale as guests typically do with 1, binding to 2 was generally fast or close to the NMR timescale. This was so even with strong binding guests such as G5–G8 which tended to bind on the NMR timescale; only strongly binding G8 revealed bound guest signals that were well defined (but often broad, see ESI†).
1 host–guest complexes with these types of cavitands.27,28 Interestingly however, rather than exchanging slowly on the NMR timescale as guests typically do with 1, binding to 2 was generally fast or close to the NMR timescale. This was so even with strong binding guests such as G5–G8 which tended to bind on the NMR timescale; only strongly binding G8 revealed bound guest signals that were well defined (but often broad, see ESI†).
We used Isothermal Titration Calorimetry (ITC) to probe the thermodynamics of complexation of the different host–guest pairs. Using a standard 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model, all but two of these afforded thermodynamic data (Table 1), with each revealing an enthalpically dominated complexation. The binding of G1 to 2 was too weak to determine either by ITC or 1H NMR spectroscopy, whereas the free energy of binding of G2 to 2 could only be determined by 1H NMR spectroscopy. In each case the presented data represents the average of at least triplicated experiments. Note that the binding thermodynamics of guests G1, G2, G5 and G6 to octa-acid 1 have been previously reported in different buffers (see footnotes in Table 1).27,28
1 binding model, all but two of these afforded thermodynamic data (Table 1), with each revealing an enthalpically dominated complexation. The binding of G1 to 2 was too weak to determine either by ITC or 1H NMR spectroscopy, whereas the free energy of binding of G2 to 2 could only be determined by 1H NMR spectroscopy. In each case the presented data represents the average of at least triplicated experiments. Note that the binding thermodynamics of guests G1, G2, G5 and G6 to octa-acid 1 have been previously reported in different buffers (see footnotes in Table 1).27,28
| Guest | Octa acid 1 | Exo-octa acid 2 | ||||
|---|---|---|---|---|---|---|
| ΔG (kJ mol−1) | ΔH (kJ mol−1) | −TΔS (kJ mol−1) | ΔG (kJ mol−1) | ΔH (kJ mol−1) | −TΔS (kJ mol−1) | |
| a Data and errors in this table were determined as follows. The ΔH and ΔG values were obtained by carrying out at least three separate experiments, averaging each set of data, and calculating the respective standard deviation. These average ΔH and ΔG values were then used to calculate an average −TΔS value, and the corresponding standard deviation calculated using the standard equation for the propagation of uncertainties (for subtraction). b Data for this host–guest combination was determined as part of SAMPL4 in 50 mM borate.27 c No binding observed. d Determined by 1H NMR spectroscopy. e Data for this host–guest combination was determined as part of SAMPL5 in 50 mM phosphate.28 | ||||||
| G1 | −20.8 ± 0.1b | −23.2 ± 0.1b | 2.4 ± 0.3b | —c | —c | —c |
| G2 | −28.9 ± 0.1b | −40.2 ± 1.1b | 11.0 ± 1.0b | −5.5 ± 1.1d | — | — |
| G3 | −33.9 ± 0.1 | −50.2 ± 0.0 | 16.3 ± 0.1 | −14.1 ± 0.3 | −25.2 ± 0.6 | 11.1 ± 0.3 |
| G4 | −28.3 ± 0.2 | −28.0 ± 0.7 | −0.3 ± 0.5 | −15.1 ± 0.1 | −30.5 ± 2.9 | 15.4 ± 2.8 |
| G5 | −19.8 ± 0.0e | −31.3 ± 0.2 e | 11.5 ± 0.2e | −23.3 ± 0.1 | −25.8 ± 0.0 | 2.5 ± 0.1 |
| G6 | −20.8 ± 0.1e | −30.5 ± 1.4e | 9.6 ± 1.4e | −24.4 ± 0.0 | −13.6 ± 0.1 | −10.8 ± 0.1 |
| G7 | −25.4 ± 0.2 | −24.0 ± 0.7 | −1.4 ± 0.5 | −29.2 ± 0.4 | −20.8 ± 0.3 | −8.4 ± 0.2 |
| G8 | −34.5 ± 0.1 | −32.7 ± 0.8 | −1.7 ± 0.6 | −32.1 ± 0.0 | −21.1 ± 0.2 | −11.0 ± 0.1 |
Looking first at anionic guests binding to host 1, as expected, smallest guest G1 binds the weakest, whilst largest and most pre-organized G3 binds the strongest. The average free energy of complexation for these four guests was found to be 〈ΔG〉G1–G41 = −28.0 kJ mol−1. One major structural difference between the two intermediate binding guests G2 and G4 is the chlorine atom of the former. When present in guests, a halogen atom is known to add a significant enthalpic contribution to binding because it forms X⋯H–C hydrogen bonds with the four electron-deficient benzal hydrogens (Hb in 1, Fig. 1) of the host pointing into the lower region of the pocket.29 Thus although slightly smaller, guest G2 binds with approximately equal affinity as G4 and with a much higher enthalpy change.
The binding of negatively charged guests to exo-octa acid 2 was expected to be weaker because of charge repulsion between the head-group of the guests and the proximal exo-carboxylates of the host. This was found to be the case. Indeed, we could not measure any affinity between 2 and guest G1, and the binding of G2 to 2 was so weak that we could only use 1H NMR spectroscopy to obtain reliable free energy data. Assuming an upper limit for the binding of G1 to 2 of Ka = 2 M−1 or ΔG = 1.7 kJ mol−1, the average free energy for negatively charged guests binding to 2 is 〈ΔG〉G1–G42 = −9.1 kJ mol−1. Thus, the binding of anionic guests to 2 is considerably weaker than to host 1: 〈ΔG〉G1–G42 − 〈ΔG〉G1–G41 = +18.9 kJ mol−1. However, as we discuss below, it is likely that complexation to these hosts is not just a simple case of coulombic (ion–ion) repulsion.
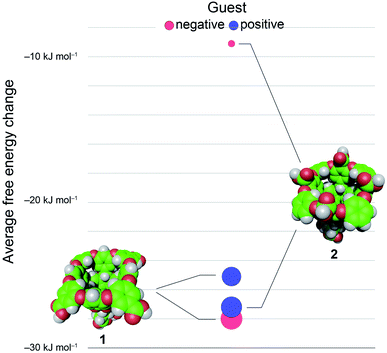
We then turned our attention to positively charged guests G5–G8. An initial consideration of Coulomb's Law might suggest that the average binding affinity of the positively charged guests G5–G8 to OA 1 would be stronger than the average affinity of the negatively charged G1–G4. This however was not found to be the case; instead the positive guests bound slightly more weakly: 〈ΔG〉G5–G81 = −25.1 kJ mol−1, i.e., 〈ΔG〉G5–G81 − 〈ΔG〉G1–G41 = +2.9 kJ mol−1. This propensity is further illustrated by adding adamantane carboxylate to the guests in Fig. 2 so as to allow the direct comparison of the binding of G8 to 1. For adamantane carboxylate the, ΔG, ΔH, and −TΔS of complexation to 1 were determined to be −37.9, −38.3 and 0.4 kJ mol−1. Thus, adamantane carboxylate binds more strongly to 1 than positively charged adamantane G8.
At a rudimentary level, the fact that negatively charged guests bind more strongly to 1 than positively charged ones suggests that, because the peri-carboxylates of 1 are remote from the bound guest, ion–ion interactions are screened. If this were the case, then the Bjerrum length (the distance that the interaction energy between charges equals kT) would be at least the distance between the peri-benzoate groups of 1 and the charge on the bound guest, i.e., ∼9 Å assuming the guest head group is aligned with the C4 axis of the host. At this distance it can be readily calculated that the average dielectric constant of the medium would need to be at least εr = 63 for the host peri-carboxylates not to influence the charged guest. If we assume this intervening space is composed of water (εr = 78) and host, then an estimation of the dielectric constant of the host reveals the amount of host and water between the charge groups necessary for screening. Thus, if we select a relatively high dielectric for the host of εr = 12.7 (c.f. benzene = 2.3, methoxybenzene = 4.3, benzyl alcohol = 12.7)30 then the water–host ratio of the intervening material between the charge groups on 1 and the guest would be 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25. This is an unrealistically high proportion of water (and would be higher with a lower dielectric for the host). Indeed, an inspection of the intervening space between the peri-carboxylates of 1 and a charged headgroup of a bound guest reveals that it is at least 50% low dielectric guest structure. Thus, the only conclusion possible is that complete screening is not occurring, and that factors other than ion–ion interactions play a significant role in guest binding.
25. This is an unrealistically high proportion of water (and would be higher with a lower dielectric for the host). Indeed, an inspection of the intervening space between the peri-carboxylates of 1 and a charged headgroup of a bound guest reveals that it is at least 50% low dielectric guest structure. Thus, the only conclusion possible is that complete screening is not occurring, and that factors other than ion–ion interactions play a significant role in guest binding.
What of the binding of guests G5–G8 to exo-octa-acid 2? If we first compare these affinities to those of the negatively charged guests binding to 2, we can see that on average the free energy of complexation of G1–G4 is weaker than the binding of G5–G8: 〈ΔG〉G1–G42 = −9.1 kJ mol−1versus 〈ΔG〉G5–G82 = −27.2 kJ mol−1, i.e., 〈ΔG〉G2–G42 − 〈ΔG〉G5–G82 = +18.1 kJ mol−1. This data suggests a significant coulombic (ion–ion) effect upon switching the charge on the guest. That noted, it is interesting to recall (vide supra) that in the case of host 2, the distance between a charge group on a bound guest (located at the portal entrance and on the C4 axis of the host) and the exo-carboxylates of the host is ∼5 Å. This means that assuming the intervening space between the charges is occupied with water (εr = 78), the difference in energy from switching a negative for a positive guest should be ∼25 kJ mol−1. This is somewhat larger than observed and suggests some competing phenomenon also play a significant role in guest binding.
Finally, a comparison of the positively charged guests G5–G8 to hosts 1 and 2 is also revealing. Here we find that 〈ΔG〉G5–G81 = −25.1 kJ mol−1versus 〈ΔG〉G5–G82 = −27.2 kJ mol−1, i.e., 〈ΔG〉G5–G82 − 〈ΔG〉G5–G81 = −2.1 kJ mol−1. Thus, moving the benzoate groups from the remote peri-positions in 1 to their proximal exo-positions in 2 only marginally enhances positive guest affinity.
En masse this data reveals an asymmetry in the complexation of positive and negative guests to hosts 1 and 2 (Fig. 3). The difference in the affinity of positive and negative guests to host 2 is only about 70% of what would be expected, but the difference between binding negative versus positive guests to 1 is inverted (negatively charged guests bind more strongly) despite a lack of screening between peri-carboxylates of 1 and the charge on the guest. Finally, the average binding of all guests to 2 is considerably weaker than the binding of these guests to host 1: 〈ΔG〉G1–G81 = −26.6 kJ mol−1versus 〈ΔG〉G1–G82 = −18.2 kJ mol−1.
So why the affinity-inverted properties of host 1, and why does 1 generally bind guests more strongly than exo-OA 2? The conclusion must be that non-covalent interactions other than electrostatic ones play key roles in guest complexation. To probe this idea, we turned to molecular dynamics (MD) simulations. In doing so we were cognizant of the fact that the (a priori affinity determination) challenge segment of the SAMPL challenge is in itself a significant undertaking for the leading experts taking part. For example, the evaluation of binding free energies between charged hosts and charged guests using MD simulations is currently challenged by the lack of inclusion of polarization effects in the majority of those calculations.31 Empirical corrections based on the scaling of charges have been proposed to account for those neglected electronic degrees of freedom,32,33 however, the accuracy of those approximations is still a matter of debate. These points are just some of the issues that the computationalists have to wrestle with during the SAMPL exercise. Because of these difficulties, here we limit our simulations to examining: (1) the hydration of individual cavitands (ion–dipole interactions); (2) how these change upon guest binding, and; (3) a small set (four host–guest pairs) of affinity determinations. Full details of the simulations are given in the ESI.† Briefly, they were performed in the isothermal–isobaric34–36 ensemble at 25 °C and 1 atm. using GROMACS 2016.3.37 The hosts were modeled using the Generalized Amber Force Field38 with partial charges assigned from AM1-BCC calculations.39 Water was modeled using the TIP4P/Ew potential.40 Lennard-Jones and electrostatic interactions (between the carboxylates and their counter ions) were respectively modeled with a mean field dispersion correction,41 and the particle mesh Ewald summation method,42 while hydrogen bonds involving the host or water were held with LINCS43 and SETTLE44 respectively. For the hydration studies, a host was placed in a bath of 2000 water molecules, with simulations conducted for 100 ns following a 5 ns equilibration time. For the affinity estimations we examined the interactions between OA 1 and exo-OA 2, and guests G3 and G4. Here, the host–guest pair was solvated in a bath of 5000 water molecules. The hosts–guest interactions were characterized using the potential-of-mean force (PMF), i.e., the free energy of interaction between the host and guest along a prescribed reaction coordinate (the 4-fold (C4) rotational axis of the host). Full details of these studies are also given in the ESI.†
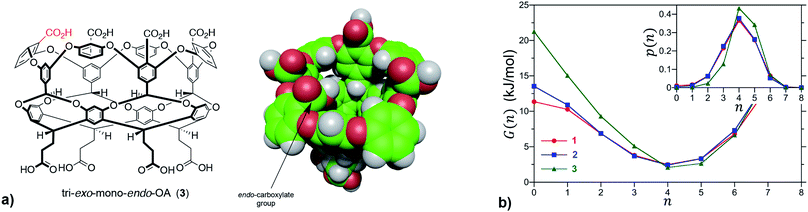
We first sought to investigate how the position of the rim carboxylate groups affects the binding of water to the non-polar pocket of hosts 1 and 2. As we explain, this comparison also led to the inclusion of theoretical host tri-exo-mono-endo-OA (3, Fig. 4a) into our studies. Host pocket hydration can be quantified by considering the probabilities and associated free energies of observing n waters inside the pocket (Fig. 4b). While the pocket hydration probability distributions for OA 1 and exo-OA 2 appear very similar (Fig. 4b inset), important differences are observed when considering the pocket hydration free energies. Notably, the free energy for emptying exo-OA 2 (n = 0) is 2.2 kJ mol−1 greater than that for OA 1. This difference was smaller than anticipated, so to probe this further theoretical host 3 was also considered. By repositioning one of the rim carboxylates of 2 from an exo-position to a neighboring endo-position, the unique carboxylate of 3 can dangle into the solvated pocket to directly hydrogen bond to bound waters. As a result, pocket hydration is significantly perturbed, with the probability distribution becoming skewed towards larger pocket hydration numbers (Fig. 4b inset). This shift manifests as a 10 kJ mol−1 greater free energy requirement to empty 3 compared to 1. As guest binding necessitates an empty host pocket, these results strongly suggest that ion–dipole interactions between the host and bound water also play an indirect role in guest binding. This noted, because of the inability to accurately model polarization effects, there are likely sizable errors to the precise magnitude of the solvation differences; ion–dipole interactions vary as 1/r2 (for fixed dipoles), thus we anticipate that the effect of placing the carboxylates at the exo-position (host 2) rather than the peri-position (host 1) might be larger than the calculations suggest. This point notwithstanding, what is clear is that the pocket of 2 is wetter than 1, and that the resulting greater competition of water for the pocket must lead to weaker guest binding.16 Importantly, this conclusion fits with the experimental observation that the average affinity of all guests to host 2 is lower than to host 1 (Fig. 3).
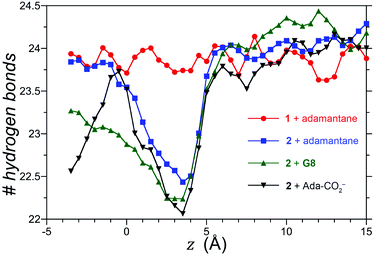
We also considered the possibility that hydrogen-bonding between the exo-carboxylates of 2 and their surrounding waters may be affected by guest complexation. To test this idea, the number of hydrogen bonds between waters and the four rim carboxylates of OA 1 and exo-OA 2 were monitored as a function of the guest position for neutral adamantane, cationic G8, and anionic adamantane carboxylate relative to the pocket (Fig. 5). For guests well outside the host pocket (z = 15 Å, see legend of Fig. 5 for definition of z), the average number of hydrogen bonds to the rim carboxylates of both hosts is approximately 24. Furthermore, as expected for host 1, hydrogen bonding to the carboxylates was found to be independent of the position and nature of each guest (for clarity, only the hydrogen bonding patterns for adamantane binding to 1 is reported in Fig. 5). In contrast, the carboxylates of 2 lost ∼1.5 hydrogen bonds upon the approach of all guests to the pocket. These were recovered as the neutral adamantane fully entered the pocket (z < 0 Å). In contrast however, hydrogen bond recovery was found to be incomplete for both charged guests, suggesting interference with the normal hydrogen bonding of the rim carboxylates. Qualitative differences in the hydrogen bond recovery for the positive and negative guests is consistent with the asymmetry in the solvation of positive and negatively charged groups.11 However, the precise energetic consequences of such changes are unclear.
For the affinity determinations we limited ourselves to hosts 1 and 2 binding G3 and G4. Our PMF calculations concluded that G3 bound to OA 1 13.9 kJ mol−1 more strongly than to host 2. This is smaller than the 19.8 kJ mol−1 observed by ITC. Similarly, the calculated affinity of G4 to OA 1 was 3.6 kJ mol−1 stronger than to host 2; again smaller than that observed by ITC (13.2 kJ mol−1). The difference between experimental and calculated (5.9 and 9.6 kJ mol−1) may reflect that the scaling of charges32,33 we utilized does not compensate for the absence of polarization factors in the model. However, our results do indicate how the wettability of the pocket of the hosts may play a key role in guest affinity.
Conclusions
Our combined experimental and simulation studies reveal an asymmetry in guest affinity for hosts 1 and 2 (Table 1 and Fig. 3) and go some way to explain the factors behind this. The affinity of all eight guests to 2 is less than that to 1, and our MD simulations point to increased wetting of the pocket of 2 and displaced hydrogen bonding as a major reason for this. Stronger ion–dipole interactions between the host and bound water in 2 means that water is a better guest and can compete more effectively for the pocket. However, looking at the difference in affinity between positive and negative guests binding to each host raises some questions. For example, the difference between positive and negative guest affinity for 2 is 70% of what might be expected. Coulombic (ion–ion) interactions are key here, but what other non-covalent interactions make up the difference? And despite the lack of complete screening, why do negative guests bind slightly more strongly to 1 than positively charged ones? We suspect that these phenomena are the result of complex ion–ion and ion–dipole interactions in the different host–guest complexes – perhaps arising in differences in the asymmetry of how groups of opposite charge are solvated – that cannot be easily modelled. With this in mind, we are synthesizing new hosts to further explore the thermodynamics of guest binding, as well as considering different ways in which to model ion–ion and ion–dipole interactions in host–guest systems. Regarding the latter, we are keen to review the data from the SAMPL7 participants to see if it can shed light on this complex, multi-faceted problem.Author contributions
PS carried out optimization of the synthesis of host 2, 50% of the ITC studies and all the described NMR analyses, and assembled the SI. TTN performed the initial synthesis of 2. NEE carried out 40% of the described ITC analysis and the syntheses of the ammonium guests. YW performed the described MD simulations. JHJ initially identified the silylation of b and the lithiation of c. CLDG performed 10% of the ITC studies and trained the other ITC users. HSA provided guidance for the MD simulations. BCG conceived the project, oversaw the described syntheses and calorimetric/spectroscopic studies, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BCG and PS gratefully acknowledge the National Institutes of Health (GM124270). NEE acknowledges the Louisiana Board of Regents for a graduate student fellowship (LEQSF(2016-21)-GF-12). BCG, YW, and HAS thank the National Science Foundation for their generous support (NSF CBET-1805167).References
- F. H. Stillinger, J. Solution Chem., 1973, 2, 141–158 CrossRef CAS.
- D. Chandler, Nature, 2005, 437, 640–647 CrossRef CAS PubMed.
- H. Ashbaugh and L. Pratt, Rev. Mod. Phys., 2006, 78, 159–178 CrossRef CAS.
- J. C. Rasaiah, S. Garde and G. Hummer, Annu. Rev. Phys. Chem., 2008, 59, 713–740 CrossRef CAS PubMed.
- M. D. Collins, G. Hummer, M. L. Quillin, B. W. Matthews and S. M. Gruner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16668–16671 CrossRef CAS PubMed.
- J. Qvist, M. Davidovic, D. Hamelberg and B. Halle, Proc. Natl. Acad. Sci., 2008, 105, 6296–6301 CrossRef CAS PubMed.
- D. M. Huang and D. Chandler, J. Phys. Chem. B, 2002, 106, 2047–2053 CrossRef CAS.
- D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638 CrossRef CAS PubMed.
- M. B. Hillyer and B. C. Gibb, Annu. Rev. Phys. Chem., 2016, 67, 307–329 CrossRef CAS PubMed.
- Y. K. Cheng and P. J. Rossky, Nature, 1998, 392, 696–699 CrossRef CAS PubMed.
- G. Hummer, L. R. Pratt and A. E. García, J. Phys. Chem., 1996, 100, 1206–1215 CrossRef CAS.
- M. D. Collins, M. L. Quillin, G. Hummer, B. W. Matthews and S. M. Gruner, J. Mol. Biol., 2007, 367, 752–763 CrossRef CAS PubMed.
- H. Yin, G. Feng, G. M. Clore, G. Hummer and J. C. Rasaiah, J. Phys. Chem. B, 2010, 114, 16290–16297 CrossRef CAS PubMed.
- J. A. Ernst, R. T. Clubb, H. X. Zhou, A. M. Gronenborn and G. M. Clore, Science, 1995, 267, 1813 CrossRef CAS PubMed.
- B. C. Finzel, L. L. Clancy, D. R. Holland, S. W. Muchmore, K. D. Watenpaugh and H. M. Einspahr, J. Mol. Biol., 1989, 209, 779–791 CrossRef CAS.
- J. W. Barnett, M. R. Sullivan, J. A. Long, D. Tang, T. Nguyen, D. Ben-Amotz, B. C. Gibb and H. S. Ashbaugh, Nat. Chem., 2020 Search PubMed , in press..
- P. W. Snyder, J. Mecinovic, D. T. Moustakas, S. W. Thomas 3rd, M. Harder, E. T. Mack, M. R. Lockett, A. Heroux, W. Sherman and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17889–17894 CrossRef CAS PubMed.
- P. Setny, R. Baron and J. A. McCammon, J. Chem. Theory Comput., 2010, 6, 2866–2871 CrossRef CAS PubMed.
- F. Biedermann, W. M. Nau and H. J. Schneider, Angew. Chem., Int. Ed. Engl., 2014, 53, 11158–11171 CrossRef CAS PubMed.
- F. Biedermann, M. Vendruscolo, O. A. Scherman, A. De Simone and W. M. Nau, J. Am. Chem. Soc., 2013, 135, 14879–14888 CrossRef CAS PubMed.
- The SAMPL Challenges, https://samplchallenges.github.io/ Search PubMed.
- https://en.wikipedia.org/wiki/SAMPL_Challenge .
- G. T. Johnson, L. Autin, D. S. Goodsell, M. F. Sanner and A. J. Olson, Structure, 2011, 19, 293–303 CrossRef CAS PubMed.
- S. Liu, S. E. Whisenhunt-Ioup, C. L. D. Gibb and B. C. Gibb, Supramol. Chem., 2011, 23, 480–485 CrossRef CAS PubMed.
- M. B. Hillyer, C. L. D. Gibb, P. Sokkalingam, J. H. Jordan, S. E. Ioup and B. C. Gibb, Org. Lett., 2016, 18, 4048–4051 CrossRef CAS PubMed.
- Z. R. Laughrey and B. C. Gibb, J. Org. Chem., 2006, 71, 1289–1294 CrossRef CAS PubMed.
- C. L. D. Gibb and B. C. Gibb, J. Comput.-Aided Mol. Des., 2014, 28, 319–325 CrossRef CAS PubMed.
- M. R. Sullivan, P. Sokkalingam, T. Nguyen, J. P. Donahue and B. C. Gibb, J. Comput.-Aided Mol. Des., 2017, 31, 21–28 CrossRef CAS PubMed.
- C. L. D. Gibb, E. D. Stevens and B. C. Gibb, J. Am. Chem. Soc., 2001, 123, 5849–5850 CrossRef CAS PubMed.
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, VCH, New York, 4th edn, 2011 Search PubMed.
- P. Sokkalingam, J. Shraberg, S. W. Rick and B. C. Gibb, J. Am. Chem. Soc., 2016, 138, 48–51 CrossRef CAS PubMed.
- M. Vazdar, E. Pluharova, P. E. Mason, R. Vacha and P. Jungwirth, J. Phys. Chem. Lett., 2012, 3, 2087–2091 CrossRef CAS.
- P. E. Mason, E. Wernersson and P. Jungwirth, J. Phys. Chem. B, 2012, 116, 8145–8153 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Phys., 2004, 25, 1157–1174 CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1987 Search PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
Footnotes |
| † Dedicated to Eric V. Anslyn on the imminent arrival of his 60th birthday. |
| ‡ A contribution of reference data for the seventh statistical assessment of modeling of proteins and ligands (SAMPL7). |
| § Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc06268h |
| ¶ Current address: Winder Laboratories, LLC, 716 Patrick Industrial Ln, Winder, GA 30680, USA. |
| || Current address: The Southern Regional Research Center Agricultural Research Service, USDA, 1100 Robert E. Lee Blvd, New Orleans, LA 70124, USA. |
| This journal is © The Royal Society of Chemistry 2020 |