Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unexpected monolayer-to-bilayer transition of arylazopyrazole surfactants facilitates superior photo-control of fluid interfaces and colloids†
Christian
Honnigfort
ab,
Richard A.
Campbell
 c,
Jörn
Droste
a,
Philipp
Gutfreund
d,
Michael Ryan
Hansen
c,
Jörn
Droste
a,
Philipp
Gutfreund
d,
Michael Ryan
Hansen
 a,
Bart Jan
Ravoo
a,
Bart Jan
Ravoo
 be and
Björn
Braunschweig
be and
Björn
Braunschweig
 *ab
*ab
aInstitute of Physical Chemistry, Westfälische Wilhelms-Universität Münster, Corrensstraße 28/30, 48149 Münster, Germany. E-mail: braunschweig@uni-muenster.de
bCenter for Soft Nanoscience (SoN), Westfälische Wilhelms-Universität Münster, Busso-Peus-Straße 10, 48149 Münster, Germany
cDivision of Pharmacy & Optometry, School of Health Sciences, University of Manchester, Oxford Road, Manchester M13 9PT, UK
dInstitut Laue-Langevin (ILL), 71 Avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
eOrganic Chemistry Institute, Westfälische Wilhelms-Universität Münster, Corrensstraße 40, 48149 Münster, Germany
First published on 8th January 2020
Abstract
Interfaces that can change their chemistry on demand have huge potential for applications and are prerequisites for responsive or adaptive materials. We report on the performance of a newly designed n-butyl-arylazopyrazole butyl sulfonate (butyl-AAP-C4S) surfactant that can change its structure at the air–water interface by E/Z photo-isomerization in an unprecedented way. Large and reversible changes in surface tension (Δγ = 27 mN m−1) and surface excess (ΔΓ > 2.9 μmol m−2) demonstrate superior performance of the butyl-AAP-C4S amphiphile to that of existing ionic surfactants. Neutron reflectometry and vibrational sum-frequency generation spectroscopy reveal that these large changes are caused by an unexpected monolayer-to-bilayer transition. This exceptional behavior is further shown to have dramatic consequences at larger length scales as highlighted by applications like the light-triggered collapse of aqueous foam which is tuned from high (>1 h) to low (<10 min) stabilities and light-actuated particle motion via Marangoni flows.
Introduction
Smart surfaces and interfaces can respond to external stimuli such as light, temperature or magnetic fields and change their physicochemical properties on demand. They have great potential to serve as hierarchical elements for responsive functional materials,1–3 light-induced actuation4,5 and have prospects to be developed further for adaptive materials with self-healing or self-learning functions. Prerequisites for such functions are distinct, precise and reproducible control of interfacial properties. Such control can be achieved by tuning molecular self-assembly through the use of an external stimulus.2,6 Here, soft interfaces are of great interest because they allow fast and reversible reconfigurations, e.g., by de- or adsorption of molecules triggered by an external stimulus.7–11 For example, tuning the properties of fluid interfaces helps to develop smart foams with self-healing and adaptive functions.3,12 In addition, Marangoni flows can be used to pattern or aggregate particles precisely and independently of their size in the tailoring of 2D colloidal crystals.13,14Previous work on photoswitchable surfactants that undergo photo-isomerization reactions from E to Z conformations when irradiated with UV and blue light has concentrated mostly on non-ionic azo surfactants with surface tension changes as high as ∼29 mN m−1 upon photoswitching.15,16 However, information on dynamic changes at interfaces like surface excess and structural information on the molecular level have not been obtained in detail, yet. That is particularly true for water-soluble photoswitches that have much greater potential to serve as building blocks for responsive as well as active colloids and interfaces. To study the underlying mechanism, kinetically resolved measurements at interfaces far outside local17 or global equilibria are required. In addition, for most azobenzene derivatives switching is incomplete due to a large spectral overlap of both isomers. Recently, Stricker et al.18,19 showed the potential of arylazopyrazoles (AAPs) as a new class of photoswitches in aqueous solutions, which exhibit optical properties superior to azobenzene derivatives and which were first introduced by Weston et al.20 Particularly, the smaller spectral overlap18 of E and Z isomers, as well as a more favourable photostationary state, which allows switching of >90% of the molecules, makes AAP derivatives highly interesting as molecular building blocks for responsive air–water interfaces.19,20
In this work, we have studied a newly designed AAP derivative – sodium n-butyl-arylazopyrazole butyl sulfonate (butyl-AAP-C4S, Fig. 1a) – that is shown to achieve massive changes in the physicochemical properties at the air–water interface which are attributable to an unexpected monolayer-to-bilayer transition. This transition is unique for the molecule we describe in this paper, which can be used to explain the superior performance of this new water soluble butyl-AAP-C4S photoswitch.
A prerequisite to unravel the monolayer-to-bilayer transition is a structural investigation of equilibrium and non-equilibrium properties that have not been discussed in detail so far. In fact, for the latter we combine the results of vibrational sum-frequency generation (SFG) spectroscopy, surface tensiometry and neutron reflectometry (NR) where NR yields a model-free quantification of the surface excess and SFG reveals structural aspects of the interface. Both SFG and NR are inherently interface specific methods where the SFG amplitude Aq ∝ Γ〈βq〉 of a vibrational band is a function of both the surface excess Γ and the orientational average 〈⋯〉 of the molecular hyperpolarizability βq, while fitted models of the NR data provide the density profile of molecules (or parts of molecules) normal to an interface (see Experimental details). Therefore, a comparison of the two techniques can reveal information about changes in the orientation, structure and coverage of interfacial molecules. Using this combined approach, we first quantify changes in surface tension, surface excess and molecular order to examine the performance of the new surfactants. Finally, the experiments are complemented by two experimental demonstrations of potential applications, which show that the unprecedented monolayer-to-bilayer transition of butyl-AAP-C4S surfactants at the air–water interface can be exploited for applications where the surfactant serves as a versatile building block for highly photo-responsive foams and light-actuated particle motion.
Results and discussion
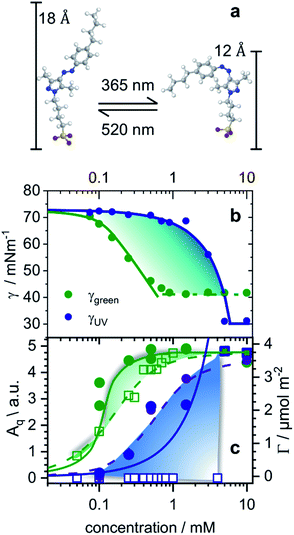
The equilibrium surface tension of butyl-AAP-C4S photoswitchable surfactants as a function of bulk concentration is shown in Fig. 1b for irradiation with 520 nm green and 365 nm UV light. Green and UV light can cause E to Z isomerization reactions of the amphiphiles, which we have confirmed by 1H high-resolution magic-angle spinning (HR-MAS) NMR spectroscopy (ESI†). In particular, 1H HR-MAS NMR demonstrates an extremely favorable photostationary state (PSS) with >99% E to Z switching and complete recovery of the E isomer at 6 mM (see Fig. S1†). This is an outstanding performance as other AAP and azo moieties have been reported to have a PSS of >98% (ref. 18 and 20) and <80%.21 For <5 mM butyl-AAP-C4S, the equilibrium surface tension of the air–water interface is systematically lower when the samples are in the E state compared to the Z state (Fig. 1b), while for >5 mM the surface tension for the surfactants in the E state reaches a plateau at a higher value.These two differences can be attributed to the different critical micelle concentrations (CMCs) of the butyl-AAP-C4S surfactants in the bulk solution and the different equilibrium constants for ad/desorption, respectively. The CMCs are 0.7 and 5 mM for the surfactants having E and Z conformations, respectively, and can be directly inferred from the kinks in the isotherms of Fig. 1b. From this analysis, we can conclude the relative surface activity of the E and Z isomers, with the E isomer being more surface active. The surface tension change Δγ upon photoswitching is as high as 27 mN m−1 for 0.5 mM butyl-AAP-C4S and is, therefore, much higher than those of the previously reported cationic amphiphiles, with a difference of ∼20 mN m−1.7,8,15 This performance of the butyl-AAP-C4S surfactant is close to the 29 mN m−1 of nonionic surfactants reported by Shang et al.15 The fact that this performance is achieved for an ionic surfactant is remarkable as small changes in surface coverage and charge density can easily destabilize these systems, as is demonstrated below.
To gain detailed information about the structural changes of butyl-AAP-C4S photoswitches at the air–water interface, we have performed experiments with NR and SFG spectroscopy. In Fig. 1c, the surface excess Γ (the number of molecules per surface area) of butyl-AAP-C4S surfactants from the low-Q analysis of NR as a function of the bulk concentration is shown for surfactants in E and Z conformations, when the samples were irradiated with green und UV light, respectively. Note that Q is the momentum transfer normal to the interface and that
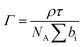 | (1) |
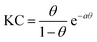 | (2) |
| γ(c) = γ0 + 2ΓmaxRT[ln(1 − θ) + aθ2] | (3) |
Comparing the model free surface excess (NR) with the one from the Frumkin model, we find excellent agreement in case where the surfactants were in the E state. This can be directly inferred from the excellent overlap of the surface excess (solid green line in Fig. 1c) taken from the Frumkin fit in Fig. 1b, with the NR data shown in Fig. 1c (green circles). We can also notice for the surfactants being in the E conformation that the SFG amplitudes Aq ∝ Γ〈βq〉 and the surface excess Γ ovelaps only at the limiting surface excess, which is reached at or above the CMC of surfactants. Below the CMC, the mismatch between Γ and Aq ∝ Γ〈βq〉 as indicated by the colour-shaded areas in Fig. 1c must be associated with the changes in the orientational average of the hyperpolarizability 〈βq〉. Thus, the molecular order of the interfacial layer increases with increasing concentration and is likely caused by attractive lateral interactions within the close-packed interfacial layer of surfactants.
Although modelling of the surface tension of the surfactants in the E conformation clearly reproduces the surface excess Γ as seen from NR, the same modelling of the results from samples in the Z state clearly fails to reproduce the NR data (Fig. 1c), even though the changes in surface tension (Fig. 1b) between the model fit and experimentally observed surface tensions are in good agreement. Application of the Frumkin model, therefore, appears not to be valid for butyl-AAP-C4S surfactants in the Z conformation. Furthermore, the difference between the surface excess Γ and the SFG amplitude Aq ∝ Γ〈βq〉 of molecules in the Z conformation is extreme for concentrations below the CMC (see the blue shaded area in Fig. 1c) because the SFG amplitude is negligible, while the surface excess is still quite substantial. This large difference for concentrations <5 mM must be directly related to the orientational average 〈βq〉 with the interfacial surfactants realizing structures with local centrosymmetry which cancel the SFG signals due to symmetry reasons (〈βq〉 = 0). This is clearly different for concentrations >5 mM, which is the bulk CMC when the molecules are in the Z state and is discussed in detail below.
In order to gain insight into the apparent interfacial rearrangements caused by photo-isomerization, we have characterized the structures that self-assemble at the interface in the two equilibrium states (Z vs. E) using NR. For that, the NR data were recorded in 4 isotopic contrasts using partially deuterated and fully hydrogenous surfactants in both D2O and air contrast matched water (ACMW), which is 8.1% by volume D2O in H2O, over the full Q-range. These data were simultaneously fitted for each system to a common structural model of stratified layers normal to the interface separated by capillary wave roughness (details are in the Experimental part and in the ESI†). From NR it is found that a layer thickness of 17 Å is created for both E and Z conformations with the molecules adopting a volume fraction of 65% in the former case and 53% in the latter case (Fig. 2a and b). To place these results in the context of the size of the molecule (Fig. 1a), it may be noted that the extended length of the molecule is ≈18 Å when the butyl-AAP-C4S molecule is in the E conformation, which reduces to ≈12 Å in the Z conformation. Consequently, the modeled NR data indicate that there is a relatively dense monolayer of butyl-AAP-C4S surfactants in the E conformation and a more hydrated and straddled (or intercalated) bilayer when the surfactants are in the Z state, which are schematically illustrated in Fig. 2c and d, respectively. In the latter case, the prevailing centrosymmetric environment can explain the complete loss of the SFG signal for surfactant concentrations <5 mM, when they are switched from the E to the Z state (Fig. 1c). This is clearly different at concentrations >5 mM, where no change in the SFG amplitude, surface excess and layer thickness (ESI, Fig. S6†) as a function of light irradiation is observed. At concentrations >5 mM, the close-packed interfacial layer of surfactants is likely to be sterically arrested in the E state due to strong lateral interactions resulting in a loss of its responsiveness to the light stimulus. In fact, this is similar to photo-switchable self-assembled monolayers which also lose their light-responsive function, when their packing becomes too dense.25
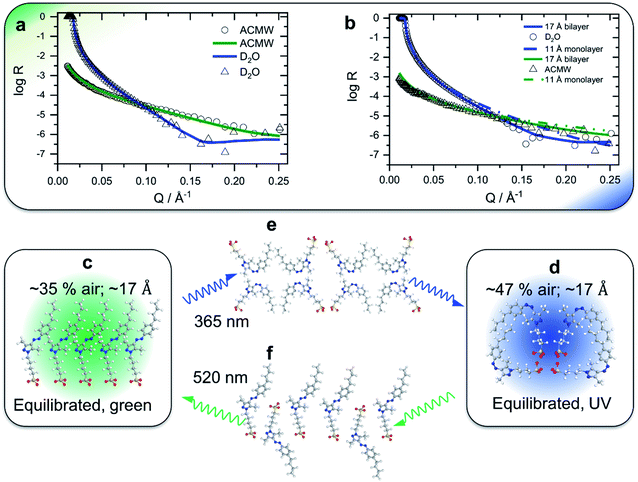 | ||
| Fig. 2 Neutron reflectivity profiles (data points) and optimized model fits (solid lines) of the 0.5 mM partially deuterated butyl-AAP-C4S surfactant at the air–D2O interface for green (a) and UV (b) irradiation; in the latter case, simulated (non-optimized) fits of a monolayer with a thickness of 11 Å are also shown (dashed-dotted lines) to demonstrate that the presence of a monolayer of surfactant molecules in their Z conformation is not supported by the experimental data. Fitting results for other NR contrasts are shown in the ESI.† Schematics of a monolayer-to-bilayer transition of butyl-AAP-C4S surfactants at the air–water interface: (c and b) structures for green and UV irradiation, respectively, when the air–water interface is in thermal equilibrium; (e and f) show suggested transition structures that are formed immediately after the E to Z and Z to E photo-isomerization reactions, respectively. Note that the presented schematics show possible structures that may be formed at the interface in spite of the simplification of representing quasi-three dimensional structures in two dimensions. We also point out that the sulfonate head groups are likely not in the same plane for electrostatic reasons. Solvating water molecules and counterions are not shown for clarity. | ||
At this point, we need to stress that the presented structures are consistent with our experimental observations, but they are also a highly schematic representation of the interfacial structure. A more detailed resolution of the specific molecular configurations is, however, outside the scope of this study.
The surprising monolayer-to-bilayer transition for an amphiphilic photoswitch is unprecedented and in fact can explain the origin of the unique performance of this surfactant in the applications we present below. We attribute this unexpected result to the bipolar character of Z-butyl-AAP-C4S, which is caused by the exposed polar azo group at one end of the molecule and the sulfonate head group at the other end, resulting in the observed bilayer structure.
This intriguing interfacial rearrangement of butyl-AAP-C4S upon photoswitching raises the question what actually happens during the conversion of one interfacial structure to the other. As such, we sought to resolve the photoswitching mechanism in real time using the same powerful set of techniques: surface tensiometry, SFG spectroscopy (S–O amplitudes) and the low-Q analysis method of NR (model-free surface excess).
During four cycles of photoswitching for 0.5 mM butyl-AAP-C4S (chosen due to the largest Δγ; Fig. 1b), a fast increase in the surface tension is observed for E to Z transitions, while the reduction in surface tension caused by the transition from the equilibrated Z to the E state is much slower (Fig. 3a). Furthermore, during two cycles of photoswitching for 0.25 mM butyl-AAP-C4S (chosen due to the largest ΔΓ; Fig. 1c), there is a complete loss in the SFG signal for switching from the E to the Z state on a time scale of just a few seconds (Fig. 3b), while the reappearance of the SFG signals by switching from the Z to the E conformation under constant green irradiation takes several minutes. The relative time scales of the response of the interfacial properties to the light stimulus are therefore qualitatively consistent for SFG spectroscopy and surface tensiometry. On the other hand, the kinetic changes in the surface excess Γ(t) in an equivalent NR experiment are strikingly different. In this case, there is a slower decrease in the surface excess for E to Z (>10 min) transitions than the corresponding increase for switching from the Z to the E state (∼1 min). We will in the following rationalize these different responses in the context of the monolayer/bilayer transition elucidated above in order to formulate an interfacial mechanism during photoswitching.
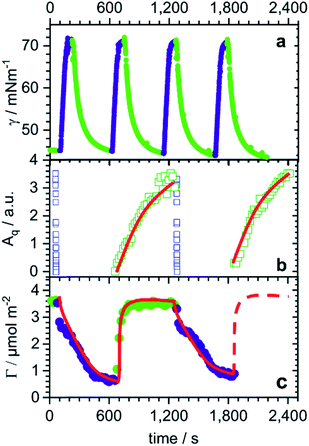 | ||
| Fig. 3 E/Z switching kinetics for changes in irradiation from 520 nm (green symbols) to 365 nm (dark blue symbols) light and vice versa: (a) dynamic surface tension γ(t) of 0.5 mM butyl-AAP-C4S, (b) time-resolved S–O amplitudes of 0.25 mM butyl-AAP-C4S from the kinetic SFG spectra shown in the ESI,† and (c) changes in surface excess Γ of 0.25 mM butyl-AAP-C4S as measured by the low-Q analysis method of NR (see Experimental section). Strikingly, timescales of changes in the surface excess are almost inverted with respect to the data from the other two techniques. | ||
In switching from a relatively dense monolayer with the surfactants in the E conformation to a more hydrated bilayer with the surfactants in the Z state, a fast loss of the molecular order (SFG) and an increase in surface tension are accompanied by a slow reduction in surface excess (NR). We infer that the monolayer-to-bilayer transition occurs quickly after the transformation from E to the sterically more demanding Z conformation, which can be interpreted in terms of a rearrangement of half of the surfactant molecules from the monolayer to adopt positions in the lower leaflet of the bilayer. The rearrangement further leads to a molecular configuration having inversion symmetry that annuls the SFG signals with a lower surface coverage, hence, resulting in a sharp increase in surface tension (schematic in Fig. 2c). As a bilayer pair of Z surfactant molecules is less amphiphilic (and thereby less surface active) than a single E isomer in the monolayer, molecules desorb from the interface, lowering the surface excess slowly without significant further changes in the molecular order or surface tension.
Conversely, in switching from the bilayer (Z conformation) to monolayer (E conformation), a fast increase in surface excess (NR) is followed by a slower gain in the molecular order (SFG) and a reduction in surface tension. In this case, we infer that the adsorption of additional surfactants from the sub-surface to the interface is fast as the E isomer is more surface active than the Z isomer (schematic in Fig. 2d). However, the transition to a complete monolayer, which results in a loss of the inversion symmetry giving rise to the SFG signal and reduces the surface tension, is relatively slow.
This interfacial picture is similar to other self-assembly processes like the formation of self-assembled monolayers at solid surfaces, where the close to maximum surface excess is established relatively fast but the assembly into the final highly ordered structures takes place on time scales of many hours.26,27 Analogous effects at fluid interfaces have so far not been reported, and indeed resolution of a structural mechanism of surfactant photoswitching at the air–water interface is without precedent.
Turning to the application of butyl-AAP-C4S, Fig. 4a presents the results for aqueous foams prepared from 0.5 mM butyl-AAP-C4S (maximum Δγ upon photoswitching; Fig. 1b). The foam lifetime in terms of decreasing foam height was ≫1 h when irradiated with green light, which is dramatically reduced to ∼150 s when the foam is irradiated with UV light. Clearly, the above discussed changes at the molecular level of the air–water interface have also dramatic consequences at a macroscopic level. Furthermore, the observed foam lifetime for green irradiation (E conformation) is much higher than that observed previously for other photo-surfactants, where the process has been shown to take several minutes.9,10
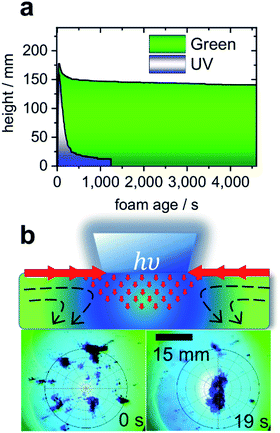 | ||
| Fig. 4 (a) Foam height as a function of foam age for solutions with 0.5 mM butyl-AAP-C4S photoswitches. Measurements under 365 nm UV and 520 nm green light irradiation are indicated by blue and green colours. (b) Schematic presentation of light-actuated Marangoni flow of surfactants (molecules not shown) caused by local surface tension gradients when the AAP modified air–water interface is irradiated locally with UV light. In addition, experiments where carbon particles are spread at the air–water interface from 0.5 mM butyl-AAP-C4S and the sample was irradiated locally with 365 nm UV light but globally with 520 nm are shown. Full video sequences are available online in the ESI.† | ||
Aqueous foams are inherently interface controlled, where the macroscopic properties can be tailored at the molecular level through structure–property relations.2,28 Since the surface excess of an ionic surfactant such as butyl-AAP-C4S determines the interfacial charging state, the latter is reduced when the samples are irradiated with UV light. This reduction in surface charge density leads to a considerable reduction in the electrostatic disjoining pressure Π(h), which results in coalescence and bursting of foam bubbles.29
In the case of AAP stabilized foams, the electrostatic disjoining pressure is the main driving force in foam stability,2 and clearly the use of butyl-AAP-C4S surfactants can render aqueous foam even more responsive to light irradiation. Indeed, the above described massive and fast light-induced changes at the air–water interface have potential to collapse foam after its desired application, enabling an easy foam removal and recycling of its ingredients in an environmentally friendly way without using antifoaming agents.
Another possibility to exploit the potential of butyl-AAP-C4S via E/Z photo-isomerization in applications involves Marangoni flows4,30 at the air–water interface, an effect that can be exploited to move micro- and nanoparticles into ordered structures at a fluid interface in the formation of colloidal crystals.13 A proof of this concept is shown in Fig. 4b, where >100 μm carbon particles were spread at the air–water interface, aggregated, and moved using light-actuated Marangoni flows of butyl-AAP-C4S during photoswitching. Due to the massive and fast changes in the interfacial structure, surface excess, and surface tension upon photoswitching, the visible Marangoni effects where interfacial surfactants migrate along existing surface tension gradients extended over several millimetres away from the UV beam, and the particles were dragged along the surfactant flow field (see ESI videos online†).
In comparison with the results of previous studies,4,13 the resulting forces produced for this system were quite remarkable as agglomerates of several millimetres were transported over distances >10 mm remotely by photoswitching on demand (see ESI videos online†).
Conclusions
Air–water interfaces modified with a new photoswitchable surfactant, butyl-AAP-C4S, have been studied using surface tensiometry, vibrational sum-frequency generation spectroscopy and neutron reflectometry. Using this powerful approach, first we demonstrate that dramatic changes in the surface tension and surface excess can be caused by E to Z photo-isomerization of the surfactant. The experimental evidence from complementary methods points to an unexpected monolayer-to-bilayer transition of the surfactant at the air–water interface, which is attributed to the unique molecular structure of butyl-AAP-C4S whose amphiphilicity varies in the two isomers. The transition structures adopted at the interface during photoswitching are proposed in an unprecedented resolution of the structural mechanism and are key to the superior performance of this new surfactant. Thus, for interface modifications, butyl-AAP-C4S seems to be the perfect photoswitch because of the unprecedented monolayer-to-bilayer transition which we have shown for the first time.The performance of the new surfactant based on the underlying monolayer to bilayer transition was demonstrated in two applications: (i) highly photo-responsive aqueous foams where the foam stability can be tuned from hours to minutes using green and UV light irradiation, respectively, and (ii) light-triggered Marangoni flows where a localized light stimulus resulted in massive and long-range particle movements. Clearly, these properties of butyl-AAP-C4S, not only at the molecular level but also at mesoscopic and macroscopic length scales, show great potential to be exploited as building blocks of adaptive materials in the future.
Experimental section
Vibrational sum-frequency generation (SFG) spectroscopy
SFG spectroscopy is an inherent interface specific method for materials with inversion symmetry and is based on a second-order nonlinear optical process. In a simplified form, the SFG intensity can be written as follows.31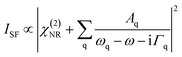 | (4) |
Neutron reflectometry (NR)
Two different implementations of NR were used to resolve either the dynamic surface excess or the interfacial structure of butyl-AAP-C4S at the air–water interface. The FIGARO instrument at the Institut Laue-Langevin (Grenoble, France) was used.35 The time-of-flight instrument was used with a broad chopper pair defining the neutron pulses to exploit high flux at the expense of loose resolution of 8% (FWHM) in the momentum transfer, Q, given by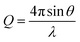 | (5) |
In the first implementation of NR, the recently established method of low-Q analysis was used,36 where data were recorded only at θ = 0.62° and in the range of λ = 2–16 Å, and they were reduced only in the range λ = 4.5–12 Å to give the Q-range 0.01–0.03 Å−1. This approach desensitized the measurements to the interfacial structure. This method has been used to good effect in the last few years to resolve kinetic and dynamic processes at fluid interfaces.22 The measurements were carried out on normal hydrogenous and partially deuterated surfactants on a subphase of ACMW, which has zero scattering length density, hence, the specular reflection is dominated by the signal from the adsorbed surfactant. As a result, the low-Q range and the nature of the measurements, a single mixed interfacial layer of surfactant tails and headgroups was used to fit the data. The surface excess Γ is calculated from eqn (1) as stated above. The background was not subtracted from the data, and the value of the background used in the model was 3.48 × 10−5 as derived from measurements of pure ACMW.
In the second implementation of NR, the data were recorded at θ = 0.62° and 3.8° in the range of λ = 2–30 Å. The measurements were carried out both on hydrogenous and partially deuterated surfactants on subphases of both ACMW and D2O. A common structural model of stratified layers normal to the interface was applied simultaneously to the data recorded in all four isotopic contrasts. The general modelling principles outlined in a recent paper37 were followed. Here, an upper layer of surfactant chains had a fitted thickness, a lower layer of surfactant headgroups had its solvation constrained so that the number of chains and headgroups was equal, and capillary wave roughness was calculated from the surface tension. As the molecules in this study include double bonds that result in constrained molecular orientations, the volume fraction of the layer of chains was fitted rather than being constrained to 1. For this measurement, the background was subtracted from the data. In the experiment, samples were measured in sequence on the standard 6-position sealed adsorption trough sample changer of the instrument. The lids of the trough were specially adapted to hold green and UV LEDs positioned 2.2 cm above the center of each liquid surface. The data were analysed using Motofit.38
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement 638278). We also thank Dana Glikman and Marco Schnurbus (University Münster) for their help with the neutron reflectivity measurements. We thank the Deutsche Forschungsgemeinschaft (SFB 858) for financial support. The authors thank the ILL for the allocation of neutron beam time on FIGARO (DOI: 10.5291/ILL-DATA.9-12-540 and DOI: 10.5291/ILL-DATA.9-10-1573) and Simon Wood for technical assistance during the experiments. Norbert Störkmann and Jürgen Kröninger are acknowledged for help with the irradiation setups.Notes and references
- (a) T. Zhao, X. Zhu, L. Zhang, H. Cang, X. Zhang, C. Li, H. Wei and N. Ma, ACS Appl. Mater. Interfaces, 2018, 10, 4095 CrossRef CAS PubMed; (b) S. Jia, W.-K. Fong, B. Graham and B. J. Boyd, Chem. Mater., 2018, 30, 2873 CrossRef CAS; (c) C. Gao, Q. Huang, Q. Lan, Y. Feng, F. Tang, M. P. M. Hoi, J. Zhang, S. M. Y. Lee and R. Wang, Nat. Commun., 2018, 9, 2967 CrossRef PubMed; (d) B. T. Worrell, M. K. McBride, G. B. Lyon, L. M. Cox, C. Wang, S. Mavila, C.-H. Lim, H. M. Coley, C. B. Musgrave, Y. Ding and C. N. Bowman, Nat. Commun., 2018, 9, 2804 CrossRef PubMed; (e) L. D. Zarzar, V. Sresht, E. M. Sletten, J. A. Kalow, D. Blankschtein and T. M. Swager, Nature, 2015, 518, 520 CrossRef CAS PubMed; (f) S. Chen, L. Fei, F. Ge and C. Wang, Soft Matter, 2019, 15, 8313 RSC; (g) R. Klajn, Chem. Soc. Rev., 2014, 43, 148 RSC; (h) D. Samanta, D. Galaktionova, J. Gemen, L. J. W. Shimon, Y. Diskin-Posner, L. Avram, P. Král and R. Klajn, Nat. Commun., 2018, 9, 641 CrossRef PubMed; (i) J. Boelke and S. Hecht, Adv. Opt. Mater., 2019, 7, 1900404 CrossRef.
- M. Schnurbus, L. Stricker, B. J. Ravoo and B. Braunschweig, Langmuir, 2018, 34, 6028 CrossRef CAS PubMed.
- E. Weißenborn and B. Braunschweig, Soft Matter, 2019, 15, 2876 RSC.
- C. Lv, S. N. Varanakkottu, T. Baier and S. Hardt, Nano Lett., 2018, 18, 6924 CrossRef CAS PubMed.
- (a) S. N. Varanakkottu, S. D. George, T. Baier, S. Hardt, M. Ewald and M. Biesalski, Angew. Chem., Int. Ed., 2013, 52, 7291 CrossRef CAS PubMed; (b) R. Klajn, P. J. Wesson, K. J. M. Bishop and B. A. Grzybowski, Angew. Chem., Int. Ed., 2009, 48, 7035 CrossRef CAS PubMed; (c) Y. Takashima, S. Hatanaka, M. Otsubo, M. Nakahata, T. Kakuta, A. Hashidzume, H. Yamaguchi and A. Harada, Nat. Commun., 2012, 3, 1270 Search PubMed.
- (a) Z. Wu, R. Xue, M. Xie, X. Wang, Z. Liu, M. Drechsler, J. Huang and Y. Yan, J. Phys. Chem. Lett., 2018, 9, 163 CrossRef CAS PubMed; (b) J. Eastoe, M. Sanchez-Dominguez, H. Cumber, G. Burnett, P. Wyatt and R. K. Heenan, Langmuir, 2003, 19, 6579 CrossRef CAS; (c) J. Eastoe and A. Vesperinas, Soft Matter, 2005, 1, 338 RSC; (d) J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103 CrossRef CAS; (e) M. Kathan and S. Hecht, Chem. Soc. Rev., 2017, 46, 5536 RSC.
- E. Chevallier, A. Mamane, H. A. Stone, C. Tribet, F. Lequeux and C. Monteux, Soft Matter, 2011, 7, 7866 RSC.
- L. Fei, F. Ge, Y. Yin and C. Wang, Colloids Surf., A, 2019, 560, 366 CrossRef CAS.
- S. Chen, Y. Zhang, K. Chen, Y. Yin and C. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 13778 CrossRef CAS PubMed.
- E. Chevallier, C. Monteux, F. Lequeux and C. Tribet, Langmuir, 2012, 28, 2308 CrossRef CAS PubMed.
- (a) J. Cheng, P. Štacko, P. Rudolf, R. Y. N. Gengler and B. L. Feringa, Angew. Chem., Int. Ed., 2017, 129, 297 CrossRef; (b) A. Theodoratou, U. Jonas, B. Loppinet, T. Geue, R. Stangenberg, D. Li, R. Berger and D. Vlassopoulos, Phys. Chem. Chem. Phys., 2015, 17, 28844 RSC; (c) A. Mamane, E. Chevallier, L. Olanier, F. Lequeux and C. Monteux, Soft Matter, 2017, 13, 1299 RSC.
- A. Carl and R. von Klitzing, Angew. Chem., Int. Ed., 2011, 50, 11290 CrossRef CAS PubMed.
- J. Vialetto, M. Anyfantakis, S. Rudiuk, M. Morel and D. Baigl, Angew. Chem., Int. Ed., 2019, 58, 9145 CrossRef CAS PubMed.
- (a) E. V. Yakovlev, K. A. Komarov, K. I. Zaytsev, N. P. Kryuchkov, K. I. Koshelev, A. K. Zotov, D. A. Shelestov, V. L. Tolstoguzov, V. N. Kurlov, A. V. Ivlev and S. O. Yurchenko, Sci. Rep., 2017, 7, 13727 CrossRef PubMed; (b) A. Diguet, R.-M. Guillermic, N. Magome, A. Saint-Jalmes, Y. Chen, K. Yoshikawa and D. Baigl, Angew. Chem., Int. Ed., 2009, 48, 9281 CrossRef CAS PubMed; (c) A. Goulet-Hanssens, C. Rietze, E. Titov, L. Abdullahu, L. Grubert, P. Saalfrank and S. Hecht, Chem, 2018, 4, 1740 CrossRef CAS.
- T. Shang, K. A. Smith and T. A. Hatton, Langmuir, 2003, 19, 10764 CrossRef CAS.
- (a) P. Brown, C. P. Butts and J. Eastoe, Soft Matter, 2013, 9, 2365 RSC; (b) R. C. Ahuja, J. Maack and H. Tachibana, J. Phys. Chem., 1995, 99, 9221 CrossRef CAS; (c) J. Maack, R. C. Ahuja and H. Tachibana, J. Phys. Chem., 1995, 99, 9210 CrossRef CAS.
- E. H. G. Backus, J. M. Kuiper, J. B. F. N. Engberts, B. Poolman and M. Bonn, J. Phys. Chem. B, 2011, 115, 2294 CrossRef CAS PubMed.
- L. Stricker, M. Böckmann, T. M. Kirse, N. L. Doltsinis and B. J. Ravoo, Chem.–Eur. J., 2018, 24, 8639 CrossRef CAS PubMed.
- L. Stricker, E.-C. Fritz, M. Peterlechner, N. L. Doltsinis and B. J. Ravoo, J. Am. Chem. Soc., 2016, 138, 4547 CrossRef CAS PubMed.
- C. E. Weston, R. D. Richardson, P. R. Haycock, A. J. P. White and M. J. Fuchter, J. Am. Chem. Soc., 2014, 136, 11878 CrossRef CAS PubMed.
- B. A. Cicciarelli, T. A. Hatton and K. A. Smith, Langmuir, 2007, 23, 4753 CrossRef CAS PubMed.
- R. A. Campbell, Curr. Opin. Colloid Interface Sci., 2018, 37, 49 CrossRef CAS.
- T. Kairaliyeva, E. V. Aksenenko, N. Mucic, A. V. Makievski, V. B. Fainerman and R. Miller, J. Surfactants Deterg., 2017, 20, 1225 CrossRef CAS PubMed.
- C. Stubenrauch, V. B. Fainerman, E. V. Aksenenko and R. Miller, J. Phys. Chem. B, 2005, 109, 1505 CrossRef CAS PubMed.
- (a) D. T. Valley, M. Onstott, S. Malyk and A. V. Benderskii, Langmuir, 2013, 29, 11623 CrossRef CAS PubMed; (b) T. Moldt, D. Brete, D. Przyrembel, S. Das, J. R. Goldman, P. K. Kundu, C. Gahl, R. Klajn and M. Weinelt, Langmuir, 2015, 31, 1048 CrossRef CAS PubMed.
- (a) D. K. Schwartz, Annu. Rev. Phys. Chem., 2001, 52, 107 CrossRef CAS PubMed; (b) T. Balgar, R. Bautista, N. Hartmann and E. Hasselbrink, Surf. Sci., 2003, 532–535, 963 CrossRef CAS.
- C. Meltzer, H. Yu, W. Peukert and B. Braunschweig, Phys. Chem. Chem. Phys., 2018, 20, 19382 RSC.
- S. Streubel, F. Schulze-Zachau, E. Weißenborn and B. Braunschweig, J. Phys. Chem. C, 2017, 121, 27992 CrossRef CAS PubMed.
- Foam Films and Foams: Fundamentals and Applications, ed. D. Exerowa, G. Gochev, D. Platikanov, L. Liggieri and R. Miller, CRC Press, 2019 Search PubMed.
- (a) M. Arangalage, X. Li, F. Lequeux and L. Talini, Soft Matter, 2018, 14, 3378 RSC; (b) L. E. Scriven and C. V. Sterling, Nature, 1960, 187, 186 CrossRef.
- P. E. Ohno, H.-F. Wang and F. M. Geiger, Nat. Commun., 2017, 8, 1032 CrossRef PubMed.
- C. D. Bain, P. B. Davies, T. H. Ong, R. N. Ward and M. A. Brown, Langmuir, 1991, 7, 1563 CrossRef CAS.
- H. B. de Aguiar, A. G. F. de Beer, M. L. Strader and S. Roke, J. Am. Chem. Soc., 2010, 132, 2122 CrossRef CAS PubMed.
- N. García Rey, E. Weißenborn, F. Schulze-Zachau, G. Gochev and B. Braunschweig, J. Phys. Chem. C, 2019, 123, 1279 CrossRef PubMed.
- R. A. Campbell, H. P. Wacklin, I. Sutton, R. Cubitt and G. Fragneto, Eur. Phys. J. Plus, 2011, 126, 107 CrossRef.
- L. Braun, M. Uhlig, R. von Klitzing and R. A. Campbell, Adv. Colloid Interface Sci., 2017, 247, 130 CrossRef CAS PubMed.
- R. A. Campbell, Y. Saaka, Y. Shao, Y. Gerelli, R. Cubitt, E. Nazaruk, D. Matyszewska and M. J. Lawrence, J. Colloid Interface Sci., 2018, 531, 98 CrossRef CAS PubMed.
- A. Nelson, J. Appl. Crystallogr., 2006, 39, 273 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and further characterization, videos of Marangoni flow. See DOI: 10.1039/c9sc05490a |
| This journal is © The Royal Society of Chemistry 2020 |