Open Access Article
Open Access ArticleSingle electron transfer events and dynamical heterogeneity in the small protein azurin from Pseudomonas aeruginosa†
Biswajit
Pradhan
 a,
Christopher
Engelhard
a,
Christopher
Engelhard
 a,
Sebastiaan
Van Mulken
a,
Sebastiaan
Van Mulken
 a,
Xueyan
Miao
a,
Xueyan
Miao
 b,
Gerard W.
Canters
b,
Gerard W.
Canters
 *a and
Michel
Orrit
*a and
Michel
Orrit
 *a
*a
aHuygens-Kamerlingh Onnes Laboratory, Leiden University, 2300 RA Leiden, Netherlands. E-mail: canters@chem.leidenuniv.nl; orrit@physics.leidenuniv.nl
bSchool of Public Health, Guilin Medical University, 541004 Guilin, China
First published on 27th November 2019
Abstract
Monitoring the fluorescence of single-dye-labeled azurin molecules, we observed the reaction of azurin with hexacyanoferrate under controlled redox potential yielding data on the timing of individual (forward and backward) electron transfer (ET) events. Change-point analysis of the time traces demonstrates significant fluctuations of ET rates and of mid-point potential E0. These fluctuations are a signature of dynamical heterogeneity, here observed on a 14 kDa protein, the smallest to date. By correlating changes in forward and backward reaction rates we found that 6% of the observed change events could be explained by a change in midpoint potential, while for 25% a change of the donor–acceptor coupling could explain the data. The remaining 69% are driven by variations in complex association constants or structural changes that cause forward and back ET rates to vary independently. Thus, the observed spread in individual ET rates could be related in a unique way to variations in molecular parameters. The relevance for the understanding of metabolic processes is briefly discussed.
Introduction
Single-molecule spectroscopy in the study of protein dynamic heterogeneity
Redox reactions, in particular electron transfer (ET) reactions are at the heart of cellular metabolism. Marcus' theory has provided a robust framework to analyze ET reactions at the ensemble level in terms of driving force, ΔG, reorganization energy, λ, and electronic donor–acceptor coupling, HDA. However, the question of the extent to which these parameters may vary across an ensemble was left out of consideration for a long time. Early time-resolved experiments by Frauenfelder1 on ensembles of myoglobin molecules revealed stretched exponential relaxation, indicative of a very large spread of the reaction rates of individual molecules. The origin of this spread was assigned to a broad distribution of barrier heights for different individual proteins, itself related to their many (slightly) different conformations and to the widely different reaction rates associated with each of these conformations. The picture thus emerging is that of a multidimensional space of conformations, in which the protein explores a rugged free-energy landscape, with widely distributed energy barriers between potential wells.2 This picture suggests a wide distribution of electron transfer rates and of Marcus' parameters,3 but it is unclear whether this also applies to small enough proteins.More recently, attempts have been undertaken to study the variation of protein reaction rates by means of single-molecule experiments. Using the fluorescence of a flavin cofactor, Lu et al.4 were the first to report single-molecule dynamical heterogeneity, i.e., the spread of reaction rates of a single enzyme, in 1998. Unfortunately, measurements on this particular enzyme have not been reproduced in the last 20 years.
Later experiments on different enzymes such as lipase, β-galactosidase, and horseradish peroxidase made use of fluorogenic reactions.5–8 These experiments, however, were subsequently revisited somewhat critically,9 mainly in view of the reactions' intrinsic stochasticity.
Yang et al.10 investigated the ET from the optically excited FAD cofactor of flavin reductase to an adjacent tyrosine and found considerable fluctuation of the rate of ET over time which they ascribed to temporal variations in the distance between cofactor and tyrosine. It is fair to say that this work is, to date, the most convincing demonstration of dynamical disorder of a single molecule. Similar distributions in ET rates were subsequently found in oxido-reductases like laccase11 and pentaerythritol tetranitrate reductase.12 General arguments on the high complexity and multi-dimensionality of a protein's free energy landscape suggest that dynamical heterogeneity should be common, if not universal, for proteins, including those with a well-defined structure.
In the more specific case of ET reactions, connecting an observed distribution of individual ET rates to variations in the parameters that figure in Marcus' theory proves challenging. Direct attempts to establish distributions of ΔG, λ and HDA have been scarce. For instance, measurements of the midpoint potential of a single redox protein by immobilizing it directly on the working electrode in a cyclic voltammetry experiment were only partially successful.13,14 Sensitivity issues limited the measurements to clusters of a few hundred or more molecules and single-molecule observations proved difficult.15 The question therefore remains whether the midpoint potential of a redox protein, and the Marcus parameters in general, should be represented by distributions rather than by single values.
Here we report on the ET between an electrode and a small protein in solution under constant potential. The study is performed in the presence of a mediator (hexacyanoferrate) and we observe the ET between protein and mediator at the single-molecule level. The distribution of midpoint potentials of individual molecules could be established (FWHM of 22 mV). Moreover, the experimental setup allowed the separate observation of the forward as well as the backward reaction. This made it possible to ascribe particular features in the observed train of ET events to variations in ΔG or HDA, and the association constants K1 and K2 (vide infra). A change in each of these parameters can be recognized from the footprint it leaves on the fluorescence trace of individual molecules.
Fluorescence probing of the azurin redox state
For our study we chose the small (14.0 kDa, 128 residues) blue copper protein azurin (Az) from Pseudomonas aeruginosa. Our choice was motivated by the fact that over the years Az has emerged as the paradigmatic test case for spectroscopic and mechanistic studies of small blue copper proteins and that the protein therefore is well characterized.16,17The ET reactions between small blue copper proteins and redox active transition metal complexes (Cr, Fe, Co, Ru) have been studied extensively in the 70's and 80's by stopped-flow and T-jump techniques.18–23 The ET reaction of Az with ferrocyanide (Fe(II)) and ferricyanide (Fe(III)) is described by:
 | (1) |
In its oxidized form Az has a strong blue color deriving from a S → Cu charge transfer at 600–625 nm involving the Cu and the sulfur of a cysteine ligand.24 This band is not strong enough to serve as a reporter for reaction dynamics at the single-molecule level. Nor can fluorescence techniques be used directly, as Az does not exhibit any fluorescence in the visible region of the spectrum. However, by appending a fluorescent label with a fluorescence overlapping the 600 nm absorption band (see ESI, Fig. S2A†), the label can report the protein's redox state:25 with the protein in the oxidized (blue, Cu(II)) form, label fluorescence is (partly) quenched by FRET, whereas, due to the negligible absorption of the Cu(I) form, quenching is absent in the reduced protein. Thus, fluorescence can be used to monitor the reaction kinetics of the protein. The technique appears sensitive enough for experiments at single-molecule level.26–29
Experimental procedures
Protein synthesis and fluorescent labeling
The copper-containing N42C Az mutant was expressed and purified as described in ref. 30. Zn–Az was obtained as a by-product of the Cu–Az synthesis.31 For fluorescent labeling, ATTO647N-maleimide was bought from ATTO-TEC GmbH and used without further purification. The Az solution was equilibrated with HEPES pH 7. ATTO647N was chosen to label the protein because of its photostability and insensitivity to the redox chemicals used in the study. A mixture of 200 μM Az and ATTO647N-maleimide (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was incubated for 2 hours. The maleimide group reacts with the Cys42 on the protein. The unreacted dyes were removed with a HiTrap desalting column. For this position of the dye, the protein construct shows a high fluorescence switching ratio of 90% between oxidized and reduced conditions (ESI, Fig. S2B†). This construct was chosen for our single-molecule experiment as its two states can be distinguished easily. The same protocol was used for Zn–Az labeling. The fluorescently labeled proteins were then reacted with biotin-PEG-NHS (MW 3400) in phosphate-buffered saline (PBS) pH 7.4 buffer with a ratio 1
1) was incubated for 2 hours. The maleimide group reacts with the Cys42 on the protein. The unreacted dyes were removed with a HiTrap desalting column. For this position of the dye, the protein construct shows a high fluorescence switching ratio of 90% between oxidized and reduced conditions (ESI, Fig. S2B†). This construct was chosen for our single-molecule experiment as its two states can be distinguished easily. The same protocol was used for Zn–Az labeling. The fluorescently labeled proteins were then reacted with biotin-PEG-NHS (MW 3400) in phosphate-buffered saline (PBS) pH 7.4 buffer with a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (Az
5 (Az![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) biotin-PEG-NHS). As the hydrolysis of NHS strongly competes with the NHS-amine reaction, not more than one biotin-PEG was bound to the protein. This was confirmed from SDS–PAGE (data not shown). The free biotin was then removed by centrifugation in a 3 kDa Amicon ultra-filter. The biotin on the protein was used for immobilization on the glass surface.
biotin-PEG-NHS). As the hydrolysis of NHS strongly competes with the NHS-amine reaction, not more than one biotin-PEG was bound to the protein. This was confirmed from SDS–PAGE (data not shown). The free biotin was then removed by centrifugation in a 3 kDa Amicon ultra-filter. The biotin on the protein was used for immobilization on the glass surface.
Functionalization of coverslips
The glass surface was functionalized according to previous work with slight modifications.28 The glass coverslips (MenzelGlaser, 22 mm × 40 mm, no. 1 thickness) were sonicated in water (15 min) and acetone (15 min). Then they were rinsed in Milli-Q water several times and incubated in a H2O/NH4OH/H2O2 (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) bath at 70 °C to remove organic impurities from the surface. The coverslips were rinsed several times with water and ethanol and finally stored in ethanol. Before functionalization, the slides were flamed and treated for 30 min with a 1% solution of [3-(2-aminoethyl)aminopropyl] trimethoxysilane in methanol containing 5% glacial acetic acid. This results in the binding of the silane to active hydroxyl groups. At this stage the silane is not yet covalently bound, but this is achieved by baking the cover slips in an oven at 65 °C for 3 h. After this treatment, the coverslips were sonicated for 10 min, washed with methanol, dried with clean nitrogen, and were left in a desiccator overnight. The next day they were treated with a mixture of 5 mg ml−1 methoxy-PEG-N-hydroxysuccinimide (MW 2000, Laysan Bio) and 0.05 mg ml−1 biotin-PEG-N-hydroxysuccinimide (MW 3400, Laysan Bio) in 50 mM phosphate buffered saline (PBS), pH 7.4. This creates a surface containing biotin and methoxy end groups. The PEG surface prevents nonspecific adsorption of the protein. The slides were dried with a gentle flow of nitrogen and stored in a desiccator until further use.
1) bath at 70 °C to remove organic impurities from the surface. The coverslips were rinsed several times with water and ethanol and finally stored in ethanol. Before functionalization, the slides were flamed and treated for 30 min with a 1% solution of [3-(2-aminoethyl)aminopropyl] trimethoxysilane in methanol containing 5% glacial acetic acid. This results in the binding of the silane to active hydroxyl groups. At this stage the silane is not yet covalently bound, but this is achieved by baking the cover slips in an oven at 65 °C for 3 h. After this treatment, the coverslips were sonicated for 10 min, washed with methanol, dried with clean nitrogen, and were left in a desiccator overnight. The next day they were treated with a mixture of 5 mg ml−1 methoxy-PEG-N-hydroxysuccinimide (MW 2000, Laysan Bio) and 0.05 mg ml−1 biotin-PEG-N-hydroxysuccinimide (MW 3400, Laysan Bio) in 50 mM phosphate buffered saline (PBS), pH 7.4. This creates a surface containing biotin and methoxy end groups. The PEG surface prevents nonspecific adsorption of the protein. The slides were dried with a gentle flow of nitrogen and stored in a desiccator until further use.
Protein immobilization
The biotin-functionalized glass slide was incubated with 20 mM PBS pH 7.4 buffer for 5 min. NeutrAvidin (Thermo Scientific, 100 nM) was incubated for another 15 min and then the slide was washed to remove unbound NeutrAvidin. The labeled protein at a concentration of 100 pM was incubated for 1 min to get isolated proteins to bind to the functionalized glass surface. The unbound proteins were then removed by washing with fresh PBS pH 7.4 buffer. This process yielded about 20 Az molecules per 20 μm × 20 μm observation area.Electrochemical-potential control
Once the unbound proteins were removed, the samples were exposed to fresh PBS pH 7.4 buffer containing 0.2 mM K3[Fe(CN)6]. The redox potential of this buffer solution was controlled by a potentiostat (Model 800B Series Electrochemical Detector, CH Instruments) using the same electrochemical setup as previously described32 with some modifications. A square platinum grid (grid side 25 mm) was used as working electrode and pressed onto the sample slide with the help of a small glass slide. The voids of the grid are nearly closed by the glass slides, forming small confined volumes where the sample slide and glass slide are the ‘floor’ and ‘roof’ and the platinum grid forms the ‘walls’. These confined volumes are on the order of nanoliters, which makes switching of the electrochemical potential of the solution possible in a matter of minutes (Fig. S2C†). The change in the solution potential changes the concentration of reductant and oxidant according to Nernst's equation.Confocal microscope
Single-molecule measurements were carried out in a home-built confocal microscope. The setup was equipped with a 635 nm pulsed diode laser (Power Technology, Little Rock, AR, USA) controlled by a PDL 828 “Sepia II” (PicoQuant) at 40 MHz repetition rate. The laser beam was passed through a narrow-band cleanup filter (Semrock LD01-640/8-25) and coupled to a single-mode optical fiber to obtain a Gaussian beam profile. The output beam was collimated and reflected by a polychroic mirror (z488/633rpc) onto the back aperture of an oil immersion objective (NA = 1.4, Olympus UPLSApo 100x). The sample holder with the glass slide and electrodes was mounted on a scanning stage (Physik Instrumente P-517.3CD) controlled by a nanopositioning system (Physik Instrumente E-710.3CD). The epifluorescence light was collected back through the same objective and focused on a 50 μm pinhole for spatial filtering, then the light passed through an emission filter (z488/635m “dual”-band emission filter, Chroma). The fluorescence beam was re-collimated and focused on a single-photon avalanche photodiode (SPCM AQRH-15, PerkinElmer Inc., USA). The signal from the photodiode was recorded by a PicoHarp 300 (PicoQuant GmbH, Berlin, Germany) in time-tagged-time-resolved mode.Data recording
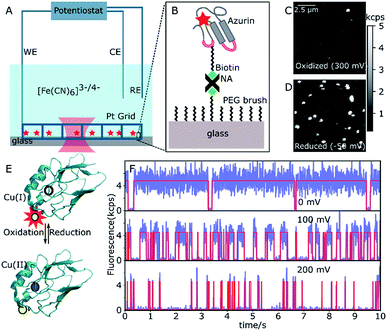
A 20 μm × 20 μm area of the sample surface functionalized with sparsely distributed ATTO647N-labeled or ATTO655-labeled Cu–Az or Zn–Az was scanned with 50 nm per pixel and with a dwell time of 1 ms per pixel. A typical fluorescence intensity image can be seen in Fig. 1. A constant potential of 200 mV vs. SCE (oxidizing) was applied by the potentiostat and an image of 10 μm × 10 μm area was taken after 2 min. Typically within one minute, the solution potential of 200 μM K3[Fe(CN)6] reaches the applied potential. Another image of this same area was recorded at 0 mV (reducing). The two images were compared to identify the active molecules, which switch from bright to dark as the potential is changed from 0 to 200 mV (Fig. 1C and D). The coordinates of the switching molecules were registered and an automatic recording was started. For each molecule, time traces were recorded for 30 s at different potentials between 0 mV and 200 mV. To observe the dynamics of a single molecule over longer times, time traces were recorded until the dye was bleached or the protein was denaturated. Zn–Az-ATTO647N was used as a control since it does not show switching at the above potentials. Time traces were recorded at the same potentials for the same durations as for the Cu–Az.Data analysis
The measurements resulted in more than 2500 time traces. Each time trace contains the absolute arrival time of each photon as well as its arrival time with respect to the excitation laser pulse. This enabled us to extract maximum information from the traces. To minimize accidental variation and improve efficiency, codes were written (in Python) to standardize the analysis of the time traces. Each trace was analyzed in three ways (i) intensity change points in the time traces were obtained using the change-point algorithm33 provided by Prof. Haw Yang (Princeton University, USA). This method is bin-free and does not require any prior knowledge of the underlying kinetics. It determines the location of intensity changes based on the photon arrival times and the algorithm is recursively applied over the whole time trace to find all the changes. A Bayesian information criterion is used to find the number of states. In the present case, only two states were identified from long time traces (about 2500 identified change points on average) of many molecules with a reported accuracy of more than 90%. This is in agreement with our expectation of two states, namely a Cu(II)-quenched (low intensity, dark) and a non-quenched Cu(I) state (bright). Consequently, the number of states for the other time traces has been set to two to minimize the computation time. Examples of traces with estimated change points and their overlap with the real time traces can be seen in Fig. 1F. (ii) Autocorrelation functions of the time traces were calculated using the SymPhoTime (PicoQuant) software. (iii) Further analysis of change-point outputs and the autocorrelation outputs were performed in Python.Results and discussion
Single-azurin observations
The N42C variant of Az was created via site-directed mutagenesis and labeled with ATTO647N maleimide.34 The position was chosen to ensure a Förster transfer efficiency of >90% (see ESI, Fig. S2B†), yielding high contrast between oxidized (quenched) and reduced (fluorescing) forms of Az. The labeled Az was allowed to react with 80-unit biotin-polyethyleneglycol (PEG)-succinimide and immobilized on a passivated PEG surface via streptavidin–biotin binding (Fig. 1A and B). The resulting PEG-NeutrAvidin-PEG tether puts the Az at a maximum distance from the glass surface of roughly 50 nm when stretched out.35 Potassium hexacyanoferrate (K3[Fe(CN)6]) was used as an electron mediator for ET, and the concentration ratio of oxidized to reduced hexacyanoferrate was controlled by varying the electrochemical potential of the solution. A platinum grid was used as the working electrode (WE) and a platinum coil as the counter electrode (CE) (see Fig. 1A). The grid was covered with a second glass slide to minimize the reaction volume. This setup allowed us to reach the desired solution potential within a few minutes after applying the potential (see ESI, Fig. S2B†). We used a saturated calomel electrode (SCE, +244 mV vs. SHE) as a reference electrode (RE), and all potential values reported hereafter are relative to the SCE.Fig. 1C shows a fluorescence image of a 10 × 10 μm2 surface area at the strongly oxidizing potential of 300 mV. Only a few bright spots can be seen, most likely stemming from either inactive Az molecules in their reduced state or those lacking a copper atom. An image of the same surface area at a reducing potential (−50 mV, Fig. 1D) shows many additional bright spots, that could be repeatedly switched on and off by cycling the potential between low and high values. The spots have a size limited by the resolution of the confocal microscope, exhibit digital blinking and bleaching, and thus correspond to individual fluorescing molecules. Therefore, these spots represent Az with active copper centers, the bright form corresponding to Cu(I)–Az and the dark form corresponding to Cu(II)–Az (Fig. 1E).
Once active Az molecules were identified, time-dependent intensity traces of individual Az molecules were recorded at different potentials using single-photon counting. Time traces at three different potentials (0, 100, and 200 mV, see Fig. 1F, blue lines) show different blinking behaviors. To ensure that the observed blinking is in fact due to protein turnover and not to redox reactions of the dye itself, the same experiments were performed with the non-redox-active Zn–Az-ATTO647N, which as expected shows negligible blinking (see ESI, Fig. S6†). Furthermore, even in its dark state, dye-labeled Cu–Az emits a measurable fluorescence signal above background, with a fluorescence lifetime of 0.6 ns, compatible with 90% fluorescence quenching; both observations confirm that the dark state is indeed the Cu(II) state.
Transition points between dark and bright states were identified by using change point analysis (CPA) formulated by Watkins et al.33 Validation of the method's reliability shows that the algorithm correctly locates the change points of a simulated trace (see ESI, Fig. S11†), except for bright times of very short duration (<3 ms) or intervals containing less than 10 detected photons. Examples of transition traces resulting from CPA are shown in Fig. 1F (red lines).
Bright and dark states
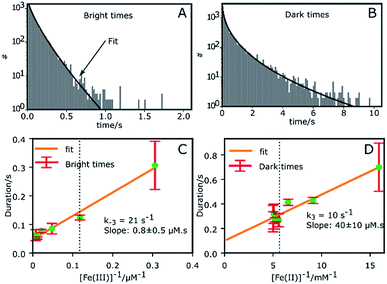
Fig. 2A and B shows the histograms of bright and dark state durations, respectively, extracted via CPA from 145 individual Az molecules at 100 mV potential. The distributions can be fitted with stretched exponentials P(t) = exp[−(t/τ)β], with the characteristic time τ and the stretching exponent β as free parameters. Lower values of β correspond to more stretched time distributions. The average time is given by 〈τ〉 = (τ/β)Γ(1/β). At 100 mV, fitting of the exponential decay results in β and τ values of β = 0.66, τ = 0.11 s, and β = 0.42 and τ = 0.26 s for bright and dark times, respectively, yielding average bright and dark times of 〈τ〉b = 0.14 s and 〈τ〉d = 0.81 s, respectively. The comparatively low values of β are indicative of bright and dark times that are distributed over a wide range of values.Average bright and dark times appear to vary linearly with the inverse of the concentrations of [Fe(III)] and [Fe(II)] (Fig. 2C and D, respectively). The concentration dependence can be fitted with the following relations (see ESI, Section 1.2†):
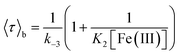 | (2) |
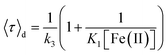 | (3) |
Single-molecule midpoint potentials
The midpoint potential of a single molecule can in principle be determined from the dark and bright times viaeqn (2) and (3). However, for K1[Fe(II)] ≪ 1 and K2[Fe(III)] ≪ 1 the midpoint potential follows from eqn (2) and (3) as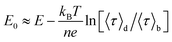 | (4) |
At Fe(CN)6 concentrations higher than 50 μM, the dependence of E0 on ln(〈τ〉d/〈τ〉b) is no longer strictly linear (ESI, Fig. S4A†). While our measurements were performed at 200 μM we still have used eqn (4) to extract E0. This introduces a systematic error of about 20 mV in the value of the midpoint potentials, but it does not affect their distribution or mutual differences.
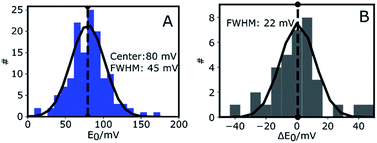
Fig. 3A shows the histogram of midpoint potentials derived from eqn (4) of 145 Az molecules. A Gaussian fit centers at 80 mV with a FWHM of 45 mV. An example of the variation of the bright and dark times as functions of potential for three different Az molecules can be found in the ESI, Fig. S4B.†
The center value of E0 = 80 mV (Fig. 3A) is compatible with previously reported values.26,36,37 The width of the distribution (45 mV) is narrower than those previously reported in single-molecule studies of Az. Davis et al.38 reported a FWHM of 150 mV in a study where each E0 was calculated from a cluster of about 1000 molecules. Salverda et al.13 reported a width of 70 mV where each value was obtained from hundreds of isolated Az molecules on the surface. The reason these studies reported broader distributions may be found in surface interactions.39,40 In our experiments the surface is passivated and is shown (see ESI, Section 1.6, Fig. S5†) to have negligible interaction with freely diffusing Az.
To gain more insight into the observed heterogeneity, we measured E0 over a period of 4 hours at 1 hour intervals (see ESI Fig. S4C†). The histogram of the changes ΔE0 in midpoint potential relative to the first measured value is shown in Fig. 3B for 10 different molecules. It again shows a Gaussian distribution, centered around 0 mV, indicative of random fluctuation rather than a systematic shift or aging. The distribution's FWHM of 22 mV is significantly narrower than the width of the distribution of midpoint potentials in Fig. 3A, but still significantly wider than the expected statistical error of 9 mV FWHM (ESI, Fig. S4D†). Hence the distribution we observe in Fig. 3B may be intrinsic to Az and may reflect slow time-dependent structural variations. The larger width observed in Fig. 3A may reflect static heterogeneity, possibly partly stemming from the various attachment points of the PEG-biotin linker to the 9 surface-exposed lysine residues.16,17
Dynamic heterogeneity
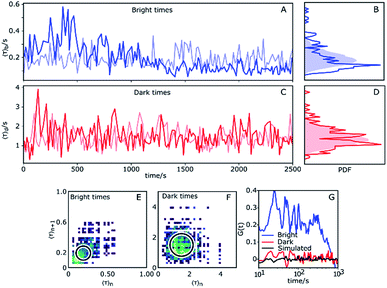
So far we have considered only the averages of the bright and dark times. It is worth examining what information can be gleaned from inspecting the variation over time of τb and τd. Fluorescent time traces of single Az molecules were recorded until the fluorescent probe attached to the protein bleached. We selected a higher potential value (100 mV), as Az populates the dark state roughly 80% of the time under these conditions, significantly lengthening the total observation time. This yielded observation times from typically hundreds up to thousands of seconds. In total, we obtained long time traces of 13 Az molecules (see ESI, Section 1.9†). Each individual trace exhibits qualitatively different dynamics (see examples in the ESI, e.g. Figs. S18, S26 and S28†).The traces were analyzed using CPA and the dark and bright times were determined. Then, for each 10 consecutive dark times, the average dark time was plotted against the center of the time window over which these dark times occurred. The result is essentially a 10-point-binned average of the dark times. The same was done for the bright times. To identify changes, we compared the measured data against simulated data with the same average bright/dark times for a stationary process (i.e., with constant switching rates), which therefore show purely random noise (light colors in Fig. 4). Hereafter, we choose the longest measured trace with ATTO647N (Fig. 4) as a basis for our discussion.
The experimental time trace shown in Fig. 4 is 2600 s long, with 1630 turnovers found by the change point algorithm, with overall average dark and bright times of 〈τ〉b = 0.18 s and 〈τ〉d = 1.4 s, respectively. The trace of bright times shows a clear deviation from the reference random trace (pale blue), characterized by sudden changes in average dwell time interspersed with regions of stability where long times tend to follow long times and short times tend to follow short times for extended periods of time. Fig. 4B shows the probability density function (PDF) of the dark times compared with the same PDF extracted from a long simulated trace. Clearly, the bright times of this Az molecule are distributed over a wider range than expected from the simulated trace with constant rates. Interestingly, there is no clear corresponding behavior of the dark times (Fig. 4C), and their measured PDF is nearly indistinguishable from the simulated homogeneous one (Fig. 4D).
We constructed 2D scatter plots of 〈τ〉n+1vs. 〈τ〉n, where 〈τ〉n indicates the n-th data point from Fig. 4A and C, i.e. again using a 10-point average for binning. The result for the bright times is shown in Fig. 4E, with the corresponding plot for the dark times in Fig. 4F. The large spread of the bright time data (Fig. 4E) beyond the circle (which corresponds to the 95th percentile of simulated data) confirms the previous indications for dynamical heterogeneity. The effect, although present, is less pronounced for the dark times of this trace (Fig. 4F).
Autocorrelations of the bright times and dark times were calculated according to
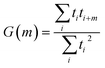 | (5) |
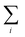 represents the sum over all events ti. The autocorrelation of bright times (Fig. 4G, blue) shows a characteristic decay time of hundreds of seconds while the autocorrelation of dark times (Fig. 4G, red) is closer to that of the simulated homogeneous trace (black), again confirming the lower dynamic variation of the dark times of this trace. Time autocorrelation curves of different Az molecules (ESI Section 1.9, Fig. S12–S37†) yield correlation decay times ranging from tens to hundreds of seconds. It should be noted that the range of measurable correlation times is limited by photobleaching of the label for long times, and by the combination of turnover rates and averaging for short times. The latter yields a time resolution of roughly 10 s.
represents the sum over all events ti. The autocorrelation of bright times (Fig. 4G, blue) shows a characteristic decay time of hundreds of seconds while the autocorrelation of dark times (Fig. 4G, red) is closer to that of the simulated homogeneous trace (black), again confirming the lower dynamic variation of the dark times of this trace. Time autocorrelation curves of different Az molecules (ESI Section 1.9, Fig. S12–S37†) yield correlation decay times ranging from tens to hundreds of seconds. It should be noted that the range of measurable correlation times is limited by photobleaching of the label for long times, and by the combination of turnover rates and averaging for short times. The latter yields a time resolution of roughly 10 s.
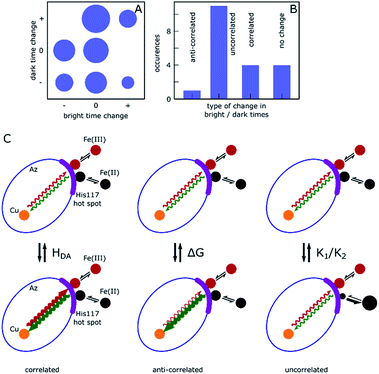
Correlated and non-correlated events
The results presented above and in the ESI† clearly demonstrate dynamic heterogeneity of bright and dark times on timescales of tens to hundreds of seconds. Remarkably, whereas simulated data show completely random fluctuations around the mean dark and bright times, as expected, the measured data of many molecules showed clear correlations where long tended to follow long and short tended to follow short dark/bright times. Moreover, these changes appear as sudden jumps within a few 10-point-averaged data bins (see Fig. 4A for examples at 500 s and 1300 s) on a timescale of tens of seconds and longer, significantly longer than the typical bright and dark times of around 0.1 s and 1 s, respectively. This indicates that the reaction rates are fairly constant over a number of turnovers before abruptly changing.We categorize the changes in dark and bright times as uncorrelated, negatively (anti-) correlated and (positively) correlated (see ESI, Section 1.11† for a full description of the followed procedure). Fig. 5 shows a qualitative summary of the observed changes: each of the change events described above was characterized as to whether only one or both times changed and in which direction. The areas of disks in Fig. 5A correspond to the number of such events. Time traces without heterogeneity were classified as one ‘no change’ event (Fig. 5A, center circle). Fig. 5B shows the same data with the direction of change omitted. As can be clearly seen, roughly two thirds of the observed events are uncorrelated, with the remainder showing predominantly a positively correlated behavior. A full list of events with their classification is given in the ESI, Table T1.†
Under the chosen experimental conditions variations in k−3 and k3 as well as in K1 or K2 may contribute substantially to variations in the bright and dark times.
The association and dissociation rates for hexacyanoferrate are much higher than the rate of electron transfer. Therefore, many binding and unbinding events occur in between any two consecutive electron transfer events. From this follows that variations due to different available binding sites being sampled would occur on a per-ET event basis, rather than the punctuated equilibrium we observe. We therefore conclude that the hexacyanoferrate binding site remains constant over long time periods, indicating that only one such site is available at any given time. It is well established that electrons on their way to and from the Cu in Az, enter or leave the protein by way of histidine 117, which is a ligand to the Cu.17,41 His117 protrudes through the protein surface and can make contact with external reactants through a water molecule that is anchored to the Nε nitrogen of the histidine. Thus the surface patch around His117 is a hot spot for electron transfer42 (see ESI Section 1.13†) and we may assume that the events we observe in our single-molecule experiment result from hexacyanoferrate associating with the protein in the neighborhood of His117.
According to Marcus, the expression for the rate of ET between a donor and an acceptor, kET, is
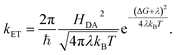 | (6) |
In the simplest version of the theory, the expressions for k−3 and k3 are identical except for the sign of the driving force. It is clear from eqn (6) that a change in donor–acceptor coupling, HDA, will lead to correlated changes of bright and dark times (Fig. 5C, left), as observed in 25% of the cases. Changes in HDA may occur through changes in the dihedral angles along the covalent path that connects donor and acceptor across the protein or through temporal changes in H-bond patterns and through-space gaps in the ET path.
As is clear from eqn (6), in the non-inverted Marcus region a change in midpoint potential E0 of Az will lead to anti-correlated changes in bright and dark times, as observed in only 6% of the cases. The midpoint potential may change, for instance, as a result of a changing charge distribution brought about by protonation/deprotonation of titratable residues. These are usually fast processes but in exceptional cases the protonation/deprotonation reaction may take place on a time scale of seconds.9
Possible changes in K1 and K2 are not necessarily correlated and may lead to uncorrelated changes in dark and bright times. As K1 and K2 refer to the formation of association complexes of Az with hexacyanoferrate moieties carrying −4 and −3 net charges, respectively, Coulomb interactions with the ferro- and ferricyanide ions will be different (as is also apparent from the 20-fold difference between K1 and K2). Solvation effects may affect the magnitude of K1 and K2 as well. It is conceivable, therefore, that slight changes in the charge distribution or the solvation around His117 may affect the two association constants differently, leading to uncorrelated changes in dark and bright times (Fig. 5C, right).
Finally, if the Marcus potential curves for forward and backward transfer significantly differ from each other, due to relaxation of the protein around the reduced or oxidized copper center, the corresponding ET rates may fluctuate in uncorrelated ways. The latter two mechanisms could explain the remaining uncorrelated changes observed in 69% of the cases. These results show that single-electron transfer events probe the sensitivity of ET parameters to protein conformational dynamics.
Conclusions
Observing single electron transfer events on single molecules showed significant rate fluctuations, a signature of dynamical heterogeneity, here demonstrated for the first time on a small protein of 14 kDa. The heterogeneous rate fluctuations are characterized by a ‘punctuated equilibrium’ behavior, where the forward and back reaction rates appear rather constant on timescales of tens to hundreds of seconds before abruptly changing, in line with existing data.43 Correlating changes in forward reaction rates with those in backward rates, we determined that in 69% of cases the two processes changed in an uncorrelated fashion, with 25% of events showing a positive and only 6% a negative correlation of the changes. Based on Marcus' theory, we can therefore conclude that changes driven purely by a change in driving force, such as would be caused by e.g. a change in protonation in the neighborhood of the Cu center, are rare in our data, in agreement with the slow variation in midpoint potentials over time mentioned above.A change of the coupling constant only, caused e. g. by sidechain reorientations or variations in H-bond patterns along the electron transfer pathway, could explain the positively correlated events observed in one quarter of cases. The latter in particular are known to have a potentially significant influence on ET.44,45 The vast majority of uncorrelated change events are thus either due to fluctuations in the complex association/disassociation constants, or to more complex structural fluctuations, e.g. those that are influenced by the formation of the complex.46 It should be noted that under physiological conditions variations in the association constants may be less prevalent since the structure of the association complex will often be unique and there will be less room for variation. It may be expected, therefore, that for biological ET reactions, in particular intramolecular ET between redox centers inside proteins, the heterogeneity in ET rates will be caused to a large extent by the dynamic heterogeneity of the electronic donor–acceptor coupling elements, i.e. it reflects the dynamic variations in the protein structure. As the protein dynamics are temperature-dependent, the dynamic heterogeneity of the ET rates should change as the temperature is lowered.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible by the NWO NanoFront PhD grant for BP, a Chinese Scholarship Council individual postdoc grant for XM, and a Deutsche Forschungsgemeinschaft postdoc grant for CE. We thank Prof Thijs J. Aartsma for his early contributions to this work and his help with Az functionalization.Notes and references
- H. Frauenfelder, S. G. Sligar and P. G. Wolynes, Science, 1991, 254, 1598–1603 CrossRef CAS PubMed.
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- Y. Gao, X. Liu, L. Sun, Y. Xu, S. Yang, C. Fan and D. Li, J. Phys. Chem. Lett., 2019, 10, 2512–2517 Search PubMed.
- H. P. Lu, L. Xun and X. S. Xie, Science, 1998, 282, 1877–1882 CrossRef CAS PubMed.
- O. Flomenbom, K. Velonia, D. Loos, S. Masuo, M. Cotlet, Y. Engelborghs, J. Hofkens, A. E. Rowan, R. J. M. Nolte, M. van der Auweraer, F. C. de Schryver and J. Klafter, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2368–2372 CrossRef CAS PubMed.
- K. Hassler, P. Rigler, H. Blom, R. Rigler, J. Widengren and T. Lasser, Opt. Express, 2007, 15, 5366–5375 CrossRef CAS PubMed.
- B. P. English, W. Min, A. M. van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. C. Kou and X. S. Xie, Nat. Chem. Biol., 2006, 2, 87–94 CrossRef CAS PubMed.
- H. M. Piwonski, M. Goomanovsky, D. Bensimon, A. Horovitz and G. Haran, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1437–E1443 CrossRef CAS PubMed.
- T. G. Terentyeva, H. Engelkamp, A. E. Rowan, T. Komatsuzaki, J. Hofkens, C.-B. Li and K. Blank, ACS Nano, 2012, 6, 346–354 CrossRef CAS PubMed.
- H. Yang, G. Luo, P. Karnchanaphanurach, T.-M. Louie, I. Rech, S. Cova, L. Xun and X. S. Xie, Science, 2003, 302, 262–266 CrossRef CAS PubMed.
- A. Gupta, T. J. Aartsma and G. W. Canters, J. Am. Chem. Soc., 2014, 136, 2707–2710 CrossRef CAS PubMed.
- C. R. Pudney, R. S. K. Lane, A. J. Fielding, S. W. Magennis, S. Hay and N. S. Scrutton, J. Am. Chem. Soc., 2013, 135, 3855 CrossRef CAS PubMed.
- J. M. Salverda, A. V. Patil, G. Mizzon, S. Kuznetsova, G. Zauner, N. Akkilic, G. W. Canters, J. J. Davis, H. A. Heering and T. J. Aartsma, Angew. Chem., Int. Ed., 2010, 49, 5776–5779 CrossRef CAS PubMed.
- A. V. Patil and J. J. Davis, Coord. Chem. Rev., 2011, 255, 1970 CrossRef CAS.
- H. A. Heering, F. G. M. Wiertz, C. Dekker and S. de Vries, J. Am. Chem. Soc., 2004, 126, 11103 CrossRef CAS PubMed.
- U. Kolczak, C. Dennison, A. Messerschmidt and G. W. Canters, in Handbook of Metalloproteins, ed. K. Wieghardt, R. Huber, T. L. Poulos and A. Messerschmidt, John Wiley & Sons, Chichester, 2001, pp. 1170–1194 Search PubMed.
- C. Dennison, Coord. Chem. Rev., 2005, 249, 3025–3054 CrossRef CAS.
- M. Goldberg and I. Pecht, Biochemistry, 1976, 15, 4197–4208 CrossRef CAS PubMed.
- B. S. Brunschwig, P. J. Delaive, A. M. English, M. Goldberg, S. L. Mayo, N. Sutin and H. B. Gray, Inorg. Chem., 1985, 24, 3743–3749 CrossRef CAS.
- A. G. Lappin, M. G. Segal, D. C. Weatherburn, R. A. Henderson and A. G. Sykes, J. Am. Chem. Soc., 1979, 101, 2302–2306 CrossRef CAS.
- A. G. Lappin, M. G. Segal, D. C. Weatherburn and A. G. Sykes, J. Am. Chem. Soc., 1979, 101, 2297–2301 CrossRef CAS.
- J. V. Mcardle, C. L. Coyle, H. B. Gray, G. S. Yoneda and R. A. Holwerda, J. Am. Chem. Soc., 1977, 99, 2483–2489 CrossRef CAS PubMed.
- M. G. Segal and A. G. Sykes, J. Chem. Soc., Chem. Commun., 1977, 764–765 RSC.
- E. I. Solomon, J. W. Hare, D. M. Dooley, J. H. Dawson, P. J. Stephens and H. B. Gray, J. Am. Chem. Soc., 1980, 102, 168–178 CrossRef CAS.
- S. Kuznetsova, G. Zauner, R. Schmauder, O. A. Mayboroda, A. M. Deelder, T. J. Aartsma and G. W. Canters, Anal. Biochem., 2006, 350, 52–60 CrossRef CAS PubMed.
- A. Andreoni, S. Sen, P. L. Hagedoorn, W. J. Buma, T. J. Aartsma and G. W. Canters, Chem.–Eur. J., 2018, 24, 646–654 CrossRef CAS PubMed.
- R. H. Goldsmith, L. C. Tabares, D. Kostrz, C. Dennison, T. J. Aartsma, G. W. Canters and W. E. Moerner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17269–17274 CrossRef CAS PubMed.
- L. C. Tabares, A. Gupta, T. J. Aartsma and G. W. Canters, Molecules, 2014, 19, 11660–11678 CrossRef PubMed.
- S. Kuznetsova, G. Zauner, T. J. Aartsma, H. Engelkamp, N. Hatzekis, A. E. Rowan, R. J. M. Nolte, P. C. M. Christianen and G. W. Canters, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3250–3255 CrossRef CAS PubMed.
- I. M. C. van Amsterdam, M. Ubbink, L. J. C. Jeuken, M. P. Verbeet, O. Einsle, A. Messerschmidt and G. W. Canters, Chem.–Eur. J., 2001, 7, 2398–2406 CrossRef CAS.
- H. Nar, R. Huber, A. Messerschmidt, A. C. Filipou, M. Barth, M. Jaquinod, M. van de Kamp and G. W. Canters, Eur. J. Biochem., 1992, 205, 1123–1129 CrossRef CAS PubMed.
- W. Zhang, M. Caldarola, B. Pradhan and M. Orrit, Angew. Chem., Int. Ed., 2017, 56, 3566–3569 CrossRef CAS PubMed.
- L. P. Watkins and H. Yang, J. Phys. Chem. B, 2005, 109, 617–628 CrossRef CAS PubMed.
- I. M. C. van Amsterdam, M. Ubbink and G. W. Canters, Inorg. Chim. Acta, 2002, 331, 296–302 CrossRef CAS.
- Z. Ma, D. N. LeBard, S. M. Loverde, K. A. Sharp, M. L. Klein, D. E. Discher and T. H. Finkel, PLoS One, 2014, 9, e112292 CrossRef PubMed.
- M. van de Kamp, G. W. Canters, C. R. Andrew, J. Sanders-Loehr, C. J. Bender and J. Peisach, Eur. J. Biochem., 1993, 218, 229–238 CrossRef CAS PubMed.
- C. S. S. Clair, W. R. Ellis and H. B. Gray, Inorg. Chim. Acta, 1992, 191, 149–155 CrossRef.
- A. V. Patil and J. J. Davis, J. Am. Chem. Soc., 2010, 132, 16938–16944 CrossRef CAS PubMed.
- L. Rivas, C. M. Soares, A. M. Baptista, J. Simaan, R. E. di Paolo, D. H. Murgida and P. Hildebrandt, Biophys. J., 2005, 88, 4188–4199 CrossRef CAS PubMed.
- D. H. Murgida and P. Hildebrandt, Chem. Soc. Rev., 2008, 37, 937–945 RSC.
- M. van de Kamp, M. C. Silvestrini, M. Brunori, J. van Beeumen, F. C. Hali and G. W. Canters, Eur. J. Biochem., 1990, 194, 109–118 CrossRef CAS PubMed.
- D. N. Beratan, J. N. Betts and J. N. Onuchic, Science, 1991, 252, 1285–1288 CrossRef CAS PubMed.
- A. Gupta, A. Milias-Argeitis and M. Khammash, J. R. Soc., Interface, 2017, 14, 20170311 CrossRef PubMed.
- J. C. Cristaldi, M. C. Gomez, P. J. Gonzalez, F. M. Ferroni, S. D. Dalosto, A. C. Rizzi, M. G. Rivas and C. D. Brondino, Biochim. Biophys. Acta, Gen. Subj., 2018, 1862, 752–760 CrossRef CAS.
- J. S. Kretchmer, N. Boekelheide, J. J. Warren, J. R. Winkler, H. B. Gray and T. F. Miller, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6129–6134 CrossRef CAS PubMed.
- C. Romero-Muniz, M. Ortega, J. G. Vilhena, I. Diez-Perez, J. C. Cuevas, R. Perez and L. A. Zotti, Biomolecules, 2019, 9, E506 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, control experiments, full data of all molecules. See DOI: 10.1039/c9sc05405g |
| This journal is © The Royal Society of Chemistry 2020 |