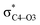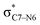Open Access Article
Open Access ArticleTipping the balance: theoretical interrogation of divergent extended heterolytic fragmentations†
Croix J.
Laconsay
 ,
Ka Yi
Tsui
and
Dean J.
Tantillo
,
Ka Yi
Tsui
and
Dean J.
Tantillo
 *
*
Department of Chemistry, University of California, Davis, CA 95616, USA. E-mail: djtantillo@ucdavis.edu
First published on 9th January 2020
Abstract
Herein we interrogate a type of heterolytic fragmentation reaction called a ‘divergent fragmentation’ using density functional theory (DFT), natural bond orbital (NBO) analysis, ab initio molecular dynamics (AIMD), and external electric field (EEF) calculations. We demonstrate that substituents, electrostatic environment and non-statistical dynamic effects all influence product selectivity in reactions that involve divergent fragmentation pathways. Direct dynamics simulations reveal an unexpected post-transition state bifurcation (PTSB), and EEF calculations suggest that some transition states for divergent pathways can, in principle, be selectively stabilized if an electric field of the correct magnitude is oriented appropriately.
Introduction
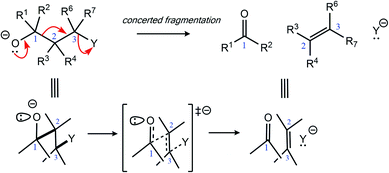
While complex molecular architectures are usually constructed using key bond-making reactions, destructive reactions, in which key bonds are broken, can also be used to advantage. Here we examine the mechanism and consequences of a particular type of molecular destruction – divergent extended heterolytic fragmentation. Carbon–carbon (C–C), carbon–heteroatom (C–X), and heteroatom–heteroatom (X–Y) heterolytic fragmentation reactions offer methods for synthesizing structural motifs (some found in complex natural products) that might be difficult to synthesize using methods focused on bond formation.1–7 Despite their continued use in organic synthesis8–17 and their relevance to reactions occurring in mass spectrometers,18 the application of heterolytic fragmentations in which multiple σ-bonds are cleaved in synthetic campaigns is limited by putative strict conformational requirements (e.g., an anti-periplanar conformation for the bonds that cleave during fragmentation; Scheme 1).4,19 Few theoretical and mechanistic studies20–24 have provided insight into the physical underpinnings for this class of reaction since the seminal work of Grob.2 Our aim in this arena is to increase the understanding of underlying mechanistic factors that govern these transformations to facilitate recognition of key patterns associated with fragmentation reactivity and thereby help guide syntheses of compounds whose construction remains a challenge.Two types of heterolytic fragmentations that have been reported in the literature but have received little theoretical attention are (1) extended fragmentations – heterolytic fragmentations that involve a chain of more than five atoms – and (2) divergent fragmentations – heterolytic fragmentations that involve the formation of two (or more) distinct products from a single substrate.4 Extended fragmentations are unsurprisingly rare due to the complexity of orchestrating many bond-breaking events in one transformation.25 Some experimental examples are shown in Fig. 1a and b.26–28 Highlighted in bold are the bonds involved in each fragmentation. Here we focus on designing systems where these sorts of cage-supported extended fragmentations can have divergent outcomes (Fig. 1d; inspired by reaction in Fig. 1c).
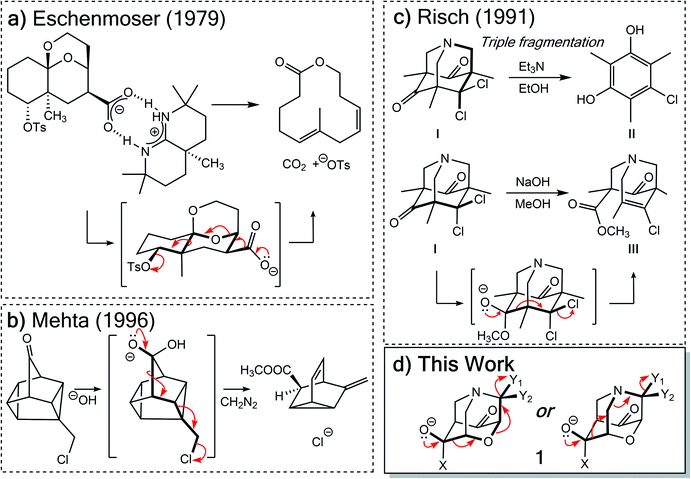 | ||
| Fig. 1 Previous extended heterolytic fragmentations.26–28 | ||
Initially, our objective was to find the length limit for a concerted extended fragmentation, but we encountered unexpected divergent fragmentations en route to this goal; our work on this length limit will be reported elsewhere. Using model systems inspired by experimentally relevant molecules,28 we show that the outcome of divergent fragmentations can be substituent dependent, is sensitive to external electrostatic environments (i.e., in external electric fields (EEFs)), and can involve unusual potential energy surfaces (PESs) with features such as plateaus and post-transition state bifurcations (PTSBs,29–34 which make these reactions subject to non-statistical dynamic effects).35–38 The particular systems we examine (Fig. 1d and Scheme 2) involve divergence after the first σ-bond has broken, complicating the issue of where along the fragmentation reaction coordinate product selectivity is determined.
Methods
All density functional theory (DFT) calculations were carried out using the Gaussian 09 suite of programs.39 Transition-state structures (TSSs) and minima were verified as such by frequency calculations. Intrinsic Reaction Coordinate (IRC) calculations were used to further characterize TSSs.40–42 Eight different functionals were tested against B3LYP-D3(BJ) for Table 1, entry 1 to verify that geometries of TSSs and minima were reasonably consistent among various methods (see Table S1 in the ESI†). However, the difference in free energy barriers identified by these functionals ranged over more than 10 kcal mol−1. Thus, B3LYP-D3(BJ) and M06-2X, each with the 6-31G(d) basis set, were tested against each other for entries 1–12 in Table 1, since, together, these two functionals covered the range of activation barriers. Employing these two functionals provided a check that DFT reasonably captured the qualitative product selectivity trends with which this study is concerned. Employing a larger basis set (that includes diffuse functions), 6-31+G(d), did not change the overall qualitative conclusions, therefore we only report 6-31G(d) results from here on (see ESI†). Quasi-classical ab initio direct dynamics simulations for entries 3 and 4 in Table 1 were initiated from optimized TSSs using the Progdyn script package provided by Singleton.43 Trajectories were propagated in time in both the reactant and product directions until they reached product or reactant wells on the PES: trajectories were allowed to propagate until either the C1–C2 bond (Scheme 2) distance dropped below 1.58 Å, for which we report the trajectory as forming reactant 1, until the O3–C4 bond distance exceeded 3.2 Å and the C5–Y1 bond distance exceeded 3.0 Å (while C5–Y1 remained below 5.5 Å), for which we report the trajectory as forming product A, or until the C7–N6 bond distance exceeded 3.2 Å and the C5–Y1 bond distance exceeded 3.0 Å (while C5–Y1 remained below 5.5 Å), for which we report the trajectory as forming product B. External Electric Field (EEF) calculations44 were implemented using the “field” keyword in Gaussian 09 (see ESI† for details).39 A more recent study, in the form of the TITAN code, expands the various types of EEFs that can be generated.45| Entry | X | Y1 | Y2 | ΔG‡B3LYP-D3(BJ), A | ΔG‡M06-2X, A | ΔG‡B3LYP-D3(BJ), B | ΔG‡M06-2X, B | Predicted kinetic product(s) |
|---|---|---|---|---|---|---|---|---|
| a The TSS computed at B3LYP-D3(BJ) leads to product A only and the TSS computed at M06-2X leads to B by an IRC. A TSS that leads to A at M06-2X was also identified, but it does not connect to minimum 1 by an IRC. | ||||||||
| 1 | N(CH3)2 | O(CO)Cl | H | 33.8 | 46.9 | — | — | A |
| 2 | N(CH3)2 | Cl | Cl | — | — | 32.9 | 44.1 | B |
| 3 | NH2 | O(CO)Cl | H | 28.5 | 39.4 | — | — | A |
| 4a | NH2 | Cl | Cl | 28.2 | 41.5 | — | 38.8 | A & B |
| 5 | OCH3 | O(CO)Cl | H | 34.4 | 46.8 | — | — | A |
| 6 | OCH3 | Cl | Cl | — | 48.2 | 33.6 | 43.8 | B |
| 7 | OCH(CH3)2 | O(CO)Cl | H | 36.7 | 47.9 | — | — | A |
| 8 | OCH(CH3)2 | Cl | Cl | 37.3 | 51.1 | 35.9 | 47.0 | B |
| 9 | H | O(CO)Cl | H | 35.2 | 47.5 | — | — | A |
| 10 | H | Cl | Cl | 36.4 | 49.4 | 34.6 | 44.6 | B |
| 11 | F | O(CO)Cl | H | 38.1 | 50.6 | — | — | A |
| 12 | F | Cl | Cl | 39.2 | 52.7 | 37.6 | 47.7 | B |
Results and discussion
Substituent effects on product selectivity
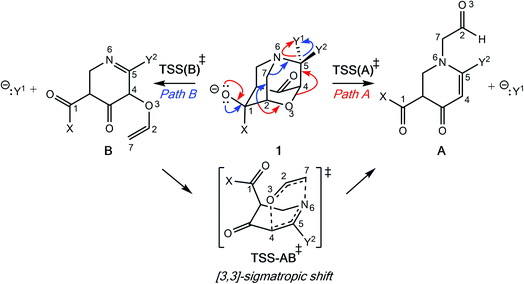
In the course of our search for the length limit in concerted fragmentation, we found inspiration in Risch's 1-aza-adamantane (I in Fig. 1c).28,46 These 1-aza-adamantane structures have played a significant role in work done by the Castellano group in studying donor–acceptor through-bond interactions for crystal and materials design.47–49 A simplified model system was designed such that it satisfied the expected structural and stereoelectronic requirements50 for concerted fragmentation (1, Scheme 2). We hypothesized that this model system would undergo one of two possible concerted 7-atom fragmentations (red and blue arrows in Scheme 2). We successfully found a TSS, TSS(A)‡, that connects 1 to a product of extended fragmentation (A; verified by IRC calculations; see ESI†), where X = OCH3, Y1 = Cl and Y2 = Cl (red arrows, Scheme 2).28 We also postulated that changing Y1 to chloroformate (O(CO)Cl) with Y2 = H might lead to a TSS that involves a concerted 9-atom fragmentation, given that chloroformate could decarboxylate to form CO2 and Cl−, which would break one additional bond (C–Cl). However, following multiple relaxed potential energy surface scans, candidate TSSs only optimized to TSS(B)‡ (for breaking the C7–N6 bond; blue arrows in Scheme 2; verified by IRC calculations; see ESI†) instead of TSS(A)‡ (for breaking the O3–C4 bond), i.e., TSS(B)‡ connects 1 to B.Calculations at the B3LYP-D3(BJ)/6-31G(d) and M06-2X/6-31G(d) levels reveal that the outcome of this divergent fragmentation (1 can form A or B) is dependent on substituents X, Y1 and Y2 (Table 1). For example, changing the leaving group (or nucleofuge1), Y1, from chloroformate (O(CO)Cl) to chlorine (Cl) and Y2 = hydrogen (H) to chlorine (Cl) switched the energetically preferred fragmentation pathway from Path A to Path B. Additionally, some entries (entries 4, 6, 8, 10, and 12) in Table 1 have competing pathways, i.e. we could identify two TSSs on the PES that either lead to products A or B (products that are kinetically favored are bolded). Attempts to identify competing TSSs for entries including chloroformate at the Y1 position (odd numbered entries in Table 1) proved unfruitful, as TSS(A)‡ was the only TSS we could identify. We suspect that different through-space and through-bond electronic effects are the cause of different energetically preferred fragmentation mechanisms—this possibility will be discussed further below.51–53 Products A and B can be interconverted by a [3,3]-sigmatropic shift (TSS-AB‡), but the TSS for this interconversion consistently lies >30 kcal mol−1 uphill in free energy relative to the less thermodynamically stable product (see ESI†). Therefore, the influence of this interconversion on product selectivity is presumably negligible at reasonable experimental temperatures. Products A and B could be of synthetic utility, although synthesis of 1 presents its own challenges. DFT calculations predicted inconsistent results for entries 3 and 4 (vide infra). Worth noting here, too, is the effect of polar solvent on product selectivity: for all entries computed at the M06-2X level in an implicit solvent model (CPCM)54,55 of water, no change in product selectivity was observed; at the B3LYP-D3(BJ) level in the same solvent, entries 2, 6, and 8, switched from B to A as the predicted kinetic product (see ESI† for additional details). Since results in polar solvent are inconclusive, we focus on gas-phase results from here on.
The behavior of the system in entry 4 proved to be sensitive to the theoretical method used. M06-2X calculations predict that product B formation is kinetically preferred over product A, which means that the C4–O3 bond stays intact while the other key bonds fragment. A representative plot of bond length changes along the reaction coordinate (Fig. 2) reveals that this concerted fragmentation reaction is asynchronous: the C1–C2 bond cleaves before the C5–Cl or C7–N6 bonds.56–58 However, a search for TSS(B)‡ at the B3LYP-D3(BJ) level only yielded a TSS connected to product A, TSS(A)‡; after re-optimizing this TSS(A)‡ at the M06-2X level, we identified a product-A-forming TSS that does not directly connect to reactant 1 as a minimum by an IRC. Instead, this TSS(A)‡ connected to an enolate structure that is similar to, but lower in energy than, 1, i.e., a potential precursor to the reactant. Thus, we do not directly compare barriers for two TSSs at the M06-2X level, but we note that TSS(A)‡ is 2.7 kcal mol−1 higher in energy than is TSS(B)‡ if we compare the two TSS's free energies to that of 1. The peculiarities of the system in entry 4 will be discussed in more detail below.
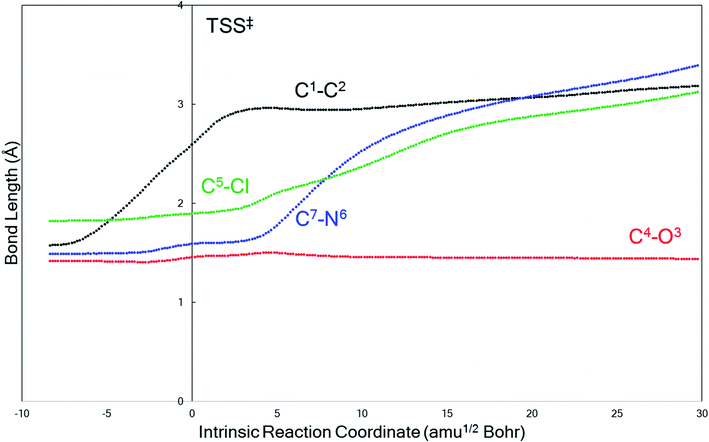 | ||
| Fig. 2 A representative example (from entry 4 of Table 1, M06-2X/6-31G(d)) of the evolution of key bond lengths involved in the fragmentation as the reaction progresses along the IRC. The transition state structure is at reaction coordinate = 0. | ||
Stereoelectronic effects
Why do different substituents have such a strong influence on which product is favored? We initially hypothesized that what drives the fragmentation towards one product or another is the net sum of stereoelectronic effects within the molecule that would favor breaking either the C4–O3 or the N6–C7 bond. We postulated that the change of one or two substituents would result in a tip in the delicate balance of donor–acceptor interactions and drive reactivity toward one product versus the other. Alabugin previously discussed fragmentation reactions in the context of donor–acceptor interactions (see “Remote Stereoelectronic Effects”, chapter 8 in ref. 50).50 For example, the concept of double hyperconjugation was introduced to explain the extra stabilization (δ-effect) from substituents in δ-cyclohexyl cations.59–61 We hypothesized that the geometric restrictions in our 1-aza-adamantane structure would enforce through-bond, ‘double-hyperconjugation-like’ communication through the σ-bond framework. However, in our case, strong double hyperconjugation is not present, since the σC1–C2 orbital is not parallel to the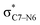 and
and 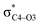 orbitals (Scheme 3).
orbitals (Scheme 3).
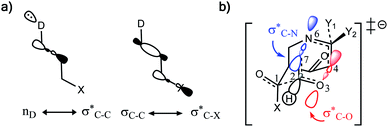 | ||
Scheme 3 (a) Double hyperconjugation. (b) The σC–H orbital is parallel with respect to antibonding molecular orbitals 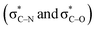 of 1. of 1. | ||
To elucidate the key donor–acceptor interactions that might lead to a change in product selectivity, we used NBO calculations, a standard approach for quantifying the magnitude of such interactions.50,62,63 A sum of second-order perturbation energies E(2) for TSSs for entries 1, 2 and 4 (Table 1), at the M06-2X/6-31G(d) level, are shown in Table 2 (for the source of these values, see ESI†). The E(2) energies are qualitatively consistent with what is observed in the TSS free energy calculations. For instance, the greater donation of electron density into 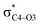 for entry 1 is consistent with formation of product A. The opposite is true for entry 2. Entry 4's TSS has a similar amount of donation into the σ* orbitals of both C4–O3 and C7–N6 bonds, which is consistent with different preferred products at different levels of theory (vide supra). It is difficult to assign ‘responsibility’ to any one donor–acceptor interaction that favors cleavage of either the C4–O3 or C7–N6 bonds (acceptors), when in fact, it is a multitude of donors that donate electron density into these σ* orbitals (see ESI†). One of the major factors contributing to this challenge is the difficulty delineating inductive and field effects in remote stereoelectronic effects.50 This is especially prevalent in 1, which as a cage-supported molecule has many through-bond and through-space interactions.
for entry 1 is consistent with formation of product A. The opposite is true for entry 2. Entry 4's TSS has a similar amount of donation into the σ* orbitals of both C4–O3 and C7–N6 bonds, which is consistent with different preferred products at different levels of theory (vide supra). It is difficult to assign ‘responsibility’ to any one donor–acceptor interaction that favors cleavage of either the C4–O3 or C7–N6 bonds (acceptors), when in fact, it is a multitude of donors that donate electron density into these σ* orbitals (see ESI†). One of the major factors contributing to this challenge is the difficulty delineating inductive and field effects in remote stereoelectronic effects.50 This is especially prevalent in 1, which as a cage-supported molecule has many through-bond and through-space interactions.
The results above are mirrored by computed Wiberg bond indices, or ‘bond orders’ (BO).64,65 Wiberg BOs (computed in an NBO calculation) for the C4–O3 or C7–N6 bonds of the reactants alone are not predictive of which bond will break (all range from 0.91–0.94, with only slightly lower BOs for the bond that breaks; see Table 3), consistent with a “dilution” of delocalization between the O− lone pair and the bonds that will break, due to the intermediacy of another σ-bond that must break. We also computed the change in the Wiberg BO, ΔBO, which gives us insight into the perturbation each bond experiences upon reaching the TSS (Table 3). Not surprisingly, for most cases, the product formed can be predicted by which bond has the larger ΔBO (i.e., smaller BO in the fragmentation TSS). For the system in entry 4 (Table 1), the ΔBO values are relatively close, however, precluding a clear prediction (vide infra).
| Entry | Wiberg BO, reactantC–O | Wiberg BO, reactantC–N | Wiberg BO, TSSC–O | Wiberg BO, TSSC–N | ΔBOC–O | ΔBOC–N | Predicted kinetic product(s) |
|---|---|---|---|---|---|---|---|
| 1 | 0.92 | 0.95 | 0.53 | 0.92 | 0.39 | 0.03 | A |
| 2 | 0.92 | 0.92 | 0.89 | 0.48 | 0.03 | 0.44 | B |
| 3 | 0.91 | 0.94 | 0.55 | 0.92 | 0.36 | 0.02 | A |
| 4 | 0.92 | 0.93 | 0.87 | 0.77 | 0.05 | 0.16 | A & B |
| 5 | 0.92 | 0.94 | 0.49 | 0.92 | 0.43 | 0.02 | A |
| 6 | 0.93 | 0.93 | 0.89 | 0.44 | 0.04 | 0.49 | B |
| 7 | 0.92 | 0.94 | 0.48 | 0.92 | 0.44 | 0.02 | A |
| 8 | 0.92 | 0.93 | 0.89 | 0.46 | 0.03 | 0.47 | B |
| 9 | 0.91 | 0.94 | 0.45 | 0.93 | 0.46 | 0.01 | A |
| 10 | 0.92 | 0.93 | 0.88 | 0.40 | 0.04 | 0.53 | B |
| 11 | 0.92 | 0.93 | 0.51 | 0.93 | 0.41 | 0.00 | A |
| 12 | 0.92 | 0.93 | 0.88 | 0.37 | 0.04 | 0.56 | B |
Post-transition state bifurcations
The inconsistency between the B3LYP-D3(BJ) and M06-2X results in entries 3 and 4 in Table 1 prompted us to explore the potential energy surfaces for these two systems using ab initio molecular dynamics (AIMD) simulations.33,66–68 Previous work suggests that IRCs obtained with two different theoretical methods that lead to different products despite originating at ostensibly the same TSS could indicate that a PTSB follows this TSS.69–71 In all dynamics simulations, trajectories were initiated from the DFT-optimized TSSs and propagated in reactant and product directions until structures were reached that closely resembled minima on the PES (see Methods section for details).31,33,72–74For the system in entry 3 (Table 1), downhill trajectories from TSS(A)‡ predominantly form A, with a small number forming B (Fig. 3) at the M06-2X level. Product A can also originate from a shallow carbanion intermediate, Int, formed viaTSS(i)‡. Int is not found on the B3LYP-D3(BJ) PES (see ESI† for IRC).75,76 Mandal and Datta reported a similarly shaped PES in a gold(I)-catalyzed Diels–Alder reaction with a single intermediate well leading to two different products where the product selectivity is steered by dynamic effects.77 Trajectories originating from TSS(i)‡ also predominantly form A, with a slightly larger number forming B. Product A is thermodynamically favored, which may manifest in lower energy exit channels from both TSSs on the relatively flat energy surface in the vicinity of TSS(i-A)‡, Int and TSS(i)‡. No downhill trajectories from TSS(A)‡ result in formation of the imine product (B) when using B3LYP-D3(BJ) (Fig. 3a). While the formation of some product B is consistent with the presence of a PTSB, the product distribution for this system is probably better described as arising from molecular motion on a flat energy surface.
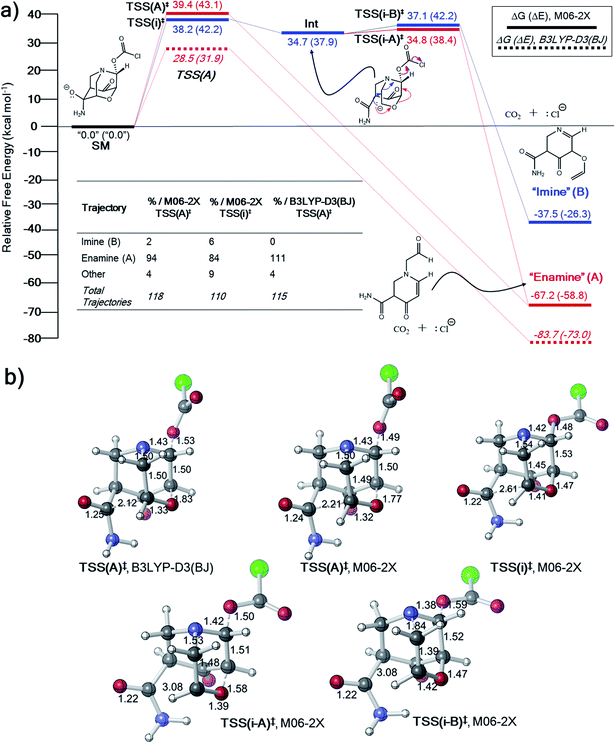 | ||
| Fig. 3 (a) Free energy profile (electronic energies in parentheses) and “downhill” dynamics results for entry 3 (Table 1). Product distributions from AIMD simulations originate from either TSS(A)‡ or TSS(i)‡. (b) CYLview images78 of key TSSs on the PES for entry 3. Bond lengths in units of Å. | ||
For the system in entry 4, no intermediate was found at either level of theory (Fig. 4). Again, product A is much more favorable in free energy than product B. However, our AIMD calculations predict that products A and B are produced in comparable amounts using either functional. These results are consistent with a PTSB on the PES and non-statistical dynamic control of the product distribution.31
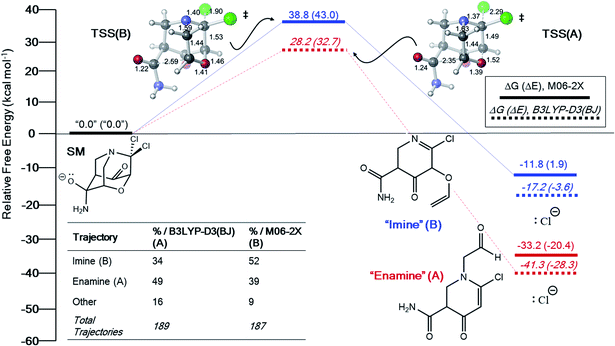 | ||
| Fig. 4 Free energy profile (electronic energies in parentheses) and “downhill” dynamics results from B3LYP-D3(BJ) and M06-2X PES's for entry 4 (Table 1). Products that are connected by a solid or dotted line to the TSS indicate that they are connected by an IRC to the reactant. | ||
External electric fields
Since changing substituents X, Y1, and Y2 altered the outcome of divergent fragmentations of 1, we questioned what might happen under the influence of an external perturbation like an external electric field (EEF). EEFs have recently received considerable attention, being referred to as “smart reagents” for catalysis because of their ability to control reactivity and selectivity.44,79–81 A seminal study by Shaik and co-workers demonstrated that not only can an EEF lower or raise the barrier for a Diels–Alder reaction when oriented in one direction or the other along the “reaction axis”—that is, the (approximate) axis along which electrons reorganize (on average) to make and break bonds—but an electric field oriented perpendicular to the reaction axis can induce endo/exo selectivity.82 The potential for EEFs to control chemical transformations has captured the curiosity of many groups83–92 since Coote and co-workers experimentally demonstrated electrostatic catalysis of a Diels–Alder reaction in 2016.93 For example, a recent experimental study demonstrated EEF-induced selective catalysis in a two-step reaction.94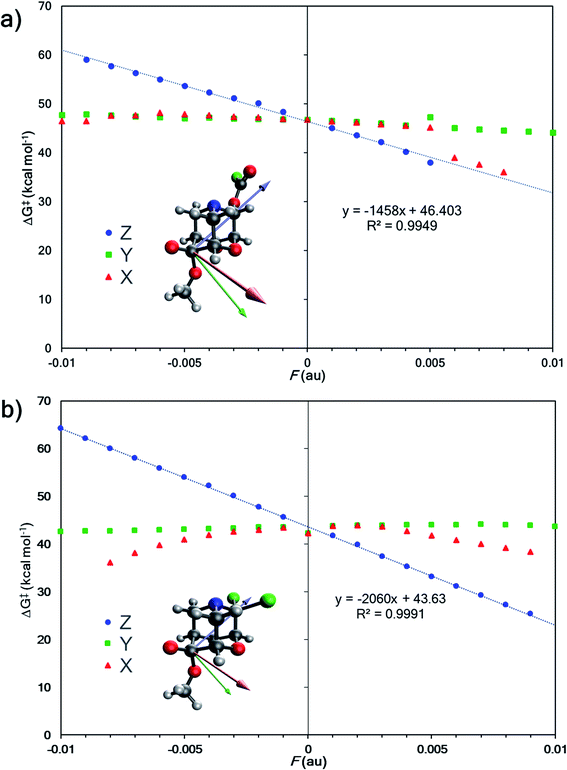 | ||
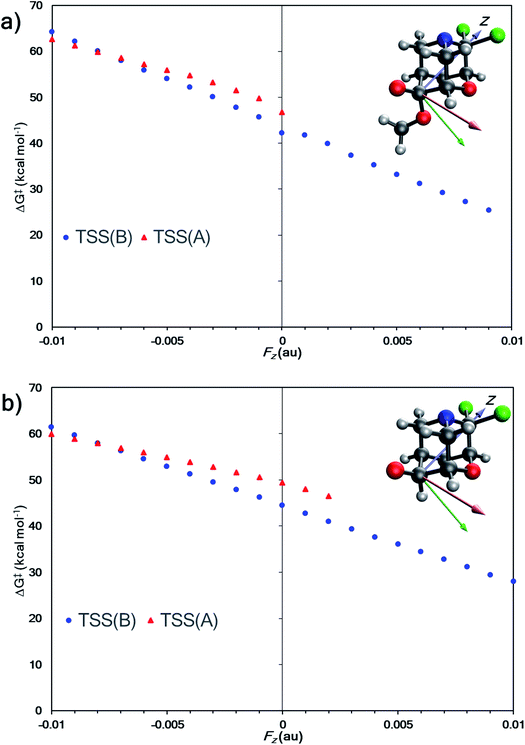
| Fig. 5 (a) External electric field effects on divergent fragmentation of 1 (entry 5, TSS for formation of A from Table 1). The high green data point at Fy = +0.005 results from a change in the reactant structure geometry in the presence of an EEF. Reactant structures optimized in EEFs of Fy ≥ 0.005 au result in a structure shown in Fig. S3 in ESI.† (b) Effects on divergent fragmentation of 1 (entry 6, TSS for formation of B from Table 1). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.95 Over time, they observed that this ratio decreased to 3
1 ratio.95 Over time, they observed that this ratio decreased to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 favoring the allene. Our computed enthalpies and free energies agree qualitatively with their reported computational results and are consistent with experimental observations that initial allene formation is faster than alkyne formation: the predicted ΔΔG‡ between TS-II and TS-I is 2.6 kcal mol−1 with B3LYP-D3(BJ) and 1.9 kcal mol−1 with M06-2X (see Table S5† for details). We envisioned that, since EEFs have a rate accelerating/decelerating effect, they also may have the ability to induce product selectivity in divergent fragmentations.
1 favoring the allene. Our computed enthalpies and free energies agree qualitatively with their reported computational results and are consistent with experimental observations that initial allene formation is faster than alkyne formation: the predicted ΔΔG‡ between TS-II and TS-I is 2.6 kcal mol−1 with B3LYP-D3(BJ) and 1.9 kcal mol−1 with M06-2X (see Table S5† for details). We envisioned that, since EEFs have a rate accelerating/decelerating effect, they also may have the ability to induce product selectivity in divergent fragmentations.
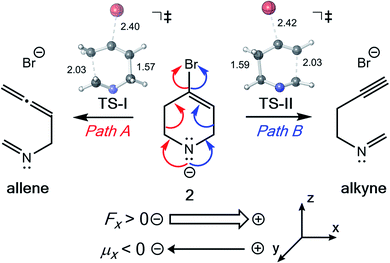 | ||
| Fig. 6 Fragmentation reaction of Williams and co-workers examined in the presence of EEFs. M06-2X/6-31G(d) optimized TS-I and TS-II are shown with key bond lengths in Å. | ||
The directional flow of electrons (reaction axis44) in this system is assumed to point from the N atom to the Br atom down the +z axis (Fig. 6). We postulated that, perpendicular to that axis, along the ±x axis, electron flow would be polarized so as to favor either Path A or Path B, i.e., one of TS-I and TS-II would be selectively stabilized while the other would be destabilized. This prediction is borne out in our computations (Fig. 7). With a field of magnitude 0.004 au oriented in the −x direction, the free energy barriers for formation of the allene and alkyne are predicted to be equal, but different products are favored at higher or lower field strengths, i.e., there exists a mechanistic crossover point somewhere along the EEF spectrum. While the crossover point might occur at a different field strength with a different level of theory, this example serves as a proof-of-concept that one might be able to selectively produce either product of a divergent fragmentation with an appropriately oriented electric field.
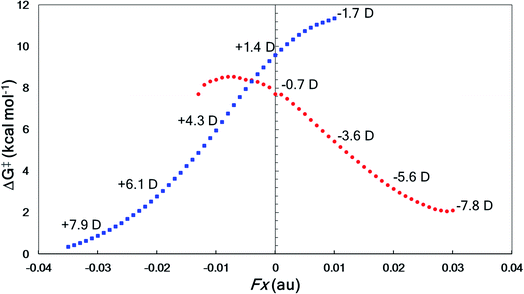 | ||
| Fig. 7 EEF effects on divergent fragmentation of 2, examined using M06-2X/6-31G(d). The x component of the molecular dipole moment (μx in Debye) is shown at each hundredth of an atomic unit (au) representing the magnitude of the electric field oriented in the in the ±x direction. Red circles correspond to Path A in Fig. 6 and blue squares correspond to Path B. At points where the trendline falls off, we find that either the reactant structure and/or the TSS are not stationary points on the PES. | ||
Do EEF's have a similar effect on product selectivity in the fragmentation of 1? To answer this question, we selected entries 6 and 10 (from Table 1) for our case studies because these entries each have two TSSs—one leading to product A (TSS(A)‡) and one leading to product B (TSS(B)‡). In both cases, product B is kinetically preferred in the absence of an EEF (with both B3LYP-D3(BJ) and M06-2X). The results of the EEF calculations in Fig. 5 indicate that the z axis induces the most significant change to the free energy barrier. We hypothesized that an EEF along the ±z axis might have a significant (de)stabilizing effect on the free energy barriers, enough to switch product selectivity. Fig. 8 displays the results of the calculations. Both TSS(A)‡ and TSS(B)‡ experience a linear change in the free energy barrier. However, only the barrier for formation of B is lowered in the presence of positive z (+Fz) fields: attempts to optimize TSS(A)‡ in the presence of EEFs of +Fz > 0.001 au for entry 6 and +Fz > 0.003 for entry 10 led to TSS(B)‡. This suggests that fields oriented in that direction might completely shut down the pathway to form product A. We also carried out calculations in which an EEF is oriented along the ±x or ±y axes, to test for switches in product selectivity (see ESI, Fig. S7 and S8†), but observed no crossing of the free energy barriers for TSS(A)‡ and TSS(B)‡. This means that there is no switch in selectivity for the divergent fragmentation of 1 in the presence of EEFs oriented in the x or y directions within the −0.01 au to +0.01 au magnitude range.95 Nevertheless, as EEFs in the −Fz direction increase in magnitude, the ΔΔG‡ between TSS(A)‡ and TSS(B)‡ decreases (making the path to form A more competitive), and at some field, the selectivity switches. This, in principle, means that EEFs oriented down the ±z axis can alter product selectivity.
Conclusions
Since the 1950s, with the identification and categorization of fragmentations as a class of organic reaction by Eschenmoser96 and its further development by Grob (with “…glaring disregard of the earlier contributions”3),1,2 the heterolytic fragmentation has become a useful tool in organic synthesis. Nonetheless, we believe that additional interesting chemistry remains to be discovered in this area. In this study, we have expanded the concept of heterolytic fragmentation by exploring a model fragmentation in which a single substrate can fragment via two distinct pathways to different products after an initial σ-bond cleavage – a divergent extended fragmentation.4 We demonstrated that substituents, electrostatic environment and dynamic effects can influence pathways to competing products. Direct dynamics simulations on some systems reveal flat regions of energy surfaces where selectivity is determined and yet another unexpected PTSB in a reaction of a complex organic molecule.33 Finally, EEF calculations suggest that divergent pathways can, in principle, be selected between if an electric field is oriented appropriately.97Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was inspired in part by a friendly competition between the groups of DJT and Roald Hoffmann (Cornell) to find the limit for combining substitution events into concerted processes. Financial and computational (XSEDE) support from NSF is gratefully acknowledged.References
- C. A. Grob and P. W. Schiess, Angew. Chem., Int. Ed., 1967, 6, 1–106 CrossRef CAS.
- C. A. Grob, Angew. Chem., Int. Ed., 1969, 8, 535–622 CrossRef CAS.
- K. Prantz and J. Mulzer, Chem. Rev., 2010, 110, 3741–3766 CrossRef CAS PubMed.
- M. A. Drahl, M. Manpadi and L. J. Williams, Angew. Chem., Int. Ed., 2013, 52, 11222–11251 CrossRef CAS PubMed.
- P. Weyerstahl and H. Marschall, in Comprehensive Organic Synthesis, 1991, pp. 1041–1070 Search PubMed.
- T. T. Hoang, G. B. Dudley and L. J. Williams, Comprehensive Organic Synthesis, Elsevier Ltd., 2nd edn, 2014, vol. 6, pp. 842–860 Search PubMed.
- J. Yang, T. T. Hoang and G. B. Dudley, Org. Chem. Front., 2019, 6, 2560–2569 RSC.
- E. J. Corey, R. B. Mitra and H. Uda, J. Am. Chem. Soc., 1963, 85, 362–363 CrossRef CAS.
- E. J. Corey, R. B. Mitra and H. Uda, J. Am. Chem. Soc., 1964, 86, 485–492 CrossRef CAS.
- T. T. Hoang, M. Birepinte, N. M. Kramer and G. B. Dudley, Org. Lett., 2016, 18, 3470–3473 CrossRef CAS PubMed.
- M. M. Uteuliyev, T. T. Nguyen and D. M. Coltart, Nat. Chem., 2015, 7, 1024–1027 CrossRef CAS PubMed.
- J. Shi, H. Xu, D. Qiu, J. He and Y. Li, J. Am. Chem. Soc., 2016, 139, 623–626 CrossRef PubMed.
- E. J. Rastelli, A. A. Bolinger and D. M. Coltart, Chem, 2018, 4, 2228–2238 CAS.
- J. R. Donald and W. P. Unsworth, Chem. – Eur. J., 2017, 23, 8780–8799 CrossRef CAS PubMed.
- L. Cao, C. Wang and P. Wipf, Org. Lett., 2019, 21, 1538–1541 CrossRef CAS PubMed.
- B. Ma, Y. Zhao, C. He and H. Ding, Angew. Chem., Int. Ed., 2018, 57, 15567–15571 CrossRef CAS PubMed.
- Q. Gu, X. Wang, B. Sun and G. Lin, Org. Lett., 2019, 21, 5082–5085 CrossRef CAS PubMed.
- D. P. Demarque, A. E. M. Crotti, R. Vessecchi, J. L. C. Lopes and N. P. Lopes, Nat. Prod. Rep., 2016, 33, 432–455 RSC.
- R. M. Wilson and S. J. Danishefsky, J. Org. Chem., 2007, 72, 4293–4305 CrossRef CAS PubMed.
- R. L. Davis, C. A. Leverett, D. Romo and D. J. Tantillo, J. Org. Chem., 2011, 76, 7167–7174 CrossRef CAS PubMed.
- J. Andrés, J. J. Queralt, V. S. Safont, M. Canle L and J. A. Santaballa, J. Phys. Chem., 1996, 100, 3561–3568 CrossRef.
- J. J. Queralt, V. S. Safont, V. Moliner and J. Andrés, Chem. Phys., 1998, 229, 125–136 CrossRef CAS.
- L. M. LeBlanc, S. W. Powers, J. S. Grossert and R. L. White, Rapid Commun. Mass Spectrom., 2016, 30, 2133–2144 CrossRef CAS PubMed.
- P. Batsomboon, B. A. Gold, I. V. Alabugin and G. B. Dudley, Synth, 2012, 44, 1818–1824 CrossRef CAS.
- M. Castiñeira Reis, C. S. López, O. Nieto Faza and D. J. Tantillo, Chem. Sci., 2019, 10, 2159–2170 RSC.
- G. Mehta and C. Ravikrishna, Tetrahedron Lett., 1996, 37, 2655–2658 CrossRef CAS.
- D. Sternbach, M. Shibuya, F. Jaisli, M. Bonetti and A. Eschenmoser, Angew. Chem., Int. Ed., 1979, 18, 634–636 CrossRef.
- N. Risch, M. Langhals and T. Hohberg, Tetrahedron Lett., 1991, 32, 4465–4468 CrossRef CAS.
- D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601 CrossRef CAS PubMed.
- J. Rehbein and B. K. Carpenter, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922 RSC.
- S. R. Hare and D. J. Tantillo, Beilstein J. Org. Chem., 2016, 12, 377–390 CrossRef CAS PubMed.
- S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698 CAS.
- Z. Yang and K. N. Houk, Chem. – Eur. J., 2018, 24, 3916–3924 CrossRef CAS PubMed.
- N. Mandal and A. Datta, J. Phys. Chem. B, 2018, 122, 1239–1244 CrossRef CAS PubMed.
- B. K. Carpenter, Angew. Chem., Int. Ed., 1998, 37, 3340–3350 CrossRef PubMed.
- P. Collins, B. Carpenter, G. Ezra and S. Wiggins, J. Chem. Phys., 2013, 139, 154108 CrossRef PubMed.
- B. K. Carpenter, Chem. Rev., 2013, 113, 7265–7286 CrossRef CAS PubMed.
- D. J. Tantillo, Dynamic Effects on Organic Reactions in Reference Modules in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier Inc., Waltham, MA, 2018 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, B. Scuseria, G. E. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, H. P. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, M. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, T. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, J. A. Nakajima, P. Honda, Y. Kitao, O. Nakai, H. Vreven, T. Montgomery, Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, V. N. Staroverov, V. N. Keith, T. Kobayashi, R. Normand, J. C. K. Rendell, A. Burant, J. C. Iyengar, S. S. Tomasi, J. B. M. Rega, N. Millam, J. M. Klene, M. Knox, J. E. Cross, R. E. Y. Bakken, V. Adamo, C. Jaramillo, J. Gomperts, R. Stratmann, M. O. Austin, R. Cammi, C. Pomelli, R. L. J. W. Ochterski, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, D. J. O. Foresman, J. B. Ortiz, J. V. Cioslowski and J. Fox, Gaussian Inc., 2009.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269 CrossRef CAS.
- D. A. Singleton, C. Hang, M. J. Szymanski and E. E. Greenwald, J. Am. Chem. Soc., 2003, 125, 1176–1177 CrossRef CAS PubMed.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, J. Comput. Chem., 2020, 41, 74–82 CrossRef CAS PubMed.
- D. Kardel, W. Knoche and N. Risch, J. Chem. Soc., Perkin Trans. 1, 1993, 2, 1455–1459 RSC.
- A. J. Lampkins, Y. Li, A. Al Abbas, K. A. Abboud, I. Ghiviriga and R. K. Castellano, Chem. – Eur. J., 2008, 14, 1452–1463 CrossRef CAS PubMed.
- H. Li, E. A. Homan, A. J. Lampkins, I. Ghiviriga and R. K. Castellano, Org. Lett., 2005, 7, 443–446 CrossRef CAS PubMed.
- L. Yuan, B. G. Sumpter, K. A. Abboud and R. K. Castellano, New J. Chem., 2008, 32, 1924–1934 RSC.
- I. V. Alabugin, Stereoelectronic Effects Stereoelectronic Effects A Bridge Between Structure and Reactivity, John Wiley & Sons, Ltd, 2016 Search PubMed.
- R. Hoffmann, Acc. Chem. Res., 1971, 4, 1–9 CrossRef CAS.
- R. Gleiter, Angew. Chem., Int. Ed., 1974, 13, 696–701 CrossRef.
- M. N. Paddon-Row, Acc. Chem. Res., 1982, 15, 245 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- D. J. Tantillo and J. Tantillo, J. Phys. Org. Chem., 2008, 21, 561–570 CrossRef CAS.
- A. Williams, Concerted Organic and Bioorganic Mechanisms, CRC Press LLC, 1st edn, 2000 Search PubMed.
- M. J. S. Dewar and A. B. Pierini, J. Am. Chem. Soc., 1984, 106, 203–208 CrossRef CAS.
- W. Adcock, J. Coope, V. J. Shiner, Jr. and N. A. Trout, J. Org. Chem., 1990, 55, 1411–1414 CrossRef CAS.
- J. B. Lambert, L. A. Salvador and J. H. So, Organometallics, 2005, 12, 697–703 CrossRef.
- I. V. Alabugin and M. Manoharan, J. Org. Chem., 2004, 69, 9011–9024 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- D. E. Ortega, S. Gutiérrez-Oliva, D. J. Tantillo and A. Toro-Labbé, Phys. Chem. Chem. Phys., 2015, 17, 9771–9779 RSC.
- S. Pratihar, X. Ma, Z. Homayoon, G. L. Barnes and W. L. Hase, J. Am. Chem. Soc., 2017, 139, 3570–3590 CrossRef CAS PubMed.
- X. Ma and W. L. Hase, Philos. Trans. R. Soc., A, 2017, 375, 20160204 CrossRef PubMed.
- M. Paranjothy, R. Sun, Y. Zhuang and W. L. Hase, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 296–316 CAS.
- S. R. Hare and D. J. Tantillo, Chem. Sci., 2017, 8, 1442–1449 RSC.
- D. H. Nouri and D. J. Tantillo, J. Org. Chem., 2006, 71, 3686–3695 CrossRef CAS PubMed.
- Y. J. Hong and D. J. Tantillo, Nat. Chem., 2014, 6, 104–111 CrossRef CAS PubMed.
- U. Lourderaj, K. Park and W. L. Hase, Int. Rev. Phys. Chem., 2008, 27, 361–403 Search PubMed.
- B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89 CrossRef CAS PubMed.
- U. Lourderaj and W. L. Hase, J. Phys. Chem. A, 2009, 113, 2236–2253 CrossRef CAS PubMed.
- M. D. Wodrich, C. Corminboeuf and P. V. R. Schleyer, Org. Lett., 2006, 8, 3631–3634 CrossRef CAS PubMed.
- V. N. Staroverov and E. R. Davidson, J. Am. Chem. Soc., 2000, 122, 7377–7385 CrossRef CAS.
- N. Mandal and A. Datta, J. Org. Chem., 2018, 83, 11167–11177 CrossRef CAS PubMed.
- C. Y. Legault, CYLview, 1.0b, Univ. Sherbrooke, 2009 Search PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1–25 CrossRef PubMed.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Perez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- T. Stuyver, D. Danovich, J. Joy and S. Shaik, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, e1438 Search PubMed.
- R. Meir, H. Chen, W. Lai and S. Shaik, ChemPhysChem, 2010, 11, 301–310 CrossRef CAS PubMed.
- M. Akamatsu, N. Sakai and S. Matile, J. Am. Chem. Soc., 2017, 139, 6558–6561 CrossRef CAS PubMed.
- K. Bhattacharyya, S. Karmakar and A. Datta, Phys. Chem. Chem. Phys., 2017, 19, 22482–22486 RSC.
- W. M. Sun, C. Y. Li, J. Kang, D. Wu, Y. Li, B. L. Ni, X. H. Li and Z. R. Li, J. Phys. Chem. C, 2018, 122, 7867–7876 CrossRef CAS.
- T. Dudev, S. Ilieva and L. Doudeva, Phys. Chem. Chem. Phys., 2018, 20, 24633–24640 RSC.
- L. Yue, N. Wang, S. Zhou, X. Sun, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2018, 57, 14635–14639 CrossRef CAS PubMed.
- A. A. Arabi and C. F. Matta, J. Phys. Chem. B, 2018, 122, 8631–8641 CrossRef CAS PubMed.
- Z. Wang, D. Danovich, R. Ramanan and S. Shaik, J. Am. Chem. Soc., 2018, 140, 13350–13359 CrossRef CAS PubMed.
- Y. Zang, Q. Zou, T. Fu, F. Ng, B. Fowler, J. Yang, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- C. Geng, J. Li, T. Weiske, M. Schlangen, S. Shaik and H. Schwarz, J. Am. Chem. Soc., 2017, 139, 1684–1689 CrossRef CAS PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef PubMed.
- X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li, J. Liu, Y. Yang, J. Shi, Z. Chen, M. Bai, H.-L. Zhang, H. Xia, J. Cheng, Z.-Q. Tian and W. Hong, Sci. Adv., 2019, 5, eaaw3072 CrossRef PubMed.
- R. V. Kolakowski, M. Manpadi, Y. Zhang, T. J. Emge and L. J. Williams, J. Am. Chem. Soc., 2009, 131, 12910–12911 CrossRef CAS PubMed.
- Perhaps product selectivity switches at greater magnitudes or under the influence of EEFs oriented in other directions.
- A. Eschenmoser and A. Frey, Helv. Chim. Acta, 1952, 35, 1660–1666 CrossRef CAS.
- Altogether, these EEF results may have implications for fragmentation reactions that occur in a variety of environments, for example, in the active sites of enzymes or in solvent in a synthetic laboratory. It is important to recognize that our EEF analysis suffers from some limitations: (1) electric fields are not always homogenous EEFs, (for example in enzymes) and (2) gas-phase quantum calculations can only elucidate EEF effects on static electronic structure and energies of stationary points on our potential energy surface. Perhaps in solution, other significant effects, such as solvent effects, might induce other phenomena that cannot be modeled here. Solvent–solute dynamic effects modeled by explicit solvent were not considered in this study, but it has been discussed recently that local electric field effects due to explicit solvent molecules can alter the PES of the Claisen rearrangement of cis-2-vinylcyclopropanecarboxaldehyde, changing the concerted mechanism into a stepwise one (J. Phys. Chem. Lett. 2019, 10, 2991–2997). However, as a proof-of-concept, we have demonstrated that electrostatic effects have significant impacts on fragmentation reaction barriers. These conclusions lead to interesting questions on the effect of EEFs and more generally, local electrostatic environment, on dynamic effects such as dynamic matching and PTSBs. Work in our group is currently being carried out to answer these questions.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05161a |
| This journal is © The Royal Society of Chemistry 2020 |