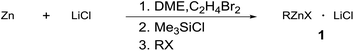Uncatalyzed conjugate addition of organozinc halides to enones in DME: a combined experimental/computational study on the role of the solvent and the reaction mechanism

Abstract

Both aryl and alkylzinc halides prepared by direct insertion of zinc into organic halides in the presence of LiCl underwent the conjugate addition reaction to nonenolizable unsaturated ketones in excellent yield, provided that DME was used instead of THF as the solvent. Diffusion NMR measurements highlighted that the species undergo considerable aggregation under the experimental conditions used in the synthetic procedure, but no substantial differences have been found between the two solvents. Density functional theory calculations, prompted by the experimental aggregation study, revealed an unexpected reaction mechanism, where the coordinating capabilities of DME stabilize a transition state involving two organozinc moieties, lowering the activation energy of the reaction with respect to that seen for THF, enough to explain the fast and quantitative reactions observed experimentally and the different behaviors of the two solvents.

---

Introduction

The conjugate addition of organometallic reagents to electron-poor alkenes represents one of the most important carbon–carbon bond-forming reactions in synthetic organic chemistry.¹ Notably, a broad range of organometallic reagents, as well as different acceptors, have been successfully employed, clearly showing the high versatility of the synthetic method.^2–5 Two kinds of organometallic species can add to electron poor alkenes: those having high intrinsic nucleophilicity and soft character, such as organocopper reagents,⁶ and those having low intrinsic nucleophilicity but aptitude to transmetallate easily to transition-metal complexes, such as organoboronic acids^7,8 or organozinc reagents.^9,10 The first ones are obtained by transmetallation starting from other organometallic precursors, such as Grignard or organolithium reagents or organozinc halides.¹¹ The others require the use of a transition metal catalyst to be converted into a nucleophilic organometallic species.¹² In both cases, the use of two metallic species is required and despite the amply recognized efficiency of these synthetic methods, the cost and toxicity of transition metals urge the development of new procedures that overcome these drawbacks. In the search for procedures that enable the formation of C–C bonds with high selectivity, operational simplicity, functional-group tolerance, and environmental friendliness, using easily available starting materials, we focused our attention on the use of organozinc halides as organometallic reagents for conjugate addition to electron poor alkenes. They are easily obtained by direct insertion of zinc metal into organic halides,^13–17 which is the most practical and atom-economical way to obtain organometallic reagents, but, to the best of our knowledge, they have not been used directly as nucleophiles for conjugate addition reactions. During our ongoing research toward organozinc halides, we have found that these reagents show different reactivities towards electron poor alkenes, depending on the method used for their preparation. Organozinc halides stabilized with TMEDA¹³ are completely unreactive, whereas those prepared according to the Knochel protocol (in the presence of one equivalent of LiCl)¹⁸ modified for the solvent (1,2-dimethoxyethane, DME, instead of THF), react with unsaturated ketones. However, in the presence of unsaturated ketones having enolizable positions, no addition product was detected and complex mixtures of condensation products were obtained. These results suggested that the basic character of these organozinc halides promoted condensation reactions faster than conjugate addition, which did not take place under these conditions. On moving towards conjugated ketones devoid of enolizable positions, we were delighted to find that phenylzinc iodide, prepared according to the modified Knochel method, cleanly achieved conjugate addition to chalcone under mild reaction conditions. This kind of reactivity for these organozinc halides, to the best of our knowledge, has never been reported. Only some isolated examples of conjugate addition to electrophilic alkenes of “in situ” obtained organozinc species from halides can be found in the literature.^19–22 Furthermore, the remarkable difference in reactivity obtained by going from THF to DME, two apparently very similar solvents, struck us as completely unexpected. For these reasons, we were prompted to gain some insight into the reaction applicability, the role of the solvent and also the reaction mechanism. These challenging problems were faced by a combined experimental-computational approach. We report herein the results of the conjugate addition of organozinc halides, having different structures, to non-enolizable enones, the diffusional analysis of the organometallic reagents in the different solvents and a computational study of the reaction in the two solvents, aimed at elucidating the reaction mechanism and the role of the solvent in determining the reactivity.

Results and discussion

Preparation of organozinc halides and conjugate addition to enones

Aryl and alkylzinc compounds were prepared by direct insertion of commercially available Zn powder in the presence of LiCl into DME. Thus, the halide was treated with commercial zinc powder (1.5 equiv., <46 μm, activated by the addition of 1,2-dibromoethane (3 mol%) and TMSCl (1 mol%)) and LiCl (1.5 equiv.) at the reflux of DME until complete conversion of the substrate (GC analysis). Under these conditions, aryl iodides were converted into the corresponding organometallic reagents in two hours, whereas alkyl bromides required longer reaction times (from 3 to 22 hours) to be completely reacted (Table 1). The titer of the organozinc compounds was determined by GC analysis after iodolysis of the reaction products.¹⁷ To obtain some insight into the reactivity of organozinc compounds towards conjugate addition to unsaturated enones devoid of enolizable positions, differently prepared phenylzinc reagents were assayed in the conjugate addition to chalcone and the results are provided in Table 2. The reaction of the phenylzinc prepared according to our protocol afforded almost quantitative conversion of chalcone in the corresponding addition product in 24 h at r.t., both in DME/toluene mixture and in DME only (entries 1 and 2).

Table 1 Preparation of the organozinc halides

Entry	RX	1	Time	% conv^a	Titer^b
a Apparent conversion determined by GC analysis after hydrolysis of the reaction mixture. b Determined by GC analysis after iodolysis of the reaction mixture.^17
1	PhI	1a	2 h	99	0.89 M
2	4-MeO2CC6H4I	1b	2 h	99	0.90 M
3	c-HexBr	1c	22 h	97	0.86 M
4	n-C8H17Br	1d	4 h	98	0.87 M
5	4-CF3C6H4I	1e	2 h	99	0.95 M

---

Table 2 Conjugate addition of phenylzinc halides to chalcone^a

Entry	“PhZnX”	Solvent	% conv^c	Time
a Chalcone (1 mmol), “PhZnX” (1.5 mmol), solvent (2 mL). b Toluene was used as a cosolvent in the conjugate addition step. c Apparent conversion determined by GC analysis. d Reaction performed at 50 °C.
1	PhZnI + LiCl	DME^b	97	24 h
2	PhZnI + LiCl	DME	98	24 h
3	PhZnI + LiCl	THF	23	24 h
4	PhMgBr + ZnBr2	DME	30	24 h
5	PhMgBr + ZnBr2	THF	11	24 h
6	TMEDA + Zn(Ag)	DME	0	24 h
7	PhZnI + LiCl	DME^d	99	2 h

---

By contrast, the use of THF as a solvent gave a scarcely reactive organometallic species, which afforded, under the same conditions, a low conversion of the substrate (entry 3): this huge difference in reactivity points out the unexpected importance of DME for the success of the reaction. Even organozinc halides obtained by transmetallation from Grignard reagents, used both in DME and THF (entries 4 and 5), poorly reacted with chalcone, whereas the organometallic reagent obtained by direct metallation using a different procedure¹³ (entry 6) was completely unreactive. In order to minimize the risk of cross contamination, in particular with other transition metals, the glassware and stirring bars used for the reactions were carefully washed with hot aqua regia. To further reduce the risk of contamination, several trials have also been conducted using new glassware and a new stirring bar.²³ Furthermore, the zinc powder used has a negligible content of transition metals, as certified by the producer.

These results suggest the fundamental role of LiCl in the formulation, which probably leads to the formation of a zincate anion²⁴ rather than an organozinc halide. Furthermore, it highlights the importance of using DME as a solvent for the preparation of the organozinc species. Finally, the reaction temperature had a strong effect on the reaction rate: almost complete conversion of the substrate into the product was achieved in only two hours at 50 °C (entry 7).

The optimized reaction conditions were used to react other enone substrates with different organozinc halides and the results are shown in Scheme 1. The reaction proceeded smoothly for the conjugate addition of phenylzinc iodide to differently substituted 1,3-diphenylprop-2-enones, affording high yields of the isolated products 3a–g in short reaction times (from 2 to 6 hours). It is worth noting that the pure products were obtained just after work-up of the reaction mixtures, without any further purification. The steric hindrance on the enone substrates affects the reaction rate: as a matter of fact, the conjugate addition of phenylzinc iodide to enones bearing bulky groups, such as 9-anthryl, tert-butyl or even 2-naphthyl, afforded high yields of pure products 3h–j in 24–30 h at the reflux of the solvent (115 °C). The presence of an electrophilic group on the substrate was well tolerated and the product 3k was obtained in high yield.

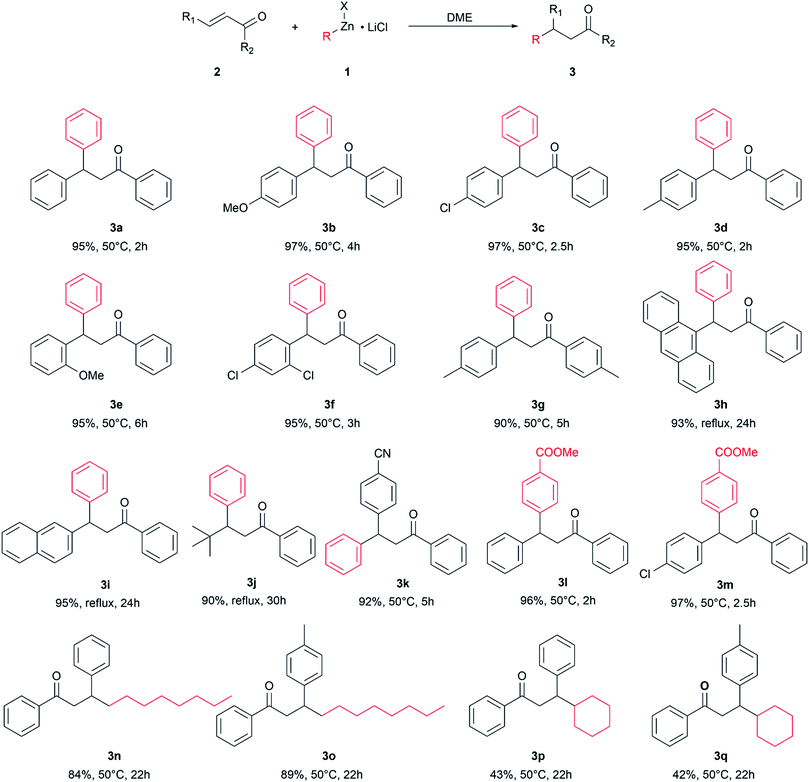Scheme 1 Conjugate addition of organozinc halides to enones. Isolated yield, reaction temperature, and reaction time.

The use of different organozinc halides was also effective, giving the desired conjugate addition products with results depending on the chemical structure of the organometallic reagent. The arylzinc iodide bearing an electron withdrawing group on the phenyl ring behaved as phenylzinc iodide, affording the conjugate addition products 3l and 3m in excellent yield, under mild reaction conditions and in short reaction times. Alkylzinc bromides reacted slower than arylzinc iodides: longer reaction times and higher temperatures were required to obtain 3n–q, which were obtained as pure products only after chromatographic purification. Under these conditions, 3n and 3p were obtained in good yields, whereas only moderate yields of 3p and 3q were achieved, suggesting some influence of the bulkiness of the organometallic reagent on the outcome of the reaction.

It is noteworthy that the reaction well tolerated electrophilic groups both on the substrate and organometallic reagents: as a matter of fact, products 3k–m were obtained in high yields.

NMR study

With the aim of explaining the dramatic solvent effect, we verified whether the aggregation processes are different in DME and THF. Despite their similar values of ε₀ (7.5), it is known that the two solvents can significantly modify the structure and nuclearity of lithium phenolates.²⁵ We used the pulsed-field gradient spin echo (PGSE) NMR technique^26,27 to quantitatively obtain the diffusion coefficient (D_t) of the species in solution and, from it, accurate information about the average hydrodynamic volume (V_H), which is a direct probe of all the aggregation processes. Because of the severe overlapping of peaks in the ¹H NMR spectra and the difficulty in using deuterated DME, we decided to use non-deuterated solvents, an internal capillary containing C₆D₆ for lock, and a fluorine nucleus-containing substrate namely 4-trifluoromethylphenylzinc iodide, 1e. As an internal standard for diffusion, C₆H₅CF₃ has been used, under the hypothesis that it is unable to participate in any aggregation process under our experimental conditions.

For both solvents, three concentrations have been considered, in order to have not only the values of V_H, but also its trend with concentration (Table 3). As can be seen, the V_H values increase as the concentration increases, going from 649 to 1704 ų in THF and from 556 to 1486 ų in DME.

Table 3 Concentration (C), diffusion coefficients (D_t), hydrodynamic volume (V_H) and aggregation number (N) of 1e in different solvents

Solvent	C (M)	10^10Dt (m^2 s^−1)	V H (Å^3)	N
THF	1.0	5.97	1704	6.7
THF	0.48	7.27	1028	4.0
THF	0.10	8.75	649	2.5
DME	0.95	6.40	1486	5.6
DME	0.42	8.41	786	3.0
DME	0.08	9.44	556	2.1

---

Therefore, the values are significantly lower for the latter than for the former (the experimental error in V_H is about 10%). Taking into account the volume of isolated 1e coordinated by one molecule of the solvent as a monomer (V⁰_H = 265 and 255 ų in the case of DME and THF, respectively, estimated by calculating their van der Waals volume by computational tools), the aggregation number N can be defined as the ratio between the experimental values of V_H and V⁰_H. The values of N show that aggregates are always present in solution and are always slightly larger in THF. Also, the aggregates are formed on average by two monomers at low concentration and by 6 (in DME) or 7 (in THF) monomers at high concentration. On the other hand, these differences are not enough to satisfactorily explain the different reactivities in the two solvents. For this reason, a computational study of the reaction mechanism has been performed.

DFT calculations

The NMR diffusional study provided us with the important information that aggregation phenomena play a significant role, but was unable to quantitatively explain the reactivity difference between THF and DME. This prompted us to hypothesize that a different reaction mechanism may be responsible for such a difference. Thus, we performed density functional theory (DFT) calculations on the species and possible aggregates reasonably involved in the transformation.

The postulated aggregates include the reactants, a LiCl ionic pair and a molecule of the solvent coordinated with the metallic centers. The calculations were performed with the B3LYP functional²⁸ in conjunction with the 6-31+G* basis set.^29,30 The polarizable continuum model (PCM) was used to account for long-range solvation effects^31–33 and Grimme's D3 corrections for dispersion interactions.³⁴ The computational protocol was validated by performing some of the calculations with a larger basis set (6-311+G** (ref. 35)), producing consistent results (see the ESI†). We selected the reaction illustrated in Scheme 2 as a model to perform calculations on the reaction pathway. The structures of the reactants, products, and transition states were optimized with analytical gradients. Once a transition state had been identified, we performed an intrinsic reaction coordinate (IRC) search and, following the found path in the direction of the reactants, we optimized the structure in order to determine whether a stable intermediate, showing some form of aggregation, could be found. The activation energies where then computed using the stable aggregates as a reference, even if such aggregates were unstable from a thermodynamic point of view, as we believe that the formation of such intermediates is an important step of the reaction mechanism, which is supported by the experimental aggregation measurements. Frequency calculations were performed in order to characterize the structures found as minima or transition states and in order to compute Gibbs free energies for all the involved species.

Scheme 2 Model reaction for DFT calculations.

We started from the simplest scenario, in which a single molecule of the organometallic reagent, one of enone, one of the solvent, and a LiCl ionic pair are involved. The reaction mechanisms found under this scenario are represented in Scheme 3, together with a 2D sketch of the structures of the intermediates and transition states. A 3D representation of all the aforementioned species can be found in the ESI (Schemes S1–S4†)

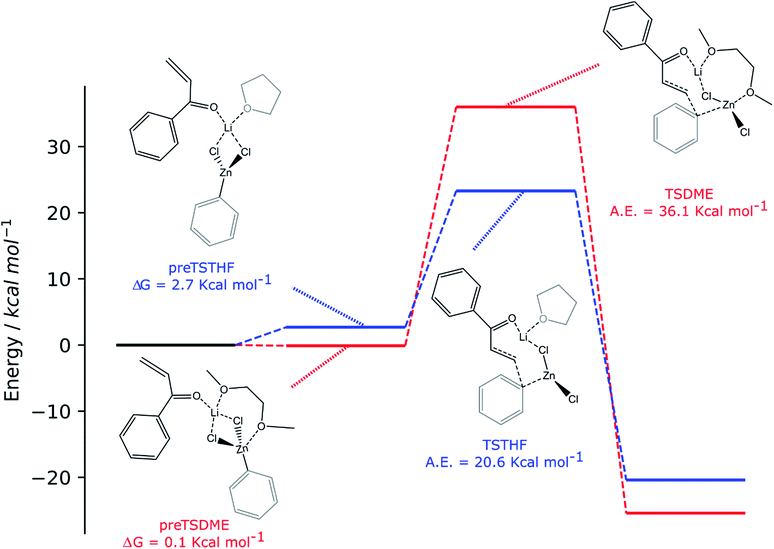Scheme 3 Computed reaction pathways (red path: RZnX and DME, blue path: RZnX and THF, and red path: 1 RZnX molecule and DME).

For both solvents, the lithium cation interacts with the oxygen of the enone, polarizing the overall enonic system (the C=O bond goes from 1.235 to 1.246 and 1.244 Å for preTSTHF and preTSDME, respectively, while the carbonyl–Cα bond goes from 1.485 to 1.471 and 1.475 Å, respectively) and, consequently, making the β carbon more electrophilic. At this stage, the presence of two oxygen atoms in DME is important in determining a difference: in preTSDME, DME can coordinate both zinc and lithium at the same time, whereas THF interacts only with lithium. Unfortunately, the computed activation energy was found to be quite high in both the cases: 20.6 and 36.1 kcal mol⁻¹ for TSTHF and TSDME (Scheme 3), respectively, values that are not acceptable for a reaction that is complete after 24 h at room temperature. On the other hand, the participation of the zinc enolate, formed at the end of the reaction, in this process can be reasonably excluded on the basis of the reaction rate trend. None of the above-discussed reactions showed that the reaction rate increases with time, suggesting that this species, formed during the reaction, does not contribute to promote the addition.

We thus searched for a more complex reaction path. We have postulated that two organozinc halide molecules participate in the reactant complex, together with the enone, two LiCl moieties and one molecule of the solvent.

The reaction mechanisms that we found under these assumptions are schematized in Scheme 4, together with a 2D sketch of all the intermediates and transition states. A 3D representation of all such species can be found in the ESI (Schemes S5–S8†).

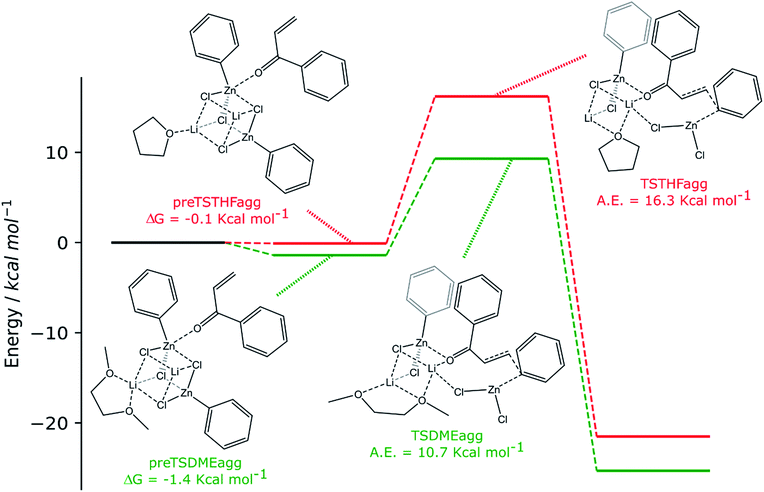Scheme 4 Computed reaction pathways (green path: 2 RZnX molecules and DME and red path: 2 RZnX molecules and THF).

The two organozinc moieties, together with the two LiCl ionic pairs and the enone, have been found to form stable aggregates for both solvents, as ΔG = −0.1 and −1.4 kcal mol⁻¹ for preTSTHFagg and preTSDMEagg, respectively.

It is interesting to note that both the stable aggregates and transition states are characterized by a highly regular spatial arrangement of all sites bearing a partial charge, i.e., Cl, Li, Zn and O atoms. In the two stable aggregates, as can be clearly seen from the 2D sketches in Scheme 4, a cube-like structure is formed, where the vertices are occupied by alternating positively and negatively charged Li, Cl and Zn ions. This arrangement seems to be ideal, as it minimized the repulsion between similarly charged sites while maximizing their favorable interaction with the oppositely charged ones, and is observed to be unchanged in both solvents. Another conserved element is the interaction between the carbonyl oxygen of the enone and the Zn atom belonging to the unreactive RZnX moiety. Furthermore, the solvent coordinates one of the two Li atoms, further stabilizing the two intermediates. In the transition states, the cubic structure is partially broken, with one of the vertices being left unoccupied. For both solvents, we observe the following rearrangements. First, the enone rotates so that its aromatic ring can interact via π stacking with the unreactive organozinc³⁶ and its oxygen atom replaces one Cl atom at a vertex of the cube-like structure. The displaced Cl atom remains coordinated to the Zn of the reactive organozinc moiety, which is ejected from the cubic structure, together with the second Cl atom. The position formerly occupied by such a Cl atom is taken by an oxygen atom belonging to a solvent molecule, which stabilizes the transition state by at least partially retaining the balance of interaction between oppositely charged sites.

In preTSTHFagg, the THF interacts with two lithium cations, the chloride anions bridge the various cations and the oxygen of the enone interacts with both zinc and lithium, leading to a longer C=O bond than before, 1.304 Å. In preTSDMEagg, both the oxygen atoms of the DME interact with one lithium cation, which is connected by chloride bridges to all the other moieties. Zinc atoms are tetracoordinated with a chlorine bridge between them, whereas the carbonyl oxygen occupies one of the coordinating positions of one of the two zinc atoms with a O–Zn bond length of 2.037 Å (C=O distance 1.254 Å). Such intermediates represent the starting point of the reaction and their formation is compatible with the aggregation properties of the organozinc halides and the experimental setup.

In the transition state found for the reaction in DME (TSDMEagg), the solvent chelates a lithium atom and interacts also with the other one, increasing the number of Li⋯O interactions with respect to those present in the reactant complex preTSDMEagg. The oxygen of the enone interacts with both the unreactive zinc and a lithium atom (O–Zn and O–Li distances of 2.074 Å and 1.918 Å, respectively), polarizing the enone more than in the case where only one organozinc molecule is involved in the reactive complex (C=O distance 1.304 Å), making the β carbon more electrophilic. This effect is reflected in the activation barrier, which is now only 10.7 kcal mol⁻¹ (Scheme 3). It is important to note that we used an unsubstituted enone (CH₂CHC(=O)Ph) that, having practically no steric hindrance around the β carbon, is likely to be more reactive than the substrates experimentally investigated. Note that the detrimental effect of the steric hindrance at this carbon atom has been discussed above. Considering again an intermediate involving two organozinc molecules and substituting the DME molecule with THF in the TS (TSTHFagg), both the additional Zn⋯O interaction and the π stacking between the unreactive organometallic moiety and the enone are again present. Indeed, the C=O bond is elongated to the same extent (1.304 Å). There is however one very noticeable difference in the arrangement of the solvent. In TSTHFagg the two lithium cations are bridged by the THF's oxygen atom, which occupies one of the vertices of the cube-like structure. By focusing on the Li atom that was coordinated by the solvent in the preTSTHF aggregate, we note that such an atom has lost a ligand and is now only three-coordinated. In contrast, when DME is employed, the transition state TSDMEagg sees not only one of the DME's oxygen atoms bridging the two lithium cations, but also the second oxygen atom chelating one of the two lithium atoms, retaining a more balanced electrostatic picture. This cannot happen with THF, as only one oxygen atom is available. This missing O⋯Li interaction is what makes the activation barrier about 6 kcal mol⁻¹ higher than in the case of TSDMEagg (16.3 kcal mol⁻¹) (Scheme 3). It must be reported that all our efforts to find a transition state with two coordinated molecules of THF failed because of the excessive hindrance.

Conclusions

The use of DME, instead of THF, in the preparation of organozinc halides according to the Knochel method has allowed an unprecedented reactivity to be disclosed, thanks to which conjugate addition to non-enolizable unsaturated ketones was achieved without the use of any catalyst. The reaction has general applicability, giving excellent to good yields with both alkyl and arylzinc halides and ketones having different structures, under mild reaction conditions.

The different reactivity in the two apparently similar solvents, THF and DME, has been initially investigated through diffusion NMR measurements. The results evidenced a large aggregation of the organozinc species in both solvents, with too small differences to explain the different reactivities, but they showed us the way to the solution.

In fact, the DFT calculations demonstrated that by only postulating an intermediate and a transition state involving more than one organozinc moiety, it is possible to explain the fast and quantitative reactions observed experimentally. Our proposed mechanism accounts not only for the fast kinetics observed in DME but also for the difference in the reactivity between DME and THF used as solvents. In fact, we observed that the ability of DME to chelate one of the lithium cations present in the transition state with both its oxygen atoms plays a crucial role in lowering the activation energy. The different reactivity is therefore explained in terms of the different coordinating capabilities of the two ethers.

In conclusion, a new and unexpected reaction has been presented, which allows C–C bond formation by direct conjugate addition of organozinc halides to enones. The surprising reactivity and the different behaviors observed changing between two very similar solvents have been quantitatively explained by determining that, as aggregation phenomena are present under the experimental conditions, a reaction mechanism involving more than one organozinc is highly probable. The proposed mechanism provides rationalization of all the observed experimental findings.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the University of Pisa through the PRA_2018_36 grant. The authors are thankful to Prof. Benedetta Mennucci for useful discussion.

Notes and references

1. P. Perlmutter, Conjugate Addition Reactions in Organic Synthesis, Pergamon, 1992.
2. L. Palais, L. Babel, A. Quintard, S. Belot and A. Alexakis, Org. Lett., 2010, 12, 1988–1991.
3. B. J. Wakefield, Organomagnesium Methods in Organic Synthesis, Elsevier, 1995.
4. Y. Takaya, M. Ogasawara, T. Hayashi, M. Sakai and N. Miyaura, J. Am. Chem. Soc., 1998, 120, 5579–5580.
5. M. Hatano, M. Mizuno and K. Ishihara, Org. Lett., 2016, 18, 4462–4465.
6. N. Yoshikai and E. Nakamura, Chem. Rev., 2012, 112, 2339–2372.
7. Y. Takaya, M. Ogasawara, T. Hayashi, M. Sakai and N. Miyaura, J. Am. Chem. Soc., 1998, 120, 5579–5580.
8. C. Wu, G. Yue, C. D.-T. Nielsen, K. Xu, H. Hirao and J. Steve Zhou, J. Am. Chem. Soc., 2016, 138, 742–745.
9. J. D. Hargrave, J. C. Allen and C. G. Frost, Chem. - Asian J., 2010, 5, 386–396.
10. J. Le Nôtre, J. C. Allen and C. G. Frost, Chem. Commun., 2008, 3795.
11. M. Schlosser, Organometallics in Synthesis A Manual, John Wiley & Sons, Ltd, 2002.
12. A. Cordova, Catalytic Asymmetric Conjugate Reactions, Wiley-VCH Verlag GmbH & Co. KGaA, 2010.
13. G. Casotti, A. Iuliano and A. Carpita, Eur. J. Org. Chem., 2019, 2019, 1021–1026.
14. A. D. Benischke, G. Le Corre and P. Knochel, Chem. –Eur. J., 2017, 23, 778–782.
15. A. D. Dilman and V. V Levin, Tetrahedron Lett., 2016, 57, 3986–3992.
16. M.-Y. Jin and N. Yoshikai, J. Org. Chem., 2011, 76, 1972–1978.
17. R. Ikegami, A. Koresawa, T. Shibata and K. Takagi, J. Org. Chem., 2003, 68, 2195–2199.
18. A. Krasovskiy, V. Malakhov, A. Gavryushin and P. Knochel, Angew. Chem., Int. Ed., 2006, 45, 6040–6044.
19. B. S. Bronk, S. J. Lippard and R. L. Danheiser, Organometallics, 1993, 12, 3340–3349.
20. T. Shono, I. Nishiguchi and M. Sasaki, J. Am. Chem. Soc., 1978, 100, 4314–4315.
21. R. A. Kjonaas and E. J. Vawter, J. Org. Chem., 1986, 51, 3993–3996.
22. W. Langer and D. Seebach, Helv. Chim. Acta, 1979, 62, 1710–1722.
23. E. O. Pentsak, D. B. Eremin, E. G. Gordeev and V. P. Ananikov, ACS Catal., 2019, 9, 3070–3081.
24. K. Koszinowski and P. Böhrer, Organometallics, 2009, 28, 771–779.
25. T. S. De Vries, A. Goswami, L. R. Liou, J. M. Gruver, E. Jayne and D. B. Collum, J. Am. Chem. Soc., 2009, 131, 13142–13154.
26. A. Macchioni, G. Ciancaleoni, C. Zuccaccia and D. Zuccaccia, Chem. Soc. Rev., 2008, 37, 479–489.
27. X. Xie, C. Auel, W. Henze and R. M. Gschwind, J. Am. Chem. Soc., 2003, 125, 1595–1601.
28. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
29. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
30. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229.
31. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
32. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
33. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
34. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
35. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
36. J. Ribas, E. Cubero, F. J. Luque and M. Orozco, J. Org. Chem., 2002, 67, 7057–7065.

---

Footnote

† Electronic supplementary information (ESI) available: General information, experimental details, computational details, NMR spectra (PDF), and optimized geometries (xyz). See DOI: 10.1039/c9sc04820k

---