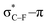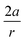Open Access Article
Open Access ArticleThe hunt for reactive alkynes in bio-orthogonal click reactions: insights from mechanochemical and conceptual DFT calculations†
Tom
Bettens
 ,
Mercedes
Alonso
,
Mercedes
Alonso
 ,
Paul
Geerlings
,
Paul
Geerlings
 and
Frank
De Proft
and
Frank
De Proft
 *
*
Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: fdeprof@vub.be
First published on 23rd December 2019
Abstract
In our effort to implement the mechanical force used to activate single molecules in mechanochemistry in the context of conceptual density functional theory, we present a theoretical investigation of strained alkynes for rationalizing structural trends as well as the reactivity of cyclic alkynes that are of great importance in in vivo click reactions. The strain on the triple bond in cyclic alkynes is modeled by angular constraints in a 2-butyne fragment and the corresponding bending force is calculated by means of an extended COGEF (constrained geometries simulate external forces) model. In general, the force required to bend the triple bond is smaller with electron-withdrawing groups on the propargylic C-atom, which elegantly results in smaller angles around the triple bond in cyclic alkynes with such substitution pattern. By means of conceptual DFT descriptors, the electrophilic and nucleophilic character of bent triple bonds was investigated revealing moderate activation for small distortions from the linear geometry (0° to 15°) and a drastically more reactive π-space if the triple bond is bent further. This analysis of the intrinsic reactivity of the triple bond is in line with experimental observations, explaining the reactive nature of cyclooctynes and cycloheptynes, whereas larger cyclic systems do not drastically activate the triple bond.
1. Introduction
Under the impetus of Bertozzi and co-workers, research on highly selective and bio-orthogonal (denoting inertness to the biochemical environment in a living organism) processes has flourished and has led to in vivo imaging of bio-molecules using small-molecule probes.1 Among the examples of chemical reactions suitable for such in vivo applications, strain-promoted azide–alkyne couplings (SPAAC) have attracted particular interest due to the stability of both the azide and strained (cyclic) alkyne in a biological environment, high selectivity without the need of a potentially toxic catalyst and favorable reaction rates.Many computational studies confirm the low reaction barriers in cycloadditions with cyclic alkynes, with 8-membered rings being the most popular member of the family because of their stability and commercial availability.2Fig. 1 illustrates the cycloaddition between acetylene and the strained cyclooctyne and an azide, in which the azide is typically considered the electron donor, although rapid inverse-electron demand SPAAC reactions are known.3
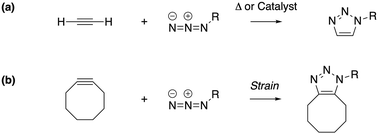 | ||
| Fig. 1 The cycloaddition of an alkyne with an azide requires (a) thermal or catalytic activation, or (b) a strained alkyne to accelerate the reaction. | ||
A critical aspect of the strain-promoted coupling in Fig. 1b is the stability of the cyclic alkyne, which is governed by the ring size.4 Therefore, the smallest cycloalkynes (3 to 6-membered rings) are not suited for reactions of this type, with total ring strain increasing from 41 kcal mol−1 for cyclohexyne to 133 kcal mol−1 in cyclopropyne.5 Whereas cyclopropyne is an intriguing test system in theoretical studies with no application in SPAAC reactions,6 the very reactive 4, 5 and 6-membered cyclic alkynes are prone to rearrangements and di- and trimerization, but can be trapped in transition metal complexes or bicyclic compounds.7–9 Cycloheptyne and its derivatives are the smallest members of the stable cycloalkyne family, although cycloheptyne itself is not thermally stable.10
Driven by the wide range of possible applications in biochemistry and assisted by computational simulations, the hunt for reactive cyclic alkynes (mainly cyclooctynes) has identified a family of compounds that undergo quick SPAAC reactions, some even under physiological conditions.1d,3,11 But what does this strain exactly do to the triple bond? Evidently, the bent triple bond in Fig. 1b lowers the deformation energy of the alkyne to form the 1,2,3-triazole. Less evidently, the intrinsic reactivity of the triple bond is also fascinatingly affected by the strained ring-structure.
Alkyne bending lifts the degeneracy of both the bonding and anti-bonding π-orbitals in the linear geometry, as a result of mixing of the C2s and the in-plane C2p atomic orbitals with one π and one π*-orbital, leading to a higher energy of the filled orbital and a lower energy of the vacant orbital.12,13 This is a strong indication that the high rate constants in SPAAC reactions originate not only from the geometrical distortion but are additionally due to the enhanced chemical reactivity of the triple bond, as can be expected from a decreasing HOMO–LUMO gap. This phenomenon gained recent attention by Bickelhaupt and co-workers who analyzed the decrease in activation barriers of SPAAC reactions with the reduction of the cycloalkyne ring size in terms of distortion/interaction–activation strain analyses.14
In mechanochemistry, external forces are used to enhance the reactivity of molecules typically by stretching and, thus, constraining bond lengths and angles. Through computational strain analysis, the connection between mechanochemistry and cyclic alkynes was explored recently by Stauch et al., revealing that bicyclic cycloheptynes can sufficiently stabilize the alkyne, whereas photoswitches (i.e. a popular source for mechanical strain in laboratory experiments) cannot.10a,15 Interestingly, in their work, the use of mechanical force was investigated for stabilizing cycloheptyne, rather than using force as a means of activation which is the common direction followed in mechanochemistry.
Recent experimental advances allow for mechanical activation at the single molecular level, where the directional character of mechanical activation through external forces is known to selectively enhance reactivity.16 Besides impressive experimental advances thanks to ingeniously set-up experiments, mechanochemistry also witnessed in recent years the development of several quantum chemical techniques for quantitative studies on the response of molecular systems to external mechanical forces.17 The COGEF method, for example, models external stretching forces through geometrical constraints.18 In a recent contribution, we casted this approach in a conceptual density functional theory (CDFT) context to enhance the chemical interpretation of these responses in the case of diatomics, leading to an extension of the energy functional E[N,v(r)] to E[N,v(r),Fext].19 In this expression, the molecular energy does not only depend on the number of electrons N and the external potential between the nuclei and the electrons v(r), but also on external mechanical forces acting on the system, leading to global response functions of the type 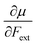 and
and 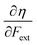 where μ and η are the electronic chemical potential and chemical hardness, respectively.
where μ and η are the electronic chemical potential and chemical hardness, respectively.
With this study, we exploit the natural connection between angular strain and mechanochemistry. The influence of an external mechanical force on the energy, structure and reactivity is scrutinized for alkynes and it is demonstrated that structural trends in cycloalkynes can be elegantly interpreted from a mechanochemical perspective. Our CDFT based approach for quantifying mechanochemical reactivity is thereby logically extended by investigating these bent alkynes and the response of local reactivity indices, such as the Fukui function and the local softness, revealing the influence of strain on the intrinsic reactivity of the triple bond in angle-strained alkynes.
2. Methods
2.1. Mechanochemical approach: extending COGEF towards forces on angles
The force acting on a molecule can be conveniently calculated by means of the COGEF (constrained geometries simulate external forces) method which simulates the effect an external force through a geometrical constraint, i.e. the structural effect of applying a force to a molecular system.18 This method has been widely adopted to estimate the force required to achieve a certain geometrical change or vice versa. While this method is generally used to simulate stretching of a molecule, it is possible to extend the model for estimating the force on bond angles in e.g. strained cyclic systems and even torsional angles. We developed a simple model to connect angular strain with single-molecule mechanochemistry.Regardless of the mathematical model used to describe the Born–Oppenheimer (BO) potential energy curve in the case of bond stretching, the contribution of a constant external force (Fext) can be written as
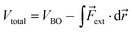 | (1) |
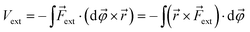 | (2) |
![[small variant phi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c5.gif) is introduced. This vector is oriented perpendicular to the plane of bending and parallel to
is introduced. This vector is oriented perpendicular to the plane of bending and parallel to ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ×
× ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext. The integration over φ then goes from zero to a certain angle and, evidently, the upper limit of the integration depends on the magnitude of
ext. The integration over φ then goes from zero to a certain angle and, evidently, the upper limit of the integration depends on the magnitude of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext: a larger force will result in a larger deviation from the equilibrium structure. The vector
ext: a larger force will result in a larger deviation from the equilibrium structure. The vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ×
× ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext has the meaning of an intramolecular torque (
ext has the meaning of an intramolecular torque (![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) ; moment of force), which provides information on the tendency of a molecule to rotate intramolecularly in a certain direction.22 Importantly,
; moment of force), which provides information on the tendency of a molecule to rotate intramolecularly in a certain direction.22 Importantly, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext is now perpendicular to the bond defined by
ext is now perpendicular to the bond defined by ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , i.e. a bending force. Fig. 2 shows a schematic picture of all vectors involved in this extended COGEF model in the case of an infinitesimally small bend on an alkyne in which the triple bond is held into place.
, i.e. a bending force. Fig. 2 shows a schematic picture of all vectors involved in this extended COGEF model in the case of an infinitesimally small bend on an alkyne in which the triple bond is held into place.
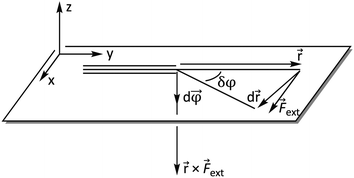 | ||
| Fig. 2 Vector model of alkyne bending used for the extension of the COGEF approach towards bending forces. | ||
Similar to the original COGEF model, a minimum on the potential energy surface is achieved when the internal restoring force and the external force cancel each other. In other words, the first derivative of eqn (1) should equal zero. Substituting the expression from eqn (2) yields
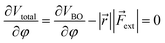 | (3) |
In this expression, the vector product has been taken out of the integral and eqn (2) is simplified to a simple product because ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext are assumed to be perpendicular to each other. For the sake of simplicity, let us now also suppose that both vectors are independent of φ (see the ESI† for an extended treatment). Eqn (3) connects the magnitude of an external bending force with an angular deviation and allows an estimation of bending forces in e.g. strained molecules, if an expression for VBO is available. In the case of a harmonic model for the bending around the triple bond [see eqn (4)], the magnitude of the external bending force, |
ext are assumed to be perpendicular to each other. For the sake of simplicity, let us now also suppose that both vectors are independent of φ (see the ESI† for an extended treatment). Eqn (3) connects the magnitude of an external bending force with an angular deviation and allows an estimation of bending forces in e.g. strained molecules, if an expression for VBO is available. In the case of a harmonic model for the bending around the triple bond [see eqn (4)], the magnitude of the external bending force, |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext|, holds a simple relationship with the harmonic force constant, a, and the length of the bond adjacent to the triple bond, |
ext|, holds a simple relationship with the harmonic force constant, a, and the length of the bond adjacent to the triple bond, |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) |, in the linear alkyne:
|, in the linear alkyne:
| VBO = aφ2 | (4) |
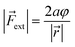 | (5) |
In these equations, φ is the deviation from the angle at equilibrium due to ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext. Eqn (5) is now the working equation in this extended COGEF model as it connects the magnitude of the external bending force to a specific angular distortion φ, in analogy to the original COGEF approach formulated by Beyer.18 The two remarkably simple ingredients in eqn (5), being a bond distance and a force constant, allow for an easy assessment of the flexibility of different bond angles. This equation will be used for quantifying the angular force acting on the triple bond in strained systems by imposing geometrical constraints to a 2-butyne fragment, creating a bridge between angle-strained alkynes and mechanochemistry. Moreover, in the ESI,†eqn (5) is validated by calculating the gradient on the propargylic C-atom in an angle-constrained acetylene, which is shown be practically equal to |
ext. Eqn (5) is now the working equation in this extended COGEF model as it connects the magnitude of the external bending force to a specific angular distortion φ, in analogy to the original COGEF approach formulated by Beyer.18 The two remarkably simple ingredients in eqn (5), being a bond distance and a force constant, allow for an easy assessment of the flexibility of different bond angles. This equation will be used for quantifying the angular force acting on the triple bond in strained systems by imposing geometrical constraints to a 2-butyne fragment, creating a bridge between angle-strained alkynes and mechanochemistry. Moreover, in the ESI,†eqn (5) is validated by calculating the gradient on the propargylic C-atom in an angle-constrained acetylene, which is shown be practically equal to |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ext|. It is also shown that this atomic gradient is almost perfectly perpendicular to the C–C bond and oriented in the plane of the three C-atoms in Fig. 2. Both methods are therefore equivalent for calculating bending forces. However eqn (5) provides valuable insight into the mechanical strength of a bond angle in terms of a and |
ext|. It is also shown that this atomic gradient is almost perfectly perpendicular to the C–C bond and oriented in the plane of the three C-atoms in Fig. 2. Both methods are therefore equivalent for calculating bending forces. However eqn (5) provides valuable insight into the mechanical strength of a bond angle in terms of a and |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) |. Importantly, this model can be adopted for any bond angle as well as torsional angles. However, a different expression for VBO might be advised in such cases.
|. Importantly, this model can be adopted for any bond angle as well as torsional angles. However, a different expression for VBO might be advised in such cases.
2.2. Conceptual DFT descriptors
As stated above, in conceptual DFT (CDFT), the energy of a chemical many-body system is expressed as a unique functional of the number of electrons, N, and the external potential between the electrons and nuclei, v(r). When the system is exposed to a perturbation in N and/or v(r), the change in the total energy, ΔE, can be written as a functional Taylor expansion.23 Please note that, for the sake of readability, vectors in this CDFT part are simply written with bold symbols.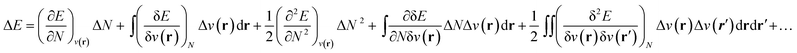 | (6) |
Insight into chemical reactivity is obtained by analyzing the partial derivatives in eqn (6), representing the response of the system to the perturbation at stake (response functions). The first and second order response functions of E with respect to N are termed the electronic chemical potential (μ) and the chemical hardness (η).24 In a previous study, the present authors revealed the response of these global descriptors as well as the electrophilicity index (ω)25 defined as 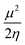 when a chemical bond is subjected to an external force, showing clear trends that can be easily understood in terms of simple chemical concepts.19 In the present work, also local descriptors will be considered.
when a chemical bond is subjected to an external force, showing clear trends that can be easily understood in terms of simple chemical concepts.19 In the present work, also local descriptors will be considered.
The electron density ρ(r) is the first derivative of E with respect to v(r). The Fukui function f(r) is the first mixed derivative of E[N,v(r)] with respect to both N and v(r) and, therefore, it is a quantitative tool for describing the change in electron density when a perturbation to the total amount of electrons is applied.26 Just like ρ(r), f(r) is a local descriptor, i.e. varying from point-to-point in space. The Fukui function can be calculated when one electron is added or removed from the system, probing the electrophilic or nucleophilic properties of a molecule, respectively, but also the reactivity of an alkyne in cycloaddition reactions both in case of the normal or inverse electron demand interactions.
The local softness is defined in eqn (7) as the product of the Fukui function and the global softness (S) of the molecular system, where the global softness is the inverse of the global hardness (η). It can be interpreted as the result of partitioning the softness through space by the Fukui function picturing the softest and less soft regions in the molecule (for a detailed discussion, see ref. 27).
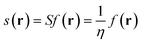 | (7) |
2.3. Computational details
All geometry optimizations were carried out with Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 using the M06-2X functional29 in combination with the 6-311+G(d,p) basis set, as computed activation free energies correlate well with experimental values.2a The external bending force was simulated by means of the extended COGEF method described above through geometry constraints on one of the C
28 using the M06-2X functional29 in combination with the 6-311+G(d,p) basis set, as computed activation free energies correlate well with experimental values.2a The external bending force was simulated by means of the extended COGEF method described above through geometry constraints on one of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C bond angles in 2-butyne fragments in steps of 5° and repeated for different substituents on the sp3 hybridized C-atom (see Fig. 3a). On this propargylic C-atom, oxygen and fluorine substituents are common1b,d and, in this work, other groups were selected to systematically investigate the electron-withdrawing/donating effect of the substituent on the mechanical rigidity of the triple bond angles as well as other effects. The external bending force was calculated with eqn (5) using the distance |
C–C bond angles in 2-butyne fragments in steps of 5° and repeated for different substituents on the sp3 hybridized C-atom (see Fig. 3a). On this propargylic C-atom, oxygen and fluorine substituents are common1b,d and, in this work, other groups were selected to systematically investigate the electron-withdrawing/donating effect of the substituent on the mechanical rigidity of the triple bond angles as well as other effects. The external bending force was calculated with eqn (5) using the distance |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | in the equilibrium geometry. The reactivity of the triple bond in cyclic systems was simulated by imposing the geometry constraint on both angles and, at the same time, freezing the C–C
| in the equilibrium geometry. The reactivity of the triple bond in cyclic systems was simulated by imposing the geometry constraint on both angles and, at the same time, freezing the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C dihedral angle to 0° to prevent the trans-bending, as illustrated by Fig. 3b. The CDFT reactivity indices (Fukui function, softness and local softness) were computed using the smaller 6-311G basis set, in order to artificially bind the additional electron to the molecule;30 this routine is especially crucial in the case of unstable anions, which typically allocate the electron to diffuse orbitals.31
C–C dihedral angle to 0° to prevent the trans-bending, as illustrated by Fig. 3b. The CDFT reactivity indices (Fukui function, softness and local softness) were computed using the smaller 6-311G basis set, in order to artificially bind the additional electron to the molecule;30 this routine is especially crucial in the case of unstable anions, which typically allocate the electron to diffuse orbitals.31
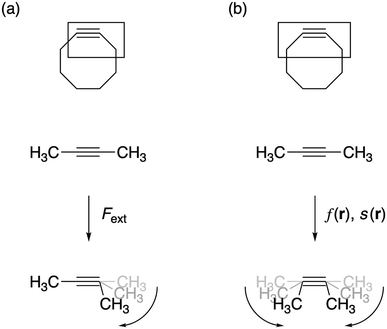 | ||
| Fig. 3 (a) The bending force was calculated by constraining one bond angle; (b) the reactivity of the triple bond in cyclic alkynes was modeled by constraining both angles around the triple bond. | ||
3. Results and discussion
3.1. Bending linear alkynes with an external force
The extended COGEF model described above leads to eqn (5) for calculating the force corresponding to a given angular distortion. As a prelude to the investigation of cyclic alkynes, which impose this geometrical constraint on the triple bond through ring strain, we discuss in this paragraph the angular force in simple linear alkynes.For different substituents (CH3, H, F and CHO) on the propargylic C-atom, the external bending force was calculated and plotted as a function of the deviation from the equilibrium geometry (φ) in Fig. 4, allowing us to scrutinize the effect of electron-withdrawing effects. Clearly, for φ equal to zero, the force also converges to zero for all substituents and a linear relation is found overall, according to eqn (5). Importantly, the magnitude of Fext is of the order of 1 nN, which is in the same range as the stretching force typically required for bond length elongations.16,19 In the ESI,† the extended COGEF model is improved by varying |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | as a function of φ, i.e. |
| as a function of φ, i.e. |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) |(φ) (|
|(φ) (|![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | typically increases for larger bends); however, no significant deviation from the linear correlation was found.
| typically increases for larger bends); however, no significant deviation from the linear correlation was found.
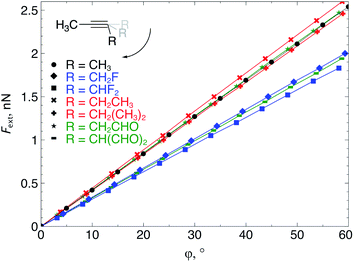 | ||
| Fig. 4 The required bending force in acetylenes increases linearly with the bending angle φ, according to eqn (5) but clearly varies upon substitution. | ||
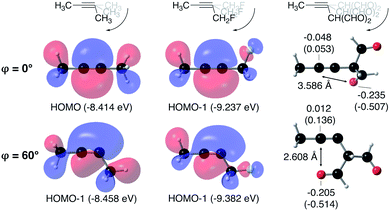
From Fig. 4, it seems that for R = CH2F, CHF2 and CH(CHO)2, the required bending force is significantly lower than for the other substituents. In the case of the fluorinated 2-butyne fragment, Gold et al. revealed that the hyperconjugative effect between the 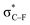 orbital and the in-plane π-orbital lowers the energy required for bending compared to unsubstituted 2-butyne and, elegantly, this effect is also reflected in a lower bending force. Fig. 5 illustrates the frontier π-orbital for 2-butyne and the σ*–π orbital in the fluorinated variant. Upon bending, the σ*–π overlap increases and the orbital is stabilized by 0.145 eV (or 3.3 kcal mol−1) whereas the HOMO/HOMO−1 orbital in the unsubstituted 2-butyne is only stabilized by 0.044 eV (or 1.0 kcal mol−1). This effect is enhanced when adding a second F-atom.
orbital and the in-plane π-orbital lowers the energy required for bending compared to unsubstituted 2-butyne and, elegantly, this effect is also reflected in a lower bending force. Fig. 5 illustrates the frontier π-orbital for 2-butyne and the σ*–π orbital in the fluorinated variant. Upon bending, the σ*–π overlap increases and the orbital is stabilized by 0.145 eV (or 3.3 kcal mol−1) whereas the HOMO/HOMO−1 orbital in the unsubstituted 2-butyne is only stabilized by 0.044 eV (or 1.0 kcal mol−1). This effect is enhanced when adding a second F-atom.
For R = CH(CHO)2, one of the carbonyl groups aligns itself with the triple bond upon bending, however, no benefit from orbital overlaps was found in this case. Instead, from Fig. 5, one can hypothesize that electrostatic interactions are responsible for the lower bending force. In particular the Natural Population Analysis (NPA) charges indicate a positively charged sp-hybridized C-atom and a strongly negatively charged O-atom.
3.2. Structural trends in cyclic alkynes
As stated before, the hunt for reactive cyclic alkynes has led a number of stable compounds with different substituents on the C-atoms next to the triple bond. In this section, structural trends in asymmetrically substituted cyclooctynes are interpreted in a mechanochemical context, that is, the influence of the substituents on the propargylic C-atom on the required bending force.In Fig. 6, structural properties of a series of cyclooctynes are shown. It is important to remark that two minimum structures exist if only one substituent is used on the propargylic C-atom and, according to the general scheme in this figure, the two structures are distinguished by the position of the substituent (see the dihedral angle, δ). For X = F, it is already clear that the bond angle β is smaller than for X = H showing that the 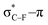 overlap, which weakens the angle for bending, also has a structural impact in the cyclic structure. Moreover, the substituents are ordered from least electron-withdrawing at the top (with CH3 being even slightly electron-donating) to most electron-withdrawing at the bottom. From Fig. 6, it is obvious that the angle β decreases from top to bottom, indicating that the
overlap, which weakens the angle for bending, also has a structural impact in the cyclic structure. Moreover, the substituents are ordered from least electron-withdrawing at the top (with CH3 being even slightly electron-donating) to most electron-withdrawing at the bottom. From Fig. 6, it is obvious that the angle β decreases from top to bottom, indicating that the 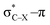 overlap increasingly distorts the symmetry around the triple bond, as expected along the series X = CH3 > NH2 > OH > F, according to Fig. 7. That is, the σ*–π energy gap decreases and the σ*-orbital is more localized on the propargylic C-atom along this series, both enhancing the stabilizing effect of the π-orbital. Additionally, the bond angle β is also smaller when the C
overlap increasingly distorts the symmetry around the triple bond, as expected along the series X = CH3 > NH2 > OH > F, according to Fig. 7. That is, the σ*–π energy gap decreases and the σ*-orbital is more localized on the propargylic C-atom along this series, both enhancing the stabilizing effect of the π-orbital. Additionally, the bond angle β is also smaller when the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C–X dihedral angle, δ, is closer to 180° corresponding to the anti-periplanar arrangement, which is favorable for the σ*–π overlap.
C–C–X dihedral angle, δ, is closer to 180° corresponding to the anti-periplanar arrangement, which is favorable for the σ*–π overlap.
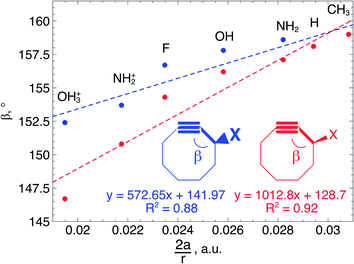
In order to understand these structural trends imposed by ring strain in the cyclic alkynes from a mechanochemical perspective, we correlated the angles at the substituent side in Fig. 6 with the factor 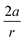 in eqn (5), which determines how large the perpendicular force component should be to bend the C
in eqn (5), which determines how large the perpendicular force component should be to bend the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C angle from linearity to a certain angle φ, according to our model in Fig. 2. The harmonic force constant, a, was computed with the substituent in anti-periplanar arrangement. Because the orientation of the substituent in Fig. 6 can have a significant influence on the angle β, two correlation graphs are shown in Fig. 7.
C–C angle from linearity to a certain angle φ, according to our model in Fig. 2. The harmonic force constant, a, was computed with the substituent in anti-periplanar arrangement. Because the orientation of the substituent in Fig. 6 can have a significant influence on the angle β, two correlation graphs are shown in Fig. 7.
From Fig. 7, a clear correlation is found between the angle in the cyclooctyne and 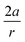 , showing that the mechanically weaker angle indeed gives rise to a larger bend in the cyclic systems. It should also be pointed out that
, showing that the mechanically weaker angle indeed gives rise to a larger bend in the cyclic systems. It should also be pointed out that 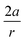 was calculated using the very simple bending model in Fig. 2, while constraining the other angle of the triple bond to linearity, which is obviously not representative for a cyclic alkyne. Nevertheless, this simple model based on classical mechanical principles (work, force and torque) provides insight into the degree of geometrical deformation when a molecule is subjected to stress in the form of an external force or, in this case, ring strain.
was calculated using the very simple bending model in Fig. 2, while constraining the other angle of the triple bond to linearity, which is obviously not representative for a cyclic alkyne. Nevertheless, this simple model based on classical mechanical principles (work, force and torque) provides insight into the degree of geometrical deformation when a molecule is subjected to stress in the form of an external force or, in this case, ring strain.
For the particular case of cyclic alkynes, our rationalization of structural trends has focused on the hyperconjugative effect between the 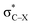 orbital and the π-system of the triple bond. In the ESI,† the effect of the electron-withdrawing character of substituents was tested by means of monobenzocyclooctynes, which have a conjugated π-system with the out-of-plane π-orbital of the triple bond analogous to the dibenzocyclooctynes, being an important family of reactive species in SPAAC reactions.2e,11c–e From this analysis, we infer that the strong dependence of the angle β in Fig. 7 is due to the simultaneous effect of the hyperconjugation and the electron-withdrawing effect of the substituent.32 The optimized structures of the benzocycloalkynes are shown in Fig. S5.†
orbital and the π-system of the triple bond. In the ESI,† the effect of the electron-withdrawing character of substituents was tested by means of monobenzocyclooctynes, which have a conjugated π-system with the out-of-plane π-orbital of the triple bond analogous to the dibenzocyclooctynes, being an important family of reactive species in SPAAC reactions.2e,11c–e From this analysis, we infer that the strong dependence of the angle β in Fig. 7 is due to the simultaneous effect of the hyperconjugation and the electron-withdrawing effect of the substituent.32 The optimized structures of the benzocycloalkynes are shown in Fig. S5.†
3.3. Reactivity of bent alkynes
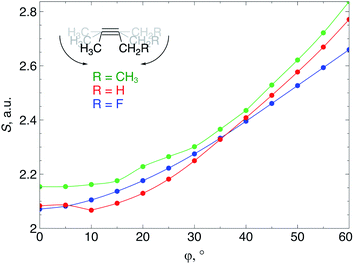
When an alkyne is bent, the mixing of C2s and C2p atomic orbitals with the in-plane π-orbital lifts the degeneracy of the π-space, which is a clear indication that not only a lower deformation energy is required when a cyclic alkyne takes part in a SPAAC reaction, but also that the reactivity of the cyclic alkyne with respect to a nucleophilic or electrophilic substrate is changed, compared to a linear system. In this section, these changes in reactivity are probed through the Fukui function and the local softness. These descriptors were calculated using the 6-311G basis set in order to bind the additional electron to the molecule in the case of the electrophilic Fukui function, f+(r).The loss of degeneracy of the π-system in bent (or cyclic) acetylenes is due to an increase of the in-plane π-HOMO energy and a decrease of the in-plane π-LUMO energy, while the out-of-plane orbitals are unaffected by bending.12 The global chemical hardness, which can be approximated by the HOMO–LUMO gap if orbital relaxation is ignored, should therefore decrease when a bending force is applied to the triple bond or, equivalently, the global chemical softness should increase. Fig. 8 illustrates the increase of the chemical softness as a function of the deviation from linearity (φ) in the 2-butyne fragment with H, F and CH3 substituents on the propargylic C-atom. The geometrical constraint was here applied to both angles in order to model a cyclic structure, according to Fig. 3b. The softness was computed by calculating the energy of the anionic and cationic species. However, a frontier orbital analysis revealed that the decrease in LUMO energy is more significant than the increase in HOMO energy. Importantly, the curves in Fig. 8 do not readily increase when the system is bent, instead S starts to increase after a deformation of about 15°.
Because the decrease of the LUMO energy is more significant than the increase of the HOMO energy upon bending, the electrophilic character of the triple bond is more affected by bending than its nucleophilic properties. Also, in SPAAC reactions, the alkyne is typically substituted with electron-withdrawing substituents (such as fluorides or O-containing chains) promoting the reaction with the electron-rich azide.1b,d,33 Hence, the electrophilic Fukui function, f+(r) which monitors the local change in the electron density when one electron is added to the system to model a nucleophilic attack, is discussed in here. In the ESI,† a fully equivalent analysis of the nucleophilic Fukui function is provided. The change in electron density was condensed to each atom of the triple bond, according to the Hirshfeld population analysis,34 in the bent alkyne providing quantitative information about the change in chemical reactivity due to an external bending force in Fig. 9a. The same analysis based on the NPA integration method35 is provided in the ESI† and yields identical conclusions.
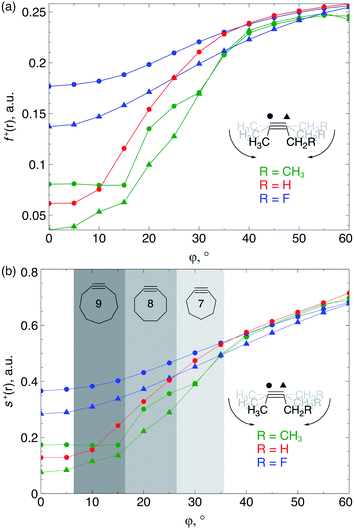 | ||
| Fig. 9 (a) f+(r) increases when the triple bond is bent, indicating that smaller cyclic alkynes become more electrophilic; (b) s+(r) increases when the triple bond is bent. | ||
From Fig. 9a, f+(r) clearly increases when the alkyne is bent, indicating that the triple bond becomes more prone to nucleophilic attacks upon bending. Also, the electron-withdrawing fluorine substituent increases the electrophilic character of the alkyne for smaller values of φ. Similar to S, the f+(r) curves are flat around φ = 0° and steeper for φ = 15° onwards. Interestingly, the separation of the curves corresponding to each C-atom of the triple bond diminishes when the angle around the triple bond becomes smaller and seems to converge at an angle of 120°, i.e. the double bond geometry. In a previous contribution, we explored the response of the electrophilicity of a chemical bond in diatomic molecules with an external stretching force revealing an increase in electrophilicity when a chemical bond is being stretched.19 This trend was interpreted in terms of a principle of least nuclear motion,36 that is, when a (homonuclear) diatomic molecule is being stretched, it becomes geometrically more similar to the geometry of the reduced form. For example, when the S2 molecule is stretched, it becomes geometrically similar to two HS˙ moieties and, therefore, the electrophilicity of S2 will increase upon stretching. The electrophilic Fukui function in Fig. 9a shows a similar behavior for alkynes: the electrophilic character increases and, more interestingly, it seems to converge at the double bond geometry (i.e. the geometry of the reduced compound). These observations indicate that an interesting relation might exist between mechanochemistry and redox chemistry.
The local softness [s(r)], which is the product of the global softness and the Fukui function, provides a predictive measure for the effectiveness of frontier orbital interactions in e.g. SPAAC reactions. In Fig. 9b, the analysis of s+(r) is shown for a nucleophilic attack to the alkyne. Similar to S and f+(r) individually, s+(r) is rather flat near φ = 0°. The reactivity of the triple bond is also strongly dependent on the substituent for small distortions with R = F being significantly more electrophilic than R = H or CH3. However, as φ increases, the reactivity of the triple is much less influenced by the substituent on the propargylic C-atom.
Recently, Bickelhaupt and co-workers investigated the [3 + 2] cycloaddition reaction of methylazide with 2-butyne, cyclononyne, cyclooctyne and cycloheptyne, revealing that the increased reaction rate along this series of alkynes can be attributed to reduced deformation energy of the reactants as well as a more stabilizing interaction energy along the reaction pathways.14 The most important contribution to the difference in interaction energy were more favorable frontier orbital interactions, which is completely in line with our analysis. Smaller energy gaps and increased orbital overlap between the frontier orbitals of the alkyne and methylazide are consistent with the analysis of the global softness in Fig. 8 and the Fukui function in Fig. 9, respectively. Moreover, cyclononyne with a triple bond angle of 168° in the cyclic structure (corresponding to φ = 12°) did not benefit from a significantly stronger interaction energy, which also emerges from the analysis of CDFT descriptors. The benefit is larger when going to the 8-membered ring (158° or φ = 22°) and even more significant for the 7-membered ring (146° or φ = 34°), again fitting nicely into the trends observed for s+(r) in Fig. 9b and s−(r) in Fig. S7b.†
The analysis in this work shows that strained alkynes have enhanced chemical reactivity compared to linear alkynes and that the substituents on the propargylic positions can influence the triple bond angle with electron-withdrawing groups giving rise to mechanically weaker angles. It is important to remark that any steric effects or attractive intermolecular interactions between the azide and (cyclo)alkyne, such as H-bonding, are not covered by this analysis based on CDFT descriptors.
4. Conclusions
Using a simple bond angle model, the COGEF approach to mechanochemistry for bond stretching forces was successfully extended to external bending forces. In the case of substituted alkynes, the angular force required to bend (linear) alkynes was calculated and shown to rely on the substituents on 2-butyne fragments. Electron-withdrawing substituents make the angles mechanically weaker and can be further weakened by a hyperconjugative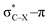 overlap, where X is a heteroatom. This effect of electron-withdrawing substituents results in smaller angles in cyclic alkynes. Smaller triple bond angles are desirable in SPAAC reactions, which rely on angular strain of alkynes to accelerate the coupling of alkynes and azides. Moreover, using the 2-butyne fragment, the chemical reactivity of the triple bond was probed upon bending (similar to cyclic alkynes) with the global softness, Fukui function and local softness. The global softness as well as the Fukui function revealed enhanced reactivity with respect to both nucleophiles and electrophiles. Importantly, the angles of the alkyne must be distorted at least 15° to be significantly more reactive than the linear system and the influence of substituents on the electrophilic character of the triple bond diminishes when it is bent further away from linearity.
overlap, where X is a heteroatom. This effect of electron-withdrawing substituents results in smaller angles in cyclic alkynes. Smaller triple bond angles are desirable in SPAAC reactions, which rely on angular strain of alkynes to accelerate the coupling of alkynes and azides. Moreover, using the 2-butyne fragment, the chemical reactivity of the triple bond was probed upon bending (similar to cyclic alkynes) with the global softness, Fukui function and local softness. The global softness as well as the Fukui function revealed enhanced reactivity with respect to both nucleophiles and electrophiles. Importantly, the angles of the alkyne must be distorted at least 15° to be significantly more reactive than the linear system and the influence of substituents on the electrophilic character of the triple bond diminishes when it is bent further away from linearity.
This study on angle-strained alkynes is part of our effort to rationalize and quantify mechanochemical reactivity within the framework of conceptual density functional theory. With this approach, different regions in complex molecules can be fragmented in order to reveal how certain bonds and (torsional) angles should be affected by external forces for selectively enhancing or reducing molecular reactivity for certain reactions. This approach paves the path for designing mechanically responsive molecules and identifying ideal attachment positions in mechanical experiments.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Computational resources and services were provided by the Shared ICT Services Centre funded by the Vrije Universiteit Brussel (VUB), the Flemish Supercomputer Center (VSC), and the Fund for Scientific Research Flanders (FWO). M. A. thanks the FWO for a postdoctoral fellowship (FWO-12F4416N) and the VUB for financial support. The authors acknowledge the Strategic Research Program funding of the VUB. F. D. P. also acknowledges the Francqui foundation for a position as ‘Francqui research professor’.References
- (a) E. M. Sletten and C. R. Bertozzi, Angew. Chem., Int. Ed., 2009, 48, 6974 CrossRef CAS PubMed; (b) S. T. Laughlin, J. M. Baskin, S. L. Amacher and C. R. Bertozzi, Science, 2008, 320, 664 CrossRef CAS PubMed; (c) J. M. Baskin, J. A. Preschner, S. T. Laughlin, N. J. Agard, P. V. Chang, I. A. Miller, A. Lo, J. A. Codelli and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16793 CrossRef CAS PubMed; (d) N. J. Agard, J. A. Prescher and C. R. Bertozzi, J. Am. Chem. Soc., 2004, 126, 15046 CrossRef CAS PubMed.
- (a) F. Liu, Y. Liang and K. N. Houk, Acc. Chem. Res., 2017, 50, 2297 CrossRef CAS PubMed; (b) E. G. Burke, B. Gold, T. T. Hoang, R. T. Raines and J. M. Schomaker, J. Am. Chem. Soc., 2017, 139, 8029 CrossRef CAS PubMed; (c) J. Garcia-Hartjes, J. Dommerholt, T. Wennekes, F. L. van Delft and H. Zuilhof, Eur. J. Org. Chem., 2013, 3712 CrossRef CAS; (d) B. Gold, G. B. Dudley and I. V. Alabugin, J. Am. Chem. Soc., 2013, 135, 1558 CrossRef CAS PubMed; (e) C. G. Gordon, J. L. Mackey, J. C. Jewett, E. M. Sletten, K. N. Houk and C. R. Bertozzi, J. Am. Chem. Soc., 2012, 134, 9199 CrossRef CAS PubMed; (f) Y. Liang, J. L. Mackey, S. A. Lopez, F. Liu and K. N. Houk, J. Am. Chem. Soc., 2012, 134, 17904 CrossRef CAS PubMed; (g) F. Schoenebeck, D. H. Ess, G. O. Jones and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 8121 CrossRef CAS PubMed.
- J. Dommerholt, O. van Rooijen, A. Borrmann, C. Fonseca Guerra, F. M. Bickelhaupt and F. L. van Delft, Nat. Commun., 2014, 5, 5378 CrossRef CAS PubMed.
- H. Hopf and J. Grunenberg, in Strained Hydrocarbons, ed. H. Dodziuk, Wiley-VCH, Weinheim, 2009 Search PubMed.
- R. P. Johnson and K. J. Daoust, J. Am. Chem. Soc., 1995, 117, 362 CrossRef CAS.
- (a) M. S. Schuurman, J. Giegerich, K. Pachner, D. Lang, B. Kiendl, R. J. MacDonell, A. Krueger and I. Fischer, Chem.–Eur. J., 2015, 21, 14486 CrossRef CAS PubMed; (b) P. Hemberger, B. Noller, M. Steinbauer, K. Fischer and I. Fischer, J. Phys. Chem. Lett., 2010, 1, 228 CrossRef CAS; (c) Q. Wu, Q. Cheng, Y. Yamaguchi, Q. Li and H. F. Schaefer III, J. Chem. Phys., 2010, 132, 044308 CrossRef PubMed; (d) R. A. Seburg, E. V. Patterson, J. F. Stanton and R. J. McMahon, J. Am. Chem. Soc., 1997, 119, 5847 CrossRef CAS.
- (a) Z. Su and H. F. Schaefer III, J. Org. Chem., 2019, 84, 5548 CrossRef PubMed; (b) R. D. Adams, G. Chen, X. Qu, W. Wu and J. H. Yamamoto, Organometallics, 1993, 12, 3029 CrossRef CAS.
- (a) J. M. Medina, T. C. McMahon, G. Jiménez-Osés, K. N. Houk and N. K. Garg, J. Am. Chem. Soc., 2014, 136, 14706 CrossRef CAS PubMed; (b) L. K. Montomery, F. Scardiglia and J. D. Roberts, J. Am. Chem. Soc., 1965, 87, 1917 CrossRef.
- C. Wentrup, R. Blanch, H. Briehl and G. Gross, J. Am. Chem. Soc., 1988, 110, 1874 CrossRef CAS.
- (a) T. Stauch, B. Günther and A. Dreuw, J. Phys. Chem. A, 2016, 120, 7198 CrossRef CAS PubMed; (b) A. Krebs and H. Kimling, Angew. Chem., Int. Ed., 1971, 10, 509 CrossRef CAS.
- (a) M. K. Narayanam, Y. Liang, K. N. Houk and J. M. Murphy, Chem. Sci., 2016, 7, 1257 RSC; (b) X. Ning, R. P. Temming, J. Dommerholt, J. Guo, D. B. Ania, M. F. Debets, M. A. Wolfert, G.-J. Boons and F. L. van Delft, Angew. Chem., Int. Ed., 2010, 49, 3065 CrossRef CAS PubMed; (c) M. F. Debets, S. S. van Berkel, S. Schoffelen, F. P. J. T. Rutjes, J. C. M. van Hest and F. L. van Delft, Chem. Commun., 2010, 46, 97 RSC; (d) J. C. Jewett, E. M. Sletten and C. R. Bertozzi, J. Am. Chem. Soc., 2010, 132, 3688 CrossRef CAS PubMed; (e) X. Ning, J. Guo, M. A. Wolfert and G.-J. Boons, Angew. Chem., Int. Ed., 2008, 47, 2253 CrossRef CAS PubMed.
- D. M. Hoffmann, R. Hoffmann and C. R. Fisel, J. Am. Chem. Soc., 1982, 104, 3858 CrossRef.
- Technically, the resulting frontier molecular orbitals can no longer be labeled π-orbitals because a π-orbital requires a defining plane, which no longer exists upon bending away from linearity.
- T. A. Hamlin, B. J. Levandowski, A. K. Narsaria, K. N. Houk and F. M. Bickelhaupt, Chem.–Eur. J., 2019, 25, 6342 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Acc. Chem. Res., 2017, 50, 1041 CrossRef CAS PubMed.
- (a) T. Stauch and A. Dreuw, Chem. Sci., 2017, 8, 5567 RSC; (b) M. Krupička, P. Dopieralski and D. Marx, Angew. Chem., Int. Ed., 2017, 56, 1 CrossRef PubMed; (c) M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377 CrossRef CAS PubMed.
- (a) T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137 CrossRef CAS PubMed; (b) J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412 CrossRef CAS PubMed; (c) M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921 CrossRef CAS PubMed.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307 CrossRef CAS.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2019, 21, 7378 RSC.
- W. Kauzmann and H. Eyring, J. Am. Chem. Soc., 1940, 62, 3113 CrossRef CAS.
- (a) J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190 CrossRef CAS PubMed; (b) M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377 CrossRef CAS PubMed.
- R.-Q. Zhang, Y.-L. Zhao, F. Qi, K. Hermann and M. A. Van Hove, Phys. Chem. Chem. Phys., 2016, 18, 29665 RSC.
- (a) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press and Clarendon Press, New York and Oxford, 1989 Search PubMed; (b) P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793 CrossRef CAS PubMed.
- (a) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef CAS; (b) R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801 CrossRef CAS.
- (a) R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922 CrossRef CAS; (b) P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065 CrossRef CAS PubMed; (c) F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Org. Lett., 2007, 9, 2721 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049 CrossRef CAS.
- (a) M. Torrent-Sucarrat, F. De Proft, P. Ayers and P. Geerlings, Phys. Chem. Chem. Phys., 2010, 12, 1072 RSC; (b) M. Torrent-Sucarrat, F. De Proft, P. Geerlings and P. Ayers, Chem.–Eur. J., 2008, 14, 8652 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- W. Langenaeker, M. De Decker, P. Geerlings and P. Raeymaekers, J. Mol. Struct.: THEOCHEM, 1990, 207, 115 CrossRef.
- (a) N. Sablon, F. De Proft, P. Geerlings and D. J. Tozer, Phys. Chem. Chem. Phys., 2007, 9, 5880 RSC; (b) D. J. Tozer and F. De Proft, J. Phys. Chem. A, 2005, 109, 8923 CrossRef CAS PubMed.
- The effect of electron-donating groups was explored by substituting X = O− and NH− on the propargylic C-atom, according to the structures in Fig. 6. The bond angle β was 161.3° (smaller δ) and 163.5° (larger δ), for X = O− and 158.7° (smaller δ) and 161.7° (larger δ), for X = NH−, which does show a clear increase of the angle when a strong inductive electron-donating group is used. However, due to the instability when bending the 2-butyne fragments, only the inductive electron-withdrawing effect were considered. The substituted 2-butyne dissociates into formaldimine (X = NH−) or formaldehyde (X = O−) and a carbanion when performing a bending experiment as illustrated by Fig. 3a.
- N. J. Agard, J. M. Baskin, J. A. Prescher, A. Lo and C. R. Bertozzi, ACS Chem. Biol., 2006, 10, 644 CrossRef PubMed.
- F. L. Hirshfeld, Theor. Chem. Acc., 1977, 44, 129 Search PubMed.
- (a) A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066 CrossRef CAS; (b) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- J. Hine, Adv. Phys. Org. Chem., 1977, 15, 1 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04507d |
| This journal is © The Royal Society of Chemistry 2020 |