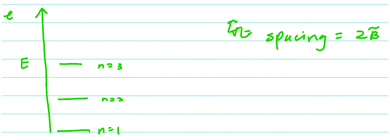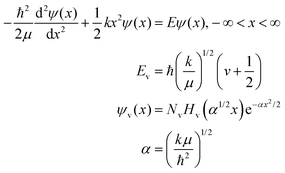Physical chemistry students’ navigation and use of models to predict and explain molecular vibration and rotation
Jordan P.
Beck
*a,
Marc N.
Muniz
 *b,
Cassidy
Crickmore
c and
Logan
Sizemore
c
*b,
Cassidy
Crickmore
c and
Logan
Sizemore
c
aConcordia University Wisconsin, Mequon, Wisconsin 53097, USA. E-mail: jordan.beck@cuw.edu
bRutgers University – New Brunswick, Piscataway, New Jersey 08854, USA. E-mail: marc.muniz@rutgers.edu
cWestern Washington University, Bellingham, Washington 98225, USA
First published on 3rd February 2020
Abstract
Models that are used to predict and explain phenomena related to molecular vibration and rotation are ubiquitous in physical chemistry, and are of importance in many related fields. Yet, little work has been done to characterize student use and application of these models. We describe the results of a multi-year, multi-institutional qualitative study to investigate how students work with and apply models of molecular vibration and rotation. Our findings indicate that a sizable fraction of students (1) struggle to interpret the meaning of wavefunctions, (2) do not appropriately build potential and kinetic energy terms into models, and (3) conflate portions of various model systems. The data suggests that the ordering of content in the quantum chemistry course impacts students’ ideas about the rotational and vibrational behavior of molecules. The results are analyzed through the lenses of a two theoretical frameworks: one for scientific modeling, and one for heuristics in the context of chemistry. Implications for research and teaching practice are provided.
Introduction
Quantum chemical models form the basis of our modern understanding of chemistry. Our ability to predict and explain the behavior of atoms and molecules directly impacts our ability to construct novel materials, make medical advances, and build fundamental knowledge about the universe. As such, it is important that undergraduate students pursuing a degree in the chemical sciences be equipped to appropriately conceptualize and apply quantum chemical models. To date, however, few studies have examined how chemistry students work with these models at the upper-division undergraduate level (Dick-Perez et al., 2016; Muniz et al., 2018; Roche Allred and Bretz, 2019).Students’ initial exposure to quantum chemical models typically comes in general chemistry in the context of the Bohr model and, perhaps, a conceptual treatment of the Schrödinger model to describe atomic structure. Both are typically revisited in more comprehensive detail in upper-division coursework. It is in the upper-division environment that students typically gain familiarity with models concerning molecular vibration and rotation. These models are important in a number of contexts including the interpretation of infrared (IR) and microwave spectra. As one prominent example, astrochemists and spectroscopists rely on vibrational and rotational models (often rovibronic models) to interpret emission and/or absorption spectra to characterize the chemical composition and temperature of celestial bodies such as a planets, stars, and interstellar clouds (Maier et al., 2001; Herbst, 2005; Cernicharo et al., 2008; Henning and Semenov, 2013; Oka, 2013; van Dishoeck et al., 2013; Fortenberry, 2015). It is the utility and wide applicability of these models which lead to their prevalence in the physical chemistry curriculum and why, we contend, undergraduate students of chemistry should be guided to develop a fundamental understanding of simple quantum mechanical models related to molecular vibration and rotation.
Published investigations of student understanding of models of internal motion (e.g. oscillatory behavior and rotational motion) are limited in the chemistry education research literature (Partanen, 2018). In physics, they are largely limited to the study of general and modern physics courses—contexts that are quite different than the typical upper-division chemistry classroom environment. Work at the general and intermediate undergraduate physics levels demonstrates that students experience significant difficulties in (1) framing the rotational and/or vibrational motion of the system they are investigating (e.g. appropriately designing a coordinate system), and (2) mathematizing the model to make quantitative predictions about such motion (Rimoldini and Singh, 2005; Sayre and Wittmann, 2008).
In the context of upper-division quantum physics, Singh and Marshman have summarized work from across the discipline of physics education research concerning common student challenges (Singh and Marshman, 2015). Among these challenges, two examples pertinent to our research are: difficulty reconciling quantum with classical behavior (especially in the context of the harmonic oscillator), and difficulties in interpretation of the wavefunction. The former difficulty manifests itself in our work across various quantum model systems (including the work described below), indicating that it exists in quantum chemistry learning environments in addition to those already described in quantum physics. The latter is especially prominent in our present work, and takes on a new form in the sense that students tend to associate the wavefunction exclusively with the behavior of an electron. This is unsurprising given that much of chemistry is driven by electronic behavior. However, when students make such generalizations, the connection between general quantum principles and the system they are modeling is compromised. In fact, we find that students experience challenges connecting the models to the systems about which the models are supposed to predict and explain: an observation noted by Singh and Marshman in their review, albeit in the context of Hilbert space vs. 1-D quantum mechanical systems (e.g. particle-in-a-box).
Our previous work has documented upper-division chemistry students’ difficulties navigating quantum chemical models in the context of atomic structure (Muniz et al., 2018). Participants’ responses to a think-aloud interview protocol revealed three broad categories of problematic student reasoning. First, the student participants tended to retain a deterministic thought processes (i.e. that electron(s) in atom(s) follow a specific trajectory). Similar results were subsequently reported by Allred and Bretz where a group of general and physical chemistry students indicated their preference for a Bohr model representation of a helium atom over, or in addition to, an electron density plot representation (Roche Allred and Bretz, 2019). Second, many students neither mathematized their models, nor directly invoked the Schrödinger equation to formulate a model of the atom. Third, students conflated models and model components that relate to quantum mechanical systems other than the hydrogenic atom. This result of conflation was reminiscent of work from Ferguson and Bodner in the context of reaction mechanisms in organic chemistry where “Concepts that [students] remember were often misapplied or confused with competing ideas” (Ferguson and Bodner, 2008).
Our previous work, along with the other reports in the literature, led us to develop a model rating task—one in which participants were asked to rate, on a four-point Likert scale, the degree to which a model is helpful or unhelpful for solving a quantum chemical problem. The results indicated that model conflation extends well beyond the hydrogen atom context and into such disparate sub-domains as the particle-in-a-box and quantum harmonic oscillator models. We interpreted our findings through the lens of a framework that casts students’ struggles with developing robust knowledge structures in a given domain as a problem of ontology (Chi et al., 1981; Slotta et al., 1995). The resulting analysis suggested that students experienced challenges in classifying the nature of a problem (e.g. does the problem focus on electronic behavior in molecules or translational behavior of an isolated atom?). Those challenges in classification led to problems in developing, or selecting, and applying the appropriate type of model. Since the rating task results, in part, indicated that students conflated models and model components pertaining to molecular rotations and vibrations, we decided to create think-aloud interview protocols that aim to investigate students’ understanding of these molecular motions. In this study, we investigated two principal research questions:
(1) How do upper-division chemistry students develop, apply, and revise simple quantum mechanical models of molecular vibration and rotation?
(2) What, if any, themes of model conflation arise when upper-division chemistry students solve problems involving molecular vibration and rotation?
When considering the data from the think-aloud interviews reported in this study, we found that the use of an ontological theoretical perspective led to a “piecemeal” approach to our analysis. In other words, only some of the data lent itself readily to interpretation along ontological lines. Our principal research questions target students’ development and application of models in an abstract context (quantum chemistry). Thus, a primary lens through which we interpreted this data is a framework for models and modeling. Bodner, Gardner, and Briggs (Bodner et al., 2005; Briggs, 2007) articulated several important features of models and modeling practice. The following is a condensation of their description, represented in a tiered fashion:
A model…
…must relate to a system or phenomenon…
…should focus attention to some particular aspect of that system or phenomenon.
…should, through the relationship between the system and the model, help us to make sense of the world.
We chose this perspective, in part, because much current instruction in the physical chemistry course context heavily favors what Bodner and coworkers refer to as a “problem solving mindset.” (Gardner and Bodner, 2007) This means that students believe that a primary goal of the course is to solve multiple problems, achieve a correct answer or expression, and move on to the next one. While the authors note that developing strong problem-solving skills is not problematic, they suggest that a course structure that emphasizes this mindset may dilute students’ abilities to genuinely engage in the scientific practice of modeling. Similarly, Tsaparlis has reported that in the realm of quantum chemistry “algorithmic behavior does not presuppose conceptual understanding, and vice versa.” (Tsaparlis, 2013) Recent literature, including the development of the next generation science standards (NGSS) and its framework for K-12 education, indicates that modeling as a scientific practice is necessary for learners to build scientific literacy (Council, 2012). Here, we aim to use the framework to explain the themes in the current state of students’ development and application of models in the quantum chemistry context. This current state is in the absence of targeted, modeling-based instruction and therefore serves as a baseline from which iterative improvements to curriculum and instruction in such courses could be made.
Finally, in order to broaden our perspective, we have also examined the student data using the set of heuristics described by Talanquer (Talanquer, 2014). The former affords us insight into the students’ reasoning with models, while the latter allows us to examine which cognitive processes are implicated in students’ challenges with successfully applying quantum chemical models. We believe that interpreting the data through the lens of models and the lens of heuristics gives us the opportunity to more fully understand students’ use of models in the context of quantum chemistry.
Research methodology, participants, and settings
Participants were all students taking the quantum chemistry component of an undergraduate physical chemistry course sequence. Student participates came from three different institutions: a large regional comprehensive in the Pacific northwestern US, a small liberal arts college in the midwestern US, and a large research-intensive institution in the midwestern US. All of the data was collected during the 2017 and 2018 calendar years. Each student participant completed only one protocol, so the total number of participants was 32. The following table provides a comprehensive description of the number of students who participated in the research, delineated by protocol (vibrational motion or rotational motion) and institution (Table 1).| Vibration | Rotation | Total | |
|---|---|---|---|
| Large Regional Comprehensive University | 8 | 11 | 19 |
| Small Liberal Arts University | 6 | 3 | 9 |
| Large Research-intensive University | 4 | 0 | 4 |
| Total | 18 | 14 | 32 |
We designed and implemented two think-aloud research interview protocols: one focused on vibrational motion, and one on rotational motion. The research team obtained informed consent, per IRB standards, from prospective participants and commenced the one-on-one, Smart-pen recorded (audio + real-time writing) interviews toward the end of the academic term at each institution. This ensured that the relevant material (quantum vibrational and rotational motion) had been covered in the students’ classes prior to their participation in the research. Each interview protocol was triphasic (see Appendices 1 and 3 for the full versions of the protocols): the first phase involved the development of a model, the second phase focused on model application, and the final phase involved refinement of the model to better account for experimental results that are not fully explained or predicted by the original model. Student participants were guided by the interviewer to think-aloud during the entire interview process (i.e. talk about whatever was going through their mind at a given moment, even if they were not thinking of anything concrete or were “stuck” on some part of the protocol). This afforded us insight into students’ thought processes while they were engaging in the modeling process, as well as their rationale for making the decisions they made about which representations to incorporate into their models and how to apply them to empirical evidence.
Think-aloud approaches have a long history (Bowen, 1994) of being used in discipline-based education research (DBER), as well as in related fields, and are considered powerful qualitative methods for investigating students’ ideas about a wide variety of constructs. Naturally, think-aloud interview data lends itself well to analysis that considers both the emergent themes from the data as well as those that are grounded in the literature. In our prior work (Muniz et al., 2018), we described a coding scheme that was partially-emergent and partially literature-grounded. This scheme afforded us the opportunity to characterize patterns and themes in students’ responses during their interviews. The same approach, which can be considered a thematic analysis (Braun and Clarke, 2006), was used for the work described here. For this report, students were assigned random pseudonyms.
Results and discussion
The interview protocols were designed for participants to construct, modify, and interact with certain physical chemical models. The protocols, along with their corresponding resource sheets, are provided in the appendices. Ideally, participants would use a variety of representations in their models, including mathematical representations. Ultimately, the participants should incorporate appropriate kinetic and potential energy terms into the Schrödinger equation as well as identify and be able to use/interpret the relevant wavefunctions and associated quantized total energies. The data presented below is organized to highlight three major themes that emerged when coding the student responses to the protocol prompts.Theme 1: interpretation of the wavefunction
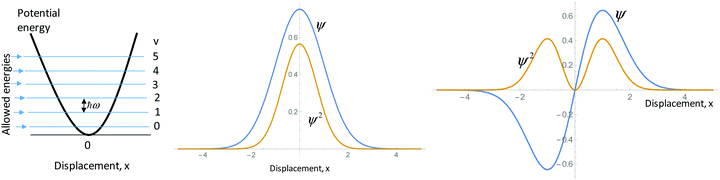
An important part of the process of modeling quantum mechanical systems is connecting the model with the physical system being modeled. The data from this study reveal that students struggled with this fundamental skill. For example, the harmonic oscillator interview protocol described a system of two atoms, held together with a covalent bond, that move with respect to each other in a coordinated fashion. In this system, the physical entity being modeled is the position of the two atoms of the diatomic molecule with respect to each other. Students were asked to describe the information provided by various representations, including graphs of the wavefunction, ψ, and its square, for two solutions of the quantum harmonic oscillator Schrödinger equation (see the harmonic oscillator protocol, question g, in Appendix 1). A fairly scientifically—normative response to this part of the protocol comes from Megan:Megan: “That's [the square of the wavefunction] just telling you like the probability…Those are just probabilities of where that displacement is going to be for that diatomic molecule at that wavefunction.”
Megan has identified the square of the wavefunction as representing a probability of displacement (from the equilibrium position) of the diatomic molecule being modeled. Contrast this with the following common response variety, exemplified here by Alan:
Alan: “And the second diagram plots the, uh, wavefunction psi and psi square, so psi is the wavefunction and psi square gives you the probability of finding an electron at a certain position…And the last picture is also a psi function, uh, wavefunction plot. And also this square of this wavefunction gives you the probability of, uh, finding an electron.”
In the excerpt above, Alan correctly identifies the wavefunction, ψ, and it's square, ψ2. He also correctly links ψ2 with a probability. The interpretive challenge comes when he tries to link ψ2 with the system being modeled. Rather than describing ψ2 as a probability distribution of displacement from an equilibrium bond length, Alan describes ψ2 as representing “the probability of finding an electron at a certain position.” This major mischaracterization of the meaning of ψ2 for this system was a common occurrence among the student participants. In fact, six of the 18 student participants who completed the harmonic oscillator protocol made a similar claim.
The framework on models and modeling articulates that models and their components must relate to a particular target system in order to be useful for predicting and explaining phenomena. One postulate of quantum mechanics is that the square modulus of a wavefunction has a probabilistic interpretation. This probabilistic interpretation affords one the ability to make predictions about and explain the outcomes of quantum measurements. Thus, the wavefunction in this capacity can be considered to be a model of the behavior of the particular system under investigation. The grain size is relatively large, since the construct of a wavefunction applies to many different quantum mechanical systems. In this sense, a wavefunction plays the role of a “one to many” model or model component: one that can be useful for a wide array of systems.
Our excerpts provide evidence that students find it challenging to appropriately invoke the general property of a wavefunction's square modulus (the probability density function) in a specific context (internal motion of a molecule). The evidence to support this claim is exemplified in excerpts similar to those of Alan's: some students appear to automatically assume that the probabilistic interpretation of the wavefunction only applies to electrons.
From the perspective of heuristics, one could argue that the cognitive process of generalization applies. Generalization, in brief, is the tendency for learners to assume that some pattern or theme applies to all situations and under all conditions in some context. While a wavefunction is, certainly, a very general construct that applies to many different systems, students’ generalization appears to invert the normative relationship between wavefunctions and target systems: they seem to tacitly assume that all wavefunctions describe electronic behavior (a many-to-one relationship) while the normative relationship is that each model system has a particular type (or a set of types) of wavefunctions. Thus, we argue that a generalization heuristic, coupled with challenges connecting a model to the appropriate target system, explains our observations.
Theme 2: kinetic and potential energies
In both the harmonic oscillator and rigid rotator protocols, student participants were prompted to construct a model, then asked how kinetic and potential energy were incorporated into their model. An important feature of the interview protocol is that it was scaffolded in the sense that the students were first asked, very broadly, to generate pictures, diagrams, sketches, figures, and mathematical formulae to model the system with no other context about what the models will be used for. Thus, student responses to the initial questions give a glimpse of students’ ideas about what model components they consider to be most general or fundamental to the system being modeled. The students were then asked more directed questions as the interview proceeded in an attempt to have them focus on specific components of their models or to have them modify or expand their models. A representative sample of student responses in the context of the harmonic oscillator to the initial, broad prompts (prompts a and b) is presented in Fig. 1.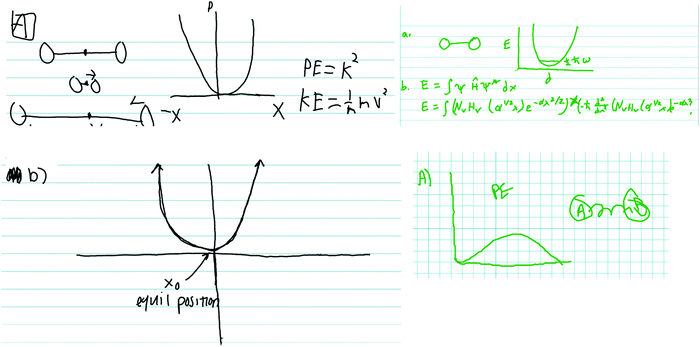 | ||
| Fig. 1 Sampling of student responses to the first two prompts of the harmonic oscillator protocol (see Appendix 1 for the protocol questions). | ||
The most common model components included by the students were potential energy diagrams and drawings of two circles connected by a straight or curvy line (i.e.Fig. 1 upper left, upper right, and lower right). Some students did attempt to include quantum mechanical ideas into their models and responses. For example, some of the models included quantized energy levels and, in some cases, zero point energy (Fig. 1, upper right).
The third question in the harmonic oscillator protocol asked students specifically how kinetic and potential energy play a role in their model. Even after this prompt, only one-third of the respondents attempted to include a formulation of the Schrödinger equation with the harmonic oscillator Hamiltonian. That only one-third of participants even attempted to invoke the Schrödinger equation is problematic from a pedagogical perspective. The Schrödinger equation is the principal framework within which we account for total (potential + kinetic) energy for the system being modeled. Despite this, the most common approach from the students was to discuss energy in a classical context. Consider these two representative examples.
Erin: Written response: “When the system oscillates back and forth, potential and kinetic energy constantly change. Potential energy is greatest where the maximum distance from the equilibrium bond length is reached and kinetic energy is greatest at the equilibrium bond length.”
Grace: “So for kinetic and potential energy I know that, um, once the spring's fully expanded, the molecule's completely stretched it's going to be all, um, potential. And then when it's completely compressed it's going to be all potential and then in between those it's going to be somewhat kinetic and somewhat potential.”
This type of description given by Erin and Grace of the kinetic and potential energies oscillating is evidence of a retention of determinism. In other words, students have great difficulty moving beyond classical explanations when dealing with systems on the quantum level. This effect has been well documented in the context of the hydrogen atom: a domain in which students retain a deterministic Bohr model when describing the position of the electron relative to the nucleus (Tsaparlis and Papaphotis, 2009; Dangur et al., 2014; Muniz et al., 2018).
Student descriptions of kinetic and potential energies in the context of the rigid rotator also provided interesting results. Half of the student participants were able to articulate that the energy for the rigid rotator is kinetic and that the potential energy for this model is zero. Some were able to express these ideas in the language of quantum mechanics by considering terms of the Hamiltonian operator. A terse, representative example of this type of response is from Sam.
Sam: “Hmm, well I know there's a potential and a kinetic, no actually the potential would be zero, I think. And then kinetic would be the Hamiltonian.”
The more interesting results come from the students who did not describe the energy of the model system properly. A not-uncommon response (3 out of the 14 students) was that there was a potential between the atoms, holding them together. Todd provided this type of reasoning in his verbal and written (Fig. 2) responses.
Todd: “Well obviously there's, there's kinetic energy in each atom. Uh, in each, um, atom, there you go. Um, because they’re moving around, um, potential energy… I’m… There's the, I guess I would say it's a potential energy that's binding the two together. Um, that keeps both of, both the atoms, um, together and stops them from falling apart.”
The problem with this type of response is not that it is wrong per se. Rather, it fails to use the model to focus on the relevant part of the system to be modeled.
Considering student responses to the question of energy in their models as a whole, it appears that many students did not use the models to properly make sense of the world. In the case of the harmonic oscillator, the major difficulty was the connection between the model and system to be modeled (i.e. the energy was introduced classically whereas the system to be modeled requires a quantum description). In the case of the rigid rotator, the major difficulty was focusing on the correct aspect of the system (i.e. the rotational kinetic energy rather than the internuclear potential).
Perhaps a more tangible interpretation of this data is that students were using the heuristics of rigidity and recognition. Despite formal instruction in quantum mechanics, many students were hesitant to move beyond classical thinking, presumably because classical thinking has worked for them to describe oscillatory motion in their prior experiences. Furthermore, classical experiences are more concrete to students based on their everyday experiences in a macroscopic world. This is an example of the cognitive process termed rigidity. When describing the potential energy of the rigid rotator some students described the potential energy between the atoms. This is a form of recognition, a heuristic where “people often rely on the information that is easier to retrieve from memory, either because it is computed quickly or it has been reinforced by frequent exposure” (Talanquer, 2014). In this particular case, the ubiquitous parabolic potential energy of a diatomic oscillator, which is critical to describe oscillatory motion, is easily recalled by students and applied out of its proper context.
Theme 3: conflation of model systems and components
Further investigation of student responses in the context of potential energy within the rigid rotator model revealed evidence of conflation of two types: conflation with harmonic oscillator and conflation with electronic structure of the atom. In the former case, students focused on the potential energy between the two atoms. As mentioned above, this type of conflation is associated with the improper connection between the model and the system being modeled. This conflation of the potential energy with the harmonic oscillator system carries over into describing the energetics of the whole system, as expressed by Glen when describing the energy spacings in a rotational spectrum as shown in Fig. 3.In the latter case, the conflation stems, apparently, from the presence of the spherical harmonics in the solution to both the electronic wavefunction for the hydrogen atom (the entry point to discussion of electronic structure in most curricula) and the rigid rotator. Consider, the response from Alicia when asked about the angular momentum of the diatomic molecule (question d in the rigid rotator protocol):
Alicia: “I think that the angular momentum of the electrons within the diatomic molecular system would be added together for the two systems. Um,”
Interviewer: “Why do you think that?”
Alicia: “I think that, uh, because if we have two atoms that are coming together from a molecule, each of those atoms’ electrons are going to have um, some sort of angular momentum, um, and so… I think that like, there are two… like two atom system that there is, but those angular momentums can be added together for a total angular momentum.”
In this case, Alicia is considering the ideas of angular momentum coupling relevant to electronic structure of atoms and molecules. In another example, Billie is more explicit when describing the connection between the rigid rotator and the hydrogen atom:
Billie: “Yeah, so this would be similar to the rigid rotor, rotator model that we used with a single electron with the um, nucleus focused at the center and the electron was at a fixed lengths at all points around, um, this sphere, like, independent of, like, any sort of angle, like, it's always sort of a fixed distance away and so this… I’m kind of saying that the, um, in, in, B the atoms are along some arbitrary axis, I’ve labeled it y, and so I’m saying that the origin is at the center of this sphere and A and B are going to rotate, um, and maintain the distance R, or R over 2, I guess, away from the origin. Like the electron in the hydrogenic rigid rotator.”
It is interesting that Billie tries to make the explicit connection between the rigid rotator model and the hydrogen atom model, going as far as describing a “hydrogenic rigid rotator”. Finding such connections is important for a deep understanding of the material in a quantum chemistry course. However, it is apparent that the connections are not totally clear for Billie, particularly when her response to the prompt about sketching an energy level diagram for the rigid rotator (question e in the rigid rotator protocol), as displayed in Fig. 4, is considered.
Examining Billie's responses holistically, she tries to connect the solution to the rigid rotator to the solution to the hydrogen atom. This ultimately leads to an energy level diagram reminiscent of that for the hydrogen-atom, complete with quantum number n. The use of quantum number n was not unique to Billie. In fact, the use of imprecise notation was taken to be an indicator of model conflation. Many students described the angular momentum and rotational quantum number using quantum numbers l or L, which are more conventionally used for electronic orbital angular momenta. In a revealing comment, Carl addressed this directly:
Carl: “I drew the model for the energy levels back up in B but I will say again that they are not equidistant, um… and this again has to do with again that fact that the energy is proportional to J-squared. And so as you increase, um, J… also J and l are the same thing, just for the record, um, if I’m calling it little l over here, is equal to J. Um, the angular quantum number, but they’re not equidistant.”
This sort of model conflation is, presumably, due in part to how the material is presented in a standard course. Consider, for example, the progression of the topic of the rigid rotator in a commonly-used physical chemistry text (McQuarrie and Simon, 1997).
Chapter 5: The Harmonic Oscillator and the Rigid Rotator: Two Spectroscopic Models
The Hamiltonian is discussed and the Schrödinger equation presented. The authors then state “The solutions to [the Schrödinger equation] are the rigid-rotator wave functions, which we won’t need in this chapter. We will encounter [this Schrödinger equation] when we solve the Schrödinger equation for the hydrogen atom in Chapter 6…you might be interested to know that the solutions to [this Schrödinger equation] are very closely related to the s, p, d, and f orbitals of a hydrogen atom.” The energy eigenvalues are then presented, using quantum number J.
Chapter 6: The Hydrogen Atom
Section 6.2: The Wave Functions of a Rigid Rotator are Called Spherical Harmonics
The wavefunction solutions to the rigid rotator problem are first presented in this section. In this context, they are labeled with quantum numbers l and ml. The authors state “The solutions to [the Schrödinger equation], which are not only the angular part of the hydrogen atomic orbitals, but also the rigid-rotator wave functions, are P|m|l(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)Φm(ϕ).”
θ)Φm(ϕ).”
Chapter 13: Molecular Spectroscopy
The discussion of the rigid rotator system resumes in chapter 13, focusing on the rotational terms, again using the conventional J as the quantum number.
Although an example from only one textbook is presented, the progression of harmonic oscillator, rigid rotator, hydrogen atom, then spectroscopy is fairly general and applies to many commonly used texts in physical chemistry (McQuarrie and Simon, 1997; Atkins and De Paula, 2009; Ball, 2015).
From a models and modeling perspective, the notion that one should be able to use a model to make sense of the world in some way is compromised by the fact that some students do not use the appropriate model components in the appropriate contexts. The model components are being related to a target system or phenomenon but not one that is physically appropriate. This differs subtly from students' difficulties that were described in theme 1, but is similar to what is described in theme 2: instead of incorrectly characterizing the system that is under study, students invoke an inappropriate model component. Consider the following: One can certainly describe the probability density of an electron in a given system with the square modulus of its wavefunction. However, one cannot describe molecular vibration with the use of the spherical harmonics. Nor can one describe microwave spectra—the result of changes in quantum rotational states—with a model that involves a harmonic oscillator potential. Hence, we conclude that the principal aspect of models and modeling practice that is violated in this theme is the sense-making requirement.
From a heuristics and cognitive bias perspective, it is arguable that the recognition heuristic is at play once again. The model conflation between harmonic oscillator and rigid rotator is, largely, one-way: it is more likely that students will invoke harmonic oscillator attributes in the context of rigid rotator than the other way around. A notable exception to this is the fact that some students invoke “spherical harmonics” as a relevant model component for the harmonic oscillator. This is likely a case of surface similarity: the term “harmonic” is present in each of the constructs, so students are likely basing their decision to call upon that set of functions in a context to which it does not apply (Muniz et al., 2018). The apparent unidirectionality of students’ model conflation, intriguingly, coincides with the order in which the models are presented to students in most quantum chemistry classes: harmonic oscillator is taught prior to rigid rotator. Additionally, it appears that heuristic of attribute substitution is being used. Taking Glen's response in Fig. 3 as an example, in an attempt to address the more complex question of how the energy levels relate to spectral features, he substitutes the attributes of the energy levels (nominally an easier question to answer) to the attributes of the spectral features. Due to the typical sequence of topics in the course, the parabolic potential energy well—in addition to the equidistant energy eigenvalues—is available for students to form a schema prior to their exploration of quantum molecular rotation. Molecular rotation is introduced immediately after molecular vibration and the pure microwave spectra have—to a first approximation—equidistant spacing in their lines. Students recognize this attribute of the spectrum: that it has equidistant lines, and assume that the origin of such lines must be equidistant energy level spacings. This means that they consider neither the structure of the energy eigenvalues: that the energy depends on the quantum number, J, in a quadratic fashion, nor the fact that the population of rotational states is such that multiple ΔJ = +1 transitions are possible. It is much simpler for students to rely on the recognition of the evenly spaced lines in the spectrum and simply relate it to evenly spaced energy levels—which likely couples to thoughts of the recently-explored harmonic oscillator model. In this sense, it is unsurprising that students use such a heuristic rather than engage in the comparatively complex cognitive task of comparing the forms of the energy eigenvalues in conjunction with the selection rules.
Summary of themes and conclusion
The data from the harmonic oscillator and rigid rotator interview protocols revealed a wealth of information that was grouped and presented as three themes above. These three principal themes are summarized in Table 2. The data has been interpreted through two theoretical lenses which are also summarized in Table 2.| Theme | Modeling challenge | Heuristic(s) |
|---|---|---|
| Interpretation of the wavefunction | Failure to relate model to target system: students assume ψ only describes electron behavior | Generalization: students invert the normative relationship between wave functions and target systems |
| Kinetic and potential energies | Difficulty with use of models to make sense of the world: | Rigidity: students do not “set aside” classical mechanical interpretations in the quantum context |
| Harmonic oscillator: students describe behavior in classical context | Recognition: students draw upon the ubiquitous parabolic energy diagram | |
| Rigid rotator: students focus on the incorrect aspect of the system | ||
| Conflation of model systems and components | Difficulty with use of models to make sense of the world: students incorrectly characterize the system that is under study | Recognition: Students recognize features of the harmonic oscillator model (e.g. parabolic potential; equidistant energy levels) and invoke them in the context of molecular rotation |
| Attribute substitution: students assume that quantum descriptions of angular behavior in rotating molecules have the same notation as that of angular behavior in atoms | ||
Using the theoretical lenses of models/modeling, and heuristics, has allowed us to categorize the data in various ways that may ultimately prove helpful in guiding further research and pedagogical interventions. Viewed through the lens of models and modeling, the data indicates that students tend to mischaracterize the system under consideration or misapply certain model components. An example of mischaracterization of the system was using the harmonic oscillator potential energy function in the context of the rigid rotator. A similar example, the improper relation of energy level spacings to spectral features, constituted a difficulty in applying components of a model to predict and explain phenomena. In the former case, students misclassified a rigid rotator problem as a harmonic oscillator problem. In the latter, rather than starting with the fundamental ideas about spectroscopy and using the energy level expressions to predict spectral features, students rather tried to classify the problem as one that should be memorized. They proceeded to try to recall certain aspects of their memorized solution. Another prime example of problematic development and application of models evident in the data is that students have transferred ideas about the meaning of the electronic wavefunction to the harmonic oscillator wavefunction. Students describe ψ2 for a harmonic oscillator as representing electron probability. Thus, the target system for which the model is to be applied was mischaracterized by some students.
Finally, the major themes of our data were described in terms of heuristics summarized by Talanquer (Talanquer, 2014). We found in our data examples of attribute substitution, generalization, rigidity, and recognition. For example, students tended to conflate aspects of the rigid rotator with the hydrogen atom. This was due, in part, to the surface similarities between the solutions to these two systems. Both rely on spherical harmonics, which tended to enhance the conflation and attribute substitutions from the hydrogen atom solutions to the rigid rotator solutions. Ultimately, the use of such heuristics couples with the fact that students experience challenges engaging in the scientific modeling process. One will arguably experience significant difficulty (1) “relating a model to a target system or phenomenon”, (2) “focusing attention on a particular aspect of the system or phenomenon”, and (3) “using the relationship between the system and the model to make sense of the world” if one makes errant connections between model components based on surface similarities, or improperly substitutes attributes between unrelated models and/or systems.
Implications for teaching and research
Our work generates several implications for teaching and research, some of which exist at the boundary of practice and scholarship. Students’ challenges with respect to applying general quantum chemical principles to specific contexts constitute a significant barrier to meaningful learning in quantum chemistry. Thus, we propose that instructors structure their approach to these fundamental ideas by (1) applying the postulates directly to different entities (i.e. not only electrons) while the content is being introduced and (2) guiding students to reflect explicitly on when general principles are necessarily invoked during the exploration of content as the course progresses. For example, instructors could have students explore the probabilistic interpretation of the wavefunction in terms of an electron in a bound system modeled by particle-in-a-box as well as in the context of a vibrating diatomic (harmonic oscillator approximation). Students can be guided to generate explanations of how the wavefunction can be used. In each context, the underlying principle of using the square modulus of the wavefunction as a probability density function to compute probability of finding the entity modeled by the wavefunction is invoked. In addition to this, instructors can have students explicitly identify general quantum mechanical principles throughout each specific context explored in the course. For instance, when one applies quantum mechanical models to predict and explain spectral results, one must always subtract the energy of the initial state from that of the final state (and that the energy difference corresponds to the position of one given peak on the spectrum). If students are guided to reflect on this, and write it explicitly in the contexts of vibrational, rotational, and electronic spectroscopies, it is possible that they will be able to better relate the spacing between energy levels with the absolute and relative locations of peaks in spectral data. Such an approach aims to facilitate the development of a less-compartmentalized viewpoint of the models encountered during the course. It also encourages the constant discussion of approaching the material from the “first principles”, spiraling back to these principles in a metacognitive fashion as more content is covered in class. From a research perspective, student responses to items designed to target the particular constructs (i.e. the quantum principles situated in a number of different contexts) could be used to assess the outcomes of any changes to pedagogy.We aim to further characterize student navigation of fundamental quantum chemical principles in a broader range of systems and topics. As such, a valid and reliable means of assessing the degree to which students are able to achieve gains in these areas is required. In our previously reported work on student modeling, we developed a preliminary model rating task with the aim to characterize which models and model components students consider relevant for solving various quantum chemical problems (Muniz et al., 2018). We are currently in the process of aligning these models and model components, as well as the items themselves, with the QCCI (Dick-Perez et al., 2016). In doing so, we will be able to use both instruments (our novel model rating task, and the existing QCCI) to more thoroughly address the following two research questions: (1) What is the nature of undergraduate students’ conceptions about fundamental quantum chemical principles after a term of instruction?, and (2) What patterns and themes emerge in students’ decisions about which models and model components are relevant for solving quantum chemical principles across a variety of subdomains (contexts)?
This future work will set the stage for a research-practice design cycle in which the results of curricular modifications in the manner articulated above will be measured by the QCCI, our novel model rating task, and subsequent think-aloud interview protocols. The analysis and interpretation of this data will, in turn, inform subsequent curricular modifications based on any additional patterns and themes that emerge. The tools we are currently developing, in conjunction with published tools such as the QCCI and the classroom observation protocol for undergraduate STEM (COPUS) (Smith et al., 2013), can be used to determine whether components of particular pedagogical approaches, and modes of instruction, are associated with certain desirable student outcomes. For example, it is possible that other yet-to-be-measured subdomains of quantum chemistry may be correlated with student conflation of models or focus on surface-level features. If such a theme emerges, curricular materials can be modified as an attempt to directly address the problems and the success of the intervention will be measured with the research tools. Research-informed educational practice has been shown to be effective at multiple levels (elementary through college and university) of schooling. We anticipate that it will be effective in the context of upper-division quantum chemistry as well.
Conflicts of interest
There are no conflicts to declare.Appendix 1: harmonic oscillator interview protocol
Interview protocol (harmonic oscillator)
Instructions: Say, out loud, what comes to your mind as you go through the process of solving the following problems. Use your resource sheet to help you shape your responses.Consider a diatomic molecule held together with a covalent bond. The two atoms of the molecule move with respect to each other in a coordinated fashion that we will model as a harmonic oscillator:
a. Draw a picture to represent this system.
b. Use sketches, diagrams, and mathematical formulae to construct a model of the interaction between the two atoms in the molecule.
c. How do potential and kinetic energy play a role in your model (if at all)? Explain.
d. Address the question: “What is the distance between the two atoms in the diatomic molecule?” Draw upon your model to support your response.
e. Explain what is represented by this diagram:
f. Kwame and Jean, upon observing the diagram presented above, disagree about how the diagram relates to using the harmonic oscillator to model a diatomic molecule.
• Kwame suggests that the diagram represents the introduction of a center-of-mass coordinate to model a two-body system as a one-body problem.
• Jean argues that the diagram represents the two atoms of the original diatomic molecule fusing into one with a new mass of μ.
Whose response do you most agree with? Use what you have developed in parts (a) through (d) to support your response.
g. What information does each of the plots below give you about the diatomic molecule modeled as a harmonic oscillator? Use your model to support your response.
h. Can real diatomic molecules dissociate into two separate atoms? Explain why or why not.
i. Does the harmonic oscillator model account for the possibility of the diatomic molecule dissociating into two separate atoms? Explain why or why not.
j. What (if anything) about your model of a diatomic molecule would need to change if you wanted to include the possibility of dissociation? Explain your answer.
Note: The images for item g are adapted from Fig. 8.18, 8.20, and 8.21 on pp. 301–302 of Atkins and De Paula (Atkins and De Paula, 2009).
Appendix 2: harmonic oscillator resource sheet
Appendix 3: rigid rotator interview protocol
Interview protocol (rigid rotator)
Instructions: Say, out loud, what comes to your mind as you go through the process of solving the following problems. Use your resource sheet to help you shape your responses.Consider a diatomic molecule held together with a covalent bond. The two atoms of the molecule are considered to be fixed in place relative to one another, and so we will describe its rotational motion using a quantum rigid rotator model:
a. Draw a picture to represent this system.
b. Use sketches, diagrams, and mathematical formulae to construct a model of the rotation of the molecule under consideration.
c. How do potential and kinetic energy play a role in your model (if at all)? Explain.
d. How does angular momentum play a role in your model? Explain.
e. Sketch an energy level diagram for the quantum rigid rotator. Are the spacings between adjacent energy levels equidistant? How about the predicted spacings between adjacent absorption peaks in a pure rotational spectrum? Explain.
f. Address the question: “What is the distance between the two atoms in the diatomic molecule?” Draw upon your model to support your response.
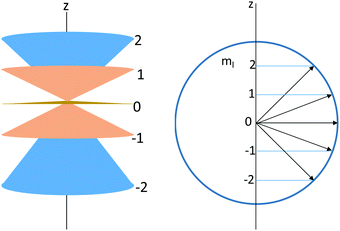
g. Explain what is represented by the following diagrams:
h. Kwame and Jean, upon observing the diagrams presented above, disagree about how the diagram relates to using the quantum rigid rotator to model a diatomic molecule.
• Kwame suggests that the cones represent the distinct ways in which the molecule can rotate (in a plane perpendicular to the z-axis) and that the values on the z-axis represent the total angular momentum of each rotational state. The arrows represent the bond length of the molecule under consideration.
• Jean argues that the cones represent uncertainty of the rotating molecule's angular momentum in the xy plane, and that the molecule rotates in a plane that is perpendicular to the total angular momentum (which is represented by the arrows). The values of the z-axis represent the z-component of angular momentum.
Whose response do you most agree with? Use what you have developed in parts (a) through (f) to support your response.
i. The solutions to the Schrodinger equation for this system are the spherical harmonics, 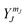 . What information is provided by
. What information is provided by 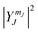 ?
?
j. It is observed that the separation between peaks in the microwave spectrum of a diatomic molecule decreases at higher frequencies. Does the quantum rigid rotator model take this into account? Explain why or why not.
k. What (if anything) about your model of a diatomic molecule would need to change if you wanted to account for a decrease in separation of these peaks for increasing frequency? Explain your answer
Note: The images for item g are adapted from Fig. 8.37 on p. 315 of Atkins and De Paula (Atkins and De Paula, 2009).
Appendix 4: rigid rotator resource sheet
References
- Atkins P. and De Paula J., (2009), Physical Chemistry, 9th edn, Oxford, UK: Oxford University Press.
- Ball D. W., (2015), Physical Chemistry, 2nd edn, CT: Cengage Learning.
- Bodner G. M., Gardner D. E. and Briggs M., (2005), Models and Modeling, in Pienta N., Cooper M. and Greenbowe T. (ed.), Chemists' Guide to Effective Teaching, Prentice-Hall, pp. 67–76.
- Bowen C. W., (1994), Think-Aloud Methods in Chemistry Education: Understanding Student Thinking, J. Chem. Educ., 71(3), 184, DOI:10.1021/ed071p184.
- Braun V. and Clarke V., (2006), Using thematic analysis in psychology, Qual. Res. Psychol., 3(2), 77–101, DOI:10.1191/1478088706qp063oa.
- Briggs M., (2007), Models and Modeling: A Theory of Learning, in Bodner G. M. and Orgill M. (ed.), Theoretical Frameworks for Research in Chemistry/Science Education, Prentice Hall, pp. 72–85.
- Cernicharo J., Guélin M., Agúndez M., McCarthy M. C. and Thaddeus P., (2008), Detection of C5N− and Vibrationally Excited C6H in IRC + 10216*, Astrophys. J., 688(2), L83–L86, DOI:10.1086/595583.
- Chi M. T. H., Feltovich P. J. and Glaser R., (1981), Categorization and Representation of Physics Problems by Experts and Novices, Cognit. Sci., 5(2), 121–152, DOI:10.1207/s15516709cog0502_2.
- Council N. R. (2012), A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, DC: The National Academies Press.
- Dangur V., Avargil S., Peskin U. and Dori Y. J., (2014), Learning quantum chemistry via a visual-conceptual approach: students' bidirectional textual and visual understanding, Chem. Educ. Res. Pract., 15(3), 297–310, 10.1039/c4rp00025k.
- Dick-Perez M., Luxford C. J., Windus T. L. and Holme T., (2016), A Quantum Chemistry Concept Inventory for Physical Chemistry Classes, J. Chem. Educ., 93(4), 605–612, DOI:10.1021/acs.jchemed.5b00781.
- Ferguson R. and Bodner G. M., (2008), Making sense of the arrow-pushing formalism among chemistry majors enrolled in organic chemistry, Chem. Educ. Res. Pract., 9(2), 102–113, 10.1039/B806225K.
- Fortenberry R. C., (2015), Interstellar Anions: The Role of Quantum Chemistry, J. Phys. Chem. A, 119(39), 9941–9953, DOI:10.1021/acs.jpca.5b05056.
- Gardner D. E. and Bodner G. M., (2007), Existence of a Problem-Solving Mindset among Students Taking Quantum Mechanics and Its Implications, in Advances in Teaching Physical Chemistry, American Chemical Society, vol. 973, pp. 155–173.
- Henning T. and Semenov D., (2013), Chemistry in Protoplanetary Disks, Chem. Rev., 113(12), 9016–9042, DOI:10.1021/cr400128p.
- Herbst E., (2005), Chemistry of Star-Forming Regions, J. Phys. Chem. A, 109(18), 4017–4029, DOI:10.1021/jp050461c.
- Maier J. P., Lakin N. M., Walker G. A. H. and Bohlender D. A., (2001), Detection of C3in Diffuse Interstellar Clouds, Astrophys. J., 553(1), 267–273, DOI:10.1086/320668.
- McQuarrie D. A. and Simon J. D., (1997), Physical Chemistry A Molecular Approach, Sausalito, CA: University Science Books.
- Muniz M. N., Crickmore C., Kirsch J. and Beck J. P. (2018), Upper-division chemistry students' navigation and use of quantum chemical models, Chem. Educ. Res. Pract., 19, 767–782, 10.1039/C8RP00023A.
- Oka T., (2013), Interstellar H3+, Chem. Rev., 113(12), 8738–8761, DOI:10.1021/cr400266w.
- Partanen L., (2018), Student-centred active learning approaches to teaching quantum chemistry and spectroscopy: quantitative results from a two-year action research study, Chem. Educ. Res. Pract., 19(3), 885–904, 10.1039/C8RP00074C.
- Rimoldini L. G. and Singh C., (2005), Student understanding of rotational and rolling motion concepts, Phys. Rev. ST – Phys. Educ. Res., 1(1), 010102, DOI:10.1103/PhysRevSTPER.1.010102.
- Roche Allred Z. D. and Bretz S. L., (2019), University chemistry students’ interpretations of multiple representations of the helium atom, Chem. Educ. Res. Pract., 20(2), 358–368, 10.1039/C8RP00296G.
- Sayre E. C. and Wittmann M. C., (2008), Plasticity of intermediate mechanics students' coordinate system choice, Phys. Rev. ST – Phys. Educ. Res., 4(2), 020105, DOI:10.1103/PhysRevSTPER.4.020105.
- Singh C. and Marshman E., (2015), Review of student difficulties in upper-level quantum mechanics, Phys. Rev. ST – Phys. Educ. Res., 11(2), 020117.
- Slotta J. D., Chi M. T. H. and Joram E., (1995), Assessing Students' Misclassifications of Physics Concepts: An Ontological Basis for Conceptual Change, Cognit. Instruct., 13(3), 373–400, DOI:10.1207/s1532690xci1303_2.
- Smith M. K., Jones F. H. M., Gilbert S. L. and Wieman C. E., (2013), The Classroom Observation Protocol for Undergraduate STEM (COPUS): A New Instrument to Characterize University STEM Classroom Practices, CBE –Life Sci. Educ., 12(4), 618–627, DOI:10.1187/cbe.13-08-0154.
- Talanquer V., (2014), Chemistry Education: Ten Heuristics To Tame, J. Chem. Educ., 91(8), 1091–1097, DOI:10.1021/ed4008765.
- Tsaparlis G., (2013), Learning and teaching the basic quantum chemical concepts, in Tsaparlis G. and Sevian H. (ed.), Concepts of Matter in Science Education, Innovations in Science Education and Technology, Dordrecht, The Netherlands: Springer, vol. 19, pp. 437–460.
- Tsaparlis G. and Papaphotis G., (2009), High-school students' conceptual difficulties and attempts at conceptual change: the case of basic quantum chemical concepts, Int. J. Sci. Educ., 31(7), 895–930, DOI:10.1080/09500690801891908.
- van Dishoeck E. F., Herbst E. and Neufeld D. A., (2013), Interstellar Water Chemistry: From Laboratory to Observations, Chem. Rev., 113(12), 9043–9085, DOI:10.1021/cr4003177.
| This journal is © The Royal Society of Chemistry 2020 |

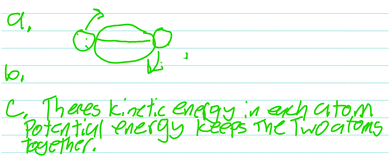

![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) J
J