Impact of basic arithmetic skills on success in first-semester general chemistry†
Vickie M.
Williamson
 *a,
Deborah Rush
Walker
*a,
Deborah Rush
Walker
 b,
Eric
Chuu
b,
Eric
Chuu
 c,
Susan
Broadway
c,
Susan
Broadway
 d,
Blain
Mamiya
d,
Blain
Mamiya
 e,
Cynthia B.
Powell
e,
Cynthia B.
Powell
 f,
G. Robert
Shelton
f,
G. Robert
Shelton
 g,
Rebecca
Weber
g,
Rebecca
Weber
 d,
Alan R.
Dabney
d,
Alan R.
Dabney
 c and
Diana
Mason
c and
Diana
Mason
 d
d
aDepartment of Chemistry, Texas A&M University, 77843-3255, USA. E-mail: williamson@tamu.edu
bDepartment of Chemistry, The University of Texas at Austin, USA. E-mail: drwalker@cm.utexas.edu
cDepartment of Statistics, Texas A&M University, TX, USA. E-mail: ericchuu@tamu.edu; adabney@stat.tamu.edu
dDepartment of Chemistry, University of North Texas, USA. E-mail: Susan.Broadway@unt.edu; Rebecca.Weber@unt.edu; Diana.Mason@unt.edu
eDepartment of Chemistry and Biochemistry, Texas State University, USA. E-mail: bmm172@txstate.edu
fDepartment of Chemistry and Biochemistry, Abilene Christian University, USA. E-mail: powellc@acu.edu
gDepartment of Science and Mathematics, Texas A&M University-San Antonio, USA. E-mail: Bob.Shelton@tamusa.edu
First published on 25th June 2019
Abstract
First-semester general chemistry is a known “gatekeeper” course due to its high failure rate. These higher education courses are taken by students who for the most part are regularly admitted freshmen, yet many struggle to succeed. In this investigation researchers from six higher-education institutions of varied sizes with student bodies of different ethnic composition teamed up to investigate the Math-Up Skills Test (MUST) as a potential tool to identify at-risk students in first-semester general chemistry (Chem I). A large population (N = 1073) was given the MUST at the beginning of the semester. The MUST had good internal consistency with the sample (Cronbach's alpha = 0.856). The MUST offers a quick 15 minute assessment of basic mathematics ability without a calculator. Instructors may find it easier than other documented predictors, which may take more time or involve obtaining student records (e.g., Math SAT). Results from the MUST support prior findings that mathematics skills correlate with course grades in chemistry. Poor arithmetic automaticity may be an underlying factor in lower performance by many students. With statistical modeling, the MUST, along with other demographic variables, was able to identify students who would go on to make a 69.5% or better in Chem I with a high percent of accuracy. The MUST, in tandem with other demographic variables, should be considered a potential tool for early identification of students at-risk for failing the class.
Background
The low success of general chemistry students has been noted since the early part of the 20th century, as measured by high attrition and high rate of unsuccessful grades (Deam, 1923; Scofield, 1927). Attrition rates of 30% or higher, in general, classifies a course as a ‘killer course’, with general chemistry falling into this category (Rowe, 1983). It is not unusual for the rate of grades of D, F, or W (withdrawal) in general chemistry to exceed this mark by several percentage points (e.g., Mason, 2015). One line of research looked for any correlations between course scores and student demographics to determine if any characteristic might signal which students would have success or difficulties. Researchers have found a number of links between course scores and student characteristics. For example, gender has been found to be a factor in chemistry course grades. Mittag and Mason (1999) found the chemistry course grades of females to be significantly higher than the grades of males, among the students who completed the course. Shibley et al. (2003) found that while gender effects had disappeared in cognitive tests based on Piagetian tasks this finding was likely due to a greater decline in the male ability than that of the female ability. These authors also found that course grades for the males were only significantly correlated with the Math SAT, while the females had course grades significantly correlated with the Math SAT, Verbal SAT, and a test of Piagetian tasks (relations, imagery, conservation, classification, and proportional reasoning). In a paper by Mason and Mittag (2001) gender and ethnicity impacted chemistry grades; the authors found that women and Hispanics withdrew at higher rates than men and non-Hispanics. Other projects have reported on underrepresented minorities (URMs) and their success, or lack thereof, in introductory chemistry (e.g., Mason and Verdel, 2001). While less than half of those entering college as STEM majors will persist, an especially high number of women, racial minorities and ethnic minorities leave (Graham et al., 2013).Student employment is also a characteristic that has been explored with the idea that simple lack of time might signal potential difficulties. Researchers remain divided on student employment and its impact on student grades. King (2006) found positive effects for those with low work hours at on-campus jobs related to the student's academic interests. Dundes and Marx (2006) suggested that there may be an optimal number of hours that is beneficial, since in their study, students who worked 10–19 hours earned higher grades than those who worked more or less hours, including those that did not work. On the other hand, Lammers et al. (2001) found that the level of academic achievement was lower for all working students.
In addition to gender, ethnicity, and employment, there seems to be a link between student success in college and the education level of the parents. For example, Sirin (2005) in a meta-review noted that student performance and dropout rates found significant effect sizes with level of parental education. Students with parents, neither of whom received a 4 year college degree (first-generation college students), performed more poorly and had higher dropout rates than students with one parent with a 4 year degree. Snibbe and Markus (2005) argued that parental education is a proxy for social class or socioeconomic status (SES), meaning that first-generation students were more likely to come from working class backgrounds and face significant economic barriers in college.
Another line of research has focused on diagnostic tests to signal potential student success or difficulty. In fact interest in early identification of struggling students in general chemistry courses has increased in recent years. Cooper and Pearson (2012) referred to several diagnostic instruments that have been used to identify potential at-risk students. These included the Toledo Chemistry Placement Exam (Hovey and Krohn, 1963), the Group Assessment of Logical Thinking (GALT) (Bunce and Hutchinson, 1993), the Test of Logical Thinking (TOLT) (Tobin and Capie, 1981), the California Chemistry Diagnostic Test (Karpp, 1995), the University of Iowa Placement Exam (Pienta, 2003) and the Math SAT (Spencer, 1996). A common component of these instruments is mathematics proficiency. Both the TOLT and the GALT assess logical-reasoning ability and require mathematics in items on proportions, probability, and correlations. These tests have been linked to achievement in chemistry by a number of researchers (e.g., Williamson et al., 2017). Lewis and Lewis (2007) found that both the TOLT and the SAT could be used to successfully identify at-risk students as have other researchers (Andrews and Andrews, 1979; Mason and Verdel, 2001). Stone et al. (2018) used the ACT at a liberal arts institution to predict success. Pyburn et al. (2013) found that language comprehension, prior knowledge, and mathematics ability, as measured by the Math SAT, significantly contributed to chemistry performance. Remaining predictors of success for students in general chemistry mentioned in the Lewis and Lewis (2007) paper include high school GPA, ACT scores, personality characteristics, and content-specific diagnostic exams. Gerlach et al. (2014) found that scale literacy was the best predictor of success on conceptual final examination scores for general chemistry students, building on the work of others (e.g., Jones and Taylor, 2009). Scale literacy relates to proportion and quantity. Jones and Taylor (2009) outlined a trajectory of scale development, with automaticity and accuracy being a characteristic of experienced scale development. Ralph and Lewis (2018) found that while at-risk students, with low Math SAT scores, struggled with all topics in general chemistry, the mole concept and stoichiometry were especially difficult for these students. These concepts are very mathematical in nature.
The idea that chemistry grades correlate with proficiency in mathematics is not new (Weisman, 1981; Spencer, 1996). Basic arithmetic skills and the automaticity of these skills have been investigated by a number of researchers with some suggesting interventions. For example, Bohning (1982) used an 84-item test, which was mailed to students with instructions not to use a calculator. Students were informed of the results and could enroll in a concurrent, supplemental course that focused on a formal, intensive review of the mathematics concepts involved on the test. A high percentage of those who took the supplemental course passed the chemistry course. Peer learning was used in chemistry laboratory by comparing the effects of grouping students of differing mathematical abilities compared to students who self-selected into a group (Srougi and Miller, 2018). These authors found that both mathematics abilities and attitudes towards working with others increased for those grouped by differing levels of mathematics ability. The 13-item mathematics instrument was given at the first and last lab and allowed calculator use. Topics included chemistry-oriented mathematics concepts, including basic operations, fractions, exponents, percentages, scientific notation, unit conversions, significant figures, graphing, and algebra. Indeed, even though many mathematics-preparatory modules and activities exist to help instructors bolster their students’ mathematics knowledge (e.g., Dahm and Nelson, 2013), students can still have issues with mathematics.
Johnstone (2000) outlined curricular changes to help students better succeed with chemistry, using his model of the nature of chemistry, which is composed of macroscopic, submicroscopic or particulate, and symbolic levels. It is this symbolic level that includes symbols, formula, equations, and mathematical treatments. Johnstone believed that students should be moved through these levels during instruction, but that introducing all levels simultaneously is a ‘sure recipe for overloading Working Space’ (Johnstone, 2000, p. 11). According to Johnstone, as students become more expert-like, they are able to easily move between the levels. These ideas fit well with the constructivist view of learning. Williamson (2008, p. 68) provided a definition of constructivism, based on the work of Piaget (1977); von Glasersfeld (1995); Osborne and Wittrock (1983); Bodner (1986):
“Constructivism is the belief that:
(a) knowledge is constructed from interactions with people and materials, not transmitted,
(b) prior knowledge impacts learning,
(c) learning, especially initial understanding, is context specific, and
(d) purposeful learning activities are required to facilitate the construction or modification of knowledge structures.”
Students who have constructed knowledge structures concerning basic mathematics should be able to move between these ideas or to have automaticity with basic mathematics skills.
Currently, faculty at many universities are responding to pressures to increase retention in course enrollments and are looking for ways to identify at-risk students (e.g., Hanover Research, 2018). In all, chemistry instructors are well aware that some proficiency in mathematics is an important prerequisite for success in college chemistry. Even with the studies previously discussed, some instructors identify a lack of easy access to instruments appropriate to measure prior mathematics knowledge as problematic. Lewis and Lewis (2007) noted that the TOLT requires a lot of class time and not all instructors have easy access to students' SAT scores. They suggested that the ease of giving the TOLT makes it a good option, especially when the SAT scores are not readily available. Other issues include rectifying the time from lecture to administer a diagnostic instrument. The California Chemistry Diagnostic Test and the Toledo Chemistry Placement Exam are time consuming, taking about 45 minutes and 55–60 minutes, respectively. One shorter, calculator-free mathematics test, described by Leopold and Edgar (2008), offers good predictability in second-semester introductory chemistry and is multiple-choice. This instrument takes 30 minutes to administer and requires 10 possible responses on the scan form for 17 of the 20 questions, making it a difficult choice for instructors limited to a standard five-response forms, have limited class time, or are hesitant to give up 30 of the standard 50 minutes in a class period.
Some have suggested that diagnostic tests should be given online or outside of class time to eliminate the drain on classroom time. Bohning (1982), as previously discussed, mailed the diagnostic to students to be completed at home that was not multiple-choice, with instructions to not use a calculator. The Bohning study did not use this diagnostic test to predict performance in the course, but to advise students whether they should take a supplemental mathematics course. Some instructors question the validity of tests taken in a non-proctored environment. Williamson et al. (2017) tested the differences between giving reasoning ability and spatial ability instruments in the classroom or as an online, un-proctored assignment. They used the TOLT for reasoning ability and used a battery of standard spatial ability tests, looking at rotation of three-dimensional objects and visuospatial transformation ability. The authors found that on items that asked students to give all possible combinations, students taking the test online failed to supply as many combinations as those in the classroom. These authors concluded that when either the TOLT or spatial ability tests were given online as compared to in the classroom, the scores will vary slightly, favoring the in-class versions, but the online versions still had a similar grade prediction value, making online administration a viable option. Regardless, many instructors prefer the reassurance of in-class administration.
In a recent publication, Albaladejo et al. (2018) noted that students can perform basic arithmetic functions with the aid of a calculator better than without on a short, open-response instrument named by the last author as the Math-Up Skills Test (MUST). While this is not surprising, a further finding was that students who enter college chemistry courses lacking automaticity in arithmetic skills needed to succeed may limit their understanding and further contribute to underling difficulties. The Albaladejo et al. paper reported on a 16-item mathematics diagnostic instrument adapted from that used by Hartman and Nelson (2016). The 16-item MUST was used to identify whether the most basic mathematics knowledge, numeracy, is lacking in students enrolled in first-semester general chemistry and whether their numeracy ability relates to their course averages. The 16-item MUST included items on: multiplication, multiplication and division with powers of ten, zeroth power application, changing fraction to decimal notation, rearranging algebraic equation (combined gas law), logarithms, determining the base-10 logarithm functions, square and square root of a number in scientific notation with a negative power, and balancing simple chemical equations. This pilot study showed that the MUST scores earned without the use of a calculator had a greater correlation with students' final course averages in first-semester general chemistry (Chem I) than the MUST scores earned with the use of a calculator (Albaladejo et al., 2018).
After the pilot study, the MUST was expanded to 20 items, and two versions of the 20-item MUST are included in the supplemental material for the Albaladejo et al. (2018) paper and in the Appendix 1, ESI† of this paper. The solutions for the items are in Appendix 2, ESI†. Added items agreed to by a committee of general chemistry instructors included simplification of a complex fraction, division by zero, simplification of a mixed operations fraction, and calculation of fraction-decimal equivalents. These additional items provide greater variation on fractions than the original MUST questions. Thus, the question that motivated the current research is how does the updated version reflect the prior knowledge of students enrolled in Chem I and can this updated version be used to accurately predict grades in first-semester general chemistry.
Research questions
Constructivism holds that students’ ability to learn depends partly on their level of knowledge when entering a course. Prior knowledge is a known predictor of learning success in most disciplines (Shell et al., 2010). Specifically, the purpose of this research was to measure how arithmetic skills impact course averages. The following questions were investigated:1. Does a diagnostic arithmetic instrument (the MUST: Math-Up Skills Test) predict students' course averages in first-semester general chemistry (Chem I)?
2. What other demographic variables will improve the predictability of the MUST?
3. To what extent does the MUST predict which students will have satisfactory course averages (69.5% or higher)?
Methodology
Research setting/population
One strength of this study lies in the fact that data were collected from universities that span across private and public institutions, small and large student populations, research-focused and community-serving, small and large class sizes, and different ethnicities served. These institutions are part of the Networking for Science Advancement (NSA) project (Albaladejo et al., 2018). Two of the institutions are classified both as Hispanic Serving Institutions (HSIs) and Minority Serving Institutions having greater than 25% of their enrollment identifying with Hispanic ethnicity. The remaining partners are from Hispanic-emerging universities. Three institutions are R1 (Carnegie classification) research universities and one of the HSIs is considered to be an R2 institution. One partner is a small, private university. Total enrollments across collaborating universities range from just under 4500 students to about 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. All researchers applied for and received approval from the Internal Review Board (IRB) at their own university. Five universities were approved as exempt research, while the sixth institution was approved as expedited research. Consent forms were constructed as per the requirements of the IRB at each university, which also included permission to have deidentified data shared.
000. All researchers applied for and received approval from the Internal Review Board (IRB) at their own university. Five universities were approved as exempt research, while the sixth institution was approved as expedited research. Consent forms were constructed as per the requirements of the IRB at each university, which also included permission to have deidentified data shared.
In the fall of 2017, collaborators distributed the 20-item MUST to Chem I students to investigate the predictive power of the MUST on course grade. Each student completed the MUST without a calculator at the beginning of the semester. Demographics were collected from a self-reported survey that included university classification, gender, ethnicity, major, college-degree attainment of parents and grandparents, and employment for each student. Students were invited to participate in the study from 13 sections of Chem I classes, which ranged in size from 30 to 305 students in each section and were across the six institutions with 10 instructors. It should be noted that these fall Chem I classes represented students taking the course on-sequence; traditionally Chem II classes are taught in the spring. Of the 1446 students who were invited, the sample size was reduced for students who did not sign their IRB-release forms at each university or who omitted significant demographic information. A total of 1127 students consented to be in the study, but 54 had missing data. The resulting student sample consisted of 1073 students who completed all study materials and gave their consent. A number of institutions required that the consent form be given late in the semester, some at the final examination, meaning that students who withdrew from the course or chose to skip the final exam could not be included.
The Chem I classes were taught by ten experienced instructors with between 1.5 to over 40 years of experience teaching Chem I, who all have an interest in chemistry education. Classes at five of the six institutions were taught for three contact hours per week in face-to-face sessions, which resulted in two or three meetings per week. Classes at one institution (school 6) had five hours of contact time per week. The classes used various textbooks and homework systems. Instructors calculated the course grade in different manners but reported the number of total points the student received and the total number of points possible in the course. For the purposes of this study, the course average for each student was calculated by dividing the points earned by points possible, then the score was reported as a percentage. The goal of this work was to investigate how the MUST predicted performance across a broad geographic setting far beyond what happens at a single institution.
Demographics were collected in a self-reported survey that was given with the MUST. These included university classification, gender, ethnicity, major, college-degree attainment of parents and grandparents, and employment for each student. Grandparent college-degree attainment was included, because a number of this generation has significant grandparent influence in their daily lives (Monserud, 2011). These variables were collected since they had been reported in the literature as predictors of success. It should be noted that the goal of predictive research, which seeks to produce the best possible predictive model, differs from the goal of explanatory research, which seeks to explain the phenomena (Pedhazur, 1997, p. 196). Our goal was to seek a predictive model.
Instrument
To accomplish the investigation, the updated MUST from Albaladejo et al., 2018 was used. The 20-item version of the MUST was designed to be completed in 15 minutes without a calculator. The MUST assessed student performance on the following tasks: multiplication, multiplication and division with powers of ten, zeroth power application, division of fractions by a fraction, changing fraction to decimal notation, rearranging algebraic equation (combined gas law), logarithms, recognition that division by zero is undefined, simplification of a fraction, determining the base-10 logarithm functions, square and square root of a number in scientific notation with a negative power, fraction-decimal equivalents, and balancing simple chemical equations. A copy of the 20-item MUST (two versions) and answer keys are available in the Appendices 1 and 2, ESI.† In the two versions of the MUST, given in Albaladejo et al., 2018, the same types of questions/concepts were presented in the same order, differing only by the exact numbers used in the problems. In order to keep the two versions as similar as possible, one version asked students to multiply 78 by 96, while the other version used the multiplication of 87 by 96. The two versions were distributed to the students on differently-colored paper in order to maintain the integrity of the test by reducing students’ chances of getting the correct answer by looking at their neighbor's paper. The content validity was established for both forms of the MUST by four professors (two full professors, each with a PhD in mathematics, one full professor with a PhD in chemistry, and one retired PhD in chemical education). These professionals investigated and confirmed that items on the instrument measured the intended tasks. Agreement on the answers and on the topic assessed for each item was 100%. For each student's MUST score, responses were identified as either correct or incorrect resulting in scores ranging from 0 to 20. No partial credit was assigned for any item. One of the benefits of the MUST is that it is not multiple choice, so students do not have the chance to get the correct answer by guessing or working backwards.Statistical modeling
The 2017 data on Chem I students was used to develop two regression models for use in predicting future student outcomes. Specifically, we built a linear regression model with Chem I course average as the numeric response and a logistic regression model with Chem I success (defined as course average of at least 69.5) as the categorical, binary response of successful or not successful. The predictor variables for both models are the MUST score (a numerical score) and the following categorical scores:• student classification (freshman, sophomore, junior, or senior),
• gender (male, female, or no response),
• race/ethnicity (Asian, Black, Hispanic, White, Mixed, or Other),
• major (STEM, medical, dual major, or other),
• which of the two MUST questionnaire versions was completed (version 78 or 87),
• whether their parents graduated from college (don’t know, no, or yes),
• whether their grandparents graduated from college (don’t know, no, or yes),
• whether they are employed on-campus (no or yes),
• whether they are employed off-campus (no or yes), and
• number of employment hours per week (0, 1–10, 11–19, 20–29, 30–39, or 40+).
We also included fixed effects in both models to account for differences between the participating universities (schools 1–6). While random effects for university differences would also be an option, they complicate the models and the methods used to tune them, and we are interested in prediction rather than explanation of relationships to enhance our ability to make accurate predictions without the random effects.
The 2017 data set was split to prepare and test the statistical model. This involved randomly selecting 2/3 of the students from each university's cohort to be used for developing, or training, the models, with the remaining 1/3 being held out for testing the models' accuracies (James et al., 2013). The LASSO method (least absolute shrinkage and selection operator) is a regression analysis method that was used to regularize, or smooth or shrink, the models in an effort to find the set of model coefficients that optimize prediction accuracies in balance with predictive effects for subject covariate variables (James et al., 2013). The LASSO shrinks the regression coefficients toward zero, with greater shrinkage applied to the coefficients for predictor variables that do not contribute substantially to the model's predictive accuracy. It is also possible for the LASSO to shrink model coefficients all the way to zero, meaning that the LASSO can also be viewed as a variable selection tool. The use of the LASSO statistical method automatically filters out variables that are not needed for making predictions.
To guide the tuning and evaluation of the predictive models for course average, we used mean squared error (MSE). MSE is an average of the squared values of the differences between true course averages and those predicted by the model. As such, the MSE will always be non-negative, and models with smaller MSEs (higher predictive accuracy) can be selected over those with larger MSEs (Sheather, 2009). To guide the tuning and evaluation of the predictive model for course success, we used balanced accuracy. Balanced accuracy is the average of sensitivity (the proportion of success cases that were correctly predicted to be successes) and specificity (the proportion of true fail cases that were correctly predicted to be failures) so that balanced accuracy is a number between 0 and 1 for which numbers closer to 1 indicate greater predictive accuracy (James et al., 2013). By averaging sensitivity and specificity, we can be confident that selected models do relatively well in making predictions of course success both for students who do indeed succeed and students who do not. All modeling was done with the R statistical programming language and the R package glmnet (Friedman et al., 2010). Our R code and data are available upon request and can be used to reproduce the results. We will also give an option for others to use our code with their data at the end of the results section.
Results
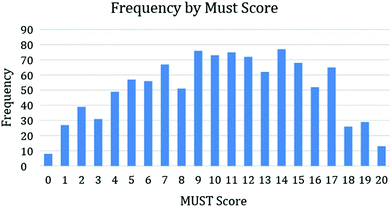
Analyses were conducted with the 1073 consenting students with all study documents, although some may have omitted a demographic question, resulting in a smaller number for that analysis. Regarding the 1073 students in this study, most of the participants (96%) were born between years 1995–2005, over 90% of the participants graduated from a Texas high school and over 98% report having taken at least one high school chemistry course prior to their current enrollment in Chem I. Over 70% of the students in this first-year course were enrolled as freshmen, 59% identified as female and 47% self-reported as being of white ethnicity (ethnicity in this study refers to ethnicity or race). Just over 25% considered themselves to be first-generation students (i.e., parents have not earned a degree), and the majority do not work on- or off-campus. The complete analysis of the demographic data is in Appendix 3, ESI.†Items on the open-response MUSTs were scored on a binary scale as either correct (1) or incorrect (0). Each student's MUST score was a sum of the correct items on a scale 0–20. Descriptive results gave a mean, standard deviation (SD), and standard error (SE) of the MUST score for the total group of students as 10.36 (SD = 4.93) (SE = 0.15). The average for all students represents a score of 52.0% on the MUST. A t-test between participant scores on the two versions of the MUST indicated no significant difference between versions (p = 0.794). This similarity was expected because the form of the question did not change between the two versions, only the exact number changed (e.g., evaluating 42° versus 47°). The 20-item MUST gave an internal consistency reliability of Cronbach's alpha = 0.856 with our population, which was above the 0.70 satisfactory level (Nunnally and Bernstein, 1994). Fig. 1 shows the frequency of MUST scores with our sample of 1073.
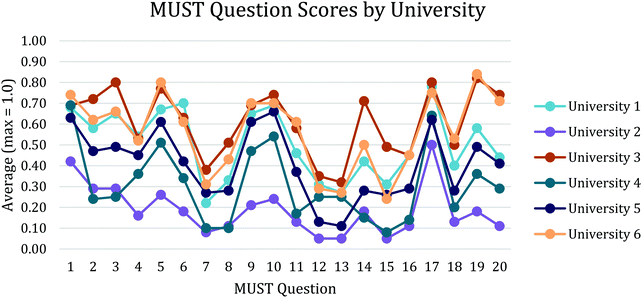
The results for each MUST question by institution were plotted (Fig. 2). Some questions were expectedly more difficult for the students as a whole. Looking beyond the individual means, similar patterns of success and difficulty were observed. Questions that were difficult for students at one institution were also difficult for students at all institutions even though some institutions consistently outperformed others. We investigate how the MUST and its questions perform across the six institutions in the statistical modeling section.
Success in a course typically spans grades of A, B, or C, whereas unsuccessful grades include D, F, or W (withdrawal). The course average for each student was used as the dependent variable. The course average was calculated by dividing the course points earned by each student, divided by the total possible points, then multiplied by 100. Students with course averages of 69.5% or higher were considered successful students, while those with course averages of 69.4% or lower were considered unsuccessful. Table 1 shows these results. As expected, successful students had higher MUST scores. The MUST scores are statistically different (p < 0.05 with a 2-tailed t-test) with successful students outperforming those who were not successful. The effect size using Hedge's for unequal groups = 1.08. This is a high effect size, since according to Cohen (1992) <0.2 is negligible, 0.2 to <0.5 is small, 0.5 to <0.8 is medium, and 0.8 and above is large. The smaller the SE calculation for a group (SE = SD/(n1/2)) would indicate a more homogeneous total group or a large sample size of the group. For example: successful students comprised 80.2% of the total group, so their SE was lower.
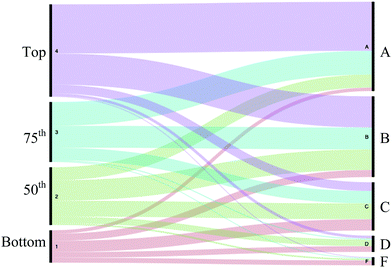
Further exploring relationships between the MUST score and course performance, the data were divided into quartiles for the MUST scores. The MUST quartiles were from 0–7, 8–11, 12–14, and 15–20 for quartiles 1–4; these have populations of 334, 275, 211, and 253, respectively. The quartiles were compared to the course grade with an alluvial diagram in Fig. 3. An alluvial diagram requires two categorical variables. The student's course average was converted into a letter grade using 69.5 to 79.4 as a C, etc. In Fig. 3, we used the student's MUST quartile versus the student's calculated letter grade. Here, students with MUST scores in the top quartile made mainly A's and B's, while those in the bottom quartile mainly made low grades. It should be noted that 30 students from the bottom quartile did make an A, but this was less than 3% of those in that quartile. While the alluvial diagram does give an interesting visual of the MUST and course performance relationship, we tried a few ineffectual models that are included in the Appendix 4, ESI† (like a linear regression from a graph of each MUST score versus the mean course average for that score, but this overfit the data by extracting the variation to 21 data points for MUST scores 0–20 and a linear regression from a graph of MUST score versus the mean course average for all 1073 points, but this showed that a simple linear relationship between the two did not accurately predict course averages). To meet our goal of a better prediction model, we turned to formal statistical modeling.
Statistical modeling for predictability
The model in Fig. 3 and the described ineffective models in Appendix 4 do not generate accurate predictions of Chem I course average, and it is not recommended that these should be used for this purpose. Instead, a more rigorous statistical approach is to use all of the data, before question-specific data summarization like that in Fig. 2, and formal model-building techniques, like train/test splits, model- and feature-selection through regularization, and model tuning with respect to a single prediction accuracy statistic (e.g., sensitivity, specificity or balanced accuracy) (Waljee et al., 2014). Without careful attention to the methods and techniques used for building a predictive model, it is likely that serious flaws in findings will follow, such as overfitting and biased predictions (James et al., 2013; Ambroise and McLachlan, 2002). Below are the methods that were used to avoid such flaws.Two regression models were performed on the 20-item MUST with the LASSO method described in the methodology using a random 2/3 of the data from each university. The first model is a linear regression for the Chem I course average. All the predictor demographic variables are categorical, compared to the numeric MUST score. With the regression model of the numeric Chem I course average, the estimated model coefficients for different levels of categorical variables are mean differences comparing to the variables' baseline levels, holding all other variables constant. In the linear regression model, the estimated coefficient for the numeric MUST variable is the mean change in course average associated with a one-point increase on MUST, again holding all other variables constant.
The second model was a logistic regression for being successful (69.5 or better average) versus unsuccessful in the course, all the predictor demographic variables are again categorical, compared to the numeric MUST score. With the logistic regression model of binary course success (course average at least 69.5) or not, a similar interpretation of coefficients applies, but with mean differences replaced by log odds ratios.
The linear regression and logistic regression models were developed using a random 2/3 of the data from each university. The predictive accuracy of these models was assessed by using them to make predictions on the remaining 1/3 data and comparing the prediction to each student's actual course average. The predictions resulted in an estimated mean squared error (MSE) of 110 for the linear regression model. While the MSE estimate is difficult to contextualize on its own, we note that the MSE of a “null” model that has only an intercept and the MUST, but no other covariate terms, was 182.8. Note that a lower MSE is better. Thus, using our predictor variables along with MUST corresponds to a substantial improvement in model fit (p-value for comparing our model to the null model was approximately 0). Thus, the MUST is an effective feature that can be successfully used to predict course averages in Chem I with the predictor, demographic variables.
For determining success and failure in the course, the logistic regression model with LASSO achieved an estimated balanced accuracy of 72.4% (the average of the correct predictions of both the successful and unsuccessful students) and an overall classification accuracy of 78% (meaning that 78% of all predictions among the test data were correct). For many, it is more important to predict success versus failure than the course average. Thus, the MUST with the demographic variables can successfully be used to predict success/failure in Chem I.
In order to see if the 20-item MUST was superior to the 16-item MUST for prediction of course average, the linear regression for MUST score versus course average was run for both forms of the MUST. The new questions were numbers 6, 16, 17, and 18 of the 20-item MUST so running the analysis without those questions closely replicates the 16-item MUST. We found an MSE = 112 for the model generated using the old 16-item MUST versus MSE = 110 for the model using the 20-item MUST. This indicates that the 20-item MUST model with the smaller MSE is better, since it had the smaller average of the squared differences between the true course averages and the actual course average for the 1/3 of our sample that was not used to develop the models. Testing for significance of the nested models gave a p-value of 0.0226, indicating that the four additional questions in the 20-question MUST jointly account for enough variance that we can reject the null hypothesis that the coefficients for the four additional questions are equal to zero. Thus, the 20-item MUST was preferred for predicting course averages. Comparing the two forms of the MUST on the logistic regression of binary course success or not, the two forms gave comparable accuracy, with no preference for either form. Since we wanted to be able to both predict course average and course success, all further analyses were done with the 20-item MUST.
The different categories of questions on the MUST were explored to see whether certain types of questions were more or less important to our models. Questions on the 20-item MUST were grouped into five question categories: multiplication (questions 1, 2, and 3), division (questions 4, 6, 7, 8, and 16), fraction simplification (questions 9, 10, 17 and 18), logarithms and exponents (questions 5, 12, 13, 14, 15), and symbolic manipulation (questions 11, 19, and 20). For both the linear and logistic models, all categories were needed. The previous analyses indicated that all items of the 20-item MUST should be included in the models.
The coefficients of our final linear regression and logistic regression models are shown in Appendices 5–8, ESI.† The p-values for the other variables can be compared to that for MUST in Appendices 5 and 7, ESI,† showing that MUST is by far the most important contributor to the ability to predict course average. While not statistically significant, a number of variables still contributed to prediction accuracy. A predictive model can be improved by adding a variable even if that variable's contribution is not statistically significant. For completeness, the coefficients for the linear regression model and logistic regression models are included in Appendices 5 and 7, ESI,† respectively. However, for the examples below and in the discussion of the results, we use the coefficients obtained from the LASSO regression models for course average and classification of success/failure that are found in Appendices 6 and 8, ESI.† The models feature the students’ institution, year in school, major, gender, ethnicity, parents’ graduation, grandparents’ graduation, employment status (on/off campus), hours worked, MUST exam version, and MUST score. Most of the predictor variables are categorical variables, with numeric values for the MUST. The model coefficients can be interpreted as, with all other predictor variables held constant, differences in average course grade (for the linear regression model) or log odds (for the logistic model). The coefficients for the categorical predictor variables compare to their baseline levels, while those for the numeric variables compare two individuals that differ by one unit. For each categorical variable with k categories, k − 1 coefficients will be reported, with the missing category accounted for in the intercept. For example, the freshman year does not have an estimate or coefficient in either Appendices 6 or 8, ESI,† meaning that the contribution from a student being in his/her freshman year is accounted for in the intercept.
As one example, consider a senior, white, female student at school 4 in a medical-related major, who worked 40 hours a week on campus, had both parents and grandparents with college degrees, and scored 10 out of 20 on version 87 of the MUST. Using the coefficients from the LASSO regression model on Appendix 6, ESI†, we can compute the following predicted course average for such a student:
| 69.3116 | +3.0867 | +0.2625 | +1.9629 | +0.0687 | −11.1646 | +(10 × 1.0733) | = | 74.2608 |
| Intercept | Senior | Female | Major med | White | Work 40 h | MUST score × coeff. | Predicted average |
The complete set of coefficient estimates can be found in Appendix 6, ESI.† In general, one can make a prediction based on our model by plugging in values for all the demographic variables in our model. Although the MSE obtained from the LASSO model does not differ substantially from the regression model with all of the features, the simplified LASSO model provides easier interpretation and allows for identification of features that are more important due to the built-in variable selection.
Similarly, the classification model can be used to compute an estimated log odds of course success. The complete set of coefficient estimates from the LASSO model can be found in Appendix 8, ESI.† For our sample student, the classification model would give a predicted log odds of success equal to −0.6997, which was computed using:
| −0.2423 | −0.4305 | +0.5858 | +0.0803 | +0.0914 | +0.2466 | +0.2993 | −0.0295 | −3.0628 | +(10 × 0.1762) |
| Intercept | School 4 | Senior | Female | White | Major med | Grands graduates | Job on campus | Work 40 h | MUST score × coeff. |
This corresponds to an estimated probability of exp(−0.6997)/(1 + exp(−0.6997)) = 0.3319 that the student will succeed in the course. The MUST coefficients in both models are highly statistically significantly different from 0, much more so than any of the coefficients for categorical variables, indicating that MUST score greatly influences predictions.
Using statistical modeling for predictability
To use our models to make predictions at one's own institution, instructors could use one of two methods. First, an instructor could make predictions based on one institution from our study that is selected from among the institutions used in our model to be most similar to his/her own in terms of the institutional summary statistics in Table 2. Care should be taken when choosing Institution 6 as data were from students who were identified as at-risk and may not be representative of all students at the institution. For example, suppose your institution is most similar to Institution 1. To compute a course average prediction for one of your students, use Appendix 6, ESI† and add the model intercept to the sum of the student's MUST score times the MUST coefficient and the model coefficient estimates for the school and demographic variables, like class, gender, ethnicity, etc. See Appendix 9, ESI† for a sample copy of a demographic survey, containing the needed items for other instructors to use.| School | Description | Undergraduate enrollment F2017 | Admitted student SAT Math F2016 |
|---|---|---|---|
| 1 | Private | 4427 | 515–600 |
| 2 | Public, Hispanic >25% | 6470 | 380–490 |
| 3 | R1 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 915 |
550–670 |
| 4 | R2, Hispanic >25% | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
470–560 |
| 5 | R1 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
490–600 |
| 6 | R1 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 427 |
580–730 |
While we have provided instructions in the previous paragraphs for readers to plug their data into our fitted models in order to make predictions for their students, we recommend that interested readers fit our linear and logistic regression models to their own institution's data and use those personalized models for predictions for their students. The models presented in this paper are somewhat limited due to their only using data from our handful of universities, and these universities are not expected to be sufficiently representative of the entire population of all global universities. Our instructions in the preceding two paragraphs can be used to make predictions for students at a university that was not part of our collaboration but using one's own university's student data for model fitting would be expected to result in more relevant predictions. Interested readers can download our code and replace our data file used for model fitting with an analogous data file, with the same exact variable names and types as ours, then run our code to obtain custom predictions on their own students. Our code is hosted online in the form of an R script file, with a short pdf document describing how to put in one's own data. These can be found at this Github address: https://github.com/echuu/ChemEd.
Discussion and limitations of the findings
Students in general chemistry courses perform better when they have the skills they need to succeed. Our findings suggest that one such skill is mathematics automaticity, an ability to perform basic mathematics calculations without a calculator and familiarity with number scale and basic rules for calculations. A result of the study is that those with greater automaticity skills as measured by the MUST appear to consistently do better in Chem I. The MUST with 20 items has been shown to be a better option than the older 16-item version, since the 20-item MUST gave a smaller MSE (mean squared error) and gave significant p-value when testing the nested models. While the MUST tests a number of skills, it has been shown that all types of questions are needed. The MUST with the demographic predictor variables does seem to be a good predictor of course averages for first-semester general chemistry students. Since the logistic regression model produced a 78% prediction accuracy in the context of a student's success or failure in the course, the MUST is useful in identifying successful vs. unsuccessful students prior to the beginning of classes or during the first few days of class. The models suggest that a low MUST should be treated as an indication of basic arithmetic skills deficiency, which may correspondingly result in a lower course average for a student with the same demographic predictor variables.We believe that predicting performance is worthwhile; however, our model did not investigate causation, only relationships or associations. Some researchers have found that concurrent courses (e.g., Bohning, 1982), requiring prerequisite courses (e.g., Stone et al., 2018), or special programs like STEM learning communities (e.g., Graham et al., 2013) have helped improve course grades for those at-risk. Our goal was to find an easy way to predict grades or success in general chemistry I.
Compared to other measures of mathematics proficiency, the MUST offers several benefits. Compared to the Toledo Chemistry Placement Exam, the TOLT, the GALT, and the California Chemistry Diagnostic Test, the MUST requires less class time at only 15 minutes compared to their 40+ minutes. Further, the MUST may be the only option for instructors unable to access their students’ Math SAT scores. The researchers in this study were not approved to get the SAT or ACT scores for our students. Additionally, a number of test-optional universities in the United States are now allowing admission without these standard examinations.
We propose that the 15 minute MUST instrument be considered as an instrument that can be used at the beginning of a Chem I class, because it is easy to obtain, takes little class time, and does not have a cost, unlike others discussed in the background section. Additionally, the MUST is free-response, lacking the various cues and limitations of multiple-choice diagnostics. Scoring of the open-response MUST might be considered a drawback; however, the required responses are specific and can be quickly scored as either correct or incorrect (no partial credit). The MUST has proven to successfully predict the scores of on-sequence, first-semester general chemistry students across multiple institutions. A multiple-institution study has advantages over a single-institution study. With different institutions, different student populations and yet very similar automaticity skills are brought to the classroom, and consistently the students with better arithmetic automaticity consistently outperform those without these foundational skills.
The limitations to the study include the fact that all institutions were from the same state with the same standards for high school graduation; however, the six institutions and student populations were varied in size, ethnicity, and SAT Math (Table 2) to help overcome this and to give a broader picture. The study looked at students in first-semester general chemistry, who were taking the course in the fall semester. The results for these on-sequence students may vary from those who take the course off-sequence, and differences in results may also exist for second-semester students. Finally, it should be noted that with a 78% prediction accuracy for success, that 22% will receive an incorrect prediction.
Summary
This study contributes to chemical education research by providing evidence that the MUST has good predictability as an early identifier of at-risk students in first-semester general chemistry. The MUST resulted in good predictions for both the numerical course average (linear regression) and the binary successful vs. unsuccessful (logistic regression). With the ease of use and accessibility for the MUST, it may be more desirable than other predictors (e.g., SAT, ACT, Toledo Chemistry Placement Exam, California Chemistry Diagnostic Test). In some cases, the MUST may be the only option for instructors who do not have the time, access, or funds to obtain the other predictors. The validity of the MUST is supported by its reliability across institutions in a large, well-populated majority-minority state in the US (spread over 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mi2 ≈ 90
000 mi2 ≈ 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 km2). Data reported from the 20-question MUST across over 1000 students attending multiple higher-education institutions are consistent with and similar to the results reported in the published pilot study, with the same questions being difficult for all institutions (Albaladejo et al., 2018). We believe the MUST is a viable option over other measures, which also show good predictability, but are hard to obtain, cost money, take much class time, etc. The MUST is an easy, practical choice for instructors.
650 km2). Data reported from the 20-question MUST across over 1000 students attending multiple higher-education institutions are consistent with and similar to the results reported in the published pilot study, with the same questions being difficult for all institutions (Albaladejo et al., 2018). We believe the MUST is a viable option over other measures, which also show good predictability, but are hard to obtain, cost money, take much class time, etc. The MUST is an easy, practical choice for instructors.
Suggestions for future research
This section discusses possible uses for the MUST in future research. The homogeneity in the types of MUST problems on which students did poorly regardless of the institution suggest that the MUST has identified an area in need of attention for college-preparation. Based on the MUST's success in differentiating students we further propose to use the MUST as a tool to measure the effectiveness of interventions that focus on improving students’ automaticity. Future research should explore the use of interventions designed to improve student numeracy skills with the end-goal of improving student success rates/retention in general chemistry. It will also be interesting to explore the efficacy of other types of interventions by using any changes in the MUST scores.Possible research questions for others to investigate could include: Would an intervention prior to beginning a Chem I course significantly improve students' number sense as measured by the MUST and would this improve course success? Could a concurrent supplemental mathematics course, similar to that used by Bohning (1982) help students with low MUST scores? Can dormant skills be reawakened by supplemental interventions? What factors lead to the lack of mathematics automaticity? The MUST in addition to other factors like language comprehension (Pyburn et al., 2013) or scale literacy (Gerlach et al., 2014) should also be investigated as should quantitative reasoning and literacy. Research has shown that attitude also plays a significant role in predicting success in chemistry (Xu and Lewis, 2011); therefore, research into the combination of MUST with attitudes and other noncognitive factors should also be investigated. How does calculator usage hinder mathematics automaticity? Does the MUST predict success for the population of off-sequence students who take first-semester general chemistry in the spring semester? Does the MUST predict success in on-sequence, second-semester general chemistry? Would grouping students by differing mathematical ability help in a general chemistry lecture class, as it did in chemistry laboratory, as reported by Srougi and Miller (2018)? With the ease of use and predictive ability, the Math-Up Skills Test or MUST has a number of possible applications.
Conflicts of interest
There are no conflicts to declare.References
- Albaladejo J. D. P., Broadway S., Mamiya B., Petros A., Powell C. B., Shelton G. R., Walker D. R., Weber R., Williamson V. M. and Mason D., (2018), ConfChem conference on mathematics in undergraduate chemistry instruction: MUST-know pilot study—math preparation study from Texas, J. Chem. Educ., 95(8), 1428–1429.
- Ambroise C. and McLachlan G. J., (2002), Selection bias in gene extraction on the basis of microarray gene-expression data, Proc. Natl. Acad. Sci. U. S. A., 99, 6562–6566.
- Andrews M. H. and Andrews, L., (1979), First-year chemistry grades and SAT Math scores, J. Chem. Educ., 56(4), 231–232.
- Bodner G. M., (1986), Constructivism: a theory of knowledge, J. Chem. Educ., 63(10), 873–878.
- Bohning J. J., (1982), Remedial mathematics for the introductory chemistry course: the “CHEM 99” concept, J. Chem. Educ., 59(3), 207–208.
- Bunce D. M. and Hutchinson K. D., (1993), The use of the GALT (group assessment of logical thinking) as a predictor of academic success in college chemistry. J. Chem. Educ., 70 (3), 183–187.
- Cohen J., (1992), A power primer. Psychol. Bull., 112, 155–159.
- Cooper C. I. and Pearson P. T., (2012), A genetically optimized predictive system for success in general chemistry using a diagnostic algebra test, J. Sci. Educ. Technol., 21(1), 197–205.
- Dahm D. J. and Nelson E. A., (2013), Calculations in chemistry: an introduction, 2nd edn, New York, NY: W.W. Norton & Company, Inc.
- Deam M. T., (1923), Diagnostic algebra tests and remedial measures. Sch. Rev., 31(5), 376–379.
- Dundes L. and Marx J., (2006), Balancing work and academics in college: Why do students working 10 to 19 hours per week excel? J. Coll. Stud. Ret., 8, 107–120.
- Friedman J., Hastie T., and Tibshirani R., (2010), Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw., 33(1), 1–22. http://www.jstatsoft.org/v33/i01/, accessed June 2019.
- Gerlach K., Traate J., Blecking A., Geissinge P. and Murphy K. L., (2014), Valid and reliable assessments to measure scale literacy of students in introductory college chemistry courses, J. Chem. Educ., 91, 1538–1545.
- Graham M. J., Frederick J., Byars-Winston A., Hunter A. B. and Handelsman J., (2013), Increasing persistence of college students in STEM, Science, 341(27), 1455–1456.
- Hartman J. R. and Nelson E. A., (2016), Automaticity in computation and student success in introductory physical science courses [online], available at: https://arxiv.org/abs/1608.05006, accessed June 2019, Quiz available at: http://bit.ly/1HyamPc, accessed June 2019.
- Hanover Research, (2018), Best practices in first year student support, Arlington, VA: Hanover Research.
- Hovey N. W. and Krohn A., (1963), An evaluation of the Toledo chemistry placement examination, J. Chem. Educ., 40(7), 370–372.
- James G., Witten D., Hastie T. and Tibshirani R., (2013), An Introduction to Statistical Learning: with Applications in R, New York: Springer.
- Johnstone A. H., (2000), Teaching of chemistry-logical or psychological? Chem. Educ. Res. Pract., 1(1), 9–15.
- Jones M. G. and Taylor A. R., (2009), Developing a sense of scale: Looking backward. J. Res. Sci. Teach., 46, 460–475.
- Karpp E., (1995), Validating the California Chemistry Diagnostic Test for local use (Paths to success, Volume III), Glendale Community Coll., CA: Planning and Research Office.
- King J. E., (2006), Working their way through college: Student employment and its impact on the college experience. ACE Issue Brief. American Council on Education Center for Policy Analysis.
- Lammers W. J., Onwuegbizie A. J. and Slate J. R., (2001), Academic success as a function of the gender, class, age, study habits, and employment of college students. Res. Sch., 8(2), 71–81.
- Leopold E. G. and Edgar B., (2008), Degree of mathematics fluency and success in second-semester introductory chemistry, J. Chem. Educ., 85(5), 724–731.
- Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
- Mason D., (2015), Knowledge decay and content retention of students in first-semester general chemistry, LUMAT – Res. Pract. Math, Sci. Tech. Educ., 3(3), 341–352.
- Mason D. and Mittag K. C., (2001), Evaluating success of Hispanic-surname students in first-semester general chemistry, J. Chem. Educ., 78(2), 256–259. [Correction: J. Chem. Educ., 78(12), 1597.].
- Mason D. and Verdel E., (2001), Gateway to success for at-risk students in a large-group introductory chemistry class, J. Chem. Educ., 78(2), 252–255.
- Mittag K. C. and Mason D. S., (1999), Cultural factors in science education: variables affecting achievement, J. Coll. Sci. Teach., 28(5), 307–310.
- Monserud M. A. and Elder G. H., (2011), Household structure and children's educational attainment: a perspective on coresidence with grandparents, J. Marr. Fam., 73, 981–1000.
- Nunnally J. C. and Bernstein I. H., (1994), Psychometric theory, 3rd edn, New York, NY: McGraw-Hill, Inc.
- Osborne R. J. and Wittrock M. C., (1983), Learning science: a generative process, Sci. Educ., 67, 489–508.
- Pedhazur E. J., (1997), Multiple Regression in Behavioral Research, 3rd edn, Fort Worth, TX: Wadsworth/Thomson Learning.
- Piaget J., (1977), The Development of Thought: Equilibrium of Cognitive Structures, NY: Viking.
- Pienta N. J., (2003), A placement examination and mathematics tutorial for general chemistry, J. Chem. Educ., 80(11), 1244–1246.
- Pyburn D. T., Pazicni S., Benassi V. A. and Tappin E. E., (2013), Assessing the relation between language comprehension and performance in general chemistry, Chem. Educ. Res. Pract., 14, 524–541.
- Ralph V. R. and Lewis S. E., (2018), Chemistry topics posing incommensurate difficulty to students with low math aptitude scores, Chem. Educ. Res. Pract., 19, 867–884.
- Rowe M. B., (1983), Getting chemistry off the killer course list, J. Chem. Educ., 60(11), 954–956.
- Scofield M. B., (1927), An experiment in predicting performance in general chemistry, J. Chem. Educ., 4(9), 1168–1175.
- Sheather S. J., (2009), A Modern Approach to Regression With R, New York: Springer Science + Business Media.
- Shell D. F., Brooks D. W., Trainin G., Wilson K. M., Kauffman D. F. and Herr L. M., (2010), The unified learning model, Dordrecht, Netherlands: Springer.
- Shibley I. A., Milakofsky L., Bender D. S. and Patterson H. O., (2003), College chemistry and Piaget: An analysis of gender difference, cognitive abilities, and achievement measures seventeen years apart, J. Chem. Educ., 80(5), 569–573.
- Sirin S. R., (2005), Socioeconomic status and academic achievement: A meta-analytic review of research, Rev. Educ. Res., 75, 417–453 DOI:10.3102/00346543075003417.
- Snibbe A. D. and Markus H. R., (2005), You can’t always get what you want: Educational attainment, agency, and choice, J. Pers. Soc. Psychol., 88, 703–720 DOI:10.1037/0022-3514.88.4.703.
- Spencer H. E., (1996), Mathematical SAT test scores and college chemistry grades, J. Chem. Educ., 73(12), 1150–1153.
- Srougi M. C. and Miller H. B., (2018), Peer learning as a tool to strengthen math skills in introductory chemistry laboratories, Chem. Educ. Res. Pract., 19, 319–330.
- Stone K. L., Shaner S. E., and Fendrick C. M., (2018), Improving the success of first term general chemistry students at a liberal arts institution. Educ. Sci., 8(1), 5.
- Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
- Waljee A. K., Higgins P. D. R. and Singal A. G., (2014), A primer on predictive models, Clin. Transl. Gastroenterol., 5, e44.
- Weisman R. L., (1981), A mathematics readiness test for prospective chemistry students. J. Chem. Educ., 58(7), 564.
- von Glasersfeld E., (1995), Radical Constructivism, London, England: Falmer Press.
- Williamson K. C., Williamson V. M. and Hinze S., (2017), Administering spatial and cognitive instruments in-class and on-line: Are these equivalent? J. Sci. Educ. Technol., 26, 12–23.
- Williamson V. M., (2008), in Bunce D. and Cole R. (ed.), Nuts and bolts of chemical education research, Washington, DC: American Chemical Society, pp. 67–78.
- Xu X. and Lewis J. E., (2011), Refinement of a chemistry attitude measure for college students, J. Chem. Educ., 88, 561–568.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9rp00077a |
| This journal is © The Royal Society of Chemistry 2020 |